Inverse probability weighting with error-prone covariates

Summary

Inverse probability-weighted estimators are widely used in applications where data are missing due to nonresponse or censoring and in the estimation of causal effects from observational studies. Current estimators rely on ignorability assumptions for response indicators or treatment assignment and outcomes being conditional on observed covariates which are assumed to be measured without error. However, measurement error is common for the variables collected in many applications. For example, in studies of educational interventions, student achievement as measured by standardized tests is almost always used as the key covariate for removing hidden biases, but standardized test scores may have substantial measurement errors. We provide several expressions for a weighting function that can yield a consistent estimator for population means using incomplete data and covariates measured with error. We propose a method to estimate the weighting function from data. The results of a simulation study show that the estimator is consistent and has no bias and small variance.

1. Introduction

Inverse probability-weighted estimates are widely used in applications where data are missing due to nonresponse or censoring (Robins et al., 1995; Robins & Rotnitzky, 1995; Scharfstein et al., 1999; Lunceford & Davidian, 2004; Kang & Schafer, 2007) or in observational studies of causal effects (Robins et al., 2000; McCaffrey et al., 2004; Bang & Robins, 2005). The estimators are consistent and asymptotically normal under very general conditions, and combining inverse probability weighting with modelling for the mean function yields doubly robust estimators which are consistent and asymptotically normal if either the model for the mean or the model for the response or treatment is correctly specified (Robins & Rotnitzky, 1995; Robins et al., 1995; Scharfstein et al., 1999; van der Laan & Robins, 2003; Lunceford & Davidian, 2004; Bang & Robins, 2005; Kang & Schafer, 2007). Recent studies have considered estimation of the response or treatment assignment functions (Hirano et al., 2003; McCaffrey et al., 2004; Lee et al., 2009; Harder et al., 2010) and have shown that nonparametric and boosting-type estimators work well in simulations and applications.

The consistency and asymptotic normality of inverse probability-weighted estimators require covariates to be free of measurement error. However, covariates measured with error are common in applications. For instance, achievement tests for school students can have very large errors, and it is clear that future achievement depends on a student’s true level of achievement rather than on the error-prone test scores. Ignoring the measurement error in the covariates can result in bias in inverse probability-weighted estimates (Pearl, 2010; Steiner et al., 2011; Raykov, 2012; Yi et al., 2012).

In the context of functional analysis of longitudinal data with missing responses and covariate measurement error, Yi et al. (2012) proposed inverse probability weighting for missing responses. They assume that response is independent of the outcomes conditional on the error-prone covariates. We consider the case where ignorability and the probability of response depend on the error-free covariates. In addition to this work, there is literature on related issues such as inverse probability-weighted estimation with missing regressors (Robins et al., 1994; Tan, 2011), error in the treatment or exposure measure (Babanezhad et al., 2010; and a 2010 unpublished report from The Pennsylvania State University by J. Kang and J. Schafer), and estimation of propensity scores when covariates are measured with error (D’Agostino & Rubin, 2000; Raykov, 2012). Pearl (2010) developed a general framework for causal inference in the presence of error-prone covariates. The framework does not provide specific solutions for weighted estimators, but it can yield weighted estimators in some cases, such as that of a binary covariate measured with error (Pearl, 2010). A shortcoming of this approach is that it relies on a model for the joint distribution of the outcome and the covariate. An analyst may want to avoid modelling with the outcomes, especially in causal inference problems (Rubin, 2001). A general advantage of inverse probability-weighted estimators is that they do not require a model for the outcome; our estimator also has this advantage.

2. Inverse probability-weighted estimator with error-prone covariates

Let Y₁, …, Y_n be the outcomes of primary interest obtained from a sample of units from a population. We are interested in the population mean, μ. Inverse probability weighting is commonly applied to two scenarios where the outcomes are observed for only a portion of the sample. The first is the case of missing data due to survey nonresponse, loss to follow-up, or censoring in which sampled units failed to provide the requested data. The second scenario involves the estimation of the causal effect of a treatment or treatments in which only one of the possible outcomes for each study unit, the outcome corresponding to the unit’s assigned treatment, is observed, and all other potential outcomes are unobserved. Let R_i be a response indicator, with R_i = 1 if Y_i is observed and R_i = 0 if Y_i is unobserved or missing.

For observational studies, each unit in the population has two potential outcomes: one that occurs when assigned to treatment Y_i1 and one that occurs when assigned to the control condition Y_i0 (Rosenbaum & Rubin, 1983). Each study unit also has an observed treatment indicator, T_i, with T_i = 1 if unit i received the treatment and T_i = 0 if the unit received the control condition. When estimating the mean of the potential outcomes for the treatment, R_i = T_i; when estimating the mean of the potential outcomes for the control, R_i = 1 − T_i. We use the generic term response indicator, but the results apply to both nonresponse and observational studies. In observational studies, we observe only Y_i1 when T_i = 1 and Y_i0 when 1 − T_i = 1, and we let Y_i,obs = Y_i1T_i + Y_i0(1 − T_i ). We assume that the potential outcomes are well-defined and unique for each unit, i.e., that the stable unit treatment assumption holds (Rosenbaum & Rubin, 1983). Although it may not hold in some studies, this assumption is commonly made when the covariates are error-free; we shall assume it holds throughout this paper in order to focus on the issue of weighting with error-prone data.

For each unit there is a covariate X_i which is unobserved and possibly related to both Y_i and R_i. We observe the covariate W_i = X_i + U_i as well as Z_i, another possibly vector-valued covariate measured without error. All data are independent across units, and we assume that the following conditions hold.

• Assumption 1. The U_i are independent of Y_i and R_i conditional on X_i and Z_i.

• Assumption 2. For all sampled units, 0 < pr(R_i = 1 | X_i, Z_i ) < 1.

• Assumption 3. The response Y_i is independent of R_i conditional on X_i and Z_i.

By the definition of W and Assumption 1, W is a surrogate for X when modelling Y and R, and measurement error is nondifferential (Carroll et al., 2006, § 2.5). Assumptions 2 and 3 are similar to strong ignorability (Rosenbaum & Rubin, 1983), which also requires Assumption 2. However, in the context of causal effect estimation for a single treatment, strong ignorability requires the conditional joint distribution of both potential outcomes, (Y_i0, Y_i1), to be independent of the treatment. We require only that each potential outcome be marginally independent of treatment assignment conditional on X_i and Z_i, i.e., the weak unconfoundedness of Imbens (2000). More importantly, independence is conditional on the error-free variable X_i and not the observed error-prone covariate W_i.

Theorem 1

Let p(x, z) = pr(R = 1 | x, z) and let A(w, z) be a function that satisfies, for any z in the support of Z,

$$E\{A(W,z)\mid X=x,Z=z\}=\frac{1}{p(x,z)}.$$ (1)

Let g be any function of Y such that E{g(Y)} = μ_g and E{ Rg(Y ) A(W, Z)} are finite. Then E{Rg(Y ) A(W, Z)} = μ_g.

Theorem 1 naturally extends to settings with multiple error-prone covariates. It guarantees that E{g(Y )} = μ_g can be recovered using a weighted mean of the observed data, even if Y_i is unobserved for a portion of the sample, i.e., R_i = 0, and covariates are measured with error, provided that the weights A(W, Z) derived from the error-prone W satisfy (1). The following corollary provides an estimator for μ_g.

Corollary 1

A consistent estimator for μ is

$$\widehat{\mu }=\frac{{\sum }_{i=1}^n{R}_i{Y}_{i}A(W_i,Z_i)}{{\sum }_{i=1}^n{R}_{i}A(W_i,Z_i)}.$$ (2)

In a similar manner, for the estimation of causal effects, the next corollary provides a consistent estimator of a treatment effect even in the presence of error-prone covariates.

Corollary 2

Let μ_t = E(Y_it ) for t = 0, 1, where the expectation is for the entire population, and let δ = μ₁ − μ₀ be the average treatment effect. Let A₁(w, z) satisfy the conditions of Theorem 1 with R = T and Y_i1, and let A₀(w, z) satisfy the conditions with R = 1 − T and Y_i0. Suppose that Assumptions 1–3 hold. Then a consistent estimator of δ is

$$\widehat{\delta }=\frac{{\sum }_{i=1}^n{T}_i{Y}_{i,\text{obs}}{A}_1(W_i,Z_i)}{{\sum }_{i=1}^n{T}_i{A}_1(W_i,Z_i)}-\frac{{\sum }_{i=1}^n(1-T_i)Y_{i,\mathit{obs}}{A}_0(W_i,Z_i)}{{\sum }_{i=1}^n(1-T_i)A_0(W_i,Z_i)}.$$ (3)

Remark 1

Suppose that A_odds(w, z) satisfies, for any z in the support of Z,

$$E\{A_{\text{odds}}(W,z)\mid X=x,Z=z\}=p(x,z)/\{1-p(x,z)\};$$

then, using an approach analogous to the proof of Theorem 1, we can show that E{(1 − T )Y A_odds(X, Z)} = E(Y₀ | T = 1) = μ_0|1, which can be estimated consistently by

$${\widehat{\mu }}_{0\mid 1}=\frac{{\sum }_{i=1}^n(1-T_i)Y_{i0}{A}_{\text{odds}}(W_i,Z_i)}{{\sum }_{i=1}^n(1-T_i)A_{\text{odds}}(W_i,Z_i)}.$$

Here μ_0|1 is the counterfactual mean of control outcomes for units that receive treatment. The average effect of treatment on the treated (Wooldridge, 2002, Ch. 18) can be consistently estimated by ${\sum }_{i=1}^n{T}_i{Y}_{i1}/{\sum }_{i=1}^n{T}_i-{\widehat{\mu }}_{0\mid 1}$.

Theorem 1 involves solving an inverse problem to obtain weights. As noted above, Pearl (2010) provided a framework for causal inference with error-prone covariates. In the case of dichotomous X and W and no additional covariates, Pearl’s approach yields estimates of μ₀ and μ₁ which are weighted sums of, respectively, the control and treatment group outcomes. However, the weights involve pr(W_i = 0 | T_i, Y_i ) and pr(W_i = 1 | T_i, Y_i ) (Pearl, 2010). In this simple case, the conditions of Theorem 1 are satisfied by A(W ) where

$$\begin{array}{l}A(0)\text{pr}(W_i=0\mid X_i=0)+A(1)\text{pr}(W_i=1\mid X_i=0)=\frac{1}{p(0)},\\ A(0)\text{pr}(W_i=0\mid X_i=1)+A(1)\text{pr}(W_i=1\mid X_i=1)=\frac{1}{p(1)}.\end{array}$$

The propensity scores for X, p(0)⁻¹ and p(1)⁻¹ can be estimated from the marginal distribution of W, the probability of treatment assignment given W, and the matrix inverse of Pearl (2010), which does not depend on Y_i. Thus, our weights are the solution of a simple linear system that does not involve the outcomes or pr(W_i = 1 | T_i, Y_i).

A closed form solution for A(w, z) also exists when U_i ~ N(0, σ²) and p(x, z)⁻¹ = 1 + exp(−β₀ − xβ₁ − z^T β₂). In this case, $A(w,z)=1+exp(-{\beta }_0-w{\beta }_1-z^{\mathrm{T}}{\beta }_2)exp(-{\beta }_1^2{\sigma }^2/2)$ satisfies (1). The weighting function plugs W into the true inverse probability function and then shrinks the value back towards 1. More generally, let X_i be a k-vector and let p(x, z)⁻¹ = 1 + exp{−(β₀ + x^Tβ₁ + z^Tβ₂ + x^TB₁x + x^TB₂z + z^TB₃z)}. Suppose that we observe W_i equal to X_i with additive, multivariate normal error, W_i = X_i + U_i with U_i ~ N(0, Σ), and suppose that A(w, z) = 1 + |Σ⁻¹V|^−1/2 exp{−(ω₀ + w^T ω₁ + z^T ω₂ + w^T M₁w + w^T M₂z + z′ M₃z)}. If V = (Σ⁻¹ + 2 M₁)⁻¹ is symmetric and positive definite, and if ${\omega }_0-0.5{\omega }_1^{\mathrm{T}}V{\omega }_1={\beta }_0,{\omega }_1-2{\omega }_1^{\mathrm{T}}{VM}_1={\beta }_1,{\omega }_2-{\omega }_1^{\mathrm{T}}{VM}_2={\beta }_2,M_1-2M_1^{\mathrm{T}}{VM}_1=B_1,M_2-2M_1^{\mathrm{T}}{VM}_2=B_2$ and $M_3-0.5M_2^{\mathrm{T}}{VM}_2=B_3$, then A(w, z) satisfies (1). Solutions for A(w, z) that satisfy all of these conditions with a positive definite V may not exist, and additional research is needed to determine the conditions under which p(x, z) and Σ yield feasible solutions. Details are given in the Supplementary Material.

Theorem 1 states that the weights need to be unbiased in the sense that the conditional mean equals the inverse probability weight calculated with the error-free X. However, because the conditional density function f (y | x, z, w, R = 1) depends only on x and z, if we could reweight the cases so that the density of x and z for the weighted cases equals f (x, z), the marginal density for the population, then we could obtain a consistent estimate of the expected value of g(Y ). This can be formalized by the following theorem.

Theorem 2

Let Ã(w, z) be a function that satisfies, for every x and z,

$$\int \stackrel{\sim }{A}(w,z)f(x,z\mid w,R=1)f(w\mid R=1)\mathrm{d}w=f(x,z).$$ (4)

Let A(w, z) = Ã(w, z)/pr(R = 1). Let g be any function of Y such that E{g(Y )} = μ_g and E{Rg(Y ) A(W, Z)} are finite. Then E{Rg(Y ) A(W, Z)} = μ_g.

Weights solving (4) also solve (1) and vice versa. Thus, to generate a weighting function, we must find weights which are unbiased for the correct weights or which reweight the conditional density of the error-free covariates given R = 1 to match their marginal density.

Proposition 1

A weight function Ã(w, z) satisfies (4) if and only if A(w, z) = Ã(w, z)/pr(R = 1) satisfies (1).

3. Estimation

3·1. Estimation of the propensity score and weighting function

Corollaries 1 and 2 provide consistent estimators in the presence of error-prone covariates, but they treat the propensity scores and weighting functions, p(x, z) and A(w, z), as known. In practice, these will need to be estimated from the observed data. The first step is to estimate p(x, z) using techniques for consistent estimation of models with error-prone covariates together with a model for the distribution of U. For example, a logistic regression model with the conditional score approach (Carroll et al., 2006, Ch. 7) could be used without assumptions on the distribution of X. If the distribution of X is known up to some parameters, then likelihood or Bayesian methods could be used with various parametric models for p(x, z); alternatively, gradient boosting corrected for measurement error could be used for nonparametric modelling (Sexton & Laake, 2008).

The next step is to calculate A(w, z) using the estimated p̂(x, z) for the unknown propensity score function. Use of Fourier transforms is a standard approach to solving integral equations like (1) in cases where there is not a closed form solution. We explored such methods but were unable to obtain the necessary transforms for p(x, z)⁻¹ when it did not have a simple functional form. We propose estimating an approximation to A(w, z) using simulated data and the estimated p̂(x, z).

First, generate a grid of x₁, …, x_J values. Second, for each x_j simulate U _j1, …, U_{j M}, error terms from the density of U given X _j and Z, and set W_jm = X _j + U _jm. Third, for each observed z, approximate A(w, z) by ${\sum }_{k=1}^K{\beta }_{zk}{\eta }_k(w)$ for a set of basis functions η_k(w) and approximate E{A(W, z) | X = x _j, Z = z} by ${\sum }_{k=1}^K{\beta }_{zk}E\{{\eta }_k(W)\mid X=x_j,Z=z\}$. Fourth, estimate E{η_k(X) | X = x _j, Z = z} by ${\overline{\eta }}_{kj}=M^{-1}{\sum }_{m=1}^M{\eta }_k(W_{jm})$; repeat this step for each x_j in the grid. Fifth, obtain a consistent estimator p̂(x, z). Sixth, estimate the coefficients of the series approximation, β̂_z1, …, β̂_zK, through linear regression of p̂(x_j, z)⁻¹ on η̄_kj, for k = 1, …, K. Repeat steps 1 to 6 for every z. Lastly, use $\stackrel{\sim }{\mu }={\sum }_{i=1}^n{R}_{i}g(Y_i){\widehat{A}}_{\widehat{p}}(W_i,Z_i)/{\sum }_{i=1}^n{R}_i{\widehat{A}}_{\widehat{p}}(W_i,Z_i)$, where ${\widehat{A}}_{\widehat{p}}(W_i,Z_i)={\sum }_{k=1}^K{\widehat{\beta }}_{zk}{\eta }_k(W_i)$, to estimate μ.

Theorem 3

Suppose that Assumptions 1–3 hold, and assume that p(x, z) meets regularity conditions, including being bounded below by a constant greater than zero for all x and z; then μ̃ is a consistent estimator of μ.

The methods for estimating p(x, z) and A(w, z) all rely on the distribution of the measurement error, which may be known or possibly estimated. Theorem 3 assumes that the measurement error distribution is known. Our simulation study tests an estimator that uses a noisy estimate of the variance of measurement errors.

3·2. Simulation study

We conducted a simulation study to test the feasibility of using μ̃ to estimate treatment and control group means and treatment effects with a finite sample. For each of 100 Monte Carlo iterations, we generated 1000 independent draws (X, Z₁, Z₂, T, W ), where X and Z₁ are both N(0, 1), with correlation 0·3, Z₂ is a Bernoulli random variable with mean 0·5, independent of (X, Z₁), and T is a Bernoulli treatment indicator with propensity score p(x, z₁, z₂) = pr(T = 1 | X = x, Z₁ = z₁, Z₂ = z₂) = G(0·5 + 1·2x + 0·5z₁ − 1·0z₂ + 0·7xz₂), where G is the cumulative distribution function of a Cauchy random variable. The Cauchy inverse link function yields fewer extreme values of p(x, z₁, z₂)⁻¹ and {1 − p(x, z₁, z₂)}⁻¹ than do the logistic or probit functions (Ridgeway & McCaffrey, 2007). The error-prone variable is W = X + U, where the U are independent and distributed as N(0, 0·09). The reliability of W is roughly 0·92, similar to that of student achievement test scores, as per a 2010 unpublished report of the Pennsylvania Department of Education. For each iteration, we also generated a working measurement error variance, S², as a scaled χ² random variable with mean 0·09 and 99 degrees of freedom. It is used in estimating the propensity scores and the weighting function to simulate analyses where the variance of the measurement error is estimated from an auxiliary dataset with 100 independent observations.

The simulated data included three outcome variables for each record: the linear outcome Y = 0·6X + 0·3 Z₁ + 0·3 Z₂ + e, where e ~ N(0, ν²) with ν² chosen such that {E(Y | T = 1) − E(Y | T = 0)}/ ν = 0·8; the tobit outcome Y ^* = Y I (Y > 0); and the cubic outcome Y ^** = Y − 0·6{h(X) − X}, where h(X) approximates the roughly cubic relationship between two consecutive years of student achievement test scores.

For each iteration, we estimated the coefficients of p(x, z₁, z₂) by maximizing the likelihood for (T, W, Z₁, Z₂) via SAS Proc NLMIXED, using the correctly specified functional form for the propensity score and a measurement model for W (Rabe-Hesketh et al., 2003) where X is normally distributed with unknown variance and W given X = x is distributed as N(x, S²).

For each observation, we estimated Â_p̂ (w, z₁, z₂) using J = 800 equally spaced pseudo-x values between −5 and 5 and M = 500 errors. We approximated A by cubic B-spline basis functions with 31 knots. We estimated the treatment effect by (3) with the unknown A(w, z₁, z₂) replaced by Â_p̂ (w, z₁, z₂). We refer to this as the weighting function estimator. The settings for approximation were chosen via exploratory analysis, which indicated that the approximation error with these settings was small and did not improve appreciably with larger samples of the X or W in the computationally feasible range, or with additional knots in the spline.

We consider two other estimators. One, the ideal estimator, is the standard inverse probability-weighted estimator with the unknown propensity scores estimated using the correct functional form and the error-free X. Obviously, this estimator would not be feasible in applications and is included as a benchmark for assessing the cost of measurement error, as this would be the standard estimator had X been observed. The other estimator we consider, the naïve estimator, is the standard inverse probability-weighted estimator with the unknown propensity scores estimated using the correct functional form and the error-prone W.

We evaluated the performance of three estimators, the ideal, naïve, and weighting function estimators, by assessing the balance of the means of the covariates between the treatment and control groups, as well as the estimated treatment effects for each of three constructed outcomes. The weights should balance the means of all the variables, so that the difference between the weighted, the treatment and the control group means of X, Z₁ and Z₂ should equal zero. Similarly, because there are no true treatment effects, the estimated treatment effects on the outcomes should be zero. We consider the bias, variance and mean squared error of the estimated treatment effects from the different weighting estimators for each of the three constructed outcomes.

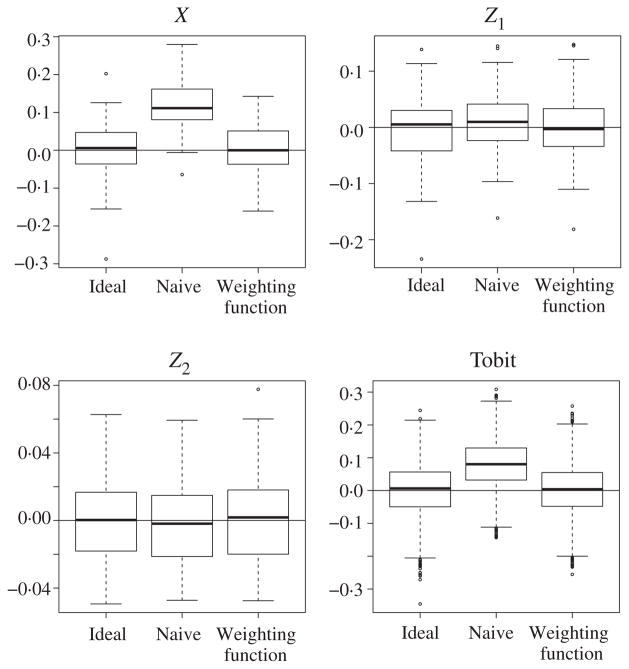
Figure 1 presents the results of the assessment of covariate balance. As expected, the ideal estimator has small bias for all three covariates while the naïve estimator has substantial bias for X, approximately 0·11, but very small bias for Z₁ and Z₂. The weighting function estimator has small bias for all three covariates, as would be expected from Theorem 3.

Fig. 1.

Box plots of the differences between the weighted treatment and control group means of X, Z₁ and Z₂, along with standardized treatment effect estimates for the tobit outcome, for three weighted estimators.

Figure 1 also shows the distribution of the estimated standardized treatment effects for the tobit outcome. Results for the other outcomes are similar and are given in the Supplementary Material. The treatment effects resemble the balance figure for X. The weighting function estimator performs similarly to the ideal estimator, with small bias, while the naïve estimator has notable bias. The variances across the different estimators are comparable but are slightly lower for the naïve estimator; however, that estimator has mean squared error 60–98% larger than that of either the ideal or the weighting function estimator due to its large bias. The mean squared errors for the ideal and weighting function estimators are approximately equal.

4. Discussion

Although our simulation study clearly demonstrates that our approach yields an estimator which can perform well in applications, methods for inference need to be investigated and the bootstrap is an obvious approach. We tested such an approach, using 100 bootstrap replicates for our first Monte Carlo iteration to estimate a standard error of our treatment effect estimates for the three outcomes. Across outcomes, the bootstrap standard error estimate ranged from about 90% to 120% of the standard error estimated from the Monte Carlo simulation. We find this encouraging, given the error in both the bootstrap and the Monte Carlo estimates, but more research is needed on the use of the bootstrap in this context.

Our simulation study suggests that the estimator can work when the parameters of the measurement distribution are estimated unbiasedly. More research is needed to determine whether the method is robust with respect to distributional assumptions about measurement error and how to adapt the method when treatment assignment and outcomes depend on latent covariates which are measured through multiple indicators (Raykov, 2012).

Future research will also need to explore the robustness of the method with respect to errors in the propensity score model and develop methods for modelling the propensity score function when the functional form is unknown. Common approaches use the distributions of covariates to select variables, terms and the functional form of the propensity score function (Dehejia & Wahba, 1999). However, it is not clear if the distribution of the error-prone covariates can proxy for the distributions of the error-free variables. Similarly, work is needed on tuning the simulation in the approximation of the weighting function.

Another area of future research is application of the weighting function estimator in the presence of heteroskedastic measurement error, for example where W_i = X_i + U_i with $U_i~N(0,{\sigma }_i^2)$. Theorem 1 and its corollaries extend naturally to this setting by allowing the weighting function to depend on i. However, this may affect the existence of solutions to (1), because the equation would depend on more than just the difference between X and W. Finally, the estimator needs to be extended to the case of multiple error-prone covariates. Theorem 1 can be extended, but work is needed to adapt the estimation methods and the existence of solutions to a multivariate version of (1).

Appendix

Proof of Theorem 1

The expected value of Rg(Y ) A(W, Z) equals

$$\begin{array}{l}E\{Rg(Y)A(W,Z)\}=\text{pr}(R=1)E\{g(Y)A(W,Z)\mid R=1\}\\ =\text{pr}(R=1)\int \int \int \int g(y)A(w,z)f(y,x,z,w\mid R=1)\mathrm{d}w\mathrm{d}z\mathrm{d}x\mathrm{d}y\\ =\text{pr}(R=1)\int \int \int g(y)\left\{\int A(w,z)f(w\mid y,x,z,R=1)\mathrm{d}w\right\}\\ \times f(y,x,z\mid R=1)\mathrm{d}z\mathrm{d}x\mathrm{d}y\\ =\text{pr}(R=1)\int \int \int \frac{g(y)}{p(x,z)}f(y,x,z\mid R=1)\mathrm{d}z\mathrm{d}x\mathrm{d}y\end{array}$$ (A1)

$$=\text{pr}(R=1)\int \int \int \frac{g(y)}{p(x,z)}\frac{\text{pr}(R=1\mid y,x,z)f(y,x,z)}{\text{pr}(R=1)}\mathrm{d}z\mathrm{d}x\mathrm{d}y$$ (A2)

$$\begin{array}{l}=\int \int \int \frac{g(y)}{p(x,z)}p(x,z)f(y,x,z)\mathrm{d}z\mathrm{d}x\mathrm{d}y\\ =\int \int \int g(y)f(y,x,z)\mathrm{d}z\mathrm{d}x\mathrm{d}y={\mu }_g.\end{array}$$ (A3)

Equality (A1) follows from Assumption 1 and condition (1); equality (A2) follows from Assumption 2; and equality (A3) follows from Assumption 3.

Proof of Corollary 1

Divide the numerator and denominator in (2) by n. By Theorem 1 with g(Y ) = Y and the weak law of large numbers, the numerator converges in probability to μ. Similarly, using Theorem 1 with g(Y ) = 1, the denominator converges in probability to 1. By Slutsky’s theorem, the ratio converges in probability to μ.

Proof of Corollary 2

By definition, when T_i = 1 we have Y_i,obs = Y_i1 and when 1 − T_i = 1 we have Y_i,obs = Y_i0. Hence, by Corollary 1, the first term on the right-hand side of (3) converges in probability to μ₁, and the second term converges in probability to μ₀.