Commensurate Priors for Incorporating Historical Information in Clinical Trials Using General and Generalized Linear Models

Abstract

Assessing between-study variability in the context of conventional random-effects meta-analysis is notoriously difficult when incorporating data from only a small number of historical studies. In order to borrow strength, historical and current data are often assumed to be fully homogeneous, but this can have drastic consequences for power and Type I error if the historical information is biased. In this paper, we propose empirical and fully Bayesian modifications of the commensurate prior model (Hobbs et al., 2011) extending Pocock (1976), and evaluate their frequentist and Bayesian properties for incorporating patient-level historical data using general and generalized linear mixed regression models. Our proposed commensurate prior models lead to preposterior admissible estimators that facilitate alternative bias-variance trade-offs than those offered by pre-existing methodologies for incorporating historical data from a small number of historical studies. We also provide a sample analysis of a colon cancer trial comparing time-to-disease progression using a Weibull regression model.

1 Introduction

1.1 Background

Clinical trials are not designed without consideration of earlier results from similar studies. Prior distributions derived from historical data, data from previous studies in similar populations, can be used prospectively to provide increased precision of parameter estimates. Our understanding of the “standard care” group in a trial can almost always be augmented by information derived from previous investigations. In a seminal article, Pocock (1976) considers incorporating historical control data into clinical trial analysis given that it satisfies six “acceptability” conditions. Conventionally, acceptable evidence from multiple trials is synthesized using random-effects meta-analyses (Spiegelhalter et al., 2004, p.268). Such borrowing of strength to assess “population averaged” effects in the full comparative evaluation of a new treatment has long been encouraged by the Center for Devices and Radiological Health (CDRH) at the U.S. Food and Drug Administration (FDA); see http://www.fda.gov/cdrh/osb/guidance/1601.html.

However, for the case of just a few historical studies, this approach is overly sensitive to the hyperprior distribution on the variance parameter that controls the amount of cross-study borrowing. Furthermore, with only one historical study, assessing the uncertainty of the between-study variability is difficult (Spiegelhalter, 2001; Gelman, 2006). Therefore, implementing the conventional meta-analytic approach to borrow strength from only one historical study requires informative prior distributions that may have drastic consequences for power and Type I error.

In this paper we propose empirical and fully Bayesian modifications to the “commensurate prior” approach (Hobbs et al., 2011) and extend the method to regression analysis using general and generalized linear regression models, in the context of two successive clinical trials. Throughout the paper we assume that the current trial compares a novel intervention to a previously studied control therapy that was used in the first trial, and thus historical data are available only for the control group. Furthermore, commensurate priors are constructed to inform about fixed regression effect parameters.

The goal of our proposed methodology is to formulate Bayesian hierarchical models that facilitate more desirable bias-variance trade-offs than those offered by pre-existing methodologies for incorporating historical data from a small number of historical studies. Sutton and Abrams (2001) consider empirical Bayesian methods in meta-analysis. Alternative solutions include “robust” Cauchy priors (Fúquene et al., 2009), meta-analytic-predictive methods (Neuenschwander et al., 2010), and power priors (Ibrahim and Chen, 2000; Neelon and O’Malley, 2010). Proper implementation of power prior models for non-Gaussian data requires formidable numerical computation that may prohibit their use in practice for clinical trial design. Therefore, we do not consider the commensurate power prior methodology proposed by Hobbs et al. (2011).

1.2 Connection to meta-analysis

Before developing our method, we briefly discuss the conventional random-effects meta-analytic approach for incorporating historical data. Let y denote a vector of i.i.d. responses of length n from patients enrolled in a current trial, such that $y_i\stackrel{\mathit{iid}}{\sim }N(\mu +d_i\lambda ,{\sigma }^2)$ where d_i is an indicator of novel treatment. Suppose that we have patient-level data for patients assigned to the current control arm from H historical trials. Let y_0,h denote response vectors of length n_0,h for the historical data, ${\mathit{y}}_{0,h}~N({\mu }_{0,h},{\sigma }_{0,h}^2)$, where h = 1, …, H. Suppose that current trial’s objective is to compare the novel treatment to the previously studied control, and thus the posterior distribution of λ is of primary interest for treatment evaluation. Historical data is incorporated for the purpose of facilitating more precise estimates of μ and λ.

The conventional random-effects meta-analytic approach for borrowing strength from the historical data (see e.g. Spiegelhalter et al., 2004, p.268) assumes that μ_0,1, …, μ_0,H, and μ are exchangeable:

$${\mu }_{0,1},\dots ,{\mu }_{0,H},\mu ~N(\xi ,{\eta }^2).$$

The model allows for both between-study heterogeneity and within-study variability. Parameters ξ and η² characterize the population mean and between-study variance, respectively. The estimate of ξ is a weighted average of the observed historical and current study effects, with weights $1/({\sigma }^2+{\eta }^2),1/({\sigma }_{0,1}^2+{\eta }^2),\dots ,1/({\sigma }_{0,H}^2+{\eta }^2)$.

The estimates of the μ_0,h and μ are “shrunk” toward ξ by an amount depending on the relative between-study and within-study variances. Following Spiegelhalter et al. (2004, p.94), B = σ²/(σ²+η²) controls the amount of shrinkage of the estimate of μ towards ξ. Relatively small values of η² suggest that the data provide little evidence for heterogeneity with respect to the effect of control among the trial populations. This results in more borrowing of strength from the historical data. Fixing η² = 0 induces a model that assumes “full homogeneity.”

Often the data provides sufficient information to estimate location parameters μ, μ_0,h, ξ, and within-study variances ${\sigma }_{0,h}^2$ and σ ² using common noninformative prior distributions, h = 1, …, H. Table 1 lists common noninformative and “weakly informative” prior distributions for η² suggested by Spiegelhalter et al. (2004, p.170), Gelman (2006), and Daniels (1999).

Table 1.

Common priors for η²

prior	form
uniform variance	p(η2) = U(0, a)
inverse gamma	p(η2) = G−1(∊, ∊)
uniform standard deviation	$p(\eta )=U(0,\sqrt{a})$
half-Cauchy	p(η) ∝ (η2 + b)−1
uniform shrinkage	p(η2) ∝ σ2/{(σ2 + η2)2}, ${\sigma }_{0,h}^2={\sigma }^2$, for all h

The first option for p(η²) considered by Spiegelhalter et al. (2004) is a uniform prior distribution with a relatively large range (a = 100). Gelman (2006) does not recommend it because it tends to unduly favor higher values, resulting in excessive heterogeneity. Spiegelhalter et al. (2004) also consider the inverse gamma prior for η² with both hyperparameters small, say ∊ = 0.001. This prior distribution is often used because it is proper and conditionally conjugate. However, it is sharply peaked near zero and thus induces strong prior preference for homogeneity. As detailed in Gelman (2006), inferences with this prior are sensitive to the choice of ∊ for datasets in which homogeneity is feasible, and in the limit (∊ → 0) results in an improper posterior density.

Both authors consider a uniform density on η, which is equivalent to p(η²) ∝ 1/η (Gelman, 2006). Assuming a uniform prior on the scale of η facilitates more homogeneity. However, for small H this prior tends overestimate heterogeneity. Gelman (2006) proposes a “weakly informative” half-Cauchy prior distribution on η with scale parameter, b, as a sensible compromise between the inverse gamma and uniform priors. For large values of b, (e.g. 25), this family of prior distributions has better behavior near 0, compared to the inverse gamma family; gentle slopes in the tails constrain the posterior away from large values and allow the data to dominate.

Daniels (1999) derives properties of the proper uniform shrinkage prior, which is equivalent to assuming a U(0, 1) prior on the shrinkage parameter, B. One attractive property of “uniform shrinkage” is that the density is maximized at zero, but less sharply peaked compared to the inverse gamma family. However, in this context, it requires identical within-study variances ${\sigma }_{0,h}^2={\sigma }^2$, for h = 1,…, H, which is an undesirable assumption.

Denote the difference between the current and hth historical intercept, or unknown bias (Pocock, 1976), by Δ_h = μ−μ_0,h, and let Δ = (μ−μ_0,1, …, μ−μ_0,H). 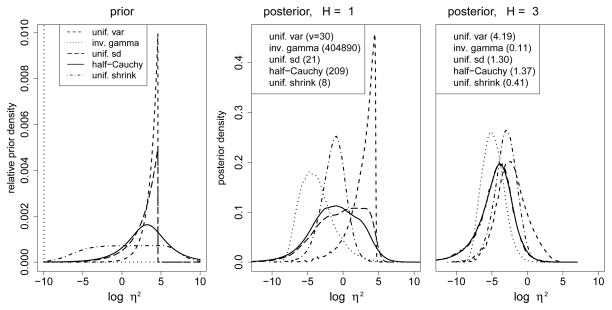Denote the parameter vector $\mathit{\theta }=(\mu ,\lambda ,\mathbf{\Delta },{\sigma }^2,{\sigma }_{0,1}^2,\dots ,{\sigma }_{0,H}^2)$, let = (y, y₀) denote the collection of current and historical response data, where y₀ = (y_0,1, …, y_0,H), and let L( |θ) denote the joint likelihood. Figure 1 illustrates the propriety of each of the aforementioned prior distributions for η² in this context on the scale of log(η²). The left plot portrays the relative prior densities, p{log(η²)} ∝ η²p(η²). The plot illustrates each prior’s relative proclivity for homogeneity. In this context, assuming η² is uniform over the interval [0, 100] induces a preference for heterogeneity, while the excessive tail behavior of the inverse gamma prior, which is characterized by a vertical dotted line on the far left side, induces a preference for homogeneity. The other three alternatives induce varying compromises. The center and right plots of Figure 1 contain marginal posterior distributions for log(η²) for truly unbiased historical data for H = 1 and = 3 historical trials. Specifically, the plots depict

Figure 1.

Prior distribution for log(η²) and posterior distributions for log(η²) for truly unbiased historical data: ${\mathrm{\Delta }}_1^{tr}=\dots ={\mathrm{\Delta }}_H^{tr}=0$ for H = 1 and = 3 historical studies. Values in parentheses are approximate posterior standard deviations on the scale η².

$$q\{log({\eta }^2)\mid {\mathit{\theta }}^{tr}\}\propto {\int }_{\mathcal{D}}\left\{{\int }_{\mathit{\theta }}{\eta }^{2}p({\eta }^2,\mathit{\theta })L(\mathcal{D}\mid \mathit{\theta })d\mathit{\theta }\right\}L(\mathcal{D}\mid {\mathit{\theta }}^{tr})d\mathcal{D},$$

where θ^tr contains fixed Δ^tr = 0. We also set true parameters λ^tr = 0 and ${\sigma }^{tr}={\sigma }_{0.1}^{tr}=\dots ={\sigma }_{0,H}^{tr}=1$; fixed historical sample sizes n_0,h = 60, and current sample size n = 180, and assumed equal allocation of patients to treatment and control in the current trial. The log-transformation of η² facilitates comprehensive characterization of the distributions over a vast portion of the parameter space. However, given the asymmetry of the parameter space (i.e., in this context homogeneity is realized for values < −3) it is difficult to assess uncertainty on the log-scale. Thus, legends in the center and right plots of Figure 1 provide approximate posterior standard deviations on the scale of η² in parentheses.

Figure 1 illustrates the primary drawback to using meta-analysis to incorporate historical data from one historical study. Looking from the left to center plots reveals that relatively little Bayesian updating of p{log(η²)} has occurred despite the fact that the historical data is unbiased. The uniform prior on η² is relatively unchanged, while the inverse gamma prior results in a posterior that covers a wide range of homogeneity, yet it is still very diffuse given that its posterior standard deviation on the η² scale is greater than 400, 000. The center plot reaffirms the aforementioned authors’ preferences for the uniform standard deviation, half-Cauchy, or uniform shrinkage priors, which facilitate sensible compromises. Yet, even these posteriors are still diffuse, facilitating little borrowing of strength from the historical data in this setting. The right plot illustrates that for H = 3, a relative “convergence” to the preference for homogeneity begins to emerge, although the priors still systematically influence the relative degree of homogeneity.

The remainder of the paper proceeds as follows. Section 2 introduces our proposed commensurate prior models and evaluates their frequentist properties for Gaussian data. Section 3 introduces general linear and general linear mixed models for Gaussian data. Then in Section 4 we expand the method to include non-Gaussian responses for generalized linear and generalized linear mixed models. Section 5 offers an illustrative time-to-event analysis that demonstrates the benefit of our proposed method, while Section 6 evaluates the frequentist and Bayesian operating characteristics of our method using simulation. Finally, Section 7 concludes, discusses our findings, and suggests avenues for further research.

2 Commensurate prior models

Hobbs et al. (2011) consider the simple case involving incorporation of data from one historical trial into the analysis of a single-arm trial. The authors define the location commensurate prior for μ to be the product of the historical likelihood and a normal prior on μ with mean μ₀ and precision or “commensurability parameter” τ. The general formulation follows from Pocock (1976), who suggested that historical parameters are biased representations of their concurrent counterparts. Pocock (1976) also suggested that models for incorporating historical information must account for unknown bias Δ = μ−μ₀ in the historical data. The commensurate prior is essentially a structural prior distribution that describes the extent to which a parameter in a new trial varies about the analogous parameters in a set of historical trials when the direction of the bias is unknown. The approach assumes that the current analysis should borrow strength from the historical data in the absence of evidence for heterogeneity. Thus, lack of evidence for large absolute bias, |Δ|, relative to the data’s informativeness, implies commensurability. A one-to-one relationship exists between the commensurability parameter and the between-study variance parameter η² for the random-effects meta-analytic models discussed in the previous section for the case of one historical study. Pocock (1976) proposes repeated analysis under several fixed values of 1/τ, while Hobbs et al. (2011) propose a fully Bayesian approach that assumes a diffuse uniform prior distribution on log(τ).

There are two issues with the pre-existing formulation. First, the diffuse prior of Hobbs et al. (2011) on log(τ) (an attempt at objectivity) is actually quite informative, in that it strongly favors either full homogeneity or heterogeneity (on the scale of η, nearly 83% of the a priori probability is placed on values less than 0.05 or larger than 10, the effective range for substantial to very little shrinkage). Second, the historical likelihood should perhaps more properly be considered data instead of a component of the prior. Nevertheless, Hobbs et al. (2011) demonstrate that analysis using commensurate priors may lead to more powerful procedures than an analysis that ignores the historical data, even when Type I error is controlled at 0.05. Henceforth, we proceed with two modifications of the preceding commensurate prior methodology. We consider the historical data to be a part of the likelihood, and propose new empirical and fully Bayesian modifications for estimating τ from the data. Our proposed commensurate prior models lead to preposterior admissible estimators that facilitate alternative bias-variance trade-offs from those offered by pre-existing methodologies for incorporating historical data from a small number of historical studies. The proposed methodology provides the most gains for the case of only one historical study. Before applying this methodology in practice we must assess frequentist properties in the context of other important factors, such as potential disparities in sample size among the historical and current studies.

2.1 One historical study

As demonstrated in Subsection 1.2, in a random-effects meta-analysis it is difficult to estimate η² if the number of historical studies is small. As illustrated in Figure 1, for only one historical trial in the above context, the data provide very little information about η². Yet, if evidence regarding the efficacy and safety profile of the current control arm derives from a single study because data is exceptionally expensive, the patient population is sparse, or the therapy is unusually hazardous, then it may be highly desirable to facilitate more borrowing of strength from the existing evidence. This is especially true if the trial implements adaptive decision rules that are designed to minimize the number of patients that are exposed to the inferior treatment. Consequently, in practice inference often proceeds under the assumption of full homogeneity, η² = 0, which violates Pocock’s (1976) proposition that one must allow for unknown bias in the historical controls. Assuming homogeneity yields designs with undesirable frequentist operating characteristics.

Let θ denote the parameter vector $\mathit{\theta }=(\lambda ,\mu ,{\mu }_0,{\sigma }^2,{\sigma }_0^2)$. For H = 1, the joint posterior distribution under the commensurate prior model is proportional to

$$q(\mathit{\theta }\mid \tau ,\mathit{y},{\mathit{y}}_0)\propto N(\mu \mid {\mu }_0,1/\tau )p({\mu }_0)p(\sigma ,{\sigma }_0)\prod _{j=1}^{n_0}N(y_{0j}\mid {\mu }_0,{\sigma }_0^2)\prod _{i=1}^{n}N(y_i\mid \mu +d_i\lambda ,{\sigma }^2).$$ (1)

Throughout this paper we refer to μ ~ N(μ|μ₀, 1/τ ) as the commensurate prior, and to p(μ₀) as the initial prior, since it characterizes information before the historical data was observed. The commensurate prior assumes that μ is a non-systematically biased representation of μ₀. For one historical study a one-to-one relationship exists between τ and the meta-analytic between-study variance, η²: τ = 1/(2η²). Larger values of τ indicate increased commensurability, and induce increased borrowing of strength from the historical data.

Define $n_d={\sum }_{i=1}^n{d}_i,{\overline{y}}_d={\sum }_{i=1}^n{d}_i{y}_i/n_d,s_0^2={\sum }_{j=1}^{n_0}{(y_{0,j}-{\overline{y}}_0)}^2,s^2={\sum }_{i=1}^n{(y_i-\overline{y})}^2,\widehat{\mu }=\frac{n\overline{y}-n_d{\overline{y}}_d}{n-n_d},{\widehat{\lambda }}_{\mu }={\sum }_{i=1}^n{d}_i(y_i-\mu )/n_d,{\widehat{\mu }}_{0,\mu }=\left(\frac{{\overline{y}}_0}{{\sigma }_0^2/n_0}+\frac{\mu }{1/\tau }\right)/\left(\frac{n_0}{{\sigma }_0^2}+\tau \right)$, and

$${\widehat{\mu }}_{\tau }=\left\{\frac{\widehat{\mu }}{{\sigma }^2/(n-n_d)}+\frac{{\overline{y}}_0}{{\sigma }_0^2/n_0+1/\tau }\right\}/\left(\frac{n-n_d}{{\sigma }^2}+\frac{1}{{\sigma }_0^2/n_0+1/\tau }\right).$$

If we assume a flat prior for μ₀ (no initial information), reference priors for the within-study variances, $p({\sigma }^2,{\sigma }_0^2)=1/({\sigma }^2{\sigma }_0^2)$, the joint posterior in (1) can be written as

$$\begin{array}{l}q(\mathit{\theta }\mid \tau ,\mathit{y},{\mathit{y}}_0)\propto N\left(\lambda \mid {\widehat{\lambda }}_{\mu },{\sigma }^2/n_d\right)N\left\{{\mu }_0\mid {\widehat{\mu }}_{0,\mu },{\left(\frac{n_0}{{\sigma }_0^2}+\tau \right)}^{-1}\right\}\\ \times N\left[\mu \mid {\widehat{\mu }}_{\tau },{\left\{\frac{n-n_d}{{\sigma }^2}+{\left(\frac{{\sigma }_0^2}{n_0}+\frac{1}{\tau }\right)}^{-1}\right\}}^{-1}\right]N\left(\widehat{\mu }-{\overline{y}}_0\mid 0,\frac{{\sigma }^2}{n-n_d}+\frac{{\sigma }_0^2}{n_0}+\frac{1}{\tau }\right)\\ \times {\mathrm{\Gamma }}^{-1}\left({\sigma }_0^2\mid \frac{n_0-3}{2},s_0^2/2\right){\mathrm{\Gamma }}^{-1}\left\{{\sigma }^2\mid n/2-2,\frac{s^2+1/(1/n-1/n_d){(\overline{y}-{\overline{y}}_d)}^2}{2}\right\},\end{array}$$ (2)

where Γ⁻¹ denotes the inverse gamma distribution. We can reduce dimensionality in the numerical marginalization of θ by replacing the product of the initial prior and the historical likelihood with a normal approximation; Section 4 discusses this approach in generality for generalized linear models. Subsection 2.3 proposes fully Bayesian as well as empirical approaches for estimating τ.

2.2 Multiple historical studies

For H > 1 historical studies, we propose an extension of the commensurate prior model in the previous subsection that assumes homogeneity among the historical studies by formulating the commensurate prior for μ conditional on the historical population mean. Usually data from only a few historical studies will be available. If the historical studies are markedly heterogenous, one may need to consider whether the historical data satisfies Pocock’s “acceptability” conditions (Pocock, 1976), or fix the degree of heterogeneity to acknowledge the conflict.

Following our previous notation, the parameter vector contains one parameter for the historical population mean, μ₀: so that $\mathit{\theta }=(\lambda ,\mu ,{\sigma }^2,{\mu }_0,{\sigma }_{0,1}^2,\dots ,{\sigma }_{0,H}^2)$, where μ_0,1 = … = μ₀,H = μ₀. Denote the hth historical within-study variance divided by the sample size by ${\omega }_{0,h}={\sigma }_{0,h}^2/n_{0,h}$. The relationship between τ and the meta-analytic between-study variance η² is more complicated than before. For H > 1, τ⁻¹ characterizes the meta-analytic between-study variability, plus the difference between the summed variability among the sample means ȳ and the ȳ_0,hs, and the population mean (previously ξ) when heterogeneity is estimated η² versus when full homogeneity is assumed,

$$\tau ={\left[{\eta }^2+{\left\{1/\left(\frac{{\sigma }^2}{n-n_d}+{\eta }^2\right)+\sum _{h=1}^{H}1/({\omega }_{0,h}+{\eta }^2)\right\}}^{-1}-{\left(\frac{n-n_d}{{\sigma }^2}+\sum _{h=1}^{H}1/{\omega }_{0,h}\right)}^{-1}\right]}^{-1}.$$

Moreover, constraining the H historical means, μ_0,h, to be equal to each other but perhaps not to the current mean, μ inserts an asymmetry into the model that is not present in the usual exchangeability model. As in the previous section, the data typically provide sufficient information to estimate parameters λ, μ₀, σ, and σ_0,h (given no initial information) under common noninformative prior distributions, h = 1, …, H. The joint posterior distribution is proportional to

$$q(\mathit{\theta }\mid \tau ,\mathit{y},{\mathit{y}}_0)\propto N(\mu \mid {\mu }_0,1/\tau )p({\mu }_0)p(\lambda ,\sigma ,{\sigma }_{0,1},\dots ,{\sigma }_0,H_0)\times \prod _{h=1}^H\prod _{j=1}^{n_0,h}N(y_0,h_j\mid {\mu }_0,{\sigma }_{0,h}^2)\prod _{i=1}^{n}N(y_i\mid \mu +d_i\lambda ,{\sigma }^2).$$ (3)

The joint posterior distribution follows from (2) by replacing ${\sigma }_0^2/n_0$ with $v_0={({\sum }_{h=1}^{H}1/{\omega }_{0,h})}^{-1}$ ȳ₀ with $v_0\left({\sum }_{h=1}^H{\overline{y}}_{0,h}/{\omega }_{0,h}\right)$, and ${\mathrm{\Gamma }}^{-1}\left({\sigma }_0^2\mid \frac{n_0-3}{2},s_0^2/2\right)$ with ${\prod }_{h=1}^H{\mathrm{\Gamma }}^{-1}\left({\sigma }_{0,h}^2\mid \frac{n_{0,h}-3}{2},s_{0,h}^2/2\right)$, where $s_{0,h}^2={\sum }_{j=1}^{n_0,h}{(y_{0,h,j}-{\overline{y}}_{0,h})}^2$

2.3 Estimation of τ

In this subsection we propose empirical and fully Bayesian methods for estimating τ, and evaluate frequentist properties of the corresponding models for estimating λ in the context of our proposed commensurate prior model.

2.3.1 Empirical Bayesian

In this subsection we consider parametric empirical Bayesian (EB) estimation (see e.g. Morris, 1983; Kass and Steffey, 1989; Carlin and Louis, 2009) in the context of our proposed commensurate prior models. Define ${\widehat{\mu }}_0=v_0\left({\sum }_{h=1}^H{\overline{y}}_{0,h}/{\omega }_{0,h}\right)$. For known σ² and v₀, the marginal distribution of the current and historical data given hyperparameter τ, m(y, y₀|τ ) = ∫_θq(θ|τ, y, y₀)dθ, follows from (2) and (3) as

$$m(\mathit{y},{\mathit{y}}_0\mid \tau )\propto N\left\{\widehat{\mu }-{\widehat{\mu }}_0\mid 0,\frac{{\sigma }^2}{n-n_d}+v_0+\frac{1}{\tau }\right\}.$$ (4)

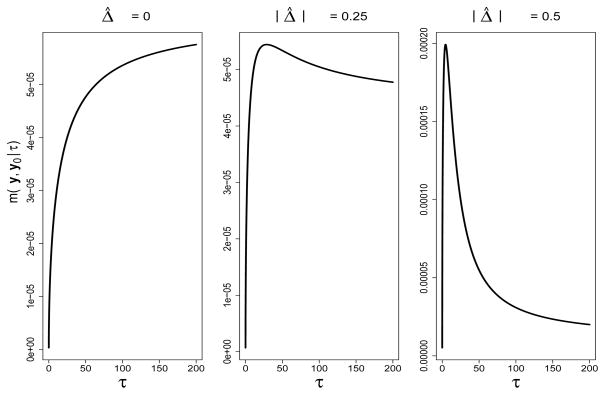
EB inference for θ proceeds by replacing the scalar hyperparameter τ in (2) and (3) with its marginal maximum likelihood estimate (MMLE). Larger values of τ indicate an increasing lack of empirical evidence for heterogeneity, and lead to increased borrowing of strength from the historical data. Figure 2 contains marginal distributions of the data in (4) for three observed values of |Δ̂ |, where Δ̂ = μ̂−μ̂₀ under the scenario that produced Figure 1 for one historical study. For sufficiently small |Δ̂ |, m(y, y₀|τ ) is monotonically increasing as a function of τ, evident in the left plot corresponding to the case when Δ̂ = 0. It follows that arg max_τ>0 m(y, y₀|τ ) = ∞, if ${\widehat{\mathrm{\Delta }}}^2<\frac{{\sigma }^2}{n-n_d}+v_0$. The center and right plots reveal that larger values of |Δ̂|, yield more peaked, unimodal functions.

Figure 2.

Marginal density of y, y₀ |τ (4) as a function of τ for three values of |Δ̂|, where Δ̂ = μ̂ – μ̂₀ and σ² = 1, u₀ = 1/n₀, n₀ = 60, n = 180, n_d = 90.

Let ν = τ^−1. We propose fixing ν* at the value that maximizes the marginal density of the data in (4), restricted to a pre-specified interval capturing the effective range of borrowing of strength. This leads to the following estimate for ν:

$${\nu }^{\ast }=arg\underset{\nu \in [l_{\nu },u_{\nu }]}{max}\{m(\mathit{y},{\mathit{y}}_0\mid 1/\nu )\}=max\left[min\left\{{\widehat{\mathrm{\Delta }}}^2-\frac{{\sigma }^2}{n-n_d}-v_0,u_{\nu }\right\},l_{\nu }\right],$$ (5)

where 0 < l_ν < u_ν. Bounding the MMLE precludes full homogeneity when evidence for heterogeneity is not strong. That is, decreasing (increasing) l_ν will induce more (less) borrowing of strength from the historical data when unrestricted maximization results in infinite 1/ν*. Restricting ν* ∈ [2(0.05²), 2(10²)], which corresponds to η ∈ [0.05, 10] for one historical study, usually captures the effective range of borrowing of strength. However, these limits should be selected via formal evaluation of the induced frequentist operating characteristics and bias-variance trade-offs in context.

Let = (y, y₀) denote the current and historical data, and ${\mathit{\theta }}^{tr}=({\lambda }^{tr},{\mathrm{\Delta }}^{tr},{\mu }^{tr},{({\sigma }^{tr})}^2,v_0^{tr})$ denote a set of fixed parameters characterizing a true state of the model. Define $Z^2=\left({\widehat{\mathrm{\Delta }}}^2\right)/\left(\frac{{\sigma }^2}{n-n_d}+v_0\right)$. Given θ^tr, Z² follows a non-central χ² distribution, $Z^2\mid {\mathit{\theta }}^{tr}~{\chi }_1^2\left\{{({\mathrm{\Delta }}^{tr})}^2/\left(\frac{{({\sigma }^{tr})}^2}{n-n_d}+v_0^{tr}\right)\right\}$. Let F_Z²|θ^tr (·) denote its cumulative density function. The probability that ν* is fixed at l_ν in the EB inference of θ is $F_{Z^2\mid {\mathit{\theta }}^{tr}}\left(\frac{l_{\nu }}{\frac{{({\sigma }^{tr})}^2}{n-n_d}+v_0^{tr}}+1\right)$.

Various maximization techniques can be used to estimate ν* for the intractable case when variances are unknown, including Markov chain Monte Carlo (MCMC) methods considered by Geyer and Thompson (1992) and Doucet et al. (2002). EB inference typically “underestimates” variability in θ, since posterior uncertainty in ν* is unacknowledged in the analysis. However, in the following sections we demonstrate that our EB procedure has several desirable properties when compared to conventional random effects meta-analytic models.

2.3.2 Fully Bayesian

The EB procedure yields approximate full homogeneity when evidence for heterogeneity is not strong (although this can be adjusted via careful selection of the lower bound, l_ν). However, even for this scenario approximate full homogeneity may not be warranted. In this subsection we discuss fully Bayesian estimation in the context of our proposed commensurate prior models. By accounting for prior uncertainty when estimating τ, the fully Bayesian approach takes full account of uncertainty in the parameter estimates. Specifically, we consider two families of priors for τ, a conditionally conjugate gamma distribution, as well as a variant of the “spike and slab” distribution introduced by Mitchell and Beauchamp (1988) for variable selection.

For known σ² and u₀, the marginal posterior distribution of τ|y, y₀ follows from (2) and (3) as

$$q(\tau \mid \mathit{y},{\mathit{y}}_0)\propto \tau N\left\{\widehat{\mathrm{\Delta }}\mid 0,\frac{{\sigma }^2}{n-n_d}+v_0+\frac{1}{\tau }\right\}p(\tau ).$$ (6)

Assuming a flat prior on τ clearly leads to an improper posterior, e.g. ${lim}_{\tau \to \infty }q(\tau \mid \mathit{y},{\mathit{y}}_0)\left(\sqrt{a+1/\tau }\right)/\tau =exp\left\{-0.5{\widehat{\mathrm{\Delta }}}^2/a\right\}$ and for ${\int }_0^{\infty }\tau {\left(\sqrt{a+1/\tau }\right)}^{-1}d\tau$ is divergent.

A default choice for p(τ ) is the gamma family of distributions, p(τ ) = Γ (cτ̃, c), since, from (1) and (3), it leads to the following conjugate full conditional posterior distribution,

$$q(\tau \mid \mathit{\theta },\mathit{y},{\mathit{y}}_0)\propto \mathrm{\Gamma }(c\stackrel{\sim }{\tau }+1/2,{\mathrm{\Delta }}^2/2+c).$$ (7)

For this parameterization τ̃ > 0 can be thought of as a prior guess at τ, while scalar c > 0 represents degree of confidence, with a smaller value corresponding to weaker prior belief.

We also propose an alternative prior for τ that derives from the aptly named “spike and slab” distribution (Mitchell and Beauchamp, 1988). As the nomenclature suggests, the distribution is locally uniform between two limits, 0 ≤ 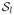< 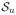except for a bit of probability mass concentrated at point 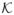> 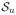. Let p₀ denote the prior probability that 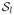≤ τ ≤ 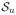. Then, formally, the prior assumes

$$\begin{array}{l}Pr(\tau <{\mathcal{S}}_l)=0,\\ Pr(\tau <u)=p_0\{(u-{\mathcal{S}}_l)/({\mathcal{S}}_u-{\mathcal{S}}_l)\},{\mathcal{S}}_l\le u\le {\mathcal{S}}_u\\ \text{and}Pr(\tau >{\mathcal{S}}_u)=Pr(\tau =\mathcal{K})=1-p_0.\end{array}$$ (8)

The reason that the spike and slab approach is appropriate in this context derives from the fact that sufficiently small values of Δ̂ result in marginal densities of the data (4) with nearly flat, gradually decreasing slopes as functions of τ, for sufficiently large τ. This is illustrated in the left plot of Figure 2. Therefore, given little evidence for heterogeneity, the marginalized likelihood prefers a large value for τ, but is virtually flat over a vast portion of the parameter space, providing little information to distinguish among values. This suggests a sensible approach may be to choose one carefully selected large value of τ (a “spike”), that characterizes commensurability. We demonstrate in the following sections that, when properly calibrated, this prior yields desirable frequentist properties. While the fully Bayesian methods are at less risk of dramatically overestimating τ, all of our methods are somewhat subjective and can therefore produce poor results if the model is incorrectly specified (the usual Bayesian “good model” assumption), thus making model checking an important component of this approach in practice.

2.3.3 Point estimation of λ

In this subsection we evaluate the proposed empirical and fully Bayesian commensurate prior models for estimating λ under squared error loss (SEL) and compare results to the full homogeneity model and the associated “no borrowing” model that ignores the historical data completely. Recall that we have assumed that the current trial’s objective is to compare a novel treatment to the previously studied control therapy. Thus, posterior inference on the novel treatment effect parameter, λ, is of primary interest. Let 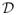= (y, y₀), and define

$$V_{\tau }={\left[{\left\{{\left(\frac{n}{n_d}\right)}^2\left(\frac{{\sigma }^2}{n}+v_0+\frac{1}{\tau }\right)\right\}}^{-1}+\frac{n_d(1-n_d/n)}{{\sigma }^2}\right]}^{-1},$$ (9)

$$\text{and}{\widehat{\lambda }}_{\tau }=\left\{\frac{\overline{y}-{\widehat{\mu }}_0}{\left(\frac{n}{n_d}\right)\left(\frac{{\sigma }^2}{n}+v_0+\frac{1}{\tau }\right)}+\frac{{\overline{y}}_d-\overline{y}}{{\sigma }^2/n_d}\right\}/V_{\tau }^{-1}.$$ (10)

For known σ² and u₀, it follows from (2) and (3) that the marginal posterior distribution of λ, τ| 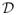can be represented as the following product:

$$\begin{array}{l}q(\lambda ,\tau \mid \mathit{y},{\mathit{y}}_0)\propto \tau q(\lambda \mid \mathit{y},{\mathit{y}}_0,\tau )m(\mathit{y},{\mathit{y}}_0\mid \tau )p(\tau )\\ \propto \tau N\left(\lambda \mid {\widehat{\lambda }}_{\tau },V_{\tau }\right)N\left\{\widehat{\mathrm{\Delta }}\mid 0,\frac{{\sigma }^2}{n-n_d}+v_0+\frac{1}{\tau }\right\}p(\tau ).\end{array}$$ (11)

If the historical data are ignored, the marginal posterior for λ|y follows as

$$q(\lambda \mid \mathit{y})\propto N[({\overline{y}}_d-\overline{y})/(1-n_d/n),{\sigma }^2/\{n_d(1-n_d/n)\}].$$ (12)

Let ${\mathit{\theta }}^{tr}=({\lambda }^{tr},{({\sigma }^{tr})}^2,{\mathrm{\Delta }}^{tr},v_0^{tr})$ denote a set of fixed parameters. The preposterior risk under squared error loss (Carlin and Louis, 2009, p. 433), conditional on θ^tr is

$$E_{\mathcal{D}\mid {\mathit{\theta }}^{tr}}\left[{\{E_{\lambda \mid \mathcal{D}}(\lambda )-{\lambda }^{tr}\}}^2\right].$$ (13)

Under fully Bayesian inference, the marginal posterior expectation of λ| 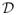follows as 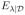(λ) = ∫ λ̂_τ q(τ| 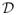)dτ. EB inference sets 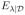(λ) = λ̂_1/ν*, where ν* is defined in (5). The no borrowing and homogeneity models result in 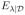(λ) = λ̂₀ and λ̂_∞, respectively.

Preposterior risk (13) can be simulated using the following relationships derived from the conditional likelihood of 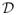|θ^tr,

$$\overline{y}-{\widehat{\mu }}_0~N\left\{{\mathrm{\Delta }}^{tr}+\frac{n_d}{n}{\lambda }^{tr},\frac{{\sigma }_{tr}^2}{n}+v_0^{tr}\right\},$$ (14)

$$\text{and}{\overline{y}}_d-\overline{y}~N\left\{\left(1-\frac{n_d}{n}\right){\lambda }^{tr},{\sigma }_{tr}^2\left(\frac{1}{n_d}-\frac{1}{n}\right)\right\}.$$ (15)

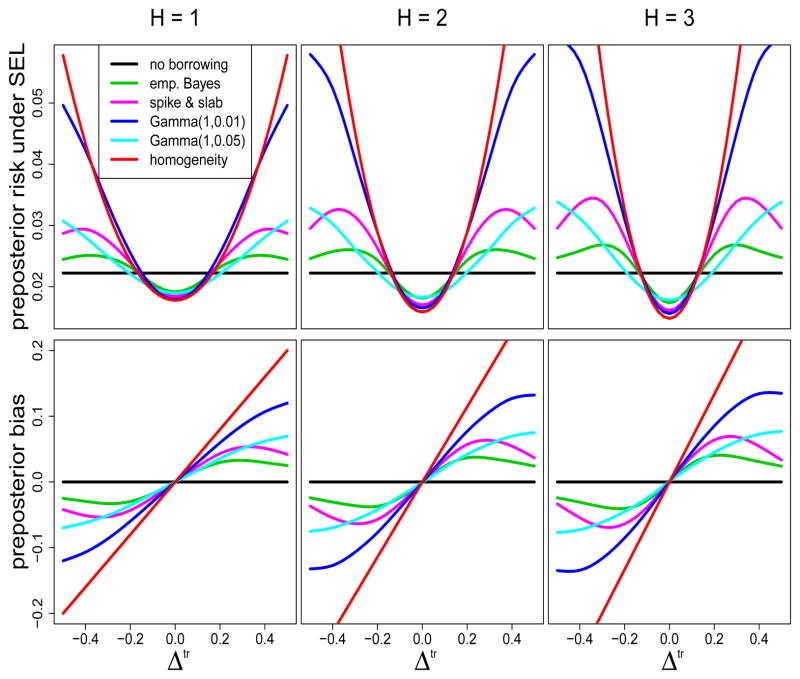
Figure 3 contains preposterior risk under SEL and bias as functions of Δ^tr resulting from inference under no borrowing, full homogeneity, as well as empirical and fully Bayesian commensurate prior models for H = 1, 2, and 3 historical studies under the same scenario that produced Figure 1: n = 180, n_d = 90, n_0,h = 60, (σ^tr)² = 1 and $v_0^{tr}={\left({\sum }_{h=1}^H{n}_{0,h}\right)}^{-1}$. Results are shown for an EB commensurate model that restricts ν* ∈ [2(0.05²), 2(10²)] = [0.005, 200], a fully Bayesian model that assumes a spike and slab prior for τ with hyperparameters, 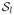= 0.005, 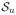= 2, 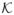= 200, and p₀ = 0.99, as well as two fully Bayesian models assuming gamma priors for τ with hyperparameters c = τ̃⁻¹ and τ̃ = 100, and 20, respectively.

Figure 3.

Preposterior risk under squared error loss and bias as functions of Δ^tr for H = 1, 2, and 3 historical studies.

Under no borrowing the posterior mean of λ| 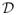is unbiased. Therefore, preposterior risk under SEL for the no borrowing inference follows from (12) as (σ^tr)²/{n_d (1 – n_d/n)}, and thus is constant as a function of Δ^tr. The plots reveal that all models obtain preposterior biases of zero when Δ^tr = 0. Assuming homogeneity a priori offers maximal variance reduction in this context, and thus is associated with the largest reductions in preposterior risk for Δ^tr near zero. Therefore, the resulting estimator is preposterior admissible. However, homogeneity leads to prohibitively biased estimators with sharply, monotonically increasing preposterior risk for |Δ^tr| > 0, rapidly trumping the gains in variance reduction. The top row of plots in Figure 3 reveal that preposterior risk for homogeneity exceeds no borrowing in this context for H = 1, 2, and 3 when |Δ^tr| > 0.2, > 0.16, and > 0.1, respectively.

In contrast to the no borrowing and homogeneity models, the commensurate prior models offer preposterior admissible estimators, with alternative bias variance trade-offs that facilitate more borrowing of strength for Δ^tr near zero and less borrowing for large values of |Δ^tr|. Numerous alternative bias variance trade-offs are attainable via adjustment to the model hyperparameters.

2.4 Comparison to meta-analysis

This subsection compares frequentist properties of our proposed commensurate prior models (2) and (3) with results for the meta-analysis models in Section 1.2 for the scenario that produced Figure 1 for the case when sampling level variances are unknown. Tables 2 and 3 augment Figure 3 and synthesize the relative bias-variance trade-offs when using the corresponding posterior expectation of λ| 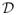as an estimator. Table 2 contains the percent change from no borrowing in preposterior risk under SEL given θ^tr for the five meta-analysis models, our proposed EB and fully Bayesian commensurate prior models, and the model that assumes full homogeneity. Negative values indicate reductions in preposterior risk. Table 3 contains the corresponding preposterior bias. Results are shown for H = 1, 2, and 3 historical studies and fixed true values of Δ^tr indicating various degrees of historical bias. Results are shown for fixed true standard deviation values ${\sigma }^{tr}={\sigma }_{0,1}^{tr}=\dots ={\sigma }_{0,H}^{tr}=1$. The spike and slab prior uses the same hyperparameters that were proposed in the previous subsection with the exception of p₀ which we now adjust to 0.7. If the historical data is ignored, the marginal posterior for λ|y now follows as

Table 2.

Percent change from no borrowing in preposterior risk under squared error loss for the specified model. For this scenario the result under no borrowing is equal to ${({\sigma }^{tr})}^2/\{n_d(1-\frac{n_d}{n})\}=0.0222$.

	Δtr = 0			Δtr = 0.25			Δtr = 0.5
	H = 1	2	3	H = 1	2	3	H = 1	2	3
unif. var.	−1	−3	−11	−1	−1	−1	0	1	4
unif. shrink	−4	−9	−14	−2	−2	−1	0	3	7
half-Cauchy	−4	−14	−21	−1	1	3	1	8	14
unif. sd	−3	−14	−21	−1	0	5	1	7	16
inv. gamma	−12	−20	−25	−1	4	9	8	20	31
emp. Bayes	−13	−17	−22	7	11	20	8	9	16
spike & slab	−13	−17	−22	1	5	11	9	10	11
Gamma(1,0.01)	−16	−22	−24	0	5	8	25	35	38
homogeneity	−19	−28	−32	25	61	86	152	337	475

Table 3.

Preposterior bias for the specified model: 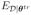{ 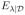(λ)}− λ^tr

	Δtr = 0			Δtr = 0.25			Δtr = 0.5
	H = 1	2	3	H = 1	2	3	H = 1	2	3
unif. var.	0.00	0.00	0.00	0.00	0.00	0.02	0.00	0.01	0.02
unif. shrink	0.00	0.00	0.00	0.01	0.02	0.03	0.01	0.02	0.03
half-Cauchy	0.00	0.00	0.00	0.01	0.03	0.04	0.01	0.03	0.04
unif. sd	0.00	0.00	0.00	0.01	0.03	0.05	0.01	0.02	0.04
inv. gamma	0.00	0.00	0.00	0.03	0.05	0.07	0.03	0.05	0.07
emp. Bayes	0.00	0.00	0.00	0.03	0.04	0.05	0.02	0.02	0.03
spike & slab	0.00	0.00	0.00	0.03	0.03	0.04	0.02	0.02	0.02
Gamma(1,0.01)	0.00	0.00	0.00	0.05	0.06	0.07	0.07	0.08	0.08
homogeneity	0.00	0.00	0.00	0.10	0.14	0.17	0.19	0.28	0.34

$$q(\lambda \mid \mathit{y})\propto t\left\{n-2,({\overline{y}}_d-\overline{y})/(1-n_d/n),\frac{s^2+1/(1/n-1/n_d){(\overline{y}-{\overline{y}}_d)}^2}{n_d(n-2)(1-n_d/n)}\right\}.$$ (16)

As in the previous subsection, preposterior risk under SEL given θ^tr follows as ${({\sigma }^{tr})}^2/\{n_d(1-\frac{n_d}{n})\}$. Note that marginal posteriors for λ| 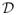corresponding to the commensurate prior models discussed in the previous subsection are now intractable due to required marginalization of the sampling variances.

First we consider the case when Δ^tr = 0. For the case of one historical study, Table 3 shows that all estimators are unbiased, yet Table 2 reveals that the meta-analysis estimators correspond to only slight reductions in preposterior risk under SEL, with the exception of the inverse gamma prior. In contrast, the commensurate models facilitate relatively large reductions in preposterior risk compared to the first four meta-analytic models. As in Figure 3, the gamma prior facilitates the largest reductions in preposterior risk, nearly approaching the reduction produced by highly subjective, full homogeneity.

When H > 1, inference using the uniform standard deviation and half-Cauchy priors in the meta-analysis framework provides considerably more reduction in preposterior risk than for H = 1. The inverse gamma prior facilitates even more reduction in preposterior risk. The uniform variance and uniform shrinkage priors offer considerably less reduction in preposterior risk. The commensurate prior models still facilitate more borrowing of strength than the first four models for meta-analysis leading to estimators with more reduction in preposterior risk, but less reduction than that obtained by full homogeneity.

When 0 < Δ^tr ≤ 0.5, the tables suggest that preposterior risk and bias are non-decreasing in H for all models. The highly subjective homogeneity model yields highly biased estimators corresponding to substantial increases in preposterior risk. The gamma model estimator is most biased among the commensurate prior estimators, which leads to large increases in preposterior risk for Δ^tr = 0.5. The spike and slab model estimator provides perhaps the best overall bias-variance trade-off among the commensurate prior estimators, given that it is least biased and results in relatively smaller increases in preposterior risk. Moreover, it provides equal or less bias than the half-Cauchy meta-analysis prior estimator when H > 1. Among the meta-analysis models, only the inverse gamma prior facilitates meaningful variance reduction from borrowing of strength for the case of one historical study. However, when Δ^tr = 0.5 the inverse gamma meta-analysis prior results in an increase in relative preposterior risk that is nearly two and three times larger than that for the spike and slab commensurate prior estimator for H = 2 and = 3, respectively.

3 General linear models

In this section we introduce general linear and general linear mixed commensurate prior models for Gaussian response data in the context of two successive clinical trials. In addition, we assume that both trials identically measure p – 1 covariates representing fixed effects which are to be incorporated into the analysis. As before, we assume that the second (current) trial compares a novel intervention to a previously studied control therapy that was used in the first trial, and thus historical data are available only for the control group. Furthermore, commensurate priors are constructed to inform about fixed regression effect parameters.

3.1 Fixed effect models

Assume y₀ is a vector of n₀ responses from patients in the historical study of an intervention that is to be used as a control in a current trial testing a newly developed intervention for which no reliable prior data exist. Let y be the vector of n responses from subjects in both the treatment and control arms of the current trial. Suppose that both trials are designed to identically measure p – 1 covariates of interest. Let X₀ be an n₀ × p design matrix and X be an n × p design matrix, both of full column rank p, such that the first columns of X₀ and X are vectors of 1s corresponding to intercepts.

Suppose ${\mathit{y}}_0~N_{n_0}(X_0{\mathit{\beta }}_0,{\sigma }_0^2)$ and y ~ N_n(Xβ + dλ, σ²) where λ is the (scalar) treatment effect and d is an n × 1 vector of 0 – 1 indicator variables for the new treatment. Let y_i,X_i, d_i represent data corresponding to the ith subject in the current trial, i = 1, …, n. Commensurability in the linear model depends upon similarity among the intercepts and covariate effects. Yet, the strength of empirical evidence for heterogeneity among the current and historical data may vary across covariates. We formulate the commensurate linear model by replacing τ in Section 2 with a vector τ = (τ₁, …, τ_p) containing a commensurability parameter, τ_g, for each associated pair of parameters in β_g and β_0g. The commensurate priors follow as $p({\beta }_g\mid {\beta }_{0g})\propto N({\beta }_g\mid {\beta }_{0g},{\tau }_g^{-1})$, for g = 1, …, p, and the β_gs are assumed a priori independent.

Let $\mathit{\theta }=(\lambda ,\mathit{\beta },{\mathit{\beta }}_0,{\sigma }^2,{\sigma }_0^2)$ and Δ = β–β₀, let diag{u} denote the diagonal matrix consisting of the elements of vector u, and let I_a denote the identity matrix of dimension a. The joint posterior distribution of θ|τ, y, y₀ follows as proportional to

$$p(\lambda ,\sigma ,{\sigma }_0)N_{n_0}({\mathit{y}}_0\mid X_0{\mathit{\beta }}_0,{\sigma }_0^2{I}_{n_0})N_n(\mathit{y}\mid X\mathit{\beta }+\mathit{d}\lambda ,{\sigma }^2{I}_n)\prod _{g=1}^{p}N({\beta }_g\mid {\beta }_{0g},{\tau }_g^{-1})p({\beta }_{0g}).$$ (17)

Let β̂_λ = (X^TX)⁻¹X^T (y–dλ) and ${\widehat{\mathit{\beta }}}_0={(X_0^T{X}_0)}^{-1}{X}_0^T{\mathit{y}}_0$, and ${\widehat{\lambda }}_{\beta }={\sum }_{i=1}^n{d}_i(y_i-X_i\mathit{\beta })/n_d$. Under a flat prior, the full conditional posterior for λ is proportional to N (λ̂_β, σ²/n_d). Let V_τ denote the precision matrix that results from averaging the commensurate prior over the historical likelihood:

$$V_{\mathit{\tau }}=\mathit{diag}\{\mathit{\tau }\}-\mathit{diag}\{\mathit{\tau }\}{(X_0^T{X}_0/{\sigma }_0^2+\mathit{diag}\{\mathit{\tau }\})}^{-1}\mathit{diag}\{\mathit{\tau }\}.$$ (18)

Thus, assuming a flat initial prior and marginalizing β₀ results in a conditional posterior for β|y, y₀, λ, σ², ${\sigma }_0^2$, τ proportional to

$$N_p\left\{\mathit{\beta }\mid {\left(V_{\mathit{\tau }}+\frac{X^{T}X}{{\sigma }^2}\right)}^{-1}\left(V_{\mathit{\tau }}{\widehat{\mathit{\beta }}}_0+\frac{X^{T}X}{{\sigma }^2}{\widehat{\mathit{\beta }}}_{\lambda }\right),{\left(V_{\mathit{\tau }}+\frac{X^{T}X}{{\sigma }^2}\right)}^{-1}\right\}.$$ (19)

Notice that the full conditional posterior mean for λ, λ̂_β, is a function of residuals (y – Xβ), whereas the conditional posterior mean of β in (19) is an average of the historical and concurrent data relative to the estimated commensurability parameter vector τ. As τ approaches 0, the posterior for β converges to a normal density with mean β̂_λ and variance ${\left(\frac{X^{T}X}{{\sigma }^2}\right)}^{-1}$, recovering the standard result from linear regression that ignores all of the historical data. In this case, λ̂_β also converges to the “no borrowing” estimate of the treatment effect. Moreover, as τ_g approaches infinity, for all g = 1, …, p, precision $V_{\mathit{\tau }}\to X_0^T{X}_0/{\sigma }_0^2$, fully incorporating the historical data, recovering full homogeneity. Full conditional posteriors for β₀, σ², and ${\sigma }_0^2$ under noninformative priors are provided in Appendix A.

3.2 Mixed models

In this subsection, we extend the model to include random effects. We begin with a familiar and useful one-way ANOVA model. Then following McCulloch and Searle (2001, p.156), we give the linear mixed model for general variance-covariance structures between and within levels of the random components.

3.2.1 One-way random effects model

Following the notation of Browne and Draper (2006), suppose y_0jk = μ₀ + u_0k + ∊_0jk, where ${\epsilon }_{0jk}\stackrel{\mathit{iid}}{\sim }N(0,{\sigma }_{\epsilon 0}^2)$ for k = 1, …, n_0j, j = 1, …, m₀, and $u_{0j}\stackrel{\mathit{iid}}{\sim }N(0,{\sigma }_{u0}^2)$. Variance component ${\sigma }_{\epsilon 0}^2$ represents the conditional variance of y_0jk|u_0j, while the marginal variance of y_0jk follows as ${\sigma }_{u0}^2+{\sigma }_{\epsilon 0}^2$. Note that observations from different subjects are assumed to be uncorrelated. The model for responses in the current trial follows y_ig = μ + u_i + d_iλ + ∊_ig, for g = 1, …, n_i; i = 1, …, m, where ${\epsilon }_{ig}\stackrel{\mathit{iid}}{\sim }N(0,{\sigma }_{\epsilon }^2)$ and $u_i\stackrel{\mathit{iid}}{\sim }N(0,{\sigma }_u^2)$. As before, d_i = 1 indicates treatment and d_i = 0 corresponds to the standard of care for the ith subject in the current trial. Therefore, fixed effects μ and λ represent the intercept and treatment effect for a patient receiving the new intervention. Given no initial information, the commensurate prior for μ is proportional to a normal distribution with mean μ₀ and precision τ.

Following the recommendations of Gelman (2006), we use independent noninformative uniform priors on σ_u0 and the current random-effects standard deviation, for large m (≥ 5), which is equivalent to a product of inverse-χ² densities with −1 degrees of freedom, $p({\sigma }_{u0}^2,{\sigma }_u^2)\propto \frac{1}{{\sigma }_{u0}{\sigma }_u}$. For small m (< 5), we use the half-Cauchy prior discussed in Section 1.2.

Let θ denote the parameter vector. The joint posterior distribution for θ|τ, y, y₀ is proportional to

$$\prod _{j=1}^{m_0}{N}_{n_{0j}}\left({\mathit{y}}_{\mathbf{0}\mathit{j}}\mid {\mu }_0{1}_{n_{0j}},{\sigma }_{u0}^2{J}_{n_{0j}}+{\sigma }_{\epsilon 0}^2{I}_{n_{0j}}\right)\prod _{i=1}^m{N}_{n_i}\left({\mathit{y}}_{\mathit{i}}\mid \mu 1_{n_i}+d_i\lambda ,{\sigma }_u^2{J}_{n_i}+{\sigma }_{\epsilon }^2{I}_{n_i}\right)\times N\left(\mu +{\mu }_0,1/\tau \right)/({\sigma }_{u0}{\sigma }_u{\sigma }_{\epsilon 0}{\sigma }_{\epsilon }),$$ (20)

where 1_u is a 1 × u column vector of 1s, and J_u is a u × u matrix of 1s. The Gibbs sampler is implemented by sampling the latent variables u_0j and u_i.

To ease the subsequent algebra required to marginalize (20), note that ${\sigma }_{\epsilon 0}^2$ times the inverted marginal estimated historical covariance for all observations in subject j, ${\sigma }_{\epsilon 0}^2{({\sigma }_{u0}^2{J}_{n_{0j}}+{\sigma }_{\epsilon 0}^2{I}_{n_{0j}})}^{-1}$, is equal to $\left(I_{n_{0j}}-\frac{{\sigma }_{u0}^2}{{\sigma }_{\epsilon 0}^2+n_{0j}{\sigma }_{u0}^2}{J}_{n_{0j}}\right)$, which has n_0j − 1 eigenvalues equaling 1 and one non-unit eigenvalue equal to $1-r_{0j}^{-1}$, where $r_{0j}=\frac{{\sigma }_{\epsilon 0}^2}{n_{0j}{\sigma }_{u0}^2}+1$. Similarly, $\left(I_{n_i}-\frac{{\sigma }_u^2}{{\sigma }_{\epsilon }^2+n_i{\sigma }_u^2}{J}_{n_i}\right)$ has n_i − 1 eigenvalues equaling 1 and one non-unit eigenvalue equal to $1-r_i^{-1}$, where $r_i=\frac{{\sigma }_{\epsilon }^2}{n_i{\sigma }_u^2}+1$. Let

$$\begin{array}{l}{M}_{\tau }=\left\{\frac{{\sum }_{j=1}^{m_0}{\sum }_{k=1}^{n_{0j}}{y}_{0jk}(1-r_{0j}^{-1})}{{\sum }_{j=1}^{m_0}{n}_{0j}(1-r_{0j}^{-1})}\right\}/\left\{\frac{1}{\tau }+\frac{{\sigma }_{\epsilon 0}^2}{{\sum }_{j=1}^{m_0}{n}_{0j}(1-r_{0j}^{-1})}\right\}\\ +\left\{\frac{{\sum }_{i=1}^m{\sum }_{g=1}^{n_i}(y_{ig}-d_i\lambda )(1-r_i^{-1})}{{\sum }_{i=1}^m{n}_i(1-r_i^{-1})}\right\}/\left\{\frac{{\sigma }_{\epsilon }^2}{{\sum }_{j=1}^m{n}_i(1-r_i^{-1})}\right\},\\ \text{and}{\mathrm{\sum }}_{\tau }={\left\{\frac{1}{\tau }+\frac{{\sigma }_{\epsilon 0}^2}{{\sum }_{j=1}^{m_0}{n}_{0j}(1-r_{0j}^{-1})}\right\}}^{-1}+{\left\{\frac{{\sigma }_{\epsilon }^2}{{\sum }_{j=1}^m{n}_i(1-r_i^{-1})}\right\}}^{-1}.\end{array}$$ (21)

After marginalizing μ₀, the conditional posterior for μ|λ, u₀, u, ${\sigma }_{\epsilon 0}^2,{\sigma }_{\epsilon }^2$, τ is proportional to $N({\mathrm{\sum }}_{\tau }^{-1}{M}_{\tau },{\mathrm{\sum }}_{\tau }^{-1})$. Full conditional posteriors for the remaining parameters can be found in Appendix B.

Several alternative prior specifications for the correlation structure may be more natural for incorporating prior information on the variance components. For example, we could formulate our prior opinion about the model smoothness by specifying a prior on the variance ratio, ${\sigma }_{\epsilon }^2/{\sigma }_u^2$ or the degrees of freedom it induces (Hodges and Sargent, 2001). For discussion about degrees of freedom and how they can be used to sensibly determine variance component priors, as well as the general marginal posterior for the variance ratio, see Reich and Hodges (2008), and Cui et al. (2010).

3.2.2 Linear mixed model

The one-way random effects model presented above is a special case of a linear mixed model for which between-subject observations are independent, all within subject observations have identical covariance (compound symmetry within groups), and there are no fixed regression effects (only intercepts). In this subsection we extend to the general linear mixed model.

Following the notation presented above, denote $n_0={\sum }_{j=1}^{m_0}{n}_{0j}$ and $n={\sum }_{i=1}^m{n}_i$. Suppose X₀ and X are n₀ × p and n × p design matrices such that the first columns contain vectors of 1s corresponding to the intercepts, β and β₀ are vectors of identically measured regression coefficients of length p representing fixed covariate effects, and d is an n × 1 new intervention indicator. Furthermore, let u₀, u and Z₀, Z denote m₀ × 1 and m × 1 random effects vectors and their respective n₀ × m₀ and n × m design matrices for the historical and current data.

Adopting the notation of McCulloch and Searle (2001, p.156), we formulate the general linear mixed model by first assuming normally distributed random effects with covariances D₀ and D, u₀ ~ N (0, D₀) and u ~ N (0, D). Models for the historical and concurrent responses are y₀ = X₀β₀ + Z₀u₀ + ∊₀ and y = Xβ + Zu + dλ + ∊, where ∊₀ ~ N_n0 (0, R₀) and ∊ ~ N_n(0, R); R₀ and R represent the conditional covariances of y₀|u₀ and y|u. The marginal covariances for y₀ and y are ${\mathrm{\sum }}_0=Z_0{D}_0{Z}_0^T+R_0$ and Σ = ZDZ^T + R, respectively. The precision matrix V_τ in (18) follows as

$$V_{\mathit{\tau }}=\mathit{diag}\{\mathit{\tau }\}-\mathit{diag}\{\mathit{\tau }\}{(X_0^T{\mathrm{\sum }}_0{X}_0+\mathit{diag}\{\mathit{\tau }\})}^{-1}\mathit{diag}\{\mathit{\tau }\}.$$ (22)

The conditional posterior distribution for β|λ, D₀, R₀, D, R, τ is proportional to

$$N_p\left\{\mathit{\beta }\mid {(V_{\mathit{\tau }}+X^T\mathrm{\sum }X)}^{-1}\left(V_{\mathit{\tau }}{\stackrel{\sim }{\mathit{\beta }}}_0+X^T\mathrm{\sum }X{\stackrel{\sim }{\mathit{\beta }}}_{\lambda }\right),{(V_{\mathit{\tau }}+X^T\mathrm{\sum }X)}^{-1}\right\},$$ (23)

where β̃_λ = (X^TΣX)⁻¹X^T (y − dλ), and ${\stackrel{\sim }{\mathit{\beta }}}_0={(X_0^T{\mathrm{\sum }}_0{X}_0)}^{-1}{X}_0^T{\mathit{y}}_0$, are the usual integrated least squares estimates. Treating the random effects as latent variables and adopting conjugate Wishart priors for D⁻¹ and R⁻¹ and their historical counterparts, namely D⁻¹ ~ W (ϕD̃, ϕ) and R⁻¹ ~ W(ρR̃, ρ), posterior inference may proceed via the Gibbs sampler. The remaining full conditional posteriors can be found in Appendix C.

If we assume that observations are uncorrelated across subjects, the covariance structures simplify to $D_0={\sigma }_{u0}^2{I}_{m_0},D={\sigma }_u^2{I}_m,R_0={\sigma }_{\epsilon 0}^2{I}_{n_0}$, and $R={\sigma }_{\epsilon }^2{I}_n$. The resulting model extends the one-way random effects model above to incorporate fixed covariate effects. Using the same priors as before, the full conditional posteriors for ${\sigma }_u^2$ and ${\sigma }_{\epsilon }^2$ follow as $q({\sigma }_{\epsilon }^2\mid \lambda ,\mathit{u},\mathit{\beta },{\mathit{y}}_0,\mathit{y})\propto {\mathrm{\Gamma }}^{-1}\{(n-1)/2,{\Vert \mathit{y}-X\mathit{\beta }-\mathit{d}\lambda -Z\mathit{u}\Vert }^2/2\}$ and $q({\sigma }_u^2\mid \mathit{u},{\mathit{y}}_0,\mathit{y})\propto {\mathrm{\Gamma }}^{-1}\left\{(m-1)/2,{\sum }_{j=1}^m{u}_j^2/2\right\}$. See Kass and Natarajan (2006) for an empirical Bayes approach using an inverted Wishart prior on Σ for general covariance structures and design matrices.

4 Generalized linear models

In this section we extend the methodology to incorporate generalized linear models for non-Gaussian error distributions. The methodology is generalized to include data from exponential families assuming Gaussian approximations of the product of the initial prior and historical likelihood using the Bayesian Central Limit Theorem (see e.g. Carlin and Louis, 2009, p.108). For a flat initial prior, the approximation takes mean equal to the historical MLE and variance equal to the inverted observed Fisher information matrix. These approximations are used frequently in Bayesian analysis for data assumed to follow from exponential families (Spiegelhalter et al., 2004, p.23; Gelman et al., 2004, p.101). While computational methods can handle the full model, the approximations facilitate dimension reduction for the numerical problem of estimating the crucial MMLE of τ when using EB inference, since β₀ is readily marginalized analytically.

We first present the general method for fixed effects models, and then discuss logistic regression models for binary outcomes and a Weibull regression model. We then extend the general method to incorporate random effects, and illustrate in two important specific cases: a probit regression model for binary outcomes, and a Poisson regression model for count data. The Weibull regression model is used to analyze patient-level data from two successive colorectal cancer trials in Section 5 for both the approximate and full commensurate prior models.

4.1 Fixed effect models

Let y₀ and y denote column vectors of length n₀ and n consisting of independent measurements from a distribution that is a member of the exponential family, f_Y (y). That is, we suppose $y_{0j}\stackrel{\mathit{indep}}{\sim }{f}_{Y_{0j}}(y_{0j})$ and $y_i\stackrel{\mathit{indep}}{\sim }{f}_{Y_i}(y_i)$ such that the log-likelihoods are of form

$$log{f}_{Y_0}(y_{0j})=\sum _{j=1}^{n_0}\{y_{0j}{\gamma }_{0j}-b_0({\gamma }_{0j})\}/{\nu }_0^2-\sum _{j=1}^{n_0}{c}_0(y_{0j},{\nu }_0)$$ (24)

$$\text{and}log{f}_Y(y_i)=\sum _{i=1}^n\{y_i{\gamma }_i-b({\gamma }_i)\}/{\nu }^2-\sum _{i=1}^{n}c(y_i,\nu ),$$ (25)

for j = 1, …, n₀ and i = 1, …, n (McCulloch and Searle, 2001, p.139). Following the notation of Section 3, let g(μ₀) = X₀β₀ and g(μ) = Xβ + dλ, for known “link” function g() where E [y₀] = μ₀ and E [y] = μ.

Using the Bayesian Central Limit Theorem, we replace the product of the initial prior and historical likelihood, f_Y0 (y₀|β₀)p(β₀), with an asymptotic normal approximation, p̂(β₀|y₀). This density is an approximate sequential Bayesian update of the initial prior for β₀. For a flat initial prior, the approximation takes mean equal to the historical MLE (computed numerically via Newton-Raphson or Fisher scoring) and variance equal to the inverted observed Fisher information matrix, $\widehat{p}({\mathit{\beta }}_0\mid {\mathit{y}}_0)=N_p\left\{{\widehat{\mathit{\beta }}}_0,{\left(X_0^T{\widehat{W}}_0{X}_0\right)}^{-1}\right\}$, where Ŵ₀ = W₀(μ̂₀) is an n₀ × n₀ diagonal matrix having jj–element

$$W_{0jj}({\mu }_0)={\left\{{\nu }^{2}v({\mathit{\mu }}_0){\left(\frac{\partial g({\mathit{\mu }}_0)}{\partial {\mathit{\mu }}_0}\right)}^2\right\}}^{-1},$$ (26)

where $v({\mu }_{0j})=\mathit{var}(y_{0j})/{\nu }^2={\partial }^{2}b({\gamma }_{0j})/\partial {\gamma }_{0j}^2$, for j = 1, …, n₀ (McCulloch and Searle, 2001, p.141). Following Subsection 3.1, the commensurate prior for β is proportional to N_p(β₀, diag{τ}⁻¹). Let θ denote the general parameter vector, θ = (β, β₀,ν, ν₀,λ). Assuming a flat prior for λ, the approximate joint posterior distribution of θ|τ, y, y₀ is proportional to

$$N_p(\mathit{\beta }\mid {\mathit{\beta }}_0,\mathit{diag}{\{\mathit{\tau }\}}^{-1})N_p\left\{{\mathit{\beta }}_0\mid {\widehat{\mathit{\beta }}}_0,{\left(X_0^T{\widehat{W}}_0{X}_0\right)}^{-1}\right\}\prod _{i=1}^n{f}_Y(y_i\mid \mathit{\beta },\lambda ).$$ (27)

After marginalizing over β₀, the precision matrix in (18) follows as,

$$V_{\mathit{\tau }}=\mathit{diag}\{\mathit{\tau }\}-\mathit{diag}\{\mathit{\tau }\}{\left(X_0^T{\widehat{W}}_0{X}_0+\mathit{diag}\{\mathit{\tau }\}\right)}^{-1}\mathit{diag}\{\mathit{\tau }\},$$ (28)

and the posterior distribution of β, λ|τ, y, y₀ is proportional to

$$N_p(\mathit{\beta }\mid {\widehat{\mathit{\beta }}}_0,V_{\mathit{\tau }}^{-1})\prod _{i=1}^n{f}_Y(y_i\mid \mathit{\beta },\lambda ).$$ (29)

Non-Gaussian data results in intractable non-conjugate full conditional distributions, therefore posterior inference requires alternative MCMC sampling methods (see e.g. Carlin and Louis, 2009), such as the Metropolis algorithm.

4.1.1 Binary response

Let y₀ and y denote the historical and current data such that y_0j ~ Ber {π₀(X_0j)}, π₀(X_0j) ∈ [0, 1], for j = 1, …, n₀, and y_i ~ Ber {π (X_i, d_i)}, π (X_i, d_i) ∈ [0, 1], for i = 1, …, n. The logistic link function transforms the expectations of y₀ and y such that $log\left\{\frac{{\pi }_0(X_0)}{1-{\pi }_0(X_0)}\right\}=X_0{\mathit{\beta }}_0$ and $log\left\{\frac{\pi (X,d)}{1-\pi (X,d)}\right\}=X\mathit{\beta }+\mathit{d}\lambda$. The diagonal elements of Ŵ₀ in (27) and (28) now consist of the estimated historical sampling variance, Ŵ_0jj = π̂₀(X_0j) {1 − π̂₀(X_0j)}, where π̂₀(X_0j) = (1 + e^{−X_0jβ̂₀})⁻¹. Assuming a flat prior for λ, the posterior distribution of β, λ|τ, y, y₀ is proportional to

$$N_p(\mathit{\beta }\mid {\widehat{\mathit{\beta }}}_0,V_{\mathit{\tau }}^{-1})\prod _{j=1}^n\pi {(X_j)}^{y_j}{\{1-\pi (X_j)\}}^{1-y_j}.$$

Sampling proceeds by Metropolis, though switching to a probit link function can lead to closed form full conditionals (Albert and Chib, 1993). Fúquene, Cook, and Pericchi (2009) propose an approach using a robust Cauchy prior for univariate logistic models.

4.1.2 Time-to-event response

Following the notation of Kalbfleisch and Prentice (2002, p.52), data for the historical and current trials consist of triples (t_0j, δ_0j, X_0j) for j = 1, …, n₀ and (t_i, δ_i, X_i) for i = 1, …, n. Here, t_0j, t_i > 0 are the observed, possibly censored, failure times; δ_0j, δ_i are noncensoring indicators (0 if censored, 1 if failure); and X_0j and X_i are row vectors of p covariates associated with historical subject j and current subject i. Let t̃_0j and t̃_i be the underlying uncensored failure times, with corresponding densities f(t_0j) and f(t_i). Denote the survival functions for the jth historical and ith current individuals by Pr(t̃_i > t) = F (t) and Pr(t̃_0j > t₀) = F (t₀).

Log-linear models are commonly used for analyzing time-to-event data. Suppose y₀ = log(t₀) = X₀β₀ + σ₀e₀ and y = log(t) = Xβ + dλ + σe where e₀ = (y₀ − X₀β₀)/σ₀ and e = (y − Xβ − d λ)/σ. Assuming that censoring times are conditionally independent of each other and of the independent failure times given X₀ and X (noninformative censoring), the historical and current data likelihoods follow as $L_0({\mathit{\beta }}_0,{\sigma }_0\mid {\mathit{y}}_0)={\prod }_{i=j}^{n_0}{\left\{\frac{1}{{\sigma }_0}f(e_{0j})\right\}}^{{\delta }_{0j}}F{(e_{0j})}^{1-{\delta }_{0j}}$ and $L(\mathit{\beta },\sigma \mid \mathit{y})={\prod }_{i=j}^n{\{\frac{1}{\sigma }f(e_i)\}}^{{\delta }_i}F{(e_i)}^{1-{\delta }_i}$. Assuming a flat prior for λ, the commensurate prior model follows from (27) where ML estimates for β₀ and σ₀ are computed numerically via Newton-Raphson or Fisher-Scoring; see Kalbfleisch and Prentice (2002, p.66–69). For discussion about censoring mechanisms see Kalbfleisch and Prentice (2002, p.193) or Klein and Moeschberger (2003, p.63).

Weibull regression arises when e₀ and e are assumed to follow the extreme value distribution, f(u) = exp {u − exp (u)}. This results in a parametric regression model which has both a proportional hazards and an accelerated failure-time representation. The hazard function, h(t) = −d log F(t)/dt, is monotone decreasing for shape parameter σ > 1, increasing for σ < 1, constant for σ = 1. We assume commensurate priors for both the regression coefficients, β, and log transformation of the shape parameter, σ. Let ${\mathit{\zeta }}_0={\{{\mathit{\beta }}_0^T,log({\sigma }_0)\}}^T$ and ζ = {β^T, log(σ)}^T denote column vectors of length p + 1. Let e₀, δ₀, and exp(e₀) − δ₀ denote vectors of length n₀ such that the jth element is equal to e_0j, δ_0j, and exp(e_0j) − δ_0j, j = 1, …, n₀. ML equations for the historical coefficients follow as $\frac{\partial log{L}_0}{\partial {\mathit{\beta }}_0}=\frac{1}{{\sigma }_0}{X}_0^T\{exp({\mathit{e}}_0)-{\mathit{\delta }}_0\}$ and $\frac{\partial log{L}_0}{\partial log({\sigma }_0)}={\sum }_{j=1}^{n_0}\{e_{0j}exp(e_{0j})-{\delta }_{0j}(e_{0j}+1)\}$. Let ê_0j = (y_0j − X_0jβ̂₀)/σ̂₀. The observed Fisher information matrix, Ψ̂₀(ζ̂₀), follows as

$${\widehat{\mathrm{\Psi }}}_0({\widehat{\mathit{\zeta }}}_0)=\left[\begin{array}{cc}{X}_0^T{\widehat{W}}_0{X}_0& X_0^T{\widehat{E}}_0\\ {\widehat{E}}_0^T{X}_0& {\sum }_{j=1}^{n_0}{\widehat{e}}_{0j}\{{\delta }_{0j}-({\widehat{e}}_{0j}+1)exp({\widehat{e}}_{0j})\}\end{array}\right],$$ (30)

where Ê₀ is the vector of length n₀ containing elements Ê_0j = (ê_0j +1) exp{ê_0j − log(σ̂₀)}− δ_0j/σ̂₀, and the diagonal elements of Ŵ₀ are ${\widehat{W}}_{0jj}=\frac{1}{{\widehat{\sigma }}_0^2}exp({\widehat{e}}_{0j})$, for j = 1, …, n₀ (see Breslow and Clayton, 1993). Assuming no initial prior information for ζ₀ and that the prior on λ is flat, the posterior distribution for ζ, λ|τ, y, y₀ follows directly from (29) by replacing $X_0^T{\widehat{W}}_0{X}_0$ in (27) and (28) with Ψ̂₀(ζ̂₀). Note that the exponential model is a special case where σ₀ = σ = 1, since this leads to probability density functions for t₀ and t following $f({\mathit{t}}_0)=\frac{1}{{\mathit{\mu }}_0}exp({\mathit{t}}_0/{\mathit{\mu }}_0)$ and $f(\mathit{t})=\frac{1}{\mathit{\mu }}exp(\mathit{t}/\mathit{\mu })$ where μ₀ = exp(X₀β₀) and μ = exp(Xβ + dλ); t₀/μ₀ is a vector of length n₀ with jth element equal to t_0j/exp(X_0jβ₀), and similarly, t/μ is a vector of length n with ith element equal to t_i/exp(X_iβ + d_iλ).

4.2 Mixed models

As with the general linear models in Section 3, we now extend our generalized linear model to the mixed model case. Following the notation of Subsection 3.2, let y_0j and y_i denote response vectors of lengths n_0j and n_i consisting of conditionally independent measurements given random effects u_0j and u_i, j = 1, …, m₀; i = 1, …, m, where u₀ and u are vectors of length m₀ and m. For generalized linear mixed models, we assume the conditional distributions of y₀ given u₀ and y given u have p.d.f.s from the exponential family, ${\mathit{y}}_{0j}\mid {\mathit{u}}_0\stackrel{\mathit{indep}}{\sim }{f}_{Y_0}({\mathit{y}}_{0j}\mid {\mathit{u}}_0)$ and ${\mathit{y}}_i\mid \mathit{u}\stackrel{\mathit{indep}}{\sim }{f}_Y({\mathit{y}}_i\mid \mathit{u})$, where log f_Y0 (y₀|u₀) and log f_Y (y_i|u) follow (24) and (25). In addition, assume that the random effects follow distributions u₀ ~ f_U0 (u₀) and u ~ f_U (u). The marginal likelihoods follow as $f_{Y_0}({\mathit{y}}_{0j})=\int {\prod }_{j=1}^{m_0}{f}_{Y_0}({\mathit{y}}_{0j}\mid {\mathit{u}}_0)f_{U_0}({\mathit{u}}_0)d_{{\mathit{u}}_0}$ and $f_Y({\mathit{y}}_i)=\int {\prod }_{i=1}^m{f}_Y({\mathit{y}}_i\mid \mathit{u})f_U(\mathit{u})d_{\mathit{u}}$.

Assuming that the conditional means are E (y₀|u₀) = μ₀ and E (y|u) = μ, let g(μ₀) = X₀β₀ + Z₀u₀ and g(μ) = Xβ + dλ + Zu, where g() is a known link function (note that Z₀, Z, X₀, X, d and parameters D, D₀ are defined in Subsection 3.2.2). Following Subsection 4.1 for normally distributed random effects, u₀ ~ N (0, D₀) and u ~ N (0, D), the posterior distribution of β, λ|τ, y, y₀, follows from (29) with Ŵ₀ in (27) and (28) replaced by ${({\widehat{W}}_0^{-1}+Z_0{\widehat{D}}_0{Z}_0^T)}^{-1}$. See McCulloch (1997), McCulloch and Searle (2001, p.263), or Breslow and Clayton (1993) for algorithms for computing ML estimates for fixed effects and prediction of random effects.

4.2.1 Binary response

Suppose that the historical responses follow y_0jk|u_0j ~ Ber {π₀(X_0j)}, where y_0jk denotes observation k for the jth patient, k = 1, …, n_0j, j = 1, …, m₀. The current responses follow y_ig|u_i ~ Ber {p(X_ig, d_i)}, where y_ig denotes observation g for the ith patient, g = 1, …, n_i, i = 1, …, m. Since the logit link function was discussed in Section 4.1.1, we will consider the probit link. Given u₀ ~ N (0, D₀), the probit uses the standard normal c.d.f., Φ(), to transform the means of y₀ and y such that π₀(X₀, Z₀) = Φ(β₀X₀ + Z₀u₀) and p(X, d, Z) = Φ(Xβ + dλ + Zu). The posterior distribution of β, λ|τ, y, y₀ follows from (29) by replacing Ŵ₀ in (27) and (28) with ${({\widehat{W}}_0^{-1}+Z_0{\widehat{D}}_0{Z}_0^T)}^{-1}$, and setting

$${\widehat{W}}_0=\mathit{diag}\left\{\frac{\varphi {(X_0{\widehat{\mathit{\beta }}}_0+Z_0{\widehat{\mathit{u}}}_0)}^2}{\mathrm{\Phi }(X_0{\widehat{\mathit{\beta }}}_0+Z_0{\widehat{\mathit{u}}}_0)\left\{1-\mathrm{\Phi }(X_0{\widehat{\mathit{\beta }}}_0+Z_0{\widehat{\mathit{u}}}_0)\right\}}\right\},$$

where ϕ() is the standard normal p.d.f. (McCulloch and Searle, 2001, p.136).

4.2.2 Count response

Suppose that the historical responses follow $y_{0jk}\mid u_{0j}\stackrel{\mathit{indep}}{\sim }\mathit{Poisson}({\mu }_{0jk})$, where log(μ0_jk) = X_0jkβ₀ + u_0j and $u_{0j}\stackrel{i.i.d.}{\sim }N(0,{\sigma }_{u_0}^2)$. Here, y_0jk denotes the kth count observed for the jth patient, where k = 1, …, n_0j and j = 1, …, m₀. Similarly, let y_ig denote the gth count observed for the ith patient, where $y_{ig}\mid u_i\stackrel{\mathit{indep}}{\sim }\mathit{Poisson}({\mu }_{ig})$, log(μ_ig) = X_igβ + u_g, and $u_g\stackrel{i.i.d.}{\sim }N(0,{\sigma }_u^2)$, for g = 1, …, n_i and i = 1, …, m. The posterior distribution of β, λ|τ, y, y₀ follows from (29) by replacing Ŵ₀ in (27) and (28) with ${({\widehat{W}}_0^{-1}+{\widehat{\sigma }}_{u0}^2{Z}_0{Z}_0^T)}^{-1}$, and setting

$${\widehat{W}}_0=\mathit{diag}\left\{exp(X_0{\widehat{\mathit{\beta }}}_0+{\widehat{\mathit{u}}}_0)\right\}.$$

5 Case study: analysis of successive colon cancer trials

In this section, we illustrate our method using data from two successive randomized controlled colorectal cancer clinical trials originally reported by Saltz et al. (2000) and Goldberg et al. (2004), respectively. The initial trial randomized N₀ = 683 patients with previously untreated metastatic colorectal cancer between May 1996 and May 1998 to one of three regimens: Irinotecan alone; Irinotecan and bolus Fluorouracil plus Leucovorin (IFL); or a regimen of Fluorouracil and Leucovorin (5FU/LV) (“standard therapy”). IFL resulted in significantly longer progression-free survival and overall survival than both Irinotecan alone and 5FU/LV and became the standard of care treatment (Saltz et al., 2000).

The subsequent trial compared three new (at the time) drug combinations in N = 795 patients with previously untreated metastatic colorectal cancer, randomized between May 1999 and April 2001. Patients in the first drug group received the current “standard therapy,” the IFL regimen identical to that used in the historical study. The second group received Oxaliplatin and infused Fluorouracil plus Leucovorin (abbreviated FOLFOX), while the third group received Irinotecan and Oxaliplatin (abbreviated IROX); both of these latter two regimens were new as of the beginning of the second trial.

Both trials recorded two bi-dimensional measurements on each tumor for each patient at regular cycles. The Saltz trial measured patients every 6 weeks for the first 24 weeks and every 12 weeks thereafter until death or disease progression, while the Goldberg trial measured every 6 weeks for the first 42 weeks, or until death or disease progression. We computed the sum of the longest diameter in cm (“ld sum”) for up to 9 tumors for each patient at baseline. In both trials, disease progression was defined as a 25% or greater increase in measurable tumor or the appearance of new lesions.

This section offers a fixed effects time-to-event analysis using the Weibull regression model presented in Subsection 4.1.2 to compare disease progression among the FOLFOX and IFL regimens. The historical data consists of the IFL treatment arm from the initial study, while the current data consists of patients randomized to IFL or FOLFOX in the subsequent trial. For simplicity, we omit data from the Irinotecan alone and 5FU/LV arms in the Saltz study, and the IROX arm in the Goldberg study. The model incorporates baseline ld sum as a predictor.

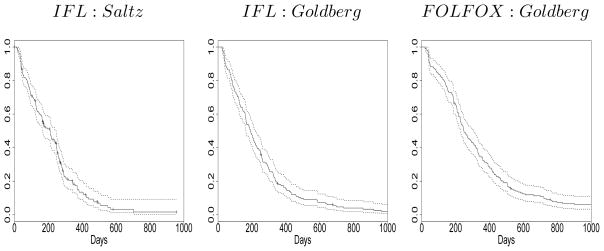
We restricted our analysis to patients that had measurable tumors and observed baseline covariates bringing the total sample size to 586: 224 historical and 362 current observations. Among the current patients, 176 are controls (IFL) and 186 are patients treated with the new regimen (FOLFOX). Figure 4 contains Kaplan-Meier estimated time to progression curves for subjects on each treatment regimen in both trials. The plots suggest that the time to progression experience for subjects on IFL was similar in both the Saltz (left panel) and Goldberg trials (center), and that FOLFOX (right) is associated with somewhat prolonged time-to-progression.

Figure 4.

Separate Kaplan-Meier curves for time to disease progression corresponding to subjects on IFL in the Saltz trial (left), IFL in the Goldberg trial (center), and FOLFOX in the Goldberg trial.

Following the log-linear model notation of Subsection 4.1.2 for progression times t₀ and t, let y₀ = X₀β₀ + σ₀e₀ and y = Xβ + dλ + σe, where y₀ = log(t₀) and y = log(t); here, X₀ and X are n₀ × 2 and n × 2 design matrices with columns corresponding to (1, ld sum at baseline), and d is the FOLFOX indicator. Thus, the β₀ and β parameters contain intercepts as well as a regression coefficient corresponding to the baseline covariate, while exp(λ) represents the acceleration factor associated with FOLFOX. Note that since F(t|d = 1) = F (te^λ|d = 0) for all t, a negative value is indicative of decreased survival. Exploratory data analysis on the covariate and age at baseline suggested that the trials enrolled patients from comparable populations. The first, second, and third quartiles for baseline tumor sum are 5, 8.5, 12.8 in the Saltz trial and 4.7, 7.9, 12.7 in the Goldberg trial; for age they are 54, 62, 69 in the Saltz trial and 53, 61, 69 in the Goldberg trial.

Table 4 summarizes results from separate and pooled classical linear regression fits to the historical (t₀, X₀) and current (t, X, d) data. The “current” values constitute a “no borrowing” analysis. Results from the current data alone suggest that the estimated acceleration factor corresponding to FOLFOX is highly significant at the 0.05 level. Point estimates (posterior means) and posterior standard deviations corresponding to both the Gaussian approximation and full commensurate prior models are provided in Table 5. The fully Bayesian spike and slab model uses the same hyperparameters for p(τ) that were used to produce Tables 2 and 3 in Section 2.4. For the EB model ${\tau }_j=1/{\nu }_j^{\ast }$, for j = 1, 2, and 3 denote the MMLEs of the commensurability parameters corresponding to the intercept, regression coefficient for ld sum at baseline, and log-shape parameters, respectively. The ${\nu }_j^{\ast }$ s were maximized over a restriction to the interval (0.005, 200), the same interval used in Section 2.3. Table 5 reveals that posterior inferences using the Gaussian approximated and full MCMC models provide congruous results in this context. Posterior distributions for the τs are highly right-skewed, with large standard deviations inducing compromises among the evidence supplied by the historical and current data.

Table 4.

Weibull model fits to colorectal cancer data n₀ = 224, n = 362.

	Separate analyses				Pooled analysis
	Historical		Current		est	sd
	est	sd	est	sd
Intercept	5.503	0.058	5.555	0.067	5.533	0.045
BL ld sum	−0.043	0.051	−0.115	0.045	−0.092	0.034
FOLFOX	–	–	0.417	0.092	0.453	0.077
log(σ)	−0.291	0.060	−0.153	0.039	−0.186	0.033

Table 5.

Commensurate prior Weibull model fits to colorectal cancer data n₀ = 224, n = 362. Gaussian approximate model (top), full model (bottom).

	EB		Approximate		Gamma(1, 0.01)
			spike & slab
	est	sd	est	sd	est	sd
Intercept	5.540	0.054	5.544	0.058	5.546	0.059
BL ld sum	−0.100	0.040	−0.103	0.041	−0.105	0.042
FOLFOX	0.436	0.084	0.434	0.085	0.432	0.087
log(σ)	−0.152	0.038	−0.159	0.039	−0.158	0.038
τ1	200	–	153.7	84.0	123.4	106.3
τ2	200	–	157.1	81.8	124.2	106.2
τ3	40.0	–	121.6	97.2	98.7	90.7

	EB		Full Model		Gamma(1, 0.01)
			spike & slab
	est	sd	est	sd	est	sd
Intercept	5.541	0.054	5.547	0.058	5.546	0.058
BL ld sum	−0.100	0.040	−0.103	0.042	−0.105	0.042
FOLFOX	0.435	0.085	0.431	0.086	0.432	0.085
log(σ)	−0.152	0.038	−0.158	0.038	−0.158	0.038
τ1	200	–	153.2	84.4	124.8	107.3
τ2	200	–	153.8	83.9	123.8	106.7
τ3	40.0	–	126.1	96.1	102.5	93.7

Incorporating the Saltz data into the analysis of the Goldberg trial using our proposed method leads to more precise parameter estimates (i.e., reductions to the posterior standard deviation for the FOLFOX effect of nearly 9%, 8%, and 5% for the EB, spike and slab, and gamma models, respectively). The two fully Bayesian commensurate prior analyses offer relatively similar amounts of borrowing of strength from the historical data. Moreover, these models provide considerably less borrowing of strength than that provide by pooling, which facilitates a 16% reduction in posterior standard deviation for estimating the FOLFOX effect. The EB procedure leads to more precise, naive estimates, and thus more borrowing of strength overall when compared to the fully Bayesian results. However, EB inference actually leads to less borrowing of strength from the historical data for estimating log(σ).

Note that our commensurate prior models estimate time-to-progression to be nearly exp(0.43) times larger on average in the FOLFOX group, and since the posteriors for log(σ) are less than 0, the hazard rates are increasing slightly over time. This finding is consistent with those of Goldberg et al. (2004), who determined FOLFOX to have superior time-to-progression and response rate compared to IFL.

6 Simulation study

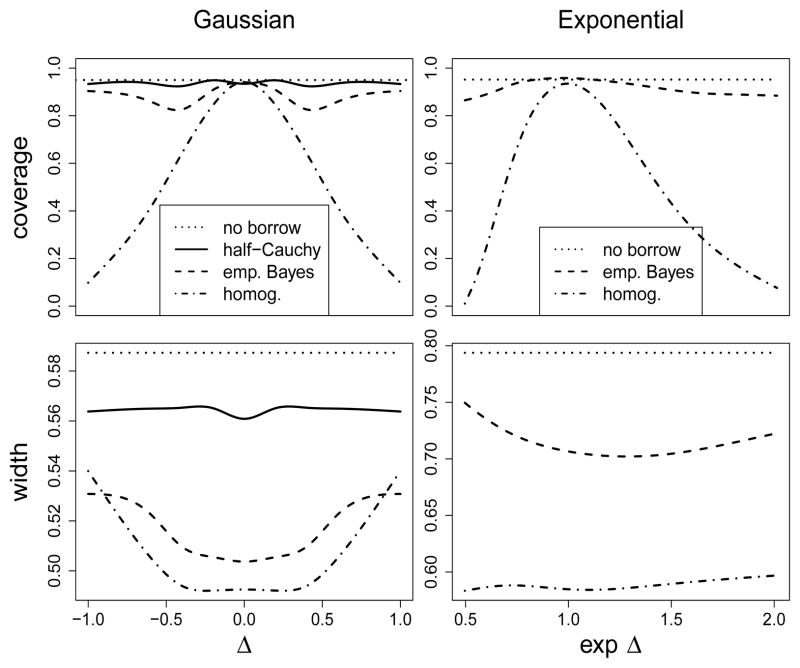
In this section we use simulation to evaluate the Bayesian and frequentist operating characteristics of our proposed empirical Bayesian commensurate prior model for the challenging case of one historical study. Figure 5 plots coverage and width of the 95% highest posterior density (HPD) intervals for λ by ${\mathrm{\Delta }}^{tr}={\mu }^{tr}-{\mu }_0^{tr}$ for the Gaussian (left) and exponential (right) time-to-event models described in Sections 3 and 4. Results for Gaussian data are compared for the no borrowing, half-Cauchy meta-analytic, EB commensurate, and homogeneity models under simulated data for n₀ = 90 historical patients, equal allocation of n = 180 current patients, and fixed true parameters, μ^tr = 0, and ${\sigma }^{tr}={\sigma }_0^{tr}=1$. Results for the exponential model are compared for the no borrowing, EB commensurate, and homogeneity models simulated for μ^tr = 2, n₀ = 200, and equal allocation of n = 100 current patients.

Figure 5.

Coverage and width of 95% HPD intervals for λ by Δ^tr or exp(Δ^tr) for Gaussian and exponential data for one historical study.

Figure 5 reveals that all four of the Gaussian models (left) provide 95% highest posterior density coverage and achieve their minimum interval widths when the historical data are unbiased, Δ^tr = 0. As |Δ^tr| > 0, we see that the interval widths increase. While coverage for the relatively conservative half-Cauchy models deviates little from the no borrowing model, the highly subjective full homogeneity model provides increasingly poorer coverage. The EB commensurate prior model offers a sensible compromise that offers more precision given lack of strong empirical evidence for heterogeneity, yet protects against poor coverage provided that the historical data is estimated to be highly biased. Results for the exponential model given in the right column of Figure 5 follow the same general trends. A referee encourages us to remind the reader that coverage probabilities of EB intervals are sometimes too small (Carlin and Louis, 2009, Chapter 5); we would expect our fully Bayesian spike and slab or gamma prior models would perform slightly better in this regard.

Next we present a sensitivity analysis for the four Gaussian models. Following Freedman et al. (1984), suppose the parameter space of λ^tr is partitioned into three intervals characterizing three true states of nature: λ^tr < −δ implies failure, −δ ≤ λ^tr ≤ δ implies equivalence, and λ^tr > δ implies efficacy. Suppose that the current trial analysis evaluates decision rules using posterior tail densities such that

$$\begin{array}{c}q(\lambda <-\delta \mid \mathit{y},{\mathit{y}}_0)>0.95,\text{failure}\\ q(\lambda \in [-\delta ,\delta ]\mid \mathit{y},{\mathit{y}}_0)>0.90,\text{equivalence}\\ q(\lambda >\delta \mid \mathit{y},{\mathit{y}}_0)>0.95,\text{efficacy}\\ \text{otherwise},\text{inconclusive}.\end{array}$$ (31)

We approximated the probability surfaces of the four stopping rules in (31) using simulation for a myriad of true values of ${\mathrm{\Delta }}^{tr}={\mu }^{tr}-{\mu }_0^{tr}$ and λ^tr for no borrowing, half-Cauchy meta-analytic, EB commensurate, and homogeneity models. We formulated a metric that facilitates comprehensive assessment of the four models by synthesizing the amount of probability allocated to the correct and incorrect decision spaces. Let 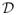= (y, y₀) denote the collection of current and historical response data, and let L(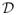|θ) denote the joint likelihood, where $\mathit{\theta }=(\mu ,\lambda ,\mathrm{\Delta },{\sigma }^2,{\sigma }_0^2)$. Let I(a) denote the indicator function of the event a, and let ϕ(·|θ^tr) denote the probability of a decision rule given a fixed set of parameters, θ^tr i.e.

$$\varphi (\lambda <-\delta \mid {\mathit{\theta }}^{tr})=\int I\{q(\lambda -\delta \mid \mathcal{D})>0.95\}L(\mathcal{D}\mid {\mathit{\theta }}^{tr})d\mathcal{D}.$$ (32)

For fixed true values σ^tr, ${\sigma }_0^{tr}$, and ${\mu }_0^{tr}$ the metric of comparison follows as

$$\begin{array}{l}M(c)={\int }_{-\infty }^{-\delta }{\int }_{-\infty }^{\infty }\varphi (\lambda <-\delta \mid {\mathrm{\Delta }}^{tr},{\lambda }^{tr})p({\mathrm{\Delta }}^{tr})p({\lambda }^{tr})d{\mathrm{\Delta }}^{tr}d{\lambda }^{tr}\\ +{\int }_{-\delta }^{\delta }{\int }_{-\infty }^{\infty }\varphi (\lambda \in [-\delta ,\delta ]\mid {\mathrm{\Delta }}^{tr},{\lambda }^{tr})p({\mathrm{\Delta }}^{tr})p({\lambda }^{tr})d{\mathrm{\Delta }}^{tr}d{\lambda }^{tr}\\ +{\int }_{\delta }^{\infty }{\int }_{-\infty }^{\infty }\varphi (\lambda >\delta \mid {\mathrm{\Delta }}^{tr},{\lambda }^{tr})p({\mathrm{\Delta }}^{tr})p({\lambda }^{tr})d{\mathrm{\Delta }}^{tr}d{\lambda }^{tr}\\ -\{{\int }_{-\infty }^{-\delta }{\int }_{-\infty }^{\infty }\varphi (\lambda >-\delta \mid {\mathrm{\Delta }}^{tr},{\lambda }^{tr})p({\mathrm{\Delta }}^{tr})p({\lambda }^{tr})d{\mathrm{\Delta }}^{tr}d{\lambda }^{tr}\\ +{\int }_{-\delta }^{\delta }{\int }_{-\infty }^{\infty }\varphi (\lambda <-\delta \cup \lambda >\delta \mid {\mathrm{\Delta }}^{tr},{\lambda }^{tr})p({\mathrm{\Delta }}^{tr})p({\lambda }^{tr})d{\mathrm{\Delta }}^{tr}d{\lambda }^{tr}\\ +{\int }_{\delta }^{\infty }{\int }_{-\infty }^{\infty }\varphi (\lambda <\delta \mid {\mathrm{\Delta }}^{tr},{\lambda }^{tr})p({\mathrm{\Delta }}^{tr})p({\lambda }^{tr})d{\mathrm{\Delta }}^{tr}d{\lambda }^{tr}\\ +c{\int }_{-\infty }^{\infty }{\int }_{-\infty }^{\infty }\varphi (\text{inconclusive}\mid {\mathrm{\Delta }}^{tr},{\lambda }^{tr})p({\mathrm{\Delta }}^{tr})p({\lambda }^{tr})d{\mathrm{\Delta }}^{tr}d{\lambda }^{tr}\}\end{array}$$ (33)

where c ∈ [0, 1] is a positive scalar that weights the relative importance of an inconclusive result. The metric M(c) ∈ [−1, 1], a generalized version of expected 0 – 1 loss, is evaluated for c = 1/2 and δ = 0.33 under prior p(Δ^tr) = N(0, s²), for three values of s: s = 0, 1, 30, characterizing likely degrees of bias. All results are computed for p(λ^tr) = N(0, 1/4). Larger values of M(c) indicate overall more desirable probability allocation among the four decision rules. The prior distributions on Δ^tr and λ^tr essentially weight the relative importance of different subsets of the decision rule probability surfaces.

Table 6 summarizes the simulation results for M(c) in (33). The top portion of the table contains results for the unrealistic case of a priori absolute certainty that the historical data is unbiased. In this scenario the highly subjective full homogeneity model exceeds our proposed EB commensurate model by 0.03. This occurs largely because borrowing of strength in this context yields unbiased results for λ. For the more likely cases when the a priori assessment of historical bias is more uncertain in the middle and bottom portions of Table 6, the EB commensurate model provides the best overall probability allocation as measured by M(c), while the highly subjective full homogeneity model provides the least desirable results. These results are sensitive to alternative weights we might subjectively assign to the outcomes we are penalizing.

Table 6.

Simulation results for M(c) and its components in (33) for p(Δ^tr) = N(0, s²) and c = 1/2.

	M(c)	s=0
		+Eff	+Fail	+Equi	−Eff	−Fail	−Equi	−Inc
no borrow	0.19	0.13	0.13	0.20	0.00	0.00	0.01	0.26
half-Cauchy	0.20	0.13	0.14	0.20	0.00	0.00	0.01	0.26
emp. Bayes	0.29	0.14	0.15	0.24	0.00	0.00	0.01	0.23
homog.	0.32	0.15	0.15	0.25	0.00	0.00	0.01	0.22
		s=1
no borrow	0.19	0.13	0.13	0.20	0.00	0.00	0.01	0.26
half-Cauchy	0.21	0.13	0.14	0.20	0.00	0.00	0.01	0.25
emp. Bayes	0.24	0.14	0.15	0.21	0.00	0.00	0.02	0.24
homog.	0.14	0.14	0.15	0.12	0.00	0.00	0.07	0.21
		s=30
no borrow	0.19	0.13	0.13	0.20	0.00	0.00	0.01	0.26
half-Cauchy	0.21	0.13	0.14	0.20	0.00	0.00	0.01	0.25
emp. Bayes	0.23	0.14	0.14	0.21	0.00	0.00	0.02	0.24
homog.	0.07	0.14	0.14	0.08	0.00	0.00	0.07	0.21

7 Discussion

In this paper, we provided empirical and fully Bayesian modifications of commensurate prior formulations (Hobbs et al., 2011), and extended the method to facilitate linear and generalized linear models. The proposed models are shown to lead to preposterior admissible estimators that facilitate alternative bias-variance trade-offs than those offered by pre-existing methodologies for incorporating historical data from a small number of historical studies. The method was also used to analyze data from two recent studies in colorectal cancer.

Future work looks toward extending the methodology to include time-dependent covariates, smoothed hazards, multiple events, Bayesian semi-parametric Cox models as e.g. Ibrahim, Chen, and Sinha (2001, p.47), and non-normal formulations of the commensurate prior itself. We are also currently pursuing the use of commensurate priors with adaptive randomization that allows the sample size or allocation ratio in the ongoing trial to be altered if this is warranted. For example, if historical and concurrent controls emerge as commensurate, we might assign fewer patients to the control group, thus enhancing the efficiency of the ongoing trial by imposing “information” balance.

Appendix A

Full conditional posterior distributions for β₀, σ, and σ₀ assuming noninformative priors for the commensurate prior linear model presented in Subsection 3.1 are as follows:

$$\begin{array}{l}q({\mathit{\beta }}_0\mid {\mathit{y}}_0,\mathit{\beta },{\sigma }_0^2,\mathit{\tau })\propto \\ N\left[{(X_0^T{X}_0/{\sigma }_0^2+\mathit{diag}\{\mathit{\tau }\})}^{-1}\left(X_0^T{X}_0{\widehat{\mathit{\beta }}}_0/{\sigma }_0^2+\mathit{diag}\{\mathit{\tau }\}\mathit{\beta }\right),{(X_0^T{X}_0/{\sigma }_0^2+\mathit{diag}\{\mathit{\tau }\})}^{-1}\right],\\ q({\sigma }^2\mid \mathit{y},\mathit{\beta },\lambda )\propto {\mathrm{\Gamma }}^{-1}\{(n-1)/2,{\Vert \mathit{y}-X\mathit{\beta }-\mathit{d}\lambda \Vert }^2/2\},\text{and}\\ q({\sigma }_0^2\mid {\mathit{y}}_0,{\mathit{\beta }}_0)\propto {\mathrm{\Gamma }}^{-1}\{(n_0-1)/2,{\Vert {\mathit{y}}_0-X_0{\mathit{\beta }}_0\Vert }^2/2\}.\end{array}$$

Appendix B

Here we present full conditional posterior distributions corresponding to the commensurate prior one-way random effects model presented in Subsection 3.2. Let

$${\widehat{\mu }}_{0,\mu }=\left[\left\{\frac{{\sum }_{j=1}^{m_0}{\sum }_{k=1}^{n_{0j}}{y}_{0jk}(1-r_{0j}^{-1})}{{\sum }_{j=1}^{m_0}{n}_{0j}(1-r_{0j}^{-1})}\right\}/\left\{\frac{{\sigma }_{\epsilon 0}^2}{{\sum }_{j=1}^{m_0}{n}_{0j}(1-r_{0j}^{-1})}\right\}+\tau \mu \right]/\left(\frac{{\sum }_{j=1}^{m_0}{n}_{0j}(1-r_{0j}^{-1})}{{\sigma }_{\epsilon 0}^2}+\tau \right)$$

and ${\mathrm{\sum }}_{0,\tau }=\frac{{\sum }_{j=1}^{m_0}{n}_{0j}(1-r_{0j}^{-1})}{{\sigma }_{\epsilon 0}^2}+\tau$. Full conditional posteriors for μ₀, λ, u, u₀, ${\sigma }_{\epsilon }^2,{\sigma }_{\epsilon 0}^2,{\sigma }_u^2$ and ${\sigma }_{u0}^2$ follow as:

$$\begin{array}{l}q({\mu }_0\mid {\mathit{y}}_0,\mu ,u_0,{\sigma }_{\epsilon 0}^2,{\sigma }_{u0}^2,\tau )\propto N\left({\widehat{\mu }}_{0,\mu },{\mathrm{\sum }}_{0,\tau }^{-1}\right),\\ q(\lambda \mid \mathit{y},\mathit{u},\mu ,{\sigma }_{\epsilon }^2,{\sigma }_u^2)\propto N\left(\frac{{\sum }_{i=1}^m{d}_i{\sum }_{g=1}^{n_i}\{y_{ig}-n_i(\mu +u_i)\}}{{\sum }_{i=1}^m{n}_i{d}_i},\frac{{\sigma }_{\epsilon }^2}{{\sum }_{i=1}^m{n}_i{d}_i}\right),\\ q(\mathit{u}\mid {\mathit{y}}_0,\lambda ,\mu ,{\sigma }_{\epsilon }^2,{\sigma }_u^2)\propto \prod _{i=1}^{m}N\left\{\frac{{\sigma }_u^2{\sum }_{g=1}^{n_i}\{y_{ig}-(\mu +d_i\lambda )\}}{n_i{\sigma }_u^2+{\sigma }_{\epsilon }^2},{\left(\frac{n_i}{{\sigma }_{\epsilon }^2}+\frac{1}{{\sigma }_u^2}\right)}^{-1}\right\},\\ q({\mathit{u}}_0\mid {\mathit{y}}_0,{\mu }_0,{\sigma }_{\epsilon 0}^2,{\sigma }_{u0}^2)\propto \prod _{j=1}^{m_0}N\left\{\frac{{\sigma }_{u0}^2{\sum }_{k=1}^{n_{0j}}(y_{0jk}-{\mu }_0)}{n_{0j}{\sigma }_{u0}^2+{\sigma }_{\epsilon 0}^2},{\left(\frac{n_{0j}}{{\sigma }_{\epsilon 0}^2}+\frac{1}{{\sigma }_{u0}^2}\right)}^{-1}\right\},\\ q({\sigma }_{\epsilon }^2\mid \mathit{y},\lambda ,\mu ,\mathit{u})\propto {\mathrm{\Gamma }}^{-1}\left(\frac{n-1}{2},\frac{{\sum }_{i=1}^m{\sum }_{g=1}^{n_i}{(y_{ig}-\mu -u_i-d_i\lambda )}^2}{2}\right),\\ q({\sigma }_{\epsilon 0}^2\mid {\mathit{y}}_0,{\mathit{u}}_0,{\mu }_0)\propto {\mathrm{\Gamma }}^{-1}\left(\frac{n_0-1}{2},\frac{{\sum }_{j=1}^{m_0}{\sum }_{k=1}^{n_{0j}}{(y_{0jk}-{\mu }_0-u_{0j})}^2}{2}\right),\\ q({\sigma }_u^2\mid \mathit{y},\mathit{u})\propto {\mathrm{\Gamma }}^{-1}\left(\frac{m-1}{2},\frac{{\sum }_{i=1}^m{u}_i^2}{2}\right),\text{and}\\ q({\sigma }_{u0}^2\mid {\mathit{y}}_0,{\mathit{u}}_0)\propto {\mathrm{\Gamma }}^{-1}\left(\frac{m_0-1}{2},\frac{{\sum }_{j=1}^m{u}_{0j}^2}{2}\right).\end{array}$$

Appendix C

Here we present full conditional posteriors for the general commensurate prior linear mixed model presented in Subsection 3.2. The full conditional posteriors for λ, β₀, u, u₀, D⁻¹, $D_0^{-1}$, R⁻¹, and $R_0^{-1}$ follow as:

$$\begin{array}{l}q(\lambda \mid \mathit{\beta },\mathit{u},R,\mathit{y})\propto N\left\{{({\mathit{d}}^T{R}^{-1}\mathit{d})}^{-1}{\mathit{d}}^T{R}^{-1}(\mathit{y}-X\mathit{\beta }-Z\mathit{u}),{({\mathit{d}}^T{R}^{-1}\mathit{d})}^{-1}\right\},\\ q({\mathit{\beta }}_0\mid {\mathit{y}}_0,\lambda ,\mathit{\beta },R_0,\mathit{\tau })\propto \\ N_p\left[{(X_0^T{\mathrm{\sum }}_0{X}_0+\mathit{diag}\{\mathit{\tau }\})}^{-1}\left(X_0^T{\mathrm{\sum }}_0{X}_0{\stackrel{\sim }{\mathit{\beta }}}_0+\mathit{diag}\{\mathit{\tau }\}\mathit{\beta }\right),{(X_0^T{\mathrm{\sum }}_0{X}_0+\mathit{diag}\{\mathit{\tau }\})}^{-1}\right]\\ q(\mathit{u}\mid \lambda ,\mathit{\beta },D,R,\mathit{y})\propto \\ N_m\left\{{(D^{-1}+Z^T{R}^{-1}Z)}^{-1}{Z}^T{R}^{-1}(\mathit{y}-X\mathit{\beta }-\mathit{d}\lambda ),{(D^{-1}+Z^T{R}^{-1}Z)}^{-1}\right\},\\ q({\mathit{u}}_0\mid {\mathit{\beta }}_0,D_0,R_0,{\mathit{y}}_0)\propto \\ N_{m0}\left\{{(D_0^{-1}+Z_0^T{R}_0^{-1}{Z}_0)}^{-1}{Z}_0^T{R}_0^{-1}({\mathit{y}}_0-X_0{\mathit{\beta }}_0),{(D_0^{-1}+Z_0^T{R}_0^{-1}{Z}_0)}^{-1}\right\},\\ q(D^{-1}\mid \lambda ,\mathit{\beta },\mathit{u},\mathit{y})\propto W\left\{\left(\mathit{u}{\mathit{u}}^T+\varphi \stackrel{\sim }{D}\right),m+\varphi \right\},\\ q(D_0^{-1}\mid {\mathit{\beta }}_0,{\mathit{u}}_0,{\mathit{y}}_0)\propto W\left\{\left({\mathit{u}}_0{\mathit{u}}_0^T+{\varphi }_0{\stackrel{\sim }{D}}_0\right),m_0+{\varphi }_0\right\},\\ q(R^{-1}\mid \lambda ,\mathit{\beta },\mathit{u},\mathit{y})\propto W\left[\left\{{\Vert \mathit{y}-X\mathit{\beta }-\mathit{d}\lambda -Z\mathit{u}\Vert }^2+\rho \stackrel{\sim }{R}\right\},n+\rho \right],\text{and}\\ q(R_0^{-1}\mid {\mathit{\beta }}_0,{\mathit{u}}_0,{\mathit{y}}_0)\propto W\left[\left\{{\Vert {\mathit{y}}_0-X_0{\mathit{\beta }}_0-Z_0{\mathit{u}}_0\Vert }^2+{\rho }_0{\stackrel{\sim }{R}}_0\right\},n_0+{\rho }_0\right],\end{array}$$

where || . || denotes the inner product.