Bridging gaps between statistical and mathematical modeling in ecology

Congratulations to Heisey and colleagues (2010) for an analysis of complex ecological data within a process-oriented framework and an equally thoughtful discussion of the ongoing challenges of linking process and pattern. Their work joins a growing literature linking modern statistical methods for describing patterns in data with expanded sets of ecologically-motivated mathematical models of population dynamics. My comments build on the authors’ framework and discussion to describe a continuum that (I feel) encompasses a conceptual path between process and pattern and illustrates how hierarchical models provide a convenient area within which to explore this continuum.

As pointed out by the authors, interactions between observed data and proposed models always operate in a tension between theoretical process and phenomenological pattern, a tension increased in the past by the relatively small intersection between individuals working in mathematical modeling and those working in statistical methodology, and the differences in training and “that’s-how-it’s-done” assumptions perpetuated within each group. Happily, this intersection is growing and a new literature is blossoming in the gap, influencing both the current and next generations of researchers on both sides of the fence. Hilborn and Mangel’s (1997) Ecological Detective set the stage for expanding the toolbox when, as their subtitle suggests, “confronting models with data.” This call has been followed up by ecological texts such as Ellner and Guckenheimer (2006), Clark (2007), and Bolker (2008) and statistical texts such as Clark and Gelfand (2006) and Royle and Dorazio (2008). These recent texts and related literature incorporate both sophisticated models and sophisticated statistical techniques while sidestepping the ultimate futility of uniquely inferring process from an observed pattern in favor of determining what new features the given data pattern allows us to learn about the underlying process.

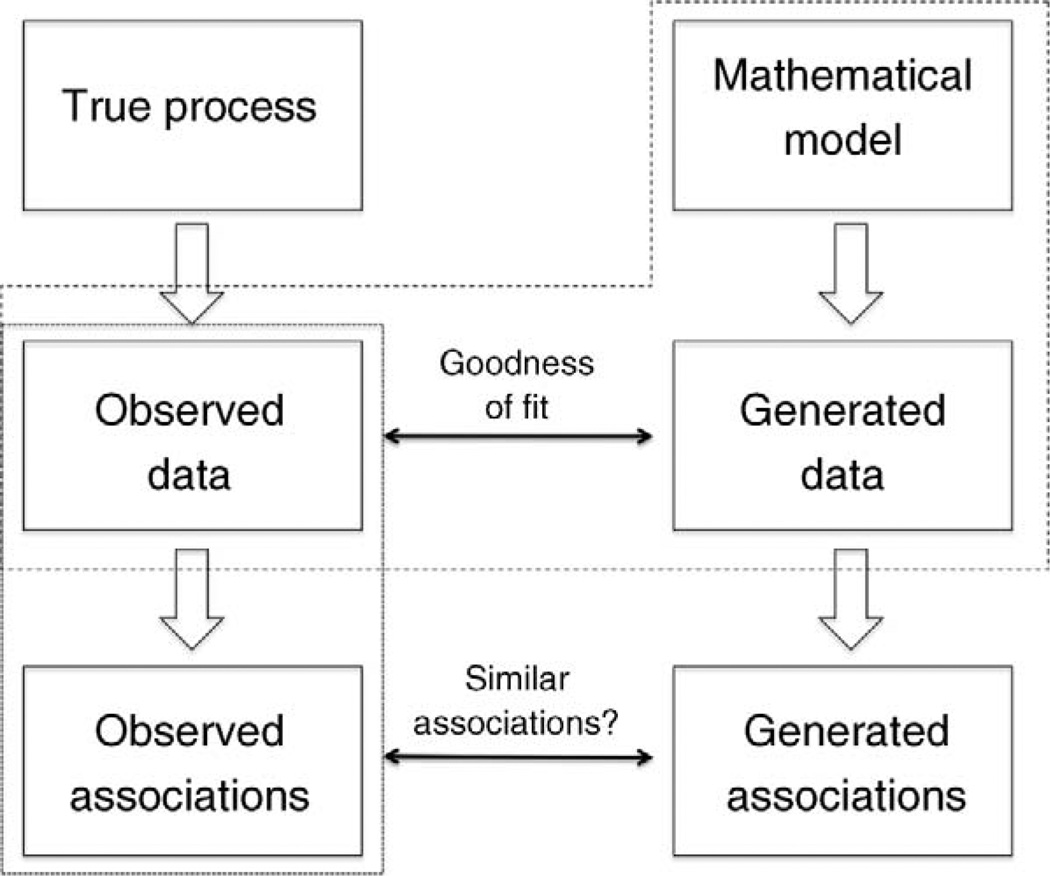
To illustrate this concept, consider Fig. 1. Starting in the box at the top left of the figure, the true (but unknown) process generates the observed data which contain various phenomenological associations that can be measured through traditional regressions, correlations, or other statistical summaries. The observed data and the observed associations within the data traditionally represent the worldview of a statistical approach to analysis. On the right hand side of the figure, we begin with a proposed theoretical model of reality, which generates data. The goal of the modeler is to have this proposed mathematical model be as representative of the true process as possible (to a level of acceptable generality). The generated data may be compared with data observed by the modeler or reported in the literature and the appropriateness of the proposed theoretical model typically is assessed by comparing the generated data to the observed data via statistical tests of goodness-of-fit or through likelihood methods. The dashed box in Fig. 1 represents this traditional worldview of the mathematical modeler. A detailed assessment of the phenomenological associations in either the observed or the generated data is often missing in this approach. While clearly an oversimplification, Fig. 1 suggests that a traditional statistical approach tends to ignore process in favor of a detailed description of pattern in the data and the revealed associations therein, while a traditional modeling approach tends to ignore pattern beyond that readily apparent in basic summaries of the data.

Fig. 1.

Potential links between statistical and modeling viewpoints. Solid-line boxes indicate elements of the process-to-pattern flow for a real system (left side) and a modeled system (right side). Dotted boxes outline the elements of primary concern to traditional mathematical modelers (model to generated data to observed data) and to traditional statistical modelers (observed data to observed associations). Double-headed arrows indicate areas of traditional (goodness of fit) and potential (similar associations?) application of statistical comparisons to assess reliability and accuracy of modeled outcomes.

As illustrated by Heisey et al., hierarchical models are well-suited to fill the gap between mathematical models of process and statistical summaries of pattern and such models provide a flexible set of tools for both modelers and statisticians. A very general framework illustrating this is provided by Berliner (1996) and expanded in Berliner et al. (2000), with an excellent overview provided by Wikle (2003). The basic frame-work involves three stages of the model: the data model, the process model, and the parameter model. The three stages are linked hierarchically as follows: first, the probability distribution of any possibly observed data is dependent on the process and some parameters ([data | process, data parameters]), next, the probability of any given process is a function of process parameters ([process | process parameters]), and, third any prior information regarding data or process parameters can be expressed in the distribution [data parameters, process parameters] using bracket notation to denote any general probability distribution. The hierarchical structure allows us to draw inference on data and process parameters via the posterior distribution: [data parameters, process parameters | data]. A particularly nice feature of this formulation is the link between the term “parameters” in an inverse problem setting (termed “process parameters” in Berliner’s setting) and the different use of the term “parameters” in direct modeling (“data parameters” in Berliner’s nomenclature). Note that the structure is fairly standard, but its effective implementation can be far from routine, often involving complex computing to implement.

While the Berliner structure is an attractive conceptual link between data (pattern) and process, in real applications such as that of the authors, the hierarchical structure also allows a mechanism for building a bridge between pattern and process, a bridge composed of probabilistic elements to summarize the impact of unobserved elements and/or data restrictions. Most often these elements are defined as random effects which induce, say, similarity between repeated observations on the same experimental unit or spatial correlation between observations taken at neighboring locations. Such random effects fit into the general framework above where the collection of data parameters includes the random effects, i.e., [data | process, data parameters] can be expanded to read: [data | process, data parameters, random effects][random effects | random effect parameters]. In this setting the random effects reflect an intermediate model structure bridging the gap between process and data to reflect, for example, spatial correlation between observed data elements via a spatial model for [random effects | random effect parameters]. These random effects may “soak up” elements of the process that are not readily observed in the data, yet are elements that influence observations nonetheless. The conditionally autoregressive (CAR) model is an example: CAR random effects allow spatial similarity between observations, similarity that may (on the process level) be due to local behavior that reaches across regional boundaries. The CAR model is not a direct process model of such features, rather the CAR model is flexible enough to capture the resulting impact of such features as best it can. In other words, the random effects may not capture the process directly (the process is not a CAR model) but instead they capture additional echoes of the process within the observed data by adding another layer or texture to the pattern.

While the value of hierarchical formulations is generally recognized, some discussion remains regarding the appropriateness of Bayesian or classical implementations. Briefly, in addition to the role of prior distributions, the two approaches also differ on which components comprise the likelihood. For the classical statistician, the likelihood includes the distribution of the data and the distributions of the random effects. For the Bayesian, the random effect distribution represents a first level of prior distributions. While the distinction is primarily definitional, it reflects a distinction between the goals and approaches typical to each approach. That is, the Bayesian maintains a relatively simpler likelihood often comprised of conditionally independent components, while the classical statistician incorporates the dependencies induced by random effects into the likelihood to be maximized. The authors point out that an advantage of a Bayesian formulation is that it allows for model-specified motivation of penalties to the likelihood resulting from random effects and a transparent mechanism for data to inform on the level of smoothing.

Regardless of mode of implementation, the hierarchical framework clarifies that all inference involves an intersection of available data, proposed models (statistical and mathematical), and associated assumptions. When all three elements align, model-based inference provides analytic possibilities that expand farther than design-based analysis in complex observational settings, but it is important to stress that model-based inference will only go as far as the underlying models allow. That is, a complex model structure allows complex inference, but only within the possibilities allowed by the models, data, and assumptions. For instance, consider the authors’ use of CAR priors to allow spatial smoothing. CAR models are flexible in allowing spatial correlation among observations, but CAR models are also dependent on the underlying neighborhood structure and the geographic units under consideration. In particular, CAR models do not scale up or down in space and it is difficult to use CAR-based results to transfer results from the relatively large regions under consideration in the authors’ analysis to either smaller or larger subdivisions of the study area. The authors’ choice of regions has some advantages in terms of the palatability some simplifying assumptions, namely, assumptions of locational accuracy limited to the scale of relatively large areas and assumptions of no animal movement between regions (a result of the assumption of a constant hazard over the lifetime of an individual animal). However, scaling the process up or down will require both a redefinition of the process model (to address the situation where these assumptions are no longer realistic) and a different spatial structure.

This line of thought leads to a few specific comments regarding the authors’ analysis. First, does frailty represent part of the process or a random effect to better describe the pattern? From the discussion above, I argue that frailty serves to build a better bridge between pattern and process, but it is not inherently a model of process. I feel that frailty allows the statistical model to move closer to the underlying process but it still involves a description of phenomenological pattern observed in the data. It provides a better and more informative description, to be sure, but not a complete solution to the puzzle. Second, the authors’ decision to work with the cumulative hazard has the advantage of parameterizing the model at the level desired for conclusions, not necessarily at the finest level possible. This choice defines the process at a level where the model will inform directly on the impact of proposed actions, rather than at the individual animal/environment level at which the disease operates (e.g., individual-based modeling as in Grimm and Railsback [2005]). In short, as illustrated by the authors, one parameterizes initially for process, but should be willing to reparameterize as needed for analytic convenience or computational efficiency, provided one can get back to the process parameters of interest. Third, the authors’ discussion of predicted declines illustrates that, even though inference is based on a process-defined model, our conclusions often involve describing a phenomenological pattern in the results through the lens of the fitted model.

In conclusion, I applaud the authors’ thoughtful work in better linking process to pattern. While no single analysis will completely reveal process from pattern, analyses such as these illustrate how process-defined structures and inference based on hierarchical elements can work together to provide a longer, more stable bridge between the two.