Complementary ensemble clustering of biomedical data

Abstract

The rapidly growing availability of electronic biomedical data has increased the need for innovative data mining methods. Clustering in particular has been an active area of research in many different application areas, with existing clustering algorithms mostly focusing on one modality or representation of the data. Complementary ensemble clustering (CEC) is a recently introduced framework in which Kmeans is applied to a weighted, linear combination of the coassociation matrices obtained from separate ensemble clustering of different data modalities. The strength of CEC is its extraction of information from multiple aspects of the data when forming the final clusters. This study assesses the utility of CEC in biomedical data, which often have multiple data modalities, e.g., text and images, by applying CEC to two distinct biomedical datasets (PubMed images and radiology reports) that each have two modalities. Referent to five different clustering approaches based on the Kmeans algorithm, CEC exhibited equal or better performance in the metrics of micro-averaged precision and Normalized Mutual Information across both datasets. The reference methods included clustering of single modalities as well as ensemble clustering of separate and merged data modalities. Our experimental results suggest that CEC is equivalent or more efficient than comparable Kmeans based clustering methods using either single or merged data modalities.

1. Introduction

Clustering is the arrangement of objects into groups (i.e., the clusters) wherein the objects in the same cluster are more similar (in one or more characteristics) than those in other clusters, and represents an important branch of unsupervised learning. Clustering [1–9] has been an active area of research in data mining and machine learning due to the rapidly growing data in different domains such as biology and clinical medicine. In biology, for instance, there is an avalanche of data from novel high throughput and imaging technologies. When applied to cancer images, clustering has been effective in identifying malignant and normal breast images [10]. Biomedical publications often present the results of biological experiments in figures and graphs that feature detailed, explanatory footnotes and captions. This annotation comprises a simple, textual representation of the images. In the clinical literature, a new semantic representation has evolved as a result of mapping the words in physicians’ clinical notes to the corresponding semantic descriptors in the Unified Medical Language System (UMLS). Each representation of the data, e.g. images, captions and semantic descriptors, is a unique data modality generated by a particular process wherein the objects have different features, structure and dimensionality. Although each data modality can be used to separately define clusters, differential encoding of the features of each modality generates assignment variability which can be interpreted as noise in the clustering process. As a result, the partitions obtained from clustering around one data modality will not necessarily be the same as those obtained from clustering around a different modality. In this discussion we explore alternative methods of building clusters around the complementary data modalities of a particular dataset to obtain more cohesive clusters. Unlike algorithms which cluster on a single data modality, complementary ensemble clustering (CEC) [6] creates clusters by extracting information from completely different domains of information that describe the same data.

There have been recent efforts to perform multiple modal clustering. Chen et al. [11] demonstrated a coclustering method using textual data that employs non-negative matrix factorization (NMF) that draws from two data modalities: textual documents and their corresponding categories. Their method, however, is semisupervised and requires user input to allow the algorithm to “learn” the distance metric. Comar et al. [12] proposed the joint clustering of multiple social networks to identify cohesive communities characterized by reduced levels of noise. Ensemble clustering on one modality [4,5,9,13,14,17] has been shown to be effective for improving the robustness and stability of clustering results. It aggregates different clusters of a single data modality in a coassociation matrix that measures the number of times each pair of data points is placed into the same cluster. In contrast, complementary ensemble clustering (CEC) draws information from ensemble clusters pertaining to complementary data modalities, thereby facilitating the exploitation of different aspects of the data while simultaneously reducing the distortion characteristic of clustering on a single modality. By integrating data from the two separate, complementary domains, CEC constructs a coassociation matrix that more clearly identifies the underlying clusters in a given dataset. CEC can be useful for any data described with multiple sources of information, i.e., the complementary modalities. We use CEC to enhance the performance of the Yale Image Finder YIF [15], an image retrieval tool developed by our lab members. YIF supports keyword queries based on images’ captions as well as on their visual features. We are investigating different means to enhance the usability of our system, such as organizing the results by image type. Rodriguez-Esteban and Iossivof [16] have proposed the use of supervised machine learning to classify images by their type (gels, diagrams etc.), and have presented a system which lets users make explicit choices when submitting a search query. We aim to achieve a similar goal in YIF by replacing its search criteria with CEC, which will group the images based on their type. We demonstrate the utility of CEC by applying it to two clinical datasets that each has information from two modalities. The first dataset is a subset of the YIF database that contains images and their corresponding text captions. The second features textual notes reported by a clinical radiologist and their corresponding semantic descriptors.

When CEC was introduced it was demonstrated using two benchmark datasets whose data modalities were both text based. The major contribution of this paper is its application of CEC to biomedical datasets, which often possess multiple data dimensions that are not restricted to text. The chief advantage of CEC is enhanced clustering via the exploitation of information from complementary data modalities.

The remainder of this paper is organized as follows. Section 2 describes related work on ensemble clustering. A brief, conceptual derivation of CEC is presented in Section 3. Section 5 presents experimental results and Section 6 provides summary remarks.

2. Background

Data clustering is a very difficult inverse problem and is ill posed in the sense that numerous clustering algorithms yield different partitions. Ensemble clustering [4–6,8,9,13,14] aggregates a number of clustering solutions obtained for a particular dataset in order to produce an overall clustering scheme with less distortion. It has proven particularly effective for improving the robustness and stability of clustering results. Ensemble clustering methods use one or more clustering algorithms and variations of the associated clustering parameters to yield a single, coassociation matrix that incorporates the incidence matrices of the distinct clustering solutions. In Ref. [4] Fred derived a consistent data partition by examining the coassociation matrix of clustering partitions based on majority voting. The clusters are populated with objects whose coassociation matrix values exceed a fixed threshold. Instead of comparing coassociation values with a fixed threshold, Fred and Jain [5], form partitions by applying single linkage clustering to the coassociation matrix. In related work Greene et al. [13] have shown that both the generation of the ensemble clusters and the specific base clustering algorithm have major effects on the efficiency of ensemble clustering. Several studies have investigated this issue. For instance Kuncheva and Hadjitodorov [14] proposed randomly choosing the number of anticipated clusters and overproducing them for every ensemble member. Their method increased the spread of the diversity within the ensemble, subsequently leading to clustering with less noise. Instead of using the coassociation matrix, Topchy et al. [8] achieved ensemble clustering from a solution of the maximum likelihood problem for a finite mixture model of the ensemble of partitions. The space of cluster labels is assumed to follow a mixture of multivariate multinomial distributions.

3. Methods

This section describes complementary ensemble clustering (CEC), a recently introduced method [6] for extracting information from different data modalities through an enhanced form of ensemble clustering. Ensemble clustering extracts information from different clusterings of a given data modality based on one or many clustering algorithms and their corresponding parameters. Our implementation of single modality ensemble clustering employs the Kmeans algorithm, a popular clustering method that partitions a set of data points into k clusters wherein each object is assigned to the cluster with the nearest multivariate mean. In each iteration of the ensemble the Kmeans algorithm produces a clustering solution that is encoded into an incidence matrix based on a random sample of the features that describe a particular modality [14]. The incidence matrices of each iteration are subsequently aggregated into a coassociation matrix. Once all the iterations are completed, we again apply Kmeans to the values residing in the coassociation matrix to derive component clusters of that particular data modality. We provide an overview of the technical details of single modality ensemble clustering in the next section.

3.1. Single modality ensemble clustering

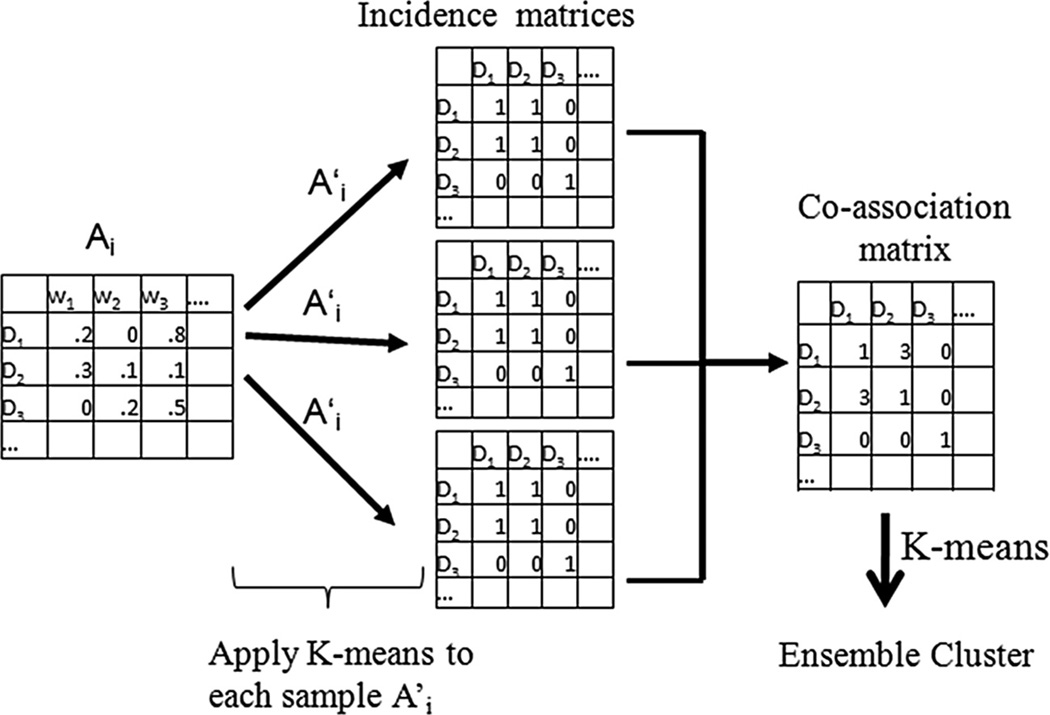
A vector space model is used to represent the data where each data point is represented by a vector. The collection of these vectors comprises the data matrix. Let A_i be a data matrix that corresponds to a single data modality i. Different types of information can be encoded in this matrix relevant to the nature of the corresponding data modality. For example, the frequencies of the words are encountered for each text fragment in the text data while correlation, inertia and density are computed to summarize the visual representation of the image data. A single modality ensemble E_i is generated by repeatedly applying Kmeans to ${\mathit{A}}_{\mathit{i}}^{\prime }$ (includes a subset of the features of A_i) and aggregating the resulting incidence matrices into the coassociation matrix S_i. For each clustering solution, i.e., each iteration of the ensemble, the number of features in ${\mathit{A}}_{\mathit{i}}^{\prime }$ is randomly set between (m/2) and (m − 1), where m is the total number of features that are randomly sampled. The coassociation matrix shows the number of times a pair of data points is assigned to the same cluster in the ensemble. It effectively encodes the likelihood that two data points belong to the same cluster. Formally, it is iteratively computed as follows:

$$S_i^{(t+1)}=S_i^{(t)}+C_i^{(t)}{C}_i^{(t)T}$$ (1)

where the matrix product $C_i^{(t)}{C}_i^{(t)T}$ is a binary 0/1 matrix that indicates whether a pair of objects belongs to the same cluster during the tth iteration of the ensemble. The matrix product $C_i^{(t)}{C}_i^{(t)T}$, is also known as the incidence matrix in the literature. The incidence matrices are not stored in our implementation because their contents are contained in the coassociation matrix. A second application of Kmeans to the final coassociation matrix S_i yields the final clusters of the ensemble cluster E_i. This result is necessary to evaluate the performance of CEC. Fig. 1 illustrates the single modality ensemble clustering approach.

Fig. 1.

Single data modality ensemble clustering.

3.2. Complementary ensemble clustering (CEC)

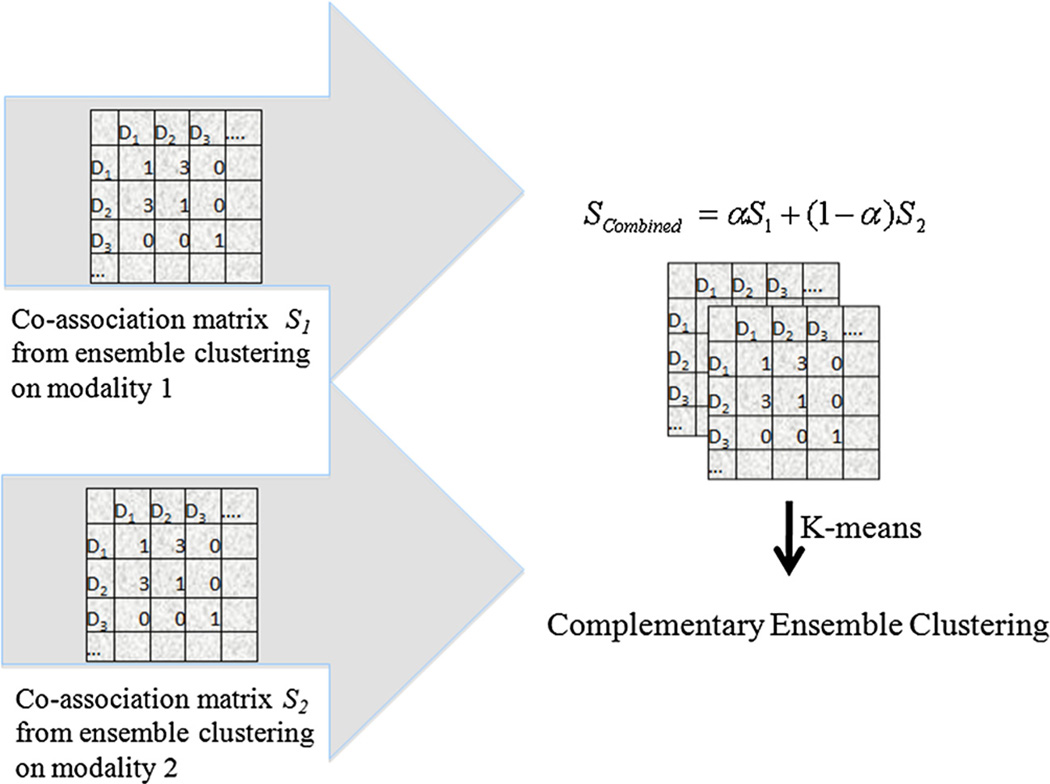
CEC is an extension of ensemble clustering [6] that combines the coassociation matrices of ensemble clusters from different modalities into one aggregate coassociation matrix that is subsequently used for obtaining the consensus clusterings. Specifically, the joint coassociation matrix is computed by adding the coassociation matrices of the different data modalities. In effect, each modality of the data contributes a weighted proportion of the overall clustering coassociation matrix.

$$S_{\mathit{\text{combined}}}={\alpha }_1{S}_1+{\alpha }_2{S}_2+\cdots +{\alpha }_n{S}_n$$ (2)

where α is a parameter that governs the weight of each modality and n is the total number of data modalities. Applying Kmeans to the combined coassociation matrix S_combined yields the final clusters. Fig. 2 describes CEC for two modalities.

Fig. 2.

Complementary ensemble clustering of two modalities.

The CEC framework is an incremental generalization of our previous work [6], however the previous algorithm generates a weighted co-association matrix for a single data modality. Specifically, each incidence matrix is weighted based on the quality of its respective Kmeans solution before being added to the coassociation matrix. In our algorithm below, we skipped the calculation of the weighting factor since it increases the computational complexity of the algorithm and requires more resources, especially for applications with big datasets such as those typically found in the medical domain. The pseudo code of our algorithm is summarized below and details are explained in the following sections.

Algorithm 1.

Inputs: n: number of data modalities, Ai: one data

modality, i={1, 2, …,n}, k: number of clusters, Max.:

maximum number of iterations in an ensemble

Outputs: Clusters C.

1. for each data modality Ai

for j = 1 to Max do

a. Cj ← KmeansCluster(Ai, k)

b. Si = Si ∪ {Cj}

end

2. Scombined ← Combine(S1, S2, …,Sn)

3. C ← KmeansCluster(Scombined, k)

3.3. Ensemble clustering of merged modalities

In order to compare CEC with a similar method that draws information from multiple data modalities, as a comparative approach we computed the ensemble clusters of the merged modalities. In this method, the data matrices A₁ and A₂ are first combined, whereupon ensemble clustering is applied to the combined matrix. This contrasts with CEC, wherein the coassociation matrices are first generated from each data modality separately and subsequently combined. The performance of the two methods depends on their respective emphases on forming a complementary ensemble cluster from various modalities versus combining different features of the data modalities prior to the formation of clusters.

3.4. Datasets

We evaluated CEC on two biomedical datasets and demonstrated its effectiveness by comparing its output clusters with the two sets of ensemble clusters computed for each individual data modality. Furthermore, we compare CEC with classic Kmeans of the full data sample and with the ensemble clustering of the two modalities merged.

3.4.1. Pubmed images dataset

This is a collection of articles from the digital archives of Pub-Med Central (PMC). A set of 3000 images were extracted from these articles. Some of these images, however, did not have captions. Images with no captions were dropped from the study and 2607 were retained. The sample includes images with multiple panels (subgraphs) as well as single panels. The images in the dataset were classified into five different categories by annotators with domain expertise. Discrepancies among the annotators were resolved by assigning the image to the category receiving the majority votes. The following image categories were used in the study: experimental, graph, diagram, clinical and others. Experimental images were defined as those depicting gel electrophoresis, fluorescence microscopy, or tissue experimental results. Graph images include bar, line, curve, or scatter graphs, while diagrams are comprised of pathway representations, flowcharts and protein structures. Clinical images correspond to various medical imaging scans (e.g. Magnetic Resonance Imaging MRI, X-ray, Computed Axial Tomography CAT). The final category “others” contains images that do not belong to any of the above categories such as screen snapshots and photographs. Table 1 shows the distribution of images across the five categories. We generated two modalities for the images. In one modality the images are represented using the pictorial and textural features computed using the Haralick method [18]. The other modality is a Bag of Words (BOWs) [19] representation generated from the captions of the images.

Table 1.

Pubmed images dataset. Distribution of images across the dataset.

Image type	Number of images
Experimental	564
Graph	1131
Diagram	645
Clinical	86
Others	181

3.4.2. Radiology reports dataset

This second dataset consists of radiology reports collected from clinical records of patients for research purposes. The radiology reports were annotated by domain experts and classified into four categories as shown in Table 2: abdominal MRI, abdominal CAT, abdominal ultrasound and non abdominal radiology reports.

Table 2.

Radiology reports dataset. Classes and their distributions.

Radiology report type	Number of reports
Abdominal CAT	486
Abdominal MRI	35
Abdominal Ultrasound	248
Non Abdominal	500

MRI: Magnetic Resonance Imaging.

CAT: Computed Axial Tomography.

These reports are represented using two data modalities: Textual features BOW and Bag of Concepts (BOCs). In the BOW modality, the reports are represented using the original words that appear in the clinical narratives and are weighted by frequency.

In the BOC modality, the vectors are indexed by semantic concepts derived from cTAKES [20]; a natural language processing tool that maps text to concepts from the UMLS ontology.

3.5. Evaluation metrics

The clustering results are evaluated by comparing to gold standard annotations of images and radiology reports. A cluster is annotated by the class label of its majority samples. We use two measures to evaluate the quality of the clusters: micro-averaged precision and Normalized Mutual Information (NMI). Micro-averaged precision is an average over all data points whose default gives higher weight to those classes with many data points, and is computed as follows:

$$\mathit{\text{Micro Averaged Precision}}=\sum _{i=1}^{k}T{P}_i/\sum _{j=1}^k(T{P}_j+F{P}_j)$$ (3)

where TP is true positive, FP is false positive, and k is the number of clusters. The second metric is Normalized Mutual Information (NMI) which is defined as follows:

$$NMI=I(X;Y)/(\text{log}k+\text{log}c)$$ (4)

where c is the number of classes, X corresponds to the cluster assignments and Y to the class labels. I(X;Y) is the mutual information shared by the classes and the clusters. NMI measures the amount of information shared between X and Y, i.e. the amount of information by which our knowledge about the classes increases upon definition of the clusters.

4. Results

We tested our method using datasets with two modalities each. Six clustering solutions were computed for each dataset: namely, Kmeans clustering of each modality, separate ensemble clustering of each modality, ensemble clustering of the merged modalities, and finally complementary ensemble clustering (CEC).

4.1. Pubmed images data

Two modalities of the images were utilized for clustering. In the first modality the images are represented using the pictorial and textural features of the Haralick method [18], in which the contents of an image were summarized over the following 13 features: Energy, Correlation, Inertia, Entropy, Inverse Difference Moment, Sum Average, Sum Variance, Sum Entropy, Difference Average, Difference Variance, Difference Entropy, and Information measures of correlation 1 and correlation 2. For computational details please refer to [18,21]. The Haralick features of all images are stored in the Haralick matrix A₁. The second modality was the use of words and phrases within the captions corresponding to the images as summarized by the Bag of Words (BOW) approach [19].

Based on our analysis, we observed that not all the Haralick features are equally suited for representing the different image types, i.e. one or more of the Haralick features may be sufficient to summarize the contents of a specific image type. Moreover different combinations of the Haralick features led to different insights about the same image. Ensemble clustering, which is based on the aggregation of different clustering solutions by taking random samples of the features in each solution, adjusts for this sampling related issue. Ensemble clustering was applied to the Haralick matrix A₁ that represents the images to produce the clustering solutions contained within EnsembleHaralick E₁. Extracted from the corresponding captions of the images, the BOW modality is stored in a matrix called the images captions matrix A₂, in which the frequencies of the words indicate their weights. Note that the stop words are removed from the captions and the Porter stemmer [22] and TFIDF [23] are applied for word normalization. The captions Ensemble Cluster, E₂, is then generated by applying ensemble clustering to the captions matrix A₂. Both ensemble clusters E₁ and E₂ are each composed of 10 iterated solutions. We have noticed that increasing the number of iterations beyond 10 does not tend to improve the results of the ensemble cluster substantially. The second modality was the use of words and phrases within the captions corresponding to the images as summarized in the Bag of Words (BOWs) approach [19]. Table 3 gives a comparison of the performance of several clustering methods: Kmeans clusters of each data modality, the cluster ensembles of each data modality, the ensemble clustering of merged modalities, i.e., EnsembleMerged, and CEC. Recall that in the EnsembleMerged method the data matrices A₁ and A₂ are first combined and ensemble clustering is subsequently applied to the combined matrix. This method differs from CEC, which generates separate ensemble clusters of each data modality prior to forming a linear combination of their corresponding coassociation matrices. We observed a marked improvement in NMI and micro-averaged precision with CEC, which achieved values of NMI and micro-averaged precision that were 41% and 32% better, respectively, referent to EnsembleMerged. Unlike EnsembleMerged, which had worse performance than EnsembleCaptions, CEC outperformed the single modality ensemble clusters (EnsembleCaptions and EnsembleHaralick) in NMI while tying EnsembleCaptions for best micro-averaged precision. While forming the complementary ensemble clusters, the coassociation matrix corresponding to EnsembleCaptions was assigned a higher weight than the EnsembleHaralick, i.e., α = 0.8. For want of a gold standard of annotation, this value of α was learned empirically. However, if the annotations are not available, different heuristics can be applied to optimize α. One possibility is to weight on the respective quality of the ensemble clusters yielded by discrete data modalities, with the ensemble cluster with lowest distortion receiving highest weight (greatest α). Another possibility is to combine the ensemble clusters with different values of α and choose the value of α that yields the better consensus clustering of the combined ensemble.

Table 3.

Results of the different clustering methods for the Pubmed images data.

Method descriptor	Clustering algorithm	Data modality utilized	Micro-Averaged Precision* (95% confidence interval)	NMI* (95% confidence interval)
KmeansHaralick	Kmeans	Haralick	0.338 (0.332, 0.343)	0.136 (0.135, 0.138)
KmeansCaptions	Kmeans	Captions	0.433 (0.43, 0.44)	0.182 (0.177, 0.186)
EnsembleHaralick	Ensemble	Haralick	0.340 (0.335, 0.346)	0.154 (0.153, 0.155)
EnsembleCaptions	Ensemble	Captions	0.465 (0.460, 0.470)	0.179 (0.177, 0.182)
EnsembleMerged	Ensemble of merged modalities	Haralick and captions merged	0.360 (0.351, 0.370)	0.134 (0.131, 0.137)
Complementary Ensemble Clustering	Linear combination of coassociation matrices from ensemble clustering of each modality separately	Haralick and captions separately	0.474 (0.468, 0.480)	0.189 (0.186, 0.192)

NMI: Normalized Mutual Information.

Bold font indicates highest performing method(s).

^*Larger is better.

Interestingly, single modality ensemble clustering does not always perform better than simple Kmeans in the performance metrics NMI and micro-averaged precision. As seen with the images data, the EnsembleHaralick outperforms KmeansHaralick in terms of NMI but not with respect to micro-averaged precision. In fact EnsembleHaralick yields a solution that is only 0.5% better than KmeansHaralick in terms of micro-averaged precision. We also explored the utility of deploying CEC in our image retrieval tool, the Yale Image Finder (YIF), to make it a cluster based rather than instance based information retrieval tool. This was done so that images are retrieved from the cluster as specified by their respective queries. This modification will enable the user to request images based on image type, a very useful query option. As a demonstration of how the proposed clustering method performs in terms of selecting similar images the five most similar images in what we refer to as the “experimental” clusters yielded by the different clustering methods were compared. The most similar images in a cluster are those with the lowest distance scores among them. We have selected to examine the images in the cluster of type “experimental” because the graphical characteristics of these images lend themselves to a cursory visual inspection. This is because the “experimental” cluster contains the largest number of images yielded from experimentation and includes those from gel electrophoresis, fluorescence microscopy, and from samples of tissue. Because CEC consistently produced the best clusters in terms of NMI and micro-averaged precision, we limit our comparison groups to only those resulting from the cluster approaches that yielded the second best results in terms of NMI and micro-averaged precision.

Specifically, we compared CEC with the EnsembleCaptions method which produced the second best micro-averaged precision, and the KmeansCaptions method that yielded the second best NMI as shown in Figs. 3–5.

Fig. 3.

Top 5 images in the cluster labeled with type “Experimental” and their corresponding labels or gold reference produced by Complementary ensemble clustering method (micro-Averaged Precision = 0.474 and NMI=.189).

Fig. 5.

Top 5 images in the cluster labeled with type “Experimental” and their corresponding labels or gold reference produced by the kmeansCaptions clustering method clustering (NMI = 0.182).

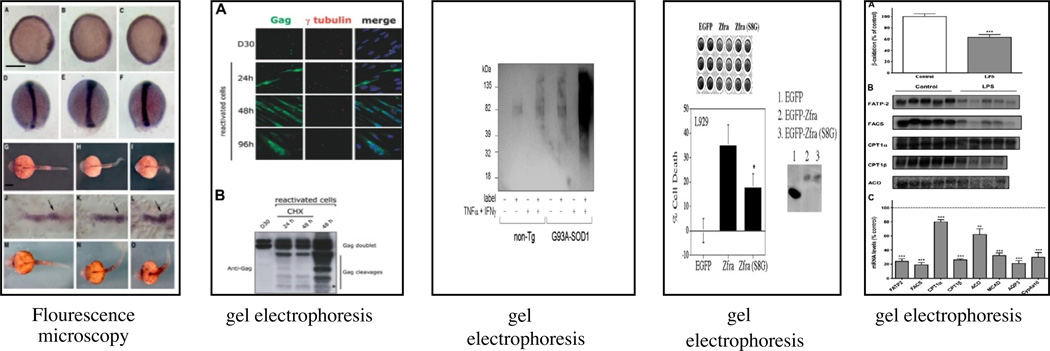
The five most similar images In Fig. 3 are all experimental images, mostly gel and fluorescence images. This result emphasizes the ability of the CEC method to group the gel images in one cluster using the images’ visual features as well as their corresponding captions. Furthermore, the similarity among the displayed images in Fig. 3 reflects the underlying bases of the mathematical measures. The images shown in Fig. 4 corresponding to the “experimental” cluster of the EnsembleCaptions method are not consistent as suggested by the high micro-averaged precision score of this clustering approach. Although this clustering method yielded the second highest average micro-averaged precision, the high average value represents the entire group of clusters and is therefore likely attributable to one of the non experimental clusters yielded by this approach. In fact, an examination of the precision of the individual clusters reveals that one of the non experimental clusters was characterized by higher precision than this cluster. For the kmeansCaptions method, whose result is shown in Fig. 5, 80% of the five most similar images are fluorescence images which are “experimental” type of images. Because this method exploits the captions when forming clusters, a review of the captions corresponding to these images reveals a small number of words that are frequently repeated, such as: fluorescence, transfect, cell, and treated. The highly frequent appearance of this group of words mathematically increased their respective similarities and eventually caused them to be grouped in the same cluster. Even though the last image in Fig. 5 is not fluorescent, it was assigned to this cluster because it shared the words (cell, treat) with the captions from the other images that happened to be fluorescent. Evaluating this cluster, which was produced by the kmeansCaptions method, one might say that these images are a good result from a query requesting experimental images. To investigate the robustness of this assertion, we expanded this post hoc examination to include the ten most similar images. We noticed that among the ten most similar images produced by the kmeansCaptions method, only 40% of the images assigned to this cluster were truly of the “experimental” type. On the other hand, an examination of the top ten images in the “experimental” cluster from CEC showed that 90% of the corresponding images were in fact experimental images. Among the clusters annotated as “experimental” yielded by the different methods, CEC produced the most graphically cohesive set of experimental images.

Fig. 4.

Top 5 images in the cluster labeled with type “Experimental” and their corresponding labels or gold reference produced by the EnsembleCaptions clustering method clustering (micro-Averaged Precision = 0.465).

4.2. Radiology reports data

The two modalities used for this dataset are the BOW and BOC. In the BOW modality, the reports are represented using the original words that appear in the clinical narratives and weighted by frequency. This data is stored in the notes and words matrix A₁, to which the cluster ensemble algorithm is applied to generate the clustering solution labeled EnsembleWords E₁. In the BOC modality the clinical notes are represented by their semantic concepts and stored in the notes and concepts matrix A₂.

The EnsembleConcepts E₂ is then computed from A₂. Once both ensembles (E₁, E₂) are computed, their corresponding coassociation matrices are combined into one coassociation matrix to which Kmeans is applied to produce the final clusters. Because it consistently gave more reliable clusters than EnsembleWords, we set the α value of EnsembleConcepts to 0.8, i.e., giving it higher weight. We plan to research the automation of learning α_i such that the each component of the cluster ensemble is weighted by its commensurate contribution to the final clustering solution.

The results from applying the different clustering methods to the Radiology reports data are shown in Table 4. Similar to our observations in the Pubmed data, CEC outperformed the EnsembleMerged method in terms of NMI and micro-averaged precision. These results emphasize the advantage of combining the ensemble clusters of individual modalities rather than their corresponding feature sets. Furthermore, the performance of the CEC clusters was notably better for both measures than those yielded by the KmeansWords, EnsembleWords and KmeansConcepts solutions. For example, in terms of NMI, relative improvements of 133%, 160%, and 18% were observed, respectively. In contrast, the proposed method was tied for best NMI performance with EnsembleConcepts. Conversely, while ensemble clustering produced better results than Kmeans in the concepts modality, it did not maintain that same advantage in the modality based on words in terms of NMI. This could be related to the feature set size, i.e., the number of concepts is greater than the number of words, which also introduces greater variability in its respective cluster ensemble solution. Furthermore, as opposed to Micro-Averaged Precision, NMI as a measure was not capable of capturing the difference in both solutions.

Table 4.

Results of the different clustering methods for Radiology reports data.

Method descriptor	Clustering algorithm	Data modality utilized	Micro-Averaged Precision* (95% confidence interval)	NMI * (95% confidence interval)
KmeansWords	Kmeans	Words	0.510 (0.506, 0.514)	0.236 (0.234, 0.238)
KmeansConcepts	Kmeans	Concepts	0.560 (0.555, 0.565)	0.468 (0.447, 0.490)
EnsembleWords	Ensemble	Words	0.551 (0.534, 0.567)	0.211 (0.204, 0.218)
EnsembleConcepts	Ensemble	Concepts	0.591 (0.588, 0.594)	0.565 (0.551, 0.579)
EnsembleMerged	Ensemble of merged modalities	Words and concepts merged	0.589 (0.584, 0.593)	0.487 (0.485, 0.489)
Complementary Ensemble Clustering	Linear combination of coassociation matrices from ensemble clustering of each modality separately	Words and concepts separately	0.609 (0.599, 0.620)	0.550 (0.540, 0.560)

NMI: Normalized Mutual Information.

Bold font indicates highest performing method(s).

^*Larger is better.

5. Discussion

Whereas the complementary ensemble clustering (CEC) framework was introduced in a previous publication, the technique was demonstrated on two standard benchmarking datasets that consist of text only, i.e., the publically available Reuters and Newsgroups datasets. Those two datasets are comprised of news articles that are known to be structured and well-written in formal English which makes the data less noisy and less challenging for the clustering algorithm. The examples in this article demonstrate the special strengths of CEC with regards to biomedical data. The first demonstration showed that by extracting information from purely visual data (images) and the corresponding captions (text), CEC was able to show as good or better performance than the reference methods. While the reference method EnsembleCaptions did yield performance on precision that was statistically no worse than CEC, the latter provided a statistically higher value of NMI. Furthermore, the images selected by CEC for the experimental cluster were visually and thematically more cohesive than those selected by EnsembleCaptions. This visual cohesiveness serves as a reflection of CEC’s superior performance in NMI and implies improved effectiveness as the basis of clustering in the Yale Image Finder. In the second dataset of radiologic data CEC did as good or better than the references methods by clustering on information drawn from two modalities, i.e., words and concepts. Whereas the NMI of EnsembleCaptions was no worse than that of CEC, the latter provided a statistically higher value of precision. In summary, across these two realistically noisy biomedical datasets, CEC provided statistically better performance in at least one clustering metric while beating or tying the reference methods in a second metric. Several limitations of this study merit comment. While the CEC falls short of demonstrating uniformly superior results in all metrics, it does display an incrementally improved performance in a much more demanding data environment. A second limitation shared by this study is the challenge of finding the optimal value for a combination parameter or weighting factor. Often times, a parameter is estimated empirically from the data within hand, which does not necessarily mean that the estimated value suits other samples of the data. Because we had the gold standard for each dataset, we utilized this information to decide which is the most informative data modality based on two different measures. We pointed out two different ways to estimate the combination parameters in case there is no existing information about how to categorization the data. We systematically conducted our experiments while varying the values of α and selected the value of 0.8, which gave more weight to the modality with the better clusters. Such empirical selection means this value is good for this data but may not be for any other.

6. Conclusion

In this paper, we demonstrate the utility of CEC by applying it to two biomedical datasets in which it demonstrated equivalent or enhanced performance on two standard measures relative to ensemble clustering based on single and merged modalities. Relative to ensemble clustering from each discrete modality, CEC exhibited notable improvement in the Pubmed images dataset and incremental improvement in the Radiology reports data. Compared to ensemble clustering based on merged data modalities, in all cases CEC showed superior performance in both datasets in at least one of two metrics. We conclude that CEC may be advantageous for enhanced biomedical data clustering and potentially useful for data from other domains. Because this algorithm could be computationally expensive for large data sets, we are currently working on parallel computation of each member of the complementary ensemble.