Abstract
Purpose
To evaluate fetal cerebral venous blood oxygenation, Yv, using principles of MR susceptometry.
Materials & Methods
A cohort of 19 pregnant subjects, with a gestational age of 31.6 +/- 4.7 weeks were imaged using a modified susceptibility weighted imaging (SWI) sequence. Data quality was first assessed for feasibility of oxygen saturation measurement and data from 5 subjects (mean +/- std gestational age of 33.7 +/- 3.6 weeks) was finally chosen for further quantitative analysis. SWI phase in the superior sagittal sinus was used to evaluate oxygen saturation using the principles of MR susceptometry. Systematic error in the measured Yv values was studied through simulations.
Results
Simulations showed that the systematic error in Yv depended upon the assumed angle of the vessel, θ, relative to the main magnetic field and the error in that vessel angle δθ. For the typical vessel angle of θ=30° encountered in the fetal data analyzed, a δθ as large as ±20° led to an absolute error, δYv, of less than 11%. The measured mean oxygen saturation across the 5 fetuses was 66% ± 9.4% (range 55.7% to 74.4%). This average cerebral venous blood oxygenation value is in close agreement with the value in the published literature.
Conclusion
We have reported the first in-vivo measurement of human fetal cerebral venous oxygen saturation using MRI.
Keywords: Susceptibility weighted imaging, SWI, fetal, brain, oxygen saturation, susceptometry
Introduction
Utilization of oxygen for aerobic metabolism during development is an integral part of the growth process of the human fetus, particularly from the second trimester onwards(1). The oxygen demand for metabolic purposes of the feto-placental unit increases with increasing gestational age(1,2). Disruption of this oxygen supply could lead to fetal cerebral hypoxia-ischemia, eventually leading to hypoxic ischemic injury (HII) to the developing brain. HII is a debilitating condition, often associated with postnatal developmental delay/deficits(3–5). The severity of brain injury depends on the nature and severity of the hypoxic-ischemic insult and gestational age of the fetus at the time of insult(3). A large number of clinical risk factors are associated with HII or stroke in the fetal brain including but not limited to: pre-eclampsia, placental abruption, maternal or fetal infection, congenital heart disease, maternal drug abuse etc(3,6–9). Recent studies show that the incidence of perinatal stroke is 1 in 1600 to 5000 births(8,10). While it is known that fetuses who suffer strokes in-utero are at increased risk of neurodevelopmental disorders(3,11), particularly hemiplegic cerebral palsy(12,13), the epidemiology of these strokes and pathways for prevention remain unclear(14,15). A major issue in studying brain damage in-utero in humans is that it remains undiagnosed until late(9). Methods for in-utero identification of ischemic injury to the fetal brain are limited and in some cases the diagnosis has to wait until the post neonatal period when injury becomes evident in neuroimaging or when affected children fail to reach developmental milestones(9,16–18). Hence, non-invasive imaging methods for identifying HII in-utero are of clinical interest and may help in the better prediction of long-term outcome(19).
Fetal magnetic resonance imaging (MRI) is increasingly gaining prominence as a clinical tool for radiologic evaluation of congenital anomalies in the developing fetus; especially neuro-developmental abnormalities(20). MR imaging has been shown to be more sensitive and provides greater specificity compared to ultrasound in the evaluation of central nervous system (CNS) abnormalities in the fetus(20–23). HII, cerebrovascular disorders (occlusive type like focal stroke or non occlusive type like aneurysms, arterio-venous malformations etc.) and intracranial hemorrhages are some of the few CNS anomalies that are often evaluated using MR(6). Cerebral hypoxic-ischemia often involves decreased arterial oxygen supply to the brain and a concomitant change in cerebral venous oxygen saturation. The ability to measure fetal cerebral blood oxygenation would make it possible to evaluate the oxygen extraction fraction; and along with blood flow rate measurements also evaluate the cerebral metabolic rate of oxygen consumption (CMRO2)(24), an important parameter in the evaluation of cerebral oxygen metabolism(25). While fetal cerebral blood flow rates may be measured using Doppler ultrasound, other methods are required for measuring fetal blood oxygenation. The current methods for measuring human fetal blood oxygenation are often invasive and/or can only be applied to fetuses intrapartum(26–28). Recently, a non-invasive method for blood oxygenation measurement in-utero was developed based on trans-abdominal near infra red spectroscopy (NIRS)(29). However, this method can only be applied to near term fetuses (>36weeks gestation) due to methodological limitations of NIRS.
Blood oxygen level dependent (BOLD) MR imaging is highly sensitive to changes in blood oxygenation levels(30–32) and has been used in quantitative assessment of cerebral metabolic rate in stroke and multiple sclerosis patients(33–35). Susceptibility weighted imaging (SWI) is an MR imaging methodology which takes advantage of the BOLD mechanism to generate not only venograms of the brain, but also to quantify venous oxygenation levels(36–40). In this work, we applied SWI and the principles of MR susceptometry to evaluate fetal cerebral blood oxygenation in humans. Specifically, we used the SWI phase images to evaluate putative venous oxygen saturation from the superior sagittal sinus of the fetal brain in-utero. The superior sagittal sinus, which carries most of the cerebral venous return, was chosen for measurement due to its relatively large size compared to other venous structures in the developing brain. Possible systematic error in this SWI-phase based venous oxygenation measurement was also assessed through simulations.
Materials & Methods
Theory
Phase from a gradient echo MRI experiment provides a direct measure of the field perturbation within a tissue relative to its immediate background via Eq. [1]. Here, γ is the proton gyromagnetic ratio, ΔB is the field perturbation, TE is the echo time of the experiment and Δφ is the phase difference between the tissue and its immediate background. For an infinitely long cylinder with a magnetic susceptibility difference of Δχ, inside a uniform external magnetic field, the field perturbation is given by Eq. [2] where θ is the angle made by the long axis of the cylinder with the main magnetic field Bo (see Figure 1a):
| [1] |
| [2] |
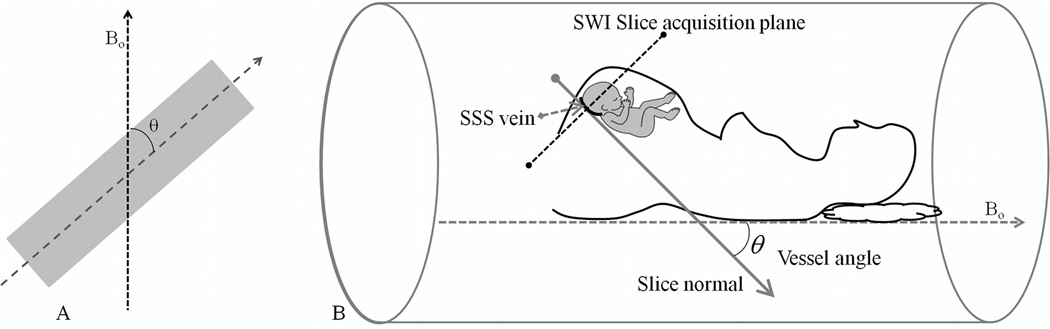
Figure 1.
A) Illustration of vessel angle made with respect to the main magnetic field Bo. B) Determination of the vessel angle in fetal imaging; illustration of the vessel angle made by the superior sagittal sinus in the fetal brain when the fetus is arbitrarily oriented within the maternal womb. With the acquisition of SWI data axial to fetal brain, determination of the angle made by the SSS in the posterior aspect of the brain is carried out using the vector normal to the slice. An implicit assumption in this angle determination is that the SSS vessel segment is perpendicular to the SWI imaging slice.
Due to the paramagnetic nature of deoxyhemoglobin, veins carrying deoxygenated blood have a magnetic susceptibility, Δχvein, different from the surrounding parenchyma. This susceptibility is dependent on the deoxyhemoglobin content in the vein(41). The relation between the venous oxygen saturation, Yv, and their magnetic susceptibility is given by Eq. [3] where Δχdo is the magnetic susceptibility difference between fully deoxygenated and fully oxygenated blood and Hct is the blood hematocrit.
| [3] |
| [4] |
Making the assumption that superior sagittal sinus (SSS) vessel could be modeled as an infinitely long cylinder, SSS oxygen saturation can be evaluated using Eq. [4] which is in turn obtained(42,43) from Eqs. [1] to [3]. Here Δφsss is the difference between the phase inside the SSS vein and the background parenchyma. The value of Δχdo for fetal blood is assumed to be the same as that for the adult blood, which is 0.27 parts per million (ppm) in cgs units(44,45) or 4· π ·0.27 = 3.39 ppm in SI units. Fetal blood hematocrit values appropriate for gestational age (GA) were obtained from the literature(46). They were estimated using the linear regression equation Hct = 22.9% + GA*0.5% which provides the normal range of fetal blood hematocrit across different gestational ages(46). Here GA is gestational age in weeks. Using Eqs. [1] through [4], the error in measured Yv is obtained by propagating error in phase to error in Δχvein and consequently error in Yv:
| [5] |
| [6] |
where δ (parameter) denotes the error within that parameter.
Subject Recruitment
Nineteen pregnant women who were receiving routine obstetric care at XXXX, were non-consecutively recruited in this study. Pregnant women, between the age of 18 to 38 years and who were between 19 and 40 weeks gestation were approached for recruitment. Singleton, uncomplicated pregnancies with normal ultrasound examination, reporting no contraindications for MRI were eligible to participate. The imaging study was approved by the local institutional review board and was compliant with HIPAA regulations and written informed consent was obtained prior to the research MRI scan. The mean gestational age of the fetuses included in this study was 31.59 +/− 4.65 weeks (range 19 6/7 to 38 5/7 weeks). Study participants were followed longitudinally to assure that they developed no complications during pregnancy.
MR Imaging
Fetal MR imaging was carried out on a 3T Siemens Verio system (Erlangen, Germany) using a 4 channel body flex array coil, along with the spine coil. In some cases of subjects with large girth, an additional 2 channel flex extremity coil was used. Image data from the fetal brain was acquired using routine anatomical scans followed by SWI sequences. Anatomical data was acquired using T2-HASTE sequence with the following parameters: TR=3000msec, TE=140msec, slice thickness = 3mm, in-plane resolution = 0.87 × 0.87mm2, acquisition matrix size = 320×320, BW = 372 Hz/pixel and flip angle = 75°.
Fetal Susceptibility Weighted Imaging (fetal-SWI)
The conventional SWI sequence(37) was adapted in the following manner for both two dimensional (2D-SWI) and three dimensional (3D-SWI) data acquisition versions for fetal imaging. The modification was to allow for fast data acquisition within a single maternal breath-hold. For the 2D version, a single echo 2D SWI sequence was implemented at 3.0T with the following imaging parameters: TR= 280msec, TE between 15 to 18.7msec, bandwidth = 199Hz/pixel, flip angle = 32°, acquisition matrix size between 448 × 168 and 448 × 175, in plane resolution between 0.78mm x 1.56mm and 0.85mm x 1.7mm and slice thickness = 3.5mm. Images were interpolated to a square pixel size in-plane to either 0.78×0.78mm2 or 0.85×0.85mm2. A total of 10 to 11 slices were collected within a total acquisition time of 22 to 24seconds.
For the 3D fetal SWI sequence, the following imaging parameters were used: TR 23msec, TE between 13.5 to 17.3msec, flip angle-10°, bandwidth of 219Hz/pixel, voxel size of 0.78mm x 1.56mm in-plane with a slice thickness of 3 or 3.5 mm and an acquisition matrix size of 448 × 175. Images were interpolated to a square pixel size in-plane, i.e., to 0.78×0.78mm2. A total of 16 slices were acquired. In addition to a parallel imaging factor of 2, partial-Fourier reconstruction in both phase and slice direction was used to reduce the total data acquisition time to between 22 and 24 seconds. Both 2D-SWI and 3D-SWI sequences were acquired under maternal breath-hold condition.
In all subject scans, both T2-HASTE and SWI data (either 2D-SWI or 3D-SWI or both) were acquired multiple times to achieve appropriate fetal brain coverage or when fetal motion was encountered. SWI data was always acquired axial to the fetal brain. In some subjects, both 2D and 3D SWI data were acquired when scan time restrictions permitted.
Data Analysis
Fetal-SWI image data were first reviewed for general quality and artifacts. SWI data from two subjects could not be analyzed due to unavoidable fetal motion or severe magnitude aliasing artifacts. In the remaining 17 subjects, fetal-SWI data were reviewed for proper visualization of superior sagittal sinus (SSS) in both magnitude and phase images. Due to severe partial voluming and/or very small vessel size, in twelve of the subjects, phase from SSS could not be properly measured. Only in the remaining 5 subject datasets was the phase data in the SSS amenable for further quantitative oxygen saturation analysis. Hence, the following description of data analysis procedure pertains only to the 2D or 3D data from these 5 subjects. Since SWI scans were often repeated in each subject to ensure complete fetal brain coverage, the SSS was often visualized in more than one acquisition for a given subject. Table 1 provides a summary of the subject information and the number of fetal-SWI scan sets analyzed. The average gestational age of these 5 subjects was 33.7+/−3.6 weeks (range 28 2/7 – 36 3/7 weeks).
Table 1.
Summary of fetal SWI data-sets analyzed
| GA (Weeks) | Hematocrit (Hct) | # of Fetal-SWI data sets analyzed |
|
|---|---|---|---|
| Subject-1 | 35 | 0.508 | 3 |
| Subject-2 | 36 3/7 | 0.517 | 4 |
| Subject-3 | 37 1/7 | 0.522 | 2 |
| Subject-4 | 28 2/7 | 0.465 | 2 |
| Subject-5 | 32 | 0.489 | 1 |
Oxygen Saturation Measurement from Phase
Raw phase images from the fetal-SWI data were first filtered using a mild homodyne high pass filter(47) of size 32×32 to remove background field inhomogeneities due to air-tissue interface. In each of the fetal brain SWI data sets from a given subject, 3 consecutive slices were chosen such that there is no considerable displacement of the SSS vessel lumen between these three consecutive slices. This was to ensure that the segment of SSS with the least curvature was chosen which was relatively perpendicular to the imaging slice. Mean and standard deviation of the phase values from the SSS, seen in the posterior aspect of the fetal brain in the three consecutive slices, were then measured. Phase images were zoomed by a factor of 4 and a region of interest (ROI) was manually drawn within the vessel to avoid the boundary voxels to minimize partial volume effects. A nearest neighborhood algorithm was used for image zooming. The average number of voxels within these ROIs across all subjects was 41.5+/−15.14 voxels after mapping the boundary back into the original images. In each slice, mean and standard deviation of phase from a reference region, was also measured from the white matter of the fetal brain. The phase difference Δφsss was then obtained by subtracting the phase measured in the reference region from the phase measured in the SSS vessel ROI. The fetal head is usually in an arbitrary orientation within the mother's womb, as illustrated in Figure 1b. Since SWI data were acquired axial to the fetal brain, the slice normal vector from the image header information (Digital Imaging and Communications in Medicine - DICOM standard) was utilized to evaluate the angle, θ, that the SSS vessel segment made with the main magnetic field Bo. Substituting the values of Δφsss, θ, TE, Hct, Δχdo, γ and Bo into Eq. [4], the value of Yv was obtained. The error associated with each measurement from a given slice was evaluated using Eqs. [5] and [6], taking into account the standard deviations of both background and SSS ROI phase measurements. Finally, the oxygen saturation values obtained from each slice and each fetal-SWI dataset for a given subject were averaged to obtain the mean Yv value for that subject. Associated standard error was also evaluated.
Simulations
To evaluate the systematic errors expected from measurement methods employed in this study, a digital phantom of an adult brain was used (40,48). Specifically, errors expected due to deviation from the assumption of the SSS being an infinitely long cylinder (which includes the influence of vessel shape and vessel curvature) and due to the influence of high pass filtering of phase data were evaluated. A 3D digital brain phantom(40,48) with isotropic voxel size of 0.5 mm was constructed by segmenting structures from adult brain MRI data, containing the cerebrum, the cerebellum, gray matter (GM), white matter (WM), red nucleus (RN), substantia nigra (SN), crus cerebri (CC), thalamus (TH), caudate nucleus (CN), putamen (PUT), globus pallidus (GP), cerebrospinal fluid (CSF), and the major venous vessels including the superior sagittal sinus. Tissue magnetic susceptibility values in parts per million (ppm) for the structures SN, RN, PUT, and GP, were adapted from Haacke et. al(39) and others were from Wharton et. al.(49). The following are the susceptibility values in ppm used in the model: RN = 0.13, SN = 0.16, CC = 0.03, TH = 0.01, CN = 0.06, PUT = 0.09, GP = 0.18, venous vessels = 0.45, GM = 0.02, CSF =0.014, and WM = 0. A susceptibility of 0.45 ppm used in the venous vessels corresponded to a venous oxygen saturation (Yv) of 70% for a hematocrit (Hct) value of 0.44. All structures were set inside a 512 × 512 x 512 zero filled matrix and phase was simulated from this susceptibility matrix using the forward field perturbation method(50,51). To study the situation of arbitrary fetal brain orientation, the field for the digital brain phantom was simulated for three different slice-normal angles relative to Bo: +30°, 0°, −30°, as illustrated in Figure 2. Imaging parameters used for simulation were Bo=3T and a TE of 18msec which is similar to the TE used for fetal imaging. Random noise and background field inhomogeneities from sinuses(52) were not included as they did not have a direct influence on the primary goals of these simulations which were to: a) evaluate the influence of an infinitely long cylinder approximation for the superior sagittal sinus and b) evaluate the influence of the amount of phase information lost from the SSS due to high pass filtering on the final oxygen saturation measurements.
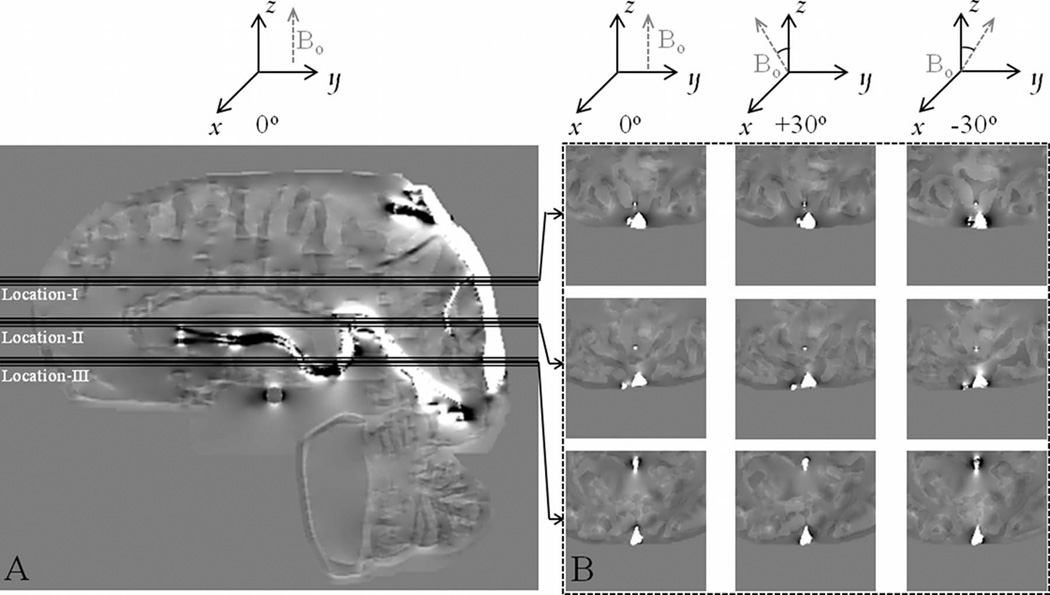
Figure 2.
Phase images from simulations with corresponding θ values as illustrated. Simulations were carried out for 3 different relative orientations of the axial slice-normal relative to Bo, i.e., three different θ values. A) Sagittal phase image illustrating the three locations where phase measurements for determination of Yv were carried out. B) Axial images corresponding to the central slice at the locations shown in (A). Images were zoomed by a factor of 4 and cropped to show phase in the SSS for the three different θ values of 0°, +30° and −30°.
Simulated phase data was homodyne high pass filtered(47) using a 32×32 filter size. Following the same procedure used on fetal SWI data described above, measurements of oxygen saturation were obtained from both the original simulated phase (Yv,sim) and high pass filtered phase data (Yv,sim–HPfilt) in 3 consecutive slices and averaged. Vessel angle was taken to be 0° for calculation of Yv because the SSS vessel segment in the posterior aspect of the brain is almost parallel to Bo when a person is laying in supine position within the MRI system. The measured Yv values were then compared with the initially assumed value of 70% and absolute error in, δYv, was calculated relative to this value. This procedure was carried out at 3 different locations along the length of the SSS as shown in Figure 2, to evaluate the influence of SSS curvature. The locations were chosen such that the SSS vessel segment at location-I deviated slightly from being parallel to Bo by 20°±1°. At location-II, the vessel segment angle was 12°±1° and at location-III, the vessel segment was almost parallel (0°±1°) to Bo. These angles were measured manually by determining the angle made by a vector tangential to the vessel centerline with a vector parallel to Bo. The value of Yv is dependent on cos θ and hence is independent of the sign of θ. Thus, the simulation of the brain volume at +30 and −30 relative to Bo is equivalent to a θ value of 30° and δθ values of ±20° (location-I), ±12° (location-II) and ±1° (location-III) for the SSS.
Finally, from filtered and unfiltered simulation data, deviation of the measured oxygen saturation, δYv,sim = (70 – Yv,sim))% and δYv,sim–HPfilt = (70 – Yv,sim–HPfilt))% respectively was evaluated and compared for these three different locations. For an infinitely long cylinder, the theoretically expected absolute error δYv due to an error in vessel angle θ can be given by:
| [7] |
Here δθ is the error in vessel angle, i.e., the actual vessel angle is θm + δθ, whereas the assumed vessel angle is θm, Δφm is the measured phase inside the cylinder, Yv,m is the measured oxygen saturation in the cylinder and Yv is the actual oxygen saturation (or ground truth). Results from the simulations were compared with the theoretically predicted error. A brain model phantom, rather than a vessel-only model(53) was used in simulations to enable us to use the white matter as the reference region and follow the same measurement procedure for measuring Δ φsss as used in the fetal data.
Results
Simulations
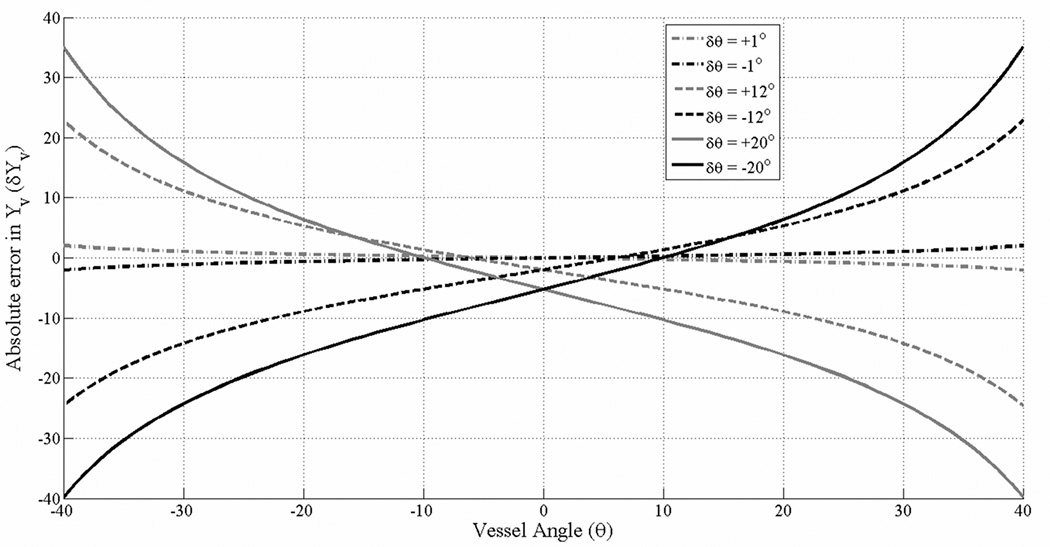
For an infinitely long cylinder, figure 3 plots the theoretically expected δYv as a function of assumed vessel angle θ for different values of δθ (±1°, ±12°, ±20°) using Eq. [7]. Following parameter values were used in generating the plot in Figure 3: Bo= 3 Tesla, TE 18ms, Hct=0.44, Yv=70% and Δχdo = 4· π · 0.27 ppm. It is evident from Figure 3 that δYv is dependent not only on the magnitude and sign of δθ, but also on the assumed vessel angle θ.
Figure 3.
Absolute error in Yv for an infinitely long cylinder, plotted as a function of the vessel angle, θ, for different values of δθ. The various curves are calculated using Eq. (7) for which the following parameters were used: Hct=0.44, Δχdo = 4 · π · 0.27 ppm, TE = 18ms, Bo = 3 Tesla and Yv=70%. The curves are plotted for 6 different values of δθ, ±1°, ±12° and ±20° closely matching the parameters in the simulations.
Table 2 summarizes the results from simulations. There is systematic under- or over-estimation of Yv, which is dependent on the initial angle of the vessel segment. Deviation from the assumed value of θ for a given vessel segment due to curvature also influences the error which is evident in the varying absolute error in Yv from location-I to location-III for a fixed vessel angle.
Table 2.
Results from the simulations.
| Location | δYv,sim = 70 – Ysim % | δYv,sim–HPfilt = 70 – δYv,sim–HPfilt % |
|---|---|---|
| theta=0° | ||
| I | −5.5 | −7.3 |
| II | −2.1 | −4 |
| III | −1.6 | −3 |
| theta = −30° | ||
| I | −7.6 | −9.3 |
| II | −4 | −6.6 |
| III | 5.7 | 3.5 |
| theta = +30° | ||
| I | 9.2 | 6.4 |
| II | 10.4 | 8 |
| III | 6.9 | 5.4 |
| (-ve deviation implies an overestimation ofYv) | ||
| Hct = 0.44, Bo=3T, TE=18msec and input Yv value of 70% were used in simulations. | ||
Table 2: The table summarizes results from the simulations. Systematic absolute error, δYv,sim, in the quantified Yv relative to the input value of 70% is tabulated. Absolute error in Yv due to high pass filtering of phase, δYv,sim–HPfilt, is also shown. Yv,sim - Measured oxygen saturation in SSS from simulated phase. Yv,sim–HPfilt - Measured oxygen saturation in SSS from phase images obtained after high pass filtering the simulated phase using a 32×32 filter size.
Theoretical predictions from Eq. [7] of absolute error in Yv for an infinitely long cylindrical vessel which is parallel to the field, are in good agreement with corresponding errors from simulations at θ=0° (see Figure 3 and Table 2). For example, for a δθ of ±20° a δYv of −5.27% is found in Figure 3 which is in very good agreement with δYv,sim= −5.5% measured from location-I in the simulations where the SSS vessel segment is making an angle of +20° with Bo (see Figure 2). Furthermore, Figure 3 also shows that while for θ=0, a positive or negative δθ always leads to a δYv with the same sign and amplitude, the same is not true for non-zero vessel angles. For example, for θ = +30° the value and sign of δYv is different for δθ=+20° and δθ= −20°. This is also seen in the results from simulations (Table 2). Quantitatively, for a θ=30° and δθ of −20°, −12° and −1°, Figure 3 predicts an error value +15.7%, +11.1%, ∓1.1% respectively for δYv. These values are larger than those obtained from simulations for δYv,sim: +9.2%, +10.2% and 6.9% respectively, for corresponding values of θ and δθ. The same is true for δθ values of +20°, +12° and +1° (location-III) where the error values δYv,sim obtained from the SSS in simulations is less than the theoretically predicted δYv for an infinitely long cylinder (Figure 3). This could be due to the influence of the shape of the vessel cross-section which is not cylindrical and is changing along the length of the vessel as can be seen from Figure 2. Nonetheless, simulations show that even for large values of δθ=+20° and θ = −30°, the systematic absolute error in Yv is less than 11% (Table 2). High-pass filtering of phase did lead to a loss of phase information from the vessel which led to Yv,sim being different from Yv,sim–HPfilt. The absolute difference between Yv,sim and Yv,sim–HPfilt was, however, less than 3% in all the cases.
Fetal SWI data
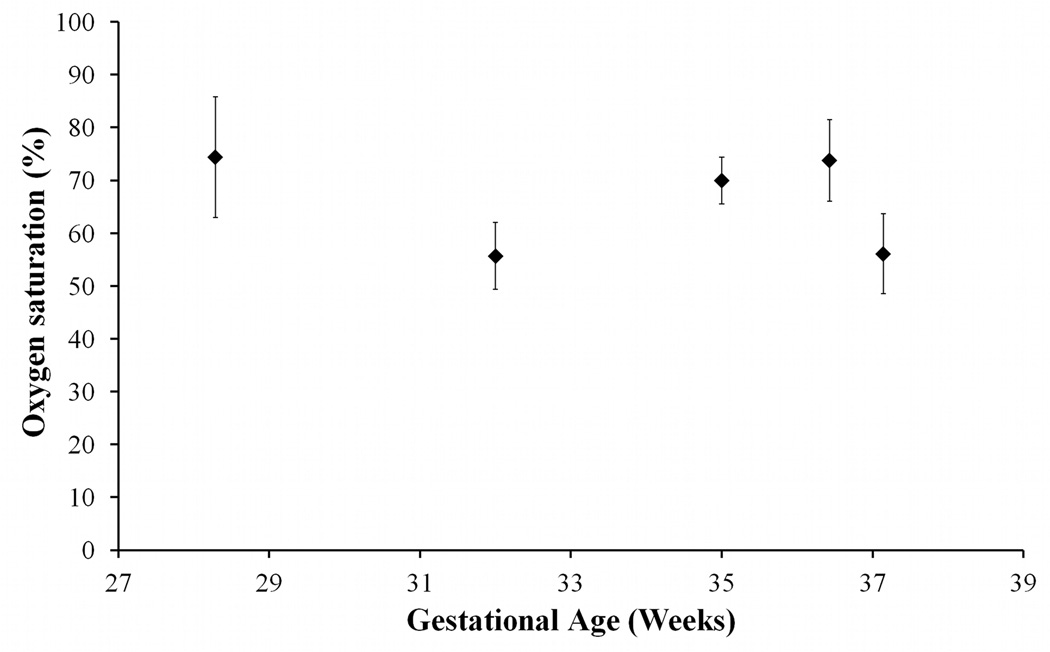
In the analyzed data from the 5 fetuses, the values of θ that the SSS vessel segments made with Bo ranged from 26.9° to 36.8° degrees. A representative set of fetal SWI magnitude and phase images are shown in Figure 4. The SSS is clearly visualized in the posterior aspect of the brain on the axial images. The measured oxygen saturation values from the SSS from the 5 fetuses are plotted in Figure 5 across their respective gestational ages. Oxygen saturation values in the SSS along with the corresponding standard errors were 70±4.4% in subject-1, 73.8±7.7% in subject-2, 56.1±7.5% in subject-3, 74.4±11.4% in subject-4, and 55.7±6.4% in subject-5. Averaged over the 5 fetuses, the oxygen saturation within the SSS is 66±9.4%. The standard deviation of 9.4 quoted here represents the variation of the mean values across subjects and not the standard error.
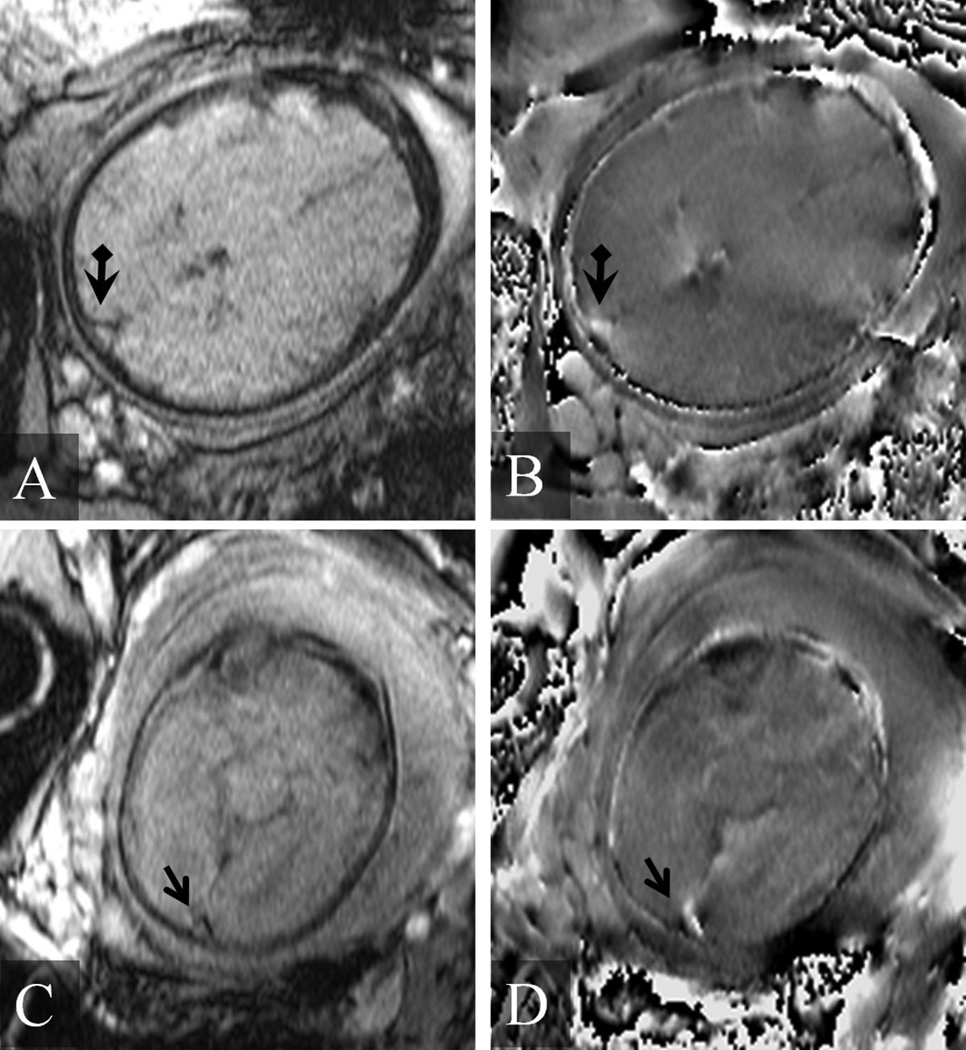
Figure 4.
Representative examples of magnitude and phase images from several fetal SWI data sets. A) Magnitude image of the fetal brain from a fetus at 36 3/7 weeks gestation. B) The corresponding phase image. The arrow head points to the superior sagittal sinus. C) Magnitude image of the fetal brain from a fetus at 28 2/7 weeks gestation. D) The corresponding phase image. In this second example, the extra-vascular dipolar phase associated with the magnetic susceptibility of the superior sagittal sinus vein (arrow) is evident in (D).
Figure 5.
Oxygen saturation values measured from 5 fetal brain SWI data plotted across their gestational age. The mean oxygen saturation across 5 fetuses was 66% ± 9.4%. The standard deviation here represents across-subject variation.
Discussion
In this study, phase from susceptibility weighted images was used to evaluate oxygen saturation of the SSS in the fetal brain. To the best of our knowledge, this is the first study applying MRI for measuring cerebral venous oxygenation in the human fetus. The method employed in this paper for measuring Yv is quite similar to the one used in the adult brain previously(42,43,54). Recently, various Fourier Transform based methods for quantitative susceptibility mapping from MR phase data have been developed(39,40,49,55,56). These methods make it possible to create a map of venous oxygenation throughout the brain (39,40). Unfortunately these methods could not be applied in this study due to poor image resolution.
Results from simulations provided an indication of the systematic errors that could be expected due to deviations from model assumptions, i.e., when the assumption that the SSS vessel segment could be modeled as an infinitely long cylinder, is violated. Influence of violation of these assumptions had been investigated previously by Li et. al.(53) for the SSS vessel segment in adults. For the case of θ=0°, our simulation results for absolute error δYv,sim in the SSS (Table 2) are in good agreement with those obtained by Li et. al., and are also in good agreement with the theoretically predicted errors from Eq. [7] for an infinitely long cylinder (see Figure 3). While for θ=0° the systematic absolute errors in Yv are on the order of 5%, when the assumed vessel angle deviates from zero, these errors increase. Nonetheless, δYv,sim is still within 11% for δθ as large as ∓20° and assumed vessel angle of ∓30° (see Table 2). The deviation of the errors obtained in simulations for non-zero vessel angles of ∓30°, from those predicted by Eq. [7] for an infinitely long cylinder could be due to the non-cylindrical shape of the SSS. In the analyzed fetal data, the vessel angle was generally close to 30° which is why the situation of θ=±30° was simulated to evaluate the magnitude of expected systematic error in Yv.
The standard errors for the measured Yv varied from one subject to another due to a) different number of SWI datasets analyzed and b) due to different magnitude signal to noise ratios partially owing to different echo times used. The average magnitude SNR was 9.4+/−3.4 across all the fetal-SWI datasets analyzed. Despite these errors, the average value of the oxygen saturation measured is in good agreement with fetal cerebral venous oxygen saturation values in the literature. Vintzileos et al(29) measured cerebral venous oxygen saturation using trans-abdominal near infra-red spectroscopy in 6 fetuses who were of 36 weeks or older gestational age. They measured this to be 61% ± 14.8%, which is in close agreement with the average oxygenation in the SSS across the 5 subjects in this study which is 66% ± 9.4%.
Hematocrit values within the fetus vary with gestational age(46). Furthermore, the relative ratios of fetal hemoglobin and adult hemoglobin within the red blood cells also changes as a function of gestational age(57). In this study, Hct values for fetuses at different gestational ages were obtained from the reference curves calculated by Boulot et al(46). These reference curves were obtained through measurements from 541 normal fetal blood samples obtained through cordocentesis. It is important to note that for absolute oxygen saturation measurement using MRI, we require the knowledge of fetal blood hematocrit. Nonetheless, the methods presented here could be employed to evaluate relative oxygen saturations within a fetus.
Due to lack of appropriate studies on magnetic properties of fetal blood, in this work it is assumed that the Δχdo value of fetal blood is same as that of the adult blood. It is known that fetal blood contains predominantly fetal hemoglobin (HbF) which has a different chemical conformation and slightly different optical absorption properties(58) in the near infrared range compared to that of adult hemoglobin (HbA). It also has considerably higher oxygen affinity compared to HbA. Furthermore, relative ratios of HbF and HbA within the red blood cell changes with gestational age of the fetus(57). All of these factors could lead to fetal blood having Δχdo–fetal different from Δχdo of the adult blood. However, this remains to be investigated.
Long echo times are typically required for SWI and this makes it challenging in its application to fetal imaging due to fetal motion and maternal breathing. Larger fields of view in fetal imaging necessitate larger matrix size in data sampling which further increases scan time. Keeping in view the above aspects, in this work, appropriate parameter changes were applied to the conventional SWI sequence for fetal-SWI imaging. However, due to severe partial voluming, magnitude aliasing and fetal motion, data from only 5 of the 19 fetuses scanned were usable in this work. This low data usability issue could largely be improved with higher resolution imaging. Higher resolution data helps to ensure that the venous vessel of interest occupies a sufficient number of voxels and that there is sufficient phase information within and outside the vessel allowing for more accurate susceptibility mapping(59) . Moreover, since susceptibility maps can be reconstructed from shorter echo time data as well(40) , higher resolution may in turn help to reduce the scan time further by relaxing the long echo time requirement for SWI. Higher through plane resolution data also allows for proper ascertainment vessel angle. The challenge in acquiring high resolution fetal imaging data is fetal motion which necessitates high speed data acquisition. High resolution and fast data acquisition are usually mutually competing goals and often require employing novel and tailored methods(60–64). Development of appropriate fast imaging methods with high resolution reconstruction of both magnitude and phase MRI data would greatly benefit MR based quantitative oxygenation assessment methods in the fetus.
In conclusion, in this work, MR susceptibility weighted imaging is applied for quantitative assessment of fetal cerebral venous blood oxygenation. Measured oxygen saturation values are in agreement with those published in the literature. In contrast to the few non-invasive methods currently available for quantitative assessment of fetal blood oxygenation(26,28,29), using MRI allows us to make these measurements in the fetus at gestational ages earlier than 36 weeks. The ability to measure fetal cerebral oxygenation is very important as it opens the doors to the possibility of quantitatively studying hypoxic ischemic injury in-utero in at risk pregnancies. With blood flow measurements from ultrasound or from MR imaging itself, it may be possible to obtain global cerebral metabolic rate of oxygen(24) in the fetal brain.
Acknowledgments
Grant support: This research was supported, in part, by the Perinatology Research Branch, Division of Intramural Research, Eunice Kennedy Shriver National Institute of Child Health and Human Development, NIH, DHHS.
This research was supported in part by the STTR grant from NHLBI, 1R42HL112580-01A1.
This research was also supported in part by the Perinatal Research Initiative of the Wayne State University School of Medicine, Detroit, Michigan, USA.
References
- 1.Burton GJ, Jaunaiux E. Maternal vascularisation of the human placenta: does the embryo develop in a hypoxic environment? Gynecologie, obstetrique & fertilite. 2001;29(7–8):503–508. doi: 10.1016/s1297-9589(01)00179-5. [DOI] [PubMed] [Google Scholar]
- 2.Schneider H. Oxygenation of the placental-fetal unit in humans. Respiratory physiology & neurobiology. 2011;178(1):51–58. doi: 10.1016/j.resp.2011.05.009. [DOI] [PubMed] [Google Scholar]
- 3.Rees S, Harding R, Walker D. The biological basis of injury and neuroprotection in the fetal and neonatal brain. International journal of developmental neuroscience : the official journal of the International Society for Developmental Neuroscience. 2011;29(6):551–563. doi: 10.1016/j.ijdevneu.2011.04.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Volpe JJ. Brain injury in premature infants: a complex amalgam of destructive and developmental disturbances. Lancet neurology. 2009;8(1):110–124. doi: 10.1016/S1474-4422(08)70294-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Walker SP, Wachs TD, Gardner JM, et al. Child development: risk factors for adverse outcomes in developing countries. Lancet. 2007;369(9556):145–157. doi: 10.1016/S0140-6736(07)60076-2. [DOI] [PubMed] [Google Scholar]
- 6.Stevenson DK. Fetal and neonatal brain injury. Cambridge, UK ; New York: Cambridge University Press; 2009. xiii, 628 p., 628 p. of plates p. [Google Scholar]
- 7.Lynch JK. Epidemiology and classification of perinatal stroke. Seminars in fetal & neonatal medicine. 2009;14(5):245–249. doi: 10.1016/j.siny.2009.07.001. [DOI] [PubMed] [Google Scholar]
- 8.Raju TN, Nelson KB, Ferriero D, Lynch JK, Participants N-NPSW. Ischemic perinatal stroke: summary of a workshop sponsored by the National Institute of Child Health and Human Development and the National Institute of Neurological Disorders and Stroke. Pediatrics. 2007;120(3):609–616. doi: 10.1542/peds.2007-0336. [DOI] [PubMed] [Google Scholar]
- 9.Ozduman K, Pober BR, Barnes P, et al. Fetal stroke. Pediatric neurology. 2004;30(3):151–162. doi: 10.1016/j.pediatrneurol.2003.08.004. [DOI] [PubMed] [Google Scholar]
- 10.Laugesaar R, Kolk A, Tomberg T, et al. Acutely and retrospectively diagnosed perinatal stroke: a population-based study. Stroke; a journal of cerebral circulation. 2007;38(8):2234–2240. doi: 10.1161/STROKEAHA.107.483743. [DOI] [PubMed] [Google Scholar]
- 11.Wu YW, March WM, Croen LA, Grether JK, Escobar GJ, Newman TB. Perinatal stroke in children with motor impairment: a population-based study. Pediatrics. 2004;114(3):612–619. doi: 10.1542/peds.2004-0385. [DOI] [PubMed] [Google Scholar]
- 12.Himmelmann K, Ahlin K, Jacobsson B, Cans C, Thorsen P. Risk factors for cerebral palsy in children born at term. Acta obstetricia et gynecologica Scandinavica. 2011;90(10):1070–1081. doi: 10.1111/j.1600-0412.2011.01217.x. [DOI] [PubMed] [Google Scholar]
- 13.Bax M, Tydeman C, Flodmark O. Clinical and MRI correlates of cerebral palsy: the European Cerebral Palsy Study. JAMA : the journal of the American Medical Association. 2006;296(13):1602–1608. doi: 10.1001/jama.296.13.1602. [DOI] [PubMed] [Google Scholar]
- 14.Lynch JK, Nelson KB. Epidemiology of perinatal stroke. Curr Opin Pediatr. 2001;13(6):499–505. doi: 10.1097/00008480-200112000-00002. [DOI] [PubMed] [Google Scholar]
- 15.Nelson KB, Lynch JK. Stroke in newborn infants. Lancet neurology. 2004;3(3):150–158. doi: 10.1016/S1474-4422(04)00679-9. [DOI] [PubMed] [Google Scholar]
- 16.Golomb MR, MacGregor DL, Domi T, et al. Presumed pre- or perinatal arterial ischemic stroke: risk factors and outcomes. Annals of neurology. 2001;50(2):163–168. doi: 10.1002/ana.1078. [DOI] [PubMed] [Google Scholar]
- 17.Kirton A, Deveber G, Pontigon AM, Macgregor D, Shroff M. Presumed perinatal ischemic stroke: vascular classification predicts outcomes. Annals of neurology. 2008;63(4):436–443. doi: 10.1002/ana.21334. [DOI] [PubMed] [Google Scholar]
- 18.Kirton A, Shroff M, Pontigon AM, deVeber G. Risk factors and presentations of periventricular venous infarction vs arterial presumed perinatal ischemic stroke. Archives of neurology. 2010;67(7):842–848. doi: 10.1001/archneurol.2010.140. [DOI] [PubMed] [Google Scholar]
- 19.Huang BY, Castillo M. Hypoxic-ischemic brain injury: imaging findings from birth to adulthood. Radiographics. 2008;28(2):417–439. doi: 10.1148/rg.282075066. quiz 617. [DOI] [PubMed] [Google Scholar]
- 20.Prayer D. Fetal MRI. Berlin: Heidelberg: Springer; 2011. XIII, 528 S. p. [Google Scholar]
- 21.Garel C, Delezoide AL, Elmaleh-Berges M, et al. Contribution of fetal MR imaging in the evaluation of cerebral ischemic lesions. AJNR American journal of neuroradiology. 2004;25(9):1563–1568. [PMC free article] [PubMed] [Google Scholar]
- 22.Griffiths PD, Widjaja E, Paley MN, Whitby EH. Imaging the fetal spine using in utero MR: diagnostic accuracy and impact on management. Pediatric radiology. 2006;36(9):927–933. doi: 10.1007/s00247-006-0234-y. [DOI] [PubMed] [Google Scholar]
- 23.Vazquez E, Mayolas N, Delgado I, Higueras T. Fetal neuroimaging: US and MRI. Pediatric radiology. 2009;39(Suppl 3):422–435. doi: 10.1007/s00247-009-1221-x. [DOI] [PubMed] [Google Scholar]
- 24.Fan AP, Benner T, Bolar DS, Rosen BR, Adalsteinsson E. Phase-based regional oxygen metabolism (PROM) using MRI. Magn Reson Med. 2012;67(3):669–678. doi: 10.1002/mrm.23050. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Sette G, Baron JC, Mazoyer B, Levasseur M, Pappata S, Crouzel C. Local brain haemodynamics and oxygen metabolism in cerebrovascular disease. Positron emission tomography. Brain. 1989;112(Pt 4):931–951. doi: 10.1093/brain/112.4.931. [DOI] [PubMed] [Google Scholar]
- 26.Hobbins JC, Grannum PA, Romero R, Reece EA, Mahoney MJ. Percutaneous umbilical blood sampling. American journal of obstetrics and gynecology. 1985;152(1):1–6. doi: 10.1016/s0002-9378(85)80165-4. [DOI] [PubMed] [Google Scholar]
- 27.Henderson Z, Ecker JL. Fetal scalp blood sampling - Limited role in contemporary obstetric practice: Part I. Lab Med. 2003;34(7):548–553. [Google Scholar]
- 28.East CE, Chan FY, Colditz PB, Begg LM. Fetal pulse oximetry for fetal assessment in labour. Cochrane database of systematic reviews. 2007;(2):CD004075. doi: 10.1002/14651858.CD004075.pub3. [DOI] [PubMed] [Google Scholar]
- 29.Vintzileos AM, Nioka S, Lake M, Li P, Luo Q, Chance B. Transabdominal fetal pulse oximetry with near-infrared spectroscopy. American journal of obstetrics and gynecology. 2005;192(1):129–133. doi: 10.1016/j.ajog.2004.07.022. [DOI] [PubMed] [Google Scholar]
- 30.Ogawa S, Lee TM, Kay AR, Tank DW. Brain magnetic resonance imaging with contrast dependent on blood oxygenation. Proceedings of the National Academy of Sciences of the United States of America. 1990;87(24):9868–9872. doi: 10.1073/pnas.87.24.9868. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.An H, Lin W. Quantitative measurements of cerebral blood oxygen saturation using magnetic resonance imaging. Journal of cerebral blood flow and metabolism : official journal of the International Society of Cerebral Blood Flow and Metabolism. 2000;20(8):1225–1236. doi: 10.1097/00004647-200008000-00008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.He X, Yablonskiy DA. Quantitative BOLD: mapping of human cerebral deoxygenated blood volume and oxygen extraction fraction: default state. Magn Reson Med. 2007;57(1):115–126. doi: 10.1002/mrm.21108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Lee JM, Vo KD, An H, et al. Magnetic resonance cerebral metabolic rate of oxygen utilization in hyperacute stroke patients. Annals of neurology. 2003;53(2):227–232. doi: 10.1002/ana.10433. [DOI] [PubMed] [Google Scholar]
- 34.Geisler BS, Brandhoff F, Fiehler J, et al. Blood-oxygen-level-dependent MRI allows metabolic description of tissue at risk in acute stroke patients. Stroke; a journal of cerebral circulation. 2006;37(7):1778–1784. doi: 10.1161/01.STR.0000226738.97426.6f. [DOI] [PubMed] [Google Scholar]
- 35.Holst B, Siemonsen S, Finsterbusch J, et al. T2' imaging indicates decreased tissue metabolism in frontal white matter of MS patients. Multiple sclerosis. 2009;15(6):701–707. doi: 10.1177/1352458509103713. [DOI] [PubMed] [Google Scholar]
- 36.Reichenbach JR, Jonetz-Mentzel L, Fitzek C, et al. High-resolution blood oxygen-level dependent MR venography (HRBV): a new technique. Neuroradiology. 2001;43(5):364–369. doi: 10.1007/s002340000503. [DOI] [PubMed] [Google Scholar]
- 37.Haacke EM, Xu Y, Cheng YC, Reichenbach JR. Susceptibility weighted imaging (SWI) Magn Reson Med. 2004;52(3):612–618. doi: 10.1002/mrm.20198. [DOI] [PubMed] [Google Scholar]
- 38.Neelavalli J, Cheng YC, Haacke EM. Method for Susceptibility Calculation in Multiple Source Object Distribution with Arbitrary Susceptibilities: A Preliminary Report.#2333; Miami. Proceedings of international Society of Magnetic Resonance in Medicine.2005. [Google Scholar]
- 39.Haacke EM, Tang J, Neelavalli J, Cheng YC. Susceptibility mapping as a means to visualize veins and quantify oxygen saturation. J Magn Reson Imaging. 2010;32(3):663–676. doi: 10.1002/jmri.22276. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Tang J, Liu S, Neelavalli J, Cheng YC, Buch S, Haacke EM. Improving susceptibility mapping using a threshold-based K-space/image domain iterative reconstruction approach. Magn Reson Med. 2012 Jun 26; doi: 10.1002/mrm.24384. PubMed PMID: 22736331. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Weisskoff RM, Kiihne S. MRI susceptometry: image-based measurement of absolute susceptibility of MR contrast agents and human blood. Magn Reson Med. 1992;24(2):375–383. doi: 10.1002/mrm.1910240219. [DOI] [PubMed] [Google Scholar]
- 42.Fernandez-Seara MA, Techawiboonwong A, Detre JA, Wehrli FW. MR susceptometry for measuring global brain oxygen extraction. Magn Reson Med. 2006;55(5):967–973. doi: 10.1002/mrm.20892. [DOI] [PubMed] [Google Scholar]
- 43.Langham MC, Magland JF, Floyd TF, Wehrli FW. Retrospective correction for induced magnetic field inhomogeneity in measurements of large-vessel hemoglobin oxygen saturation by MR susceptometry. Magn Reson Med. 2009;61(3):626–633. doi: 10.1002/mrm.21499. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Spees WM, Yablonskiy DA, Oswood MC, Ackerman JJ. Water proton MR properties of human blood at 1.5 Tesla: magnetic susceptibility, T(1), T(2), T*(2), and non-Lorentzian signal behavior. Magn Reson Med. 2001;45(4):533–542. doi: 10.1002/mrm.1072. [DOI] [PubMed] [Google Scholar]
- 45.Jain V, Abdulmalik O, Propert KJ, Wehrli FW. Investigating the magnetic susceptibility properties of fresh human blood for noninvasive oxygen saturation quantification. Magn Reson Med. 2012;68(3):863–867. doi: 10.1002/mrm.23282. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Boulot P, Cattaneo A, Taib J, et al. Hematologic values of fetal blood obtained by means of cordocentesis. Fetal Diagn Ther. 1993;8(5):309–316. doi: 10.1159/000263845. [DOI] [PubMed] [Google Scholar]
- 47.Wang Y, Yu Y, Li D, et al. Artery and vein separation using susceptibility-dependent phase in contrast-enhanced MRA. J Magn Reson Imaging. 2000;12(5):661–670. doi: 10.1002/1522-2586(200011)12:5<661::aid-jmri2>3.0.co;2-l. [DOI] [PubMed] [Google Scholar]
- 48.Buch S, Liu S, Haacke EM, Neelavalli J. Simulated 3D Brain Model to Predict the Phase Behaviour of Brain Geometries; Melbourne, Australia. 20th Annual Meeting of ISMRM; 2012. p. 2332. [Google Scholar]
- 49.Wharton S, Schafer A, Bowtell R. Susceptibility mapping in the human brain using threshold-based k-space division. Magn Reson Med. 2010;63(5):1292–1304. doi: 10.1002/mrm.22334. [DOI] [PubMed] [Google Scholar]
- 50.Salomir R, De Senneville BD, Moonen CTW. A fast calculation method for magnetic field inhomogeneity due to an arbitrary distribution of bulk susceptibility. Concepts in Magnetic Resonance Part B-Magnetic Resonance Engineering. 2003;19B(1):26–34. [Google Scholar]
- 51.Marques JP, Bowtell R. Application of a fourier-based method for rapid calculation of field inhomogeneity due to spatial variation of magnetic susceptibility. Concepts in Magnetic Resonance Part B-Magnetic Resonance Engineering. 2005;25B(1):65–78. [Google Scholar]
- 52.Neelavalli J, Cheng YC, Jiang J, Haacke EM. Removing background phase variations in susceptibility-weighted imaging using a fast, forward-field calculation. J Magn Reson Imaging. 2009;29(4):937–948. doi: 10.1002/jmri.21693. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Li C, Langham MC, Epstein CL, et al. Accuracy of the cylinder approximation for susceptometric measurement of intravascular oxygen saturation. Magn Reson Med. 2012;67(3):808–813. doi: 10.1002/mrm.23034. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Jain V, Langham MC, Wehrli FW. MRI estimation of global brain oxygen consumption rate. Journal of cerebral blood flow and metabolism : official journal of the International Society of Cerebral Blood Flow and Metabolism. 2010;30(9):1598–1607. doi: 10.1038/jcbfm.2010.49. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Schweser F, Deistung A, Lehr BW, Reichenbach JR. Differentiation between diamagnetic and paramagnetic cerebral lesions based on magnetic susceptibility mapping. Medical physics. 2010;37(10):5165–5178. doi: 10.1118/1.3481505. [DOI] [PubMed] [Google Scholar]
- 56.de Rochefort L, Brown R, Prince MR, Wang Y. Quantitative MR susceptibility mapping using piece-wise constant regularized inversion of the magnetic field. Magn Reson Med. 2008;60(4):1003–1009. doi: 10.1002/mrm.21710. [DOI] [PubMed] [Google Scholar]
- 57.Bard H, Makowski EL, Meschia G, Battaglia FC. The relative rates of synthesis of hemoglobins A and F in immature red cells of newborn infants. Pediatrics. 1970;45(5):766–772. [PubMed] [Google Scholar]
- 58.Zijlstra WG, Buursma A, Meeuwsenvanderroest WP. Absorption-Spectra of Human Fetal and Adult Oxyhemoglobin, De-Oxyhemoglobin, Carboxyhemoglobin, and Methemoglobin. Clin Chem. 1991;37(9):1633–1638. [PubMed] [Google Scholar]
- 59.Liu S, Neelavalli J, Cheng YC, Tang J, Mark Haacke E. Quantitative susceptibility mapping of small objects using volume constraints. Magn Reson Med. 2012 May 8; doi: 10.1002/mrm.24305. PubMed PMID: 22570268. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Haacke EM, Tkach JA. Fast MR imaging: techniques and clinical applications. AJR American journal of roentgenology. 1990;155(5):951–964. doi: 10.2214/ajr.155.5.2120964. [DOI] [PubMed] [Google Scholar]
- 61.Irarrazabal P, Nishimura DG. Fast three dimensional magnetic resonance imaging. Magn Reson Med. 1995;33(5):656–662. doi: 10.1002/mrm.1910330510. [DOI] [PubMed] [Google Scholar]
- 62.Larson PEZ, Gurney PT, Nishimura DG. Anisotropic field-of-views in radial imaging. IEEE transactions on medical imaging. 2008;27(1):47–57. doi: 10.1109/TMI.2007.902799. [DOI] [PubMed] [Google Scholar]
- 63.Pisani L, Bammer R, Glover G. Restricted field of view magnetic resonance imaging of a dynamic time series. Magn Reson Med. 2007;57(2):297–307. doi: 10.1002/mrm.21115. [DOI] [PubMed] [Google Scholar]
- 64.Studholme C. Fetal brain mapping. Biomedical Imaging (ISBI), 2012 9th IEEE International Symposium on. 2012:495–498. [Google Scholar]