Computational and Experimental Characterization of RNA Cubic Nanoscaffolds

Abstract

The fast-developing field of RNA nanotechnology requires the adoption and development of novel and faster computational approaches to modeling and characterization of RNA-based nano-objects. We report the first application of Elastic Network Modeling (ENM), a structure-based dynamics model, to RNA nanotechnology. With the use of an Anisotropic Network Model (ANM), a type of ENM, we characterize the dynamic behavior of non-compact, multi-stranded RNA-based nanocubes that can be used as nano-scale scaffolds carrying different functionalities. Modeling the nanocubes with our tool NanoTiler and exploring the dynamic characteristics of the models with ANM suggested relatively minor but important structural modifications that enhanced the assembly properties and thermodynamic stabilities. In silico and in vitro, we compared nanocubes having different numbers of base pairs per side, showing with both methods that the 10 bp-long helix design leads to more efficient assembly, as predicted computationally. We also explored the impact of different numbers of single-stranded nucleotide stretches at each of the cube corners and showed that cube flexibility simulations help explain the differences in the experimental assembly yields, as well as the measured nanomolecule sizes and melting temperatures. This original work paves the way for detailed computational analysis of the dynamic behavior of artificially designed multi-stranded RNA nanoparticles.

1. Introduction

In the process of constructing nanoscale shapes out of RNA, it is now possible to incorporate RNA-based functional moieties such as aptamers, riboswitches, ribozymes, or short interfering RNAs (siRNAs), highlighting the capacity of RNA nanoscaffolds to simultaneously deliver specific therapeutics targeting selective human tissues while controlling the composition and stoichiometry of the delivered drugs [1–10]. These potentially therapeutic nanoparticles utilize internal biochemical processes, such as RNA interference (RNAi) that is activated by RNA markers to shut down diseases at their source [11–13]. Techniques for constructing nanoparticles that can both diagnose and target diseased cells have given RNA a new role in nanomedicine. Such functionalized nanostructures are able to down-regulate specific gene expression in cancerous cells, with positive results being confirmed by animal studies [5, 6, 8, 13, 14]. All this suggests that RNA molecules may offer a high degree of natural versatility and biologically relevant functionality when used as building blocks in the construction of nanomaterials [3, 5, 6, 15–20]. The correspondences between the fields of DNA and RNA nanotechnology, as well as the uniqueness of each, are discussed in the following reviews [5, 8, 21].

Earlier work in RNA nanotechnology demonstrated the assembly of modular RNA units into functional dimers [22–25], trimers [10, 26–29], tetramers [9, 10], pentamers [10], hexameric nano-rings [30–33], heptamers [10] together with non-functionalized octameric squares [34], 1D and 2D arrays composed of filaments [35], and tecto-squares [36]. Recently, we have explored the structural potential of RNA self-assembly for designing 3D supra-molecular RNA architectures by engineering an RNA antiprism decorated with proteins [37] and several different cubic nanoscaffolds [38, 39] functionalized with aptamers [38] and therapeutic siRNAs [7, 33]. All these studies suggest that RNA nanoscaffolds have become promising candidates for therapeutic purposes. Therefore, it is desirable to do detailed studies of the existing RNA nano-constructs in order to better understand and possibly improve their further design and fabrication. In this work, we report on the computer-aided design and analysis supported by experimental studies that aim to improve the assembly properties of the existing RNA cubic nanoscaffolds which are composed of six single-stranded RNAs designed to interact with each other through canonical Watson-Crick base pairing. These types of interactions are somewhat analogous to those found in DNA-based nanoparticle formation [39, 40].

This is the very first application of Elastic Network Modeling to large, multi-stranded and non-compact nano-scale structures engineered from ribonucleic acids, in the effort to characterize their dynamic behavior. The limits of the dynamic distortions can help to predict melting characteristics, the expected effective dimensions, and to assess the potential impact of the differences in the dynamics of the nanocube design variants on the efficiency of assembly, and thus the experimental yield. Elastic Network Models and normal mode analysis offer fast and powerful methods to describe the dynamic properties of molecules. Elastic networks are composed of nodes and connecting springs, and with normal mode analysis they can predict the biologically relevant low frequency collective motions of biomolecules [41–43]. The Gaussian Network Model (GNM) introduced by Bahar et al. assumes a Gaussian distribution of node fluctuations around their positions at equilibrium and uses uniform springs (i.e. springs with a uniform harmonic spring constant) [44]. GNM can be used to determine the magnitudes of network node fluctuations, which are assumed to be the same in all directions, i.e. isotropic. The Anisotropic Network Model (ANM), used in this study, takes into account the directionality of the positional fluctuations by calculating for each node of the network their fluctuation vectors in addition to their relative magnitudes of motion [45, 46]. Compared to molecular dynamics (MD) simulations, the ANM calculations take orders of magnitude less time. For example, an all-atom (i.e. each atom is a network node) ANM calculation of the top 150 modes of a nanocube assembled out of a total of 288 RNA nucleotides (9,134 atoms) takes approximately 42 minutes on a single 3.0GHz Intel Xeon processor workstation, whereas an explicit solvent molecular dynamics trajectory of approximately 50 ns would take from two weeks to a month to compute, depending on the choice of processors. A recently published method for characterizing nanoscale models employs symmetry with hierarchical degrees of freedom [47, 48]. It combines all-atom energy functions with fast sampling to find favorable structure states.

This paper is organized to follow the logic of our computational and experimental work, which informed each other, to optimize and characterize the cubic nano-scaffold designs. Results are immediately discussed to aid the presentation. First, we present in detail the in silico design of eight cube variants, in which the helical edges of either 10 or 11 bps long were connected in the cube corners by single-stranded bridges varying in size from 1 nt to 3 nt and a design without any single-stranded links. The initial modeling also included optimization of the helix sizes. The predicted design strengths and weaknesses were verified in a series of assembly experiments that excluded, as computationally predicted, the unbridged (0 nt) cubes from further consideration. Next, we present the determination of the nanoparticle sizes. The sizes of the assembled nanocubes were measured via Dynamic Light Scattering (DLS) experiments that indicated nanoparticles of sizes larger than those of the initial models. Therefore, we rescaled our models and characterized their flexibility (distortion limits) as a way of determining their potential apparent size changes with the aid of the Anisotropic Network Model. The sizes of the distorted cubes matched the DLS results, and the distortions of the initial models were energetically neutral. Finally, we present examination of the relative strains and stabilities of the cubes’ components and their possible relationship to the melting properties of the two best (most efficiently assembling) cube designs. The melting temperatures of the two best-assembling nanocubes were obtained by Thermal Gradient Gel Electrophoresis (TGGE) experiments. Computational analysis of the cubic nanoscaffold models revealed clear differences in their stiffness and in the computed B-factors. These results seem to reflect the melting temperature differences. Thus, we showed that the computational design and characterization of the nanoscaffolds can improve the assembly properties and help in predicting and explaining the characteristics of the assembled nanoparticles.

2. The use of coarse-grained structure dynamics characterization with ANM

While we have shown in the past that it is possible to employ Molecular Dynamics to characterize even relatively large nanostructures, the method is computationally intensive and time consuming [49]. Therefore, in this study we employed an Elastic Network Model (ENM), specifically the Anisotropic Network Model (ANM), to characterize the dynamic properties of the RNA nanoscaffolds with different structural design parameters. The ANM methodology is capable of predicting both relative magnitudes and directions of the major modes of motion (normal modes) of a molecule. Refer to the Methods section for more details on ANM and to Brooks et al. [50] and Atligan et al. [45] for a mathematical description of the method. Unlike Molecular Dynamics (MD) simulations, which model motions of all atoms based on empirically derived force fields [51–53], ANM focuses on the harmonic motions of a set of points (network nodes) representing the initial coordinates of a molecule. These points are connected with springs approximating interactions among them, as illustrated in Figure 1. Even though it is a coarse-grained method, it has been shown that the predicted motions correspond closely to the principal components derived from MD trajectories, multiple crystal structure conformations, or NMR ensembles [42, 54]. Numerous studies comparing ANM-predicted motions with the available experimental data demonstrated applicability of the method to characterization of naturally occurring proteins, protein-RNA complexes and self-folded single-stranded RNAs alone [55–59]. For example, Wang et al. [57, 58] showed that ANM-based lowest frequency normal modes can predict anti-correlated, experimentally known ratchet-like motions of the ribosomal subunits [60] within the full ribosome, as well as motions facilitating translocation of tRNA inside the ribosome (based on the crystal structures PDB#: 1J5E, 1GIY and 1GIX reported by Wimberley et al. [61] and Yusupov et al. [62]). These studies demonstrated that the dominant motions predicted by ENMs for a representative structure correspond to the ensembles of experimentally captured conformational variants. The emerging consensus is that the collective motions of structural domains are responsible for the major, biologically relevant, low frequency motions of molecular structures, that these motions depend mostly on the shape of the molecules, and that they are well characterized by ANMs. In addition, it has been shown that elastic networks are capable of reproducing experimentally measured B-factors [42, 44, 63–65]. In this study we present a successful application of the ANM methodology to characterization of multi-stranded, engineered RNA-based nanoparticles that are less atomistically dense than the natural RNAs (in terms of number of atoms per unit volume).

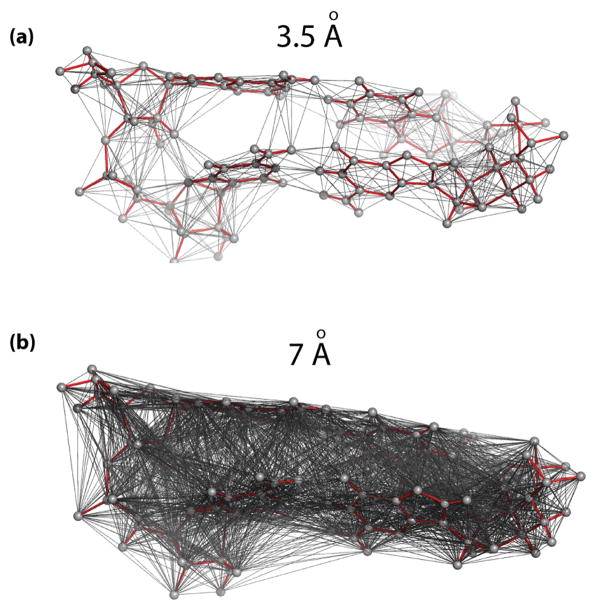
Figure 1.

Elastic Network Model (ENM) representation of RNA structures. (a) A small, 2bp-long fragment of an RNA helix (red sticks) is overlaid with its ENM representation. A set of network nodes (gray spheres) represents the initial coordinates of a molecule. The nodes are connected with uniform springs approximating interactions among them (grey lines). Connectivity based on a cutoff distance of 3.5Å is shown to make the illustration more legible. The connectivity network captures intra and inter nucleotide, base pair and stacking interactions. (b) The same two base pairs shown with a connectivity network based on a cutoff distance of 7Å, the parameter used in the Anisotropic Network Model (ANM, a type of ENM) simulations in this study (see also Supplementary Figure S4).

The ENM-based calculations are orders of magnitude faster than MD simulations for the same molecules. Whether the nodes of the network correspond to all the atoms of the simulated molecule or a coarse-grained subset of it, which influences the speed of computations, the complexity and time of calculations can be further reduced by limiting the number of modes to be calculated. This focuses the calculation on the relatively small subset of lowest frequency modes, which are responsible for the majority of total motions. The high frequency modes capture localized motions that do not impact the overall dimensions of the structures, and thus, can be viewed as irrelevant to this study and ignored.

3. Computational and Experimental Nanocube Design and Assembly

Computational design of eight cube variants is outlined in the next section and discussed in more detail in the Supporting Information. The helical edges of the cubes were designed to be connected by single-stranded bridges from 1 nt to 3 nt long. However, a design variant without any single-stranded links was also explored. The computer modeling phase also optimized the helix sizes on the cube edges, considering either 10 or 11 bps in each helix. The predicted design strengths and weaknesses were verified by assembly experiments. As it was predicted in silico, the cube design without any single-stranded linkers (i.e. unbridged, 0 nt) has been eliminated from further consideration.

3.1 Computational generation of RNA cube models predicts best design choices

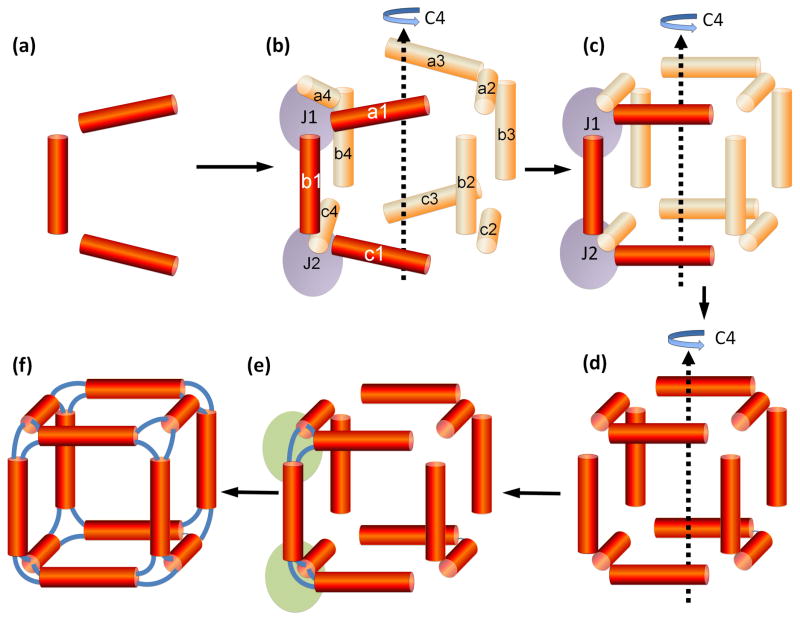
Key design considerations in the RNA cube structure design are (i) the number of base pairs the helices should contain and (ii) the number of residues at the single-stranded corner loop regions (each corner can be viewed as an internal loop with the emanating helices, or a three-way junction). Both of these questions have been successfully addressed using several novel approaches to RNA 3D modeling. In Figure 2, we present a general method for generating RNA 3D structural models. This approach (called the helix-centric approach) can be viewed as a coarse-grained method that places helices (treated as rigid bodies) such that the flanking residues of the helical strands are to be connected within a specified distance range. This is modeled within the NanoTiler [66] software as a special type of constraint, called a “junction constraint.” A junction constraint is a data structure that can be used to compute a score that indicates how well a set of n helix ends could form an RNA n-way junction (a cube-corner in this case), possibly involving single-stranded linker regions that connect the flanking residues. The junction constraint data structure keeps track of which helix ends form a junction, and the minimum and maximum distance between the 3′ and 5′ residues that are to be connected. Once the junction constraints are specified, a simulated annealing algorithm optimizes the helix orientations using as an objective function the sum of the junction constraint scores as well as a repulsive potential that favors structures without steric clashes. For the case of the RNA cube, an additional constraint of 4-fold rotational symmetry (C4) has been applied (see the Supporting Information). In other words, instead of optimizing the position of 12 helices (corresponding to the 12 edges of the cube), the positions of only 3 helices are optimized; the remaining helices are treated as symmetry copies. The number of base pairs per helix as well as the maximum distance between the terminal residues of the strands that are to be connected can be viewed as parameters. The results of this procedure indicated that 10nt helices correspond to 3D structural models with the smallest amount of steric hindrance. The identified minimal loop distance of 8Å suggested that the cube corners should be at least 1nt. The Supporting Information contains detailed descriptions of this and two other variants of the cube model generating procedures. Uracils were selected for use in the single-stranded corner linkers due to their small size, and because in the long term they are particularly suitable to co-transcriptional chemical modification increasing the resistance of the full nanoparticle to ribonucleases [33].

Figure 2.

Nanocube model building procedure employing the NanoTiler program: helix-centric approach. This figure illustrates geometric aspects of the design procedure. Refer to Figure 3 for the illustration of how this cube is experimentally assembled from six single strands of RNA. (a) Atomic coordinates of 3 idealized RNA double-helices (b) Two “junction constraints”, indicated as J1 and J2 are defined, corresponding to two cube corners (purple). Each junction constraint defines a connectivity of a 3-way junction (a cube corner). It keeps track of the 3′ and 5′ ends of the helices that are connected by single-stranded regions (simulated as distance constraints). Notably, only the helices a1, b1 and c1 are represented by virtual atom coordinates. The other helices are mirror copies (due to the four-fold rotational symmetry, indicated as C4) and are not at this stage represented by atom coordinates. For example, helix a4 is a 270 degree rotational copy of helix a1. The positions of the helices a1, b1 and a4 contribute to the junction constraint J1; the positions of the helices b1, c1, and c4 correspond to the junction constraint J2. (c) The positions of the three helices a1, b1 and c1 are optimized in order to minimize the sum of the error scores that corresponds to the junction constraints J1 and J2. Only coordinate systems representing translational and rotational offsets of those three helices are being optimized; i.e. those 3 helices are treated as rigid bodies. (d) Using rotational symmetry copies, atom coordinates for all 12 helices of the cube are generated. These steps also involve a visual or automated inspection of the generated structure, because the generated structure might contain steric clashes. (e) Bridging loops consisting of 2 nucleotides are generated using NanoTiler. Only 6 bridges, corresponding to two cube corners (indicated as purple ovals) are distinct. All other loop regions are symmetry copies of those initial loop regions. (f) Strands are fused and nicks are inserted at the appropriate positions. The original place-holder sequence is mutated to the desired final sequence. The steps in stage f break the four-fold rotational symmetry.

3.2 Native PAGE experiments justify design choices

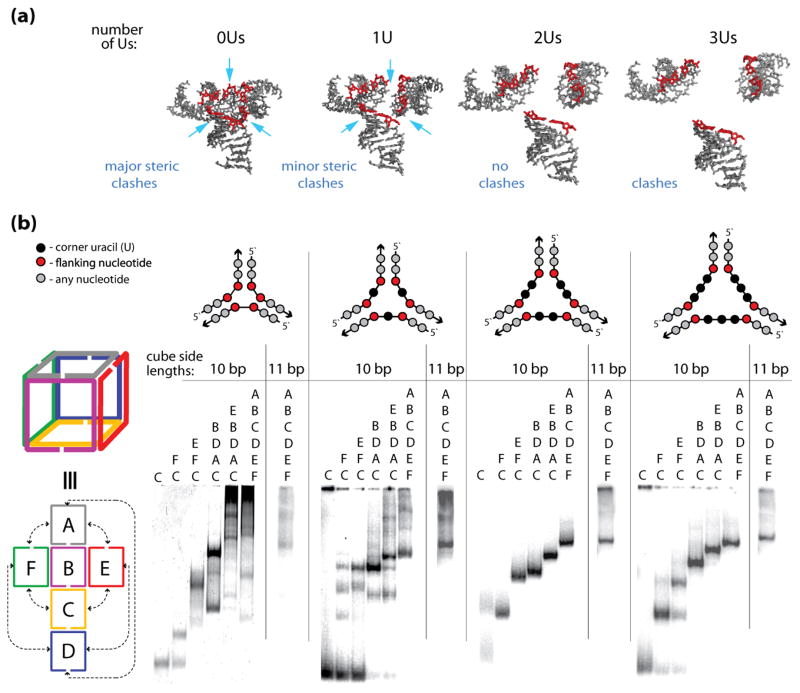
To check the computer aided predictions, eight design variants with identical sequences but different numbers of Us (0, 1, 2, or 3) at the corners and a different number (10 or 11) of bps per cube side (sequences are presented in the Supporting Information) were engineered and tested by gel experiments (Figure 3b). The native polyacrylamide gel electrophoresis (native-PAGE) is an electrophoretic separation technique typically used for characterizations of radiolabeled RNA assemblies [25, 67, 68]. Native PAGE separations, shown in Figure 3b, are run in non-denaturing conditions with major dark bands corresponding to the main products of the assemblies. These products are electrophoretically separated based on their molecular mass, intrinsic charge and more importantly size and shape of the overall structure. The more complex assemblies migrate on the gel at lower rates hence, staying closer to the loading well. Major dark bands on the gels shown in Figure 3b correspond to the main products of the assemblies. Assembled RNA cubes are expected to migrate as a single band with the lowest mobilities (upper bands). The native PAGE results indicate that the designs without any Us at the corners tend to aggregate and do not form any desirable nano-scaffolds. Designs with 1U at the corner assemble with yields not exceeding 50%, while constructs with 2 and 3Us, show reproducible assemblies with yields higher than 95%. The increase in lengths of the cube sides from 10 to 11bp, negatively affects the results of all assemblies. All results are in a good agreement with the computer modeling estimates and prove that the dimensions of the cubic RNA nanoscaffolds play a critical role in their formations. The 2U cube formation has also been verified and explored experimentally by other methods in an earlier study, including imaging by cryo-electron microscopy (cryo-EM) [38].

Figure 3.

The sizes of the cube corners define the efficiencies of the cube assemblies. (a) 3D models of the cube junctions that were generated to find the minimum number of nucleotides required to link corner helices. The nucleotides indicated in red are the end base pairs that are connected to the single stranded uracil bridges (not shown). The structures correspond to linker loop sizes of 0–3 uracils (Us) respectively. These linker loop sizes are simulated as distance constraints between edge O3′ and P atoms of helices that are designed to be linked. Structure 0U has a distance constraint of maximally 4 Ǻ distance between O3′ and P atoms. This corresponds to no linker loops and the structure has significant steric clashes. A larger distance constraint (1U) of maximally 9 Ǻ corresponds to a structure with 1 residue linker regions. The structural model suggests that the electrostatic interactions between the negatively charged phosphate groups could be somewhat unfavorable and that the cube formation would benefit from the linkers being at least 2 nt-long (structures 2Us and 3Us). (b) native-PAGE experiments indicating the assembly patterns of the RNA nanocubes having zero, one, two, and three single-stranded corner uracils (0U, 1U, 2Us, and 3Us respectively) and corresponding cubes with additional base-pair per each side (11 bp). Color-coded three-dimensional and two-dimensional schematic representations of interactions for the A–F cube sequences (shown to the left of the gel lanes) and schematic representations of cube corners (above the gels) are shown. Corresponding sequence strands are indicated above each lane of the gel.

4. Experimental and Computational Determination of Nanocubes’ Sizes

As determined by the Dynamic Light Scattering experiments, the sizes of the assembled nanocubes were larger than those of their initial in silico models. This finding led us to scale-up (and rebuild) our models and predict their distortion limits with the aid of the Anisotropic Network Model. The potential apparent size changes predicted by the ANM matched the experimental results.

4.1 Dynamic light scattering (DLS) experiments

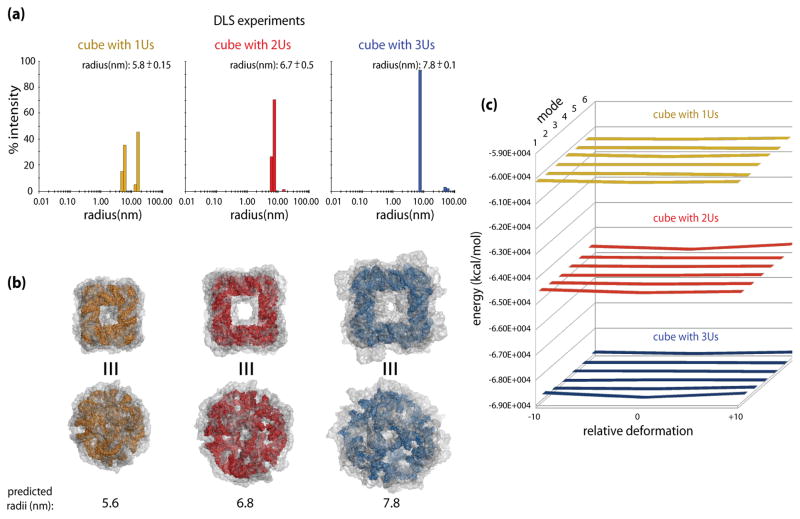
Using dynamic light scattering (DLS), the hydrodynamic radii (Rh) of the RNA cubes with a different number of Us per corner were determined to be 5.8 ±0.15, 6.7 ±0.5, and 7.8 ±0.1 nm for cubes with 1U, 2Us and 3Us, respectively (Figure 3a). For the 2U cube the dimension determined from the Cryo-EM data was approximately 7.0 nm. Also, the peak of larger assemblies in the DLS plot (Figure 4a) for 1U cube is consistent with the native-PAGE experiments (Figure 3) demonstrating approximately half of the cube fragments assembled in malformed constructs with lower gel mobilities. The DLS experimental values match well the predicted radii of circumscribed spheres around the geometric cubes, assuming an ideal geometry of a cube and idealized A-form helix dimensions. However, the more accurate models we are dealing with here have truncated corners because of the single-stranded corner bridges (Figure 4b and 5a), and their initial sizes (of 4.8, 5.3, and 6.1 nm for 1U, 2Us and 3Us cubes, respectively, measured as the maximum radii from the all atom centroid) fall short of the experimental data (Figure 4a). For this reason we explored the changes in the apparent cube dimensions, as described in the following computational sub-section. The results considering the dynamics of the models showed very good agreement with the DLS data.

Figure 4.

Predicted and measured dimensions of the nanocubes with 1U, 2U and 3U single-stranded corner linkers, connecting 10bp-long helical edges. (a) Dynamic light scattering (DLS) experiment results for RNA nanocubes having one, two, and three single-stranded corner uracils respectively (1U in yellow, 2Us in red, and 3Us in blue). (b) Colored models of the maximum size cubes (refer to the text for details); dark yellow for the 1U cube, red for the 2U cube, and blue for the 3U cube. Top views show cube faces, while the bottom views focus on one of the truncated corners linked with single strands. The transparent gray envelopes of motion around the cubes illustrate maximum extents of the distortions predicted by the ANM simulations for the top six normal modes. The envelopes delineate the increase in the apparent dimensions of the cubes due to distortions of their initial shapes, which bring them into agreement with the experimentally observed results. (c) The energy plots for the 1U, 2U, and 3U cubes (color-coded as elsewhere) based on the minimized energies of the starting models (relative deformation of 0) and the maximum distortions (−10 and +10). Relative deformations correspond to structural snapshots at discrete points in the calculated distortion trajectories. Data for the top six modes of motion is shown, with mode 1 being the closest to the viewer. The plots show nearly flat (within a fraction of one percent) energy landscapes for the top 6 mode distortions, indicating free mobility of the models to the limits of steric clashes. Refer to the text for details.

Figure 5.

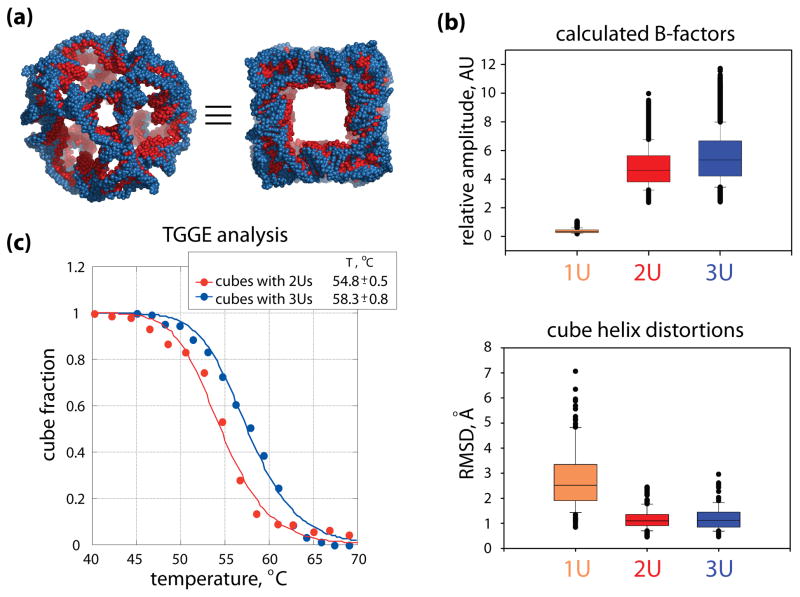
Structural dynamics yields insights into melting temperature differences between the 2U and 3U cubes. (a) Two views of the maximum size (refer to the text for details) overlaid models of the 2U (red) and 3U (blue) cubes, featuring the truncated corners linked with single strands of uracils (left) and the cube faces (right). In both cubes the helical, 10 bp-long edges have the same nucleotide make-up. (b) Box plots of the calculated normalized B-factors (top) and the geometric distortions in the helices (bottom). In both plots the medians are marked as horizontal lines inside each box, and the 25^th and 75^th percentile values are indicated by the bottom and the top extents of the boxes. Error bars below and above each box indicate the 10^th and 90^th percentile values. Outliers are shown as overlapping black dots. In the top plot, the B-factors were calculated for the top 6 normal modes of motion (cumulatively) for all the atoms in each of the three cube models (in arbitrary units, marked as AU). The difference in the atomic fluctuations in the 1U cube and the 2U and 3U cubes is striking, but the smaller difference between the atomic mobility in the 2U and 3U cubes is also statistically significant. The median values for the 1U, 2U and 3U cubes are, respectively, 0.4, 4.6, and 5.3. Pair-wise comparisons of the data sets show statistically significant differences with the p-value P =< 0.001 in Mann-Whitney tests. The lower box plots capture geometric distortions measured for the helices of the three cube models subjected to normal mode motions. Helices in the 2U and 3U cubes experience minimal distortions while the motions of the whole cubes increase with their size (top b panel). RMSDs were calculated for the P atoms of the helical backbones, between the initial ANM states and the extreme distortion frames in the top 6 normal modes. The median values for the 1U, 2U and 3U cubes are 2.5Å, 1.1Å and 1.1Å, respectively. The differences between the 2U and 3U cube helix distortions are not statistically significant. Together with the energy data calculated for the cubes (refer to the text), the results shown in (b) suggest that corner linkers contribute to the melting temperature differences measured for the 2U and 3U cubes. (c) Melting curves obtained from thermal gradient gel electrophoresis (TGGE) analysis for the nanocubes with two and three corner uracils (2Us and 3Us respectively). From the TGGE experiments (Supporting Information, Figure S1), T_m for 3Us cubes was determined to be higher by ~ 3.5°C than for the cubes with 2Us. These results are in a good agreement with UV melting experiments (data not shown).

4.2 Applying ANM to predict the size limits of nanocube motions

Because the initial cube model dimensions were smaller than the DLS-based experimental results, we rebuilt the models in search for maximum sizes that would retain the original topology (base pairing) after energy minimization in Amber. Such models’ dimensions still fell short of the DLS results. Therefore, they were subjected to Anisotropic Network Model (ANM) simulations in order to explore other dynamic states that could increase the apparent sizes of the models. The methodology developed in this study is described in detail in the Supporting Information. Briefly, combining ANM dynamics and Amber minimizations required using all atom models (see Supplementary Figure S4) [51–53]. Analysis of the ANM normal modes indicated that the majority of motions of the studied nanocubes are captured by the first 25 modes. Most importantly, the largest distortions to nanocube geometry, a focus of the ANM simulations in this study, were observed in the top 6 modes for all the models. The largest distortions pushed the cube models to the limits of internal steric clashes, but those states could be structurally cleaned-up (corrected) and minimized to a nearly constant energy level for each cube, as shown in Figure 4c. For this reason we concluded that collisions limited the maximum extents of the cube distortions, and that such dynamic states could correspond to the maximum observable nanoparticle sizes and should be analyzed further. The key results are discussed next and illustrated in Figure 4b and 4c.

The dimensions of the initial computational models (maximum radii from the all atom centroid) were 47.7Å, 52.7Å, and 60.9Å for the 1U, 2U, and 3U-bridged corner cube models, respectively. The Amber-minimized ANM-distorted cube models increased their maximum dimensions. By overlaying the Amber-minimized normal mode motions states for the top 6 ANM modes we created distortion envelopes illustrated in Figure 4b. The measured maximum radii for the distorted cubes were 56.4Å for 1U, 68.2Å for 2U, and 78.0Å for the 3U cube model. These are approximately 97%, 102%, and 100.0% of the DLS-based (hydrodynamic) radii for the 1U, 2U, and 3U cubes, respectively. Higher modes produced distortions resulting in lower maximum radii and are not shown in Figure 4b for the sake of clarity. The absolute increases in the radii of the maximally distorted 1U, 2U, and 3U cubes, relative to those of the starting models, are 8.7Å, 15.5Å, and 15.9Å respectively. These represent a relative increase of 18% for the 1U cube, 29% for the 2U cube, and 26% for the 3U cube. Another striking difference between the cube models is that the eigenvalues calculated for the 1U cube model are an order of magnitude larger than those predicted for the 2U and 3U cube models (the last two are comparable with each other). Because eigenvalues correspond to the inverse squared motion frequencies these results indicate that all the motions of the smallest cube have higher frequencies, and this observation is consistent with the hypothesis that the 1U cube is much more restrained in its motions by the tight corner bridges.

5. Melting properties of the cubes

Given the above results that bring modeling and experiments into agreement, further exploration of the cube dynamics was undertaken with the idea of gaining insight into the observed melting temperature differences between the two larger (2U and 3U) and better self-assembling cubes.

5.1 Thermal gradient gel electrophoresis (TGGE) experiments

To determine the relative thermodynamic stability between the cubes having either 2Us or 3Us at each corner (Figure 5a), melting temperatures for these constructs were determined by TGGE experiments (Figure 5c). In these experiments (Supporting Information, Supplementary Figure S1), the fractions of the cubes (f) derived from the gel quantifications are plotted versus the corresponding temperatures and the temperature at which f = 0.5 is the melting temperature, T_m. The T_m’s for the cubes with 2Us and 3Us were measured to be 54.4°C and 57.8°C respectively and are in a good agreement with UV melting experiments (data not shown).

5.2 Calculating the relative strain and flexibility of cubes’ structural components

We have also analyzed the cumulative mobility of the individual atoms (network nodes) predicted by ANM across the first 6 modes (Figure 5b). The plotted values are mean-square fluctuations, which are comparable to B-factors [42, 63–65]. Although we do not have experimentally measured B-factors, which could be used to normalize the calculated data, we did scale the individual mode amplitudes based on the available physical parameters for each cube model, i.e. structure energy and physical collision limits. In the calculations of the B-factors, the contributions of individual modes were normalized based on the maximum amplitude scaling factor for each nanocube, allowing us to compare the three cube models (refer to section Applying ANM to predict the dimensional limits of nanocube motions and the Supporting Information).

The mean scaled B-factor values calculated for all atoms (and normalized by the number of atoms in each cube model) show a large gap between the values for the 1U and 2U cubes and a smaller but clear difference between the 2U and 3U cube models subjected to ANM. For example, for the first non-zero mode (lowest frequency), the values are 0.2 ±0.1, 1.2 ±0.9, and 2.1 ±1.5 for the 1U, 2U, and 3U cubes, respectively. This trend holds for the means of the first six modes taken cumulatively, for which the 1U, 2U, and 3U cube B-factors are 0.4 ±0.2, 4.8 ±1.4, and 5.6 ±1.7, respectively (see Figure 5b). The difference in the median values between the calculated scaled B-factors for the top 6 modes (cumulatively) for the 2U and 3U cubes, 4.6 and 5.3, respectively, showed a statistically significant difference using the Mann-Whitney Test with a p-value P < 0.001. The same is true for the other pair-wise comparisons of the calculated B-factors. Comparisons between the cubes also show that the calculated B-factors for the atoms of only the corner nucleotides (i.e. evaluated separately) grow with the increase in their length and are statistically significantly different between the pairs of compared cube models (means at 0.6 ±0.2, 4.5 ±0.7, and 4.9 ±1.2 for the 1U, 2U, and 3U cube corner bridges, respectively). The rate of increases in the B-factors of the helical regions (the sets of twelve helices making up each cube are identical in size and sequence in all the cube models) is even faster (means of 0.4 ±0.1, 4.9 ±1.4, and 5.7 ±1.8 for the 1U, 2U, and 3U cube helices, respectively). This measure, however, may be due to collective motions or relatively undistorted helices and requires further examination, as described below.

The geometric distortions of the helices in all the cube models for the top 6 normal modes were measured by calculating the root-mean-square deviations (RMSDs) for the helix backbone P atoms between the ANM equilibrium state and the previously determined maximum distortions in each mode (all after structure-correcting full cube energy minimizations). The results show that in the 2U and 3U cubes the helices undergo minimal distortions in the top 6 normal modes (see Figure 5b). The mean RMSDs of the 2U and 3U cubes are 1.2 ±0.4Å and 1.2 ±0.5Å, respectively. The differences in RMSDs between the corresponding P atoms of the 2U and 3U cube helices are not statistically significant (P=0.798, Mann-Whitney test). The 1U cube helices experience statistically significant higher distortions in comparison to the 2U and 3U cubes (P=<0.001, Mann-Whitney test). The mean RMSD value of these distortions in the 1U cube model is 2.8 ±1.2Å. In general, distortions of the opposite cube faces tend not to be symmetric. Thus, considering that the helices in the 2U and 3U cubes experience minimal distortions while the motions of the whole cubes increase with their size, the calculated B-factors point to the nucleotides in the single-stranded corner bridges as individually most mobile, or flexible. The distortion “trajectories” which can be viewed as movies for individual normal modes, also clearly show that all the cubes tend to use the corner linkers as pivot points in bending (see Supplementary Figure S5). The idea that the stress of distortions is relieved in the single-stranded corner bridges appears to be consistent with the observed flat energy landscape of the minimized distorted cubes. Motions in the helical regions observed in the top normal modes are either collective rotations or translations around the corner bridges. Torsional compressions and elongations mostly affect the helices in the 1U cube.

The energy of the minimized 1U cube is −60,197 kcal/mol. For the 2U cube it is −64,691 kcal/mol, and for the 3U cube it is −68,824 kcal/mol (see Figure 4c). However, these differences are in part due to different numbers of nucleotides in each model. To assess the strain that each cube model exerts on its helices, which have identical sizes and sequences in all models, we calculated the energies of the helices alone in the minimized full cube models. These results were −33,682 kcal/mol, −34,606 kcal/mol, and −36,396 kcal/mol for the 1U, 2U, and 3U cube helices, respectively. They can all be minimized (relaxed in the absence of the single stranded bridges) to a common level of approximately −53,000 kcal/mol. The elevated energy components point to stretched bond lengths and distorted angles as the main contributors, i.e. again, strain resulting from geometric distortions. These results indicate clearly that the most geometrically constrained 1U cube subjects its helices to most strain (distortions) and that the longer the single-stranded corner bridges (within the tested limits from 1nt to 3nt), the less strain (distortion) on the helices (i.e. the lower their energy).

Thus, we have shown that the mean mobility of the cubes increases with the increase in the length of their corner bridges. At the same time the strain of the helices, indicated by the decrease in their energies measured within the context of the full cube models, decreases with the increase in the length of the corner bridges. Low geometric distortion levels were measured for helices subjected to the predicted normal mode motions of the cubes. These low geometric distortions, especially low for the 2U and 3U cubes, indicate that the helices are moving as minimally distorted units. Combined, all of these observations indicate that the differences in the single stranded regions are a key factor contributing to the observed melting temperature increase in the 3U cube relative to the 2U cube. One could argue that the flexibility of the single-stranded corner linkers adds to their entropy with the increasing length. In addition, one has to remember that, even though we focused on the maximum-sized cubes, the 2U and 3U linkers can accommodate a large variability of separations between the helices, thus adding to the number of possible states of the cubes. For example, relative to the initial model of the 2U cube, (see section Computational generation of RNA cube structures justifies design choices) the maximum size used in ANM simulations increases the distances between the helices parallel to each other by 15%. For the 3U cube it is 21%. Thus, the number of states, even before all the distortions are considered, is growing with the increasing length of the single-stranded linkers. It is also reasonable to assume that the occurrences of reversible base-pair breaks within the helical ends nearest to the single-stranded corner links are more likely for the less strained helices connected with longer single-stranded bridges. All of the above observations combined are in good agreement with the experimentally measured melting temperature differences for the 2U and 3U cubes, illustrated in Figure 5. In addition, the much more limited flexibility of the 1U cube may explain the experimental evidence of a much lower experimental efficiency of its assembly (yield). It may be that in the design where the full nanostructure assembly requires six strands to anneal together, the flexibility needed for the whole process to succeed is negatively impacted by the 1U corners, leading to the observed approximately 50% success rate. The larger dimensions of the species in the second DLS peak (Figure 4a), too large to correspond to properly formed 1U cubes, suggest that these are unknown malformed species, the characterization of which is beyond the scope of this paper.

6. Conclusions

In summary, we have demonstrated the power of rational design and, to the best of our knowledge, the very first application of coarse-grained Elastic Network Modeling to designed multi-stranded, non-compact nano-structures made out of nucleic acids. Initial design exploration with the aid of the NanoTiler program indicated that single-stranded bridges linking helices in the cube corners are necessary for assembly, and that 10 bps, rather than 11 bps long helices forming the edges of the nanocubes would produce less-strained and better assembling nanoparticles. These findings were confirmed experimentally. Evaluation of another design factor – the lengths of the single-stranded corner linkers – required characterization of the dynamics (flexibility) of the nanoparticles. ANM proved to be a sufficiently precise method to evaluate the gross dynamic characteristics of the three cube designs and to differentiate between them. ANM simulations of the three nano-cube variants showed that flexibility of the models has to be considered in order to account for the experimentally measured dimensions. The initial cube model sizes fall short of the DLS data, whereas the dimension changes resulting from the predicted distortions of the initial cube models are in excellent agreement with the experimental data. One has to keep in mind that our evaluations are based on the lowest frequency normal modes and each mode is used independently. It is possible that the combination of multiple modes would further increase the maximum dimensions of the cube models. However, at this stage we have no means (no phasing information) to accurately combine the modes. One way of partially exploring this combinatorial problem could be by starting the combined simulations with the same phase for all the modes and letting the frequency differences between them naturally shift the relative mode phasing over long periods of time. We are currently exploring this issue and hope to report on it in the future. Cube characterization via ANM revealed more constrained motions in the 1U cube in terms of absolute increases in the maximum dimensions, relative to the 2U and 3U cubes, as well as an order of magnitude higher frequency of motions in the 1U cube. Flat energy landscapes for the deformations in all the cubes indicated that the differences in their deformability are solely due to limitations imposed by the steric clashes resulting from deformations. These characteristics are consistent with the experimentally observed ~50% lower assembly yield for the 1U cube. Computational characterization indicated elevated energy levels calculated for the helices (alone) in the cubes with shorter corner bridges, indicating more strain in the 2U cube than in the 3U cube. The relative geometric distortions levels of the helices in the 2U and 3U cube modes subjected to normal mode motions are indistinguishable. At the same time the differences in the flexibility of the 2U and 3U cubes, as captured in the calculated B-factors, indicate their relationship with the single-stranded corner link lengths. These results taken together are consistent with the difference in the melting temperatures measured for the 2U and 3U cubes. The longer single-stranded corners can tolerate more motion inherent to the higher temperature environment.

In summary, we demonstrated how computational RNA 3D modeling can be used to optimize nanostructure design decisions, and help predict the best experimental strategy. A detailed discussion of the design approaches that can be adapted to building models of different nanostructures and sample NanoTiler scripts used in nanocube modeling are provided in the Supporting Information. Following the previously validated application of the ANM methodology to naturally occurring nucleic acids and their complexes, we have demonstrated here a successful application of this modeling method to less dense (less structurally compact), multi-stranded engineered RNA-based nanoparticles. The methodology presented, combining the optimization of the geometric aspects of the design with the help of NanoTiler and the characterization of the nanostructure dynamics via coarse-grained ANM simulations that are orders of magnitude faster than molecular dynamics and effectively capable of dealing with much larger structures, is generally applicable in the field of RNA-based nanobiology.

7. Experimental and Computational Procedures

Listed below are details of the experimental and computational protocols used and developed for this study. Further extensions and discussions are included in the Supporting information.

7.1 Experimental Methods

7.1.1 RNA preparation

RNA molecules were prepared by transcription of PCR amplified DNA templates. Synthetic DNA molecules coding for the antisense sequence of the designed RNA were purchased from IDT DNA and amplified by PCR using primers containing the T7 RNA polymerase promoter. PCR products were purified using the QiaQuick PCR purification kit and RNA molecules were prepared enzymatically by in vitro transcription using home-made T7 RNA polymerase. Samples were incubated at 37 °C for four hours in a buffer containing 15 mM MgCl₂, 2 mM spermidine, 50 mM Tris buffer (pH 7.5), 2.5 mM NTPs, 10 mM DTT, 0.1 μg/μl IPP, and 0.8 u/μl RNAsin; the reaction was quenched by adding 5 μl of RQ1 RNAse-free DNase (10u/μg) for a reaction volume of 200 μl, followed by 30 additional minutes of incubation. Samples were purified on a denaturing urea gel (PAGE) (8% or 10% acrylamide, 8M urea). The RNA was eluted from gel slices overnight at 4 °C into buffer containing 300 mM NaCl, 10 mM Tris pH 7.5, 0.5 mM EDTA. After precipitating the RNA in two volumes of 100% ethanol, samples were rinsed twice with 90% ethanol, vacuum dried, and dissolved in TE buffer.

7.1.2 [³²P]Cp labeling of RNA molecules

T4 RNA ligase was used to label the 3′-ends of RNA molecules by attaching [³²P]Cp. Labeled material was purified on denaturing polyacylamide gels (8% or 10% acrylamide, 8M urea).

7.1.3 Non-denaturing PAGE experiments

All constructs were annealed as per the desired protocol described earlier [7, 38]. Once assembled, the RNA solutions were placed on ice and combined with an equal volume of loading buffer consisting of 2 Mg(OAc)₂, 50% glycerol, 0.01% bromophenol

7.1.4 Thermal Gradient Gel Electrophoresis (TGGE) experiments

For TGGE experiments, analysis was performed with 2 mM Mg(OAc)₂, and a linear temperature gradient, typically from 40 to 70 °C, was applied perpendicular to the electric field. Cube concentration was typically 1 μM. Gels were run for 1 hour, at 30 W.

7.1.5 Dynamic Light Scattering

For DLS, 50 μL of sample solution containing preassembled RNA cubes were measured by a DynaPro NanoStar (Wyatt Technology, Inc.) at a wavelength of 662 nm. Samples were kept on ice until the time of measurement, and measured at 25 °C under a constant flow of nitrogen gas. Both acquisition time and the number of acquisitions for each batch measurement varied between 5, 10, 15, and 20. The theoretical R_h’s were calculated by measuring the distance between the center of mass and the most-distant atom of the cube 3D CPK model.

7.2 Computational Methods

7.2.1 Modeling

Cube models were produced with the aid of our program NanoTiler. The tool has been described in detail in Bindewald et al. [66]. The algorithm used is described in detail in sections on computational nanocube design exploration and ANM-predicted nanocube motions in the body of the text and in the Supporting Information. A sample NanoTiler script that outlines the construction of the initial model of a nanocube with 2U corner bridges is provided with the Supporting Information. The program NanoTiler is available for downloads from http://www.ccrnp.ncifcrf.gov/~bshapiro/software.html.

7.2.2 Anisotropic Network Model

Anisotropic Network Models are constructed using the following procedure. First, for a network reflecting the three-dimensional coordinates of the modeled molecule (with a chosen granularity) a connectivity matrix is constructed, based on a cutoff radius applied to each node of the network (see Figure 1 and Supplementary Figure S4). All the nodes within that radius are connected with identical springs, providing the potential energy for the model. In this study all ANM calculations were performed for an all atom network with a cutoff distance of 7Å (see Supplementary Figure S4). Next, the matrix of second derivatives of the potential energy is computed, from which the eigenvectors and eigenvalues are calculated. Eigenvectors are also called normal mode shapes because they indicate the direction and relative amplitude of distortions for each node in the network. Eigenvalues correspond to the inverse squared frequencies of motion for each mode. In a 3D network of N nodes ANM can calculate up to 3N-6 modes (the 6 full network/structure translations and rotations relative the x, y, and z axis are ignored). Refer to Atligan et al. [45] for mathematical description of the method. We employed the Anisotropic Network Model implemented in the software package MAVENs [69]. In addition, certain ANM simulation and analysis functions utilize MatLab functions (® Version 2010a, The MathWorks, Natick, MA).

MAVENs function calc_ISO_scale was used to calculate mean-square fluctuations of all ENM nodes (i.e. all atoms in this case), which are comparable to B-factors [42, 63–65]. The scaling (normalization) procedure is presented in the Supporting Information. The results are plotted in Figure 5b.

Visualization and analysis of the results was performed with the aid of MAVENs, PyMOL (http://www.pymol.org/) and VMD (http://www.ks.uiuc.edu/Research/vmd/) [70].

7.2.3 Energy Minimization

Energy minimizations resulting in the structural corrections of the cube models subjected to ANM were performed with Amber 10, employing the Cornell force field for RNA (ff99bsc0) and the implicit solvent method GBSA [51–53]. To improve the accuracy of the process, a large electrostatic interactions cut-off of 999Å was used to effectively include all the atoms of the models in these energy component calculations.

For the calculation of the energy of the set of twelve helices making up each cube (identical in size and nucleotide make-up across the cube models) we removed the single-stranded corner bridges from the minimized cube models and subjected the remaining helices to new full minimizations. The first step energy output was used to collect and analyze data on the energy components from the helices, since it reflects their energy state at the end of minimization with the corner bridges restraining the process. The final results of the helix-only model minimizations for each of the cubes showed energy convergence to a common level, thus providing a control on the method.

Highlights.

• We describe computational methodologies for designing RNA nanocubes

• 3 different cube designs are computationally and experimentally characterized

• An anisotropic network model is used to understand the dynamic nature of the cubes

• Computational results explain and predict the experimental outcomes

• Outcomes include cube sizes, melting temperatures and assembly yields