Transverse propagation of action potentials between parallel chains of cardiac muscle and smooth muscle cells in PSpice simulations

Abstract

Background

We previously examined transverse propagation of action potentials between 2 and 3 parallel chain of cardiac muscle cells (CMC) simulated using the PSpice program. The present study was done to examine transverse propagation between 5 parallel chains in an expanded model of CMC and smooth muscle cells (SMC).

Methods

Excitation was transmitted from cell to cell along a strand of 5 cells not connected by low-resistance tunnels (gap-junction connexons). The entire surface membrane of each cell fired nearly simultaneously, and nearly all the propagation time was spent at the cell junctions, the junctional delay time being about 0.3 – 0.5 ms (CMC) or 0.8 – 1.6 ms (SMC). A negative cleft potential (V_jc) develops in the narrow junctional clefts, whose magnitude depends on the radial cleft resistance (R_jc), which depolarizes the postjunctional membrane (post-JM) to threshold. Propagation velocity (θ) increased with amplitude of V_jc. Therefore, one mechanism for the transfer of excitation from one cell to the next is by the electric field (EF) that is generated in the junctional cleft when the pre-JM fires. In the present study, 5 parallel stands of 5 cells each (5 × 5 model) were used.

Results

With electrical stimulation of the first cell of the first strand (cell A1), propagation rapidly spread down that chain and then jumped to the second strand (B chain), followed by jumping to the third, fourth, and fifth strands (C, D, E chains). The rapidity by which the parallel chains became activated depended on the longitudinal resistance of the narrow extracellular cleft between the parallel strands (R_ol2); the higher the R_ol2 resistance, the faster the θ. The transverse resistance of the cleft (R_or2) had almost no effect. Increasing R_jc decreases the total propagation time (TPT) over the 25-cell network. When the first cell of the third strand (cell C1) was stimulated, propagation spread down the C chain and jumped to the other two strands (B and D) nearly simultaneously.

Conclusions

Transverse propagation of excitation occurred at multiple points along the chain as longitudinal propagation was occurring, causing the APs in the contiguous chains to become bunched up. Transverse propagation was more erratic and labile in SMC compared to CMC. Transverse transmission of excitation did not require low-resistance connections between the chains, but instead depended on the value of R_ol2. The tighter the packing of the chains facilitated transverse propagation.

Introduction

An electric field (EF) mechanism was first proposed in 1977 by Sperelakis and Mann [1] for the transmission of excitation between cardiac muscle cells. The EF mechanism and the relevant literature from a number of laboratories were summarized in two recent review articles by Sperelakis & McConnell [2,3]. One key feature of the EF mechanism is that the junctional membranes must be excitable, and reach threshold slightly before the surface membrane [1]. It has been shown that, in cardiac muscle, fast Na⁺ channels are in higher density in the junctional membranes than in the surface membrane [2,4-6]. The mathematical model of Sperelakis and Mann [1] is in close agreement with our new PSpice model (see below). The PSpice model accurately depicts excitation and propagation in cardiac muscle and smooth muscle.

The EF mechanism for propagation was recently modeled on the PSpice program by Sperelakis and colleagues for cardiac muscle and visceral smooth muscle [7,8], using short chains of 6 or 10 cells. Although these strands of cells were not connected by low-resistance pathways (gap-junction connexons), propagation occurred by means of the EF that develops in the narrow junctional clefts when the prejunctional membrane (pre-JM) fires an action potential (AP). The magnitude of the cleft potential (V_jc) that is generated is a function of the radial cleft resistance (R_jc). Propagation not only can occur at very high external resistance (R_O), but in some cases, propagation velocity (θ) actually increases and propagation was facilitated, indicating that local-circuit current is not important for transmission from cell to cell [9]. In addition, elevating the longitudinal resistance of the junctional cleft up to one million times had no effect on θ.

When the EF mechanism was combined with the gap junction mechanism by placing a variable shunt resistor across each junction, the two mechanisms were facilitory [10]. That is, adding gap junctions (G.J.) channels in parallel with the EF mechanism allows both mechanisms to act in concert to facilitate transmission of excitation between contiguous cells of a chain [10]. When there were many connecting tunnels (e.g., low shunt resistance of 1.0 MΩ or 10 MΩ), the tunnel mechanism became dominant. But addition of 1,000 or 10,000 G.J. channels caused propagation velocity to become greatly increased and out of the physiological range. So in those species in which gap junctions are present, most of the G.J. channels may be closed during propagation. Thus, when the G.J. channels are blocked/ inhibited by Ca⁺⁺ or substances released during ischemia, propagation can still occur at a fast velocity by the EF mechanism. Hence, the EF mechanism is important under pathophysiological conditions.

To determine whether transverse propagation could occur between parallel chains of myocardial cells without low-resistance connections between the parallel chains, two (2 × 3) and three (3 × 4) strands were placed in parallel [11]. It was found that transmission of excitation by the EF mechanism can occur between myocardial cells lying close together in parallel. In the present paper, the parallel chains were expanded so that there were 5 parallel chains of 5 cells each (5 × 5 model) for both cardiac muscle and smooth muscle. It was found that transverse propagation between the parallel chains also occurred in smooth muscle, like in cardiac muscle, but propagation was more labile.

Methods

The full version of the PSpice software for circuit analysis/design was obtained from the Cadence Co. (Portland, OR). Details of the methods and assumptions were given previously, including the entire circuit that was used [8]. An abbreviated version of the circuitry is given in the first two figures. The surface membrane of each myocardial cell was represented by 2 units and each junctional membrane by 1 unit (Figs. 1, 2). The values for the circuit parameters used under standard conditions are listed in Table 1 for both the surface units and junctional units in both types of muscle. The cell was assumed to be a cylinder 150 μm long and 16 μm in diameter (CMC) or 200 μm long and 5 μm in diameter (SMC). The myocardial cell capacitance was assumed to be 100 pF, and the input resistance to be 20 MΩ; the corresponding values for the smooth muscle cells were 50 pF and 25 MΩ. A junctional tortuosity (interdigitation) factor of 4 was assumed for the CMC junction, and a factor of 5 for the SMC junction.

Figure 1.

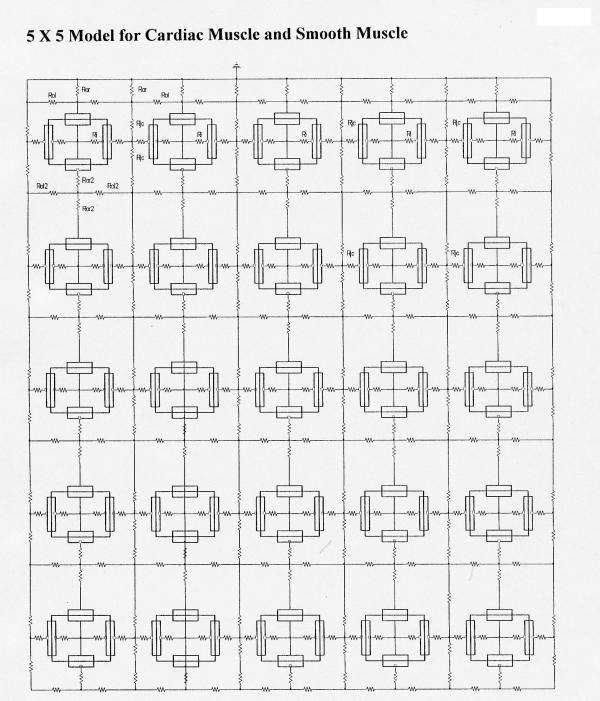
Diagrams of the arrangement of the myocardial cells and smooth muscle cells, basic units, and key resistances for the 5 × 5 model: 5 parallel chains (A – E) of 5 cells each (1 – 5). There were no low-resistance connections between cells within a chain or between chains. The surface membrane of each cell was represented by 2 basic units (one upwards and one inverted), and each junctional membrane by one unit each. The radial junctional cleft resistance (R_jc) is depicted, as is the longitudinal resistance of the interstitial space between the chains. Propagation of simulated action potentials was examined when only one cell of one chain was electrically stimulated (usually cell ^#1 of the A-chain (cell A1)).

Figure 2.

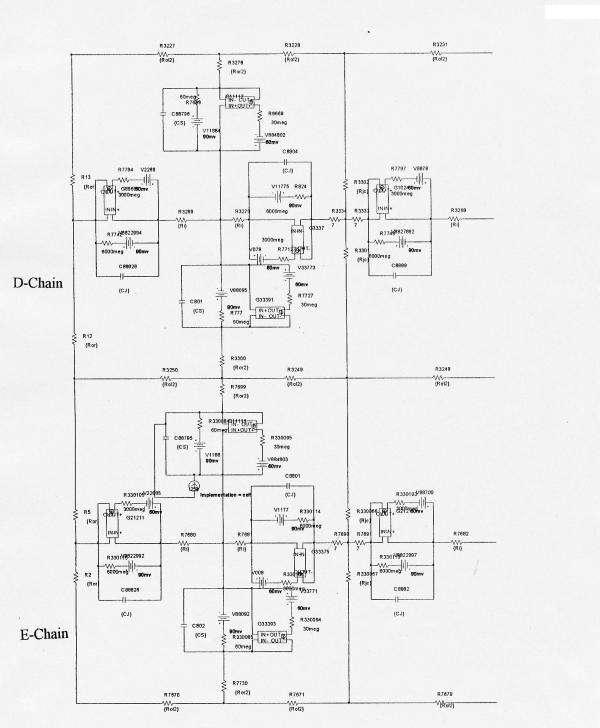
Printout of a portion of the circuits used for PSpice simulation of 2-dimensional propagation of action potentials in smooth muscle in the 5 × 5 model. The electrical circuits consisted of many repeat units, so only the upper left portion of the 5 × 5 model is illustrated. Doing this allowed the circuit elements and labels to be larger, and therefore more easily resolved by the reader. R_or2 is the transverse resistance of the interstitial space between the chains. R_or is the radial resistance of the Ringer solution bathing the upper chain (A-chain) of the bundle, R_ol is the corresponding longitudinal resistance. R_i is the longitudinal intracellular resistance. R_jc is depicted as two parallel pathways, one directed upwards and one downwards. Stimulus (0.5 ms; 0.5 nA) was usually applied at zero time to inside of cell ^#1 of the upper chain (cell A1), but for some experiments, stimulus was applied to the first cell of the other four chains.

Table 1.

Listing of standard values of circuit parameters used.

	Values
Parameters	Cardiac Muscle	Smooth Muscle
Rjc	25 MΩ	10 MΩ
Rol2	100 KΩ	200 KΩ
Ror2	100 Ω	100 Ω
Ror	1.0 KΩ	1.0 KΩ
Rol	1.0 KΩ	1.0 KΩ
Cj	4 pF	4 pF
Cs	16 pF	4 pF
EK	-94 mV	-90 mV
ENa	+60 mV	----
Eca	----	60 mV
RK (surf)	70 MΩ	60 MΩ
RK (junc)	70 M Ω	600 M Ω
R'Na (surf)	14 M Ω	----
R'Na (junc)	14 M Ω	----
R'Ca (surf)	----	30 M Ω
R'Ca (junc)	----	300 M Ω

^# Two 50 MΩ resistors in parallel. R_jc = Radial junctional cleft resistance. R_ol2 = Longitudinal resistance of the interstitial space between chains. R_or2 = Transverse resistance of the interstitial space between the parallel chains. R_or = Radial resistance at the surface of the bundle. R_ol = Longitudinal resistance at the surface of the bundle. C_j = Capacitance of junctional membranes. C_s = Capacitance of the surface membranes. E_K = Potassium equilibrium potential. E_Na = Sodium equilibrium potential. E_Ca = Calcium equilibrium potential. R_K(surf) = Potassium resistance of the surface membrane units. R_K(junc) = Potassium resistance of the junctional membrane units^. R'Na (surf) = Sodium resistance of the surface membrane during excitation. R'Na (junc) = Sodium resistance of the junctional membrane during excitation. R'Ca (surf) = Calcium resistance of the surface membrane during excitation. R'Ca (junc) = Calcium resistance of the junctional membrane during excitation.

The circuit used for each unit was kept as simple as possible, using only those ion channels that set the resting potential (RP) and predominate during the rising phase of the AP. We wanted to only inscribe the rising phase of the APs to study propagation in the chain and in the 2-dimensional sheet. The RP was -80 mV in myocardial cells, and the overshoot potential was +30 mV (AP amplitude of 110 mV). For smooth muscle, the corresponding values were -55 mV, +11 mV, and 66 mV. The related calculations were given previously (8). Propagation velocity was calculated from the measured total propagation time (TPT) (measured as the difference between when the APs of the first cell and last cell crossed -20 mV) and cell length.

Because the PSpice program does not have a V-dependent resistance to represent the increase in conductance for Na⁺ ions in CMC cells or Ca⁺⁺ ions in SMC cells during depolarization and excitation, this function had to be simulated by a V-controlled current source (our "black-box") in each of the basic circuit units (Fig. 2). The current output of the black-box, at various membrane voltages, were calculated assuming a sigmoidal relationship between membrane voltage and resistance between -60 mV and -30 mV (CMC) or between -40 mV and -10 mV (SMC). The V values used in the GTABLE were those recorded directly across the membrane. The excitabilities of the basic units (both cardiac muscle and smooth muscle) was the same as in our previous papers.

The upper chain of cells was assumed to be bathed in a large volume of Ringer solution connected to ground. The external resistance (R_o) of this fluid was divided into two components: a radial resistance (r_or) and a longitudinal resistance (r_ol). The longitudinal resistance values (R_ol2) between the upper chain and middle chain, and between the middle chain and lower chain, were increased over a wide range to reflect packing of parallel chains into a bundle of fibers, with different degrees of tightness of the packing (Fig. 1). The higher the R_ol2 value, the tighter the packing of the chains. The transverse resistance of the interstitial fluid space (R_or2) was also varied to reflect the closeness between the chains: the lower the R_or2 value, the closer the chains are packed. The cells in each chain were not interconnected by low-resistance pathways (gap junction channels), so that transmission of excitation from one cell to the next had to be by the EF developed in the narrow junctional cleft. There were five parallel chains (chains A, B, C, D, and E) of five cells each (5 × 5 model). Electrical stimulation (rectangular current pulses of 0.50 nA and 0.50 ms duration) was usually applied to the inside of the first cell of chain A (cell A1), but for some experiments, stimulation was applied to either cell B1, C1, D1, or E1.

As shown in Figure 1, there were two surface membrane units in each cell (one facing upwards and one inverted) and one unit for each of the junctional membranes (intercalated disks in the case of cardiac muscle). To improve clarity, in some runs the V-recording markers were placed on only one chain at a time. When all cells in a model were being recorded simultaneously (25 cells), the V markers were removed from some of the basic units to minimize confusion. That is, the voltage was recorded from only one surface unit (upward-facing) in each cell. The junctional cleft potential (V_jc) was recorded across R_jc, the radial resistance of the narrow and tortuous junctional cleft. Under standard conditions, R_ol2 was 100 KΩ, R_or2 was 100 Ω, and R_jc and was 25 MΩ (50 MΩ ÷ 2) for cardiac muscle and 10 MΩ for smooth muscle.

Results

Cardiac muscle

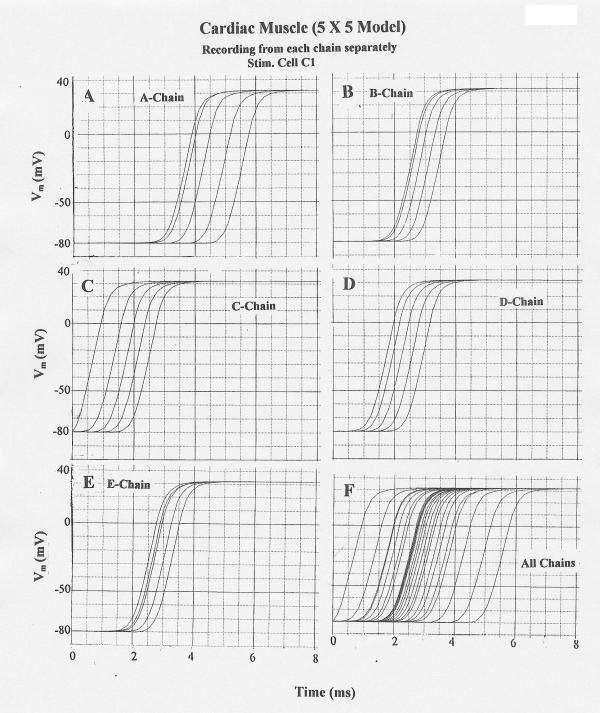
The results obtained from this 5 × 5 model under standard conditions are illustrated in Figure 3 for stimulation of cell A1. In this figure and the following one, the APs from each chain were recorded separately (A-E) and together (F). Propagation down chain A was uniform and about 33 cm/sec. Physiological values for propagation longitudinally in cardiac muscle usually range between 30–50 cm/sec. Transverse propagation into chain B occurred at multiple sites along chain A, but primarily near the end of chain A. This caused the action potential (AP) responses in chains B, C, D, and E to have a higher apparent velocity.

Figure 3.

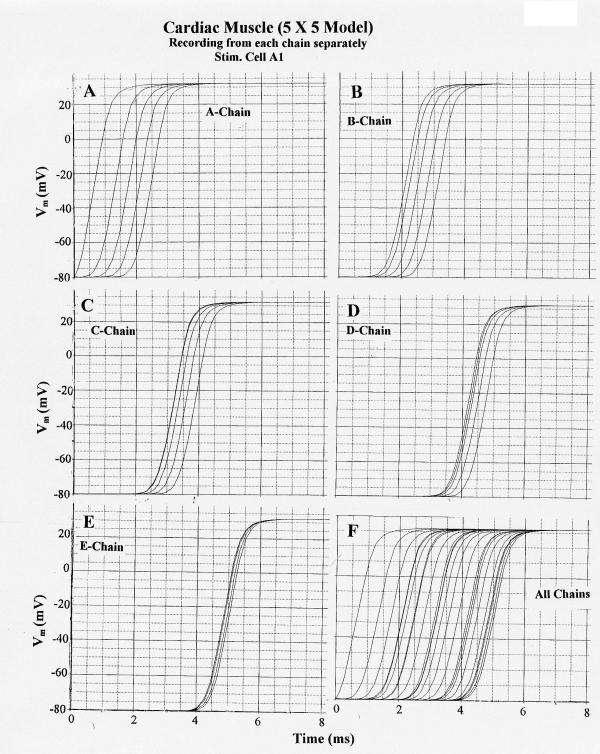
Propagation of cardiac action potentials (APs) in the 5 × 5 model (5 parallel chains of 5 cells each). First cell of the A-chain (cell A1) was electrically stimulated by a rectangular current pulse (0.5 nA, 0.5 ms) applied internally. PSpice simulation. A: V recording from the A-chain only. B: V recording from the B-chain only. C: V recording from C-chain only. D: V-recording from the D-chain only. E: V-recording from the E-chain only. F: V recording simultaneously from all 5 chains. (The ordinate scale in this panel is slightly different from panels A – E because the computer must list more data numbers at the bottom of the plot, hence compressing the ordinate scale.) All parameters were the standard values (R_jc = 25 MΩ; R_ol2 = 100 KΩ). Note that excitation spreads from the A-chain to the B-chain after a delay (from when cell A1 responded) of about 1.4 ms. Also note that once excitation entered the B-chain, it spread more quickly over the 5 cells in that chain. The same was true of the other chains, e.g. in the E-chain the 5 APs were bunched closely together.

Stimulation of cell C1 gave uniform propagation down chain C at about 32 cm/sec and transverse propagation nearly simultaneously into chains B and D, followed by propagation into chains A and E (Fig. 4). Thus, propagation transversely occurred nearly simultaneously from the stimulated chain C into the two adjacent chains B and D. As when cell A1 was stimulated, the apparent propagation velocities in the adjacent chains were much faster, e.g. about 63 cm/sec in chain B.

Figure 4.

Propagation of cardiac APs in the 5 × 5 model when cell C1 was stimulated. R_ol2 = 1.0 MΩ. (When R_ol2 was at the standard value of 100 KΩ, failure occurred at the border between chains D and E.) All other parameters were at standard values. A–E: V recording from only one chain at a time: A-chain (A), B-chain (B), C-chain (C), D-Chain (D), and E-chain (E). F: V recording simultaneously from all 5 chains. Transverse propagation occurred nearly simultaneously from the C-chain to the B and D chains, followed by excitation of the E and A chains.

The effect of varying the longitudinal resistance of the interstitial space between the chains (R_ol2) was determined (all other parameters held constant at their standard values). When R_ol2 was increased from the standard value of 100 KΩ (Fig. 5A) to 1.0 MΩ (Fig. 5B) and to 10 MΩ (Fig. 5C), θ of chains B, C, D, and E increased markedly. Further increase to 100 MΩ caused θ to increase further (Fig. 6A, Fig. 7A). In contrast, θ in chains B, C, D, and E were slowed when R_ol2 was lowered from 100 KΩ to 10 KΩ (Fig. 5D) and to 1.0 KΩ. In these cases, failure occurred at the border between chains C and D. The AP propagation velocity (θ) in chain A was unaffected, as expected. These data are summarized in Table 2. The data show that the tighter the packing of the chains, the greater the interaction between the chains.

Figure 5.

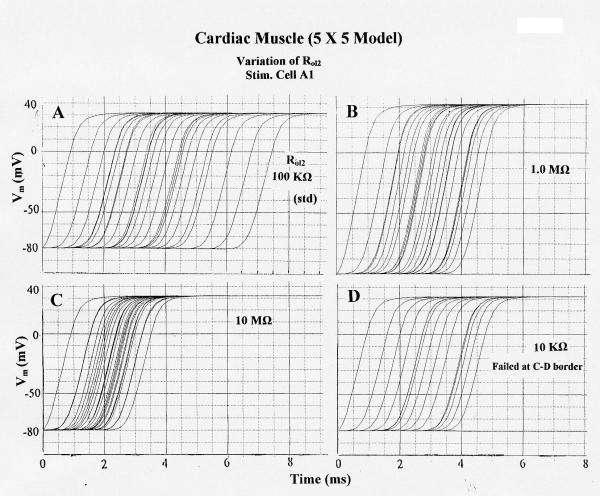
Effect of varying the longitudinal resistance of the interstitial space (R_ol2) between the 5 parallel chains on propagation of APs simulated by PSpice in the 5 × 5 model. All other parameters held at their standard values (e.g., R_jc = 25 MΩ). Stimulation applied to cell A1. A: R_ol2 = 100 KΩ (standard). B: R_ol2 = 1.0 MΩ. C: R_ol2 = 10 MΩ. D: R_ol2 = 10 KΩ. Failure occurred at the border between C-chain and D-Chain. Propagation over the 25-cell network was fastest in C (TPT = 2.6 ms) and slowest in A (TPT = 6.5 ms). Propagation in the stimulated A-chain was unaffected by changing R_ol2.

Figure 6.

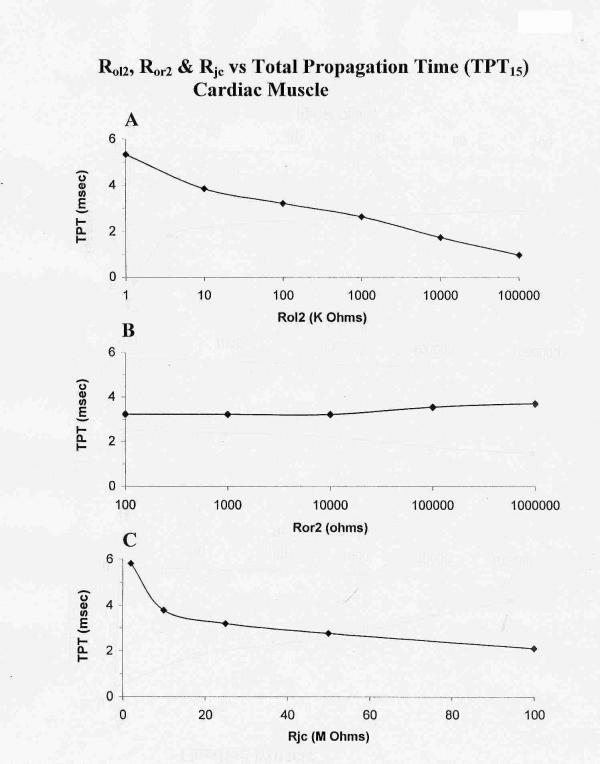
Graphic summary of the effects of varying R_ol2 (A), R_or2 (B), and R_jc (C) on the total propagation time (TPT) over the first 15 cells (TPT₁₅) of the 25-cell network (5 × 5 model) of cardiac muscle cells. As shown in A, TPT decreased as R_ol2 (longitudinal resistance of the interstitial space between chains of the bundle) was increased (reflecting tighter packing of the chains). Hence, average velocity of propagation was increased. Elevation of R_or2 (transverse resistance of the interstitial space) had only a slight effect on TPT (B), indicating that transverse current flow was small and not important to transverse transmission. Elevation of R_jc (radial shunt resistance of the junctional cleft) decreased TPT. A high R_jc value reflects a narrow junctional cleft. TPT was measured over only 15 cells, because in a few cases, failure occurred between chains C and D or between D and E.

Figure 7.

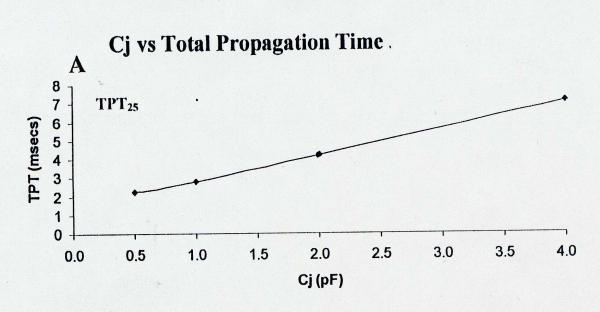
Plot of total propagation time (TPT) over the entire 25-cell network as a function of the capacitance of the junctional membrane (C_j). Data were collected at more C_j values (e.g., 0.75, 8.0, and 10 pF), but these data are not plotted because all cells did not fire. Lowering C_j greatly decreased TPT₂₅ and therefore increased velocity.

Table 2.

Summary of effect of varying R_ol2 on total propagation time(TPT) & average velocity (θ_avg) over the entire network of the 5 × 5 models.

Rol2	Cardiac Muscle		Smooth Muscle
	TPT (msec)	θ (cm/sec)	TPT (msec)	θ (cm/sec)
1.0 KΩ	5.3	36.2	----*	----*
10 KΩ	3.83	54.8	16.2	12.9
100 KΩ	3.2	65.6	13.7	15.5
1.0 MΩ	2.62	80.1	10.5	19.8
10 MΩ	1.72	122	9.25	22.7
100 MΩ	0.95	221	8.50	24.7

Only 15 cells were marked because, in some cases, all 25 cells did not respond. *Only 12 of the 15 cells marked responded

The total propagation time (TPT) required for excitation to spread through all 25 cells in the model (from when AP of cell A1 crosses -20 mV until when the AP of the last cell of chain E crosses -20 mV) was measured (Fig. 6A). As shown in Fig. 5, there is a decrease in TPT as R_ol2 is increased from 100 KΩ (A, standard value) to 1.0 MΩ (B) and to 10 MΩ (C). Lowering the R_ol2 to 10 KΩ (D) produced failure at the C-D border. A graphic summary of these measured TPT data is given in Fig. 6A.

Varying the transverse resistance of the interstitial space between the chains (R_or2) from the standard 100 Ω up to 1.0 MΩ had only little effect on TPT (Fig. 6B). Thus, there is almost no effect on the interaction between the chains, indicating that almost no current flows transversely between the chains.

The effect of varying the radial resistance of the junctional cleft (R_jc) was also determined (all other parameters held constant at their standard values). In these experiments, the voltage across Rjc (namely, the cleft potential V_jc) was also recorded. From the standard value of 25 MΩ (50 MΩ ÷ 2), R_jc was raised to 50 MΩ and to 100 MΩ. As expected, raising R_jc markedly increased the cleft potential and propagation velocity in chain A and in chains B, C, D, and E. Thus, the interaction between the parallel chains is augmented at higher R_jc values. When Rjc was lowered to 10 MΩ and to 5 MΩ, TPT was increased and θ decreased. A graphic summary of all the data is given in Figures 6C (TPT). V_jc increased as R_jc was increased. Peak V_jc was about -8 mV at the standard R_jc of 25 MΩ and was -33 mV at 100 MΩ.

The effect of varying the capacitance of the junctional membranes (Cj) was also assessed. Decreasing Cj from the standard value of 4.0 pF to 1.0 pF and to 0.5 pF markedly decreased TPT and increased the averaged propagation velocity. A graphic summary of these data are given in Figure 7 for TPT. When Cj was increased above the standard 4.0 pF, all 25 cells did not respond.

To more accurately measure transverse velocity, all five cells of the A-Chain (Cardiac Muscle) or E-chain (Smooth Muscle) were simultaneously stimulated. This produced a small effect on transverse velocity, and these results are shown in Fig. 8A,8B for cardiac muscle and Fig. 8C,8D for smooth muscle, and summarized in Table 3.

Figure 8.

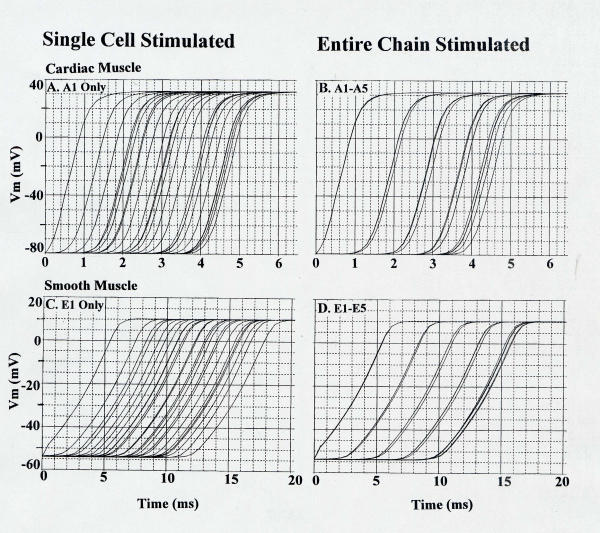
Simultaneous stimulation of all five cells of the A-Chain in cardiac muscle (B) and E-Chain in smooth muscle (D). This was done to obtain a more accurate measurement of tranverse propagation velocity. These values were compared with stimulations of only one cell(A and C).

Table 3.

Transverse velocity (θ_tr) versus longitudinal velocity (θ_lo).

	cm/sec
	θtr		θlo	θlo/θtr
A. Cardiac Muscle	1.56	1.62	33	20.4
B. Smooth Muscle	0.16	0.19	10	52.6
A/B Ratio (CMC/SMC)	9.75	8.53	3.3	0.39

Assumed cell length and diameter: 150 μm by 16 μm (cardiac muscle) and 200 μm by 5 μm (smooth muscle). Thus, the ratio of cell diameters (CMC/SMC) was 0.31. θ_tr: The first value is with stimulations of single cell (A1 for CMC and E1 for SMC). The second value is with stimulations of the entire chain (A-Chain for CMC and E-Chain for SMC) θ_lo/θ_tr: That ratio was calculated using θ_tr with stimulation of entire chain.

Smooth muscle

The results obtained from this model under standard conditions are illustrated in Figure 9 for stimulation of cell E1. In this figure and the following one, the APs were recorded separately from each chain (A-E) and together (F). Propagation down chain E was uniform at about 9.9 cm/sec. Transverse propagation into chain D occurred, and excitation of chain D was followed by transverse propagation into chains C, B, and A (Fig. 9). The AP responses in chains D, C, B, and A were bunched up, as compared to those in chain E, causing an apparent faster propagation velocity in these chains. For example, the apparent velocity was about 22.2 cm/sec in chain B. This effect may be due to the transverse transmission of excitation occurring at multiple points. An additional factor is that, since θ in a single chain is enhanced when the extracellular resistance is raised (9), this would produce faster propagation in the other chains compared to the E chain.

Figure 9.

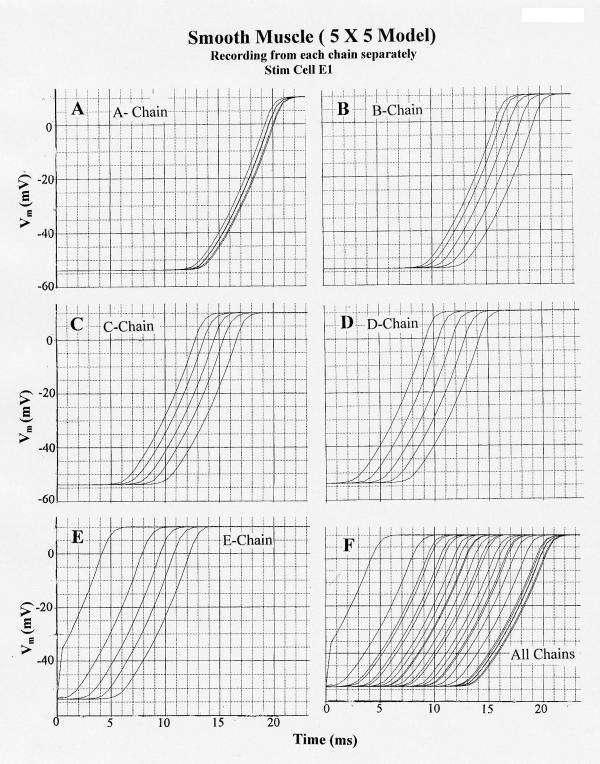
Propagation of smooth muscle action potentials (APs) in the 5 × 5 model (5 parallel chains of 5 cells each) when the first cell of the E chain (cell E1) is electrically stimulated (0.5 nA, 0.5 ms rectangular current pulse applied internally). PSpice simulation. A: V recording markers placed on the A-chain cell units only. B: V markers on the B-chain only. C: V recording from the C-chain only. D: V recording from D-chain. E: V recording from E-chain. F: V recording from all 5 chains simultaneously. All parameters were the standard values (R_jc = 10 MΩ; R_ol2 = 100 KΩ). Note that excitation spreads from the E-chain to the D-chain after a delay (from first response of A-chain) of about 5.0 ms, and that excitation spreads from the D-chain to the C-chain after a delay (from first response of D-chain) of about 3.7 ms. Once excitation entered the D, C, B and A chains, it propagated very quickly over the 5 cells of each chain. The effect of bunching of the APs is greatest in the last chain (A-chain).

Stimulation of cell C1 gave uniform propagation down chain C (θ = 15.4 cm/s) and transverse propagation simultaneously into chain B and chain D (not illustrated). In this case, apparent fast propagation occurred in chains B-A and D-E. For example, the apparent velocity was about 42 cm/s in the B-chain and 84 cm/s in the A-chain. Stimulation of cell A1 produced uniform propagation down chain A and transverse transmission into chain B, followed by excitation of chains C, D, and E (not illustrated).

The effect of varying R_ol2 between the five chains was also determined in this enlarged model. All other parameters were held constant at their standard values (R_jc = 10 MΩ). θ in chain E (stimulation applied to cell E1) was only slightly affected. In contrast, θ of the other chains were markedly affected. TPT was > 17.4 ms at the standard R_ol2 value of 200 KΩ (but 2 cells in chain A failed to fire), 16.6 ms at R_ol2 of 1.0 MΩ, and 19.0 ms at 10 KΩ. The data on TPT for only 15 cells are summarized in Table 2. The data indicate that the tighter the packing of the parallel chains (higher R_ol2), the greater the interaction between the chains.

The total propagation time, TPT, required for excitation to spread through all 25 cells in the model (from when the AP of cell E1 crosses -20 mV until when the AP of the last cell excited (A chain) crosses -20 mV) was measured (Fig. 10A) and average θ calculated. As shown, TPT decreased as R_ol2 increased (Fig. 10A). θ_avg increased as R_ol2 was increased from 100 KΩ to 100 MΩ.

Figure 10.

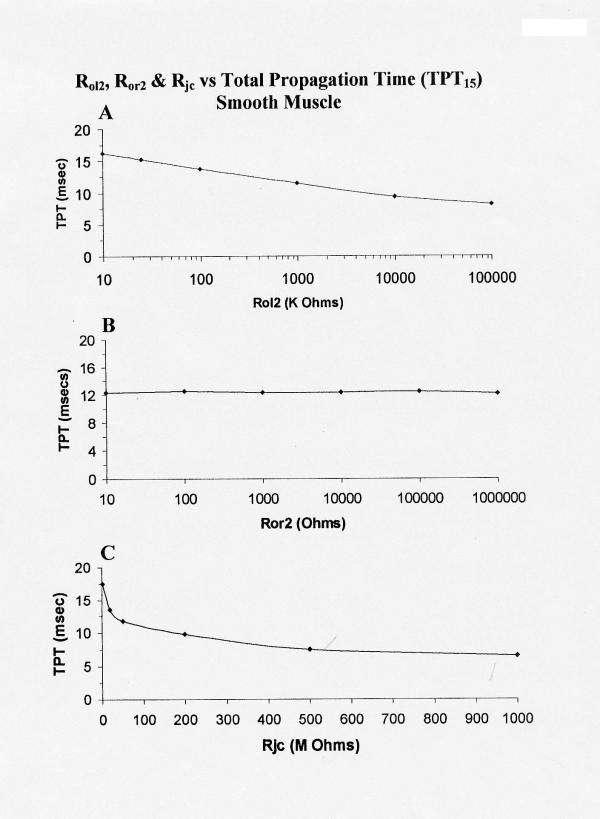
Graphic summary of the effects of varying R_ol2 (A), R_or2 (B), R_jc (C) on TPT over the first 15 cells of the network (5 × 5 model) of smooth muscle cells. Increasing R_ol2 (A) produced a decrease in TPT. Increasing R_or2 (B) had only slight effect on TPT₁₅ (as in cardiac muscle). Increasing R_jc (C) decreased TPT₁₅, much like in cardiac muscle.

As in the cardiac model, varying the transverse resistance of the interstitial space between the chains (R_or2) from the standard 100 Ω up to 1.0 MΩ had no effect on TPT (Fig. 10B) and on the averaged propagation velocity or on the interaction between the chains. This again indicates that almost no current flows transversely between the cells. Therefore, the transverse spread of excitation between chains must be by the electric field developed in the narrow interstitial clefts.

The effect of varying R_jc was also determined (all other parameters held constant at their standard values). In these experiments, the voltage across R_jc (namely V_jc) was also recorded. From the standard value of 10 MΩ (20 MΩ ÷ 2), R_jc was raised to 25 MΩ, to 50 MΩ, and to 200 MΩ. Raising R_jcgreatly increased the junctional cleft potential (V_jc) and decreased TPT and increased θ_avg. These data are plotted in panel C of Figure 10. As shown, TPT was decreased and average velocity was increased when R_jc was increased. Hence, the interaction between the parallel chains is enhanced and speeded at higher R_jc values.

Calculations for the velocity of transverse propagation gave a value of about 1.62 cm/sec for cardiac muscle and 0.19 for smooth muscle. These values were based on the assumed diameter of the fiber cells of 16 μm for cardiac muscle and 5 μm for smooth muscle. The transverse velocities (θ_tr), were measured from when the AP voltage crossed -20 mV in the last cell #5 of the first chain (A) until that of cell #5 of the fifth chain (E). Excitation jumped across four interstitial-space junctions. Thus, from Figure 8 for cardiac muscle (Table 3):

and for smooth muscle:

Hence θ_tr was about 10-fold faster in cardiac muscle than in smooth muscle, even though the ratio of diameter was only about 3-fold. The discrepancy is probably due to differences in maximum rate of rise of the APs, and therefore in magnitude of the cleft potential. From Figures 3 and 9, the longitudinal velocity (θ_lo) within a single chain (the stimulated chain, A-chain for cardiac muscle and E-chain for smooth muscle) was 33 cm/sec for cardiac muscle and 10 cm/sec for smooth muscle (Table 3):

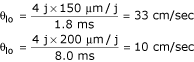
Thus the ratio of velocities, longitudinal to transverse, was about 20.4 (33/1.62) for cardiac muscle and 52.6 (10/0.19) for smooth muscle (Table 3). This difference is consistent with the approximately 3-fold smaller cell diameter in smooth muscle compared to cardiac muscle. Boundary (edge) effects may affect the quantitative measurement of velocity to a small extent. Adding many gap junctions between the cells in the five chains actually inhibited transverse propagation to a moderate extent (unpublished observation).

Discussion

The present results clearly demonstrate that electrical interaction between parallel strands of myocardial cells and smooth muscle cells occurs in the complete absence of any low-resistance connections between the strands. As we previously showed for a smaller cardiac muscle model [11], transverse spread of excitation also occurs between parallel strands of smooth muscle cells that are not interconnected by low-resistance connections. We believe that the electrical interaction between strands occurs by means of the electric field potential that develops in the narrow interstitial space between the strands. This mechanism would be similar to that which operates at the end-to-end junctions between cells within a given chain. We demonstrated that the electric field (EF) that develops in the narrow junctional clefts (V_jc), when the prejunctional membrane fires an AP, depolarizes the postjunctional membrane to threshold by a patch-clamp action [8]. The EF magnitude is determined by several factors, including the magnitude of R_jc (reflecting a shorter junctional gap between the cells). For transverse transmission, the value of R_ol2 may be equivalent to R_jc for longitudinal transmission. If so, this would explain why transverse propagation was enhanced at higher value of R_ol2 (reflecting a tighter packing of the strands).

The electrical interaction between the parallel strands does not occur via current flow between the strands in both the cardiac muscle model and the smooth muscle model. Strong evidence for this includes the fact that varying the transverse resistance of the interstitial space (R_or2) over a wide range had only little effect on propagation over the 5-strand models. This indicates that significant current does not flow in the transverse direction between strands. This is similar to our finding that increasing the 7 Ω longitudinal resistance of the junctional cleft stepwise up to 7 MΩ had no effect on the cleft potential and propagation velocity in our single-strand model [11]. In addition, when the APs were recorded from each chain individually, and the stimulated chain (i.e., A-chain) was excited, the neighboring chain (e.g. B-chain) was quiescent at the resting potential for most of the A-chain's propagation time (compare Fig. 3A and 3B). This indicates that no transverse current flows between chains.

Therefore, if significant current does not flow transversely between strands, we infer that the electrical transmission of excitation between the parallel strands probably occurs by means of the EF potential that develops in the narrow interstitial space between strands when the surface membrane of the cells in chain A fire an AP. This effect may be greater near the end of each strand because of a reflection phenomenon at the end of the chain. The fact that transverse propagation is strongly dependent on Rol2, the longitudinal resistance of the interstitial space, suggests that it should be affected by cardiac edema (lowered R_ol2) and by short episodes of ischemia where the interstitial space is decreased (elevated R_ol2).

The transverse transmission of excitation between parallel strands is faster when R_jc was increased. Increasing R_jc increases θ in the stimulated strand, which, in term, transfers excitation to the contiguous strand more quickly. And that strand transmits excitation more quickly to its neighboring strand. In addition, propagation velocity within the neighboring strands should be enhanced. The amplitude of the cleft potential V_jc, for a given value of R_jc, is much greater in cardiac muscle than in smooth muscle, probably reflecting the greater rate of rise of the cardiac AP.

The fact that lowering the capacitance of the junctional membranes (C_j) greatly speeded the longitudinal velocity in the stimulated chain and the transverse velocity in the neighboring chains is consistent with the EF mechanism. The longitudinal capacitive current (I_c) through the junctional membrane would be greater if C_mj were larger, not smaller (X_c = 1/ 2πfC, where X_c is the capacitive reactance and f is the frequency). That is, for a given frequency (AP rising velocity), the larger the capacitance C, the lower the capacitive reactance, and so the lower the impedance (Z). This means that less longitudinal capacitive current would flow from one cell to the next across the post-JM when C_j is lowered. But velocity greatly increases.

The staircase propagation in the EF model causes a discontinuous conduction. This finding is in good agreement with the results of other investigators, in both experimental and theoretical studies. For example, Spach et al. [12] showed that propagation in normal cardiac muscle was discontinuous in nature and they reported similar findings in computer simulations [Spach et al., [13]]. In theoretical simulations, Diaz et al. [14] concluded that continuous cable theory does not apply to propagation in cardiac muscle, and that excitation jumps from cell junction to cell junction. These findings were further explored by Rudy and Quan [15] and in a book that covers numerous aspects of discontinuous conduction in heart muscle [Spooner et al., [16]].

Discontinuous conduction is caused by a high junctional resistance, and one evidence for the latter is a high input resistance measured for a myocardial cell within a bundle. Sperelakis and colleagues have reported high input resistances of about 5 – 30 MΩ for cardiac muscle [for references, see [2,3]]. Others have observed similar high values of about 25 MΩ in isolated cell pairs [17,18]. Another evidence for high junctional resistance is a short length constant. Sperelakis and colleagues have reported values of about one cell length (e.g., ca 150 μm) for several different myocardial bundles [for references, refs [2,3]]. Kleber et al. reported [19] a λ value of about 350 μm, a value much shorter than that previously reported [e.g. Weidman, [20]].

A number of other studies on propagation in cardiac muscle, including inclusion of gap-junction channels, were done using the DiFrancesco-Noble model [21]. The simulation studies by Rudy and colleagues [22,23]and by Henriquez et al. [24] did not incorporate the role played by the negative potential developed in the junctional cleft (V_jc). This oversight was corrected in a very recent paper by Kucera et al. [6] in which they incorporated our EF mechanism into their gap-junctional model for propagation in cardiac muscle. Their updated model also incorporated our demonstration that the intercalated disk membranes have a higher density of fast Na⁺ channels than does the surface membrane [see refs. [2,3]] Their model confirmed the presence of a large negative potential in the junctional cleft that produced a suprathreshold depolarization of the post-JM. They concluded that our EF mechanism facilitates transmission from cell to cell and increases conduction velocity.

Some additional recent studies that are consistent with the EF mechanism for propagation include experiments on connexin knockout mice. For example, in connexin-43 (C×43) deficient knockout mice, propagation was slowed by about 30% [Vaidya et al., [25]]. And in C×40 knockout mice, conduction velocity in the His-Purkinje system was slowed to ca. 59% of the control [Tamaddon et al., [26]]. Others did not observe any significant slowing [Morley et al., [27]]. In C×43 knockout (restricted to the heart) mice, C×43 expression was reduced to about 5% of control, but conduction velocity was slowed by only about 50% [Gutstein et al., [28]]. These results are in good agreement with our PSpice simulation study that combined gap-junction channels with the EF mechanism.

Some other investigators studied theoretically transmission of excitation between myocardial cells not connected by low-resistance pathways. For instance, Hogues et al., [29] observed the cleft potential, and concluded that the EF mechanism could provide an important contribution to the transmission process. Pertsov and Medvinskii [30] concluded that propagation can occur between excitable cells without the necessity of gap-junction channels.

Finally, we demonstrated years ago that excitation can jump from one smooth muscle bundle to a neighboring one that was artificially pushed up against the first one for a short distance [Prosser & Sperelakis, [31]]. A similar demonstration was done more recently for two cardiac muscle bundles [Suenson, [32]]. Barr and Plonsey [33] reported electrical interaction between parallel fibers of excitable cells via the interstitial space. These results are consistent with our present PSpice simulation of transverse propagation in parallel chains of cardiac muscle cells and smooth muscle cells.

In summary, we have expanded (to 25 cells) our previous studies of propagation in two or three strands of cardiac muscle cells (not connected by gap junction channels) via the EF mechanism to examine transverse spread of excitation between more parallel strands with longer chains (5 × 5). We also extended these studies to smooth muscle. It was demonstrated that electrical interaction between the closely-abutting strands does not occur by means of transverse current flow. But rather the electrical interaction may occur by means of the EF that develops in the narrow interstitial space between strands. The longitudinal resistance of this interstitial space is a key parameter in determining the degree of transverse interaction between strands. Transverse propagation occurs at multiple points along the stimulated chain, causing the apparent velocity in the neighboring chains to be markedly faster. Limitations of the present study include boundary (edge) effects, possible load effects, and small electrotonic effects.