Assembling evidence for identifying reservoirs of infection

Highlights

• •We review the problem of identifying reservoirs of infection for multihost pathogens and provide an overview of current approaches and future directions.
• •We provide a conceptual framework for classifying patterns of incidence and prevalence.
• •We review current methods that allow us to characterise the components of reservoir-target systems.
• •Ecological theory offers promising new ways to prioritise populations when designing interventions.
• •We propose using interventions as quasi-experiments embedded in adaptive management frameworks.
• •Integration of data and analysis provides powerful new opportunities for studying multihost systems.

Abstract

Many pathogens persist in multihost systems, making the identification of infection reservoirs crucial for devising effective interventions. Here, we present a conceptual framework for classifying patterns of incidence and prevalence, and review recent scientific advances that allow us to study and manage reservoirs simultaneously. We argue that interventions can have a crucial role in enriching our mechanistic understanding of how reservoirs function and should be embedded as quasi-experimental studies in adaptive management frameworks. Single approaches to the study of reservoirs are unlikely to generate conclusive insights whereas the formal integration of data and methodologies, involving interventions, pathogen genetics, and contemporary surveillance techniques, promises to open up new opportunities to advance understanding of complex multihost systems.

Advancing our understanding of reservoirs

Most disease-causing organisms, including many important human, livestock, and wildlife pathogens, are capable of infecting multiple hosts 1, 2, 3. Therefore, determining how hosts enable persistence [4] and which hosts are crucial for the persistence of these multihost pathogens [5] is essential for the design of effective control measures. Failure to establish this understanding can hamper policy formulation and lead to ineffective or counter-productive control measures with costly implications for socially, economically, or ecologically important populations.

Reservoirs of infection can be ecologically complicated structures comprising one or more interacting populations or species (Box 1 [5]). Although a range of developments has led to better theoretical conceptualisation of reservoirs 5, 6, 7, 8, 9, their empirical characterisation remains a challenge. In this article, we review methods currently used to characterise each of the components that comprise a reservoir according to the framework in Box 1. Specifically, we first present a conceptual approach for classifying patterns of incidence and prevalence (see Glossary) that result from the connectivity between source and target populations (black arrows in Figure I in Box 1). We then review methods that allow us to identify maintenance or nonmaintenance populations (squares or circles in Figure I, Box 1), how they are connected (arrows in Figure I, Box 1), and the role that each of these populations has in maintaining the pathogen (i.e., reservoir capacity).

Box 1. Disease reservoirs framework.

Our study of epidemiology is usually motivated by the need to control disease in a particular host population or a subset of a population. Following Haydon et al. [5], we refer to this as the ‘target population’. Populations that are direct sources of infection for the target are termed ‘source populations’. A ‘reservoir of infection’ is defined with respect to a target population as ‘one or more epidemiologically connected populations or environments in which a pathogen can be permanently maintained and from which infection is transmitted to the target population’ [5]. Some reservoirs can be simple and comprise a single nontarget host population (Figure I A). However, they can comprise a more structured set of connected host subpopulations termed ‘maintenance community’ (Figure IB–D). Individually, some of these populations can maintain the pathogen (‘maintenance populations’), whereas others cannot (‘nonmaintenance populations’).

Thus, infection reservoirs can be constituted in a variety of ways. Reservoirs can be wildlife species [e.g., possums (Eichosurus vulpecula) as a reservoir of bovine TB in cattle in New Zealand; or wildebeest (Connochaetes taurinus) as a reservoir of malignant catarrh fever for cattle in Tanzania]; domesticated species (e.g., dogs as a reservoir of rabies for humans in many developing countries; cattle as a reservoir of Escherichia coli 0157 for humans in the UK), or subsets of the same species (e.g., adults as a reservoir of respiratory syncytial virus for children, men as an element of the reservoir of human papillomavirus for women).

Other definitions of reservoirs have been proposed 7, 55. Although Ashford's [7] definition is appealing for its generality, and Drexler et al.’s [55] for its evolutionary perspective, we use Haydon et al.’s [5] due to not only its acceptance within the epidemiological literature, but also its direct application for designing interventions.

Figure I.

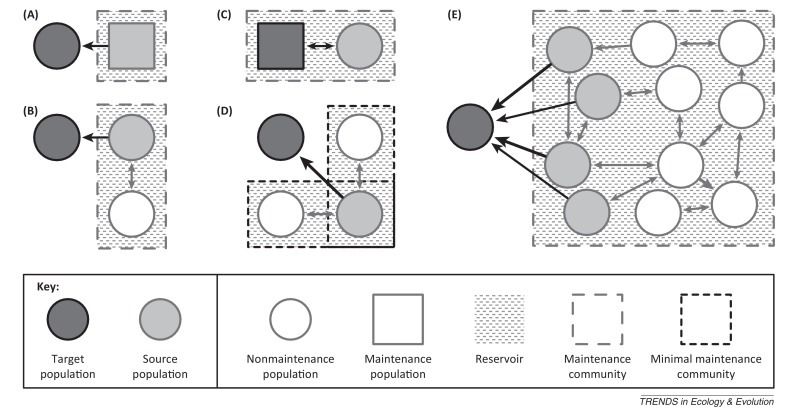
Illustrative examples of reservoir–target systems. Arrow thickness denotes rate of transmission. In (A), the reservoir comprises a single source maintenance population that transmits to a nonmaintenance target population. In (B), the reservoir comprises two connected nonmaintenance populations (of which one is the source) that together form a maintenance community. In (C), the target is a maintenance population and a source of infection and, thus, is part of the reservoir. In (D), the reservoir comprises three nonmaintenance populations, together forming two minimal maintenance communities each capable of maintaining the pathogen; together, these form a larger maintenance community. In (E), the reservoir comprises a maintenance community of multiple connected nonmaintenance populations, four of which are source populations. Modified from [5].

Long-term ecological data on multihost systems are sparse and challenging to collect 10, 11, 12; this, combined with the inherent difficulty of identifying reservoirs of infection, means that each data set or approach in isolation is unlikely to result in a sufficient evidence base to inform control strategies. Here, we further discuss how to enrich this evidence base. Almost inevitably, the need to intervene will precede adequate understanding of the dynamics of reservoir-target systems. Our central thesis is that interventions that are meticulously planned to optimise both the immediate short-term benefits to the target population and the longer-term understanding of how reservoirs function, applied together with a formal integration of data and methods [13], can provide powerful new opportunities for studying complex multihost systems (e.g., [14]).

Patterns of incidence and prevalence in the target

Data on patterns of incidence and prevalence provide indirect information on the connectivity between source and target populations (i.e., black arrows in Figure I, Box 1). Building upon the ‘community-epidemiology continuum’ framework developed by Fenton and Pedersen [15], specific patterns can be assigned to ‘zones’ (Figure 1 and Table 1 ) defined in relation to the relative magnitudes of the force of infection from one or more source(s) (x-axis in Figure 1; thickness of arrows in Figure I, Box 1), and R _0,T, the basic reproduction number of the pathogen within the target.

Figure 1.

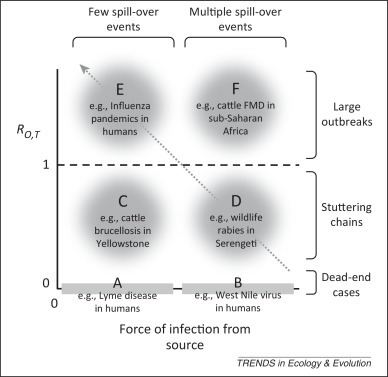
Illustration of disease zones characterised by low and high frequencies and/or rates of transmission from an external source of infection (force of infection, x-axis) and target-to-target transmission represented here by the basic reproduction number in the target population (R₀,_T; y-axis). We note that the source of infection can be a reservoir, a maintenance population, or a nonmaintenance population. Further details of the dynamic and genetic signatures of each zone are provided in Table 1 (main text).

Table 1.

Description of the dynamics and genetic signature of each disease zone captured in Figure 1 (main text)

Zone	Process	Observation		Example
		Dynamics	Genetics
A	Low frequency of spillover infection with no onward transmission in the target population. Low incidence with isolated, epidemiologically independent cases	Low incidence with long gaps between outbreaks that exceed the average combined incubation and infection periods	Genetic independence between cases	Lyme disease in humans
				Human rabies
B	Frequent, dead-end spillover leads to cases at a rate that could appear to indicate target-to-target transmission (but it is not)	Sometimes low incidence with frequent outbreaks (e.g., West Nile virus in humans). However, low frequency with high incidence can also occur (e.g., Rift Valley fever in humans)	Genetic independence between cases allows distinction from zones with similar incidence rates arising from target-to-target transmission (zones C/D)	West Nile virus in humans and horses
				Rift Valley fever in humans
				Wildebeest-associated malignant catarrhal fever in cattle
				Vampire bat rabies in humans and/or livestock
C	Limited target-to-target transmission causes isolated stuttering chains of transient nature and, thus, self-limiting outbreaks	Low-to-medium incidence with frequent small outbreaks	Genetics reveals that stuttering chains are unlinked based on cases having shared ancestry only in the distant past. Critical to distinguish from zones B/D	Monkeypox
				Cattle brucellosis in Yellowstone
				Early severe acute respiratory syndrome
				H5N1 avian influenza
				Food-borne Escherichia coli
D	Similar dynamics to zone C but chains initiated at high enough frequency to create a pseudo-endemic pattern (i.e., cases are always present in the target population)	Medium-to-high incidence with frequent small outbreaks. Reveals pseudo-endemicity	Genetics reveal that chains are separate and temporally superimposed (rather than linked), showing frequent transmission from source. Critical to distinguish from zone C	Wildlife CDV in the Serengeti
				Possibly TB in African lions
				Wildlife rinderpest (but see [78])
E	Rare introductions that result in large and usually sustained outbreaks due to R0,T >1. Size of target population is important because higher R0,T leads to a faster depletion of susceptibles, increasing the CCS required for persistence	High incidence with endemic circulation influenced by, for example, seasonal dynamics	Invasion can be traced to a single or a small number of spillover events	HIV
				Influenza in humans
				Mycoplasma ovipneumonia in bighorn sheep
				Bat rabies in skunks
F	Frequent introductions and large outbreaks associated with a high number of spillover events. Difficult to identify dynamically. Contribution from source unclear due to high R0,T in target population	High incidence	Genetics reveal multiple co-circulating lineages in the target population, with new lineages appearing through spillover events. Multiple spillovers from the source mean that it is more difficult to eliminate	Southern African Territories strains of cattle foot-and-mouth disease in sub-Saharan Africa
				Bovine TB in UK
				Jackal-dog rabies in southern Africa

If the target population is a ‘dead-end’ host from which transmission does not occur, then R _0,T  = 0. For a sufficiently low force of infection, the interval between cases in the target host is longer than the infectious period of single cases (Figure 1, zone A) and cases are not directly linked. As the force of infection from alternative sources increases, we observe cases in the target population with increasing frequency. At higher values, cases can overlap in time and space but remain epidemiologically unlinked and, as long as variability in the pathogen is high enough, genetically distinct (Figure 1, zone B).

Target populations in which limited transmission can occur but R _0,T <1 will, when the force of infection from the source is low, exhibit the classic ‘stuttering chain’ dynamics (Figure 1, zone C) in which outbreak sizes follow an overdispersed distribution [16]. As R _0,T →1, these outbreaks can become large. However, as the interval between introductions becomes shorter than the average duration of outbreaks, we observe a pseudo-endemic pattern in which the target population can appear to be a maintenance population even when it is not (Figure 1, zone D). Systems in which R _0,T is close to 1 present particular threats because small changes in their epidemiology within the target population, through either pathogen evolution or changes in the target population structure, can cause R _0,T to exceed 1 and lead to an endemic situation and/or epidemic behaviour [17].

If R _0,T >1 then any spill-over events can give rise to substantial epidemics. Stochastic extinction will still occur frequently if R _0,T is only slightly greater than 1 (Figure 1, zone E); however, if the outbreak ‘takes off’ or R _0,T >>1, then there are three broad possible outcomes: (i) the target population sustains a major epidemic after which the pathogen becomes extinct in the target population [e.g., distemper virus in wolves (Canis lupus) and harbour seals (Phoca vitulina)]; (ii) the target population sustains a major epidemic after which the pathogen proceeds towards an endemic state in the target population (e.g., HIV; the target population is then a square in Figure I, Box 1); (iii) control measures within the target population reduce R _0,T to below 1, so a major epidemic is averted and the pathogen becomes extinct in the target population (e.g., severe acute respiratory syndrome). If R _0,T >1 and the force of infection from the reservoir is large (Figure 1, zone F), fadeout is unlikely (e.g., Southern African Territories strains of foot-and-mouth disease in cattle in sub-Saharan Africa).

Dynamics ranging from pseudo-endemicity to true endemicity lie on an ascending diagonal from right to left (Figure 1, arrow), along which increasing R _0,T compensates for a declining force of infection from the reservoir. These different situations are likely to be hard to distinguish using patterns of incidence and prevalence alone. However, higher resolution spatiotemporal data and pathogen genetic sequence data, together with sophisticated analytical techniques such as state-space modelling, can provide some of the necessary tools to examine these patterns (See ‘Connectivity within the reservoir’).

Analysis of serology data

Given the challenges of isolating pathogens from wildlife populations, patterns of incidence and prevalence are typically obtained from longitudinal seroprevalence surveys or age-seroprevalence curves. These have been used to investigate infection dynamics of various multihost systems, such as canine distemper virus (CDV) in carnivore communities of the Serengeti 18, 19, Kenya [20], and Yellowstone [21], Trypanosoma cruzi in wildlife hosts in the USA [22] and hepatitis E in wild boars (Sus scrofa) in Europe [23]. However, their interpretation remains fraught with uncertainties mainly owing to cross-reactivity, declining antibody titres, cut-off thresholds used to distinguish positive and negative reactions, and difficulties with the detectability of antibodies because these depend on the relation between immunity and infection resistance (e.g., a detectable antibody does not always imply protection and the time of exposure remains unknown for pathogens that create life-long immunity in the host) [24]. New statistical approaches, such as latent class methods and site-occupancy modelling, have been suggested recently to improve estimates of prevalence from imperfect tests by allowing uncertainty in the detection of infection state [25]. Although still in early stages of development, advanced modelling techniques, such as Bayesian process models, can enable inferences of timing of exposure from age-seroprevalence data, accounting for non-stationary epidemiological dynamics [26], and/or detect cross-species transmission [27], to identify which host species is the most likely source of infection.

Identifying maintenance populations

Methods to identify plausible reservoirs typically focus on thresholds that define individual populations as maintenance or nonmaintenance (squares or circles in Figure I, Box 1). Therefore, we discuss critical community size (CCS) as an intuitive measure of persistence that can be traced back to the reservoir framework proposed by Haydon et al. [5].

CCS can be loosely defined as the host population size below which a pathogen cannot persist 28, 29. Thus, a maintenance population can be defined as a host population in which a pathogen persists because the population size is greater than CCS, whereas a nonmaintenance population is one smaller than CCS [5]. However, there are several challenges to the study of CCS in practice.

The first challenge is to define the population in which persistence is to be measured. Given that persistence is sensitive to the complex relation between demographic and epidemiological factors, it is difficult to estimate in the presence of population structure 30, 31; therefore, CCS is most commonly discussed in the context of single well-mixed populations, although these are rare in natural systems. The second challenge is in defining persistence, particularly because any estimate of CCS is likely to be sensitive to the choice of persistence metric [32]. In his original work, Bartlett defined CCS as the size of a population in which extinction was as likely as not following a major outbreak [29]. However, persistence might also be measured from an initial condition corresponding to the endemic equilibrium 33, 34. Lloyd-Smith et al. [35] point out that the relation between persistence and population size is not well described as a step function, but instead increases in a gradual manner. CCS can also be thought of in relation to the probability of extinction within a given time or the time until a given proportion (usually 50%) of introductions (or simulations) have gone extinct [36]. Once appropriate definitions are adopted, the final challenge is estimating CCS. The main approaches used are: (i) empirical observation, which consist of plotting incidence data against population size 28, 37, 38, 39; (ii) analytic expressions 34, 40, 41, 42, although all approximations so far exclude many processes relevant to CCS, such as latency, spatial heterogeneity, seasonality, age structure, and nonexponential infectious periods 40, 43; and (iii) stochastic computer simulations, in which parameterised compartmental models are used to generate distributions of persistence times for populations of different sizes and from which CCS can be estimated 33, 34. However, these studies assume a linear relationship between population size and recruitment, which is unrealistic in natural systems [35]. Beyond studies of measles 44, 45, 46, little work has been done to estimate CCS.

Next-generation matrix (NGM) methods have also been used to identify reservoir communities from endemic prevalence data. This method estimates a threshold that is similar to R ₀ (or the effective reproduction number in the endemic case) separately for individual host populations within a multigroup population rather than averaging across all populations [47]. For example, using NGM, mallards and other dabbling ducks were reported to be part of the most likely reservoir community of influenza A in the global water bird population [8]. However, this method focuses strictly on whether persistence is possible (i.e., whether the appropriate reproductive number exceeds 1), and ignores the stochasticity and nonequilibrium dynamics that are central to classical thinking on CCS. Also, implementations of the method have relied on the strong assumption that infection prevalence is at endemic equilibrium in all host species.

Connectivity within the reservoir: tracing transmission

Identifying which populations constitute the reservoir requires understanding how the populations are epidemiologically connected to each other. Here, we discuss two approaches used to trace transmission within the reservoir and between the reservoir and a target population: simulations and modelling, and genetics. Evidence to test the hypothesis that a particular population is a source of infection can also be acquired through real-world interventions that either reduce prevalence of disease in the putative source or block source-to-target transmission while monitoring incidence in the target. These are discussed in a subsequent section.

Tracing transmission using simulations and modelling

Statistical modelling is increasingly used to identify plausible sources of infection. One of the advantages of modelling is that they can be used for partially observed processes [e.g., approximate Bayesian computation 48, 49, state-space models (SSM; [50]), and Markov models 50, 51, 52]. For example, SSMs make an explicit distinction between data that can be observed (e.g., infected individuals detected by surveillance) and the underlying process itself, which might be largely unobserved (e.g., all infection events). Beyer et al. [50] constructed an SSM of rabies persistence in the Serengeti District in Tanzania that used records of humans reporting to hospital with dog bite injuries. Using a state-space implementation of a metapopulation process describing the unobserved process of dog-to-dog transmission between villages, they were able to estimate parameters capturing the effects of intervillage distance and the size of dog populations on rabies dynamics. Based on these, they inferred that it was more likely that dog rabies infections were being imported from unvaccinated domestic dogs in outlying districts, or from wild peri-urban carnivores in the Serengeti district itself, rather than from wildlife residing within the National Park. Despite their advantages, inferences rely on valid assumptions being made about the biological processes embodied in model structure.

Given a possible set of transmission parameters, plausible reservoirs of infection can also be identified using simulation models 43, 53, 54. Transmission parameters are typically obtained from epidemiological, demographic, or genetic data, and can be manipulated to explore the sensitivity of the reservoir dynamics to these parameters. For example, Cross et al. [54] used an age-structured model of two interacting elk populations (free-ranging and those receiving supplemental feeding) to investigate the extent to which dispersal from feeding grounds could explain changes in brucellosis seroprevalence in elk around the Yellowstone ecosystem. They found that R ₀ in the free-ranging elk population (the target population) had increased to above 1 over the past 20 years, probably due to changes in elk aggregations that led to enhanced elk-to-elk transmission (i.e., moved from zone C to E in Figure 1).

Tracing transmission using genetics

Genetic inference of cross-species transmission has so far tended to borrow analytical approaches from population genetics and phylogeography 55, 56, 57 (Box 2 ). Genealogy-based methods have particular appeal because, for many pathogens, the accumulation of mutations takes place on approximately the same timescale as transmission. If transmission chains are genetically distinguishable, they can provide complementary information to incidence and prevalence data. For example, given sufficient pathogen genetic variability in the reservoir, genetic data should readily distinguish rare spillover and subsequent transmission in the target from scenarios involving the same incidence due only to a high force of infection from outside the target population (Figure 1, zones B and C, and zones D and E) 57, 58.

Box 2. Using pathogen genetics to untangle reservoir–target dynamics.

Methods based on discrete ancestral state inference offer an appealing statistical way to approach the problem of multihost transmission by fitting probabilistic models to pathogen sequence data [79]. In these methods, genealogies are constructed from the data, and host associations (states) observed at the tips of the trees are used to estimate the conditional probability of being affiliated with a particular host population along all interior branches. Transmission events between host populations and, thus, the net contribution of the reservoir to dynamics in the target, can be enumerated through Markov jump counts 56, 80. A more formal population genetic framework, centred on joint estimation of population sizes and migration rates across all patches 81, 82, can similarly be adapted to deal with pathogen gene flow [83].

Although novel approaches based on genetic data open up intriguing opportunities, their resolution has defined limits. As introductions into the target become more frequent, it is increasingly difficult to distinguish contributions of the reservoir from continuous transmission within the target. Increasing genetic resolution by using longer sequences can compensate for this, but only to the point of sequencing entire pathogen genomes. The ability of genetic markers to resolve cross-species transmission processes will also be reduced by potential pathogen flow from the target population back into the reservoir [84].

Genetic inference of reservoir–target dynamics has so far also received little formal testing. There is strong reason to suspect that biased sampling can have a profound influence on the inferences generated. For example, genetically unsampled sources of infection will not only remain undetectable, but their contribution will also be wrongly attributed to populations included in the sample (a problem akin to that caused by ‘ghost populations’ in population genetics [85]). Moreover, inferred transmission dynamics can depend on the relative spatial and temporal density of sampling among host populations. Finally, stuttering chains within the target population can boost the frequency of cases (compare zones A and C in Figure 1, main text) and, hence, the likelihood of detection under sparse sampling; if unaccounted for, this can lead to overestimation of cross-species transmission rates. These complexities can generate significant challenges for the investigation of reservoir–target systems because balanced, representative sampling, proportional to the incidence in each host, is rarely achievable. Therefore, developing robust ways to deal with problems related to sampling in the context of genealogical inference and the reconstruction of transmission histories remains an important focal area for future research.

Reservoir capacity

A reservoir can comprise multiple connected populations of the same or different species (see Figure 1E in Box 1), and, thus, can be represented as a metapopulation. To assess whether this metapopulation is capable of supporting pathogen persistence, we can draw a parallel with ecological theory. Representing the reservoir as a metapopulation, we can extend the notion of metapopulation capacity [59] to that of reservoir capacity (Box 3 ). Reservoir capacity, λ’_M, is a measure of the potential of a structured host population to support pathogen persistence in the absence of external imports and, thus, can be used to assess whether a population constitutes a reservoir. A useful benefit is that associated patch values V _i (i.e., the relative contribution of each population to overall persistence; Box 3) can be used to prioritise populations when designing interventions. The modelling framework encapsulates three processes (within-population processes, transmission between populations, and community-level persistence) and is normally used to investigate one of these processes when it is possible to parameterise the other two.

Box 3. Reservoir capacity of a metapopulation.

The notion of ‘metapopulation capacity’ [59] captures in a single number λ′ _M the capacity of a fragmented landscape, comprising patches, to support the long-term persistence of a species in the absence of external imports. By analogy, we define ‘reservoir capacity’ as the capacity of a metapopulation to support the long-term persistence of a pathogen. It can be regarded as a measure of effective host abundance, weighted to take into account structural factors, such as local population sizes and connectivity, that influence fadeout rates within populations and transmission between them.

The dynamics of a general metapopulation are governed by Equation I (Figure I ), in which invasion and fadeout rates are functions of infection status of other populations, as well as factors such as population sizes and transmission rates. Persistence in the metapopulation is controlled by the ratio of population invasion events to disease fadeouts, and these are balanced at equilibrium. Reservoir capacity for this general model is defined in Equation II (Figure I). Reservoir capacity also suggests a persistence threshold. In this deterministic model, a pathogen persists in a given landscape if and only if λ′ _M >1, corresponding to the threshold above which Equation I has a stable nontrivial equilibrium. Although parameterising this kind of metapopulation model is challenging, methodology shared between ecologists and epidemiologists [86] can allow assessments of likely persistence.

Figure I.

Metapopulation model and definition of reservoir capacity.

An attractive feature of this approach is the ability to estimate patch values, V _i, which are measures of the contribution of individual populations to the persistence threshold that is used to guide interventions. For example, Figure II shows the relative contribution of 75 villages in the Serengeti District, Tanzania, to local rabies reservoir capacity, estimated from the Beyer et al. 50, 87 model discussed in the main text. Although the village shaded in red is the biggest both in terms of size and patch value, for villages with approximately 400 dogs, the patch values range from 0.00 to 0.04 depending on their spatial location relative to other villages (Figure IIB).

Figure II.

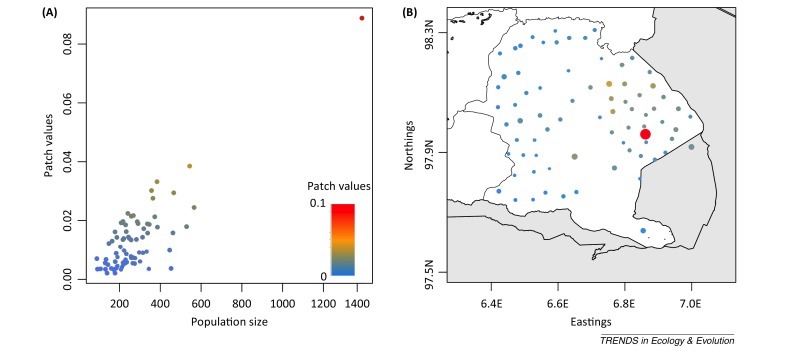
Dog population size against relative patch values (A) estimated for rabies in 75 villages of the Serengeti District, Tanzania, and their geographic location (B). Colour gradient represents patch values V_i and circle sizes (B) are proportional to dog population size.

Enriching the evidence base

No one line of evidence is likely to support unambiguous inferences about the structure and functioning of a reservoir system. However, two general strategies are worth emphasising: interventions embedded into adaptive management and data integration.

Interventions embedded into adaptive management programs

Interventions are normally designed to maximise the benefits of disease control [60]. However, they must often be devised with an incomplete understanding of the overall disease dynamics. We argue that using interventions as quasi-experiments can provide valuable opportunities to learn more about the functioning of a reservoir (see examples in Table 2 ). Through adaptive management 61, 62, disease control objectives can be met while generating and enriching the evidence base to improve future control policies and resource allocation.

Table 2.

Intervention studies shedding light on maintenance host status

Pathogen	Focal (other) species	Location	Type of intervention: intervention	Outcome	Is focal species a maintenance host?	Refs
Mycobacterium bovis	Wild boar (red deer)	Spain	Block: isolated and/or fenced from livestock hosts for over 20 years	Pathogen persisted	Yes	[88]
	Red deer (possum)	New Zealand	Pulse: possum density reduced by poisoning	Incidence in deer dropped to approximately zero in treatment plots	No	[89]
	Possum (pigs, deer, and ferrets)	New Zealand	Press: reduced possums by poisoning to 22% of former population density, followed by maintenance through trapping and shooting	Major reduction in TB prevalence in possums and TB incidence in cattle	Yes	[90]
	Badgers (cattle)	England	Pulse: randomised controlled trial of badger culling	Mixed results, but evidence for temporary decrease in incidence	Insufficient evidence	[91]
Brucella spp.	Red deer (cattle, sheep, and goats)	Spain	Press: controlled in livestock through a yearly ‘test-and-slaughter’ program; no control in deer	Pathogen eliminated in deer	No	[92]
Louping ill virus	Hares (grouse)	Scotland	Press: hare density reduced by shooting and snaring; control plot without intervention	Huge drop in tick burden and viral prevalence in grouse on treatment plot	Yes	[93]
Leishmania chagasi	Dogs (humans)	Brazil	Pulse: seropositive dogs eliminated in two valleys, no treatment in two other valleys	No difference in human incidence across treatments	No (although see [69])	[94]
Rabies virus	Red foxes (skunks, dogs, cats, and bats)	Ontario	Press: oral vaccination of foxes	Elimination from foxes, followed by elimination from skunks	Yes	[95]
	Red foxes (carnivores and dogs)	Europe	Press: oral vaccination of foxes	Elimination	Yes	[96]
	Dogs (wild carnivores, livestock, and humans)	Serengeti, Tanzania	Press: long-term mass vaccination of dogs	Elimination in parts of the ecosystem	Yes	[97]
Rinderpest virus	Cattle (wildlife)	Africa	Press: coordinated large-scale vaccination of cattle with sudden interruption to identify remaining affected areas	Eradication in cattle and wildlife	Yes	[78]

Interventions that generate substantial (and, thus, more easily measurable) changes to the system are the most likely to provide useful information. Such interventions can be akin to ‘press’ (sustained action; e.g., long-term vaccination) or ‘pulse’ (one-off action; e.g., single culling or vaccination campaign) phenomena that are familiar to ecologists [63], or ‘block’ perturbations (where potential transmission between reservoir and target is impeded; e.g., fences). Power can be assessed from predictions based on classical sensitivity or elasticity analysis [64]. Interventions that induce no changes can also be informative if, for example, they allow us to rule out a particular transmission route or source population. What can be learned from such interventions is dependent on whether they enable relevant hypotheses to be tested. It is also important to note that these interventions can alter the target-reservoir transmission dynamics, leading to difficulties in distinguishing causes and effects of the intervention. For example, the Randomised Badger Culling Trial conducted over 3000 km² and a 10-year time period [65] generated a wealth of data and analysis that should be instrumental in determining the circumstances in which badger culling might usefully contribute to the effective control of bovine TB in the UK. However, it might not be simple to determine whether particular changes in the reservoir–target disease transmission dynamics were a direct or indirect (due to dispersal and behaviour change) consequence of the culling.

The main challenge in using adaptive management lies in balancing knowledge gain that enables improved future control with achieving the best short-term outcome based on current knowledge [66]. It might be that an intervention that optimises the short-term outcome (e.g., one resulting in the greatest reduction of disease prevalence in the target) is also the one that provides the greatest statistical power to test the hypothesis of interest. In other situations, there can be a trade-off between the short-term goals of rapid disease control and the longer-term goals of learning about the system to optimise future control. This is particularly true given the cost of allocating resources to monitoring, the need to include experimental control areas [67], and the challenge of defining efficient experimental designs (e.g., stepped wedged trial; [68]) for the hypothesis being tested 62, 69. For example, faced with limited knowledge about the dynamics of chronic wasting disease (CWD) in Wisconsin (US), the US Department of Natural Resources established an adaptive management programme to eradicate CWD from the area [70]. The intervention was based on random deer culling, but a key component of the program was the collection of lymph nodes and brain tissue from the culled and harvested deer to assess the spatial distribution of CWD and provide further insights into its epidemiology.

Integration of data and findings

In most cases, understanding reservoirs dynamics requires the use of multiple data sources. Integration of findings can occur at the analysis or study design stage [71] or later, using techniques such as meta-analysis or mathematical modelling (e.g., [69]). Triangulation of multiple sources should improve understanding of the validity and generalisation of inferences [72]. By synthesising several lines of evidence, Lembo et al. [14] found support for the hypothesis that domestic dogs, rather than wildlife, constitute the maintenance population for canine rabies in northern Tanzania. Their analyses included post-hoc integration of long-term case monitoring data (suggesting that rabies can persist in high-density domestic dog populations), genetic data (showing that a single rabies virus variant circulates among a range of species), and analysis of incidence patterns (indicating that spillover from domestic dog populations initiated only short-lived chains of transmission in other carnivores, consistent with zone C in Figure 1).

Ultimately, we seek a formal statistical integration of different sources of evidence that can be used to characterise reservoir systems. Such integrative approaches are rare, but increasingly powerful methods are being developed. For example, genetic, spatial, and epidemiological data can now be combined to enable detailed reconstruction of transmission within and between host populations (e.g., 73, 74) and time-calibrated phylogenies can be layered with geographical and epidemiological data in a joint framework that enables estimation of the frequency and directionality of interspecies transmission (e.g., 56, 75). For example, based on viral gene sequences and epidemiological data, Faria et al. [75] reconstructed the cross-species transmission history of rabies virus between North American bats and identified ecological and evolutionary constraints on transmission patterns. Latent variable models that explicitly parameterise both process and observation models are also well suited to combining data types, particularly when observations are sparse [26]. Developing statistically rigorous analytical methods that integrate multiple data layers is a challenging but exciting area, and key to future progress in infectious disease ecology 76, 77. Box 4 summarises outstanding questions in the study of reservoirs of infection.

Box 4. Outstanding questions.

Although there are increasingly powerful tools to characterise different components of reservoir–target systems, there are two central challenges that remain to be overcome: (i) determining persistence thresholds for different host populations; and (ii) estimating the rates of cross-species transmission. Instead, we typically make qualitative inferences (as shown in Table 2, main text), which inevitably results in less effective control policies. Advances in the use of genetic data and widely available serology data sets, including their integration with relevant ecological theory such as reservoir capacity, offer promising new ways to approach these challenges.

The use of interventions as quasi-experiments can provide robust empirical ‘top-down’ approaches to characterising reservoirs, particularly if they are designed as ‘crucial experiments’ [98] that test among multiple hypotheses to eliminate host populations progressively as contributing to a reservoir. However, this approach raises two other challenges: (iii) how to design interventions that allow us to test the quantitative predictions of the level of control needed to eliminate infection in one population; and (iv) how to coordinate the close engagement of the research community with managers charged with improving veterinary and public health.

Concluding remarks

Each of the approaches discussed here provides important threads of evidence on its own. However, these threads are part of a more extensive tapestry and, when viewed in isolation, they convey only a fragmentary understanding of how reservoirs work. Appropriately designed interventions can simultaneously provide direct tests of disease control methodology, deliver health benefits within the target population, and create important research opportunities that can advance understanding of reservoir dynamics. However, to realise these benefits fully, we must form broad-based interdisciplinary teams, engage with their full range of expertise from the earliest planning stages, and support them throughout the lifetime of the intervention. Understanding reservoir structure and function requires not only an integration of approaches to data collection and analysis, but also a step-change in the way that research communities integrate their activities with animal and human health practitioners.

Glossary

Basic reproduction number (R₀)

expected number of secondary cases caused by a single infectious individual in a fully susceptible population.

Critical community size (CCS)

host population size below which a disease cannot persist in the long term.

Effective reproductive number

expected number of secondary cases caused by each infectious individual in a partially immune population.

Endemic

an infection is endemic in a population when it is maintained without the need for external introductions.

Force of infection

hazard rate of infection from a defined source to susceptible host individuals in a defined population.

Incidence

number of new cases in a particular time interval.

Maintenance community

any set of connected host (sub)populations that together can maintain a pathogen over the long term. A minimal maintenance community is a maintenance community of which all subsets are nonmaintenance. Trivially, a maintenance population is also a (minimal) maintenance community.

Maintenance population

single host population capable of maintaining a pathogen over the long term.

Metapopulation

set of populations that are connected by transmission. It can comprise structured populations of the same species (e.g., in space), populations of different species, or a combination thereof.

Patch value

measure of the contribution of individual populations to the reservoir capacity of a metapopulation.

Prevalence

proportion of positive cases in a population at a particular time point.

Reservoir capacity

measure of the potential of a host metapopulation to support long-term pathogen persistence in the absence of external imports.

Reservoir of infection

one or more epidemiologically connected populations or environments in which a pathogen can be permanently maintained and from which infection is transmitted to the target population.

Stuttering chain

pattern of cases in the form of short chains when transmission among hosts occurs but is too weak to support endemic or epidemic transmission.