Computational models for large-scale simulations of facilitated diffusion

Abstract

The binding of site-specific transcription factors to their genomic target sites is a key step in gene regulation. While the genome is huge, transcription factors belong to the least abundant protein classes in the cell. It is therefore fascinating how short the time frame is that they require to home in on their target sites. The underlying search mechanism is called facilitated diffusion and assumes a combination of three-dimensional diffusion in the space around the DNA combined with one-dimensional random walk on it. In this review, we present the current understanding of the facilitated diffusion mechanism and identify questions that lack a clear or detailed answer. One way to investigate these questions is through stochastic simulation and, in this manuscript, we support the idea that such simulations are able to address them. Finally, we review which biological parameters need to be included in such computational models in order to obtain a detailed representation of the actual process.

Introduction

Transcription factors (TFs) control gene activity in both prokaryotic and eukaryotic cells. These DNA-binding proteins bind to specific target sites in the genome, where they can either increase or reduce the rate at which genes are transcribed¹. While in prokaryotic organisms genes are often regulated by single TFs in the bacterial cytoplasm², eukaryotic transcription relies on combinations of different TFs that bind to nucleosome free regions of the highly compacted chromatin in the nucleus. In both settings, the ability of these proteins to locate their target sites becomes a critical aspect in the process of gene regulation.

A naive model of this search process may suggest that the TF molecules move by random three-dimensional diffusion in the cytoplasm (or nucleoplasm, in the case of eukaryotic cells; for reasons of simplicity, we will use cytoplasm throughout the text although the same mechanisms likely apply for the nucleoplasm) and then bind only to the target sites on the DNA. This model would further assume that there is no non-specific binding of the TF molecules to the DNA. In reality, the target finding problem is much more complicated.

More than 40 years ago, Riggs et al. ³ were the first to observe that the rate at which the lac repressor (a bacterial TF) locates its target site is much faster than the rate predicted by pure three-dimensional diffusion (using the Smoluchowski limit⁴) and hypothesised that a different mechanism is involved in this process. While their original calculations³ were found to contain errors⁵, their overall conclusion was correct and it is now well-established that, at least in prokaryotic systems, TF molecules do not rely on three-dimensional diffusion alone, but also bind non-specifically to the DNA, from where they perform an one-dimensional random walk. This combination of three-dimensional diffusion in the cytoplasm and one-dimensional random walks along the DNA is called facilitated diffusion. Berg et al. ⁶ were the first to formulate this model of facilitated diffusion and supported the idea that by reducing the dimensionality of the search process from three to one dimensions speeds up the search process significantly. In particular, Berg et al. ⁶ found that the association rate to a specific site increases by increasing the non-specific absorption rate. Nevertheless, this increase in association rate is limited by a maximum value above which increase in the non-specific absorption rate does not increase the association rate to the specific site. This result was proven theoretically and experimentally and seems to be correct, under the assumption of linear DNA (no three-dimensional structure)⁶, when the DNA is assumed to be a random globule^7,8 and even in the case when the DNA is assumed to be a fractal globule⁹.

In the model of facilitated diffusion, the TF molecules are allowed to perform three types of movements, namely: (i) sliding, (ii) hopping and (iii) jumping¹⁰; see Figure 1. Sliding and hopping are both one-dimensional random walk mechanisms, but during sliding the TF molecule is in constant contact with the DNA, while during hopping the TF molecule is allowed to perform short dissociations from the DNA each followed by a correlated rebinding to the DNA, i.e., the molecule will bind in close proximity (up to 100 base pairs) from the site where it unbound from the DNA. Finally, jumping is a mechanism of three-dimensional diffusion, which assumes that the TF molecule completely dissociates from the DNA and releases into a cytoplasmic pool of TFs, from where it can rebind anywhere on the DNA.

Fig. 1. TF one-dimensional random walk on the DNA.

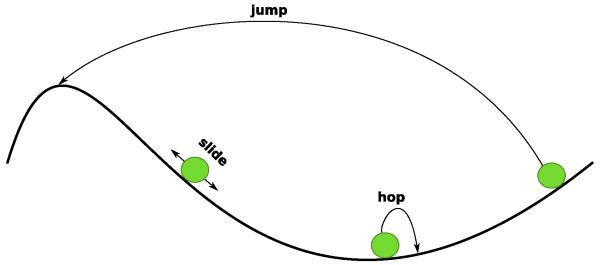
A TF molecule (green circle) can move on the DNA (black line) by either: (i) sliding (moving to a nearby position without losing contact with the DNA), (ii) hopping (disassociations and fast reassociations in close proximity from the unbinding position) and (iii) jumping (disassociation, release in the bulk and reassociation anywhere on the DNA).

In this paper, we review the literature on the TF search process with results from both experimental as well as theoretical studies. First, we present previous experimental and analytical results of the facilitated diffusion mechanism and identify areas where theoretical results do not agree with experimental measurements. Next, we propose stochastic simulations as an alternative approach to address these discrepancies and we review previous and current ways to computationally model the facilitated diffusion mechanism. Finally, we draw the conclusions and identify possible questions related to the facilitated diffusion mechanism where the stochastic simulations can provide answers. Note that this is not an exhaustive review, but is aimed to support the idea that stochastic simulations have the potential to answer several questions that are currently not amenable to experimental studies.

The facilitated diffusion mechanism

While the model proposed by Berg et al. ⁶ was essentially correct, it took almost two decades and several lines of investigation to provide experimental proof.

One-dimensional random walk

The first experimental evidence for the one-dimensional random walk came from Shimamoto and co-workers^11,12, who observed a linear movement of fluorescent molecules along the DNA in vitro. Technical limitations made it impossible to provide sufficient resolution to differentiate between sliding and hopping as the underling mechanisms for the one-dimensional random walk. This differentiation would require a temporal resolution of 1 ms and a spatial resolution of 1 nm, constraints that make further improvements currently unfeasible¹³. Consequently, a significant amount of work was invested to infer the answer from several experiments as we detail below.

Sliding

What is the nature of the sliding mechanism? Originally, the non-specific binding of TFs to the DNA was modelled to be mainly electrostatic^14,15. This hypothesis was supported by the fact that the contacts between lac repressor and non-specific DNA are totally electrostatic¹⁶. The sliding mechanism assumes that condensed monovalent salt cations that reside on one side of the TF-DNA complex are displaced from the DNA and they rebind fast to the DNA on the other side of the TF-DNA complex^14,15. Due to the fact that the dynamics of the ions are much faster that the movement of the TF on the DNA, sliding represents a one-dimensional diffusion^14,15.

Xie and co-workers support the idea that sliding is the most important one-dimensional random walk mechanism. First, Blainey et al. ¹⁷ tried to exploit the fact that, by increasing the salt concentration, the non-specific affinity is decreased and, conversely, hopping will be faster. Their experiment showed little dependence between the one-dimensional random walk and salt concentration, suggesting that sliding is the main one-dimensional random walk mechanism. However, DeSantis et al. ¹⁸ showed through simulations that lowering the non-specific affinity has limited effects on the hopping kinetics and, thus, one should not rely on this strategy (to alter the salt concentration) to infer the hopping rate.

Secondly, Xie and co-workers investigated whether the one-dimensional random walk is linear or helical, following the shape of the DNA^19,20. Their experimental results could best be fitted by a helical move of the protein, which indicates that the TF might follow the shape of the DNA and, consequently, the protein might be in permanent contact with the double helix. The fact that the experimental data was fitted best by a helical move does not mean necessary that this mechanism is the correct one. Actually, Schonhoft and Stivers ²¹ showed that a specific enzyme (hUNG) is able to slide both on double and single strand DNA, although in the latter case the one-dimensional random walk is reduced. This means that DNA binding proteins might not follow a helical movement on the DNA during their one-dimensional random walk, but another type of movement might be involved.

Hopping

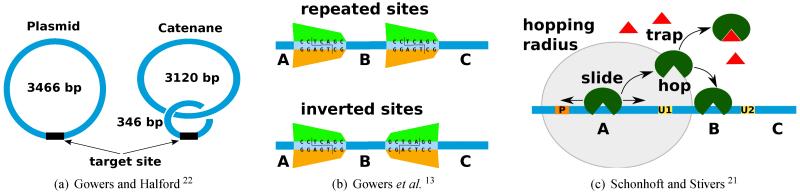
Halford and co-workers dedicated a series of articles on trying to investigate whether hopping exists or the one-dimensional movement is purely due to sliding^5,13,22,23. In one experiment they observed that, by adding non-specific DNA, the rate at which EcoRV enzyme cleaved the DNA at the recognition site was increased, but there was no difference between adding the non-specific DNA co-linear to the restriction site (one ring of 3466 bp) or by catenation (two interlinked rings of DNA one of 3120 bp with only non-specific DNA and one of 346 bp with the recognition site)²²; see Figure 2(a). This suggested that three-dimensional proximity (three-dimensional diffusion is the only way to reach the restriction site from the non-specific DNA in the catenane) is as important as one-dimensional proximity (one-dimensional random walk is one way to reach the restriction site from the non-specific DNA in the plasmid), and this is true only if hopping is taken into account.

Fig. 2. Experimental strategies aimed to prove the existence of hopping.

(a) The addition of non-specific DNA co-linear with an enzyme restriction site leads to similar cleavage rate as in the case when the non-specific DNA is added by catenation²². In the second scenario the restriction site is reachable from the catenane only if hopping exists. (b) The experimental setup assumes two DNAs each with two restriction sites, but while in the first DNA, the sites are repeated (and no reorientation of the enzyme is required), in the second DNA, the sites are inverted (and the enzyme needs to invert its orientation which is possible only through hopping). Ensuring that only one enzyme is bound to the DNA, Gowers et al. ¹³ observed that for distances longer than 50 bp the two strands display similar cleavage rates at both sites. The processivity of the two sites is measured as P = ([A] + [C] − [BC] − [AC])/([A] + [C] + [BC] + [AC]). (c) This is a similar strategy as in (b), but the experiments assumes only one DNA with two damaged uracil sites where the hUNG enzyme can excise the DNA. The protein is released from a P site and if the protein leaves the DNA for long excursions then it gets inactivated by a trap molecule and, thus, only a pure sliding mechanism will ensure a similar excision rate as in the case of a system without the trap molecule.

In another experiment, Gowers et al. ¹³ designed two DNA strands with two sites that are cut by restriction enzymes. The first DNA strand contained two sites that had the same orientation, while the second one contained two sites with different orientations; see Figure 2(b). In the absence of hopping, the cleavage of the first DNA strand should be higher than that of the second one. However, their experiments showed similar cleavage rate for distances between sites greater than 50 bp, which suggested that molecules slide and scan ≈ 50 bp of DNA before performing a hop event.

Recently, Schonhoft and Stivers ²¹ performed an in vitro experiment where a specific enzyme (hUNG) would excise a damaged uracil base; see Figure 2(c). Setting two uracil sites at various distances and using trap molecules which would inactivate the enzyme only during their three-dimensional excursions, they were able to quantify that the enzyme has an average sliding length of 4 bp and at least one hopping occurs every 10 bp. This is a higher rate than predicted by Gowers et al. ¹³ and could be explained by the fact that the two experiments used different enzymes. Thus, these parameters could be highly specific to each DNA binding protein and extra care should be taken before assuming their generality.

In vivo experimental evidence

All the experimental validation presented above were performed on isolated DNA in reconstituted in vitro test systems, but there was no proof that the facilitated diffusion mechanism actually exists in vivo. Elf et al. ²⁴ were able to visualise the movement of fluorescent lac repressor molecules in a live E.coli cell. In this study, they used fluorescence correlation spectroscopy (FCS) to measure the pure three-dimensional diffusion coefficient (lacI without DNA binding domain) and the apparent diffusion coefficient (lacI with DNA binding domain). In addition, the one-dimensional diffusion coefficient was determined from in vitro experiments. Using these measurements they approximated that the molecules spend approximately 90% of the time performing one-dimensional random walks on the DNA and the remaining time performing three-dimensional diffusion in the cytoplasm. Finally, Elf et al. ²⁴ were able to measure that the molecules have a residence time of t_R = 5 ms (the time a molecule spends on the DNA before it unbinds by jumping) and using the in vitro diffusion coefficient they estimated that the sliding length is $s_l^{\mathrm{obs}}\approx 90bp$ (the number of base pairs scanned before it unbinds by jumping).

Recently, Hammar et al. ²⁵ estimated that the in vivo sliding length of lac repressor is $s_l^{\mathrm{obs}}\approx 45\pm 10bp$. This study used a strategy similar to the one used in in vitro by Ruusala and Crothers ²⁶. The experimental setup considers that two target sites are added on the DNA at various distances. If the distance between two target sites is smaller than the sliding length, then the association rate of a protein to any target site reduces by up to a half of the original value. This is caused by the fact that when the two target sites are far enough they appear as two target sites, while when they are close they behave as a single target (leading to a reduction in the association rate). This measure of sliding length of lac repressor in vivo is half of the value proposed in Elf et al. ²⁴, but both studies estimate these parameters (these values are not direct measures of the sliding length). This suggests, that there is an error in measuring these parameters which is not generated by the differences in the systems, but rather by the methods that are used to estimate the parameters. One solution to surpass these errors is to provide a direct measure of these parameters, but this is not achievable with current technologies.

Elf and co-workers^24,25 provided conclusive evidence that the facilitated diffusion mechanism exists in vivo in prokaryotic cells. Target site identification seems more complicated when we consider eukaryotic cells. Here the DNA displays a higher level of organisation than in prokaryotic cells and it is packed in chromatin, which will make large regions of DNA inaccessible. For example, during early developmental stages of the D.melanogaster, only 3.5% of the DNA is accessible²⁷. Furthermore, this is not a static but rather dynamic system, in which the accessible regions are in constant flow depending on the biological context. Gehring and co-workers^28,29 used FCS and found that the Drosophila homeobox transcription factor Sex combs reduced (Scr) displays three different diffusion constants in live salivary gland. They attributed these diffusion constants to three-dimensional diffusion, non-specific one-dimensional random walk on the DNA and to TF molecules tightly bound to specific sites. These results seem to suggest that the facilitated diffusion mechanism might exist even in eukaryotic cells, but there is still no strong proof that what Gehring and co-workers^28,29 observed was actually facilitated diffusion, or only a slower diffusion in a denser environment.

Interestingly, Gehring and co-workers^28,29 estimated that the diffusion coefficient of Scr is significantly higher compared to the one of the lac repressor²⁴. This is surprising, as one would expect slower movements in a eukaryotic cell, because of higher crowding on the DNA and a denser environment. Nevertheless, it is still not clear whether these differences are generated by the differences in the experimental methods, differences in the investigated TFs, or differences in the search mechanism between prokaryotes and eukaryotes (such as different proportion of time spent on the DNA, faster diffusion or higher crowding on the DNA).

The main disadvantage of FCS is that the method cannot obtain long trajectories of individual molecules. An alternative method was recently proposed by English et al. ³⁰. This method, which is called the stroboscopic tracking assay, has no limitation on in vivo copy number and can capture long trajectories. Nevertheless, the details of applying this method to the facilitated diffusion mechanism of TFs still needs to be investigated.

Open questions

It becomes evident from the presented work that our picture of facilitated diffusion is still partial, and while the basic mechanism is commonly accepted, still many aspects lack a detailed description.

The rate of sliding compared to the rate of hopping

It is now accepted that both sliding and hopping exist, but there is still no agreement on whether the molecules predominantly slide or hop during the one-dimensional random walk. While the analytical study of Coppey et al. ³¹ and the computational model of Wunderlich and Mirny ³² concluded that molecules perform up to 10 hops during each one-dimensional random walk, the results of DeSantis et al. ¹⁸ indicate that this rate can be three orders of magnitude higher. Both studies are theoretical and the field still awaits improved experimental measurements of the phenomenon to propose a reliable value/interval for the degree of hopping. Using the fact that the lac repressor seems to scan approximately 90 bp on each random walk on the DNA²⁴ and the fact that protein can change orientation on the DNA only for distances of at least 30 bp seems to suggest that hopping exists but that the degree of hopping is rather small, as suggested by Coppey et al. ³¹ and Wunderlich and Mirny ³².

Nevertheless, Bonnet et al. ³³ observed experimentally a high rate of long hops on the DNA (longer than 600 bp). Since it is expected that short hops are more frequent than long ones^18,32,34, it seems possible that proteins display a high rate of hopping. In addition, Schonhoft and Stivers ²¹ estimated high hopping rates (at least one every 10 bp) for a specific enzyme (hUNG).

Overall, it seems plausible that hopping rates can be high or low depending on the DNA binding protein (its conformation and charge) and even the salt concentration in the cell³⁵. This means that instead of looking for a general value for the hopping rate, one should aim to identify these parameters individually for each protein that is investigated.

Optimal partition of time

Previous theoretical work suggested that the optimal configuration is the one in which a TF molecule would spend half of its time on the DNA and the other half diffusing in the cytoplasm^31,36, but experimental measurements found that bacterial TFs spend 90% of the time bound to DNA. Mirny and co-workers^36-38 proposed that, while sliding, the protein can be in two modes, (i) a search mode or (ii) a recognition mode, and that a TF swaps randomly between these states. This model could explain why there is a difference between the optimal proportion of time spent performing one-dimensional random walk or three-dimensional diffusion³⁷. However, there is no strong evidence that this is a general mechanism used by TFs and, although this model might be true in the context of their research, it is unclear whether their experiments provide an insight into the general mechanism.

Reingruber and Holcman ³⁹ gave a different interpretation to the search/recognition mechanism: They suggested that when the TF is in search mode it actually hops, while when it is in recognition mode it slides. Consequently, during hopping a molecule will bind weakly to the DNA through electrostatic interaction with the DNA backbone, while during sliding the binding is stronger. This contradicts the model of sliding proposed by von Hippel and co-workers^14,15, where the sliding is mediated through weak electrostatic interactions. Both models (Reingruber and Holcman ³⁹ and von Hippel ¹⁵) seem biologically plausible and there is no proof of the actual mechanism by which the TFs perform the one-dimensional random walk.

Recently, Benichou et al. ⁹ showed analytically that when the DNA is assumed to be a fractal globule, the optimal partition of time assumes that the molecules spend more time bound to the DNA (≈ 85%), which is in accordance with experimental measurements. Nevertheless, Benichou et al. ⁹ used a mean-field approximation and it is not clear whether these results are still valid assuming real affinity landscapes.

Crowding

Molecular crowding is an aspect which was disregarded in most of the above mentioned studies, and which may have a significant effect on the search process. TF molecules that perform facilitated diffusion to search for their target sites are not alone on the DNA. For example, in the case of E.coli, depending on growth conditions, between 10% and 50% of the genomic DNA is covered by other DNA-binding proteins⁴⁰.

One effect of crowding on the DNA is that the target site can be totally or partially covered by other molecules (called non-cognate species), which will make locating the target site impossible⁴⁰. Nevertheless, by adding non-cognate molecules and considering steric hindrance (two molecules cannot occupy the same space), a large region of the DNA can be masked by other molecules and, consequently, the amount of free DNA, where a TF molecule needs to perform the search process, is smaller compared to naked DNA, leading to faster location of the target site³⁷.

Murugan ⁴¹ found that there is an amount of crowding that minimises the search time of one TF molecule. Nevertheless, in deriving this result, Murugan ⁴¹ considered that the sliding length was inversely proportional to the number of molecules bound to the DNA⁴², which is true only if the sliding length is higher than the length of the DNA segment. In addition, Murugan ⁴¹ did not consider the probability that the target site can be covered by the non-cognate species or the effect the crowding has on reducing the association rate of the TF to non-specific DNA (non-cognate molecules bound to the DNA reduce the association rate of free cognate molecules by reducing the amount of available non-specific sites)⁴⁰. Li et al. ⁴³ took into account these aspects and showed analytically that by increasing the crowding on the DNA, the search time actually increases.

One solution to avoid the slow down of the search process caused by crowding is to increase the abundance of the TF of interest. Li et al. ⁴³ found that by increasing the copy number of the TF of interest, and the copy number of other DNA binding proteins in E.coli by the same factor, leads to an increase in search speed when the total number of DNA binding proteins is below 10⁴ and a significant decrease in the search speed for more than 1.6 × 10⁵ molecules. This result seems to indicate that the actual number of DNA binding molecules in E.coli (≈ 3 × 10⁴) lies within an optimal interval. However, in the works of Flyvbjerg et al. ⁴⁰ and Li et al. ⁴³, crowding was assessed assuming “immobile obstacles”, which is a crude approximation that can lead to biases in the results. It is reasonable to approximate that the most DNA-binding proteins move on the DNA at similar speeds (with an average diffusion constant). This new regime of “moving obstacles” on the DNA may influence the results presented by Flyvbjerg et al. ⁴⁰ and Li et al. ⁴³, but further work is required to test these new hypotheses.

Crowding on the DNA does not only reduce the association rate of TFs to their target sites, but it also increases the fluctuations in the occupancy of the target site⁴⁴. On crowded DNA, non-cognate TFs have a higher probability to bind ‘empty’ target sites. One solution to this noise in gene activity is to have target sites that are occupied almost all the time and, thus, the cognate TFs act like insulators. Sasson et al. ⁴⁴ found that the variation in the lac promoter activity decreases when the promoter has a higher cognate occupancy. One question that still needs to be answered is how the parameters of the one dimensional random walk of TFs on the DNA affect this behaviour?

In a crowded environment, hopping and jumping may play an even more important role, in the sense that a TF molecule can overcome an obstacle by hopping over it^41,45-47. Kampmann ⁴⁵ proposed that the obstacles are bypassed through a two-dimensional random walk on the DNA, where proteins do not follow the major grove of the DNA, but perform a random walk on the entire cylindrical surface of the DNA. However, Kampmann ⁴⁵ could not distinguish whether the obstacle bypass was performed by this two-dimensional random walk or by hopping. The two-dimensional random walk does not assume that proteins bound to the DNA can change their orientation and, consequently, enzymes could not cleave two sites with inverted orientation as shown in Gowers et al. ¹³. Thus, it seems more plausible that the obstacle bypass observed by Kampmann ⁴⁵ is generated by hopping rather than a two-dimensional random walk on the DNA. Similarly, Hedglin and O’Brien ⁴⁷ found that the addition of obstacles between two sites reduces the processivity of a specific enzyme only by 50%. In a pure sliding scenario the processivity should have been completely reduced and, thus, the authors of that study concluded that the enzyme has to hop to a certain degree in order to reach the second site.

Li et al. ⁴³ argued that the hopping mechanism would not lead to obstacle bypass because the molecule would need to make an excursion of ≈ 14 nm and, at these distances, the molecule has a low probability to rebind ‘correlated’ to the DNA, in the sense that the rebinding will most likely occur far away from the unbinding position. However, Bonnet et al. ³³ observed in vitro that molecules bound to the DNA can perform a large number of long hops or jumps on the DNA of lengths further than 30 nm (100 bp), which suggests that hopping could, in principle, bypass obstacles on the DNA. In addition, Murugan ⁴¹ showed theoretically that if TFs were not able to jump over obstacles on the DNA, then one should observe anomalous diffusion (sub-diffusive behaviour of molecules that are trapped in crowded regions of DNA). Experimental studies, such as the ones of Blainey et al. ¹⁷ and Elf et al. ²⁴, observed a normal diffusion of the TFs on the DNA, thus supporting the idea that TFs should be able to bypass obstacles on the DNA by hopping.

Crowding on the DNA can also lead to a reduction in the number of jumps and an increase in the number of hops³⁴, which means that the protein spends more time performing the one-dimensional random walk. Nevertheless, if obstacles occupy a large area of the DNA (think clusters of binding sites in an eukaryotic enhancer), then the TF molecule can only diffuse in the cytoplasm and attempt to rebind at a further distance, compared to where it was originally residing.

In addition, the obstacles that are generated by molecular crowding can lead to boundary effects (the TF molecule cannot slide towards the direction of the cluster), in which case, the analytical result seems to suggest that the optimal target finding strategy of being bound to the DNA half of the time, is no longer valid⁴⁸.

Finally, it has been shown both theoretically⁴⁹ and computationally^50,51 that cooperative behaviour between TF molecules (direct TF-TF contact) leads to cluster formation and all-or-none behaviour. Flyvbjerg et al. ⁴⁰ showed that the formation of bigger clusters of non-cognate TFs reduces the probability that non-cognate molecules will cover the target site of interest. The addition of non-cognate TFs to a cooperative system can also reduce this clustering effect of cognate TFs introduced by cooperativity, but this seems to work only in the case of weak cooperativity⁵¹. Nevertheless, the theoretical studies mentioned above did not consider moving TFs on the DNA (moving obstacles), while the computational ones did not consider the entire DNA sequence, which can introduce biases when the parameters of the smaller systems are not adjusted correctly from the parameters of the complete system (representing the entire DNA and all the molecules in the cell) (unpublished data).

It would be interesting to investigate whether the results presented above hold when one considers the entire DNA, all the molecules in a cell, and specific affinities between TFs and DNA or whether other emergent properties are found.

Clustering of target sites

It was found that multiple target genes of a TF seem to cluster together⁵², but there is no exact answer as to the benefits of this mechanism. One explanation is that a single site does not have enough information to offer specificity (to be distinguishable from other random sites in the genome) especially in large eukaryotic genomes, while a cluster of sites (for the same TF or for different TFs) would have the required information content to stand out from the genomic background⁵³.

In eukaryotic systems, spurious sites can get covered by nucleosomes, while clusters of TFs can compete with these nucleosomes and keep the region nucleosome free without the need of chromatin modification. Mirny ⁵⁴ computed analytically that clusters of 3–6 sites within 147 bp of DNA (the nucleosome DNA footprint) will ensure that the underlying DNA region will be free of nucleosomes. This will transform the gene activation function from a gradual response (a hyperbolic function) to a all-or-none one (a steep sigmoidal one). However, this study did not consider the dynamics of this competition between TFs and nucleosomes. In particular, it would be interesting to understand how the one-dimensional random walk of TFs on the DNA (sliding and hopping) would change this result.

An alternative explanation for this site clustering is that the same TF molecules can regulate a series of close genes by performing only one-dimensional random walks and not by taking long excursions into the cytoplasm³². Slutsky et al. ⁵⁵ proposed that, if the affinity landscape contains energetic valleys where the target site resides, then TF molecules can be captured and, consequently, the local concentration can be overall increased.

Above we assumed that the co-localization of target sites could lead to the target sites being occupied by TFs for longer. Related to this property of the system, is the time required to form clusters of identical molecules (oligomers) on these target sites. Nicodemi and Prisco ⁵⁰ found that in the case of two attractors of DNA binding molecules, the three-dimensional distance between the attractors affects the rate of formation of these clusters over the attractors. Due to lower specificity of eukaryotic TFs compared to prokaryotic ones, one way to control the activity of genes in eukaryotic cells assumes that the regulatory modules consist of multiple identical binding sites for several TFs⁵³. In this setting, co-localization of clusters of functional sites can increase the speed at which clusters of TFs are formed and, consequently, the gene regulation speed.

Overall, it is still not clearly understood how co-localization of clusters of target sites and the size of the clusters influences the time to form clusters of TFs over the target sites and the proportion of time these target sites are occupied, when real affinity landscapes are included in the model.

Computational methods

Some of the theoretical studies mentioned above proposed analytical solutions of the facilitated diffusion mechanism. While analytical solutions are preferred as they provide consistent and reproducible results, they have certain limitations. First, analytical solutions lack the capability to integrate real DNA sequences⁵⁶, but rather have to rely on using approximations, such as a non-uniform TF affinity landscape³⁷. In particular, at least in higher eukaryotic systems, there are many non-functional high affinity sites on the DNA, where the TF molecules can be trapped⁵⁷. This is a mechanism which probably evolved to cope with high copy number of TFs in higher eukaryotic organisms⁵⁷. Thus, spatial aspects can lead to significant deviations from the mean field approximation⁵⁸ and, consequently, analytical solutions can mask information encoded in the DNA, see for example Weindl et al. ⁵⁹.

Secondly, analytical models cannot consider moving obstacles and volume exclusion (mobile roadblocks)^40,43. Computational models can overcome these shortcomings. In what follows, we present a general strategy to model computationally how the search process of TFs for their target sites takes place.

How to model the facilitated diffusion mechanism?

An ideal model would entail a complete representation of the cell, in which all relevant molecules (such as DNA, all TFs, RNA polymerase and other DNA-binding proteins) are explicitly included in the model. However, there are two issues with this ideal experiment. Firstly, our current knowledge is incomplete and many crucial parameters unknown. We lack precise knowledge of many details (such as abundances, preferred binding sites and diffusion coefficients for TFs). Secondly, even if all data would be available, there is not enough computational power to simulate such a large and detailed system in feasible time. To address these two issues, computational models use two strategies: Approximation of crucial parameters and reduction of the model to the most relevant components. Thus, computational models of the facilitated diffusion mechanism must have a reduced level of detail and often focus on a smaller subsystems, i.e. a stretch of DNA rather than the genome; one TF rather than the entire repertoire; and a common affinity for all TFs rather than real properties. Hence, when working with such models it is then important to remember that the quality of the results is a direct consequence of the simulation strategy. Here we present aspects that need to be considered in models of facilitated diffusion in order to address the questions that were asked in the previous section and how parameters can be approximated..

The two essential ingredients of the model are the DNA and the DNA-binding molecules in the cell. There is usually comprehensive data for the DNA in many organisms and this data can be classified from low-resolution to high-resolution depending on the level of detail. First, at the lowest resolution we have the DNA sequence and, due to the advancements in sequencing in the last decade, a significant number of organisms have now a reference DNA sequence. At the next level, there is the three-dimensional structure of the DNA and although the data at this level is sparse, there are some crystallographic structures of TF-DNA complexes available, especially through Protein Data Bank (PDB)⁶⁰. These two levels of DNA information can be combined together in the computational model to determine the affinity between the TF and the DNA (see below).

Finally, at the highest level of resolution, we have the global organisation of the DNA. This is an area which has recently started to extend after a first map of the organisation of the human DNA⁶¹. This data contains the probability that two DNA regions of at least 1 Mbp are close to each other in the three-dimensional space. The main problems with this data are: (i) the low resolution (to include this in a computational model we need shorter segments that are at most equal to the DNA persistence length, which is approximately 150 bp⁷) and (ii) the fact that there is no time evolution of this three-dimensional structure (we do not know whether two DNA segments are always close to each other, or whether this is specific to certain biological context).

While for many species the genome sequence and their repertoire of DNA-binding proteins (both TFs and other) are known, data about the DNA-binding proteins abundance in the cell or their binding specificity is extremely sparse. This shortcoming in the available data can be surpassed by considering only those well-studied proteins that are of interest (called cognate TFs) and for which there is enough data available. In addition, the model could also consider a generic TF species called non-cognate TFs, for which one can use generic parameters with respect to size, diffusion coefficients and DNA affinity^51,62-65.

For example, for E.coli, one can consider a generic length of the DNA binding motif of 20 bp, which seems to fit in the range of many TFs in this organism⁶⁶, the binding energy of 12 ± 1 K_BT ^20,67 and use the other parameters (such as residence time t_R = 5 ms²⁴, proportion of time bound to the DNA f = 0.9²⁴, observed sliding length $s_l^{\mathrm{obs}}=90bp$²⁴ or $s_l^{\mathrm{obs}}=45bp$²⁵ and number of hops n_hops = 6³²) from the measurements of lacI. This means that the actual sliding length is ≈ 36 bp which is similar to the value previously proposed to minimize the search time⁸, but also estimated for some DNA binding proteins^13,23.

Here, we assumed average values for the unknown parameters, as this ensures that they are at least within a biologically plausible range. These approximations are prone to introducing biases in the results, but further investigations are required to determine the degree of influence these average parameters will introduce.

Most importantly, the abundance and the size of the non-cognate TFs can be usually estimated and consequently the simulation should reasonably approximate the dynamical crowding on the DNA. For example, in E.coli we know that between 10% and 50% of the DNA is covered by proteins⁴⁰, the number of DNA binding molecules in the cell⁴³ is in the range of ~ 10000 and each TF molecule will cover around 20 bp of DNA⁶⁶. Using these numbers, one can estimate that there are between 2 × 10⁴ and 10⁵ molecules each covering ≈ 20 bp on the DNA. A similar approximation was made by Flyvbjerg et al. ⁴⁰, who considered that there are between 10⁵ and 2 × 10⁵ molecules bound to the DNA each covering 10 bp. Both of these approximations are just rough estimates of the DNA binding proteins, which will not have only one size (10 bp or 20 bp), but rather a distribution of sizes centred around one of these values. In the absence of a complete set of data (size of all DNA binding proteins and their copy numbers), the only viable solution is to use one of these approximations.

A comprehensive model of the facilitated diffusion mechanism will consider each TF molecule as an object (agent), which can move through three-dimensional diffusion in the cytoplasm, but which also can bind to the DNA and perform a one-dimensional random walk. Nevertheless, simulating the three-dimensional diffusion and one-dimensional random walk of each molecule in the in-silico cell is infeasible with respect to the simulation time. Below, we review the details associated with this process and locate certain mechanisms that can be approximated, in order to increase the simulation speed.

Three-dimensional diffusion

The three-dimensional diffusion of molecules in the cell can be resolved with algorithms such as GFRD⁶⁸, which is an event driven exact algorithm. However, three-dimensional diffusion to the Smoluchowski limit is one of the most time expensive steps of spatial simulations and other approximate algorithms, such as Smoldyn⁶⁹, were developed. These algorithms are time driven and their accuracy depends on the size of the time step. In fact, if the discretisation of the algorithm is not done correctly, the results can be misleading⁷⁰. In this context, one might ask whether it is necessary to simulate this three-dimensional diffusion explicitly at all. When the TF molecules are not bound to the DNA, they can move freely in the cytoplasm or perform micro-dissociations from the DNA followed by fast re-associations (hops). van Zon et al. ⁷¹ showed that the three-dimensional diffusion of molecules from the cytoplasm to the DNA can be approximated by the Chemical Master Equation (CME), when the model takes into account the fact that a molecule that unbinds has a high probability to rebind in close proximity. This aspect is already incorporated when modelling the hopping of TF molecules on the DNA and, consequently, a good solution would be to consider molecules that flow freely in the cytoplasm as belonging to a reservoir from where molecules can arrive at the DNA with certain arrival rates and where molecules can go when they completely dissociate from the DNA^51,65. This approach does not consider crowding in the cytoplasm, which might introduce biases. However, this three-dimensional crowding will only affect the distribution of the arrival times to the DNA and as long as one has this distribution (which van Zon et al. ⁷¹ showed to be well represented by the CME), the specific details of the three-dimensional diffusion in the cytoplasm will not change the results significantly.

The arrival rate at the DNA is computed from the three-dimensional diffusion coefficients. Nevertheless, if the DNA is highly occupied, the rate at which a TF molecule locates a free site is lower compared to the case when the DNA has a lower occupancy. This effect can be incorporated in the arrival rate, by weighting the arrival rate by the proportion of free DNA^51,65. In particular, this rate of arrival does not need to be updated at every step in the simulation, but only after a significant change in the DNA occupancy was achieved⁶⁵.

The other component of the facilitated diffusion mechanism that assumes three-dimensionality is hopping. During a hopping event the TF briefly unbinds from the DNA and then it rebinds fast in close proximity. The question is now whether we need to explicitly simulate the three-dimensional diffusion or just approximate this process by a repositioning of the molecule at a close position on the DNA. Given the fact that three-dimensional diffusion is much faster than the one-dimensional random walk²⁴ and that hops are short-lived^6,37, then one can approximate the hops by a simple repositioning of the molecule on the DNA³².

Morelli and ten Wolde ⁵⁸ performed exact three-dimensional diffusion simulations of two molecules and found that when a molecule B unbinds from a molecule A, molecule B should not be repositioned in contact or close to molecule A, but should be moved far away from molecule A. This means that during a dissociation event, the TF molecule can either be repositioned on the DNA in close proximity or has to be repositioned in the TF reservoir.

In summary, it seems that the three-dimensional diffusion processes can be approximated by single steps with certain probabilities associated to them, instead of explicitly simulating this process. This approximation leads to significant speed up in the simulation and negligible errors in the results.

Positioning of the TF molecules on the DNA

The next aspect one needs to consider in the model of facilitated diffusion is where to position a molecule on the DNA once this molecule has arrived from the cytoplasm at the DNA, or when it is hopping and shortly dissociated from the DNA.

Positioning during initial binding

The location where the TF molecule is first positioned on the DNA can have significant effects on the search process³². In prokaryotic cells, where translation is co-localized with transcription, Kolesov et al. ⁷² observed that a significant number of lowly expressed genes that encode for TFs are in close proximity to the target sites of the TFs, thus supporting the idea that the position where the TF starts the one-dimensional random walk is essential for fast regulation. The reason behind this is that, if the TF has high probability to encounter the target site during the first one-dimensional random walk, then the regulation takes place faster³². Thus, it is essential that the model of the facilitated diffusion mechanism in prokaryotic cells include an initial “drop interval” for TFs.

Repositioning of a molecule after jumping

The standard approach assumes that when a TF molecule arrives at the DNA from the cytoplasm it can rebind with equal probability anywhere on the DNA^6,23,31,36. These models seem to predict no acceleration of the search process resulting from the combination of one-dimensional random walk and three dimensional diffusion, but rather the fact that facilitated diffusion leads to a slowing down of the search process^5,37,73.

Das and Kolomeisky ⁷⁴ proposed that the one-dimensional random walk and the three-dimensional diffusion are correlated, in the sense that the original position where the molecule binds after a three-dimensional excursion, has a strong correlation to the previous region of the DNA, where the molecule performed a one-dimensional random walk. This mechanism seems to increase the search speed⁷³ and is supported by the fact that molecules seem able to move in dense chromatin regions where it is more likely to associate with a three-dimensionally close DNA segment than to release into the cytoplasm and rebind anywhere on the DNA with equal probability^75,76. In addition, previous theoretical studies showed that searching on a non-linear DNA can be faster than on a linear DNA, but there is an optimal DNA density above which the search becomes inefficient^76,77.

However, in order to test the validity of this assumption one needs a three-dimensional structure of the DNA. As mentioned above, there is some advancement on determining these three-dimensional^61,78,79 structures of the genome for various species, but we still lack a high-resolution three-dimensional map of any genome and information about the dynamics of the DNA structure.

Repositioning of a molecule after hopping

We also need to consider where the molecules are repositioned after a hopping event. Wunderlich and Mirny ³² performed stochastic simulations and found that the molecules need to be repositioned at a random position on the DNA, the location of which follows a Gaussian distribution around the original position (before the molecule micro-dissociates) and with a standard deviation of 1 bp. DeSantis et al. ¹⁸ found a similar result when performing stochastic simulations of the three-dimensional diffusion mechanism, but in their case the the standard deviation was approximated to be around 0.007 bp. As long as the one-dimensional random walk also consists of sliding, both of these values will lead to similar results (unpublished data) and, thus, one can use both of these values without affecting the results. When the random walk on the DNA is made mainly of hopping events, then a standard deviation of 0.007 bp leads to extremely short sliding lengths (often just 1 bp) for a fixed number of one-dimensional random walk events, while a standard deviation of 1 bp can lead to similar sliding lengths as in the case of purely sliding events. Since there is no difference between the two approaches except on a purely hopping scenario and there seems to be a consensus in the community that sliding exists, one can use any of these values and this will not change the results significantly.

This approximation of the relocation of a molecule after a hop event by a Gaussian distribution around the unbinding position considers one-dimensional distances only. If we consider the three-dimensional structure of the DNA, one-dimensional proximity will differ from three-dimensional proximity, i.e., regions of DNA that are far away from each other when we consider the DNA as a string can be close in the third dimension. This means that during a hopping event, the repositioning should be Gaussian distributed, but the sites where the molecule can rebind need to ordered according to their three-dimensional distance and not only according to one-dimensional distance. However, we lack this information and the resolution currently provided by chromosome capture experiments^61,78,79 is by no means sufficient.

It seems that both the repositioning of a TF molecule after a jump or a hop can be influenced by the structure of the DNA. We consider that, where this data is available, it should be included in the model. Nevertheless, it seems that the three-dimensional structure of the DNA influences only the positioning of the molecules on the DNA⁷⁴. One way to include this information in the model is to construct a square matrix where the relative distances between DNA regions is specified and, when a molecule rebinds to the DNA, the new position should take this matrix into account.

Finally, the model of the facilitated diffusion mechanism should implement steric hindrance (or volume exclusion), in the sense that two molecules cannot overlap in space⁸⁰, i.e., two molecules cannot cover the same base pair at the same time. An aspect which is usually neglected in this scenario is that the number of base pairs that are obstructed by a TF molecule are not only the ones that are in direct contact with molecule, but it can also be the case that a number of base pairs are obstructed downstream or upstream of the DNA binding motif (e.g. as in⁶⁵). This additional coverage of the DNA (downstream or upstream of the DNA binding motif) can be determined by analysing the crystallographic structure of the protein-DNA complex and, when this three-dimensional structure of the protein-DNA complex is missing, the model should avoid approximations that can lead to biases in the results.

One-dimensional random walk

Once the TF molecule is bound to the DNA, it starts to perform a one-dimensional random walk, until it unbinds. During the one-dimensional random walk, the TF stays bound to a position for a certain time, which depends on the binding energy (see below). After this time interval the molecule can slide left or right, it can hop, or it can unbind from the DNA. The probability to slide left or right depends on the type of random walk, in the sense that during an unbiased random walk it is constant across the whole genome and equal in both directions (e.g. as in^62,65), while for a biased random walk this probability depends on the affinities of the new positions^36,81. The hypothesis that the random walk is biased stems from the idea that valleys in the energetic landscape can hold molecules within a confined region⁵⁵. Weindl et al. ⁵⁹ observed that the affinity landscape of RNA polymerase seems to increase when moving towards the transcription start site (TSS) and consequently the polymerase can be directed towards the TSS^55,59.

Furthermore, Weindl et al. ⁸¹ claimed that the slow-down of a DNA-binding molecule near the recognition site can be explained by this energetic trap. Near the TSS the affinity is higher, which results in the molecule spending longer time intervals in that region and, consequently, the molecule would display slower speeds. Thus, one cannot infer from slower speeds that the random walk is directed, but just that the molecule has higher affinity in the slower region.

Finally, if the random walk would be biased, then it would display an sub-diffusive behaviour on short time scales, in the sense that the TF would slow-down⁸². Nevertheless, previous studies, such as the ones of Blainey et al. ¹⁷, Elf et al. ²⁴ or Vukojevic et al. ²⁸, did not observe this anomalous behaviour when proteins performed the random walk on the DNA and, thus, one can conclude that the random walk seems to be unbiased.

Methods to estimate the affinity between DNA and TF

There are various ways to model the binding of TF molecules to the DNA. One of these models assumes that the TF molecules have a constant affinity for the DNA (non-specific affinity), which is independent of the bound DNA word, except for the target site, where the affinity is higher compared to non-specific sites (e.g. as in Das and Kolomeisky ⁷⁴ and Wunderlich and Mirny ³²). In this context, a non-specific site means every site except the specific one(s), including random background DNA, weak and medium affinity sites. A more biologically realistic model assumes that TFs have various affinities for sites on the DNA and the affinity between a TF and the DNA is determined by the preferred DNA binding motif of the TF.

Several computational strategies were used to determine the affinity of a TF to DNA^67,83,84, but the most widely used one is the Position Weight Matrix (PWM)⁸⁴. Despite the success of PWMs in sequence bioinformatics, it seems that the method is prone to high error rates and there are different views about the correct scoring of PWMs. Maerkl and Quake ⁸⁵ considered the human transcription factor Max and compared the PWM score with actual binding energies measured for single point mutations over a range of four base pairs. They found that for more than 1 mutation, the PWM underestimates the binding energy, and this means that PWMs cannot be reliably used to capture the entire binding energy landscape. This underestimation in binding energy of the PWM is a consequence of the additivity rule, where each nucleotide contributes independently and additively to the total binding energy^86,87.

One solution to address this problem is to change the affinity of specific sites and shift the distribution of the binding energies, but this comes at the cost of knowing a priori which target sites the TF has.

Another solution is the search-recognition model proposed by Slutsky and Mirny ³⁶, which assumes that the TF has two different average binding energy levels, depending on how the TF is bound. This method does not require a priori knowledge of the target sites, but assumes a model which might not be biologically realistic (i.e. there is no proof that TFs display this allosteric behaviour with stochastic switching between states).

Similarly, Hammar et al. ²⁵ proposed that the TF scans at high speeds the DNA independent of the sequence. The TF has a certain probability (which seems to be low²⁵) to ‘read’ the affinity of the underlying DNA motif at certain positions and bind to it (recognition). In this model, the probability to switch from the search to the recognition mode depends not only on the TF, but also the underlying DNA. This complicates the picture even more, because there seems to be no solution to measure these probabilities for lower affinity sites.

In this context, it is worthwhile noting the study of Marcovitz and Levy ⁸⁸, which performed coarse-grained simulations of the protein-DNA interactions taking into account the structure of the molecules. They observed that the time to switch between non-specific binding (search mode) to specific binding (recognition mode) depends on the differences in the conformation of the DNA-binding protein in the two cases. This means that if the conformation to bind the DNA non-specifically is very different from the one to bind the DNA specifically, then the protein has to pass over the target site multiple times before it can bind there. Furthermore, they considered 125 DNA-binding proteins and found that the majority have very different binding modes, which supports the idea of multiple contacts between the protein and the target site before the specific binding takes place. However, this is not the complete scenario and other features of the protein can change this switching rate between the binding modes. For example, in the case of p53, the C-tail can bind to another DNA segment and change the conformation of the protein or the orientation of the DNA binding domain⁸⁹. This means that one should not consider just the differences between non-specific conformation of the protein and the specific one, but also additional features (such as disordered regions, additional binding domains) and local configuration of the DNA.

A more detailed model for the affinity will take into account the structure of the DNA in an all-atom model. This second layer of information can significantly change the results⁹⁰. To include this into an improved facilitated diffusion model, one could perform energy minimisation calculations as performed in Alibes et al. ⁹¹ to accurately predict the binding energy between TFs and all sequence words. This approach is feasible for TFs with short DNA binding motif, because the number of DNA words against which the TF is compared is relatively small (e.g. for 8 base pairs there are 65536 possibilities). However, there are still a significant number of TFs that have motifs longer than 20 base pairs (especially in prokaryotes⁶⁶) and, in that case, it is impractical to compare a TF with all the possible DNA words.

Finally, if the TF molecules are not symmetric (if the TFs are not homo-dimers or higher-order homo-oligomers such as p53 or lac repressor), then the affinity for the DNA will depend on the orientation of the TF. In this scenario, hopping might play a significant role in the diffusion process, due to the fact that without hopping, a molecule would not be able to change orientation and, consequently, to have a different affinity for the same DNA region or to be able to cleave the DNA¹³. For example, without hopping the TF will have to rely only on jumping to ensure that the molecule is in the correct orientation at the target site, which can significantly increase the variation in the search time. Nevertheless, Givaty and Levy ³⁵ found that only longer lived hops could lead to change of orientation of the protein with respect to the DNA. This means that, when computing the probability of changing orientation, one also has to take into account the duration of the hop.

Computational models for large-scale simulations of the facilitated diffusion mechanism

As mentioned above, there is a trade-off between the level of detail included in the model and the speed at which the system can be simulated. The models that would include the highest level of detail are models that represent the molecules at their atom level, their three-dimensional diffusion and their interactions⁹¹. This type of model can simulate systems of only a few molecules at ns time scales, which makes them infeasible for simulations of facilitated diffusion. In contrast, Levy and co-workers^{35,88,89,92-96} proposed a coarse-grained model, where groups of atoms are replaced by beads and only electrostatic interactions were considered between the DNA-binding proteins and the DNA. This type of model allowed the simulation of the facilitated diffusion mechanism considering coarse-grained models of the molecules structures, their diffusion and their interactions. However, such a model can only consider a few molecules and simulate the system only on μs to ms time scales. Cellular processes take place over minutes to hours, take place on a large genome, and TFs are often represented by at least 10⁴–10⁵ molecules. It becomes clear that, in order to simulate such a large system, further simplifications are required and one of the most important ones is the exclusion of the explicit three-dimensional structure of the TFs. Nevertheless, this does not mean that one should disregard the results of all-atom models or meso-scale models, but rather to use results of those models and include them as parameters into a large-scale model.

Furthermore, in order to perform large-scale simulations in feasible time, one has to make another set of approximations and, depending on these approximations, there are two classes of large-scale computational models of the facilitated diffusion mechanism, namely: (i) those that focus on the three-dimensional aspects (such as the case of Das and Kolomeisky ⁷⁴ or Wunderlich and Mirny ³²) and (ii) those that focus on the one-dimensional random walk (such as the ones of Chu et al. ⁵¹ or Zabet and Adryan ⁶⁵).

Previous work has demonstrated that the three-dimensional diffusion can be approximated by simple one-step reactions with negligible errors (see above). However, to our knowledge, there is no proof that approximations in the one-dimensional random walk do not lead to significant deviations from the actual results. In particular, the DNA can consist of multiple high affinity sites which are non-functional and act as traps for the TFs⁵⁷. Thus, we argue that more focus should be given to the second class of computational models (those that represent the one-dimensional random walk with a high level of detail). This does not mean that the computation models that focus on the three-dimensional diffusion should be neglected, but rather their results should be incorporated in the second class of models.

In recent work, we presented a model of facilitated diffusion, which represents one-dimensional random walk with high level of detail and uses all the aforementioned features^64,65. The model is similar to those of Chu and co-workers^51,62,63, but also supports additional features, such as TF orientation on the DNA and exclusion volumes greater than the actual DNA-binding motif of the TF. In addition, the model presented in⁶⁵ comes with an implementation in Java 1.6 called GRiP⁶⁴, which is able to simulate 1 s of an E.coli K-12 cell in between 1 and 4 hours on a standard desktop computer. In particular, we were able to consider a complete system where we represented the DNA of E.coli K-12 (of 4.6 Mbp)⁹⁷ and the ~ 10⁴ non-cognate DNA binding proteins (agents)⁴³. This indicates that, despite all approximations introduced in the model (such as the approximation of three-dimensional diffusion by the Chemical Master Equation), the simulation of entire cells is still computationally expensive, even for a small organism such as E.coli.

One solution to the computational speed issue, is to consider only a smaller part of the full system. In a recent work, we found that, indeed, one can consider a smaller subsystem (such as 100 Kbp), but only if the system parameters are adjusted accordingly (unpublished data).

Conclusions and outlook

In silico experiments have the advantage that once a simulation is set up and the parameters are correctly estimated, one can reproducibly measure every aspect of the system. Especially given the notoriously difficult and therefore noisy imaging experiments that are prevalent in the facilitated diffusion field, this can be an advantage as these simulations can provide insight without having any technical bias. This is what makes computational models and, in particular stochastic simulations, such an attractive approach.

One question that can be addressed with these types of models is the target site finding process. In particular, analytical solutions are difficult to apply and certain results can be hindered due to mean-field approximation of the affinity landscape of the TF for the DNA. Thus, recently, more efforts where invested in applying these types of approaches to the facilitated diffusion mechanism^51,62-65.

In this manuscript, we enumerated several questions regarding this process that are still unanswered, such as: (i) the proportion of hopping and the proportion of sliding within the one-dimensional random walk, (ii) the optimal fraction for the TF to spend time on the DNA (during the one-dimensional random walk or during three-dimensional diffusion), (iii) the effects of moving obstacles on the DNA (crowding generated by other TF molecules performing facilitated diffusion) or (iv) the effects of target site clustering on the genome. Computational models are one way to address these questions and, here, we reviewed several strategies to computationally model this process.

How can simulations help to address these questions? For example, one can simulate a system with different rates of hopping/sliding and identify which measurements are most likely to display a high correlation with the hopping rate. Previously, it was suggested that the only way to differentiate between hopping and sliding is to change the affinity of the TF for the DNA (by changing the salt concentration in the cell^6,17). However, the degree of influence of salt on the search process is still under debate and, for example, DeSantis et al. ¹⁸ argues that salt displays only a limited effect on sliding. Thus, this question needs to be addressed using a different strategy. One such approach consists of exploiting the effect of crowding on the search time. The current hypothesis is that in a crowded environment, more hopping might lead to lower search time due to the bypass of obstacles^45,47. Thus, one could compare the times the target sites are reached for two different sets of parameters, low and high crowding on the DNA, and for several hopping rates. Next, the results of the simulations can be compared with the results from two in vitro experiments: (i) a system consisting of a restriction enzyme and DNA and (ii) a system consisting of a restriction enzyme, DNA and a different DNA binding molecule. Comparing the cleavage rate of the DNA in two setups with the ones predicted in the simulation can indicate for which relative hopping rate the simulation results match best the computational ones and, thus, determine the relative contribution of hopping to the one-dimensional random walk.

Alternatively, one could investigate the behaviour of the system using different proportions of time spend on the DNA and investigate if the value measured experimentally (of 90% time spent on the DNA) optimises any of the search process properties (such as variation in arrival times or proportion of time the site is occupied). For example, the analytical solution for the optimal fraction of time (50% of the time spent on the DNA and 50% of the time spent in the cytoplasm) might not be valid in the case of moving obstacles on the DNA and under consideration of specific affinities between TFs and the DNA.

These computational models can also be used to understand the cooperative behavior between TFs. Cooperativity is a common mechanism used by TFs to regulate gene activity^57,80 and can lead to an all-or-none response in gene expression. Despite this common observation, there are various underlying mechanisms that can account for cooperativity. For example, in the case of direct TF-TF cooperativity, the molecules can only form a stable complex with the target site when the TF is in high abundance and can form multimeric clusters on the DNA. In the case of DNA mediated cooperativity, high abundance of a TF can be required to saturate other non-functional high affinity sites or to bind to sites that increase the affinity for the target site (e.g. by making the target site available). Finally, the nucleosome-mediated cooperativity assumes that TFs can occupy nucleosome-rich areas only when they have a high abundance⁵⁴. What are these scenarios best suited for? How do the one-dimensional random walk parameters and crowding on the DNA influence the behaviour of these three mechanisms of cooperativity? These are questions that do not have a clear answer yet, and we believe this is where computational models can provide some insight.

Finally, these type of computational models could be used to investigate the effects of target site clustering on the genome⁵². In particular, one could test if this clustering of target sites reduces the TF search process time for their target site by analysing the facilitated diffusion mechanism in systems with multiple co-localized (clusters of) target sites and by including in the model the real affinity landscapes of the TFs considered.

One shortcoming of the current approaches is the lack of three-dimensional structure of the DNA on the nuclear scale in the model. As we mentioned above, currently available data has low resolution and there is no information on the dynamics of this structure. The results obtained when simulating the DNA as a string of letters, without the three-dimensional shape, might hinder some aspects. For example, Klenin et al. ⁸ found that when assuming the DNA to be a random globule, the optimal sliding length (and, thus, the time spent performing the one-dimensional random walk) has a lower value than in the case of linear DNA. Furthermore, Das and Kolomeisky ⁷⁴ found that correlated rebinding to the DNA (which is possible only if one considers the shape of the DNA) leads to an increase in the search speed of TFs for the DNA. These are just two examples that underline the importance of the DNA structure in the models of facilitated diffusion mechanism. Given the recent advancements of these methods^61,78,79, we expect that in the near future high-resolution maps of genomes will become more widely available, and one could incorporate them into the models of facilitated diffusion.

It is not only the three-dimensional structure of the DNA that can influence the facilitated diffusion mechanism, but also the conformation of the protein. For example, Levy and co-workers^92-96 observed that the presence of disordered tails or additional DNA-binding domains could increase the rate at which a protein jumps from one DNA segment to a nearby one (within 6–10 nm). More specifically, this increase in jump rate takes place for long tails with high positive charge^92,93 or additional weaker DNA-binding domains^94,96. DNA-binding proteins with disordered regions⁹⁸ or additional binding domains^2,94 are common in eukaryotes, but less present in prokaryotes. One possible explanation for this observation is that, in eukaryotes, the DNA has a higher degree of organization into chromatin and the three-dimensional distances between DNA regions are better controlled, while in prokaryotes this is not the case. Controlling that distance by chromatin reorganisation could represent an additional method of fine-tuning facilitated diffusion, in the sense that once a protein is captured on one segment, it will have a predefined probability to also scan another DNA segment (depending on the distances between them) and, thus, to achieve gene co-regulation.

Determining the occupancy-bias with computational models of the facilitated diffusion mechanism

In addition to the theoretical questions about the TF search mechanism for their target sites, the computational models described above could be used, in principle, to answer more quantitative questions regarding gene regulation. One such question is the amount of time the target site is occupied by a TF, which determines the rate at which genes are transcribed.

Determining the occupancy-bias landscape in order to compute the percentage of time a target site(s) will be occupied (under the assumption of real affinity landscapes and crowding on the DNA) becomes an essential step in finding the relative expression pattern of a gene. Usually, this occupancy-bias is determined using the statistical thermodynamic framework, which assumes that the system reaches an equilibrium^99-101. The method uses the sequence motif of the TF(s) (the preferred DNA words) determined either in vitro or in vivo¹⁰² and computes the steady state configuration of how a certain number of molecules will be distributed on the genome¹⁰³. The limited accuracy of the approach lead to the use of several new methods (such as Hidden Markov Models¹⁰⁴) and inclusion of more features into the models (such as competition/cooperativity between TFs, nucleosomes and DNA accessibility^99,100,104), but although the quality of the results increased there was still a high rate of false predictions.

One problem with the thermodynamic approach is that the cell is a dynamic environment and this raises the question of whether the regulatory elements actually reach equilibrium^99,105,106. One could argue that since transcription and translation are much slower than regulation, then this equilibrium assumption might be valid after all. However, even if regulation is much faster than transcription there is no guarantee that the regulatory system can reach a steady state.

In particular, long term behaviour (time average) will deviate from the average population behaviour (ensemble average) when the ergodicity assumption is broken (for example in the case of multiple steady states) and in that case one cannot use the statistical thermodynamic approach¹⁰⁷. Actually, we observed that, in the case of crowding on the DNA and when we assume steric hindrance between molecules on the DNA, the time average of the occupancy-bias does not equal the ensemble average (unpublished data) and in that case the thermodynamic approach cannot accurately describe the behaviour of the system.

In each cell, the expression pattern of a gene is an indication of the time the regulatory region was occupied (thus when estimating gene expression one needs to perform time averages and not ensemble ones) and then, at population level, there is an ensemble average over the behaviour of each cell. Thus, one approach would assume first a time average of the occupancy-bias from stochastic simulations for each “virtual” cell, which is then averaged over multiple “virtual” cells (ensemble average). This type of model represents a more accurate representation of the actual process that takes place in real cells and, although speculative at this stage, might increase the quality of the computational predictions of the occupancy-biases.