Abstract
Many locomotor activities require muscles to actively lengthen, dissipate energy and decelerate the body. These eccentric contractions can disrupt cytoskeletal structures within myofibrils and reduce force output. We examined how architectural features of pennate muscles can provide a protective mechanism against eccentric muscle damage by limiting fascicle lengthening. It has been previously shown that the angled fibers of pennate muscles change orientation when shortening. This change in fiber orientation can amplify fascicle shortening, resulting in a velocity advantage at the level of the muscle–tendon unit (MTU) that is characterized by a gear ratio (MTU velocity/fascicle velocity). A muscle's architectural gear ratio (AGR) has been shown to vary as a function of force during shortening, while AGR during lengthening remains largely unknown. We independently measured fascicle length and MTU length in vitro in the bullfrog plantaris. We characterized the muscle's force–velocity curve and AGR during both shortening and lengthening across a broad range of forces (10–190% peak isometric force). AGR was measured during the isotonic portion of each contraction, to eliminate possible contributions of series elasticity to MTU length changes. We found that gear ratio varies with force during both shortening and lengthening contractions. The highest AGR was observed during lengthening contractions, indicating that lengthening of the MTU can occur with relatively little stretch of the fascicle. As fascicle strain is considered an important determinant of muscle damage, a high gear ratio may afford pennate muscles protection against the damaging effects of active lengthening.
KEY WORDS: AGR, Pinnate, Pinnation, Pennation, Fiber architecture, Eccentric, Gear ratio, Variable gearing, Muscle damage
INTRODUCTION
Muscles are commonly described as the body's motors, converting chemical energy into mechanical energy to power movement. To function as a motor, muscles actively shorten while producing force, thereby generating positive mechanical work. However, many locomotor activities require muscles to dissipate mechanical energy. To dissipate energy, muscles must actively lengthen (contract eccentrically) while producing force. When an animal slows down, runs downhill or lands after a jump, muscles must dissipate mechanical energy to decelerate the body (Lindstedt et al., 2001). Energy dissipation is not limited to these specialized locomotor tasks and can also occur during specific phases of level running (Carr et al., 2011). Despite the ubiquity of muscular energy dissipation, much of our understating of how muscles function during movement is based on their role as work-generating motors.
A feature of eccentric contractions that is well established by previous studies is the fact that muscles can be damaged when actively stretched. Eccentric contractions can disrupt cytoskeletal structures and damage the Z-disks that define the boundaries of a sarcomere (Lieber and Fridén, 2002). The disruption and mis-alignment of a subset of sarcomeres reduces a muscle's capacity for force generation and often results in severe soreness and discomfort. Therefore, muscle damage following eccentric activity can impair locomotor performance.
The specific mechanical features of eccentric contractions that are responsible for muscle damage are not broadly agreed upon. Some studies have suggested that muscle damage can be primarily attributed to the magnitude of stretch applied to the muscle fibers (Lieber et al., 1991; Lieber and Fridén, 1993). Others have suggested that the best predictor of damage is the mechanical work dissipated by the sarcomere during a contraction (Brooks et al., 1995). Given that the mechanical work is the product of force and displacement, it is likely that limiting the stretch applied to the sarcomere reduces susceptibility to eccentric muscle damage.
Recent studies have shown that a muscle's architectural features can decouple the length changes that occur at the level of the whole muscle from those that occur at the level of fascicles (Brainerd and Azizi, 2005; Shin et al., 2009; Wakeling et al., 2011). In pennate muscles, where fascicles are oriented at an angle relative to the muscle's line of action, muscle fascicles not only shorten but change orientation during a contraction (Benninghoff and Rollhäuser, 1952; Gans and Bock, 1965; Otten, 1988; Fukunaga et al., 1997; Maganaris et al., 1998). The change in pennation angle during a contraction can decrease the amount of fascicle shortening needed for a given amount of muscle shortening (Brainerd and Azizi, 2005). The effect of fascicle rotation can be characterized as the muscle's gear ratio (Δ muscle length/Δ fascicle length), which is usually greater than 1 for pennate muscles. Muscles that operate with a gear ratio greater than 1 operate with a relative velocity advantage as the length changes of fascicles are amplified, thereby increasing the output velocity of the muscle.
It has recently been shown that a pennate muscle's gear ratio is not constant and may vary with load (Azizi et al., 2008). In the lateral gastrocnemius of wild turkeys, high force contractions involve little change in pennation angle and shortening occurs with a low gear ratio (Azizi et al., 2008). In contrast, during rapid contractions, changes in pennation angle are substantial and the muscle operates with a high gear ratio. It has been suggested that this automatic shift from a gear that favors force to one that favors velocity is mediated by variation in how the muscle changes shape during the contraction. This variable gearing is thought to allow muscles to better match the mechanical conditions of the contraction through dynamic changes in muscle architecture (Azizi et al., 2008).
The gear ratio with which pennate muscles operate during eccentric contractions can define the relationship between the stretch applied to the muscle–tendon unit (MTU) versus the stretch applied directly to the fibers or sarcomeres. If a pennate muscle operates with a high gear ratio, the stretch applied to fascicles will be small relative to the stretch applied to the MTU. This mechanism may be particularly important because pennate muscles might otherwise be at greater risk during active lengthening because of their relatively short fascicle lengths. With fewer sarcomeres in series, a given stretch applied to a short fascicle will require each sarcomere to lengthen more, which may increase the likelihood of muscle damage. Therefore, we predict that during eccentric contractions, pennate muscles operate with a high gear ratio in order to compensate for their shorter fascicles and protect the muscle from eccentric damage.
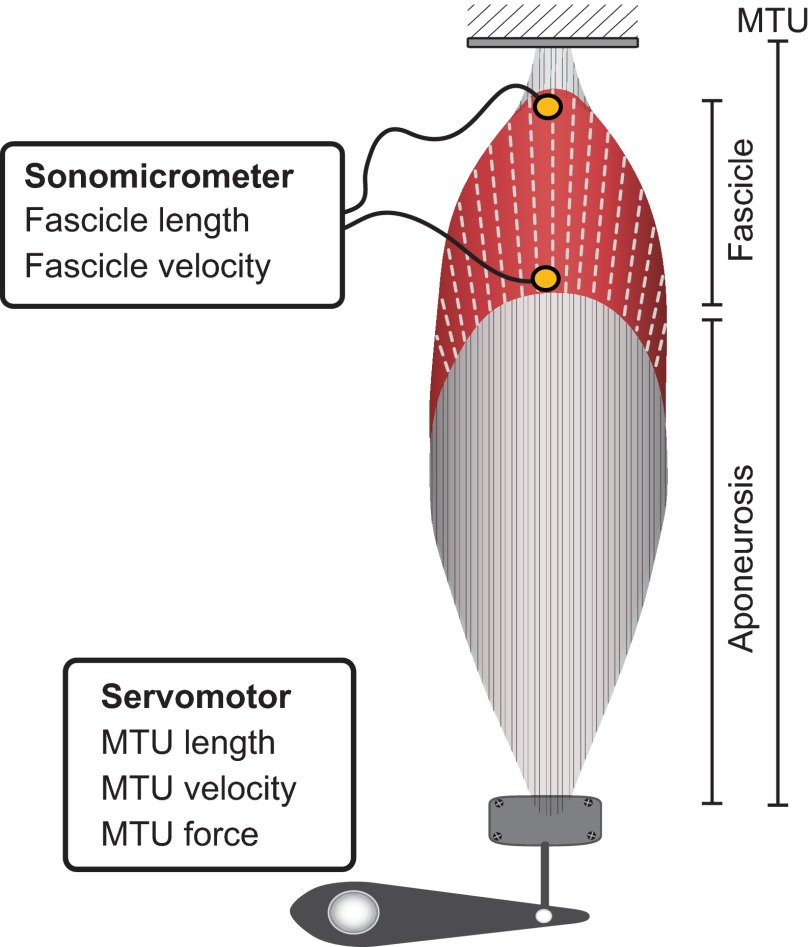
We used an isolated muscle protocol to quantify the gear ratio of a pennate muscle during eccentric contractions. We used the plantaris muscle of bullfrogs, Rana catesbeiana (Shaw 1802), a muscle with a pennation angle of ~30deg, as our model system. We determined the muscle's gear ratio by independently measuring muscle fascicle length using sonomicrometry and MTU length using a servomotor (Fig. 1). We used an isotonic eccentric protocol, which allowed muscles to lengthen while maintaining constant force (Joyce and Rack, 1969). By measuring the muscle's gear ratio during a period of constant force we were able to control for the potentially confounding effect of stretching series elastic elements (Fig. 2). Although we primarily focused on lengthening contractions, our study also included shortening contractions and spanned forces ranging from 10% to 190% of each muscle's maximum isometric force. We used this experimental protocol to test the hypothesis that pennate muscles operate with a high gear ratio during lengthening contractions in order to limit the stretch applied directly to muscle fascicles.
Fig. 1.
Schematic diagram of the in vitro preparation. The regions corresponding to the fascicle, aponeurosis and MTU are indicated. The muscle is stimulated maximally through its nerve. Sonomicrometry is used to measure fascicle length and velocity. A dual-mode servomotor is used to measure MTU force, length and velocity. The ratio of MTU velocity to fascicle velocity is used to characterize the muscle's AGR.
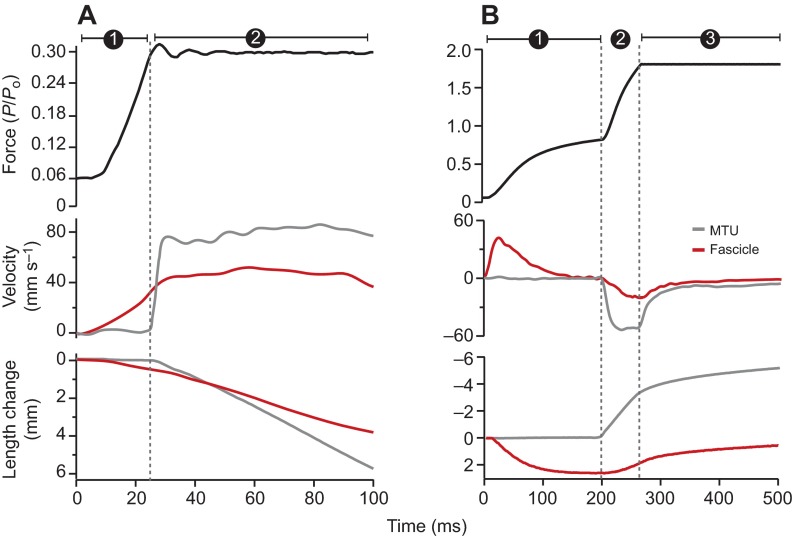
Fig. 2.
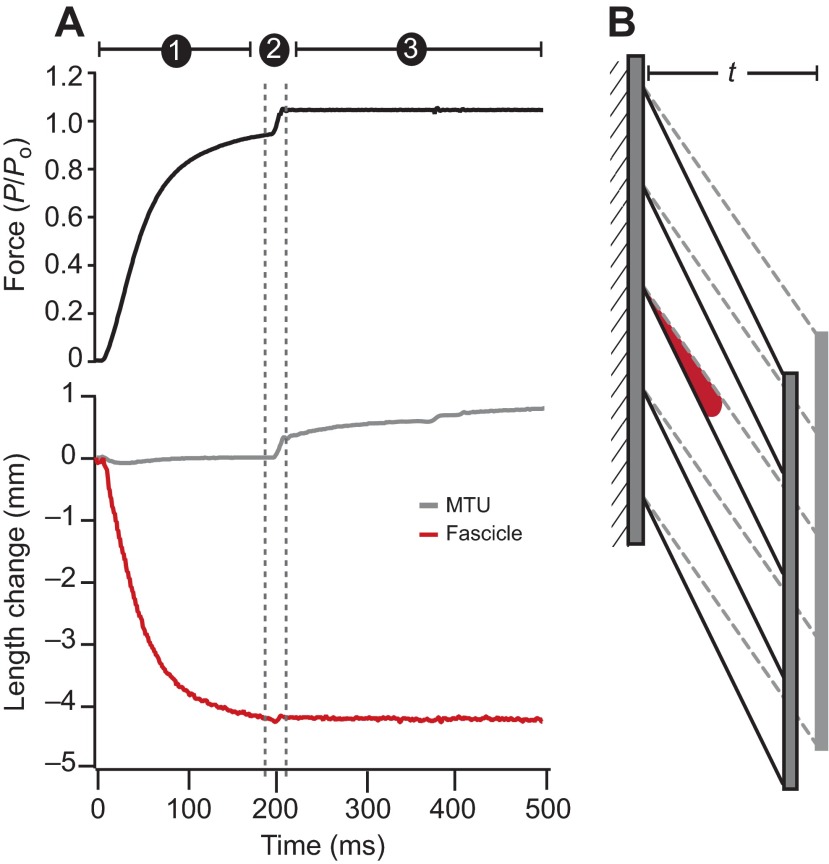
Sample concentric (A) and eccentric (B) contractions. (A) Isotonic concentric contraction at 30% of maximum isometric force (Po). Phase 1 represents a period of force development and phase 2 represents the constant force (isotonic) period of the contraction. The ratio of MTU velocity (gray) and fascicle velocity (red) measured during the isotonic period is used to quantify AGR. (B) Isotonic eccentric contraction at 170% of Po. Phase 1 represents a period of force development. During phase 2 the muscle is stretched by an isovelocity ramp until the muscle force reaches a designated force level. Phase 3 represents an isotonic period where the muscle is being stretched while the motor maintains a constant force level. Gear ratio is quantified during phase 3, where force is constant. By convention, shortening is defined as positive velocity and lengthening is defined as negative velocity.
RESULTS
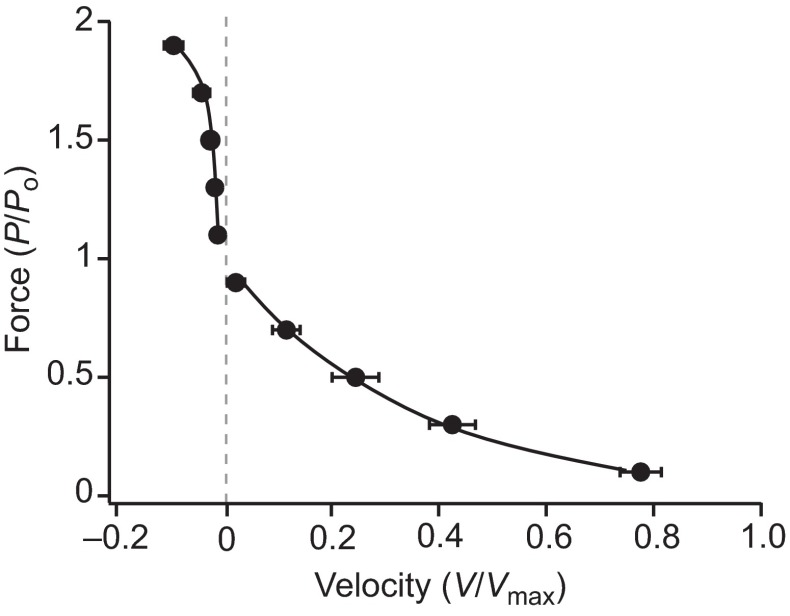
The plantaris muscles used in this study had an average muscle mass of 4.5±0.63 g and an average pennation angle of 28.6±2.1 deg (means ± s.d.). Based on fascicle lengths, muscle mass, pennation angle and standard values for muscle density, the average physiological cross-sectional area of the muscle was calculated as 2.11±0.28 cm2. The average maximum isometric force (Po) was 46.21±3.84 N and the average specific force was 22.56±3.99 N cm−2 for the muscles used in the study. The maximum shortening velocity (Vmax) was 9.62±1.52 lengths s−1 and the maximum power output was 253.1±29.7 W kg−1 (Fig. 3).
Fig. 3.
The shortening and lengthening force–velocity relationship of the muscle. Velocity data are based on the velocity of the MTU and are normalized to maximum shortening velocity (Vmax). Forces are normalized to maximum isometric force (Po). Data (means ± s.e.m.) are pooled from seven muscles and fitted according to Otten (Otten, 1987).
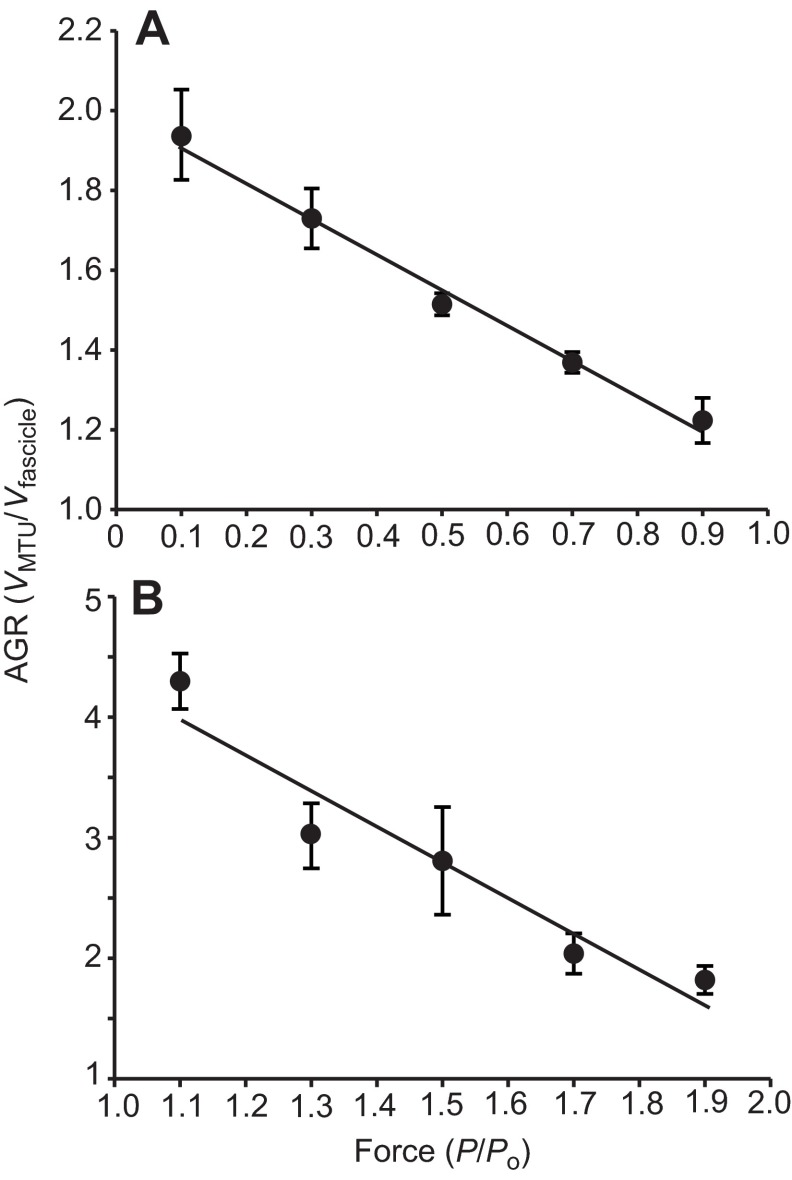
The architectural gear ratio (AGR) of the planatris muscle was significantly higher during lengthening contractions than during shortening contractions (P<0.001; Fig. 4). AGR ranged from 1.94 to 1.22 during shortening contractions and from 4.30 to 1.82 during lengthening contractions. AGR varied based on the force of the contraction during both shortening and lengthening contractions. The relationship between AGR and force was discontinuous as the contractions transitioned from shortening to lengthening (Fig. 4). AGR decreased significantly with increasing force (P<0.001) during shortening contractions and the relationship was best described by a linear least-squares fit (Fig. 4A). AGR also decreased with increasing force during lengthening contractions (P<0.001). The AGR data during lengthening were fitted with a linear least-squares fit (Fig. 4B).
Fig. 4.
Architectural gear ratio (AGR) during shortening and lengthening contractions across a range of contraction forces. Gear ratio is quantified as the ratio of muscle–tendon unit (MTU) velocity to muscle fascicle velocity measured during a period of constant force. (A) During shortening contractions, AGR decreases with increasing force. Data are fitted with a least-squares linear fit (AGR=–0.91P+2.01, where P is force; R2=0.69, P<0.001). (B) During lengthening contractions, AGR decreases with increasing force. Data are fitted with a least-squares linear fit (AGR=−2.97P+7.23; R2=0.61, P<0.001). Data are pooled from seven muscles and shown as means ± s.e.m. Po, maximum isometric force.
DISCUSSION
Our results show that muscles operate with a high gear ratio during lengthening contractions (Fig. 4). As a result of fascicle rotation, the amount and rate of fascicle lengthening is significantly reduced relative that of the whole muscle. This may protect pennate muscle fibers against eccentric muscle damage. The difference in fascicle lengthening and MTU lengthening rate can be quite large; our highest measured AGR was greater than 4, indicating that the fascicle lengthening under these conditions was less than 25% the rate of MTU lengthening.
Fascicle rotation, muscle shape changes and gearing
Architectural gearing is mediated by the rotation of fascicles as pennation angle changes (Brainerd and Azizi, 2005; Azizi and Brainerd, 2007; Azizi et al., 2008; Wakeling et al., 2011; Randhawa et al., 2013; Azizi and Roberts, 2013). The high gear ratios of some lengthening contractions result from a relatively large degree of fascicle rotation for a given amount of fascicle shortening. This mechanism is particularly well illustrated in a few contractions in which a small MTU lengthening was almost entirely accommodated by changes in pennation angle, with little or no stretch of the fascicle. Fig. 5 depicts a contraction where the MTU is lengthened slowly at a force just slightly exceeding maximum isometric force. In this contraction the MTU lengthens as the fascicles rotate to shallower angles of pennation, but the fibers undergo negligible length change (Fig. 5A). Under these conditions, the muscle's gear ratio can be very high because the muscle lengthens and absorbs energy with minimal change in fascicle length (Fig. 5B).
Fig. 5.
A sample eccentric contraction at a very slow lengthening velocity. (A) This contraction depicts the potential for high gear ratios when forces are just above maximum isometric force (Po). The three phases of the contraction are the same as those described in Fig. 2. In this contraction, MTU lengthening during a period of constant force is achieved with little or no stretch of the fascicle. This contraction suggests that small, slow stretches of the MTU can be accommodated by changes in muscle pennation angle and do not require the fascicles to be stretched. (B) A schematic diagram of how architectural changes of the muscle can limit fascicle stretch during eccentric contractions. The muscle before the contraction is shown with dashed fascicles. A decrease in the muscle thickness (t) and a decrease in pennation angle (red) can allow the MTU to be stretched without any length change in the fascicle.
We found that the AGR during both active lengthening and shortening in the frog plantaris was variable. For a series of contractions, the AGR of the bullfrog plantaris decreased with increasing force during both shortening and lengthening contractions. The relationship between AGR and force during shortening contractions is consistent with a previous study highlighting a range of AGR with changing contraction conditions (Azizi et al., 2008). Azizi and colleagues (Azizi et al., 2008) found that AGR decreases with force in the turkey gastrocnemius muscle and that AGR ranged between 1.4 and 1. In this study we found that AGR during shortening is between 2.0 and 1.2 in the plantaris muscle of bullfrogs. Given that the two studies used identical methods for quantifying AGR, this difference likely results from structural differences between the two muscles. One explanation for the differences observed in the range of AGR may be that the two muscles differ in how they change shape during contractions at varying forces. The passive elastic structures that regulate muscle shape during contraction may vary between the two muscles, thereby resulting in differences in AGR. Alternatively, differences in AGR between this and a previous study (Azizi et al., 2008) may be due to the fact that the two muscles differ in their degree of pennation. The muscle used in this study has an initial pennation angle of ~30 deg whereas the turkey lateral gastrocnemius has an initial pennation angle of ~20 deg. This interpretation is consistent with the idea that muscles with lager pennation angles will operate with higher gear ratios (Brainerd and Azizi, 2005). A similar variation in gear ratios has also been observed within a single muscle as fascicle strains were shown to vary regionally, with higher strains occurring in regions with the lowest pennation angles (Shin et al., 2009).
The relative relationship between changes in pennation angle and length changes in the fascicle is mediated by how the muscle changes shape (Azizi et al., 2008). As muscle fibers are constant volume structures, shortening in one direction must be accommodated by an expansion in other directions. Variable gearing among different shortening contractions results from variation in how the muscle changes shape as the muscle bulges in different directions during different contractions. This phenomenon also explains variable gearing during lengthening contractions. However, during lengthening, muscle fiber diameter becomes smaller, which in turn decreases the width and thickness of the muscle (Kinugasa et al., 2012). Although we did not measure muscle shape in this study, the higher gearing in low-force contractions suggests that there was a greater change in muscle thickness when compared with high-force lengthening contractions. A decrease in muscle thickness can accommodate large changes in muscle pennation angle, resulting in high gearing (Fig. 5).
Protective effects of muscle gearing in pennate muscles
The high gear ratio during lengthening contractions observed in this study may represent a mechanism that protects against eccentric muscle damage, as it may reduce the stretch applied directly to fascicles. Compared with parallel fibered muscles, the relatively short fibers of pennate muscles potentially put them at greater risk during lengthening contractions. An increase in the length of muscle fibers and the addition of sarcomeres acting in series can function to distribute a given stretch applied to the muscle over a greater number of sarcomeres, thereby reducing the strain in each contractile unit. However, unlike parallel fibered muscles, which operate with a gear ratio of 1, a relatively high architectural gear ratio in pennate muscles may limit the strain experienced by active fascicles. For example, the sarcomeres of a parallel fibered muscle operating with an AGR of 1 and a pennate fibered muscle operating with an AGR of 3 would likely undergo the same stretch if the fascicles of the parallel fibered muscle were three times as long. Previous work has shown that despite having shorter fascicles, pennate fibered muscles can be stretched to significantly longer lengths before mechanical failure (Garrett et al., 1988). This pattern suggests that operating with a high gear ratio may in part compensate for the relatively short fibers of pennate muscles and provide some degree of protection during lengthening contractions.
Pennate muscles are often associated with the presence of significant series elastic tissue. The fascicles of many uni- and bi-pennate muscles insert onto sheet-like aponeuroses, which can significantly extend the length of the free tendon and are considered to be an important site for elastic energy storage (Roberts et al., 1997; Azizi and Roberts, 2009). The presence of series elasticity can function to attenuate mechanical power during eccentric contractions by temporarily storing mechanical energy before releasing the energy to stretch the muscle at a slower rate (Roberts and Azizi, 2010). The reduction of mechanical power input to the muscle may serve a protective function during high-energy decelerations (Roberts and Azizi, 2010; Roberts and Azizi, 2011; Konow et al., 2012; Roberts and Konow, 2013).
The established relationship between gear ratio and pennation angle would suggest that a muscle's architectural features could be a potential target for muscle remodeling in response to eccentric training. Numerous studies have shown that moderate exposure to eccentric training can decrease susceptibility to muscle damage during subsequent bouts of eccentric exercise (reviewed by McHugh, 2003). The mechanism underlying this decrease in susceptibility is not broadly agreed upon. Altered motor control strategies (Warren et al., 2000; Howatson et al., 2007), changes in muscle stiffness (Lindstedt et al., 2002; Lehti et al., 2007) and the addition of sarcomeres within muscle fibers (Lynn and Morgan, 1994) have all been implicated as potential mechanisms that explain this repeated bout effect. In addition, several studies have also found that muscle pennation angle increases following an eccentric training protocol (Aagaard et al., 2001; Blazevich et al., 2007; Duclay et al., 2009). Our results suggest that such increases in pennation angle may allow muscles to operate with higher gear ratios during eccentric contractions. Therefore, changes in the architectural properties of muscles may help to minimize muscle damage following exposure to eccentric exercise.
Conclusions
Our results show that pennate muscles operate with high gear ratios during eccentric contractions, and that gear ratio varies with force in both lengthening and shortening contractions. A high gear ratio functions to minimize the stretch applied directly to fascicles when the muscle is lengthened. We conclude that operating with a high gear ratio may mitigate the potential risk of muscle damage in pennate muscles.
MATERIALS AND METHODS
Animals
Large adult bullfrogs, R. catesbeiana, ranging in body mass from 327 to 416 g were purchased from a herpetological vendor (N=7). Animals were housed in large aquaria, which included both aquatic and terrestrial regions. Frogs were maintained on a diet of large crickets provided ad libitum. All husbandry, and experimental protocols were approved by the Institutional Animal Care and Use Committee of The University of California, Irvine.
In vitro preparation
The plantaris muscle was selected as the model system for this study. The selection of this muscle was motivated by two important factors. First, the plantaris is a pennate muscle with a large and conspicuous aponeurosis, making the fascicles easy to distinguish from series elastic elements (Fig. 3). Second, the size of the muscles was large enough for sonomicrometry implantation while being small enough that the high forces developed during eccentric contractions were within the range of available muscle servomotors. The one drawback in our selection of this muscle is that the plantaris is rarely actively lengthened in vivo. However, the motivation of the study was to relate morphological aspects of muscle architecture to AGR without developing explicit links to in vivo function.
The frogs were killed with a double pithing protocol. The legs were isolated and the surrounding skin was removed. The distal tendon of the plantaris was severed and the muscle freed from the ankle and the tibiafibula. The proximal attachment of the muscle at the knee was kept intact. The musculature around the femur was removed to expose the sciatic nerve. A nerve cuff constructed from plastic tubing and silver wire was attached to the nerve to allow for stimulation. A pair of 1 mm piezoelectric crystals (Sonometrics Corp., London, ON, Canada) was implanted in the proximal region of the plantaris. Crystals were oriented along a proximal superficial fascicle that was both accessible and visible during the surgery. Both crystals were implanted proximal to the aponeurosis in order to avoid possible interference from elastic elements. Sonomicrometry transducers were secured in place using 6-0 silk.
The femur and the tibiafibula were clamped to a rigid plate and the distal end of the plantaris muscle was placed in a lightweight custom-made clamp. The preparation did not include the free tendon; however, the aponeurosis was intact during the experiments. The muscle was placed in an amphibian Ringer's solution (100 mmol l−1 NaCl, 2.5 mmol l−1 KCl, 2.5 mmol l−1 NaHCO3, 1.6 mmol l−1 CaCl, 10 mmol l−1 dextrose), which was continuously aerated with oxygen and kept at 22°C. The tendon clamp was attached to a dual-mode servomotor (310 B-LR, Aurora Scientific Inc., Aurora, ON, Canada) with stiff steel cable. Care was taken to minimize the overall compliance of the set-up.
Data collection
The implanted sonomicrometry transducers were used to independently measure muscle fascicle length while the servomotor was used to measure the length and force of the MTU (Fig .1). A series of isotonic contractions ranging from 10–190% of the muscle's maximum isometric force (Po) was used to characterize the force–velocity properties of the plantaris during active shortening and lengthening. In addition, these contractions allowed us to characterize the relationship between fascicle velocity and MTU velocity, and quantify the AGR with which the muscle operates during concentric and eccentric contractions. The use of an isotonic protocol allowed us to control two important factors. First, we controlled for the potentially confounding effects of stretching series elastic elements by measuring the muscle properties during a period of constant force. Second, we were able to take measurements of fascicle and MTU velocity at the same fascicle length to minimize variation due to the muscle's force–length properties as well as variation in the initial pennation angle of the muscle during a contraction.
Prior to the tetanic isotonic contractions, the optimum stimulation voltage and fascicle length were determined. To determine the optimum stimulation voltage, the muscle's twitch force was monitored as the voltage was increased by 1V increments. The voltage that resulted in maximum twitch force was increased by 1V and used to maximally stimulate the muscle. A series of twitches at varying fascicle lengths was then used to determine the muscle's optimal fascicle length (Lo). A single tetanic contraction at the muscle's optimal length was then used to determine the muscle's Po. All isotonic contractions were performed at varying proportions of Po and were started at fascicle lengths that ensured the muscle length would cross Lo during the constant force period.
During concentric isotonic contractions the muscle was stimulated maximally and force was allowed to develop up to a predetermined force level (10%, 30%, 50%, 70% or 90% of Po), at which point the servomotor maintained constant force as the muscle shortened (Fig. 2A). As a result, each contraction had two phases corresponding to (1) a period of force development under ‘fixed-end’ conditions and (2) a constant force period during which the muscle shortened (Fig. 2A). During eccentric isotonic contractions the muscle was initially stimulated maximally for 200 ms in order develop force close to Po. The muscle was then lengthened rapidly with a constant velocity ramp in order to get muscle force above Po up to a pre-set level (110%, 130%, 150%, 170% or 190% of Po) at which point the servomotor maintained constant force as the muscle lengthened. As a result, each eccentric contraction had three distinct phases corresponding to (1) a period of force development under ‘fixed-end’ conditions, (2) an isovelocity ramp and (3) a constant force period during which the muscle lengthened at a rate determined by servomotor feedback (Fig. 2B). Each muscle was a given a minimum of 4 min rest between tetanic contractions in order to avoid fatigue. Following the entire protocol, a final isometric contraction was performed at Lo in order to ensure that force did not drop by more than 5% throughout the experiment. All data were collected at 1000 Hz using a 16 bit A/D converter and LabView software (National Instruments, Austin, TX, USA).
Following the experiments, the muscles were fixed at a fascicle length corresponding to Lo and the fascicle length, mass and pennation angle of each muscle were measured. We used these morphological parameters to calculate the physiological cross-sectional area and calculate the maximum muscle stress. The anatomical and contractile properties of the muscles used in the study are given in Table 1.
Table 1.
Anatomical and contractile properties of the muscles used in the study

Data analysis
The force–velocity curves for both concentric and eccentric contractions were constructed using the MTU force and velocity measured with the servomotor. Measurements were taken within the period of constant force and at a fascicle length corresponding to Lo. The force–velocity data during shortening were fitted to a rectangular hyperbola of the form:
| (1) |
where P is force, Po is the maximum isometric force, V is velocity, a and b are constants (Hill, 1938). The fit for each muscle was used to calculate Po, maximum shortening velocity (Vmax), the curvature of the curve (a/Po), and the muscle's peak power output (Pmax). The force–velocity data during lengthening were fitted with a similar function of the form:
| (2) |
where c, k and q are constants that are specific to a given muscle (adapted from Otten, 1987). The constant c indicates the maximum force during eccentric contractions (Table 1).
The AGR of the muscle was calculated using the ratio of the muscle velocity (from the servomotor) and the fascicle velocity (from the sonomicrometer) during a period of constant force. When necessary, length data were smoothed using a quintic spline interpolation and differentiated to attain velocities. Velocities were measured at a fascicle length corresponding to Lo. We assume that by measuring velocities at the same length, the muscle is at a similar pennation angle for all our measurements of AGR. The degree to which the force and length history of the contraction prior to our measurements may decouple the relationship between length and pennation angle is unknown and may be a small source of variation in our measurements. In this study we also assume that changes in pennation angle are directly responsible for muscles operating with an AGR above 1. This assumption is based on previous studies that have directly measured instantaneous pennation angle during a contraction and have developed a relationship between AGR and changes in fascicle orientation (Azizi and Brainerd, 2007; Azizi et al., 2008; Wakeling et al., 2011; Randhawa et al., 2013; Azizi and Roberts, 2013). All data analysis was performed using Igor Pro software (V. 6.0; Wavemetrics, Lake Oswego, OR, USA).
A mixed model ANOVA was used to compare AGR between shortening and lengthening conditions with contraction type (eccentric or concentric) as the main factor and individual treated as a random effect. Least-squares regressions were used to assess the relationship between AGR and force. Statistics were performed using JMP software (SAS Institute, Cary, NC, USA).
ACKNOWLEDGEMENTS
We thank Emily Abbott, Greg Sawicki and Nicolai Konow for experimental assistance.
FOOTNOTES
Competing interests
The authors declare no competing financial interests.
Funding
This work was supported by National Institutes of Health (NIH) grant AR055295 and National Science Foundation (NSF) grant 1051691. Deposited in PMC for release after 12 months.
References
- Aagaard P., Andersen J. L., Dyhre-Poulsen P., Leffers A. M., Wagner A., Magnusson S. P., Halkjaer-Kristensen J., Simonsen E. B. (2001). A mechanism for increased contractile strength of human pennate muscle in response to strength training: changes in muscle architecture. J. Physiol. 534, 613-623 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Azizi E., Brainerd E. L. (2007). Architectural gear ratio and muscle fiber strain homogeneity in segmented musculature. J. Exp. Zool. A 307A, 145-155 [DOI] [PubMed] [Google Scholar]
- Azizi E., Roberts T. J. (2009). Biaxial strain and variable stiffness in aponeuroses. J. Physiol. 587, 4309-4318 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Azizi E., Roberts T. J. (2013). Variable gearing in a biologically inspired pneumatic actuator array. Bioinspir. Biomim. 8, 026002 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Azizi E., Brainerd E. L., Roberts T. J. (2008). Variable gearing in pennate muscles. Proc. Natl. Acad. Sci. USA 105, 1745-1750 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Benninghoff A., Rollhäuser H. (1952). Zur inneren Mechanik des gefiederten Muskels. Pflugers Arch. 254, 527-548 [DOI] [PubMed] [Google Scholar]
- Blazevich A. J., Cannavan D., Coleman D. R., Horne S. (2007). Influence of concentric and eccentric resistance training on architectural adaptation in human quadriceps muscles. J. Appl. Physiol. 103, 1565-1575 [DOI] [PubMed] [Google Scholar]
- Brainerd E. L., Azizi E. (2005). Muscle fiber angle, segment bulging and architectural gear ratio in segmented musculature. J. Exp. Biol. 208, 3249-3261 [DOI] [PubMed] [Google Scholar]
- Brooks S. V., Zerba E., Faulkner J. A. (1995). Injury to muscle fibres after single stretches of passive and maximally stimulated muscles in mice. J. Physiol. 488, 459-469 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Carr J. A., Ellerby D. J., Marsh R. L. (2011). Differential segmental strain during active lengthening in a large biarticular thigh muscle during running. J. Exp. Biol. 214, 3386-3395 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Duclay J., Martin A., Duclay A., Cometti G., Pousson M. (2009). Behavior of fascicles and the myotendinous junction of human medial gastrocnemius following eccentric strength training. Muscle Nerve 39, 819-827 [DOI] [PubMed] [Google Scholar]
- Fukunaga T., Ichinose Y., Ito M., Kawakami Y., Fukashiro S. (1997). Determination of fascicle length and pennation in a contracting human muscle in vivo. J. Appl. Physiol. 82, 354-358 [DOI] [PubMed] [Google Scholar]
- Gans C., Bock W. J. (1965). The functional significance of muscle architecture – a theoretical analysis. Ergeb. Anat. Entwicklungsgesch. 38, 115-142 [PubMed] [Google Scholar]
- Garrett W. E., Jr, Nikolaou P. K., Ribbeck B. M., Glisson R. R., Seaber A. V. (1988). The effect of muscle architecture on the biomechanical failure properties of skeletal muscle under passive extension. Am. J. Sports Med. 16, 7-12 [DOI] [PubMed] [Google Scholar]
- Hill A. V. (1938). The heat of shortening and the dynamic constants of muscle. Proc. R. Soc. B 126, 136-195 [Google Scholar]
- Howatson G., Van Someren K., Hortobágyi T. (2007). Repeated bout effect after maximal eccentric exercise. Int. J. Sports Med. 28, 557-563 [DOI] [PubMed] [Google Scholar]
- Joyce G. C., Rack P. M. H. (1969). Isotonic lengthening and shortening movements of cat soleus muscle. J. Physiol. 204, 475-491 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kinugasa R., Hodgson J. A., Edgerton V. R., Sinha S. (2012). Asymmetric deformation of contracting human gastrocnemius muscle. J. Appl. Physiol. 112, 463-470 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Konow N., Azizi E., Roberts T. J. (2012). Muscle power attenuation by tendon during energy dissipation. Proc. Biol. Sci. 279, 1108-1113 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lehti T. M., Kalliokoski R., Komulainen J. (2007). Repeated bout effect on the cytoskeletal proteins titin, desmin, and dystrophin in rat skeletal muscle. J. Muscle Res. Cell Motil. 28, 39-47 [DOI] [PubMed] [Google Scholar]
- Lieber R. L., Fridén J. (1993). Muscle damage is not a function of muscle force but active muscle strain. J. Appl. Physiol. 74, 520-526 [DOI] [PubMed] [Google Scholar]
- Lieber R. L., Fridén J. (2002). Mechanisms of muscle injury gleaned from animal models. Am. J. Phys. Med. Rehabil. 81 Suppl., S70-S79 [DOI] [PubMed] [Google Scholar]
- Lieber R. L., Woodburn T. M., Fridén J. (1991). Muscle damage induced by eccentric contractions of 25% strain. J. Appl. Physiol. 70, 2498-2507 [DOI] [PubMed] [Google Scholar]
- Lindstedt S. L., LaStayo P. C., Reich T. E. (2001). When active muscles lengthen: properties and consequences of eccentric contractions. News Physiol. Sci. 16, 256-261 [DOI] [PubMed] [Google Scholar]
- Lindstedt S. L., Reich T. E., Keim P., LaStayo P. C. (2002). Do muscles function as adaptable locomotor springs? J. Exp. Biol. 205, 2211-2216 [DOI] [PubMed] [Google Scholar]
- Lynn R., Morgan D. L. (1994). Decline running produces more sarcomeres in rat vastus intermedius muscle fibers than does incline running. J. Appl. Physiol. 77, 1439-1444 [DOI] [PubMed] [Google Scholar]
- Maganaris C. N., Baltzopoulos V., Sargeant A. J. (1998). In vivo measurements of the triceps surae complex architecture in man: implications for muscle function. J. Physiol. 512, 603-614 [DOI] [PMC free article] [PubMed] [Google Scholar]
- McHugh M. P. (2003). Recent advances in the understanding of the repeated bout effect: the protective effect against muscle damage from a single bout of eccentric exercise. Scand. J. Med. Sci. Sports 13, 88-97 [DOI] [PubMed] [Google Scholar]
- Otten E. (1987). A myocybernetic model of the jaw system of the rat. J. Neurosci. Methods 21, 287-302 [DOI] [PubMed] [Google Scholar]
- Otten E. (1988). Concepts and models of functional architecture in skeletal muscle. In Exercise and Sports Sciences Reviews, vol. 16 (ed. Pandolf K. B.), pp. 89-137 New York, NY: Macmillan Publishing; [PubMed] [Google Scholar]
- Randhawa A., Jackman M. E., Wakeling J. M. (2013). Muscle gearing during isotonic and isokinetic movements in the ankle plantarflexors. Eur. J. Appl. Physiol. 113, 437-447 [DOI] [PubMed] [Google Scholar]
- Roberts T. J., Azizi E. (2010). The series-elastic shock absorber: tendons attenuate muscle power during eccentric actions. J. Appl. Physiol. 109, 396-404 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Roberts T. J., Azizi E. (2011). Flexible mechanisms: the diverse roles of biological springs in vertebrate movement. J. Exp. Biol. 214, 353-361 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Roberts T. J., Konow N. (2013). How tendons buffer energy dissipation by muscle. Exerc. Sport Sci. Rev. 41, 186-193 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Roberts T. J., Marsh R. L., Weyand P. G., Taylor C. R. (1997). Muscular force in running turkeys: the economy of minimizing work. Science 275, 1113-1115 [DOI] [PubMed] [Google Scholar]
- Shin D. D., Hodgson J. A., Edgerton V. R., Sinha S. (2009). In vivo intramuscular fascicle-aponeuroses dynamics of the human medial gastrocnemius during plantarflexion and dorsiflexion of the foot. J. Appl. Physiol. 107, 1276-1284 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wakeling J. M., Blake O. M., Wong I., Rana M., Lee S. S. M. (2011). Movement mechanics as a determinate of muscle structure, recruitment and coordination. Philos. Trans. R. Soc. B 366, 1554-1564 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Warren G. L., Hermann K. M., Ingalls C. P., Masselli M. R., Armstrong R. B. (2000). Decreased EMG median frequency during a second bout of eccentric contractions. Med. Sci. Sports Exerc. 32, 820-829 [DOI] [PubMed] [Google Scholar]