Robust smoothing of gridded data in one and higher dimensions with missing values

Abstract

A fully automated smoothing procedure for uniformly-sampled datasets is described. The algorithm, based on a penalized least squares method, allows fast smoothing of data in one and higher dimensions by means of the discrete cosine transform. Automatic choice of the amount of smoothing is carried out by minimizing the generalized cross-validation score. An iteratively weighted robust version of the algorithm is proposed to deal with occurrences of missing and outlying values. Simplified Matlab codes with typical examples in one to three dimensions are provided. A complete user-friendly Matlab program is also supplied. The proposed algorithm – very fast, automatic, robust and requiring low storage –provides an efficient smoother for numerous applications in the area of data analysis.

1. Introduction

In this paper, a fast robust version of a discretized smoothing spline is introduced. The proposed method, based on the discrete cosine transform (DCT), allows robust smoothing of equally spaced data in one and higher dimensions. The next paragraphs of the present section briefly describe the underlying penalized least squares approach, in the particular case of one-dimensional data. Section 2 provides a review of the generalized cross-validation which is used to estimate the smoothing parameter. When data are evenly spaced, it is shown (section 3) that the linear system can be greatly simplified and solved by means of the DCT. An iterative robust scheme of this DCT-based penalized regression is then proposed in order to deal with weighted, missing (section 4) and outlying (section 5) values. It is finally explained, in section 6, how the smoothing technique proposed in this paper can be applied to multidimensional data. To illustrate the effectiveness of the smoother, several examples related to one-, two- and three-dimensional data are presented (section 7). Two simplified Matlab functions and one complete optimized Matlab code are also provided.

In statistics and data analysis, smoothing is used to reduce experimental noise or small-scale information while keeping the most important imprints of a dataset. Consider the following model for the one-dimensional noisy signal y:

$$y=\widehat{y}+\epsilon ,$$ (1)

where ε represents a Gaussian noise with mean zero and unknown variance, and ŷ is supposed to be smooth, i.e. has continuous derivatives up to some order (typically ≥2) over the whole domain. Smoothing y relies upon finding the best estimate of ŷ. Data smoothing is generally carried out by means of parametric or nonparametric regression. Parametric regression requires some a priori knowledge of the so-called regression equation that can represent the data well. The majority of observed values, however, cannot be parameterized in terms of predetermined analytical functions so that nonparametric regression is usually the best option for smoothing of data (Takezawa, 2005). To cite a few instances, some of the most common approaches to nonparametric regression used in data processing include kernel regression (Hastie and Loader, 1993) like moving average filtering, local polynomial regression (Watson, 1964) and the Savitzky-Golay filter (Savitzky and Golay, 1964). Another classical approach to smoothing is the penalized least squares regression. This method was first introduced in the early 1920’s by Whittaker (Whittaker, 1923) and has been extensively studied ever since (Wahba, 1990a). This technique consists in minimizing a criterion that balances the fidelity to the data, measured by the residual sum-of-squares (RSS), and a penalty term (P) that reflects the roughness of the smooth data. One thus seeks to minimize:

$$F(\widehat{y})=\text{RSS}+s\mathrm{P}(\widehat{y})={\left|\right|\widehat{y}-y\left|\right|}^2+s\mathrm{P}(\widehat{y}),$$ (2)

where || || denotes the Euclidean norm. The parameter s is a real positive scalar that controls the degree of smoothing: as the smoothing parameter increases, the smoothing of ŷ also increases. When the roughness penalty is written in terms of the square integral of the pth derivative of ŷ, the penalized regression is known as a smoothing spline (Schoenberg, 1964; Takezawa, 2005; Wahba, 1990a). Another simple and straightforward approach to express the roughness is by using a second-order divided difference (Weinert, 2007; Whittaker, 1923) which yields, for a one-dimensional data array:

$$\mathrm{P}(\widehat{y})={\left|\right|D\widehat{y}\left|\right|}^2,$$ (3)

where D is a tridiagonal square matrix defined by:

$$D_{i,i-1}=\frac{2}{h_{i-1}\left(h_{i-1}+h_i\right)},D_{i,i}=\frac{-2}{h_{i-1}{h}_i},D_{i-1,i}=\frac{2}{h_i\left(h_{i-1}+h_i\right)},$$

for 2 ≤ i ≤ n−1 where n is the number of elements in ŷ, and h_i represents the step between ŷ_i and ŷ_i+1. Assuming repeating border elements (y₀ = y₁ and y_n+1 = y_n), gives:

$$-D_{1,1}=D_{1,2}=\frac{1}{{h_1}^2}\text{and}{D}_{n,n-1}=-D_{n,n}=\frac{1}{{h_{n-1}}^2}$$

This procedure is similar to the Whittaker smoothing (Eilers, 2003; Weinert, 2007; Whittaker, 1923) apart from the repeating boundaries. Such boundary conditions lead to further numerical simplifications with evenly spaced data (Buckley, 1994), as explained further in section 3.

Now, using equations (2) and (3), minimization of F(ŷ) gives the following linear system that allows the determination of the smoothed data:

$$\left(I_n+{sD}^{\mathrm{T}}D\right)\widehat{y}=y,$$ (4)

where I_n is the n×n identity matrix and D ^T stands for the transpose of D. Because (I_n+sD^TD) is a symmetric pentadiagonal matrix, the latter equation can be numerically solved very efficiently with a technical computing software (Eilers, 2003; Weinert, 2007). Computation of ŷ using Matlab (The MathWorks, Natick, MA, USA) and equation (4) has been recently introduced by Eilers (2003) and Weinert (2007). In the case of evenly-spaced data, Weinert has proposed a relatively fast algorithm based on Cholesky decomposition (Weinert, 2007). This algorithm, however, loses efficiency when an estimation of the smoothing parameter is required, as explained in the following section.

2. Estimation of the smoothing parameter

As indicated by equation (4), the output ŷ is strongly influenced by the smoothing parameter s. Assuming the model given by equation (1), it is appropriate to use the smoothing parameter that yields the best estimate of the original data and thus avoids over-or under-smoothing as much as possible. Such a correct value can be estimated by the method of generalized cross-validation (GCV).

The GCV method has been introduced by Craven and Wahba (Craven and Wahba, 1978; Wahba, 1990b) in the context of smoothing splines. Assuming that one wants to solve the smoothing linear system

$$\widehat{y}=H(s)y,$$

where H is the so-called hat matrix, the GCV method chooses the parameter s that minimizes the GCV score (Craven and Wahba, 1978; Golub, Heath and Wahba, 1979):

$$s=\text{argmin}(\mathit{GCV})\text{with}\mathit{GCV}(s)\equiv \frac{\text{RSS}/n}{{(1-\text{Tr}(H)/n)}^2},$$

where Tr denotes the matrix trace. Finding s which minimizes the GCV score thus requires Tr(H) to be known. Here, according to equation (4), H is given by:

$$H={\left(I_n+{sD}^{\mathrm{T}}D\right)}^{-1}.$$ (5)

To calculate the GCV score, Eilers (Eilers, 2003) and Weinert (Weinert, 2007) have both proposed algorithms that involve the determination of H at each iterative step of the minimization. Such a process is very time-consuming and can be avoided. Indeed, Tr(H) can be simply reduced to:

$$\text{Tr}(H)=\sum _{i=1}^n\frac{1}{1+s{\lambda }_i^2}$$ (6)

where ${({\lambda }_i^2)}_{i=\mathrm{l}\mathrm{..}\mathrm{n}}$ are the eigenvalues of D^TD. The GCV score thus reduces to:

$$\mathit{GCV}(s)=n\sum _{i=1}^n{({\widehat{y}}_i-y_i)}^2/{\left(n-\sum _{i=1}^n{\left(1+s{\lambda }_i^2\right)}^{-1}\right)}^2.$$ (7)

Finding the s value that minimizes the GCV score yielded by equation (7) makes the smoothing algorithm fully automated. Because the components of ŷ appear in the expression of the GCV score, ŷ has to be calculated at each step of the minimization process. This can be avoided for the particular case of equally spaced data as demonstrated in the next section.

3. Smoothing of evenly spaced data

Equation (4) can be efficiently solved with a Matlab code using the so-called left matrix division (see Matlab documentation) applied to sparse matrices. Solving such a linear system, however, may rapidly become time-consuming with an increasing number of data. This algorithm can be greatly simplified and sped up if the data are evenly spaced. Indeed, in numerous conditions, experimental acquisition and data measurement lead to equally-spaced or evenly-gridded datasets. An efficient algorithm for smoothing of uniformly sampled data is described in the present section. A generalization for multidimensional data will be described in a further paragraph (section 6). Assuming now that data are equally spaced with h_i=1, ∀i, the divided difference matrix D (in equation 4) can be rewritten as the simple difference matrix:

$$D=\left(\begin{array}{ccccc}-1& 1& & & \\ 1& -2& 1& & \\ & \ddots & \ddots & \ddots & \\ & & 1& -2& 1\\ & & & 1& -1\end{array}\right).$$

An eigendecomposition of D yields

$$D=U\mathrm{\Lambda }{U}^{-1},$$

where Λ is the diagonal matrix containing the eigenvalues of D defined by (Yueh, 2005):

$$\mathrm{\Lambda }=\text{diag}\left({\lambda }_1,\dots ,{\lambda }_{\mathrm{n}}\right)\text{with}{\lambda }_i=-2+2cos((i-1)\pi /n).$$ (8)

Because U is a unitary matrix (i.e. U⁻¹ = U ^T and UU ^T = I_n), equation (4) leads to

$$\widehat{y}=U{\left(I_n+s{\mathrm{\Lambda }}^2\right)}^{-1}{U}^{\mathrm{T}}y\equiv U\mathrm{\Gamma }{U}^{\mathrm{T}}y,$$ (9)

where the components of the diagonal matrix Γ, according to equation (8), are given by:

$${\mathrm{\Gamma }}_{i,i}={\left[1+s{(2-2cos((i-1)\pi /n))}^2\right]}^{-1}\text{and}{\mathrm{\Gamma }}_{i,j}=0\text{if}i\ne j.$$ (10)

It is worth noting that U^T and U are actually n-by-n type-2 discrete cosine transform (DCT) and inverse DCT matrices, respectively (Strang, 1999). Thus, the smooth output ŷ can also be expressed as:

$$\widehat{y}=U\mathrm{\Gamma }\text{DCT}(\mathrm{y})=\text{IDCT(}\mathrm{\Gamma }\text{DCT}(\mathrm{y})\text{)},$$ (11)

where DCT and IDCT refer to the discrete cosine transform and the inverse discrete cosine transform, respectively.

In the case of equally-spaced data, the GCV score can also be simplified considerably. The trace of the hat matrix [see equations (6) and (8)] indeed reduces to:

$$\text{Tr}(H)=\sum _{i=1}^n{\left[1+s{(2-2cos((i-1)\pi /n))}^2\right]}^{-1}.$$

Note that when n becomes large, one has:

$$\frac{\text{Tr}(H)}{n}\approx \frac{1}{\pi }{\int }_0^{\pi }{\left[1+s{(2-2cosx)}^2\right]}^{-1}\mathrm{d}x=\frac{\sqrt{1+\sqrt{1+16s}}}{\sqrt{2}\sqrt{1+16s}}.$$ (12)

Moreover, using equation (9), the residual sum of squares (RSS) can be written as:

$$\begin{array}{l}\mathit{RSS}={\left|\right|\widehat{y}-y\left|\right|}^2\\ ={\Vert \left({\left(I_n+s{\mathrm{\Lambda }}^2\right)}^{-1}-I_n\right)\text{DCT}(y)\Vert }^2\\ =\sum _{i=1}^n{\left(\frac{1}{1+s{\lambda }_i^2}-1\right)}^2{\text{DCT}}_{\mathrm{i}}^2(y),\end{array}$$

where DCT_i refers to the i^th component of the discrete cosine transform. The GCV score given by equation (7) thus becomes:

$$\mathit{GCV}(s)-=\frac{-n{\displaystyle \sum _{i=1}^n}{\left(\frac{1}{1+s{\lambda }_i^2}-1\right)}^2{\text{DCT}}_{\mathrm{i}}^2(y)}{{\left(n-{\displaystyle \sum _{i=1}^n}\frac{1}{1+s{\lambda }_i^2}\right)}^2},$$ (13)

with λ_i given by equation (8).

It is much more convenient to use an algorithm based on equation (11) rather than equation (4) when data are equispaced. The DCT has indeed a computational complexity of O(n log(n)) whereas equation (4) requires a Cholesky factorization whose computational complexity is O(n³). Note also that the computation of the GCV score from equation (13) is straightforward and does not require any matrix operation and manipulation, which makes the automated smoothing very fast. A simplified Matlab code for fully automated smoothing is given in Appendix I. The abovementioned smoothing procedure requiring DCT is similar to that introduced by Buckley (1994). It is shown in the following section how this DCT-based smoother can be adapted to weighted data and missing values.

4. Dealing with weighted data and occurrence of missing values

Occurrence of missing data due to measurement infeasibility or instrumentation failure is frequent in practice. It can also be convenient to give outliers a low weight or, on the contrary, allocate a relatively high weight to high-quality data. Let W be the diagonal matrix diag(w_i) that contains the weights w_i∈[0,1] corresponding to the data y_i. In the presence of weighted data, RSS becomes:

$$\text{wRSS}={\Vert W^{1/2}(\widehat{y}-y)\Vert }^2.$$

The minimization of F(ŷ) (equation 2) thus yields:

$$\left(W+{sD}^{\mathrm{T}}D\right)\widehat{y}=Wy,$$

which can be rewritten as:

$$\left(I_n+{sD}^{\mathrm{T}}D\right)\widehat{y}=\left(I_n-W\right)\widehat{y}+Wy.$$

Letting A ≡ sD^TD + W and using the abovementioned hat matrix H, this equation can also be expressed as:

$$H^{-1}\widehat{y}=\left(H^{-1}-A\right)\widehat{y}+Wy.$$

This implicit formula can be solved using an iterative procedure:

$$H^{-1}{\widehat{y}}_{\{k+1\}}=\left(H^{-1}-A\right){\widehat{y}}_{\{k\}}+Wy\text{with}\text{an}\text{arbitrary}{\widehat{y}}_{\{0\}},$$ (14)

where ŷ_{k} refers to ŷ calculated at the k^th iteration step. It can be shown that this equation converges, for any ŷ_{0}, since the linear system is positive definite. Indeed, the matrix D is real nonsingular, then sD^TD is positive definite if s>0. In addition, W is positive semidefinite (because w_i ≥ 0); A is thus positive definite and, according to the theorem 3 of (Keller, 1965), convergence of ŷ_{k} towards the desired solution ŷ is ensured for any s > 0.

Note that, in the presence of missing values, W is simply defined by w_i = 0 if y_i is missing, while an arbitrary finite value is assigned to y_i. In that case, the algorithm performs both smoothing and interpolation. Contrarily to classical methods which usually operate with linear or cubic local interpolations, missing data are assigned to values that are estimated using the entire dataset.

In the case of evenly spaced data, one can take advantage of the DCT by rewriting equation (14) as:

$${\widehat{y}}_{\{k+1\}}={\left(I_n+{sD}^{\mathrm{T}}D\right)}^{-1}\left(W(y-{\widehat{y}}_{\{k\}})+{\widehat{y}}_{\{k\}}\right),$$

which, similarly to equation (11), becomes:

$${\widehat{y}}_{\{k+1\}}=\text{IDCT}\left(\mathrm{\Gamma }\text{DCT}\left(W(y-{\widehat{y}}_{\{k\}})+{\widehat{y}}_{\{k\}}\right)\right),$$ (15)

with Λ given by equation (10). The iterative convergent process defined by equation (15), with the additional determination of the GCV score, allows automatic smoothing with weighted and/or missing data. When weighted and/or missing data occur, equation (7) describing the GCV score, however, becomes invalid since the weighted residuals (wRSS) must be accounted for. Moreover, the number of missing data must be taken into account in the expression of the average square error. In the presence of weighted data, the GCV score is therefore given by:

$$\mathit{GCV}(s)=\frac{\text{wRSS}/\left(n-n_{\mathit{miss}}\right)}{{(1-\text{Tr}(H)/n)}^2}=\frac{{\Vert W^{1/2}(\widehat{y}-y)\Vert }^2/\left(n-n_{\mathit{miss}}\right)}{{(1-\text{Tr}(H)/n)}^2},$$

where n_miss represents the number of missing data and n is the number of elements in y. Note that the GCV score given by the latter equation, in comparison with equation (13), requires ŷ to be known, so that ŷ must be calculated at each iteration of the GCV minimization. Smoothing of weighted data will thus involve additional computation time.

5. Robust smoothing

In regression analysis, it is habitually assumed that the residuals follow a normal distribution with mean zero and constant variance, usually unknown. In spite of that, faulty data, erroneous measurements or instrumentation malfunction may lead to observations that lie abnormally far from the others. The main drawback of the penalized least squares methods is their sensitivity to these outliers. Besides outlying points, high leverage points also adversely affect the outcome of regression models. In statistics, the leverage denotes a measure of the influence (between 0 and 1) of a given point on a fitting model due to its location in the space of the inputs. More precisely, the points which are far-removed from the main body of points will have high leverage (Chatterjee and Hadi, 1986). To minimize or cancel the side effects of high leverage points and outliers, one can assign a low weight to them using an iteratively re-weighted process, as often used in robust local regression. This method consists in constructing weights with a specified weighting function by using the current residuals and updating them, from iteration to iteration, until the residuals remain unchanged (Rousseeuw and Leroy, 1987). In practice, five iterative steps are sufficient.

Several weighting functions are available for robust regression. The most common one, the so-called bisquare weight function, will be used hereinafter although other weight functions would be suitable as well (Heiberger and Becker, 1992). The bisquare weights are given by:

$$W_i=\{\begin{array}{c}{\left(1-{\left(\frac{u_i}{4.685}\right)}^2\right)}^2\text{if}\left|\frac{u_i}{4.685}\right|<1\\ 0\text{if}\left|\frac{u_i}{4.685}\right|\ge 1\end{array},$$

where u_i is the studentized residual which is adjusted for standard deviation and leverage and is defined as (Rousseeuw and Leroy, 1987):

$$u_i=\frac{r_i}{\widehat{\sigma }\sqrt{1-h_i}}.$$ (16)

In equation (16), r_i − y_i − ŷ_i is the residual of the i^th observation, h_i is its corresponding leverage and σ̂ is a robust estimate for the standard deviation of the residuals given by 1.4826 MAD, where MAD denotes the median absolute deviation (Rousseeuw and Croux, 1993). The leverage values h_i are all given by the diagonal elements of the hat matrix H (Hoaglin and Welsch, 1978). However, a faster and economical alternative for robust smoothing can be obtained using an average leverage:

$$\forall i,h_i=h=\frac{1}{n}\sum _i{H}_{ii}=\text{Tr}(H)/n,$$

where an approximated value for Tr(H)/n is given by equation (12). The approximated studentized residuals finally reduce to:

$$u_i=r_i{\left[1.4826\text{MAD}(r)\sqrt{1-\frac{\sqrt{1+\sqrt{1+16s}}}{\sqrt{2}\sqrt{1+16s}}}\right]}^{-1}.$$

The use of the bisquare weights in combination with these approximated studentized residuals provides a robust version of the abovementioned smoother. Note that if y_i represents a missing data, r_i is not involved in the calculation of the MAD(r). Appendix II contains a simplified Matlab code for robust smoothing using the method described in this paper.

6. Multidimensional smoothing of evenly gridded data

Because a multidimensional DCT is basically a composition of one-dimensional DCTs along each dimension (Strang, 1999), equation (11) can be immediately extended to two-dimensional or N-dimensional regularly gridded data. A detailed description of the extension of equation (11) to higher dimensions is given in (Buckley, 1994). In the case of N-dimensional data, equation (11) becomes:

$$\widehat{y}=\text{IDCTN}\left({\mathrm{\Gamma }}^{\mathrm{N}}\circ \text{DCTN}(y)\right),$$ (17)

where DCTN and IDCTN refer to the N-dimensional discrete cosine transform and inverse discrete cosine transform, respectively, and ∘ stands for the Schur (elementwise) product. As an extension of equation (10), Γ^N is a tensor of rank N defined by:

$${\mathrm{\Gamma }}^{\mathrm{N}}=1^{\mathrm{N}}÷\left(1^{\mathrm{N}}+s{\mathrm{\Lambda }}^{\mathrm{N}}\circ {\mathrm{\Lambda }}^{\mathrm{N}}\right).$$ (18)

Here, the operator ÷ symbolizes the element-by-element division and 1^N is an N-rank tensor of ones. Λ^N, similarly to equation (8), is the following N-rank tensor (Buckley, 1994):

$${{\mathrm{\Lambda }}^{\mathrm{N}}}_{i_1,\dots ,i_{\mathrm{N}}}=\sum _{j=1}^{\mathrm{N}}\left(-2+2cos\frac{(i_j-1)\pi }{n_j}\right),$$ (19)

where n_j denotes the size of Λ^N along the j^th dimension. Automated determination of s requires the GCV score which, in the case of multidimensional data, can be written as:

$$\mathit{GCVs}=\frac{{{\Vert \widehat{y}-y\Vert }_F}^2/n}{{\left(1-{\Vert {\mathrm{\Gamma }}^{\mathrm{N}}\Vert }_1/n\right)}^2},$$

where || ||_F denotes the Frobenius norm, || ||₁ is the 1-norm, and $n={\displaystyle \prod _{j=1}^{\mathrm{N}}}{n}_j$ is the number of elements in y. Similarly to equation (7), the GCV score with no weighted and no missing data can be rewritten as follows:

$$\mathit{GCVs}=\frac{n{\Vert \left({\mathrm{\Gamma }}^{\mathrm{N}}-1^{\mathrm{N}}\right)\circ \text{DCTN}(y)\Vert }_F^2}{{\left(n-{\Vert {\mathrm{\Gamma }}^{\mathrm{N}}\Vert }_1\right)}^2}.$$

The same procedure as described in section 5 can also be directly applied to weighted or missing data. The iterative process illustrated by equation (15) thus becomes:

$${\widehat{y}}_{\{k+1\}}=\text{IDCTN}\left({\mathrm{\Gamma }}^{\mathrm{N}}\circ \text{DCTN}\left(W\circ (y-{\widehat{y}}_{\{k\}})+{\widehat{y}}_{\{k\}}\right)\right),$$ (20)

A robust version can also be immediately obtained using the studentized residuals given by (16) with the following average leverage:

$$h={\left(\frac{\sqrt{1+\sqrt{1+16s}}}{\sqrt{2}\sqrt{1+16s}}\right)}^N.$$

7. Matlab codes and examples

Equations (11) and (15) with optimal smoothing by means of the GCV method are relatively easy to implement in Matlab. Simplified Matlab codes for automatic smoothing (smooth.m) and robust smoothing (rsmooth.m) of 1-D and 2-D datasets are given in appendices I and II. These two programs have a similar syntax and both require the 2-D (inverse) discrete cosine transform (dct2 and idct2) provided by the Matlab image processing toolbox. The input represents the dataset to be smoothed, while the output represents the smoothed data. A complete documented Matlab function for smoothing of 1-D to N-D data (smoothn), with automated and robust options, and which can deal with weighted and/or missing data, is also supplied in the supplemental material. The pseudocode for smoothn is given in Figure 1. No Matlab toolbox is needed for the use of smoothn. Updated versions of this function are downloadable from the author’s personal website (Garcia, 2009). The first four examples illustrated hereinafter can be run in Matlab using the function smoothndemo also available in the supplemental material.

Figure 1.

Pseudocode of the automatic robust smoothing algorithm. The variable names and acronyms are described in the text. The complete Matlab code is supplied in the supplemental material (smoothn.m). When robust option is required, minimization of the GCV score is performed at the first robust iterative step only (see 4.c.ii) and the last estimated smoothness parameter (s) is used during the successive steps. This makes the algorithm faster without altering the final results significantly.

2-D smoothing with missing values

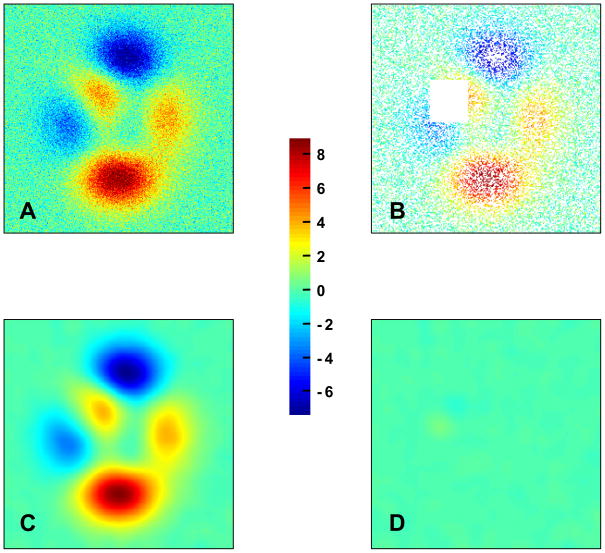
To illustrate the effectiveness of the DCT-based smoothing algorithm, highly corrupted 2-D data have been smoothed and the result has been compared with the original data. The original matrix data (300× 300) consisted of a function of two variables obtained by translating and scaling Gaussian distributions created by the Matlab “peaks” function. The corrupted data were obtained by first adding a Gaussian noise with mean zero (Figure 2A), then randomly removing half of the data, and finally creating a 50× 50 square of missing data (Figure 2B). The automatic smoother was able to recover satisfactorily the original surface (Figure 2C) with an average relative error (defined by ||smoothed – original||/||original||) smaller than 5% (see also the absolute error mapping on Figure 2D).

Figure 2.

Automatic smoothing of two-dimensional data with missing values. A. Noisy data. B. Corrupted data with missing values. C. Smoothed data restored from B. D. Absolute errors between the restored and original data.

Robust smoothing

Penalized least squares methods are very sensitive to outlying data. Figure 3A demonstrates how outliers may adversely bend the smoothed curve (see also 1-D example in Appendix II). Clearly, the smoothed values do not reflect the behavior of the bulk of the data points. To overcome the distortion due to a small fraction of outliers, the data can be smoothed using the robust procedure described in section 5. Figure 3B shows that the robust smoothing is resistant to outliers. An example for 2-D robust smoothing is also given in Appendix II.

Figure 3.

Non robust versus robust smoothing. Outliers may bend the smoothed curve (A). A robust smoothing may get rid of this drawback (B).

3-D smoothing

Figure 4 now illustrates 3-D automated smoothing by means of the smoothn program supplied in the supplementary material. Gaussian noise with mean zero and standard deviation of 0.06 has been added to a 3-D function defined by f(x,y,z) = x exp(−x² − y² − z²) in the [−2;2]³ domain (Figure 4A). Figure 4B shows that smoothn significantly reduced the additive noise. Note that smoothn could also be applied to higher dimensions.

Figure 4.

Automatic smoothing of three-dimensional data.

Smoothing of parametric curves

Discrete cosine transform (DCT) and inverse DCT are linear operators and thus work with complex numbers. This property can be used to smooth parametric curves defined by (x(t),y(t)), where t is equispaced. By way of example, Figure 5 depicts a noisy cardioid (dots) whose parametric equations are x(t) = 2 cos(t)[1-cos(t)] + (0,0.2) and y(t) = 2 sin(t)[1-cos(t)] + (0,0.2), where refers to the normal distribution and t is equally spaced between 0 and 2π. Let us now define the complex function z(t) = x(t) + i y(t), where i is the unit complex number, and its smoothed output ẑ(t). The parametric curve defined by (Re(ẑ(t)), Im(ẑ(t))), where Re and Im refer to the real and imaginary parts, respectively, provides a smooth cardioid (solid line, see Figure 5).

Figure 5.

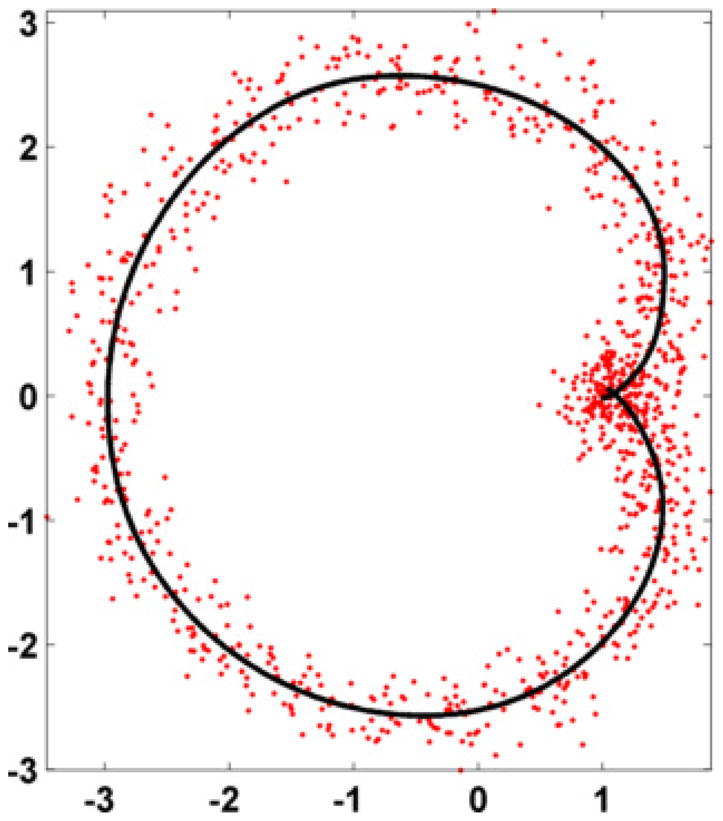
Automatic smoothing of a noisy cardioid.

Applications to surface temperature anomalies

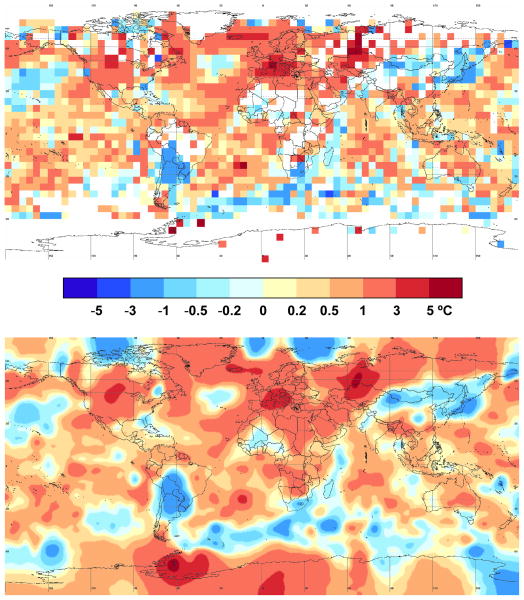
Automatic smoothing with the minimization of the GCV score has finally been tested on temperature data available in the Met Office Hadley Centre’s website (Brohan, Kennedy, Harris, Tett and Jones, 2006; Kennedy, 2007). Figure 6 illustrates the evolution of global average land temperature anomaly (in °C) with respect to 1961–1990. The smooth curve clearly depicts the continuing rise of global temperature that occurs since the 1970’s. Figure 7 shows the earth surface temperature difference of August 2003 with respect to 1961–1990. The top panel represents a mapping of the best estimates of temperature anomalies as provided by the Met Office Hadley Centre. Note that numerous temperature data are missing due to nonexistent station measurements. A smooth map of Earth temperature anomalies with filled gaps can be automatically obtained using the DCT-based algorithm described in the present paper (Figure 7, bottom panel).

Figure 6.

Global average land temperature anomaly (ºC) with respect to 1961–1990: smoothed versus original year-averaged data. Year-averaged data are available in http://hadobs.metoffice.com/crutem3/diagnostics/global/nh+sh/annual.

Figure 7.

August 2003 surface temperature difference (ºC) with respect to 1961–1990: smoothed (bottom panel) versus original year-averaged (top panel) data. Year-averaged dataset is available in http://hadobs.metoffice.com/hadcrut3/index.html. The smoothed output has been upsampled for a better visualization of the surface temperatures.

Resolution of Figure 7, bottom panel, has been increased to obtain a better visualization of surface temperatures. A basic upsampling of the smoothed data was performed by padding zeros after the last element of DCTN(ŷ) along each dimension before using the inverse DCT operator, as follows:

$${\widehat{y}}_{\mathit{upsampled}}=\sqrt{\frac{n_{\mathit{upsampled}}}{n}}\text{IDCTN}(\text{ZeroPad}(\text{DCTN}(\widehat{y}))),$$

where n_upsampled represents the number of elements after upsampling. It is worth reminding that DCT assumes repeating boundary conditions whereas periodic boundaries would have been more appropriate for the east-west edges. Such conditions caused east-west discordances at the level of New-Zealand and Antarctica.

8. Discussion

The best choice of the smoothing algorithm to be used in data analysis depends specifically upon the original data and on the properties of the additive noise. As a consequence, the search for a perfect universal smoother remains illusory (Eilers, 2003). In this paper, a robust, fast and fully automated smoothing procedure has been proposed, and its efficacy has been illustrated on a few cases in the previous section. The user, however, should be aware of some limitations of the algorithm. Better results will be obtained if ŷ itself is sufficiently smooth, i.e. if it has continuous derivatives up to some desired order over the whole domain of interest. Moreover, because the algorithm process involves a discrete cosine transform, the inherent repeating conditions may slightly distort the smoothed output on the boundaries, especially when the total number of data is small. The GCV criterion is used to make the smoothing procedure fully automated and good results are expected if the additive noise ε in equation (1) follows a Gaussian distribution with nil mean and constant variance. It has been reported, however, that the GCV remains fairly adapted even with nonhomogenous variances and non-Gaussian errors (Wahba, 1990b). Alternatively, if the measurement errors in the data present variable standard deviations and if the variances are known ( ${\sigma }_i^2$), the response variances can be transformed to a constant value using weights given by $w_i=1/{\sigma }_i^2$. In addition, if outlying data occur, it could be convenient to perform a robust smoothing. Finally, the GCV criterion may cause problems when the sample size is small, which could make the automated version unsatisfactory with a small number of data. If this occurs, the smoothing parameter s must be tuned manually until a visually acceptable result is obtained.

Appendix I

A simplified Matlab code (smooth) for 1-D and 2-D smoothing of equally-gridded data, and two examples are given below. The input represents the dataset to be smoothed and the output represents the smoothed data. This code has been written with Matlab R2007b.

function z = smooth(y)
[n1,n2] = size(y); n = n1*n2;
Lambda = bsxfun(@plus,repmat(−2+2*cos((0:n2−1)*pi/n2),n1,1),…
     −2+2*cos((0:n1−1).’*pi/n1));
DCTy = dct2(y);
fminbnd(@GCVscore,−15,38);
z = idct2(Gamma.*DCTy);
function GCVs = GCVscore(p)
     s = 10^p;
     Gamma = 1./(1+s*Lambda.^2);
     RSS = norm((DCTy(:).*(Gamma(:)−1)))^2;
     TrH = sum(Gamma(:));
     GCVs = RSS/n/(1−TrH/n)^2;
end
end

1-D Example:

x = linspace(0,100,2^8);
y = cos(x/10)+(x/50).^2 + randn(size(x))/10;
z = smooth(y);
plot(x,y,‘.’,x,z)

2-D Example:

xp = linspace(0,1,2^6);
[x,y] = meshgrid(xp);
f = exp(x+y)+sin((x−2*y)*3) + randn(size(x))/2;
g = smooth(f);
figure, subplot(121), surf(xp,xp,f), zlim([0 8])
subplot(122), surf(xp,xp,g), zlim([0 8])

Appendix II

A simplified Matlab code (rsmooth) for robust smoothing of 1-D and 2-D equally-sampled data, and two examples are given below. The syntax is similar to that of smooth (see Appendix I). A complete optimized code (smoothn) allowing smoothing in one or more dimensions is also available in the supplemental material and in the author’s personal website (Garcia, 2009).

 function z = rsmooth(y)
 [n1,n2] = size(y); n = n1*n2;
N = sum([n1,n2]~=1);
Lambda = bsxfun(@plus,repmat(−2+2*cos((0:n2−1)*pi/n2),n1,1),...
     −2+2*cos((0:n1−1).’*pi/n1));
W = ones(n1,n2);
zz = y;
for k = 1:6
   tol = Inf;
   while tol>1e−5
       DCTy = dct2(W.*(y−zz)+zz);
       fminbnd(@GCVscore,−15,38);
       tol = norm(zz(:)−z(:))/norm(z(:));
       zz = z;
   end
   tmp = sqrt(1+16*s);
   h = (sqrt(1+tmp)/sqrt(2)/tmp)^N;
   W = bisquare(y−z,h);
end
function GCVs = GCVscore(p)
   s = 10^p;
   Gamma = 1./(1+s*Lambda.^2);
   z = idct2(Gamma.*DCTy);
   RSS = norm(sqrt(W(:)).*(y(:)−z(:)))^2;
   TrH = sum(Gamma(:));
   GCVs = RSS/n/(1−TrH/n)^2;
end
end
function W = bisquare(r,h)
   MAD = median(abs(r(:)−median(r(:))));
   u = abs(r/(1.4826*MAD)/sqrt(1−h));
   W = (1−(u/4.685).^2).^2.*((u/4.685)<1);
end

1-D Example:

x = linspace(0,100,2^8);
y = cos(x/10)+(x/50).^2 + randn(size(x))/10;
y([70 75 80]) = [5.5 5 6];
z = smooth(y);
zr = rsmooth(y);
subplot(121), plot(x,y,‘.’,x,z), title(‘Non robust’)
subplot(122), plot(x,y,‘.’,x,zr), title(‘Robust’)

2-D Example:

xp = linspace(0,1,2^6);
[x,y] = meshgrid(xp);
f = exp(x+y)+sin((x−2*y)*3) + randn(size(x))/2;
f(20:3:35,20:3:35) = randn(6,6)*10+20;
g = smooth(f);
gr = rsmooth(f);
subplot(121), surf(xp,xp,g), zlim([0 8]), title(‘Non robust’)
subplot(122), surf(xp,xp,gr), zlim([0 8]), title(‘Robust’)