ESTIMATION METHOD OF THE HOMODYNED K-DISTRIBUTION BASED ON THE MEAN INTENSITY AND TWO LOG-MOMENTS

Abstract

The homodyned K-distribution appears naturally in the context of random walks and provides a useful model for the distribution of the received intensity in a wide range of non-Gaussian scattering configurations, including medical ultrasonics. An estimation method for the homodyned K-distribution based on the first moment of the intensity and two log-moments (XU method), namely the X and U-statistics previously studied in the special case of the K-distribution, is proposed as an alternative to a method based on the first three moments of the intensity (MI method) or the amplitude (MA method), and a method based on the signal-to-noise ratio (SNR), the skewness and the kurtosis of two fractional orders of the amplitude (labeled RSK method). Properties of the X and U statistics for the homodyned K-distribution are proved, except for one conjecture. Using those properties, an algorithm based on the bisection method for monotonous functions was developed. The algorithm has a geometric rate of convergence. Various tests were performed to study the behavior of the estimators. It was shown with simulated data samples that the estimations of the parameters 1/α and 1/(κ + 1) of the homodyned K-distribution are preferable to the direct estimations of the clustering parameter α and the structure parameter κ (with respective relative root mean squared errors (RMSEs) of 0.63 and 0.13 as opposed to 1.04 and 4.37, when N = 1000). Tests on simulated ultrasound images with only diffuse scatterers (up to 10 per resolution cell) indicated that the XU estimator is overall more reliable than the other three estimators for the estimation of 1/α, with relative RMSEs of 0.79 (MI), 0.61 (MA), 0.53 (XU) and 0.67 (RSK). For the parameter 1/(κ + 1), the relative RMSEs were equal to 0.074 (MI), 0.075 (MA), 0.069 (XU) and 0.100 (RSK). In the case of a large number of scatterers (11 to 20 per resolution cell), the relative RMSEs of 1/α were equal to 1.43 (MI), 1.27 (MA), 1.25 (XU) and 1.33 (RSK), and the relative RMSEs of 1/(κ + 1) were equal to 0.14 (MI), 0.16 (MA), 0.17 (XU) and 0.20 (RSK). The four methods were also tested on simulated ultrasound images with a variable density of periodic scatterers to test images with a coherent component. The addition of noise on ultrasound images was also studied. Results showed that the XU estimator was overall better than the three other ones. Finally, on the simulated ultrasound images, the average computation times per image were equal to 6.0 ms (MI), 8.0 ms (MA), 6.8 ms (XU) and 500 ms (RSK). Thus, a fast, reliable, and novel algorithm for the estimation of the homodyned K-distribution was proposed.

1. Introduction

The homodyned K-distribution appears naturally in the context of a limiting random walk modeling physical scattering process, with a constant-amplitude coherent component and with a negative binomial distribution for the number of steps [13, 15]. As a special case, the K-distribution [21, 14] corresponds to a vanishing coherent component of the amplitude of that process. Also, the Rice distribution corresponds to the limiting case where the scatterer clustering parameter implicit in the negative binomial distribution is infinite [24, 30, 15]. Finally, the Rayleigh distribution [29, 15] corresponds to the Rice distribution with a vanishing coherent component. Both the Rice and the Rayleigh distributions correspond to a Gaussian random walk, but not the homodyned K-distribution (nor the K-distribution). The random variable of these distributions is called the amplitude and is denoted by A. The intensity I is defined as the square of the amplitude.

K-distributions and, more generally, homodyned K-distributions turned out to provide a useful model for the received amplitude in a wide range of non-Gaussian scattering configurations, such as optical propagation through turbulent media [27], microwave sea echo [38], land clutter [26] and medical ultrasonics [33, 8, 23, 10, 28, 25]. See [6] for a presentation of the homodyned K-distribution and related distributions in the context of ultrasound imaging.

The homodyned K-distribution is determined by three parameters that carry a physical meaning: the mean intensity μ; the scatterer clustering parameter α (i.e. the clustering parameter in the negative binomial distribution); and the structure parameter κ (i.e. the ratio of the coherent signal power to the diffuse signal power). Given a sample of the received amplitude, one is then interested in estimating those three parameters, or related parameters, such as the signal-to-noise ratio (SNR) of the intensity and the ratio of coherent signal to diffuse signal, denoted k in [8, 11]. The goal is then to use the estimated parameters in the context of tissue characterization or quantitative ultrasound (QUS) based on medical ultrasound images. See [25, 11] as examples.

A simple estimation method of the homodyned K-distribution based on the first three moments of the intensity E[I], E[I²], and E[I³] was proposed in [8]. In [11], the SNR, the skewness and the kurtosis of two fractional orders (namely, 0.72 and 0.88) of the amplitude were used as statistics for the estimation of the homodyned K-distribution. In the case of the estimation method of [11], one obtains an overdetermined non-linear system of equations that is solved in the sense of the least mean square.

In this paper, an estimation method based on the first moment of the intensity E[I], the U-statistics E[log I] − log E[I] and the X-statistics E[I log I]/E[I] − E[log I] is proposed. These two statistics were introduced in the context of K-distributions in [26] and [4], respectively. Moreover, an algorithm with geometric rate of convergence for the computation of this new estimator is proposed.

The remaining part of this paper is organized as follows. In Section 2, the definition of the homodyned K-distribution is recalled. In Section 3, the proposed estimation method is explained. Experimental results based on simulations of sample sets and of ultrasound images are presented in Section 4. The results are discussed in Section 5, and we conclude in Section 6.

Table 1 presents the definition of the main parameters and statistics discussed in this paper. Given a sample set {A₁, …, A_N}, the notation $\overline{f(A)}$ means the average value of the function f over the sample set, i.e. $\frac{1}{N}{\sum }_{i=1}^{N}f(A_i)$. In particular, the notation I̅, for instance, means $\frac{1}{N}{\sum }_{i=1}^N{A}_i^2$. The notation $\frac{\partial }{\partial \alpha }$ is used for the partial derivative with respect to, say, α. For example, the notation P_K does not mean partial derivative, but rather that K is used as a subscript (identifying the K-distribution).

Table 1.

Main parameters and statistics discussed in this paper.

Definition	Notion
A and I = A2	amplitude and intensity
I̅	mean intensity of a sample A1, … AN
$U=\overline{logI}-log\overline{I}$	U-statistics
$X=\overline{\mathit{I}logI}/\overline{I}-\overline{logI}$	X-statistics
Homodyned K-distribution with parameters ε ≥ 0, σ2 > 0 and α > 0
α	scatterer clustering parameter
ε2	coherent signal power
2σ2α	diffuse signal power
μ = ε2 + 2σ2α	total signal power (mean intensity)
κ = ε2/(2σ2α)	structure parameter
γ = ε2/(2σ2) = κα	algorithmic parameter
$k=\sqrt{2\kappa }=\epsilon /(\sigma \sqrt{\alpha })$	ratio of the coherent to diffuse signal
Rice distribution with parameters ε ≥ 0 and ${\sigma }_{\text{R}}^2>0$
$\mu ={\epsilon }^2+2{\sigma }_{\text{R}}^2$	mean intensity
$\kappa ={\epsilon }^2/(2{\sigma }_{\text{R}}^2)$	structure parameter
$k=\sqrt{2\kappa }=\epsilon /{\sigma }_{\text{R}}$	ratio of the coherent to diffuse signal

2. The homodyned K-distribution

The reader is referred to [15] for a presentation of the homodyned K-distribution and the related Rice distribution in the context of random walks, and to [6] for a presentation in the context of ultrasound imaging. The reader may consult [2] for the notions of Bessel functions.

The 2-dimensional homodyned K-distribution is defined by

$$P_{\text{HK}}(A\mid \epsilon ,{\sigma }^2,\alpha )=A{\int }_0^{\infty }u{J}_0(u\epsilon )J_0(uA){(1+\frac{u^2{\sigma }^2}{2})}^{-\alpha }du,$$ (2.1)

where ε ≥ 0, σ² > 0 and α > 0, and J₀ denotes the Bessel function of the first kind of order 0. The limiting case of a homodyned K-distribution with parameters ε, ${\sigma }^2={\sigma }_{\text{R}}^2/\alpha$ and α, where ${\sigma }_{\text{R}}^2>0$ is a positive real number and α → ∞, yields the Rice distribution

$$P_{\text{Ri}}(A\mid \epsilon ,{\sigma }_{\text{R}}^2)=\frac{A}{{\sigma }_{\text{R}}^2}{I}_0\left(\frac{\epsilon }{{\sigma }_{\text{R}}^2}A\right)exp\left(-\frac{({\epsilon }^2+A^2)}{2{\sigma }_{\text{R}}^2}\right),$$ (2.2)

where I₀ denotes the modified Bessel function of the first kind of order 0.

The compound representation of Theorem 2.1 is useful in simulating the homodyned K-distribution, and in evaluating its values.

Theorem 2.1 (Jakeman-Tough [15])

The compound representation of the homodyned K-distribution is

$$P_{HK}(A\mid \epsilon ,{\sigma }^2,\alpha )={\int }_0^{\infty }{P}_{Ri}(A\mid \epsilon ,{\sigma }^{2}w)\mathcal{G}(w\mid \alpha ,1)dw,$$ (2.3)

where 𝒢(w | α, 1) = w^α−1e^−w/Γ(α) is the gamma distribution with mean and variance α, and Γ denotes the Euler gamma function.

Two functions of the three parameters of the homodyned K-distribution are invariant under scaling of the mean intensity μ = ε² + 2σ²α: 1) the scatterer clustering parameter α; 2) the structure parameter κ = ε²/(2σ²α), i.e. the ratio of the coherent signal power ε² to the diffuse signal power 2σ²α. Let us mention also the ratio of the coherent to diffuse signal $k=\sqrt{2\kappa }=\epsilon /(\sigma \sqrt{\alpha })$ adopted in [8, 11]. It was found convenient to also consider the parameter γ = κα = ε²/(2σ²). This parameter should not be confused with the structure parameter $\kappa ={\epsilon }^2/(2{\sigma }_{\text{R}}^2)$ of the Rice distribution $P_{\text{Ri}}(A\mid \epsilon ,{\sigma }_{\text{R}}^2)$. See Table 1 for a summary of these parameters. The special case where ε = 0 yields the K-distribution P_K(A | σ², α) [21, 15] and the Rayleigh distribution $P_{\text{Ra}}(A\mid {\sigma }_{\text{R}}^2)$ [29].

3. A new method for estimating the homodyned K-distribution

A new method for estimating the parameters (ε, σ², α) of the homodyned K-distribution based on an independent and identically distributed (i.i.d.) sample set (A₁, …, A_N) of positive real numbers is now discussed.

Two statistics will play an important role in the sequel: 1) the U-statistics defined by $U:=\overline{logI}-log\overline{I}$ and 2) the X-statistics defined as $X:=\overline{\mathit{I}logI}/\overline{I}-\overline{logI}$. For parametric models, such as the homodyned K-distribution or the Rice distribution, the U-statistics is defined as E[log I] − log E[I], where expectation is taken with respect to the distribution. Similarly, the X-statistics is defined as E[I log I]/E[I] − E[log I]. A subindex (such as “_HK”) is then used to identify the distribution (e.g. “U_HK”).

For later reference, it is instructive to observe the following result.

Lemma 3.1

1. For any non-constant random variable, the U-statistics is negative.

2. For any non-constant random variable, the X-statistics is positive.

The proof of Lemma 3.1 is presented in Appendix A.

3.1. Proposed estimator

The proposed method of estimation consists in solving the following (non-linear) system of equations in the variables ε², σ², and α:

$$E[I]=\overline{I};U_{\text{HK}}=U;X_{\text{HK}}=X.$$ (3.1)

Sufficient conditions for this system to admit a solution are presented below. For that purpose, it will be convenient to adopt the following change of variables

$$\mu ={\epsilon }^2+2{\sigma }^2\alpha ;\gamma =\frac{{\epsilon }^2}{2{\sigma }^2}.$$ (3.2)

Proposition 3.2

Let $A=\sqrt{I}$ be distributed according to the homodyned K-distribution P_HK(A | ε, σ², α). With the notation of (3.2), one has

$$\begin{array}{l}{U}_{HK}(\gamma ,\alpha )\\ =-{\gamma }_E-log(\gamma +\alpha )+\psi (\alpha )\\ -{\gamma }^{\alpha }\frac{\mathrm{\Gamma }(-\alpha )}{\alpha \mathrm{\Gamma }(\alpha )}{{}_{1}F}_2(\alpha ;1+\alpha ,1+\alpha ;\gamma )+\gamma \frac{\mathrm{\Gamma }(\alpha -1)}{\mathrm{\Gamma }(\alpha )}{{}_{2}F}_3(1,1;2,2,2-\alpha ;\gamma );\end{array}$$ (3.3)

$$\begin{array}{l}{X}_{HK}(\gamma ,\alpha )\\ =\frac{(1+2\alpha )}{(\gamma +\alpha )}-\frac{2{\gamma }^{\alpha /2+1/2}}{(\gamma +\alpha )\mathrm{\Gamma }(\alpha )}{K}_{\alpha +1}\left(2\sqrt{\gamma }\right)\\ +\frac{{\gamma }^{\alpha }}{(\gamma +\alpha )}\frac{\mathrm{\Gamma }(-\alpha )}{\mathrm{\Gamma }(\alpha )}{{}_{1}F}_2(\alpha ;1+\alpha ,1+\alpha ;\gamma )\\ -\frac{{\gamma }^{\alpha +1}}{(\gamma +\alpha )}\frac{\mathrm{\Gamma }(-1-\alpha )}{(1+\alpha )\mathrm{\Gamma }(\alpha )}{{}_{1}F}_2(1+\alpha ;2+\alpha ,2+\alpha ;\gamma )\\ +\frac{\gamma }{(\gamma +\alpha )}{{}_{2}F}_3(1,1;2,2,1-\alpha ;\gamma )-\frac{\gamma }{(\gamma +\alpha )}\frac{\alpha \mathrm{\Gamma }(-1+\alpha )}{\mathrm{\Gamma }(\alpha )}{{}_{2}F}_3(1,1;2,2,2-\alpha ;\gamma ),\end{array}$$ (3.4)

where γ_E denotes the Euler constant, ψ is the digamma function, _pF_q(a₁, …, a_p; b₁, …, b_q; z) is the generalized hypergeometric series and K_p denotes the modified Bessel function of the second kind of order p.

As one can see, Equations (3.3) and (3.4) depend only on the variables γ and α. Thus, the proposed method amounts to solving the second and third equations of (3.1) in the variables γ and α, and then using the identities

$${\epsilon }^2=\mu \gamma /(\gamma +\alpha );{\sigma }^2=\mu /(2(\gamma +\alpha )).$$ (3.5)

with the estimator I̅ of the mean intensity μ.

The proof of Proposition 3.2 is presented in Appendix A.

3.2. Estimating γ, when α is known

Let α > 0 be known. A method for finding γ > 0 satisfying Equation (3.4) is now discussed. Thus, one wants to solve the equation X_HK(γ, α) = X.

In Appendix B, the following result is shown.

Theorem 3.3

Notation as above.

1. One has the left boundary condition lim_γ→0 X_HK(γ, α) = X_K(α), where X_K(α) = 1 + 1/α.

2. One has the right boundary condition lim_γ→∞ X_HK(γ, α) = 0.

3. For any α > 0, the function X_HK(γ, α) is decreasing in the variable γ.

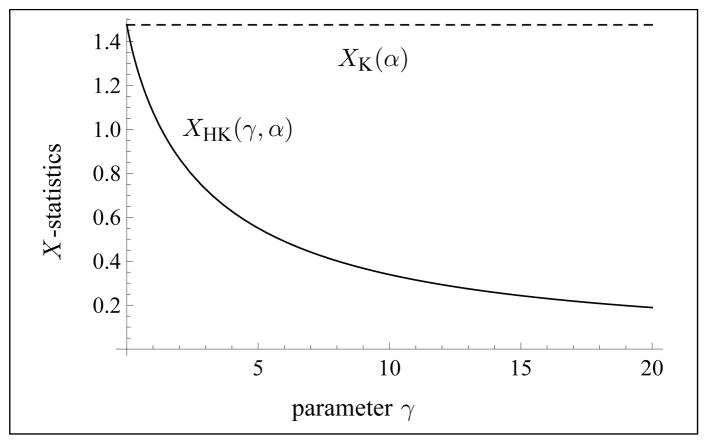
See Fig. 1 for an illustration of Theorem 3.3. Part c) of Theorem 3.3 implies that a binary search algorithm can be used to find the unique solution to Equation (3.4), whenever it exists. See Section 3.4 for details.

Fig. 1.

Illustration of the typical behavior of the X-statistics for the homodyned K-distribution as a function of γ ≥ 0 with a fixed value of α > 0 (here, α = 2.1).

Corollary 3.4

Let X > 0. Then, there is at most one solution to the equation X_HK(γ, α) = X.

1. If X ≤ 1, then there is a solution for any α > 0.

2. If X > 1, then there is a solution if and only if 0 < α = α₀, where ${\alpha }_0=X_K^{-1}(X)=1/(X-1)$.

Thus, one obtains a well-defined function

$$\gamma =\gamma (\alpha ,X),$$ (3.6)

on the domain described by Corollary 3.4.

3.3. Estimating γ and α

From Corollary 3.4, one knows that for any α in an interval of the form (0, α₀] or (0, ∞), there exists a unique solution γ = γ(α, X) to the equation X_HK(γ, α) = X. Substituting this solution in the second equation of (3.1), one obtains a function U_HK(γ(α, X), α) in the variable α. Thus, one now wants to solve the equation U_HK(γ(α, X), α) = U.

See Appendix C for a proof of the following result.

Theorem 3.5

Let X > 0.

1. One has the left boundary condition lim_α→0 U_HK(γ(α, X), α) = 0.

2. Let X > 1. One has the right boundary condition lim_α→α0 U_HK(γ(α, X), α) = U_K(α₀), where U_K(α) = − γ_E − log α + ψ(α), X_K(α) = 1 + 1/α, and ${\alpha }_0=X_K^{-1}(X)=1/(X-1)$.

3. Let X ≤ 1. One has the right boundary condition lim_α→∞ U_HK(γ(α, X), α) = U_Ri(κ₀), where $U_{Ri}(\kappa )=\mathrm{\Gamma }(0,\kappa )+log\frac{\kappa }{(\kappa +1)},X_{Ri}(\kappa )=\frac{(2-e^{-\kappa })}{(\kappa +1)}$, and ${\kappa }_0=X_{Ri}^{-1}(X)$. The function X_Ri(κ) is decreasing and has the interval (0, 1] for range.

Since the function X_Ri(κ) is decreasing on its domain [0, ∞) and has range (0, 1], the function $X_{\text{Ri}}^{-1}(X)$ is well-defined on the interval X ∈ (0, 1].

Conjecture 1

The function U_HK(γ(α, X), α) is decreasing on its domain.

See Fig. 2 for an illustration of Theorem 3.5 and the conjecture. The conjecture implies that a binary search algorithm can be used to find the unique solution to the second and third equations of (3.1), whenever a solution exists. The details are presented in Section 3.4. In Appendix D, a discussion on the Conjecture is presented.

Fig. 2.

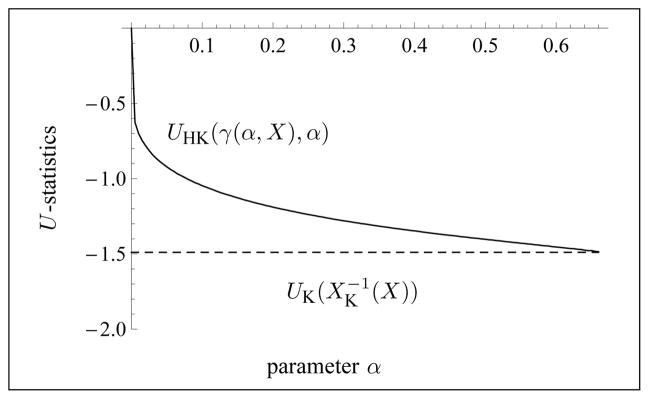
Illustration of the typical behavior of the U-statistics for the homodyned K-distribution as a function of α > 0, with a fixed value of X > 0 and γ = γ(α, X). Here, X = 2.5. Since X > 1, the upper bound for α is α₀ = 1/(X − 1).

Combining Theorems 3.3 and 3.5 with the conjecture yields the following result.

Corollary 3.6

Let U < 0 and X > 0 be given. Then, there exists a simultaneous solution to the system U_HK(γ, α) = U and X_HK(γ, α) = X if and only if

1. X > 1 and $U>U_K(X_K^{-1}(X))$

   or

2. X ≤ 1 and $U>U_{Ri}(X_{Ri}^{-1}(X))$.

Moreover, if a solution exists, it is unique.

Thus, one obtains well-defined functions

$$\gamma =\gamma (X,U);\alpha =\alpha (X,U),$$ (3.7)

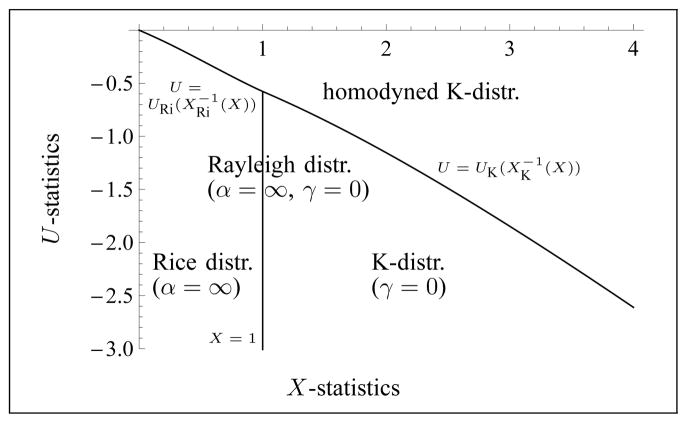
where X and U are restricted to the domain described by parts a) and b) of Corollary 3.6. See Fig. 3 for an illustration of this domain.

Fig. 3.

Illustration of the domain in the (X, U)-plane in which the parameters γ ≥ 0 and α are well-defined. The domains where either the K-distribution, the Rice distribution, or the Rayleigh distribution model apply are also indicated. The Rayleigh distribution corresponds to the vertical line.

3.4. Algorithms for solving the system (3.1)

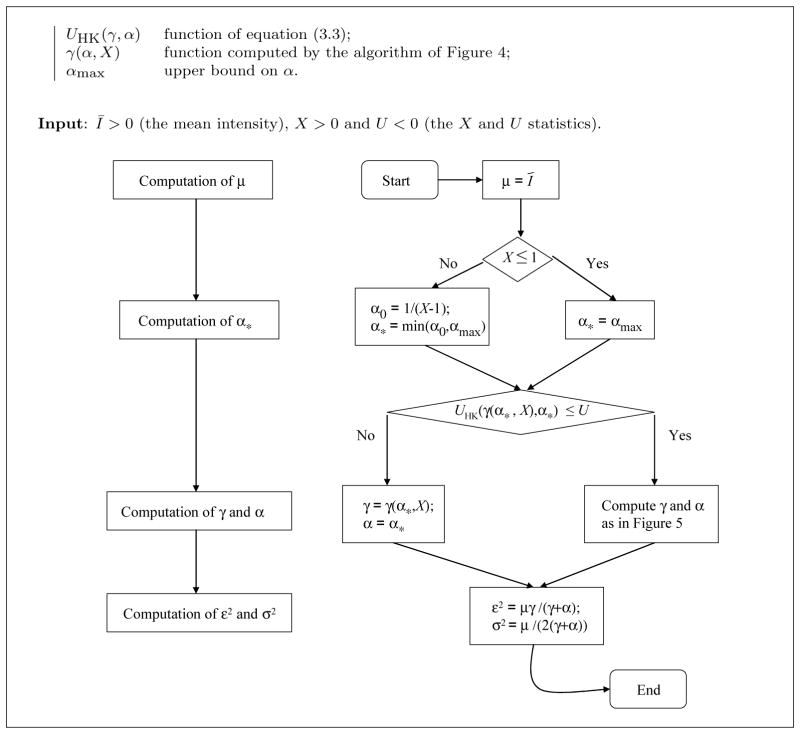
The algorithm presented in Fig. 4 is used as sub-routine in the algorithm of Fig. 5 that computes the unique solution (according to Conjecture 1) to the system (3.1), whenever U and X satisfy the conditions of Corollary 3.6.

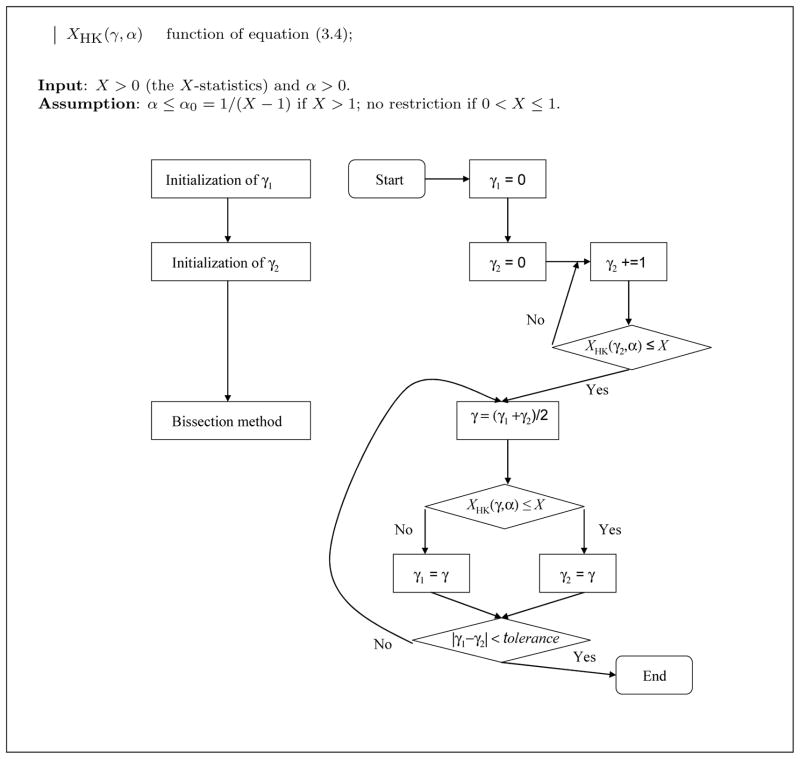
Fig. 4.

Algorithm for computing the function γ(α, X) of equation (3.6). Left: block diagram; right: flow chart.

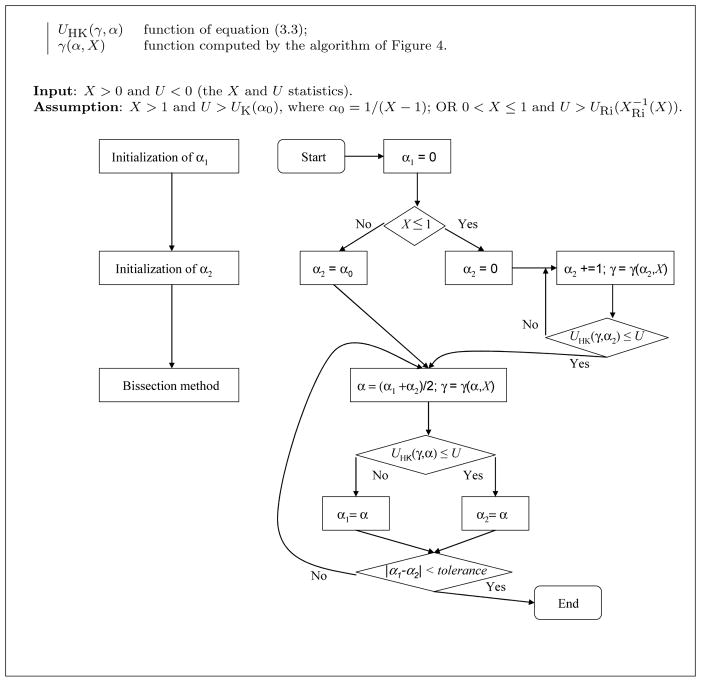
Fig. 5.

Algorithm for solving simultaneously X_HK(γ, α) = X and U_HK(γ, α) = U. Left: block diagram; right: flow chart.

First of all, Fig. 4 gives a binary search algorithm for computing the function γ(α, X) of equation (3.6) (α being known) by solving the equation X_HK(γ, α) = X. Since (from Theorem 3.3) the function X_HK(γ, α) is decreasing in the variable γ and since (by assumption) X is between the upper bound X_K(α) = 1 + 1/α and the lower bound 0, it follows that the algorithm of Fig. 4 converges to the unique solution of the equation X_HK(γ, α) = X, as follows from the Intermediate Value Theorem. Note that this binary search algorithm corresponds to the bisection method [9] and converges at a geometric rate; namely, after each iteration the distance between the current value of γ and the solution decreases by a factor of 2.

Having this algorithm as a tool, one can solve the equation U_HK(γ(α, X), α) = U using the binary search algorithm of Fig. 5 for similar reasons as above, based on Conjecture 1. Indeed, according to the Conjecture, the function U_HK(γ(α, X), α) is decreasing and Theorem 3.5 gives the upper and lower bounds of that function. Note that the assumptions on X and U of the algorithm are those of Corollary 3.6. Moreover, observe that the assumption of the sub-routine of Fig. 4 is satisfied whenever it is called in the algorithm of Fig. 5. Details on the computation of the functions X_HK and U_HK are given in Appendix E. Since the value of γ = γ(α, X) is computed for each value of α considered in the algorithm of Fig. 5, an error on that computation propagates on the error in the estimation of α. So, one has to allow enough precision. In the implementation of the reported tests, we adopted a tolerance of 10⁻⁴ and 10⁻² in the algorithms of Figs 4 and 5, respectively.

3.5. Overall algorithm

We now discuss an extension of the above method in the case where the system (3.1) has no solution, i.e. whenever U and X do not satisfy the conditions of Corollary 3.6. Also, there is a further issue on the size of α with respect to numerical considerations. On that matter, one has to know that the various functions appearing in the expression of X_HK and U_HK (such as the digamma function) have a finite support in any implementation. Therefore, in practice, one has to limit the size of α to a finite interval (0, α_max]. So, we resort to the algorithm of Fig. 6 for a practical implementation of the proposed approach. This algorithm finds a solution to the system:

$$\begin{array}{l}(\epsilon ,{\sigma }^2,\alpha )=argmin\mid U_{\text{HK}}-U\mid \\ \text{subject}\text{to}\mu =\overline{I}\text{and}{X}_{\text{HK}}=X\text{and}\alpha \le {\alpha }_{max},\end{array}$$ (3.8)

as follows directly from Conjecture 1 (i.e., the function U_HK(γ(α, X), α) is decreasing in the variable α). Observe that a solution to the system (3.1) such that α ≤ α_max is automatically a solution to the system (3.8). Note that in the algorithm of Fig. 6, a homodyned K-distribution with parameters ε, σ², α > α_max is approximated by the distribution with parameters

Fig. 6.

Algorithm for estimating the parameters ε², σ², α of the homodyned K-distribution with the constraint that α is less than an upper bound α_max. Left: block diagram; right: flow chart.

$$\stackrel{\sim }{\epsilon }=\sqrt{\mu \frac{\stackrel{\sim }{\gamma }}{(\stackrel{\sim }{\gamma }+{\alpha }_{max})}};{\stackrel{\sim }{\sigma }}^2=\frac{\mu }{2{\alpha }_{max}(\stackrel{\sim }{\gamma }+{\alpha }_{max})};{\alpha }_{max},$$ (3.9)

where $\stackrel{\sim }{\gamma }=\gamma ({\alpha }_{max},X_{\text{HK}}(\frac{{\epsilon }^2}{2{\sigma }^2\alpha },\alpha ))$.

In the reported tests, we chose α_max = 59.5, i.e. as large as possible but within a range for which the various functions used in the C++ implementation of the method could be supported numerically. In view of the numerical behavior of the function X_HK at integral values of α (see Appendix E), one might as well choose an odd integer divided by 2 for the value of α_max. Finally, we have checked numerically that the Kullback-Leibler distance [20] between a homodyned K-distribution with parameters ε, σ², α and the distribution with parameters as in equation (3.9) is less than 1.8 × 10⁻⁴ for parameter values in the range $k=\frac{\epsilon }{\sigma \sqrt{\alpha }}\in \{0,0.1,\dots ,1.9,2.0\}$ and α, α_max ∈ {59.5, 61.5, …, 79.5}. Note that the Kullback-Leibler distance is independent of the scaling factor μ, so that we assumed μ = 1 in the numerical computations. Thus, we are inclined to think that a homodyned K-distribution with α > α_max is approximated sufficiently well by the algorithm of Fig. 6 and that the choice of α_max ≥ 59.5 is not crucial, at least if k ≤ 2. However, we do not have a proof of this hypothesis because the analytical computations appeared to be intractable.

3.6. Are k and α the right parameters to estimate

The biases and normalized standard deviations reported in [11] are rather high. For instance, from [11, Fig. 3], the relative biases for k and α go up to about 600% and 100%, respectively, and their normalized standard deviations reach to about 300%. This suggests that one should consider a transformation of these parameters. In [8], the parameter β = 1/α is considered rather than α itself. For one estimation, the two solutions are equivalent, but for numerous estimations, the biases and standard deviations are not necessarily equivalent, because the averaging operator is not invariant under a transformation unless that transformation is linear. Thus, for instance, the relative bias of 1/α might be lower than the relative bias of α.

In this study, the parameters 1/(κ + 1) and 1/α were adopted. As will be presented in Section 4.1, the relative biases and normalized standard deviations were improved considerably with that choice of transformations. So, in the applications considered, the parameters 1/(κ + 1) and 1/α are estimated in each frame of a sequence of ultrasound images, and those estimated values are then averaged out over all frames. See Section 4.2 for such an application.

The advantage of the proposed choice of parameters is that, even if α = ∞ (corresponding to the Rice model), the parameter 1/α has a meaningful finite value (namely 0). In fact, the parameters 1/(κ + 1) and 1/α have values within the intervals (0, 1] and [0, ∞), respectively, even in the case of the Rice, Rayleigh or K-distribution model. See Section 5.6 for further discussion on this issue.

4. Experimental results

4.1. Comparison of estimators based on simulation of data samples

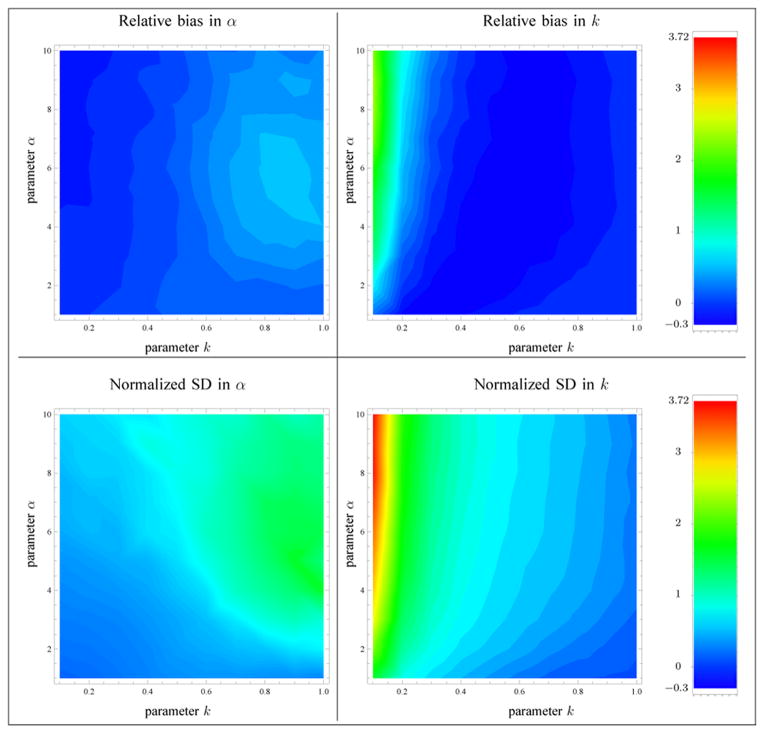
In order to compare the reported experimental results with those of [11], it was decided to present the results in terms of the scatterer clustering parameter α and the ratio of coherent to diffuse signal $k=\sqrt{2\kappa }$, where κ = ε²/(2σ²α) is the structure parameter. Following the same approach as in [11], 100 sets of values of the parameters k and α were considered in the domains k ∈ {0.1, 0.2, …, 0.9, 1.0} and α ∈ {1, 2, …, 9, 10}, and the value of σ² was taken as 1/α, so that the diffuse signal power 2σ²α = 2 was kept constant. For each of these sets, 1000 samples of size N = 1000 each were simulated, according to the homodyned K-distribution model. The parameters from each sample were then estimated using 1) the moments of intensity method [8] (MI), 2) a method based on the first three moments of the amplitude (MA), 3) the proposed method based on the mean intensity and the X and U statistics (XU), and 4) the method [11] based on the SNR, skewness and kurtosis of two fractional orders of the amplitude (RSK). For each estimation method, the relative biases (E[k̂] − k)/k and (E[α̂] − α)/α, the normalized standard deviations $\sqrt{\mathit{Var}[\widehat{k}]}/k$ and $\sqrt{\mathit{Var}[\widehat{\alpha }]}/\alpha$, and the relative root mean squared errors (RMSE) defined by $\sqrt{E[{(\widehat{k}-k)}^2]}/k$ and $\sqrt{E[{(\widehat{\alpha }-\alpha )}^2]}/\alpha$ were computed, based on the 1000 estimates k̂ and α̂ of those parameters. The relative bias and normalized standard deviation of the proposed estimator are presented in Fig. 7. As in [11], the computation of the bias and standard deviation did not include the instances where α was outside a reasonable range (i.e., α ≥ 59.5 for the MI, MA and XU methods). In Table 2, the sums of the quantities represented in Fig. 7 over the sets of parameters that were considered are presented for each of the tested methods. See Appendix F for the implementation of the MI method in the reported tests. The implementation of the MA method follows a similar strategy as the one presented in Section 3. We decided to skip the details in this paper since the MA method performed less well than the proposed estimator. For the MI and MA methods, a minimization problem similar to Equation (3.8) is considered to circumvent the case where the system of non-linear equations has no solution.

Fig. 7.

Relative bias and normalized standard deviation (SD) of the parameter estimates based on the XU estimator. The sample size is N = 1000. The computation of the biases and standard deviations excluded the instances where α was greater than α_max.

Table 2.

Improvements in bias and variance of estimators. The sample size is N = 1000. Estimation methods: 1) MI [8]; 2) MA; 3) XU (proposed method); 4) RSK [11]. The computation of the biases and standard deviations excluded the instances where α was greater than α_max for the MI, MA, XU methods. A star (*) indicates the best relative RMSE value among the four estimators.

	MI	MA	XU	RSK
Total absolute value of the relative bias of α̂	47.9	19.6	17.5	23.9
Total absolute value of the relative bias of κ̂	42.2	33.2	34.7	60.7
Total normalized standard deviation of α̂	108.9	73.7	70.3	84.5
Total normalized standard deviation of κ̂	117.0	92.0	91.1	62.1
Total value of the relative RMSE of α̂	120.3	76.7	72.7*	88.2
Total value of the relative RMSE of κ̂	126.6	99.1	99.1	92.7*

Next, the relative RMSE of the various tested estimators were evaluated for the parameters k, α, as well as the parameters κ, $\sqrt{2\gamma }=\epsilon /\sigma$, 1/(κ + 1) and 1/α, but without excluding high values of α for the MI, MA and XU methods (since 1/α = 0 is a solution). The results are presented in Table 3.

Table 3.

Relative RMSE of estimators for various parameters of the homodyned K-distribution. The sample size is N = 1000. Estimation methods: 1) MI [8]; 2) MA; 3) XU (proposed method); 4) RSK [11]. For the MI, MA, XU methods, the computation of the biases and standard deviations did not exclude any values of α, because 1/α = 0 is a solution. A star (*) indicates the best MSE value among the four estimators.

	MI	MA	XU	RSK
Mean relative RMSE of α̂	1.69	1.06	1.04	0.88*
Mean relative RMSE of $\widehat{1/\alpha }$	1.37	0.64	0.63*	0.67
Mean relative RMSE of k̂	1.26	0.99	0.99	0.93*
Mean relative RMSE of κ̂	6.90	4.29*	4.37	4.87
Mean relative RMSE of $\widehat{\sqrt{2\gamma }}$	1.04	0.86	0.85*	0.88
Mean relative RMSE of $\widehat{1/(\kappa +1)}$	0.18	0.12	0.13	0.11*

4.2. Estimation based on simulated ultrasound images

4.2.1. Experimental setup

The reported computational simulations were inspired by the work of [11, III-D-2]. Namely, radiofrequency (RF) data were simulated using the Field II ultrasound simulation program [17, 18]. A single-element oscillating focused (f/4) transducer with a focal length of 50.8 mm was used. Its center frequency was 10 MHz, and it was excited with a Gaussian windowed sinusoidal pulse with a 50% fractional bandwidth at −6 dB. The excitation pulse length was 0.616 mm, i.e. 4 times the wavelength (that information is missing from [11]). The sampling frequency was 200 MHz and the scan lines to produce an image were separated by 0.43 mm. The speed of sound was equal to 1540 m/s. These choices amount to an axial and a lateral discretization of 0.00385 mm and 0.43 mm per pixel, respectively. As in [11], no tissue attenuation was added in these simulations. The ultrasound echo envelope was computed as the norm of the Hilbert transform of the RF data (see [19]). The resulting unfiltered and uncompressed B-mode image was then decimated along the beam axis by a factor of 10 in order to have an independent identically distributed sample modeled by a single homodyned K-distribution.

A computational phantom of height 17.2 mm, length 20.7 mm, and width 1.72 mm was also considered. The center of the volume was located at the geometric focus of the transducer. The resolution cell (a volume which corresponds to the smallest resolvable detail [5]) was obtained by scanning one scatterer located at the geometric focus of the transducer and considering the −20 dB contour of the echo envelope (as in [8]). The resolution cell size was then estimated using the correlation length method (as in [8]) along the axial and lateral directions. The resolution cell volume (based on an ellipsoid model) was 0.2153 mm³ (the ellipsoid semi-principal axis in the beam direction measured 0.2180 mm and the two other semi-principal axes were 0.4856 mm long). Thus, a density (i.e., average number of scatterers per unit volume) of N_s scatterers per resolution cell corresponded to N_s × 2844 scatterers within the numerical phantom (N_s was variable in the reported tests).

4.2.2. Variation of the density of randomly located scatterers

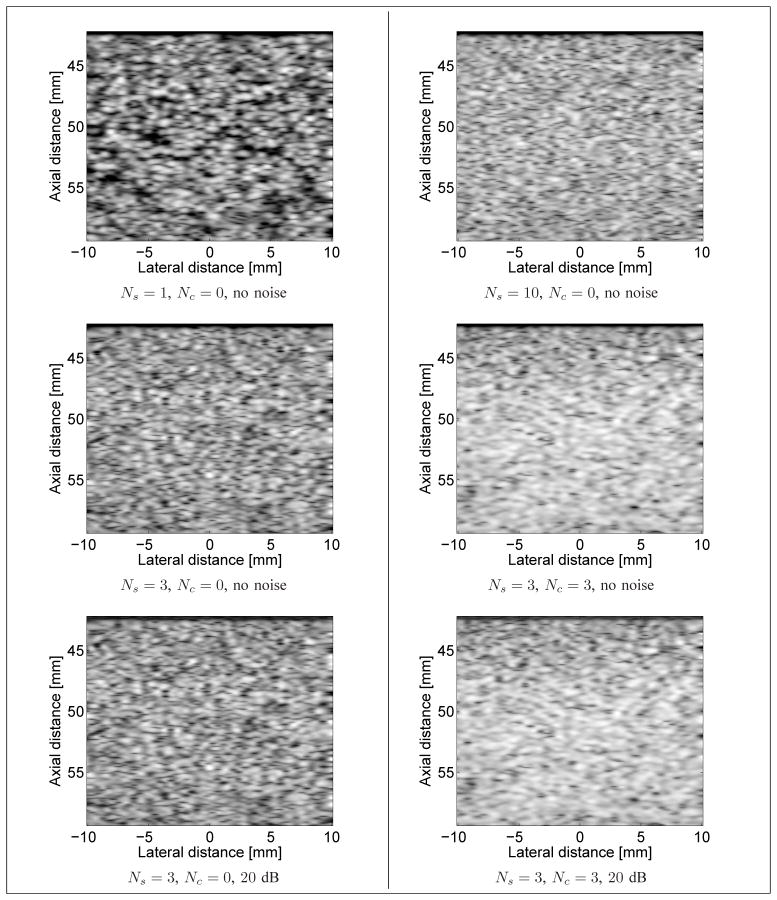
Randomly located scatterers were placed in the phantom volume at spatial locations distributed according to a uniform distribution. The amplitude of each scatterer (related to the contrast in acoustic impedance between the scatterer and the surrounding medium) was distributed according to a normal distribution of mean 0 and variance 1, as in [17] (that information is missing in [11]). Sequences of ultrasound images were simulated with an average number of randomly located scatterers per resolution cell varying from 1 to 10 (for a total of 10 simulated sequences). For each value of the scatterer density, a total of 60 images were simulated. See Fig. 8 for examples of simulated images.

Fig. 8.

Examples of simulated B-mode images with N_s randomly located scatterers per resolution cell, N_c periodic scatterers per resolution cell, with or without noise added to the RF signal. Top left: N_s = 1, N_c = 0, no noise; Top right: N_s = 10, N_c = 0, no noise. Middle left: N_s = 3, N_c = 0, no noise; Middle right: N_s = 3, N_c = 3, no noise. Bottom left: N_s = 3, N_c = 0, RF SNR of 20 dB; Bottom right: N_s = 3, N_c = 3, RF SNR of 20 dB. A log-compression was applied to the echo envelope solely for visualization purposes.

For each simulated sequence, the estimated values of 1/(κ + 1) and 1/α were averaged over the 60 images of the sequence within a region of interest (ROI), based on the XU estimator. The ROI consisted of the rectangle covered by 6 resolution cells in the axial direction and of about 35 resolution cells in the lateral direction (for a sample size of N = 13299 pixels), centered at the geometric focus of the transducer. In Fig. 9, the theoretical and estimated values (with the XU estimator) of these parameters are presented. For the theoretical values, the parameter 1/(κ + 1) should be equal to 1, since there are no periodic scatterers in this simulation (see Section 4.2.3). Also, the parameter 1/α should be inversely proportional to the number of randomly located scatterers per resolution cell. In fact, from [33, Eq. (4)], the parameter α is of the form α_sN_s, where N_s is the number of randomly located scatterers per resolution cell and α_s > 0 is related to the homogeneity of the scattering cross-sections. Thus, one obtains 1/α = 1/(α _sN_s). The constant 1/α_s was obtained with the Blacknell-Tough estimator [4], assuming a K-distribution. Namely, for each simulated sequence, corresponding to an average of i = 1, …, 10 randomly located scatterers per resolution cell, the estimated value of 1/α_[i] was averaged over the 60 images. Then, the average $\frac{1}{10}{\sum }_{i=1}^{10}i/{\alpha }_{[i]}$ was considered as the constant 1/α_s (because the index i in the sum represents N_s). In the reported tests, a value of 1/α_s = 2.243 was obtained in that manner.

Fig. 9.

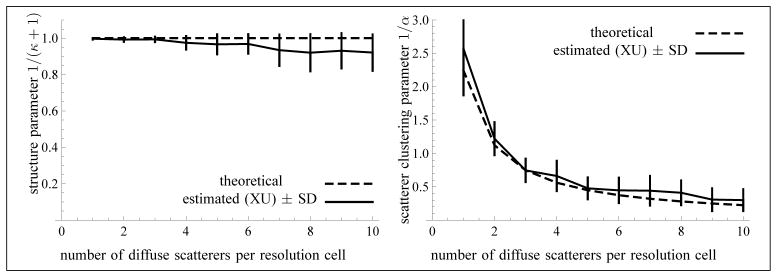
Values of the parameter 1/(κ + 1) (left) and of the scatterer clustering parameter 1/α (right) as a function of the average number of randomly located scatterers per resolution cell. No coherent component was included in these simulations. The sample size of each frame is 13299 and the number of frames is N = 60 (used for the computation of the standard deviations). The computation of the biases and standard deviations did not exclude any values of α, because 1/α = 0 is a possible solution.

4.2.3. Variation of the coherent component

A fixed density of 3 randomly located scatterers per resolution cell was considered. Coherent scattering was created by using periodically spaced scatterers along the transducer axis. So, their coordinates in the plane perpendicular to the transducer axis were random, whereas their coordinates along that axis were separated by a distance of around λ/2, where λ is the wavelength. This corresponds to a subresolvable periodic alignment of scatterers. The amplitude of the periodic scatterers was fixed to the constant 1 for each simulation of 60 images, in order to match the average intensity value of the randomly located scatterers. Indeed, the amplitude of the randomly located scatterers was distributed according to a Gaussian distribution of mean 0 and variance 1, which implies a Rayleigh distribution of mean 1 for the intensity (i.e., the square of the amplitude). The average number of periodic scatterers per resolution cell (i.e., their density) varied from 0 to 9 (with a step of 1), for a total of 10 simulations of 60 images each.

For each simulated sequence, the estimated values of 1/(κ +1) and 1/α were averaged over the 60 images of the sequence within the ROI of Section 4.2.2. In Fig. 10, the theoretical and estimated values of these parameters (with the XU method) are presented. As a first approximation, the theoretical value of κ is equal to the ratio of periodic to randomly located scatterers. Moreover, one would expect that the theoretical value of α is constant and corresponds to a density of 3 randomly located scatterers per resolution cell (and no periodic scatterers) times the constant α_s of Section 4.2.2. Hence, it can be deduced as in that section.

Fig. 10.

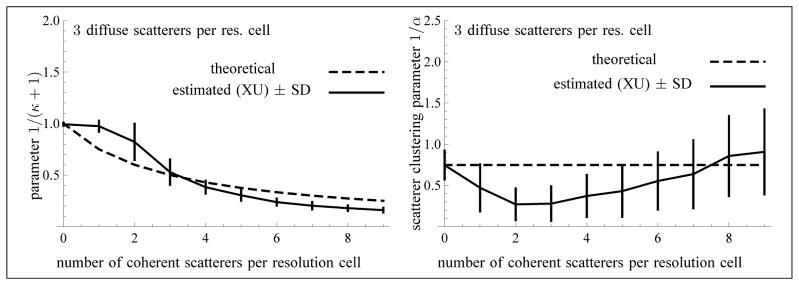
Values of the parameter 1/(κ + 1) (left) and of the scatterer clustering parameter 1/α (right) as a function of the number of coherent scatterers per resolution cell. The sample size of each frame is 13299 and the number of frames is N = 60 (used for the computation of the standard deviations). The computation of the biases and standard deviations did not exclude any values of α, because 1/α = 0 is a possible solution.

4.2.4. Presence of noise

The simulations of Sections 4.2.2 and 4.2.3 were repeated with the addition of noise on the RF signals (prior to the computation of the echo envelope) to create RF signals with SNRs of 20 dB, 10 dB or 5 dB. Namely, an SNR of n dB on the RF signal was simulated by adding to the RF signal a Gaussian noise of mean 0 and of variance τ² equal to 10^−n/10 E[I_RF], where I_RF denotes the square of the RF signal. In that manner, the SNR of the RF signal was equal to E[I_RF]/τ² = 10^n/10, which corresponds indeed to n dB. A comparison with the simulations with no added noise is presented in Table 4. Four methods were tested: 1) the MI method [8]; 2) the MA method; 3) the XU (proposed) method; and 4) the RSK method [11]. In that table, the relative RMSE are reported. Note that the value of the constant 1/α_s of Section 4.2.2 has to be evaluated for each level of noise. We obtained the values 2.225, 2.106, and 1.896 for SNRs of 20 dB, 10 dB, and 5 dB, respectively.

Table 4.

Improvements in mean relative RMSE, mean CV and mean RFJC of estimators. The sample size of each frame is 13299 and the number of frames is N = 60 (used for the computation of the standard deviations). Estimation methods: 1) MI [8]; 2) MA; 3) XU (proposed method); 4) RSK [11]. For the methods MI, MA, and XU, the computation of the biases and standard deviations did not exclude any values of α, because 1/α = 0 is a solution. A star (*) indicates the best relative RMSE value among the four estimators.

	Simulations 4.2.2					Simulations 4.2.3
Method	MI	MA	XU	RSK		MI	MA	XU	RSK
	No noise					No noise
rel. RMSE of $\widehat{1/\alpha }$	0.79	0.61	0.53*	0.67	CV of $\widehat{1/\alpha }$	0.99	0.65	0.61*	0.75
rel. RMSE of $\widehat{1/(\kappa +1)}$	0.074	0.075	0.069*	0.100	RFJC of $\widehat{1/(\kappa +1)}$	4.37	5.27	5.73*	3.95
	RF SNR of 20 dB					RF SNR of 20 dB
rel. RMSE of $\widehat{1/\alpha }$	0.80	0.62	0.53*	0.67	CV of $\widehat{1/\alpha }$	0.99	0.65	0.61*	0.74
rel. RMSE of $\widehat{1/(\kappa +1)}$	0.074	0.075	0.069*	0.100	RFJC of $\widehat{1/(\kappa +1)}$	4.37	5.25	5.78*	3.97
	RF SNR of 10 dB					RF SNR of 10 dB
rel. RMSE of $\widehat{1/\alpha }$	0.83	0.66	0.56*	0.70	CV of $\widehat{1/\alpha }$	0.99	0.64	0.61*	0.76
rel. RMSE of $\widehat{1/(\kappa +1)}$	0.076	0.078	0.071*	0.101	RFJC of $\widehat{1/(\kappa +1)}$	4.31	5.04	5.54*	3.96
	RF SNR of 5 dB					RF SNR of 5 dB
rel. RMSE of $\widehat{1/\alpha }$	0.89	0.72	0.61*	0.76	CV of $\widehat{1/\alpha }$	0.98	0.67	0.61*	0.78
rel. RMSE of $\widehat{1/(\kappa +1)}$	0.080	0.085	0.077*	0.107	RFJC of $\widehat{1/(\kappa +1)}$	4.11	4.55	5.03*	3.99

5. Discussion

5.1. Comparison of estimators based on simulations of data samples

As can be seen from Table 2, the XU method for the homodyned K-distribution yielded the lowest total relative RMSE for the parameter α. On the other hand, the total relative RMSE for the parameter k was lowest with the RSK method, whereas the MA and XU methods ranked second.

Note that the values obtained for α and k with the RSK method agree with [11, Table 1]. The values obtained for α with the MI method agree with [11, Table 1], but not the values obtained for k. This is explained by the fact that in the present study, as well as in [11], estimated values were excluded when α was outside its range. However, in [11], estimated values were excluded whenever α was outside its domain for either method [8] or [11]. In the present study, estimated values were excluded for a given estimator only if α was outside its domain for that estimator. We proceeded in that manner in order to test the performance of each method as it stands alone.

Moreover, Table 3 indicates clearly that it is preferable to estimate the parameters 1/(κ + 1) and 1/α rather than k (or κ or $\sqrt{2\gamma }$) and α. The XU method yielded a lower relative RMSE than the MI method, whereas it was barely better than the MA method, for the parameters α, 1/α and $\sqrt{2\gamma }$. On the other hand, the reported tests on simulated images indicate that the XU estimator is preferable to the MA estimator. The RSK method presented the lowest relative RMSE for the parameters α, k and 1/(κ + 1), but the XU method was best for the parameters 1/α and $\sqrt{2\gamma }$.

5.2. Estimation based on simulated ultrasound images

5.2.1. Variation of the density of randomly located scatterers

Table 4 (left part) shows that the XU estimation method performs better than the other tested methods. These results are in agreement with the RMSEs obtained on simulated data samples of Section 4.1, as far as the XU and RSK methods are concerned. On the other hand, the XU method appears to be much better than the MA method on simulated images, whereas the tests performed on simulated data samples did not stress this fact. This is explained by the fact that the X and U statistics arise in the limiting case where the fractional exponent of the fractional moment estimator is small [4] (i.e., near 0 or 1), since higher order moments are more sensitive to noise. Note that the estimates improve in the presence of less noise on the RF signal.

As can be seen from Fig. 9, the estimation of the parameters 1/(κ + 1) and 1/α is reliable up to 3 scatterers per resolution cell (1/α > 0.7) in the context of the reported tests. This is due to the behavior of the estimator for large values of α when κ = 0. Namely, the normalized bias and standard deviation of the estimator of $k=\sqrt{2\kappa }$ increase with the size of α, as can be seen from Fig. 7 (right) on the axis k = 0. Moreover, the normalized standard deviation of the estimator of α increases with the size of α (left of Fig. 7), which is consistent with the asymptotic expression 1/α² of the Fisher information of the K-distribution [1] (corresponding to k = 0). Indeed, the larger the value of α, the smaller the information revealed by the data, so that a larger sample size is needed for a finer estimation. Henceforth, the limitation of the XU estimator for large values of α is intrinsic to the model. To further study this issue, we have experimented with simulated ultrasound images with 11 to 20 scatterers per resolution cell. The relative RMSEs for 1/α were equal to 1.43 (MI), 1.27 (MA), 1.25 (XU) and 1.33 (RSK); for 1/(κ + 1), we obtained 0.14 (MI), 0.16 (MA), 0.17 (XU) and 0.20 (RSK). So, the XU estimator is better than the three others for 1/α, but for 1/(κ + 1), the MI estimator is best, whereas the XU estimator is still better than the RSK estimator.

One way to remedy this limitation is to consider the median of the estimator over a sequence of images. Fig. 11 shows that this approach yields much better results for the parameter 1/(κ + 1) and slightly better results for 1/α. Taking the median over all frames, instead of the mean, reduced the normalized bias¹ of the XU estimator for the parameter 1/(κ + 1) down to 0.08 in the case of the simulations with 11 to 20 diffuse scatterers. So, the bias was smaller when using the median instead of the mean. Moreover, the standard deviation (or the median absolute deviation - MAD -) is proportional to $1/\sqrt{N}$ for the average of an estimator over N images. Thus, taking the median value of the estimator over a sequence of images greatly improves its performance.

Fig. 11.

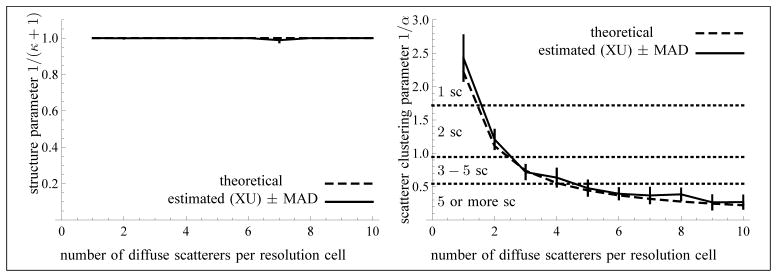
Median values of the parameter 1/(κ + 1) (left) and of the scatterer clustering parameter 1/α (right) as a function of the average number of randomly located scatterers per resolution cell. No coherent component was included in these simulations. The sample size of each frame is 13299 and the number of frames is N = 60 (used for the computation of the median absolute deviations).

Note also from Fig. 11 that although the XU estimator does not allow the exact number of scatterers per resolution cell for 1/α < 0.7 to be distinguished, this estimator nevertheless indicates the range of the number of scatterers. This is consistent with the fact that the homodyned K-distribution gets close to a Rice distribution² as α increases, so that it becomes harder to determine the exact value of α. So, again, this phenomenon is intrinsic to the model.

5.2.2. Variation of the coherent component

As can be seen from Fig. 10, the estimation of the parameter 1/(κ + 1) is quite reliable except when the number of coherent scatterers is 1 or 2. Also, the estimated parameter 1/α is smaller than the expected constant value, in the case of the simulations with a variable coherent component. So, as it stands, the proposed theoretical model is only an approximation. For that reason, we have chosen two evaluation measures that do not depend on a theoretical ground-truth in Table 4 (right). For the parameter 1/α, the coefficient of variation (CV) of the estimated parameter indicates the variability of the estimator with respect to its mean. If θ̂ is the estimator of a parameter θ, the CV is defined as $\sqrt{\mathit{Var}[\widehat{\theta }]}/E[\widehat{\theta }]$. For the parameter 1/(κ + 1), the root Fisher’s J criterion (RFJC) applied to pairs of distinct values of the parameter is an indicator of the discrimination power of the estimator. For two distinct values of a parameter θ, say θ₁ and θ₂, the RFJC is defined as $\mid E[\widehat{{\theta }_1}]-E[\widehat{{\theta }_2}]\mid /\sqrt{\mathit{Var}[\widehat{{\theta }_1}]+\mathit{Var}[\widehat{{\theta }_2}]}$.

Table 4 (right) shows that the XU estimation method performed better than the other tested methods, even with RF SNRs of 20 dB to 5 dB. Note that overall, the estimates improved in the presence of less noise on the RF signal, as expected.

5.3. Computational load

In the case of the experiments of Section 4.1, one estimation took on average 1.0 ms (MI), 1.6 ms (MA), 1.8 ms (XU) and 295.2 ms (RSK). In the case of the experiments of Sections 4.2.2 and 4.2.3, the computation times per image were equal to 6.0 ms (MI), 8.0 ms (MA), 6.8 ms (XU), and 500 ms (RSK). So, the MI, MA and XU methods share a comparable efficiency, whereas the RSK method is slower. That being said, the implementation for the first three methods was in C++, whereas the RSK method was implemented with Matlab. Nevertheless, the first three methods resort to a binary search algorithm with geometric rate of convergence, whereas the RSK method does not.

5.4. Hypothesis underlying the simulations of ultrasound images

As in [8, 11], we have made the hypothesis that the scatterers are dimensionless (upon using the Field II ultrasound simulation program [17, 18]). In the case of biological tissues, this hypothesis is false. In fact, the cell nuclei may be viewed as weak scatterers embedded in cytoplasm, considered as the ambient medium (see [31, 34]). Assuming spherical nuclei with a radius of 4.5 μm, one obtains a volume of 382 μm³. For flowing red blood cells, which do not have a nucleus, the cells themselves are viewed as scatterers (of volume 94 μm³ [32]), whereas the plasma is considered as the ambient medium. The point is that a sufficiently large density of scatterers with non-zero volume creates a scattering field that departs from the scattering behavior of uniformly distributed dimensionless scatterers, due to the so-called packing factor [36, 37]. Thus, the simulations reported in the present study are to be interpreted in the context of a low density of uniformly distributed weak scatterers of sufficiently small size (with respect to the resolution cell). The study of the homodyned K-distribution in the context of more realistic simulations with scatterers of finite dimensions would need to be addressed.

5.5. Conjecture 1

The statement that the algorithm of Fig. 4 converges to a unique solution is proved in Appendix B. For the algorithm of Fig. 5, all statements of Theorem 3.5 are proved in Appendix C. But Conjecture 1 remains to be proven to obtain the convergence of the algorithm of Fig. 5 to a unique solution of the system of equations (3.1). Yet, we have explained in Appendix D how that conjecture would follow from two claims. The former claim is illustrated in Fig. 12, whereas the latter is proved in Appendix D. We are convinced that the first claim is also true, but we do not know if this strategy for proving the conjecture is the easiest one. Note that the algorithm of Fig. 6 also relies on the conjecture.

Fig. 12.

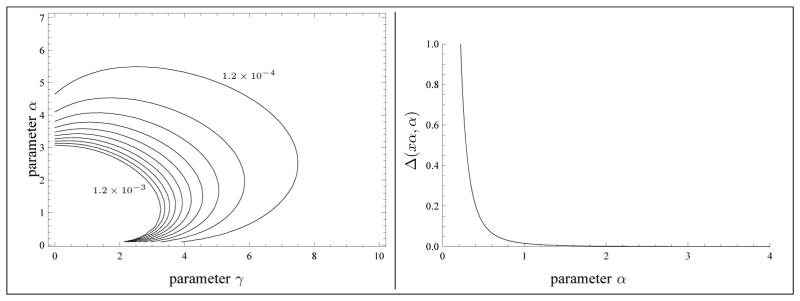
Left: A few level curves of the function Δ( γ, α) by steps of 1.2 × 10⁻⁴. The function Δ is increasing in the direction pointing to the origin. Right: Typical graph of Δ(xα, α) for a fixed value of x.

5.6. Upper bound on the parameter α

If one does not impose an upper bound on α (unlike what was done in Section 3.5), then one can consider the following minimization problem, which is similar to Eq. (3.8)

$$\begin{array}{l}(\mu ,\kappa ,\beta )=argmin\mid U_{\text{HK}}-U\mid \\ \text{subject}\text{to}\mu =\overline{I}\text{and}{X}_{\text{HK}}=X,\end{array}$$ (5.1)

where κ = ε²/(2σ²α) and β = 1/α. Observe that a solution to the system (3.1) yields automatically the solution μ = I̅, κ = ε²/(2σ²α) = γ/α and β = 1/α to the system (5.1).

The first case where the conditions of Corollary 3.6 are not satisfied (i.e., when the system (3.1) has no solution) corresponds to X > 1 and $U_{\text{K}}(X_{\text{K}}^{-1}(X))\ge U$. Since $U_{\text{K}}(X_{\text{K}}^{-1}(X))$ is the lower bound of the function U_HK(γ(α, X), α) (c.f. Theorem 3.3), it follows that |U_HK − U| is minimized at α = α₀ = 1/(X − 1), assuming the conjecture. But then, one must have γ(α₀, X) = 0, because of Theorem 3.3. Thus, one obtains the K-distribution model with μ = I̅, κ = 0 and α = α₀ (and hence β = 1/α₀).

The other case to consider corresponds to X ≤ 1 and $U_{\text{Ri}}(X_{\text{Ri}}^{-1}(X))\ge U$. Then, |U_HK − U| is minimized at α = ∞, assuming the conjecture. Indeed, the lower bound of the function U_HK(γ (α, X), α) is equal to $U_{\text{Ri}}(X_{\text{Ri}}^{-1}(X))$ and is reached asymptotically at infinity (c.f. Theorem 3.5, part c)). Thus, one obtains the Rice distribution. In fact, as α → ∞, the homodyned K-distribution with parameters ε², ${\sigma }^2={\sigma }_{\text{R}}^2/\alpha$ and α tends to the Rice distribution with parameters ε² and ${\sigma }_{\text{R}}^2$. Moreover, from Appendix B, Proof of Theorem 3.5, Part c), we have X_Ri(κ) = lim_α→∞ X_HK(γ, α), where $\kappa =\frac{{\epsilon }^2}{2{\sigma }_{\text{R}}^2}$ and $\gamma =\frac{{\epsilon }^2}{2{\sigma }^2}=\frac{{\epsilon }^2}{2{\sigma }_{\text{R}}^2}\alpha =\kappa \alpha$. Furthermore, one obtains β = lim_α→∞ 1/α = 0. The special case where X = 1 yields the Rayleigh distribution because X_Ri(0) = 1. Thus, if one is willing to include the Rice distribution to the homodyned K-distribution model as a limit case, then the system (5.1) always admits a solution.

However, the value of α is unbounded with that formulation, which is problematic in any implementation. For that reason, we adopted the minimization formulation of Eq. (3.8). Note that the MI and MA methods present a similar behavior. Moreover, the RSK method also restricts the parameters k and α to a bounded domain.

5.7. Biomedical applications

The K-distribution was used in the context of breast cancer classification in [33]. The parameters of the K-distribution have also been studied in the context of tissue characterization under shear wave propagation [3]. The homodyned K-distribution was used for cardiac tissue characterization [10], cancerous lesion classification [25, 12, 22], breast lesion classification [35] and determination of red blood cell aggregation [7]. In all these applications, the statistical parameters of the distributions considered are viewed as classifying features. The underlying assumption is that the scattering properties of the biological tissues leave a signature on the echo envelope of the received RF signal.

6. Conclusions

A method for the estimation of the parameters of the homodyned K-distribution was proposed, based on the first moment of the intensity and two log-moments (i.e., the U and X statistics). It was proven that the proposed algorithm converges to an estimation of the parameters. It was shown that it is preferable to estimate the parameters 1/(κ + 1) and 1/α, rather than k or κ, and α. The experimental results reported here show that the resulting estimator is, overall, more reliable than the method [8] based on the first three intensity moments, or a method based on the first three moments of the amplitude, or the estimator [11] based on the SNR, the skewness and the kurtosis of two fractional orders of the amplitude. These results hold even in the presence of noise corresponding to RF SNRs of 20 dB to 5 dB. For simulated data samples, the method [11] was slightly better for the parameter 1/(κ + 1). For simulated ultrasound images with more than 10 scatterers per resolution cell, the estimator [8] was slightly better for the parameter 1/(κ + 1). Otherwise, the proposed estimator ranked best among the four tested estimation methods. Moreover, the proposed method has a geometric rate of convergence, since it is based on the bisection algorithm for monotonous functions. Thus, a fast, reliable, and novel algorithm for the estimation of the homodyned K-distribution was proposed. On theoretical grounds, the uniqueness of the solution produced by the proposed method remains to be proven.

Appendix A. The statistics U and X for the homodyned K-distribution

In this appendix and those which follow, the software Mathematica (Wolfram Research, Inc., Champaign, IL, USA, version 7.0) was used whenever possible for the computations of integrals or limits. We have indicated any step that could not be obtained directly from that software.

Proof of Lemma 3.1

Part a). The function log I is concave. Therefore, from Jensen’s inequality [16], one obtains E[log I] < log E[I], since the random variable I is non-constant.

Part b). The function I log I is convex. Thus, E[I log I] > E[I] log E[I]. From part a), one concludes that E[I log I] > E[I]E[log I].

Proof of Proposition 3.2

Part a). First of all, using the change of variable I = A², one computes

$${\int }_0^{\infty }log{A}^2{P}_{\text{Ri}}(A\mid \epsilon ,a^2)dA={\int }_0^{\infty }logI\frac{1}{2a^2}{I}_0\left(\frac{\epsilon }{a^2}\sqrt{I}\right)e^{-{\epsilon }^2/(2a^2)}{e}^{-I/(2a^2)}dI,$$ (A.1)

which is a Laplace transform equal to $\mathrm{\Gamma }(0,\frac{{\epsilon }^2}{2a^2})+log{\epsilon }^2$, where Γ(0, x) is the incomplete gamma function ${\int }_x^{\infty }\frac{e^{-t}}{t}dt$. Then, taking a² = σ²w, multiplying by 𝒢(w|α, 1), and integrating with respect to w, one obtains

$$\begin{array}{l}-{\gamma }_E+log(2{\sigma }^2)+\psi (\alpha )\\ -{\left(\frac{{\epsilon }^2}{2{\sigma }^2}\right)}^{\alpha }\frac{\mathrm{\Gamma }(-\alpha )}{\alpha \mathrm{\Gamma }(\alpha )}{{}_{1}F}_2(\alpha ;1+\alpha ,1+\alpha ;\frac{{\epsilon }^2}{2{\sigma }^2})+\frac{{\epsilon }^2}{2{\sigma }^2}\frac{\mathrm{\Gamma }(\alpha -1)}{\mathrm{\Gamma }(\alpha )}{{}_{2}F}_3(1,1;2,2,2-\alpha ;\frac{{\epsilon }^2}{2{\sigma }^2}).\end{array}$$ (A.2)

Subtracting log E[I] from equation (A.2), with the identity E[I] = ε² + 2σ²α, and setting γ = ε²/(2σ²) yields the result.

Part b). Again, using the change of variable I = A², one computes

$${\int }_0^{\infty }{A}^{2}log{A}^2{P}_{\text{Ri}}(A\mid \epsilon ,a^2)dA={\int }_0^{\infty }\mathit{I}logI\frac{1}{2a^2}{I}_0\left(\frac{\epsilon }{a^2}\sqrt{I}\right)e^{-{\epsilon }^2/(2a^2)}{e}^{-I/(2a^2)}dI.$$ (A.3)

This Laplace transform is equal to $4a^2-2e^{-\frac{{\epsilon }^2}{2a^2}}{a}^2+({\epsilon }^2+2a^2)\left(\mathrm{\Gamma }(0,\frac{{\epsilon }^2}{2a^2})+log{\epsilon }^2\right)$. Then, subtracting by $({\epsilon }^2+2{\sigma }^2\alpha ){\int }_0^{\infty }log{A}^2{P}_{\text{Ri}}(A\mid \epsilon ,a^2)dA$ (corresponding to the term − E[I]E[log I]), taking a² = σ²w, and multiplying by 𝒢(w | α, 1), one obtains

$$\begin{array}{l}2{\sigma }^{2}w(-e^{-\frac{{\epsilon }^2}{2{\sigma }^{2}w}}+2)\mathcal{G}(w,\alpha )+2{\sigma }^2\mathrm{\Gamma }(0,\frac{{\epsilon }^2}{2{\sigma }^{2}w})(-\alpha +w)\mathcal{G}(w,\alpha )\\ +2{\sigma }^{2}log{\epsilon }^2(-\alpha +w)\mathcal{G}(w,\alpha ).\end{array}$$ (A.4)

Then, integrating with respect to w yields

$$\begin{array}{l}2{\sigma }^2+4{\sigma }^2\alpha -\frac{2^{3/2}\epsilon \sigma }{\mathrm{\Gamma }(\alpha )}{\left(\frac{{\epsilon }^2}{2{\sigma }^2}\right)}^{\alpha /2}{K}_{\alpha +1}\left(\frac{\sqrt{2}\epsilon }{\sigma }\right)\\ +2{\sigma }^2\frac{\mathrm{\Gamma }(-\alpha )}{\mathrm{\Gamma }(\alpha )}{\left(\frac{{\epsilon }^2}{2{\sigma }^2}\right)}^{\alpha }{{}_{1}F}_2(\alpha ;1+\alpha ,1+\alpha ;\frac{{\epsilon }^2}{2{\sigma }^2})\\ -{\epsilon }^2\frac{\mathrm{\Gamma }(-1-\alpha )}{(1+\alpha )\mathrm{\Gamma }(\alpha )}{\left(\frac{{\epsilon }^2}{2{\sigma }^2}\right)}^{\alpha }{{}_{1}F}_2(1+\alpha ;2+\alpha ,2+\alpha ;\frac{{\epsilon }^2}{2{\sigma }^2})\\ +{\epsilon }^2{{}_{2}F}_3(1,1;2,2,1-\alpha ;\frac{{\epsilon }^2}{2{\sigma }^2})-{\epsilon }^2\frac{\alpha \mathrm{\Gamma }(-1+\alpha )}{\mathrm{\Gamma }(\alpha )}{{}_{2}F}_3(1,1;2,2,2-\alpha ;\frac{{\epsilon }^2}{2{\sigma }^2}),\end{array}$$ (A.5)

which gives an expression for E[I log I]−E[I]E[log I]. Dividing equation (A.5) by E[I] = ε² +2σ²α and setting γ = ε²/(2σ²) yields the result. ■

Appendix B. Estimating γ, when α is known

Proof of Theorem 3.3

Part a). By definition of the hypergeometric series as a power series, one has _pF_q(a₁, …, a_p; b₁, …, b_q; x) = 1 at x = 0. Using this fact, one concludes that the sum of the last four terms in Equation (3.4) is equal to 0 at γ = 0. Next, from [2, p.375, (9.6.9)], one has the asymptotic behavior $K_{\alpha }(x)~\frac{\mathrm{\Gamma }(\alpha )}{2}{(\frac{2}{x})}^{\alpha }$ at x = 0. Hence, the second term of equation (3.4) admits the asymptotic form $-\frac{2{\gamma }^{\alpha /2+1/2}}{(\gamma +\alpha )\mathrm{\Gamma }(\alpha )}\frac{\mathrm{\Gamma }(\alpha +1)}{2}{\left(\frac{1}{{\gamma }^{1/2}}\right)}^{\alpha +1}=-\frac{\alpha }{(\gamma +\alpha )}=-1$, at γ = 0. Collecting all terms, one obtains ${lim}_{\gamma \to 0}\frac{1+2\alpha }{(\gamma +\alpha )}-\frac{\alpha }{(\gamma +\alpha )}=1+\frac{1}{\alpha }$. Since γ = 0 corresponds to the K-distribution, this also shows that X_K(α) = 1 + 1/α.

Part b). Writing equation (A.4) in terms of γ and α, and dividing by μ = E[I], one obtains

$$\frac{w}{(\gamma +\alpha )}(-e^{-\frac{\gamma }{w}}+2)\mathcal{G}(w,\alpha )+\frac{\mathrm{\Gamma }(0,\frac{\gamma }{w})}{(\gamma +\alpha )}(-\alpha +w)\mathcal{G}(w,\alpha )+\frac{log{\epsilon }^2}{(\gamma +\alpha )}(-\alpha +w)\mathcal{G}(w,\alpha ).$$ (B.1)

The third term of equation (B.1) is irrelevant because its integral with respect to w is equal to 0. Thus, one has

$$\begin{array}{l}{X}_{\text{HK}}(\gamma ,\alpha )={\int }_0^{\infty }F(w,\gamma ,\alpha )dw;\\ F(w,\gamma ,\alpha )=\frac{w}{(\gamma +\alpha )}(-e^{-\frac{\gamma }{w}}+2)\mathcal{G}(w,\alpha )+\frac{\mathrm{\Gamma }(0,\frac{\gamma }{w})}{(\gamma +\alpha )}(-\alpha +w)\mathcal{G}(w,\alpha ).\end{array}$$ (B.2)

Claim 1

$\mid \mathrm{\Gamma }(0,1/x)\mid =\mathrm{\Gamma }(0,1/x)\le \sqrt{x}$ for any x > 0.

Proof

Let $f(x)=\mathrm{\Gamma }(0,1/x)-\sqrt{x}$. On one hand, lim_x→0 f (x) = 0. On the other hand, $\frac{d}{dx}f(x)=\frac{e^{-1/x}}{x}-\frac{1}{2\sqrt{x}}<0$, for x > 0. This last statement is equivalent to $2/\sqrt{x}<e^{1/x}$, for x > 0, or 4z < e^2z, for z > 0 (with the change of variable z = 1/x). But now, the function g(z) = e^2z −4z has an absolute minimum at $z_0=\frac{1}{2}log2$ (because $\frac{d}{dz}g(z)<0$ for z < z₀, whereas $\frac{d}{dz}g(z)>0$ for z > z₀), and furthermore, g(z₀) = 2(1 − log 2) > 0. So, g(z) > 0 for all z > 0, which completes the proof of the claim. ■

From the claim, $\mid \mathrm{\Gamma }(0,\frac{\gamma }{w})\mid \le \sqrt{\frac{w}{\gamma }}$. Therefore, the absolute value of the function F (w, γ, α) of equation (B.2) admits the upper bound

$$\frac{2w}{(\gamma +\alpha )}\mathcal{G}(w,\alpha )+\frac{w^{1/2}}{{\gamma }^{1/2}(\gamma +\alpha )}(\alpha +w)\mathcal{G}(w,\alpha ).$$ (B.3)

Integrating equation (B.3) with respect to w yields $\frac{2\alpha }{(\gamma +\alpha )}+\frac{(1+4\alpha )\mathrm{\Gamma }(1/2+\alpha )}{2{\gamma }^{1/2}(\gamma +\alpha )\mathrm{\Gamma }(\alpha )}$. Thus, lim_γ→∞ X_HK(γ, α) = 0.

Part c). From equation (B.2), the function X_HK(γ, α) can be written as the sum of the two following functions

$$\begin{array}{l}{X}_{\text{HK},A}(\gamma ,\alpha )={\int }_0^{\infty }\frac{w}{(\gamma +\alpha )}(-e^{-\frac{\gamma }{w}}+2)\mathcal{G}(w,\alpha )dw;\\ X_{\text{HK},B}(\gamma ,\alpha )={\int }_0^{\infty }\frac{\mathrm{\Gamma }(0,\frac{\gamma }{w})}{(\gamma +\alpha )}(-\alpha +w)\mathcal{G}(w,\alpha )dw.\end{array}$$ (B.4)

It is now shown that the first function is decreasing in γ and that the second one is strictly decreasing in γ.

First of all, one computes

$$\begin{array}{l}\frac{\partial }{\partial \gamma }{X}_{\text{HK},A}(\gamma ,\alpha )={\int }_0^{\infty }\left\{\frac{1}{(\gamma +\alpha )}{e}^{-\frac{\gamma }{w}}+\frac{w}{{(\gamma +\alpha )}^2}\left(e^{-\frac{\gamma }{w}}-2\right)\right\}\mathcal{G}(w,\alpha )dw\\ \le {\int }_0^{\infty }\left\{\frac{1}{(\gamma +\alpha )}\frac{1}{(1+\gamma /w)}+\frac{w}{{(\gamma +\alpha )}^2}\left(\frac{1}{(1+\gamma /w)}-2\right)\right\}\mathcal{G}(w,\alpha )dw\\ =\frac{\alpha }{{(\gamma +\alpha )}^2}\left(-1+e^{\gamma }\alpha E(1+\alpha ,\gamma )\right),\end{array}$$ (B.5)

where $E(1+\alpha ,\gamma )={\int }_1^{\infty }{e}^{-\gamma t}{t}^{-\alpha -1}dt$. So, one concludes that $\frac{\partial }{\partial \gamma }{X}_{\text{HK},A}(\gamma ,\alpha )\le 0$, from Claim 2 below.

Claim 2

For γ > 0 and α > 0, E(1 + α, γ) ≤ e^−γ/α.

Proof

Since e^−γt ≤ e^−γ for t ≥ 1 and t^−α−1 > 0, one computes immediately ${\int }_1^{\infty }{e}^{-\gamma t}{t}^{-\alpha -1}dt\le e^{-\gamma }{\int }_1^{\infty }{t}^{-\alpha -1}dt=e^{-\gamma }/\alpha$. ■

Next, one may write X_HK,B(γ, α) as $\frac{1}{(\gamma +\alpha )}{X}_{\text{HK},C}(\gamma ,\alpha )$, where

$$X_{\text{HK},C}(\gamma ,\alpha )={\int }_0^{\infty }\mathrm{\Gamma }(0,\frac{\gamma }{w})(-\alpha +w)\mathcal{G}(w,\alpha )dw.$$ (B.6)

Hence, $\frac{\partial }{\partial \gamma }{X}_{\text{HK},B}(\gamma ,\alpha )=-\frac{1}{{(\gamma +\alpha )}^2}{X}_{\text{HK},C}(\gamma ,\alpha )+\frac{1}{(\gamma +\alpha )}\frac{\partial }{\partial \gamma }{X}_{\text{HK},C}(\gamma ,\alpha )$. Thus, in order to show that X_HK,B is strictly decreasing, it is sufficient to show that X_HK,C(γ, α) > 0 and that X_HK,C(γ, α) is decreasing. Therefore, it is sufficient to prove Claims 3 and 4 below.

Claim 3

For γ > 0 and α > 0, $\frac{\partial }{\partial \gamma }{X}_{HK,C}(\gamma ,\alpha )<0$.

Proof

One computes

$$\frac{\partial }{\partial \gamma }{X}_{\text{HK},C}(\gamma ,\alpha )={\int }_0^{\infty }-\frac{e^{-\frac{\gamma }{w}}}{\gamma }(-\alpha +w)\mathcal{G}(w,\alpha )dw=-\frac{2{\gamma }^{(\alpha -1)/2}}{\mathrm{\Gamma }(\alpha )}{K}_{\alpha -1}(2\sqrt{\gamma })<\mathrm{0.■}$$

Claim 4

For α> 0, lim_γ→∞ X_HK,C(γ, α) = 0.

Proof

Observe that |Γ(0, 1/x)| = Γ(0, 1/x) ≤ x, for x > 0. Indeed, let f(x) = Γ(0, 1/x) − x. Then, lim_x→0 f(x) = 0, and $\frac{d}{dx}f(x)=\frac{e^{-1/x}}{x}-1<0$, because e^1/x > 1/x, for x > 0. Hence, one has $\mid X_{\text{HK},C}(\gamma ,\alpha )\mid \le {\int }_0^{\infty }\frac{w}{\gamma }(\alpha +w)\mathcal{G}(w,\alpha )dw=\frac{\alpha (1+2\alpha )}{\gamma }$. But, ${lim}_{\gamma \to \infty }\frac{\alpha (1+2\alpha )}{\gamma }=0$.

This completes the proof of the Theorem. ■

Appendix C. Estimating γ and α

Lemma C.1

1. lim_α→0 X_HK(α/x, α) = ∞, for any x > 0.

2. lim_α→0 U_HK(α/x, α) = − log(1 + x), for any x > 0.

Proof

Part a). Setting γ = α/x, equation (3.4) reads as

$$\begin{array}{l}{X}_{\text{HK}}(\alpha /x,\alpha )=\frac{1}{(1/x+1)}\frac{(1+2\alpha )}{\alpha }\\ -\frac{2}{x^{\alpha /2+1/2}(1/x+1)}\frac{{\alpha }^{\alpha /2-1/2}}{\mathrm{\Gamma }(\alpha )}{K}_{\alpha +1}\left(2\sqrt{\alpha /x}\right)\\ +\frac{1}{x^{\alpha }(1/x+1)}\frac{\mathrm{\Gamma }(-\alpha ){\alpha }^{\alpha -1}}{\mathrm{\Gamma }(A)}{{}_{1}F}_2(\alpha ;1+\alpha ,1+\alpha ;\alpha /x)\\ -\frac{1}{x^{\alpha +1}(1/x+1)}\frac{\mathrm{\Gamma }(-1-\alpha ){\alpha }^{\alpha }}{(1+\alpha )\mathrm{\Gamma }(\alpha )}{{}_{1}F}_2(1+\alpha ;2+\alpha ,2+\alpha ;\alpha /x)\\ +\frac{1}{(x+1)}{{}_{2}F}_3(1,1;2,2,1-\alpha ;\alpha /x)-\frac{1}{(x+1)}\frac{\alpha \mathrm{\Gamma }(-1+\alpha )}{\mathrm{\Gamma }(\alpha )}{{}_{2}F}_3(1,1;2,2,2-\alpha ;\alpha /x).\end{array}$$ (C.1)

Using the definition of the hypergeometric series, one sees immediately that 1 ≤ ₁F₂(α; 1 + α; α/x) ≤ ₁F₂(1/2; 1, 1; α/x), for α ≤ 1/2; moreover, ${lim}_{\alpha \to 0}\frac{\mathrm{\Gamma }(-\alpha ){\alpha }^{\alpha -1}}{\mathrm{\Gamma }(\alpha )}=-\infty$. Therefore, $\frac{\mathrm{\Gamma }(-\alpha ){\alpha }^{\alpha -1}}{\mathrm{\Gamma }(\alpha )}{{}_{1}F}_2(\alpha ;1+\alpha ,1+\alpha ;\alpha /x)\ge \frac{\mathrm{\Gamma }(-\alpha ){\alpha }^{\alpha -1}}{\mathrm{\Gamma }(\alpha )}{{}_{1}F}_2(1/2;1,1;\alpha /x)$, for α sufficiently small. Now, ₁F₂(1/2; 1, 1; α/x) is a power series in the variable α; moreover, ${lim}_{\alpha \to 0}\frac{\mathrm{\Gamma }(-\alpha ){\alpha }^{\alpha -1}}{\mathrm{\Gamma }(\alpha )}\alpha =-1$ and ${lim}_{\alpha \to 0}\frac{\mathrm{\Gamma }(-\alpha ){\alpha }^{\alpha -1}}{\mathrm{\Gamma }(\alpha )}{\alpha }^n=0$, for n > 1. Therefore, $\frac{\mathrm{\Gamma }(-\alpha ){\alpha }^{\alpha -1}}{\mathrm{\Gamma }(\alpha )}{{}_{1}F}_2(\alpha ;1+\alpha ,1+\alpha ;\alpha /x)\ge \frac{\mathrm{\Gamma }(-\alpha ){\alpha }^{\alpha -1}}{\mathrm{\Gamma }(\alpha )}+\mathit{constant}$ for α sufficiently small. Arguing as above, lim_{α→0 1}F₂(1 + α; 2 + α, 2 + α; α/x) = 1. In the same manner, one sees that 1 ≤ ₂F₃(1, 1; 2, 2, 1− α; α/x) ≤ ₂F₃(1, 1; 2, 2, 1/2; α/x), for α ≤ 1/2; but, one has that lim_{α→0 2}F₃(1, 1; 2, 2, 1/2; α/x) = 1. Similarly, for ₂F₃(1, 1; 2, 2, 2 − α; α/x). From there, one obtains

$$\begin{array}{l}\frac{\mathrm{\Gamma }(-\alpha ){\alpha }^{\alpha -1}}{\mathrm{\Gamma }(\alpha )}{{}_{1}F}_2(\alpha ;1+\alpha ,1+\alpha ;\alpha /x)\ge \frac{\mathrm{\Gamma }(-\alpha ){\alpha }^{\alpha -1}}{\mathrm{\Gamma }(\alpha )}+\mathit{constant};\\ \underset{\alpha \to 0}{lim}-\frac{\mathrm{\Gamma }(-1-\alpha ){\alpha }^{\alpha }}{(1+\alpha )\mathrm{\Gamma }(\alpha )}{{}_{1}F}_2(1+\alpha ;2+\alpha ,2+\alpha ;\alpha /x)=-1;\\ \underset{\alpha \to 0}{lim}{{}_{2}F}_3(1,1;2,2,1-\alpha ;\alpha /x)=1;\\ \underset{\alpha \to 0}{lim}-\frac{\alpha \mathrm{\Gamma }(-1+\alpha )}{\mathrm{\Gamma }(\alpha )}{{}_{2}F}_3(1,1;2,2,2-\alpha ;\alpha /x)=0\times 1.\end{array}$$ (C.2)

Using the limiting form K₁(z) ~ z⁻¹ [2, p.375, (9.6.9)] valid for small arguments z, one computes

$$\underset{\alpha \to 0}{lim}-\frac{{\alpha }^{\alpha /2-1/2}}{\mathrm{\Gamma }(\alpha )}{K}_{\alpha +1}\left(2\sqrt{\alpha /x}\right)=-\frac{\sqrt{x}}{2}.$$ (C.3)

Finally, combining (C.1), (C.2), and (C.3), one has $lim{inf}_{\alpha \to 0}{X}_{\text{HK}}(\alpha /x,\alpha )\ge lim{inf}_{\alpha \to 0}\frac{1}{(1/x+1)}\frac{(1+2\alpha )}{\alpha }+\frac{1}{x^{\alpha }(1/x+1)}\frac{\mathrm{\Gamma }(-\alpha ){\alpha }^{\alpha -1}}{\mathrm{\Gamma }(\alpha )}+\mathit{constant}=\infty$.

Part b). Setting γ = α/x, equation (3.3) reads as

$$-{\gamma }_E-log(\alpha /x+\alpha )+\psi (\alpha )-{(\alpha /x)}^{\alpha }\frac{\mathrm{\Gamma }(-\alpha )}{\alpha \mathrm{\Gamma }(\alpha )}{{}_{1}F}_2(\alpha ;1+\alpha ,1+\alpha ;\alpha /x)+(\alpha /x)\frac{\mathrm{\Gamma }(\alpha -1)}{\mathrm{\Gamma }(\alpha )}{{}_{2}F}_3(1,1;2,2,2-\alpha ;\alpha /x).$$ (C.4)

Using the definition of the hypergeometric series, one sees immediately that 1 ≤ ₂F₃(1, 1; 2, 2, 2 − α; α/x) ≤ ₂F₃(1, 1; 2, 2, 3/2; α/x), for α ≤ 1/2; but, on the other hand, one has lim_{α→0 2}F₃(1, 1; 2, 2, 3/2; α/x) = 1. So, lim_{α→0 2}F₃(1, 1; 2, 2, 2 − α; α/x) = 1. Since ${lim}_{\alpha \to 0}(\alpha /x)\frac{\mathrm{\Gamma }(\alpha -1)}{\mathrm{\Gamma }(\alpha )}=0$, one concludes that ${lim}_{\alpha \to 0}(\alpha /x)\frac{\mathrm{\Gamma }(\alpha -1)}{\mathrm{\Gamma }(\alpha )}\times {{}_{2}F}_3(1,1;2,2,2-\alpha ;\alpha /x)=0$. Next, one writes ₁F₂(α; 1 + α, 1 + α; α/x) = 1 + h(x, α), where $h(x,\alpha )={\sum }_{n=1}^{\infty }\frac{{(\alpha )}_n}{{(1+\alpha )}_n{(1+\alpha )}_n}\frac{{(\alpha /x)}^n}{n!}$. Let us observe that $0\le h(x,\alpha )\le {\sum }_{n=1}^{\infty }\alpha {(\alpha /x)}^n=\frac{{\alpha }^2}{x}\frac{1}{1-\alpha /x}$ (for α sufficiently small), and from there it follows that ${lim}_{\alpha \to 0}{(\alpha /x)}^{\alpha }\frac{\mathrm{\Gamma }(-\alpha )}{\alpha \mathrm{\Gamma }(\alpha )}h(x,\alpha )=0$. Finally, one has ${lim}_{\alpha \to 0}-{\gamma }_E-log(\alpha /x+\alpha )+\psi (\alpha )-{(\alpha /x)}^{\alpha }\frac{\mathrm{\Gamma }(-\alpha )}{\alpha \mathrm{\Gamma }(\alpha )}=-log(1+x)$.

Lemma C.2

For any γ > 0 and α > 0 $\frac{\partial }{\partial \gamma }{U}_{HK}(\gamma ,\alpha )>0$.

Proof

From the proof of Proposition 3.2, part a), one has

$$U_{\text{HK}}(\gamma ,\alpha )={\int }_0^{\infty }\left(\mathrm{\Gamma }(0,\frac{\gamma }{w})+log\frac{\gamma }{\gamma +\alpha }\right)\mathcal{G}(w\mid \alpha ,1)dw.$$ (C.5)

So, one computes

$$\begin{array}{l}\frac{\partial }{\partial \gamma }{U}_{\text{HK}}(\gamma ,\alpha )={\int }_0^{\infty }\frac{\partial }{\partial \gamma }\left(\mathrm{\Gamma }(0,\frac{\gamma }{w})+log\frac{\gamma }{\gamma +\alpha }\right)\mathcal{G}(w\mid \alpha ,1)dw\\ ={\int }_0^{\infty }\frac{1}{\gamma }\left(-e^{-\frac{\gamma }{w}}+\frac{\alpha }{(\gamma +\alpha )}\right)\mathcal{G}(w\mid \alpha ,1)dw\\ \ge {\int }_0^{\infty }\frac{1}{\gamma }\left(-\frac{1}{(1+\gamma /w)}+\frac{\alpha }{(\gamma +\alpha )}\right)\mathcal{G}(w\mid \alpha ,1)dw\\ =\frac{e^{\gamma }\alpha }{(\gamma +\alpha )}\left(E(\alpha ,\gamma )-E(\alpha +1,\gamma )\right),\end{array}$$ (C.6)

where $E(\alpha ,\gamma )={\int }_1^{\infty }{e}^{-\gamma t}{t}^{-\alpha }dt$. Since the function E(α, γ) is obviously decreasing in the variable α for a fixed value of γ, the result follows. ■

Proof of Theorem 3.5

Part a). Let x > 0 be fixed for now. From Lemma C.1, part a), and Theorem 3.3, part c), one has that γ (α, X) > α/x, for α sufficiently small. Then, from Lemma C.2, one obtains that U_HK(α/x, α) < U_HK(γ (α, X), α) < 0, for α sufficiently small. Therefore, using Lemma C.1, part b), one has −log(1 + x) = lim_α→0 U_HK(α/x, α) ≤ lim sup_α→0 U_HK(γ (α, X), α) ≤ 0. Since x > 0 can be taken arbitrarily small, one deduces that lim_α→0 U_HK(γ (α, X), α) = 0.

Part b). Let X > 1. From Theorem 3.3, one has that $\alpha =X_{\text{K}}^{-1}(X)=1/(X-1)$ implies that γ( α, X) = 0. Then, taking γ = 0 and $\alpha =X_{\text{K}}^{-1}(X)$ in Equation (3.3) yields the result.

Part c). Let X ≤ 1. The homodyned K-distribution with parameters ε², ${\sigma }^2={\sigma }_{\text{R}}^2/\alpha$, α tends to the Rice distribution with parameters ε² and ${\sigma }_{\text{R}}^2$, as α → ∞. The structure parameter κ for that Rice distribution is equal to $\frac{{\epsilon }^2}{2{\sigma }_{\text{R}}^2}$, and this is the same value for the homodyned K-distribution (because $2{\sigma }^2\alpha =2({\sigma }_{\text{R}}^2/\alpha )\alpha =2{\sigma }_{\text{R}}^2$). Therefore, lim_α→∞ X_HK(κα, α) = X_Ri(κ), since γ = κα. In the same manner, one obtains lim_α→∞ U_HK(κα, α) = U_Ri(κ). Now, take $\kappa =X_{\text{Ri}}^{-1}(X)$ and let 0 < η < κ. Then, for α sufficiently large, one has (κ − η) α < γ( α, X) < (κ + η) α. Therefore, one obtains U_HK((κ − η) α, α) < U_HK(γ (α, X), α) < U_HK((κ + η) α, α), since from Lemma C.2, the function U_HK(γ, α) is increasing in the variable γ. Taking the limit as α→∞ (which is possible since 0 < X ≤ 1 implies that γ( α, X) is well-defined for any α > 0), one deduces that U_Ri(κ − η) ≤ lim inf_α→∞ U_HK(γ (α, X), α) ≤ lim sup_α→∞ U_HK(γ (α, X), α) ≤ U_Ri(κ + η). Since η > 0 can be taken arbitrarily small, the result follows.

Next, an argument similar to the proof of Theorem 3.3 (i.e., making the change of variable I = A² and computing Laplace transforms) shows that $U_{\text{Ri}}(\kappa )=\mathrm{\Gamma }(0,\kappa )+log\frac{\kappa }{(\kappa +1)}$ and $X_{\text{Ri}}(\kappa )=\frac{(2-e^{-\kappa })}{(\kappa +1)}$. Finally, from basic calculus, one obtains the statement on the function X_Ri(κ). ■

Appendix D. Discussion on Conjecture 1

Let f(α) = U_HK(γ (α, X), α) (X being known). Then, Conjecture 1 amounts to the inequality

$$\frac{d}{d\alpha }f(\alpha )=\frac{\partial }{\partial \gamma }{U}_{\text{HK}}(\gamma ,\alpha )\frac{\partial }{\partial \alpha }\gamma (\alpha ,X)+\frac{\partial }{\partial \alpha }{U}_{\text{HK}}(\gamma ,\alpha )<0,$$ (D.1)

where γ = γ (α, X). Since γ(α, X) is defined by the identity X_HK(γ (α, X), γ) ≡ X, the implicit function Theorem implies that $\frac{\partial }{\partial \alpha }\gamma (\alpha ,X)=-\frac{\frac{\partial }{\partial \alpha }{X}_{\text{HK}}(\gamma ,\alpha )}{\frac{\partial }{\partial \gamma }{X}_{\text{HK}}(\gamma ,\alpha )}$. Moreover, since $\frac{\partial }{\partial \gamma }{X}_{\text{HK}}(\gamma ,\alpha )<0$, we conclude that equation (D.1) is equivalent to

$$\mathrm{\Delta }(\gamma ,\alpha )=\frac{\partial }{\partial \gamma }{X}_{\text{HK}}(\gamma ,\alpha )\frac{\partial }{\partial \alpha }{U}_{\text{HK}}(\gamma ,\alpha )-\frac{\partial }{\partial \alpha }{X}_{\text{HK}}(\gamma ,\alpha )\frac{\partial }{\partial \gamma }{U}_{\text{HK}}(\gamma ,\alpha )>0.$$ (D.2)

In particular, it is sufficient to prove the inequality Δ(γ, α) > 0, for any γ > 0 and α > 0. For that purpose, it is sufficient to show the two following claims.

Claim 5

For any fixed value of x > 0, the function Δ(αx, α) is decreasing in the variable α > 0.

We have not succeeded in proving the Claim 5, but Fig. 12 convinced us that it is true.

Claim 6

For any fixed value of x > 0, lim_α→∞ Δ( αx, α) = 0.

Proof

Using the identity γ = xα and making the change of variable w = αw′, we obtain from Equation (C.6)

$$\begin{array}{l}\frac{\partial }{\partial \gamma }{U}_{\text{HK}}(x\alpha ,\alpha )={\int }_0^{\infty }\frac{1}{\gamma }\left(-e^{-\frac{\gamma }{w}}+\frac{\alpha }{(\gamma +\alpha )}\right)\mathcal{G}(w\mid \alpha ,1)dw\\ =\frac{1}{\alpha }{\int }_0^{\infty }\frac{1}{x}\left(-e^{-\frac{x}{w^{\prime }}}+\frac{1}{(x+1)}\right)\mathcal{G}(w^{\prime }\mid \alpha ,1/\alpha )d{w}^{\prime }.\end{array}$$ (D.3)

The distribution 𝒢(w′ | α, 1/α) is concentrated on w′ = 1 as α→∞. Therefore, $\frac{\partial }{\partial \gamma }{U}_{\text{HK}}(x\alpha ,\alpha )~{\frac{1}{\alpha }\frac{1}{x}\left\{-e^{-\frac{x}{w^{\prime }}}+\frac{1}{(x+1)}\right\}|}_{w^{\prime }=1}=\frac{O(1)}{\alpha }$, for large values of κ. Similarly, we have

$$\begin{array}{l}\frac{\partial }{\partial \alpha }{U}_{\text{HK}}(x\alpha ,\alpha )={\int }_0^{\infty }\mathrm{\Gamma }(0,\frac{\gamma }{w})(logw-\psi (\alpha ))\mathcal{G}(w\mid \alpha ,1)dw-\frac{1}{(\gamma +\alpha )}\\ ={\int }_0^{\infty }\mathrm{\Gamma }(0,\frac{x}{w^{\prime }})(log{w}^{\prime }+log\alpha -\psi (\alpha ))\mathcal{G}(w^{\prime }\mid \alpha ,1/\alpha )d{w}^{\prime }-\frac{1}{\alpha (x+1)}.\end{array}$$ (D.4)

Thus, $\frac{\partial }{\partial \alpha }{U}_{\text{HK}}(x\alpha ,\alpha )=O(1)+\mathrm{\Gamma }(0,x)(log\alpha -\psi (\alpha ))+\frac{O(1)}{\alpha }=O(1)+O(1)(log\alpha -\psi (\alpha ))$ for large values of α.

Next, we have for the X-statistics

$$\begin{array}{l}\frac{\partial }{\partial \gamma }{X}_{\text{HK}}(x\alpha ,\alpha )={\int }_0^{\infty }\left(\frac{1}{(\gamma +\alpha )}{e}^{-\frac{\gamma }{w}}+\frac{w}{{(\gamma +\alpha )}^2}(-e^{-\frac{\gamma }{w}}+2)\right)\mathcal{G}(w\mid \alpha ,1)dw\\ +{\int }_0^{\infty }\left(-\frac{(-\alpha +w)}{\gamma (\gamma +\alpha )}{e}^{-\frac{\gamma }{w}}-\frac{(-\alpha +w)}{{(\gamma +\alpha )}^2}\mathrm{\Gamma }(0,\frac{\gamma }{w})\right)\mathcal{G}(w\mid \alpha ,1)dw\\ =\frac{1}{\alpha }{\int }_0^{\infty }\left(\frac{1}{(x+1)}{e}^{-\frac{x}{w^{\prime }}}+\frac{w^{\prime }}{{(x+1)}^2}(-e^{-\frac{x}{w^{\prime }}}+2)\right)\mathcal{G}(w^{\prime }\mid \alpha ,1/\alpha )d{w}^{\prime }\\ +\frac{1}{\alpha }{\int }_0^{\infty }\left(-\frac{(-1+w^{\prime })}{x(x+1)}{e}^{-\frac{x}{w^{\prime }}}-\frac{(-1+w^{\prime })}{{(x+1)}^2}\mathrm{\Gamma }(0,\frac{x}{w^{\prime }})\right)\mathcal{G}(w^{\prime }\mid \alpha ,1/\alpha )d{w}^{\prime }.\end{array}$$ (D.5)

Hence, $\frac{\partial }{\partial \gamma }{X}_{\text{HK}}(x\alpha ,\alpha )~\frac{1}{\alpha }\left(\frac{1}{(x+1)}{e}^{-x}+\frac{1}{{(x+1)}^2}(-e^{-x}+2)\right)~\frac{O(1)}{\alpha }$ for large values of α. Also, the partial derivative of X with respect to α is given by

$$\begin{array}{l}\frac{\partial }{\partial \alpha }{X}_{\text{HK}}(x\alpha ,\alpha )={\int }_0^{\infty }\left(\frac{w}{(\gamma +\alpha )}(-e^{-\frac{\gamma }{w}}+2)+\frac{\mathrm{\Gamma }(0,\frac{\gamma }{w})}{(\gamma +\alpha )}(-\alpha +w)\right)(logw-\psi (\alpha ))\mathcal{G}(w\mid \alpha ,1)dw\\ +{\int }_0^{\infty }\left(-\frac{w}{{(\gamma +\alpha )}^2}(-e^{-\frac{\gamma }{w}}+2)-\frac{\mathrm{\Gamma }(0,\frac{\gamma }{w})}{{(\gamma +\alpha )}^2}(\gamma +w)\right)\mathcal{G}(w\mid \alpha ,1)dw\\ ={\int }_0^{\infty }\left(\frac{w^{\prime }}{(x+1)}(-e^{-\frac{x}{w^{\prime }}}+2)+\frac{\mathrm{\Gamma }(0,\frac{x}{w^{\prime }})}{(x+1)}(-1+w^{\prime })\right)(log{w}^{\prime }+log\alpha -\psi (\alpha ))\mathcal{G}(w^{\prime }\mid \alpha ,1/\alpha )d{w}^{\prime }\\ +\frac{1}{\alpha }{\int }_0^{\infty }\left(-\frac{w^{\prime }}{{(x+1)}^2}(-e^{-\frac{x}{w^{\prime }}}+2)-\frac{\mathrm{\Gamma }(0,\frac{x}{w^{\prime }})}{{(x+1)}^2}(x+w^{\prime })\right)\mathcal{G}(w^{\prime }\mid \alpha ,1/\alpha )d{w}^{\prime }.\end{array}$$ (D.6)

So, $\frac{\partial }{\partial \alpha }{X}_{HK}(x\alpha ,\alpha )=O(1)+\left(\frac{1}{(x+1)}(-e^{-x}+2)\right)(log\alpha -\psi (\alpha ))+\frac{O(1)}{\alpha }=O(1)+O(1)(log\alpha -\psi (\alpha ))$ for large values of α.

Finally, since lim_α→∞ (log α − ψ( α))/α = 0, the claim follows. ■

Appendix E. Implementation issues

Using standard identities of the Euler gamma function and permuting the terms, one rewrites (3.4) as

$$\begin{array}{l}{X}_{\text{HK}}(\gamma ,\alpha )=\frac{(1+2\alpha )}{(\gamma +\alpha )}-\frac{2{\gamma }^{\alpha /2+1/2}}{(\gamma +\alpha )\mathrm{\Gamma }(\alpha )}{K}_{\alpha +1}\left(2\sqrt{\gamma }\right)\\ +\frac{\gamma }{(\gamma +\alpha )}\times \\ \{{{}_{2}F}_3(1,1;2,2,1-\alpha ;\gamma )-\frac{\pi }{sin(\pi \alpha )}\frac{{\gamma }^{\alpha -1}{{}_{1}F}_2(\alpha ;1+\alpha ,1+\alpha ;\gamma )}{\mathrm{\Gamma }(\alpha )\mathrm{\Gamma }(1+\alpha )}\\ +\frac{\pi }{sin(\pi (\alpha +1))}\frac{{\gamma }^{\alpha }{{}_{1}F}_2(1+\alpha ;2+\alpha ,2+\alpha ;\gamma )}{\mathrm{\Gamma }(\alpha )\mathrm{\Gamma }(2+\alpha )(1+\alpha )}-\frac{\alpha }{(\alpha -1)}{{}_{2}F}_3(1,1;2,2,-\alpha ;\gamma )\},\end{array}$$ (E.1)

which is valid for α > 1. If α < 1, the last term $-\frac{\alpha }{(\alpha -1)}{{}_{2}F}_3(1,1;2,2,2-\alpha ;\gamma )$ is replaced by $\frac{\pi }{sin\pi (1-\alpha )}\frac{\alpha }{\mathrm{\Gamma }(\alpha )\mathrm{\Gamma }(2-\alpha )}{{}_{2}F}_3(1,1;2,2,2-\alpha ;\gamma )$.

Either expression can be computed directly for α > 0, if α is not an integer. When α is a positive integer, the four terms of lines three and four of (E.1) tend to ±∞. Nevertheless, it can be shown that the corresponding sum has a finite value. In the implementation used in the reported tests, we chose the simplest solution that consists in approximating X_HK(γ, α) by interpolation of the values X_HK(γ, n − 10⁻⁷) and X_HK(γ, n + 10⁻⁷) in the interval n − 10⁻⁷ ≤ α ≤ n + 10⁻⁷, where n is an integer. On the other hand, the first two terms of (E.1) are well-defined for any value of α > 0.

Similar remarks apply to the computation of U_HK. In particular, one obtains

$$U_{\text{HK}}(\gamma ,\alpha )=-{\gamma }_E-log(\gamma +\alpha )+\psi (\alpha )+\frac{\pi }{sin(\pi \alpha )}\frac{{\gamma }^{\alpha }{{}_{1}F}_2(\alpha ;1+\alpha ,1+\alpha ;\gamma )}{\alpha \mathrm{\Gamma }(\alpha )\mathrm{\Gamma }(\alpha +1)}+\frac{\gamma }{(\alpha -1)}{{}_{2}F}_3(1,1;2,2,2-\alpha ;\gamma ),$$ (E.2)

which is valid for α > 1. If α < 1, the last term $\frac{\gamma }{(\alpha -1)}{{}_{2}F}_3(1,1;2,2,2-\alpha ;\gamma )$ is replaced by $-\frac{\pi }{sin\pi (1-\alpha )}\frac{\gamma }{\mathrm{\Gamma }(\alpha )\mathrm{\Gamma }(2-\alpha )}{{}_{2}F}_3(1,1;2,2,2-\alpha ;\gamma )$. These expressions are valid for α not an integer. One uses an approximation as explained above for values of α near integers.

Appendix F. Method [8] revisited

The method [8] is equivalent to solving the following (non-linear) system of equations in the variables ε², σ², and α:

$$\begin{array}{l}E[I]=\overline{I};\\ E[I^2]/E{[I]}^2=\overline{I^2}/{\overline{I}}^2:=M;\\ E[I^3]/E{[I]}^3=\overline{I^3}/{\overline{I}}^3:=L.\end{array}$$ (F.1)

Sufficient and necessary conditions for this system to admit a solution are presented below. For that purpose, the change of variables (3.2) was adopted.

Proposition F.1

Let $A=\sqrt{I}$ be distributed according to the homodyned K-distribution P_HK(A | ε, σ², α). With the notation of (3.2), one has

$$E[I^2]/E{[I]}^2=M_{HK}(\gamma ,\alpha )=\frac{({\gamma }^2+4\gamma \alpha +2\alpha (\alpha +1))}{{(\gamma +\alpha )}^2};$$ (F.2)

$$E[I^3]/E{[I]}^3=L_{HK}(\gamma ,\alpha )=\frac{({\gamma }^3+9{\gamma }^2\alpha +18\gamma \alpha (\alpha +1)+6\alpha (\alpha +1)(\alpha +2))}{{(\gamma +\alpha )}^3}.$$ (F.3)

As one can see, Equations (F.2) and (F.3) depend only on the variables γ and α. Thus, the method [8] amounts to solving Equations (F.2) and (F.3) in the variables γ and α, and then using Equations (3.5) with μ = E[I].

Let α > 0 be known. Using Equation (F.2), one deduces the value of γ ≥ 0 explicitly.

Proposition F.2

Let M > 1 be a real number and α be fixed. Then, there exists at most one solution γ ≥ 0 to the equation M_HK(γ, α) = M, namely

$$\gamma =\left(\alpha (2-M)+\sqrt{2(M-1)\alpha +(2-M){\alpha }^2}\right)/\left(M-1\right).$$ (F.4)

1. If M ≤ 2, then there is a solution for any α > 0.

2. If M > 2, then there is a solution if and only if $0<\alpha \le {\alpha }_0=M_K^{-1}(M)=2/(M-2)$.

Thus, one obtains a well-defined function γ = γ( α, M) on the domain described by Proposition F.2. Next, proceeding as in Section 3.3, the expression of Equation (F.4) is substituted in Equation (F.3), thus yielding a function L_HK(γ (α, M), α) in the single variable α.

Proposition F.3

Let M > 1 be a real number.

1. One has the left boundary condition lim_α→0 L_HK(γ (α, M), α) = ∞.

2. If M ≤ 2, then lim_α→∞ L_HK(γ (α, M), α) = L_Ri(κ₀), where ${\kappa }_0=M_{Ri}^{-1}(M)=1/(1-\sqrt{2-M})-1$.

3. If M > 2, then lim_α→α0 L_HK(γ (α, M), α) = L_K(α₀), where ${\alpha }_0=M_K^{-1}(M)=2/(M-2)$.

4. The function L_HK(γ (α, M), α) is decreasing on its domain.

In Proposition F.3, part b), the functions M_K(α) = 2 (1+1/α) and L_K(α) = 6 (1+1/α) (1+2/α) correspond to the computation of the M and L statistics for the K-distribution. In part c), the functions $M_{\text{Ri}}(\kappa )=2-\frac{{\kappa }^2}{{(\kappa +1)}^2}$ and $L_{\text{Ri}}(\kappa )=\frac{({\kappa }^3+9{\kappa }^2+18\kappa +6)}{{(\kappa +1)}^3}$ correspond to the computation of the M and L statistics for the Rice distribution.

Part d) of the Proposition implies that a binary search algorithm can be used to find the unique solution to Equations (F.2) and (F.3), whenever a solution exists.

Corollary F.4

Let M > 1 and L > 1 be given. Then, there exists a simultaneous solution to the system M_HK(γ, α) = M and L_HK(γ, α) = L if and only if

1. M ≤ 2 and $L>L_{Ri}(M_{Ri}^{-1}(M))$.

   or

2. M > 2 and $L>L_K(M_K^{-1}(M))$.

Moreover, if a solution exists, it is unique.

Thus, one obtains well-defined functions γ = γ(M, L) and α = α(M, L), where M and L are restricted to the domain described by parts a) and b) of Corollary F.4.