Simultaneous Multi-Slice fMRI using Spiral Trajectories

Abstract

Parallel imaging methods using multi-coil receiver arrays have been shown to be effective for increasing MRI acquisition speed. However parallel imaging methods for fMRI with 2D sequences show only limited improvements in temporal resolution because of the long echo times needed for BOLD contrast. Recently, Simultaneous Multi-Slice (SMS) imaging techniques have been shown to increase fMRI temporal resolution by factors of four and higher. In SMS fMRI multiple slices can be acquired simultaneously using Echo Planar Imaging (EPI) and the overlapping slices are un-aliased using a parallel imaging reconstruction with multiple receivers. The slice separation can be further improved using the “blipped-CAIPI” EPI sequence that provides a more efficient sampling of the SMS 3D k-space. In this paper a blipped-spiral SMS sequence for ultra-fast fMRI is presented. The blipped-spiral sequence combines the sampling efficiency of spiral trajectories with the SMS encoding concept used in blipped-CAIPI EPI. We show that blipped spiral acquisition can achieve almost whole brain coverage at 3 mm isotropic resolution in 168 ms. It is also demonstrated that the high temporal resolution allows for dynamic BOLD lag time measurement using visual/motor and retinotopic mapping paradigms. The local BOLD lag time within the visual cortex following the retinotopic mapping stimulation of expanding flickering rings is directly measured and easily translated into an eccentricity map of the cortex.

1. Introduction

Sub-second whole brain imaging is of particular interest in Blood Oxygen Level Dependent (BOLD) functional Magnetic Resonance Imaging (fMRI) (9, 22, 33). Faster acquisitions with higher temporal sampling of the BOLD time course provide several advantages. One immediate benefit is the increased sensitivity in detecting functional activation for a given stimulation duration simply by acquiring a greater number of samples. Using more sophisticated data analyses, improved sampling also allows for direct observation of the underlying BOLD hemodynamic response function (HRF). If the full HRF is recorded, regional variations in shape, onset, lag time or other general characteristics can be incorporated into the model fitted to the observed data leading to lower residuals and increased statistical significance (8). Furthermore, cardiac and respiration components of the physiological noise signal can also be measured directly and filtered out, possibly improving the overall temporal SNR. Lastly, higher volume acquisition rates freeze out head motion for improved image quality.

The most commonly used strategy to accelerate image acquisition times involves parallel imaging methods (13, 24, 28), where non-acquired k-space data are estimated using receiver array coil sensitivity information. Current commercially available receiver coil designs (i.e. “soccer ball” patterns with 32 channels (30)) provide sensitivity variation along all three spatial dimensions. This favors the use of three-dimensional (3D) sequences that can be accelerated along the in-plane and slice-select spatial dimensions. Standard Cartesian two-dimensional (2D) acquisitions however can only be accelerated along the phase encoding direction, and thus make use of coil sensitivity information along a single dimension. Although two- to four-fold in-plane acceleration is easily feasible with 2D methods, the savings in sampling time especially for 2D single-shot BOLD fMRI or diffusion-weighted EPI are in practice very marginal due to the need for an adequate echo time (TE) to generate BOLD contrast. If the accelerated acquisition time is decreased beyond the optimal TE, this results in reduced BOLD amplitude, which decreases the ability to distinguish between noise and functional activation. Fast 3D single shot sequences based on Cartesian (22, 31) and non-Cartesian trajectories (1, 33) volume acquisition times below 100 ms have been demonstrated. The drawback of single shot 3D methods is that the available time for k-space data acquisition is limited to approximately two times the T2*-decay time constant. Therefore these sequences can only provide moderate spatial resolution (3-4 mm)³ and are prone to off-resonance artifacts.

Recently, Simultaneous Multi-Slice (SMS) imaging was introduced for EPI based fMRI (9, 21, 27) bridging the gap between 2D multi-slice and 3D single shot imaging. In SMS EPI multiple thin, spatially separated slices are excited at once using a multi-band RF excitation pulse (18, 20). The length of an SMS readout is the same as those for standard 2D acquisitions, and so the temporal acceleration factor is equal to the number of simultaneously excited slices. Recent work on SMS acquisitions proposed the so-called “blipped CAIPI” EPI method (27), which is the EPI analogue of the CAIPIRINHA (5) technique. The “blipped-CAIPI” EPI method use z-gradient blips played out simultaneously with the in-plane y-gradient (phase encoding) blips in order to provide z-encoding along the slice direction and for more efficient use of the coil sensitivities. This allows for improved reconstruction of simultaneously excited slices and lower g-noise penalty (27). In essence, blipped-CAIPI exploits in-plane and slice direction coil sensitivity variation to reliably separate more slices than the coil sensitivities along slice direction alone allow. Slice acceleration factors of eight and even up to 16 have been shown to be possible on standard 32 channel coils (6) when no concurrent in-plane undersampling is used. An overview of the recent developments in ultra-fast SMS Imaging can be found in (11).

Here, we present a blipped-spiral trajectory design for fast non-Cartesian SMS imaging where z-gradient blips are applied for each revolution of the spiral in analogy to blipped-CAIPI EPI. Both, the blipped versions of spiral and EPI trajectories share the concept of distributing k-space encoding for SMS imaging along all three dimensions. The SMS encoding process is furthermore presented using a 3D k-space picture that describes optimal Cartesian and non-Cartesian sampling (35) (34) in a generalized way. The blipped-spiral trajectory combines the advantageous properties of spiral fMRI with the advantages of single-shot SMS acquisitions. For a comprehensive overview of spiral fMRI please see the review by G. Glover (12). We show that a blipped spiral acquisition can achieve almost whole brain coverage at 3 mm isotropic resolution in 168 ms. We also show that blipped-spirals have a more benign response to static off-resonances compared to a stacked-spiral (1, 16) approach that was also applied to non-Cartesian SMS Imaging (25). Finally the sequence is demonstrated using visual/motor and retinotopic mapping paradigms for high temporal resolution fMRI at 3T.

2. Theory

2.1 Simultaneous multi-slice imaging and 3D k-space

We demonstrated previously that a 3D encoding space formalism can be used to describe SMS encoding and the subsequent reconstruction of N simultaneously excited slices (34). In contrast to a 2D SMS description where the encoding problem is explained as individual slices that fold onto each other during the readout, the slice direction now corresponds to a second phase encoding direction of a 3D encoding space (k-space), with a field of view along the slice select direction given by the number of excited slices times their separation. By defining a Cartesian 3D k-space that corresponds to full sampling of the simultaneously excited slices, non-Cartesian sampling strategies (either fully sampled or accelerated) can be applied readily to SMS imaging. We first present a brief summary of the SMS 3D k-space framework for SMS imaging. See Ref. (34) for a more complete description.

Given N simultaneously excited slices with slice separation Δz, the k-space in the slice direction z is defined by

$${\mathrm{FOV}}_z=N\Delta z\text{and}\Delta k_z=\frac{1}{{\mathrm{FOV}}_z}\text{and}{k}_z^{\max }=\Delta k_z\frac{N}{2}$$ [1]

FOV_z gives the field of view along the slice direction. The slice direction k-space component k_z together with k_x and k_y, for the field of view FOV_xy and resolution N_xy in the x- and y-directions, span the 3D SMS k-space for full sampling of the in-plane and slice directions. In this work, SMS 3D k-space refers to a k-space that describes SMS imaging and is defined by Eq. [1]. If the Cartesian SMS 3D k-space is fully sampled, a straightforward inverse 3D Fourier transform will reconstruct all of the simultaneous slices. If the SMS 3D k-space is undersampled, as in standard SMS imaging, coil sensitivity information and parallel imaging reconstruction techniques are needed for un-aliased reconstruction. The ratio of the fully sampled to accelerated SMS 3D k-space is the total acceleration factor R_tot which can be distributed between different k-space directions. Note that the SMS 3D k-space framework can be used to better understand all previously published Cartesian methods using SMS excitation. For example, using an unmodified 2D readout as in Ref. (20) corresponds to sampling only the central plane in the SMS 3D k-space and therefore provides only limited slice acceleration. By adding z-blips during the 2D readout as in Ref. (27), the SMS 3D k-space sampling density is more uniformly distributed in 3D and thus allows for greater SMS acceleration.

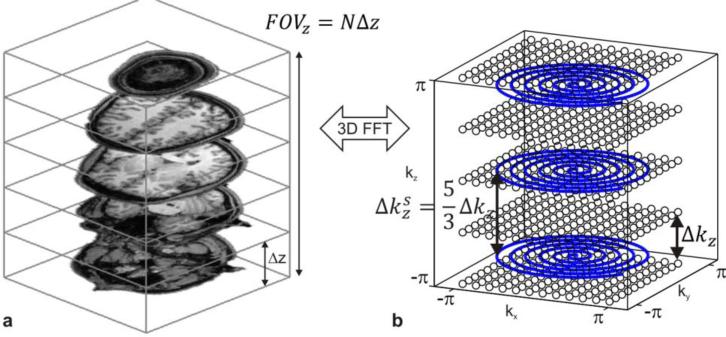
Figure 1 shows an example of N=5 simultaneously excited slices with a slice separation Δz = 20 mm and the corresponding SMS 3D k-space with N Cartesian k_x-k_y-planes at locations in generalized units depicted as black circles. As an example of an accelerated non-Cartesian acquisition a stacked-spiral trajectory is plotted in Figure 1b. The stacked-spiral trajectory is typically generated using a series of 2D spirals separated by z-gradient blips with k-space increment $\Delta k_z^s$. The number of 2D spirals in the stack is given as N_z. In this example $\Delta k_z^s=\frac{5}{3}\Delta k_z$ and the reduction factor along k_z is $R_z=\frac{\Delta k_z^s}{\Delta k_z}=5∕3$. The reduction factor along k_z can also be expressed in terms of the number of SMS slices and the number of spirals in the stack and is then given as R_z = N/N_z. It describes how undersampled the k_z direction is. Sufficient coil sensitivity variation is needed to compensate for this. For example if R_z = 1 then no coil sensitivity information along z is needed which corresponds to a k-space sampling pattern where the number of slices and the number of sampled k-space planes (stacks) are identical. Note that because of the relative rotations of each spiral along k_z any in-plane aliasing will be shifted from slice to slice analogous to CAIPIRINHA methods. The in-plane aliasing can be removed using parallel imaging reconstruction with in-plane sensitivity. In-plane acceleration is also possible with the stacked-spiral trajectory by decreasing FOV_xy by an in-plane reduction factor equal to R_xy. In-plane acceleration effectively reduces the number of spiral rotations per plane.

Figure 1.

This figure illustrates the relationship between SMS excitation and the corresponding 3D k-space dictated by the Nyquist sampling theorem. Figure a shows an example of five slices that are excited simultaneously with slice separation Δz =20 mm. The FOV in the slice direction is then 100 mm and the k-space increment for Nyquist sampling must be 10 1/m. The three spirals (blue lines in b) are an example for accelerated non-Cartesian sampling of the full k-space since only three out of the five k-space planes are sampled.

2.2 Blipped-spiral trajectories

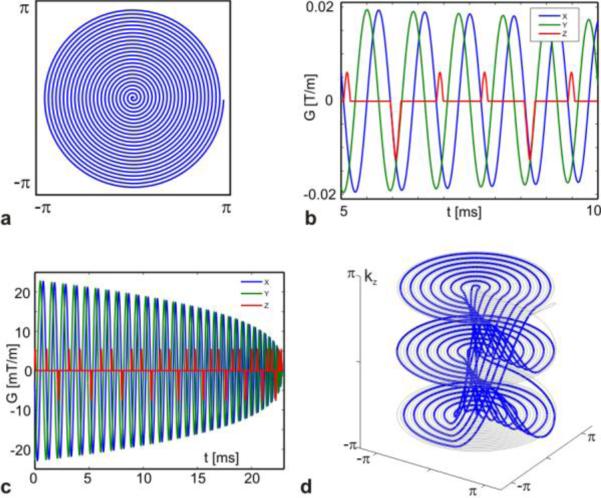
Like the stacked-spiral trajectory, the blipped-spiral method is based on a planar spiral in the k_x-k_y-plane, orthogonal to k_z (Figure 2a). Unlike the stacked-spiral trajectory, however, the gradient blips in the z-direction are added after every full rotation of the x- and y-gradients (Figure 2b and c). This difference is critical to the off-resonance response of the trajectory, as we will show later. The blip moment still determines the actual k-space increment $\Delta k_z^s$ and we assume that the trajectory starts at k-space location -$k_z^{\max }$ after the application of a pre-winder blip prior to the spiral. Similar to blipped CAIPI implementations in EPI, 2-4 blips are typically applied depending on the degree of sampling required along k_z. After $k_z^{\max }$ is reached a larger gradient pulse is substituted for the blip which rephases the k-space coordinate back to -$k_z^{\max }$. The initial 2D spiral is then distributed over N_z = N/N_z k-space planes in the k_z direction. Like the stacked-spiral trajectory, the reduction factor along k_z is given as $R_z=\Delta k_z^s∕\Delta k_z$, where Δk_z is given by Eq.[1]. In standard spiral imaging full sampling of the k_x-k_y plane with resolution N_xy requires N_xy/2 revolutions. Consequently, full sampling of N simultaneous slices requires that the generating spiral be N-fold oversampled resulting in NN_xy/2 revolutions in order to ensure that sampling of each k_z-plane fulfills the Nyquist criterion, as depicted by the gray line in Figure 2d. The effective in-plane acceleration factor depends on the oversampling factor of the initial spiral and the number of k-space planes in the k_z direction. For any given SMS parameters N and Δz, the k-space increment in the slice direction is identical for the blipped versions of spiral and EPI SMS trajectories.

Figure 2.

Blipped-spiral trajectory design in generalized k-space units. The initial planar spiral (a) is generated and after each full revolution of the spiral gradients a short gradient blip in the slice direction is added (red line in b). The full gradient waveforms for the blipped spiral are shown in c and the corresponding k-space trajectory with three k_z-planes is shown in d.

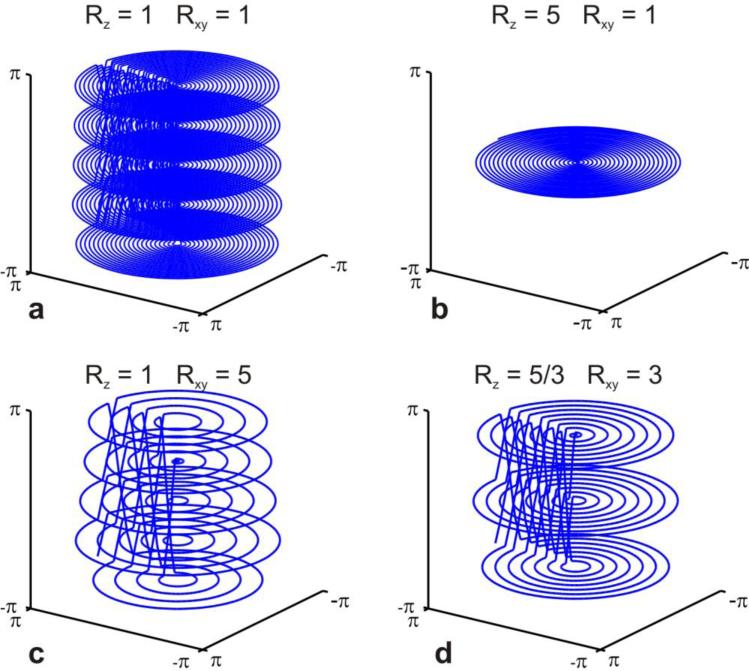
Figure 3 shows an example for N=5 slices and in-plane resolution N_xy = 48 in generalized k-space units. In Figure 3a full sampling is shown where each of the five k_z-planes contains a spiral with 24 revolutions. Figure 3b-d depicts different scenarios of in-plane acceleration versus slice acceleration, with a total acceleration factor of five in all cases. In Figure 3b only a single k_z-plane is sampled with 24 revolutions. This trajectory is fully sampled in the xy-direction and fivefold undersampled in the slice direction (R_z=5). Restoration of missing k-space points entirely relies on receiver coil sensitivity variation in the slice direction. In contrast, the trajectory in Figure 3c is fully sampled in the slice direction and five fold undersampled in the in-plane direction. No coil sensitivity variation in the slice direction is needed to restore missing k-space samples and therefore R_z = 1. A more practical distribution is shown in Figure 3d with threefold in-plane undersampling and an undersampling factor of R_z =5/3 in slice direction. This latter example is analogous to an SMS blipped-CAPIPI EPI acquisition of five simultaneous slices with a FOV/3 shift between neighboring slices (also referred to as blip factor 3).

Figure 3.

Full blipped-spiral sampling of five simultaneously excited slices is shown in a. The trajectory in b corresponds to five fold undersampling in the slice direction in contrast to c which can be seen as five fold undersampled in the k_xk_y–plane. A more practical example for an fMRI acquisition is shown in d where the total five-fold acceleration is more homogeneously distributed.

3. Material and Methods

3.1 Image acquisition

All experiments were performed on a 3T Tim Trio system (Siemens Healthcare, Erlangen, Germany) equipped with a 32-channel head coil array. Data were acquired in four healthy subjects after obtaining informed consent using an institutionally approved protocol. SMS excitation of N slices was performed using a windowed multiband sinc excitation pulse of 2.56 ms duration and with N frequency bands. The z-gradient blip waveforms were designed by employing a linear programming algorithm for optimal gradient waveforms (14) given a required k-space increment with gradient peak amplitude and slew rate constraints. For the 2D spirals optimal use of gradient slew rate was achieved by solving the differential equation describing the evolution of the slew rate vector (17). A spiral-in design was used because it offers optimal use of scan time and off-resonance behavior because the acquisition starts immediately after the excitation pulse and TE occurs at the end of the trajectory. To avoid peripheral nerve stimulation, the maximum slew rate for the design was set to 135 T/m/s. The imaging parameters for a given blipped-spiral implementation are presented below as needed. All blipped-spiral trajectories were designed off-line and uploaded to the pulse sequence. The image reconstruction was performed offline. All gradient waveform designs, as well as the image reconstructions and fMRI data analyses described below, were performed using Matlab (The Mathworks, Natick, MA).

3.2 Image reconstruction

The method of conjugate gradients and a nuFFT gridding algorithm were used to reconstruct the blipped-spiral images (www.eecs.umich.edu/~fessler/irt/irt). Since no additional regularization was employed, it closely follows the generalized SENSE approach described in (23). Coil sensitivity and off-resonance maps were derived from a dual gradient echo (GRE) pre-scan covering the entire FOV spanned by the SMS acquisitions (FOV = 192×192×96 mm³, TR = 168 ms,TE₁/TE₂ = 2.38/4.76 ms, flip angle 25 degrees). Off-resonance correction was implemented by a time-segmented formulation of the signal equation which approximates the continuous off-resonance induced phase evolution by piecewise constant phase maps and interpolates in between segments as proposed by Ref. (29). For this work Hanning window interpolation with ten time segments was used.

To examine the performance of the blipped-spiral trajectory three sets of images with the following parameters were acquired in a subject: (1) 3 mm isotropic resolution with FOV = 192×192×96 mm³, N = 8, TR = 168 ms, TE = 35 ms, R_tot = 5.1 and R_z =8/3; (2) 2.5 mm isotropic resolution with FOV = 200×200×100 mm³, N = 8, TR = 215 ms, TE = 35 ms, R_tot =6.4 and R_z =8/3; and (3) 2 mm isotropic resolution with FOV = 192×192×96 mm³, N = 8, TR = 294 ms, TE = 42 ms, R_tot = 7.5 and R_z = 8/3. Maps of the noise enhancement (g-factor maps) due to the accelerated imaging were then calculated using an approach inspired by the pseudo replica method in (26). For a given accelerated k-space trajectory and 32-channel sensitivity maps, the raw data vector was replaced by a noise vector with uniform noise distribution (drawn from the interval [-1; 1] assuming negligible noise correlation between coil elements) and reconstructed. This was repeated 50 times and the noise enhancement maps were given as the standard deviation of the noise for each pixel in the pseudo time series. In the same way noise enhancement maps were calculated for a non-accelerated blipped spiral trajectory which serves as a reference. The g-factor maps were then generated from the noise maps by pixel-wise division with the fully sampled noise map and accounting for the reduced number of sampled by dividing by the square root of the total acceleration factor. The g-factor maps then show the total noise enhancement relative to a fully sampled SMS 3D k-space and not only the contributions from multi-band acceleration.

3.3 Comparison between blipped-spiral and undersampled stack-of-spirals

The 3D k-space coverage of the blipped-spiral acquisition can also be accomplished by a single shot stacked-spiral trajectory (1). In that work it was shown that changing the phase encoding direction along z, the direction of the strongest off-resonance gradients (e.g. above the sinuses), reduces off-resonance induced signal loss and blurring. In order to compare the off-resonance behavior of the stacked-spiral approach with the proposed blipped-spiral approach, trajectories of equal sampling time and approximately identical k-space coverage where designed. Images were then acquired in a subject with the following parameters: FOV = 192×192×75 mm³, N = 5, TR = 200 ms, TE = 35 ms, R_tot = 4, R_z = 1. The trajectories are plotted in Figure 4c and g. In addition, g-factor maps for the stacked-spiral and the blipped-spiral images were calculated as described above. No off-resonance correction was employed in calculating the g-factor maps.

Figure 4.

A direct comparison between five simultaneous slices acquired with blipped-spiral and stack-of-spirals trajectories is shown. Both trajectories acquire approximately identical k-space samples and the acquisition times are both around 35 ms. Figures a and b show the blipped-spiral slices without and with the field map based off-resonance correction. Figure c shows the trajectory and d the g-factor maps. Corresponding figures for the stack-of-spirals trajectory are shown in (e-h) respectively. The off-resonance map is shown in i. All of the displayed slices are subject to off-resonance deviations that the field map based reconstruction mitigates to some degree in the blipped-spiral images. The stack-ofspirals acquisition however shows significantly distorted image quality compared to the blipped-spiral and the off-resonance corrected reconstruction is not able to improve the overall image quality. The g-factor values are comparably low for both trajectories.

3.4 Functional stimulation and statistical analysis

Two visual activations paradigms were used to evaluate the utility of the blipped-spiral SMS sequence. The first was a flickering checkerboard task with a total duration of 60 s. The task consisted of four blocks where each block consisted of 5 s of stimulation and 10 s of rest. During each stimulation period the subject was asked to perform bilateral finger tapping as well. In this manner the delay between the visual and motor responses could be measured. The functional images were acquired with 2 mm isotropic spatial resolution (FOV = 192×19×96 mm³, N=8, TR=294 ms, TE=42 ms, R_tot =7.5, R_z=8/3).

The second paradigm was for dynamic eccentricity mapping of the visual cortex (4). The stimulation consisted of expanding flickering rings (angular width 15°), with a periodicity of 18 s defined as the time from central to peripheral stimulation of the visual field (see Figure 8a). One time series consisted of five stimulation cycles resulting in a total scan time of 90 s. The functional time series was acquired using a FOV = 200×200×100 mm³, N=8, TR=215 ms, TE=35 ms, R_tot =6.7, R_z=8/3 resulting in 2.5 mm isotropic spatial resolution.

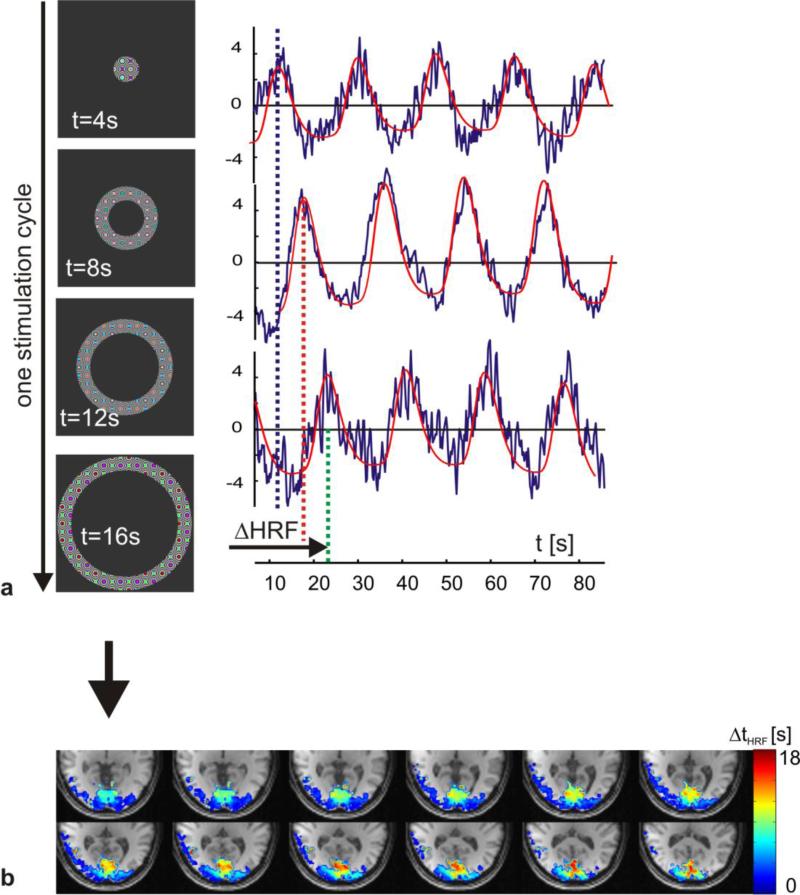
Figure 8.

This figure shows results from the dynamic eccentricity stimulation and mapping of the visual cortex fMRI experiments. The left column in figure a shows the temporal and spatial progression of the visual field stimulation. On the right three single voxel time courses corresponding to short, medium and long delay relative to the stimulation onset are shown. The horizontal lines indicate the time of maximum BOLD response, which is translated into a phase within one stimulation period. The BOLD delay relative to the stimulation onset can then directly be transformed into an eccentricity map of the visual cortex (b).

Prior to the activation analysis the reconstructed time series was spatially smoothed with an isotropic Gaussian filter (kernel width 5 mm) and slow drifts in the temporal domain were removed by subtracting linear and second order fits. No motion correction or realignment was performed. The ECG and respiration components of the time series were identified manually by performing a spectral analysis. The first and second order components were then removed by applying a notch filter in the spectral domain (filter width ±0.1Hz around each component's spectral peak). A general linear model (GLM) activation analysis was then performed with a canonical HRF, taken from SPM8 (www.fil.ion.ucl.ac.uk/spm/software/spm8) with default values, that was convolved with the stimulus onset function yielding the BOLD model function. The voxel-specific lag in the HRF delay was found by shifting the BOLD model in the GLM-analysis in steps of TR spanning ±10xTR and calculating the corresponding T-map for every delay. For every voxel the optimal HRF delay was assumed to be given by the highest T-value along the delay domain. The first 18 s of each time series were discarded to allow a transition into a steady state, both for the MR signal and the BOLD response.

4. Results

4.1 SMS imaging with blipped and stacked spiral trajectories

Figure 4 compares the five simultaneous slices acquired with the blipped-spiral trajectory (Figs. 4a-d) to the stacked-spiral approach (Figs. 4e-h). Figures 4a and 4b show the result of blipped-spiral acquisitions, reconstructed without and with off-resonance correction (ORC). The blipped-spiral trajectory is shown in 4c and the corresponding g-factor maps are shown in 4d. The stacked-spiral trajectory images are shown without (4e) and with (4f) off-resonance correction as well. The stacked-spiral trajectory and corresponding g-factor maps are shown in 4g and 4h. Data were acquired within a few seconds and the off-resonance maps displayed in 4i are hence valid for both scans.

The g-factor maps in 4d and 4h demonstrate that both trajectories experience very low additional g-factor penalty (around 10%) with slightly better performance by the stacked-spiral trajectory. One reason for the differences in g-factor penalty is the missing k-space samples during the transition period of the blipped spiral. The wedge shaped “holes” in k-space reduce the local sampling density and thus leading to increased g-factor noise. The total amount of off-resonance induced blurring should be approximately identical for both trajectories due to their similar lengths and sampling, however the stacked-spiral images show significantly more off-resonance artifact compared to those obtained using the blipped-spiral. In both cases off-resonance leads to a more pronounced blurring of the point spread function (PSF) along the k-space dimension that is acquired slowly over the entire duration of the acquisition. For the stacked-spiral trajectory, blurring is predominantly along the slice-select direction and for the blipped-spiral it is along the in-plane directions. In-plane blurring of neighboring voxels is a local effect reducing the effective spatial resolution, whereas the through-plane blurring of simultaneously excited slices is a non-local effect since neighboring slices in the reconstructed volume are generally from different regions of the brain up to several centimeters apart.

4.2 Accelerated imaging and g-factor noise

In Figure 5 shows the reconstruction of 35 slices with 3 mm isotropic resolution is displayed as an example of a typical fMRI scan in which off-resonance correction was performed. The parameters for the blipped-spiral trajectory were: FOV = 192×192×105 mm³, N=7, TR=205 ms, TE=35 ms, R_tot =7.5, R_z=8/3). The total acquisition time for one volume was 200 ms. Because of the relatively short readout time of only 35 ms, off-resonance induced signal loss and blurring especially above the sinuses is mostly suppressed.

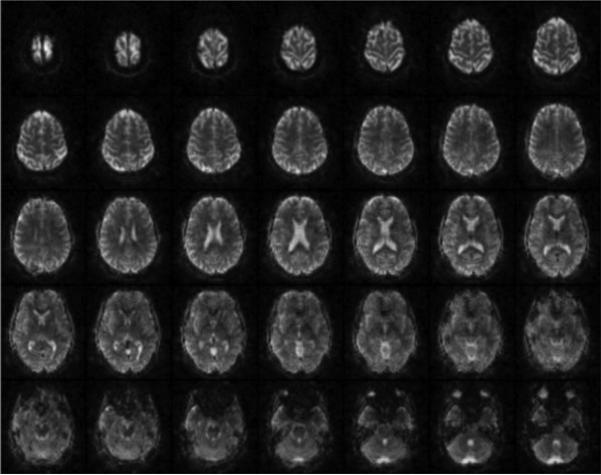
Figure 5.

This figure shows an example of 35 slices with 3 mm isotropic resolution acquired with five excitations in a total of 200 ms using an N = 7 SMS blipped-spiral acquisition.

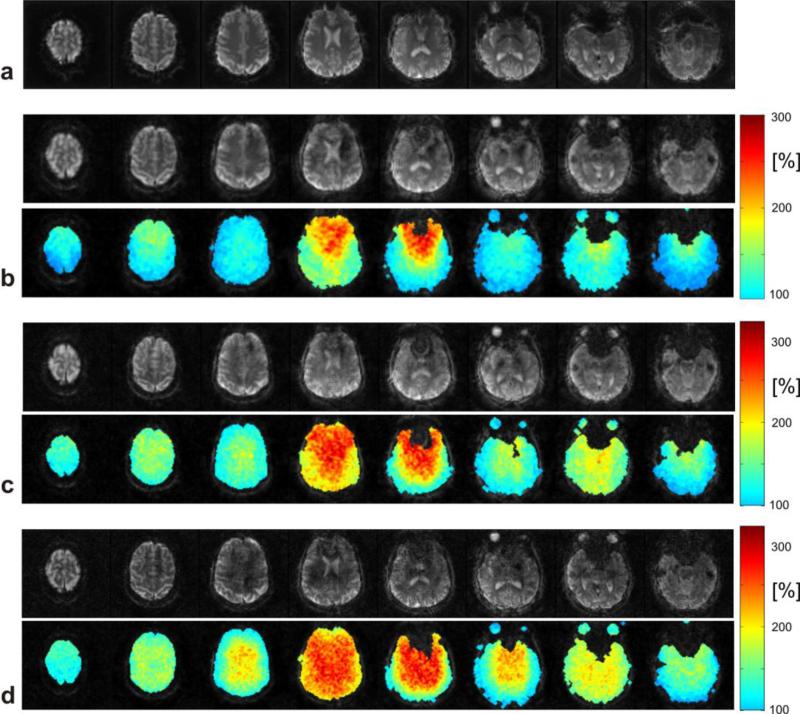
Figure 6 shows a comparison of images from different blipped-spiral acquisitions and the corresponding g-factor maps for completeness. The examples represent acquisition parameters that we found to be feasible for high temporal resolution fMRI applications. The scans covered a FOV_z of approximately 100 mm in the slice direction, which in most fMRI applications provides sufficient coverage of the brain yet does not cover the brain completely. The first row 6a shows eight fully encoded standard (N = 1) spiral reference slices with an isotropic resolution of 3 mm. Figure 6b shows eight slices out of the 32 acquired slices with 3 mm isotropic spatial resolution using the blipped-spiral trajectory. The g-factor maps are displayed below the slices and show pronounced noise enhancement only for the two inner slices. For Figure 6c the spatial resolution was increased to 2.5 mm. The g-factor maps now show increased noise as expected for a higher total acceleration factor. For 2 mm spatial resolution and 48 slices (Figure 6d) the acquisition time per excitation had to be increased to 42 ms to provide sufficient in-plane k-space sampling density due to the higher total acceleration factor. The g-factor penalty compared to the previous exampled is thus further increased. Despite the definition of in-plane and multi-band acceleration factors, in general, a g-factor map contains contributions from both sampling directions depending on the undersampling pattern of the 3D k-space. Especially for higher slice acceleration factors (>6) and additional in-plane undersampling, the 3D SMS k-space for both Cartesian and non-Cartesian sampling has the same properties as a regular k-space for 3D imaging.

Figure 6.

Images acquired with an N = 8 SMS blipped-spiral acquisitions with 100 mm brain coverage in the slice direction and their corresponding g-factor noise enhancement maps. Reference images from a fully sampled standard 2D spiral acquisition is shown in a. Blipped-spiral images with increasing spatial resolution over a fixed FOV are shown in b-d. In b images with a 3 mm isotropic voxel size with minimum TR of 168 ms are shown. Only the two middle slices experience significant g-factor penalty. For 2.5 mm and 2 mm (c and d) spatial resolutions the g-factor penalty increases as does the TR and the total acceleration factor (TR = 215 ms and R_tot = 6.4 for c; TR = 294 ms and R_tot = 7.5 for d).

The g-factor penalty generally is strongest in the center of the FOV as a result of the lower sensitivity variation of the receiver coil elements there. The higher g-factor values for the frontal regions of the brain can be explained with the opening of the helmet coil and the consequently lower coverage with individual coil elements.

4.3 Visual/motor fMRI

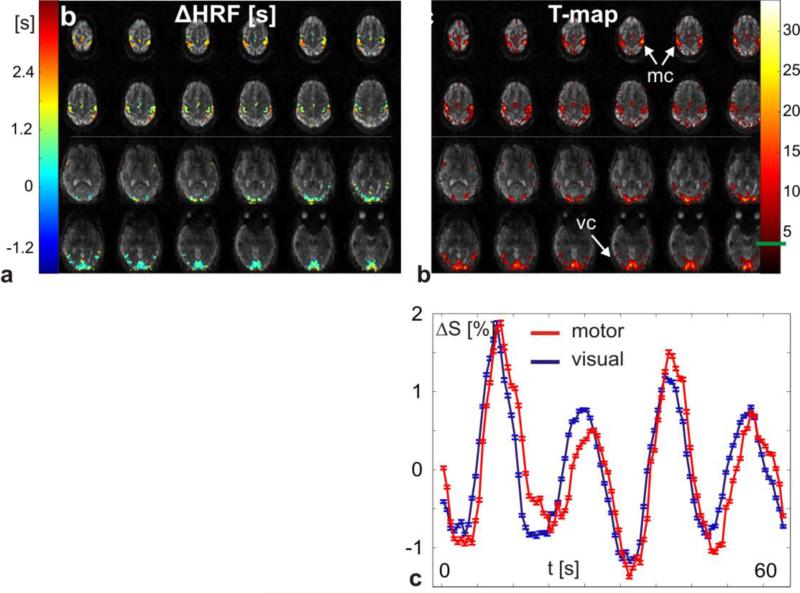
In Figure 7 the results from the flashing checkerboard visual/motor stimulation task are shown. The functional maps are overlaid on the first volume of the time series and only the top and bottom 12 slices are displayed. The relative HRF onset for the motor cortex in Figure 7a lags behind the visual cortex by 1-2s. The spatial variability of BOLD signal arrival times within the visual cortex was also previously shown in Ref. (32). The T-map corresponding to the GLM analysis with the optimal HRF delay is shown in Figure 7b with an uncorrected T-threshold of 4.5 (uncorrected p-value 0.000005). The average percentage BOLD signal time courses from the motor (red) and visual (blue) cortex in Figure 7c also display the relative temporal shift of the motor response. The error bars display the standard error of all voxels that were averaged.

Figure 7.

In this figure the results from the combined visual/motor flashing checkerboard fMRI task are displayed. In a, the HRF delay is plotted on top of the first reconstructed time frame of the time series (2 mm isotropic spatial resolution at TR = 294 ms). The uncorrected T-value (T-threshold 4.5) for the optimal delay is plotted in b. Average signal time courses (change relative to baseline) from the motor (red) and the visual (blue) cortex are plotted in c visualizing the delayed response of the motor cortex relative to the response of the visual cortex.

4.4 Dynamic eccentricity mapping fMRI

Figure 8 shows the results from dynamic eccentricity mapping. The left row of Figure 8a displays the temporal evolution of the flickering visual field stimulation pattern at various time points in steps of 4s. On the right, three voxel time courses together with the fitted BOLD response are plotted representing a short, medium, and long delay relative to the stimulation onset. The vertical dashed lines indicate the first maximum of the fitted BOLD model. Together with the intrinsic delay from the stimulation onset to the actual peak of the vascular response the phase of each voxel within the stimulation cycle can be calculated. Figure 8b shows a map of the measured delay within the stimulation cycle Δt_HRF overlaying a structural T1 weighted scan that was co-registered to the blipped-spiral fMRI data. The parametric map only shows voxels with an uncorrected T-value above the chosen threshold of five (uncorrected p-value 0.00000041). The range of Δt_HRF corresponds to one stimulation cycle (18s). The characteristic cortex representation of the visual field (posterior for the focal part of the visual field and anterior for peripheral stimulation of the visual field) is clearly visible in this single-subject data.

5. Discussion

In summary we presented a novel blipped-spiral sequence for SMS imaging for fast fMRI. The method only requires the addition of an alternating blipped z-gradient, which is a simple modification to a standard 2D spiral imaging sequence. We did observe some loss in image quality due to residual slice aliasing when compared to standard 2D spiral imaging as seen in Figure 6. Compared to a 2D spiral readout for SMS excitation, however, we found that considerably reduced g-factors and more homogeneous g-factor distributions are achieved by distributing the 2D spiral trajectory over multiple planes using the gradient blips in the slice direction to effectively sample an SMS 3D k-space. This SMS 3D k-space picture allows for the straightforward extension of non-Cartesian parallel imaging reconstruction methods to SMS imaging. Note that the SMS 3D k-space picture is completely general and applies to blipped-CAIPI EPI as well. The total spiral-in sampling duration and therefore the total in-plane resolution is restricted by the desired TE, which at 3 Tesla is approximately 35 ms for maximum BOLD contrast. For the case of a 32-channel coil we found that N =8 slices could be acquired simultaneously if the spiral trajectory is distributed over N_kz=3 k-space planes. If N is further increased more k-space sampling density in slice direction is required. This can be achieved by distributing the spiral over more than three planes at the cost of in-plane sampling density of each plane since the total number of spiral rotations is a constant. Whole brain acquisition times for 3 mm isotopic resolution were 168 ms without dramatic g-factor penalty using these parameters. For 2 mm isotropic resolution the acquisition rate was less than 300 ms, which is fast enough to at least capture the first harmonic of cardiac induced pulsatility. The imaging parameters for the examples shown were derived heuristically. A more optimal blipped-spiral trajectory certainly is a compromise between in-plane acceleration, number of slices, which affects the slice gap for a constant FOV in slice direction, and k-space sampling density in the slice direction.

We have also shown that SMS acquisitions in fMRI have the advantage of improved temporal resolution of the BOLD HRF. This was demonstrated with the visual/motor flashing checkerboard task as well as with dynamic eccentricity mapping of the visual cortex. An eccentricity map with distinctive spatial features can be acquired from a single subject in less than two minutes using the blipped-spiral SMS acquisition. Because of the proof-of-concept nature of this experiment we did not calibrate for locally varying vascular response delays by performing a second experiment with modified or inverted stimulation paradigm. The BOLD time courses in Figure 8 show the direct recording of the HRF response, which allows the extraction of locally varying features like onset time or variations in shape. This also shows how the high temporal resolution simplifies the analysis of dynamics within the functional response. No jittering or multiple repetitions, which are based on the assumption of identical responses to identical stimuli over the course of an experiment, need to be employed to indirectly measure BOLD latencies. We expect that blipped-CAIPI EPI methods will show similar results.

The main advantage of the spiral approach compared to EPI is that the gradient utilization is more efficient, making optimal use of slew-rate, and as a result spiral readouts are approximately 30% shorter when matched for coverage. Also the use of spiral-in makes use of all available time such that immediately after TE another group of simultaneous slices can be acquired. This produces improvement in the fMRI temporal resolution and increased sampling power. In terms of the maximum number of slices that can be acquired simultaneously using the blipped-spiral readout, we expect a very similar behavior as EPI based SMS approaches since both acquire the slice direction of k-space with Cartesian spacing. The main difference between spiral and EPI based acquisition is the PSF response to off-resonances. In EPI off-resonances lead to a shift of the PSF along the slow phase encoding direction, which can be corrected in a post-processing step after the actual image reconstruction. For spiral like acquisition the PSF experiences in-plane blurring which, if uncorrected, effectively reduces the spatial resolution. Additional acceleration in EPI can be also achieved using Partial Fourier techniques and Simultaneous Image Refocusing (SIR) (10). A direct comparison between spiral and EPI based acquisitions in terms of minimum volume TR however is beyond the scope of this work and needs to be investigated further.

Compared to other non-Cartesian 3D trajectories, like stacked-spiral approaches, the blipped-spiral trajectory avoids having the z phase encoding along the slice direction as the slow direction. Although blipped-spiral has the in-plane dimension as the slow direction, advancing from the periphery to the center of the 3D k-space leads to in-plane blurring in contrast to through-slice blurring as in the case of a stack of k-space planes that are acquired sequentially. The result is a significant improvement in image quality for the blipped-spiral trajectory compared to the stacked-spiral approach. The use of the spiral-in readout of only 35 ms duration keeps in-plane blurring at acceptable levels and contributes to the good overall image quality. We found no blipped-spiral g-factor improvement using the CAIPI style sampling compared to stacked-spirals, which actually showed slightly lower g-factors. This is likely due to the specific nature of spiral aliasing where the aliased signal is distributed over the complete FOV. Adding undersampled slices together therefore does not lead to a higher concentration of aliasing energy in the center of the image as in Cartesian sampling. Consequently, no improvement is expected by modifying the distribution of the spiral undersampling artifact in image space. The slightly higher g-factor for the blipped-spiral may be due to applying the z-gradients during the spiral readout creating unwanted undersampling. This g-factor penalty however is minimal compared to the gains in off-resonance robustness and blipped-spiral still produces images of superior quality compared to stacked-spirals. In practice it might be difficult to distinguish between pure g-factor effects on the image quality and signal dephasing due to local off-resonances when both effects have comparable magnitude. Furthermore recent work shows that off-resonance impacts g-factor measurements in phase constrained SMS reconstruction (2). Future investigation of the effects of off-resonance on SMS g-factor is needed. Additional improvements in image quality for high acceleration factors could be achieved by including regularization in the iterative image reconstruction (3, 15).

The temporal resolution for the blipped-spiral for a 3 mm isotropic voxel size is only reduced by approximately a factor of two compared to the reported values for single shot 3D k-space acquisitions (100 ms for the latter case). However, the gain in image quality, the drastically reduced signal loss around the sinuses, and the effective spatial resolution being close to the nominal resolution outweighs the loss of temporal resolution compared to 3D single shot techniques. For the 32-channel receive coil array with its circular distribution of coil elements a homogenous (under)-sampling of the SMS 3D k-space seems promising. An advantage of SMS methods over 3D techniques is also that the separation between slices is a more efficient use of coil sensitivity variations, which allows greater acceleration along the slice direction compared to the in-plane directions. Because of the low volume TR both 3D and SMS methods have some signal loss due to the lower Ernst flip angle (15 – 25°) compared to an fMRI sequence with higher TR. This loss of in-plane SNR, however, is compensated by the ability to remove the fast physiological noise components by direct filtering and therefore increasing temporal SNR and by the unique ability to directly record the voxel specific HRF.

The blipped-spiral technique also has the flexibility of utilizing more sophisticated spiral sampling strategies. For example, further reduction in both g-factor penalty and acquisition times with a minimized tradeoff in spatial resolution can easily be achieved by replacing the spiral-in trajectory with a variable density spiral-in trajectory (19) where the periphery of k-space is sampled less densely than the center of k-space. An even more sophisticated approach would also allow for variable density sampling along the slice direction which can be achieved by reducing the k-space increment in the slice direction as the spiral moves to the center of k-space. Furthermore, the trajectory's k_z-component (slice direction), which in the current implementation follows a Cartesian sampling pattern, can be replaced by a continuously oscillating gradient in the slice direction as done by (7). The effectiveness of these approaches, however, has to be further investigated.