The mutagenic footprint of low-fidelity Pol I ColE1 plasmid replication in E. coli reveals an extensive interplay between Pol I and Pol III

Abstract

ColE1 plasmid replication is unidirectional and requires two DNA polymerases: DNA polymerase I (Pol I) and DNA polymerase III (Pol III). Pol I initiates leading-strand synthesis by extending an RNA primer, allowing the Pol III holoenzyme to assemble and to finish replication of both strands. The goal of the present work is to study the interplay between Pol I and Pol III during ColE1 plasmid replication, in order to gain new insights into Pol I function in vivo. Our approach consists of using mutations generated by a low fidelity mutant of Pol I (LF-Pol I) during replication of a ColE1 plasmid as a footprint for Pol I replication. This approach allowed mapping areas of Pol I replication on the plasmid with high resolution. In addition, we were able to approximate the strandedness of Pol I mutations throughout the plasmid, allowing us to estimate the spectrum of the LF-Pol I in vivo. Our study produced the following three mechanistic insights: 1) we identified the likely location of the polymerase switch at ~200 bp downstream of replication initiation; 2) we found evidence suggesting that Pol I can replicate both strands, supporting earlier studies indicating a functional redundancy between Pol I and Pol III 3) we found evidence pointing to a specific role of Pol I during termination of lagging-strand replication. In addition, we illustrate how our strand-specific footprinting approach can be used to dissect factors modulating Pol I fidelity in vivo.

Introduction

ColE1 plasmids represent convenient models for mechanistic studies of DNA repair and replication. ColE1 replication requires the action of two DNA polymerases: DNA polymerase I (Pol I) and DNA polymerase III (Pol III). Here we use mutations generated by a low fidelity mutant of Pol I (LF-Pol I) to establish the relative contribution of Pol I versus Pol III to ColE1 plasmid replication and to estimate the mutation spectrum of Pol I in vivo. This approach can be used more broadly as a tool to dissect out genetic or physiological factors modulating the fidelity of error-prone polymerases in vivo.

ColE1 plasmid replication is unidirectional (Lovett et al. 1974; Martin-Parras et al. 1991). Replication is initiated by the transcription of a ~600 nt sequence known as the plasmid origin of replication (ori), generating an RNA pre-primer known as RNA II. Following processing of the 3′ end by RNAseH, the primer is extended by Pol I (Itoh and Tomizawa 1979). This extension initiates leading-strand synthesis, and facilitates replisome assembly by exposing a primosome assembly signal on the leading strand (Masai and Arai 1996). Once assembled, at a point known as “polymerase switch”, the replisome finishes replication of both strands.

A critical component of the replisome is the Pol III holoenzyme (Pol III HE). This complex contains two core subassemblies. Each core subassembly consists of three tightly bound subunits: α (dnaE, the DNA polymerase), ε (dnaQ, the 3′→5′ proofreading exonuclease), and θ (holE, stabilizer for the ε subunit). The two cores are connected by a linker subunit (τ), creating a dimeric polymerase unit that replicates both strands of the DNA duplex coordinately at high speed (for reviews see (Langston et al. 2009; McHenry 2011)).

While leading-strand synthesis by the Pol III HE is continuous, by elongation of the Pol I-synthesized leading-strand, the lagging strand is synthesized in fragments that are assembled together. The DnaG primase synthesizes short RNA primers that are elongated by Pol III; when Pol III reaches the end of the Okazaki fragment, it is replaced by Pol I, which removes the RNA primer through its 5′→3′ exonuclease activity and fills in the remaining gap. Fluorescence localization of tagged core Pol III subunits using single- molecule microscopy during replication in living E. coli cells indicates that a new Pol III molecule is used for each Okazaki fragment (Lia et al. 2012).

We previously created a low fidelity variant of Pol I (LF-pol I) by mutating three key determinants of fidelity: I1709N in motif A, A759R in motif B, and A424D in the proofreading domain (Camps et al. 2003). Expression of this variant in JS200 cells, a polA12 (Pol I temperature-sensitive) strain of E. coli, under restrictive conditions leads to the introduction of random mutations during ColE1 plasmid replication (Camps et al. 2003). Based on the mutation frequency of LF-Pol I mutagenesis, 3–4 orders of magnitude above spontaneous mutagenesis, we can assume LF-Pol I replication to be the source of the vast majority of mutations included in this analysis.

In a previous article (Allen et al. 2011), a thorough analysis of the footprint of error-prone Pol I replication of ColE1 plasmids allowed us to establish the following: 1) that Pol I replication extends well beyond the ~100 nt of RNA II primer extension reported in vitro; 2) we found the likely location of Okazaki processing sites on the lagging strand of the plasmid; 3) we estimated the extent of 5′→3′ exonuclease processing by Pol I at Okazaki processing sites to be ~20 nucleotides.

The main limitation of our previous article was our inability to resolve strandedness down to the level of individual mutations. All we could say was that mutations were more likely to correspond to leading or lagging strand, based on an asymmetric representation of complementary pairs. Here we refine our original approach by estimating the mutation spectrum of LF-Pol I on the leading strand and by using that information to resolve the strandedness of the remaining mutations. Reasoning that the mutation spectrum is an intrinsic property of the polymerase, we validated our approach by deriving comparable mutation spectra from either strand and before and after the polymerase switch.

Our current analysis identifies the location of the polymerase switch 170 to 250 nt downstream of DNA replication initiation. Downstream of the polymerase switch, the mutation footprint of Pol I replication shows little strand preference, suggesting Pol I may be capable of coordinated double-strand replication. This observation is consistent with previous reports of a functional redundancy between Pol I and the α subunit of Pol III (Maki et al. 1989). In addition, at the 3′ end of plasmid replication we discovered a clear bias for lagging-strand synthesis, pointing to a role for Pol I in termination of lagging-strand replication.

Results

Replication of a neutral sequence by LF-Pol I generates random mutations whose distribution identifies Pol I templates with high resolution (Allen et al. 2011). The main limitation of this polymerase template-mapping approach is our inability to identify the strand where mutations originally occurred. In a previous article, we addressed this problem using biases in the distribution of complementary mutations to define probabilistic markers, i.e. markers that indicated a higher probability of originating in one strand vs. the other (Allen et al. 2011). For each complementary pair, the most frequent mutation (A→G; C→T; A→T; G→T) was designated as a marker for leading-strand synthesis and the least frequent, complementary mutations (T→C; G→A; T→A; C→A), as markers for lagging-strand synthesis. Combined with a clustering analysis of marker lagging-strand mutations, this approach identified sites of Okazaki primer processing by Pol I. However, without knowing the mutation spectrum of LF-Pol I on a single strand, we were unable to adequately interpret the mutation footprint outside areas of Okazaki primer processing.

Here our goal is to use LF-pol I mutations outside of Okazaki processing sites to discriminate between Pol I and Pol III synthesis during ColE1 plasmid replication. The present analysis includes two new libraries: one targeting GFP and another one targeting human ALKBH1. These libraries are of high quality because they underwent multiple rounds of mutagenesis (n=4), which increases the mutation density and facilitates the identification of Okazaki processing sites (Allen et al. 2011), and because they involve sequences that are neutral, i.e. sequences that provide no significant fitness advantage or disadvantage to the host. The sequence coverage for these libraries on their respective plasmids is shown in Fig. 1 and their metrics are summarized in Table 1. The new LF-Pol I mutagenesis data can be found in Suppl. Table 1, broken down by individual clones. In addition, our previously reported GFP library (Allen et al. 2011) was also included in the present analysis (Table 1).

Fig 1. Sequence coverage.

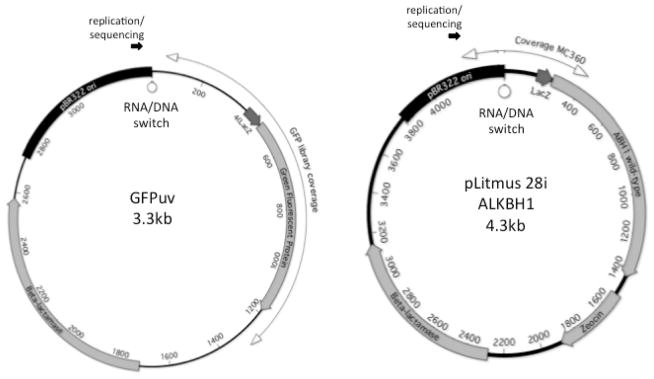
The sequence coverage for the two libraries presented here is shown on a circular representation of the plasmid showing ORFs, Col E1 plasmid origin of replication, and point of replication initiation a. GFP library. b. ALKBH1 library.

Table 1.

Metrics for the libraries included in this study.

Library	Form	# cycles	# clones	Coverage (kbp)	# mut	Mut frequ x103	Mut freq/cycle
GFP-A	Suspension	1	154	305	184	0.60	0.60
GFP-B	Suspension	2	185	55.9	55	0.98	0.49
GFP-C	Colony	4	105	116.7	262	2.24	0.56
ALKBH1	Colony	4	120	80.2	272	3.39	0.85
Total plankt.				360.9	239
Total colony				116.7	522
Total				477.6	761

We found little evidence of clonal selection in our GFP or ALKBH1 libraries, confirming that these genes represent largely neutral targets in our system.

In addition, generating a footprint for Pol I replication requires a random distribution of mutations along the sequence. We investigated the spatial distribution of mutations by calculating an index (which we named hotspot index) that measures local clustering of mutations (Methods; Suppl. Fig. 1). In both libraries we found strong evidence of mutation clustering (Suppl. Fig. 2). The local sequence in these areas of decreased Pol I fidelity is shown in Suppl. Table 2. These hotspots tend to be GC-rich, with fifteen of these sites (out of a total of twenty) occurring in runs of three or more C or G residues. We also found one recognizable motif: 5′-CCA/TA/T-3′, which is found in seven of the hotspots. Given the non-random spatial distribution of these mutations (with multiple hits in the same or adjacent positions) and their apparent sequence-context dependence, mutations in these clusters were analyzed separately.

Our clustering analysis aimed at identifying potential Okazaki Processing Sites (OPS)(Allen et al. 2011) identified the following candidate OPSs in our new GFP library: positions 179–191; 559–578; 910–926; and 1035–1045 (sites I–IV in Suppl. Fig. 3a). Of these, site I (comprising positions 179–191) is likely artifactual because it falls squarely in a mutation hotspot as defined in Suppl. Fig. 1a and it does not show the same level of enrichment for lagging-strand mutations seen in the other three sites (Suppl. Fig. 3b). For the remainder of the analysis, we considered only sites II, III and IV as legitimate Okazaki processing sites. These sites were removed from our replication footprint, as they are associated with a separate role of Pol I in plasmid replication (processing of Okazaki primers).

Fig. 2 shows the ratio of leading-strand vs. lagging-strand marker mutations at 50nt intervals for the whole area of coverage for the GFP and ALKBH1 libraries (Fig. 2a and Fig. 2b, respectively). In our GFP libraries, we noticed an area (between positions 70 and 170) where the ratio between marker leading- and marker lagging-strand mutations, is extraordinarily high, in the order of ten-to-one (dark grey arrows). This trend encompassed all complementary pairs, suggesting that this unique distribution of mutations is likely attributable to strand preference. Indeed, we found a similar area of very high (>10-fold) bias in our new ALKBH1 library (dark grey arrow), which has a different sequence than the GFP library at these positions, confirming this bias is independent of sequence context. We interpret the end of the high bias for leading-strand synthesis as indicative of the polymerase switch (inverted, white triangle). In addition, we found an area of substantial bias for leading-strand replication in our ALKBH1 library, indicated with white arrows (Fig. 2b).

Fig. 2. Ratio of leading-strand vs. lagging-strand marker mutations.

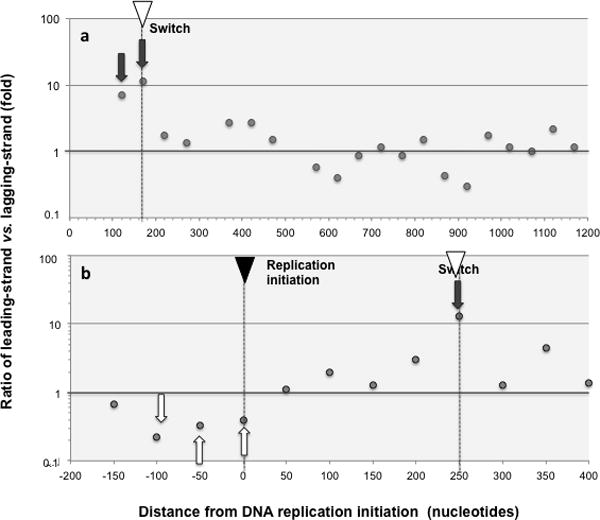
Ratios of marker leading- versus lagging-strand mutations (as defined in Methods) are shown for 50 nucleotide intervals at increasing distance from replication initiation. Only intervals with at least 10 mutations are shown and hotspots, defined as areas with 5 or more mutations in the same or contiguous positions (Methods) were removed. On the X-axis the number means the end of the interval, so “50” means 0–50 sequence interval, and “− 200” means −250 to −200 sequence interval. The location of DNA replication initiation and switch are indicated with a black and a white inverted triangle, respectively. Areas of high bias for leading-strand replication are highlighted with dark grey arrows, and high bias for lagging-strand replication with white arrows. Mutation hotspots and OPS were removed prior to the analysis (Methods) a. GFP libraries. Both liquid and solid plate libraries are included. The following 3 (out of 21) intervals comprised fewer than 10 mutations and were excluded from the analysis as unrepresentative: 470–520, 1170–1220 and 1220–1270. b ALKBH1 library.

Beyond the putative polymerase switch, the ratio of marker leading vs. marker lagging strand mutations for the GFP library stayed around 1. The average leading vs. lagging strand ratio over 18 intervals was 1.3, with a standard error of 0.33 (Fig. 2a). In addition, we did not detect a statistical difference in the absolute frequency of Pol I mutagenesis between leading and lagging-strand mutations in the area beyond the putative switch (p value for Wilcoxon test=0.2). These results indicate that Pol I does replicate plasmid sequence beyond the switch, and strongly suggest that Pol I has little strand preference in this area of sequence. An average above 1 (1.3) may indicate a slight preference for leading-strand synthesis but this observation doesn’t detract from the conclusion that both strands are being replicated in this area.

Finally, we found another sharp change in the leading vs. lagging-strand mutation ratios at the end of directional plasmid replication, going from close to 1 (no strand preference) to strongly below 1 (predominantly lagging; Fig. 2b, white arrows). This new switch in strand specificity is likely associated with replication termination and points to a special role of Pol I during lagging-strand synthesis in this area (see Discussion).

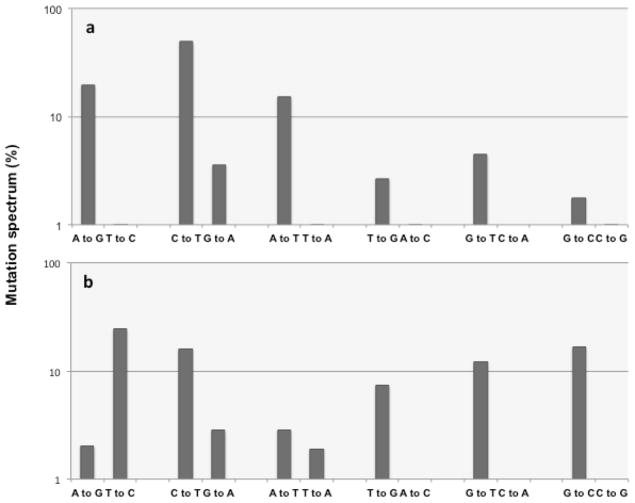
Given a representative sample size, if both strands are replicated with comparable frequency, each mutation of a complementary pair should be equally represented (Fig. 3). The strong bias for marker Pol I leading-strand mutations upstream of the polymerase switch suggests that in this particular section of sequence Pol I plays little or no role in lagging-strand replication. Therefore mutations found in this section of sequence likely represent the mutation spectrum of the LF-Pol I polymerase on a single-stranded template in vivo. This inferred spectrum of LF-Pol I in live cells is shown in Fig. 4a, with individual mutations grouped by complementary pairs in order to facilitate seeing differences indicative of possible strand bias. For comparison, Fig. 4b shows the mutation spectrum reported for proofreading-deficient (Pol I exo-) mutant in vitro (Bebenek et al. 1990). The overall profile is consistent between the two error-prone Pol I mutants, with the A→G/T→C pair being the only clear exception (see Discussion).

Fig. 3. Rationale for determining strand specificity based on frequency of complementary mutations.

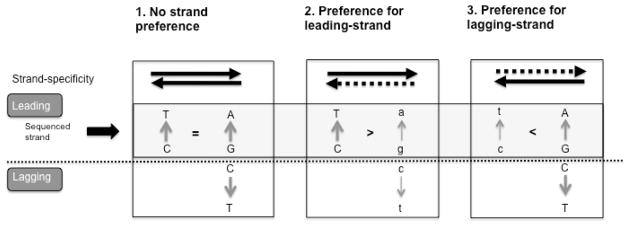
C→ T is shown as an example. If the error rate of the polymerase for C→ T ⋙ G→ A, leading-strand mutations appear as C→ T and lagging-strand mutations as G→ A. The frequency of complementary strand mutations is indicative of the strand preference of the polymerase: individual C→ T mutations approximating leading-strand replication, and individual G→ A mutations approximating lagging-strand replication. This is in contrast to the scenario where C→ T >G→ A, in which case C→ T is only more likely to be leading-strand but not an unambiguous marker of strandedness, since it can also correspond to a G to A in the lagging strand. In either case the ratio of C→ T vs. G→ A can be used then to establish the strand preference of the polymerase. Three scenarios are shown: 1) no strand preference; 2) preference for leading-strand; 3) preference for lagging-strand. Both strands are shown, and the light grey box highlights the leading (sequenced) strand. Dashed lines represent decreased replication preference. Mutations introduced during replication of the non-preferred strand are denoted in small letters.

Fig. 4. Mutation spectrum for error-prone Pol I.

a Area of high leading-strand replication bias. Each complementary pair is shown on the x-axis, with the frequency of occurrence (%, in logarithmic scale) on the y-axis. The mutations include GFP and hTK libraries generated in suspension culture described in (Allen et al. 2011) (n=33 and 30 mutations, respectively), and GFP and ALKBH1 libraries generated on solid plates (n=20 and 40 respectively). Hotspots, defined as areas with 5 or more mutations in the same or contiguous positions (methods) were excluded form this analysis. b. In vitro fidelity of 3′→5′ exo domain-knockout is shown for each complementary pair, as reported in (Bebenek et al. 1990). In order to facilitate visual comparison with panel a, mutation frequencies are expressed as percentage, in logarithmic scale.

Note the sharp differences in frequency found between the complementary pairs. In the case of LF-Pol I (Fig. 4a), the differential representation between the three most abundant mutation pairs (A→G/T→C; C→T/G→A; and A→T/T→A), is dramatic: between 10- and 20-fold. This strong bias between complementary pairs means that certain mutations can now be approximated to be physical indicators of strandedness, with the most frequent mutation of the pair representing leading-strand synthesis and the other partner representing lagging-strand synthesis. This concept, originally used by Dr. Buehler to study directional evolution in vertebrate genomes (Albrecht-Buehler 2009) is illustrated in Fig. 3 for the C→T/G→A complementary pair. If the frequency of C→T mutations introduced by the polymerase is much higher than that of G→A mutations, and the sequenced strand is the leading strand, C→T mutations can be approximated to indicate leading-strand synthesis and G→A mutations to indicate lagging-strand synthesis. The same applies to other complementary pairs with strong differences in frequency.

We reasoned that since the mutation spectrum is largely an intrinsic property of the polymerase, we should derive a consistent mutation profile regardless of strand or section of the plasmid considered. Specifically, we made the following three predictions:

1. The leading-strand mutation spectrum should be comparable regardless of whether the spectrum is derived from mutations occurring before of after the polymerase switch.

2. The mutation spectrum derived from lagging-strand sequence should be consistent with the spectrum derived from leading-strand sequence.

3. Perturbing the mutation spectrum of the polymerase should produce consistent changes across the three sequence compartments: 1) leading strand before the polymerase switch, 2) leading-strand downstream of the switch, and 3) lagging-strand downstream of the switch.

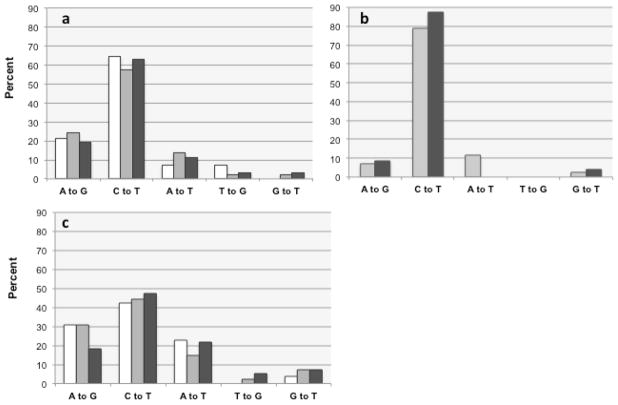
Fig. 5a compares the mutation spectra of GFP derived from three different areas of sequence: leading before polymerase switch (white columns), leading-strand after the switch (light grey columns), and lagging-strand after the switch (dark grey columns). The results are strikingly similar in all three areas, with C→T representing around 60% of the total, A→G ~20%, A→T ~10%, and the remainder constituting <5%. Fisher’s exact test confirms that there is no statistical difference between the spectra derived from leading before switch, leading after switch, and lagging after switch sequence (p values=0.94), thus confirming predictions #1, and #2. In the hotspots, we find a different mutation profile, with a stronger predominance of C→T mutations (80%) at the expense of A→G mutations, which represent less than 10%. However, again we derive very similar numbers from either strand, further supporting the accuracy of our strand mapping (Fig. 5b).

Fig. 5. Concordance between mutation spectra.

The relative proportion of indicator leading-strand mutations inferred from our analysis is shown, in percentage, as derived from leading-strand sequence before functional replisome assembly at position 170 (white columns), from leading-strand sequence after assembly (light grey columns), and for lagging- strand sequence (dark grey) a. Plate mutagenesis protocol, excluding hotspots and OPS; n=17 (<170), n=155 (>170 leading), n=62 (>170 lagging). b Plate mutagenesis protocol, hotspots only, excluding OPS; n=69 (>170 leading), 25 (>170 lagging). c. Suspension culture mutagenesis protocol, excluding hotspots and OPS; n=26 (<170), 139 (>170 leading), 55 (>170 lagging).

To test prediction #3, we reasoned that growth conditions might affect the fidelity of LF-Pol I in vivo. We compared our new GFP library (generated using a solid plate protocol), to our original random mutant libraries generated in cultures grown in suspension in liquid media. While the overall mutation frequency was comparable in both libraries (Table 1), we did detect significant differences in the mutation spectrum: in our liquid culture libraries, C→T mutations represented only ~40% of the total (compared to 60% for cells grown as colonies), while the representation of A→G and A→T mutations increased substantially, from 20 to 30% and from 10 to 20%, respectively. Differences in spectrum between the two libraries were confirmed statistically using the Fisher’s exact test (p=0.046). Notably, comparing liquid and solid libraries, we observed again consistent differences in the mutation spectrum of LF Pol I regardless of whether we looked at mutations on the leading-strand before the polymerase switch or at mutations on either strand downstream of the polymerase switch (Fisher’s exact test p value 0.74; Fig. 5c). A shift in mutation spectrum upon perturbation of polymerase fidelity in vivo that is consistent across strands and areas of sequence neatly confirms prediction #3.

Our ability to derive a consistent mutation spectrum regardless of strand or section of sequence (predictions #1,2), and observing a consistent shift in the mutation spectrum upon perturbation of replication fidelity (prediction #3) support the accuracy of our strand mapping approach. Finally, our ability to detect subtle differences in replication fidelity produced by changes in culture conditions illustrates how our mutation footprinting approach can be used as a tool to dissect genomic and physiologic variables modulating Pol I fidelity in vivo.

Discussion

The present work is based on random mutant library data generated by LF-Pol I replication of a ColE1 plasmid. Based on the high frequency of LF Pol I mutagenesis (3 to 4 orders of magnitude above spontaneous mutation levels), and on the fact that the observed mutation frequency in vivo correlates with the fidelity of Pol I in vitro (Shinkai and Loeb 2001), the primary source of mutations in our system can be assumed to be error-prone Pol I replication. The spectrum of LF-Pol I mutations we see in vivo, however, has in all likelihood been modulated by mismatch repair (MMR) and possibly other proofreading mechanisms operating in live cells.

While the MMR capacity of the cell can be depleted by extensive mutagenesis (Schaaper and Radman 1989), specially under conditions of prolonged starvation (reviewed in (Foster 2007; Galhardo et al. 2007)), two lines of evidence argue for the presence of significant MMR activity in our LF-Pol I expressing cells: (1) We see a very low frequency of T→C transitions (Fig. 4a); given that these transitions are the most frequent mutations made by exo- Pol I in vitro (Fig 4b) and are also the preferred substrate for MMR in E. coli (Lee et al. 2012), our observations strongly suggest active A:T→G:C proofreading by MMR. (2) We see a very low frequency of insertions and deletions (<1%), even when hotspots are included; this observation again points to significant MMR activity, as one of the functions of MMR is postreplicational control of frameshifts caused by polymerase slippage in repetitive sequences (Drotschmann et al. 1999; Schaaper 1993), with mismatch repair-deficient strains typically showing a high frequency of frameshifts (>10%) (Lee et al. 2012; Schaaper 1993). The presence of MMR activity in our model system, however, would be unlikely to affect our analysis, as mismatch repair should not depend on strand or distance from the plasmid origin of replication.

To use LF-Pol I mutations as a footprint for Pol I replication, areas of unusual mutation density needed to be analyzed separately as unlikely to be representative of baseline errors made by the polymerase. We identified these areas by defining a hotspot index that measures local mutation density (see Methods), and finding clusters deviating from the expected distribution (Suppl. Fig. 2). The mutation spectrum of the polymerase at these sites differed from the spectrum elsewhere, with a with a stronger predominance of C→T mutations (80% compared to 60%) at the expense of A→G mutations (7% compared to 20%), supporting the unusual character of these mutations.

The mutation clusters we identified (15 for the GFP library and 5 for our ALKBH1 library) are listed in Suppl. Table 2. Each cluster comprises a moderate number of mutations, with an average of 9 mutations per cluster and a standard deviation of 2.5. We also found an overrepresentation of GC runs and of the CCA/TA/T motif. This profile suggests that our hotspots correspond to areas of moderate sequence instability that is at least partially dependent on local sequence context.

We also mapped the presence of Okazaki processing sites in our GFP library to distinguish mutations originating from Okazaki primer processing from mutations generated by Pol I extension. Our new analysis confirmed two of the four Okazaki processing sites in pGFPuv plasmid sequence tentatively identified in our previous study: II (at positions 559–578) and IV (at positions 1035–1045) (Allen et al. 2011). Our analysis also identified a new candidate Okazaki processing site (site III), at positions 910–926. The new site is less than 100 nt away from site IV, and may represent an alternate location for that site.

A key finding of the present work is a ~100 nt area of leading-strand that appears to be replicated exclusively by Pol I (Fig. 2, dark grey arrows). The mutation spectrum for LF-Pol I in this section of sequence is highly biased between complementary pairs, allowing us to approximate mutations to strandedness indicators. The resulting strand-specific mutation footprint of LF-Pol I is diagrammed in Fig. 6. Based on the ratio of leading vs. lagging-strand mutation, we found three distinct areas: 1) sequence close to plasmid replication initiation (up to position ~200), with a clear predominance of leading-strand mutations; 2) most of the remaining sequence, which shows little strand bias; and 3) an area associated with replication termination, where we see a clear predominance of lagging-strand mutations.

Fig. 6. Footprint of LF-Pol I plasmid replication.

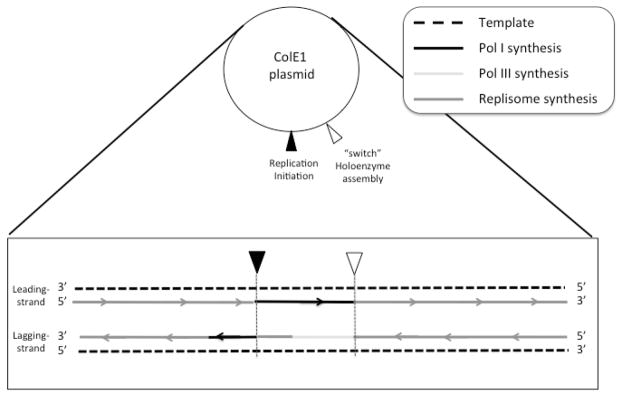
Mutation patterns are mapped on each strand of a generic ColE1 plasmid. The points of replication initiation and Pol III holoenzyme assembly are indicated with inverted triangles. Replication is shown as solid lines, with arrows pointing the direction of replication. Dark grey lines represent areas of no significant strand bias. Black lines represent Pol I replication in areas showing significant Pol I strand bias. During replication initiation, lagging-strand synthesis is attributed to Pol III, to the α subunit or to the lagging-strand core subassembly before complete assembly of the Pol III replisome (light grey line), beginning at the switch but not extending on the leading strand all the way to the point of DNA replication initiation in the 5′ direction. During termination of DNA synthesis, a bias for lagging-strand synthesis is attributed to filling of a gap left by premature disassembly of the holoenzyme.

The practical absence of Pol I lagging-strand mutations in an ~100 nt area of sequence close to replication initiation suggests that Pol III may be taking over lagging-strand replication in this section of sequence. How it does so is unclear, since the Pol III HE generally replicates both strands. Pol III replication here may involve the Pol III HE subassembly responsible for lagging-strand replication, suggesting this subassembly may assemble earlier than the core subassembly responsible for leading-strand synthesis. Alternatively, the polymerase subunit of Pol III (α) may be responsible for the replication of this stretch of sequence on its own. Given this ambiguity in Fig. 6, this area has been designated as “Pol III” to distinguish it from “Pol III HE” replication.

A second area of strand bias for LF-Pol I that we identified is the end of directional replication of the plasmid. In this case, lagging-strand mutations are the predominant type (Fig. 2b, white arrows), suggesting a special role of Pol I during termination of lagging-strand synthesis. Pol I may be involved in resolving gaps produced by asynchronous termination between the two strands. If leading-strand replication was completed first, disassembly of the Pol III HE would leave a gap in the lagging strand. Given that Pol I is a polymerase specialized in short-gap repair (Lieb and Bhagwat 1996; Savic et al. 1990), a gap-filling role during termination of ColE1 plasmid replication is a very plausible mechanism to account for the observed lagging-strand template preference at the end of directional replication of the plasmid.

Downstream of the putative polymerase switch, we found that LF-Pol I replication produces mutations in both strands with comparable frequency (Fig. 2), strongly suggesting that in this area Pol I shows little strand preference. Extensive double-stranded plasmid replication by LF-Pol I likely accounts for the remarkably balanced base pair substitution profile reported for LF Pol I-generated libraries (Wong et al. 2006) despite the imbalanced spectrum reported in vitro for Pol I exo- (Bebenek et al. 1990) and inferred in vivo in this work. For example, on a given strand LF-polymerase makes almost exclusively C→T mutations, but since at the same time the polymerase makes a comparable number of G→A mutations when it replicates the opposite strand, a balanced representation for this complementary pair is achieved (Fig. 3). Thus, for polymerases that replicate both strands of DNA, achieving a balanced mutation spectrum only necessitates a high frequency of mutation of one nucleotide substitution for each complementary pair. It would be surprising if this strategy for achieving a balanced generation of genetic diversity hasn’t been exploited more often in nature.

The most parsimonious explanation for double-stranded replication by Pol I is the functional incorporation of Pol I into the Pol III holoenzyme. This proposition is supported by three types of arguments: (1) It is hard to envision a mechanism that would produce balanced double-strand synthesis without any coordination between synthesis of the two strands; the Pol III HE has the molecular machinery already in place for the coordinated replication of the two strands. (2) Topologically, the change in Pol I template preference coincides with the polymerase switch, suggesting that double-strand replication by Pol I and Pol III HE assembly may be mechanistically linked (3). There are precedents for polymerase exchanges during DNA replication: examples of this “polymerase tool belt” scenario include Pol II, Pol IV and Pol V (reviewed in (Fijalkowska et al. 2012; Sutton 2010)). While these examples involve highly localized transactions in the context of tolerization to DNA damage, the earlier observation that Pol I is essential for survival in the absence of a functional Pol III α subunit (Maki et al. 1989), is consistent with the idea that Pol I can functionally replace the polymerase subunit of Pol III during normal replication. We ignore the functional significance of Pol I double-stranded replication since it appears to be redundant with Pol III HE replication. Since our libraries were generated in saturated cultures, the apparent partial functional replacement of Pol III by Pol I may be a component of a more general stress response of cells under conditions of starvation.

A critical test for our approach for generating a strand-specific mutation footprint was showing that we derive the same spectrum (which is likely an intrinsic property of the polymerase) from either strand. We also derived a consistent spectrum from sequence before and after the polymerase switch. In addition, perturbations in polymerase fidelity produce consistent changes regardless of the section sequence the spectrum is derived from (Fig. 5a,c). These striking results strongly support our strand-specific footprinting approach.

We found that changing culture conditions from growth in the structured environment of a colony to growth in planktonic form produces a shift in the mutation spectrum of LF-Pol I without substantially changing the mutation frequency. Differences in mismatch repair capacity or in levels of genotoxic stress are likely between these two culture conditions (Boles and Singh 2008; Conibear et al. 2009; Foster 2007; Galhardo et al. 2007). However, if Pol I is the primary source of mutations, the observed shift in mutation spectrum may reflect physiological factors directly modulating the fidelity of the polymerase such as differences in dNTP pools, whose effect on replication fidelity in vivo has been elegantly established through ribonucleotide reductase overexpression (Gon et al. 2011).

In sum, we found a way to estimate the strand-specific mutation footprint for LF-Pol I in vivo. This approach provided new insights on the role of Pol I in the cell, strongly suggesting that Pol I can replicate both strands downstream of the switch and that it likely plays a role during termination of lagging-strand plasmid replication. Finally, we provide an example to illustrate how our approach can be used more generally to investigate the impact of genomic and physiologic variables on the polymerase fidelity of Pol I in vivo.

Methods

Bacterial strains

JS200 (SC-18 recA718 polA12ts uvrA355 trpE65 lon-11 sulA1) cells were used as our host strain. The polA12 allele encodes a point mutation in Pol I (G544D) that likely interferes with the coordination between the polymerase and the 5′→3′ exonuclease activities (Camps and Loeb 2005). This Pol I mutant exhibits reduced temperature stability and activity at 42 °C (Uyemura and Lehman 1976). RecA718 is a sensitized allele of RecA, resulting in SOS induction under conditions that are restrictive for polA12 (Fijalkowska et al. 1989).

Plasmid constructs

Our mutagenic plasmid expressing LF-Pol I (muta-plasmid) was generated by cloning of the Pol I sequence bearing the three low-fidelity mutations (I709F A759R D424A) into pHSG576 (a pSC101 plasmid) between the HindIII/EcoRI restriction sites, and bears chloramphenicol resistance (Shinkai and Loeb 2001). pGFPuv (with carbenicillin resistance) was obtained from Clontech (Mountain View, CA). The pLitmus ALKBH1 plasmid was generated by cloning the ALKBH1 cDNA sequence (GenBank: BC025787.1) into the multi-cloning site of the pLItmus 28i vector between the XhoI/HindIII restriction sites.

Media and Supplies

LB Agar and LB broth were purchased from Fisher Scientific and prepared according to vendor specifications. Some mutagenesis experiments were carried out in 2XYT rich media containing 0.016g/ml Bacto Tryptone, 0.01g/ml Bacto Yeast Extract and 0.005g/ml NaCl suspended in deionionized water. The antibiotic concentrations used for marker selection are: 30μg/ml (chloramphenicol), and 100μg/ml (carbenicillin). All DNA isolation procedures were performed using Machery Nagel’s Nucleospin Plasmid miniprep. Sequencing was carried out by Sequetech (Mountain View, CA) using the following sequencing primers; attP2 (CAGGAAACAGCTATGAC) and Blac5 (TTACGGTTCCTGGCCTTTTGC) for pGFPuv and MC360 (CTTGCCACTTGCTGACGG) for ALKBH1 libraries, respectively.

Error-prone pol I Mutagenesis

The target plasmid, a ColE1 plasmid bearing the gene of interest, was transformed into JS200 cells carrying muta-plasmid, the pSC101 (Pol I-independent) plasmid bearing our low-fidelity Pol I. When these transformants are grown under restrictive conditions, low-fidelity Pol I is the functional polymerase present in the cell, introducing random errors during replication of the ColE1 target plasmid.

Liquid mutagenesis: mutagenesis in liquid culture was performed by switching a culture grown under permissive conditions (LB, 30°C, exponential) to restrictive conditions (2XYT, 37°C, saturation) as described in (Camps et al. 2003). Briefly, ~100ng of the target plasmids (pGFPuv or pLitmusALKBH1) were transformed into electrocompetent JS200 muta-plasmid cells (for preparation of competent cells, see (Troll et al. 2011)). The transformants were resuspended in 1ml LB broth, recovered for 1h at 30°C, and plated at 30°C on LB Agar plates containing 100 μg/ml carb. A single colony was picked from each plate, inoculated into 4ml LB broth and grown at low density at permissive temperature (30°C). For mutagenesis, an aliquot of the overnight culture (dilution factor 1:10³ to 1:10⁵) was transferred into 4ml of 2XYT media (pre-warmed at 37°C), and grown shaking at 37°C for 1 or 3 days to reach complete saturation or hypersaturation (Troll et al. 2011). Following mutagenesis, plasmid DNA was isolated using Machery Nagel’s Nucleospin Plasmid miniprep kit.

Solid plate mutagenesis: electrocompetent JS200 cells carrying muta-plasmid, the pSC101 (Pol I-independent) plasmid bearing our low-fidelity Pol I, were transformed with ~100ng of the target plasmids (pGFPuv or pLitmusALKBH1). Cells were allowed to recover at 37°C in LB broth for one hour. Cells were then plated on pre-warmed Petri dishes containing chloramphenicol and carbenicillin (to select for both the pSC101 and the target plasmid) at a high colony density (>100,000 colonies). Petri dishes were left in the 37°C to grow over night. In the morning the Petri dishes were washed with 2ml of LB broth and then subsequently mini-prepped. This constituted one round of solid plate mutagenesis.

Iteration of mutagenesis and sequencing

The mutagenesis procedures described above were repeated to increase the mutation frequency as described in detail in (Troll et al. 2011). Briefly, the plasmid library recovered from the initial round of mutagenesis was retransformed into fresh JS200 muta-plasmid cells at 30°C, and transformant colonies were washed, inoculated into 4ml of 2XYT media and grown to saturation at 37°C (liquid protocol) or retransformed JS200 muta-plasmid cells were directly plated at 37°C (solid plate mutagenesis). These procedures were repeated until the desired mutation frequency was reached. Individual plasmids were identified through transformation of a small amount of plasmid DNA (50–100ng) into BL21 cells. From this transformation, individual colonies were sequenced. In Supplementary table 1 we list number of mutagenesis cycles, sequence coverage, and mutations found for each clone present in our libraries. This information is summarized in Table 1 of the main text.

Hotspot identification

We investigated the spatial distribution of mutations by calculating the distribution of distances between mutant positions for all the mutations included in this study (501 mutations at 335 positions for GFP and 260 mutations at 179 positions for ALKBH1). A “hotspot index” was calculated, defined as the number of mutations that can be grouped as being in the same or adjacent positions. Moving along the sequence we start counting at 1 until we have exhausted the number of mutations at that position. We then check the next nt position and continue to raise the count if it has one or more mutations. If not, the count is logged and the count starts over, continuing forward on the strand. Individual hotspot indexes are plotted in Suppl. Fig. 1 and the cluster size distribution for these indices is shown in Suppl. Fig. 2. The vast majority of clusters fall in the 1–2 mutation category (n=303). However, 16 of these clusters deviate from the overall distribution, with ≥ 6 mutations. The sequence of these clusters in shown in Suppl. Table 2. Each cluster comprises a moderate number of mutations, with an average of 9 mutations per cluster and a standard deviation of 2.5. These hotspots tend to be GC-rich, with fifteen of these sites occurring in runs of 3 or more C or G residues. The only recognizable motif was “5′-CCA/TA/T-3′”, found in seven of the hotspots (highlighted with a grey box in Suppl. Table 2). Mutations in these clusters (133 mutations in total) were considered “hotspots” and excluded from the footprint as unrepresentative of randomly distributed mutations made by the polymerase.

Strandedness markers

Leading-strand marker mutations are defined as the most frequent of the complementary pairs: A→G, C →T, A→T, and G→T. Lagging-strand marker mutations are defined as the least frequent of the complementary pairs: T→C, G→A, T→A, and C→A. Due in part to low representation in our database, the strandedness of C→G vs. G→C was inconclusive. The frequency of T →G and A→C mutations in the area of single-stranded Pol I replication was also too low to ascribe strandedness unambiguously but we designated T →G as a marker for leading-strand synthesis based on the fact that we did see a moderate enrichment for T→G mutations in that area and that we saw the converse in putative Okazaki processing sites: an enrichment for A→C mutations.

Identification of Okazaki processing sites

Putative Okazaki processing sites within the sequence coverage area were identified using the approach previously described in (Allen et al. 2011). Briefly, clusters of consecutive maker lagging-strand mutations located at a short distance from each other (d≤5; the average distance being 7.4) were plotted. Based on the cluster size distribution, clusters with 6 or more mutations were considered significant. This identified the following positions as likely Okazaki processing sites: positions 179–191; 559–578; 910–926; and 1035–1045 (sites I–IV in Suppl. Fig. 3a). Of these, site I (comprising positions 179–191) is likely artifactual because it falls squarely in a mutation hotspot as defined in Suppl. Fig. 1a and it does not show the same level of enrichment for lagging-strand mutations seen in the other three sites (Suppl. Fig. 3b). For the remainder of the analysis we considered only sites II, III and IV as legitimate Okazaki processing sites.

Statistical methods

To aid in the identification of the hotspots, we simulated the null distribution of hotspots under the assumptions that for each library, coverage was the same across clones and that mutations occurred independently with probability p at each nt position in each clone. We calculated 1,000,000 Monte Carlo replicates for each library, then estimated the right tail probabilities using the empirical distribution.

To test for a statistically significant difference in mutation frequency between leading and lagging strands in the area beyond the putative switch, we binned the mutation counts into 50 nt intervals, then performed a Wilcoxon Signed Rank test using these counts (p= 0.26).

In several instances, we performed a Fisher’s exact test on observed mutational spectra from different locations or libraries in order to ascertain whether or not they were different at a statistically significant level. The reported p-values were estimated by Monte Carlo with 100,000 simulations.

All simulations and statistical tests were performed using standard R packages.