Evaluation of template matching for tumor motion management with cine-MR images in lung cancer patients

Abstract

Purpose: Accurate determination of tumor position is crucial for successful application of motion compensated radiotherapy in lung cancer patients. This study tested the performance of an automated template matching algorithm in tracking the tumor position on cine-MR images by examining the tracking error and further comparing the tracking error to the interoperator variability of three human reviewers.

Methods: Cine-MR images of 12 lung cancer patients were analyzed. Tumor positions were determined both automatically with template matching and manually by a radiation oncologist and two additional reviewers trained by the radiation oncologist. Performance of the automated template matching was compared against the ground truth established by the radiation oncologist. Additionally, the tracking error of template matching, defined as the difference in the tumor positions determined with template matching and the ground truth, was investigated and compared to the interoperator variability for all patients in the anterior-posterior (AP) and superior-inferior (SI) directions, respectively.

Results: The median tracking error for ten out of the 12 patients studied in both the AP and SI directions was less than 1 pixel (= 1.95 mm). Furthermore, the median tracking error for seven patients in the AP direction and nine patients in the SI direction was less than half a pixel (= 0.975 mm). The median tracking error was positively correlated with the tumor motion magnitude in both the AP (R = 0.55, p = 0.06) and SI (R = 0.67, p = 0.02) directions. Also, a strong correlation was observed between tracking error and interoperator variability (y = 0.26 + 1.25x, R = 0.84, p < 0.001) with the latter larger.

Conclusions: Results from this study indicate that the performance of template matching is comparable with or better than that of manual tumor localization. This study serves as preliminary investigations towards developing online motion tracking techniques for hybrid MRI-Linac systems. Accuracy of template matching makes it a suitable candidate to replace the labor intensive manual tumor localization for obtaining the ground truth when testing other motion management techniques.

INTRODUCTION

Intensity modulated radiation therapy (IMRT) has the ability to deliver escalated radiotherapeutic doses to tumors while sparing the surrounding healthy tissues.¹ However, the required high conformity of dose distribution to the tumor poses a challenge especially for thoracic and abdominal tumors due to respiratory and cardiac motions. Motion compensated radiotherapy that uses motion management techniques, such as respiratory gating,^{2, 3} dynamic multileaf collimators (MLCs),³ and the use of dynamic couch,^{4, 5} have been developed to restrict radiation doses accurately to tumors by incorporating the time-resolved positional information. However, obtaining accurate tumor position is the key to successful implementation of any of these motion compensated radiotherapy techniques.

Several techniques have been developed to track tumor positions by inferring the motion from either external or internal surrogates. Abdominal motion measured by the motion of external infrared markers placed on the patient's abdomen has been used as a surrogate for tumor motion.^{5, 6} Others have used the patient's spirometric measurement during therapy as a surrogate for tumor motion, and it has been shown to perform better than the abdominal displacement.^{7, 8} While external surrogates perform well, the relationship between external surrogate motion and internal tumor position is often valid for just a few minutes (∼10 min) and has to be reevaluated following that duration.^{9, 10} Internal surrogates, i.e., fiducial markers surgically embedded in or around the tumor, have proven to be accurate in tracking tumor position and hence have been extensively used during radiation treatment.^{11, 12} However, it has some drawbacks, such as the risk of migration of these markers¹ and the risk of pneumothorax when implanted in the lung.¹³ Therefore, other techniques that do not resort to the external surrogates or surgically implanted fiducial markers are needed.

Several groups have explored marker free techniques that use image features to aid in tumor tracking.^{2, 3, 13, 14, 15} Template matching,^{16, 17, 18} a simple and efficient image processing technique, has been recently applied to track tumor motion during radiation treatment. Berbeco et al. used a combination of template matching and information about the respiratory phase to extract the tumor positional information for gated radiation therapy.² To improve the robustness of this technique, template matching based on multiple templates was proposed.^{3, 13} Others also used the correlation between tumor position and surrounding surrogate anatomic features for tumor tracking.¹⁵ Most of these tumor tracking techniques were developed using fluoroscopic images that often suffer from poor soft tissue contrast. The performance of template matching is often improved by the implantation of fiducial markers before fluoroscopic imaging.¹ While there are several advantages of using fluoroscopy, one major disadvantage in addition to the poor soft tissue contrast is the use of ionizing radiation that can sometimes lead to unacceptable levels of radiation dose during real-time tumor tracking.¹⁹

Magnetic resonance imaging (MRI) is gaining traction within the radiation oncology community due to the use of nonionizing magnetic field for imaging combined with its superior soft tissue contrast. Tumor tracking using MR images is gaining popularity especially with the development of hybrid MRI-Linac systems.^{20, 21} Specifically, template matching has been widely used to track the vascular structures and tumors in the lung with dynamic MR images for various studies in the radiotherapy context.^{22, 23, 24, 25, 26, 27, 28, 29, 30} However, validation of this technique with ground truth established by physicians has rarely been provided. Recently, with the help of manually determined ground truth, Cervino et al. validated the superior performance of template matching in tracking the position of vascular structures with cine-MR images of healthy volunteers.¹⁴ They further inferred that the performance of template matching would be comparable if it is used to track tumors. While this is a good initial proof of concept study, pulmonary tumor mass may have different motion characteristics due to its irregular shape when compared to tubular vascular structures. Additionally, there is no data in the literature comparing the performance of template matching in determining tumor position to the manual determination that often suffers from interoperator variability. Therefore, the overall goal of this study was to examine the performance of template matching to track tumor motion in cine-MR images of lung cancer patients undergoing radiotherapy. Specifically, the objectives were (1) to test the performance of template matching by estimating the tracking error when compared to the manually determined ground truth tumor positions and (2) to compare the tracking error to the interoperator variability of three human reviewers.

MATERIALS AND METHODS

Patient information and imaging parameters

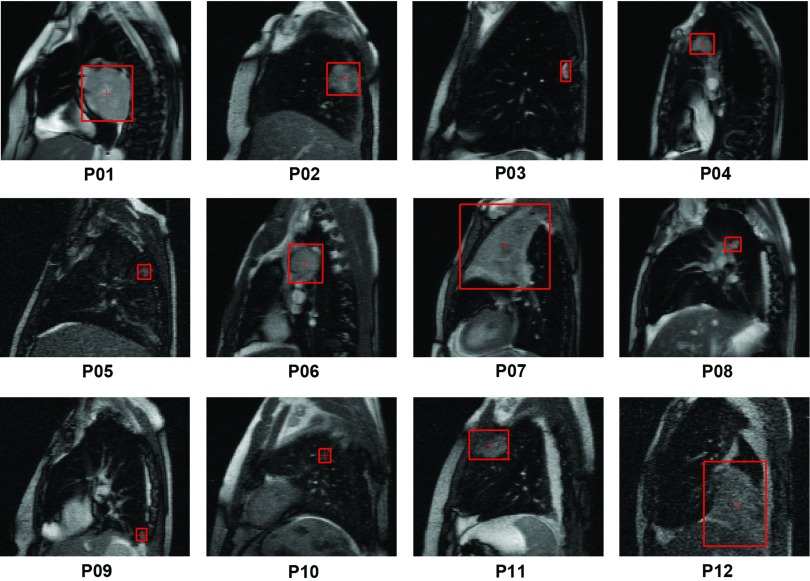
Twelve patients with nonsmall cell lung cancer (NSCLC), who were undergoing treatment using concurrent chemoradiotherapy, were recruited in a larger prospective study (Table 1 and Fig. 1). The study was approved by the Institutional Review Board at University of Maryland School of Medicine. Imaging was carried out on a 1.5 T clinical MRI scanner (MAGNETOM Avanto, Siemens Medical Solutions, Malvern, PA). For this work, imaging data collected prior to the start of the radiation treatment were used for further analysis.

Table 1.

Patient and tumor information.

			Tumor dimensions	Tumor	Magnitude of tumor	Magnitude of tumor
	Gender	Age (yr)	(AP × SI, mm)	location1	motion2 (AP, mm)	motion2 (SI, mm)
Patient 1	F	66	73 × 80	LP	3.5	10.9
Patient 2	F	75	47 × 47	MP	3.0	11.9
Patient 3	M	64	14 × 29	MP	1.3	1.0
Patient 4	F	64	34 × 29	UA	4.5	3.3
Patient 5	M	58	19 × 20	MP	3.3	4.9
Patient 6	M	55	49 × 56	UA	7.3	12.8
Patient 7	M	68	130 × 122	UA	11.7	11.7
Patient 8	M	87	22 × 20	UP	5.0	3.9
Patient 93	F	54	15 × 18	LP	5.0	27.2
Patient 10	M	46	17 × 20	UA	21.8	31.2
Patient 11	M	72	57 × 42	UA	22.2	11.9
Patient 12	M	53	90 × 122	LP	15.2	21.0

¹L: Lower; M: Middle; U: Upper; A: Anterior; P: Posterior.

²Calculated as the distance between the two extreme tumor positions in the AP and SI directions, respectively.

³Enlarged template was used.

Figure 1.

The tumor position and size, as determined by a radiation oncologist, were illustrated on the first frame of the cine-MR images (acquired in the sagittal plane) for all 12 patients.

Images were acquired using a multislice 2D TrueFISP (fast imaging with steady-state precession) sequence with an echo time (TE) of 1.29 ms, a repetition time (TR) of 2.57 ms, a matrix size of 176 × 256, a flip angle of 60º, and an in-plane spatial resolution of 1.95 mm. Following the localizer scan, five sagittal slices, with slice profile thickness ranging from 12 to 16 mm for different patients to ensure complete tumor coverage, were positioned across the tumor for data collection. The field-of-view in the sagittal plane covered the entire thoracic region. The effective frequency of imaging for any given slice location within the imaged slab was 0.4 Hz. Imaging was carried out for ∼8 min resulting in a series of 200 frames for each patient. A single 2D slice that showed the largest extent of the tumor in the first frame was identified, and subsequently the same slice from each frame was selected to create a time series containing 200 2D slices for each dataset. Patients were instructed to breathe normally during the entire imaging session.

Manual determination of tumor position

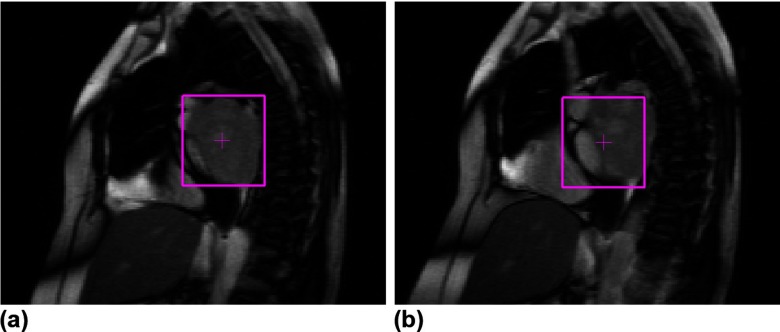
A radiation oncologist established the ground truth of the tumor location by manually drawing the smallest box that enclosed the tumor on each of the 200 slices for all datasets (Figs. 12, the box labeled with “r”). The original images were upsampled by a factor of 2 using bicubic interpolation in MATLAB (MathWorks, Natick, MA) to facilitate the manual tumor localization. The center of mass of the enclosing box, using grayscale intensity as the weight, was used as the tumor position (${{\mathbf{x}}^{\rightharpoonup }}_{man1}$) for subsequent analysis. This manually determined tumor position was used as the ground truth to test the performance of the automated template matching technique.

Figure 2.

One representative slice from Patient 1 showing the tumor localized automatically with template matching (labeled with “m”) as well as manually by 3 reviewers (labeled with “r”, “c”, and “g”, respectively). The box labeled with “y” shows the motion magnitude of the tumor (Table 1). The crosshairs indicate the corresponding tumor positions.

To assess interoperator variability, two additional reviewers trained by the radiation oncologist made independent assessments of the tumor position (${{\mathbf{x}}^{\rightharpoonup }}_{man2}$ and ${{\mathbf{x}}^{\rightharpoonup }}_{man3}$) as shown in Fig. 2 (the boxes labeled with “c” and “g”). During the training, the radiation oncologist made sure the tumor positions determined by the two reviewers were satisfactory for the first ten frames of each dataset.

Template matching

Template matching uses a brute-force search for a predefined template in a local region of the dynamic image by maximizing an objective function to determine a good match. The objective function used in this study is normalized cross-correlation, which is calculated using the equation

$$\gamma (u,v)=\frac{{\sum }_{x=u+1}^{u+N_x}{\sum }_{y=v+1}^{v+N_y}(f(x,y)-{\overline{f}}_{u,y})(t(x-u,y-v)-\overline{t})}{\sqrt{{\sum }_{x=u+1}^{u+N_x}{\sum }_{y=v+1}^{v+N_y}{(f(x,y)-{\overline{f}}_{u,y})}^2{\sum }_{x=u+1}^{u+N_x}{\sum }_{y=v+1}^{v+N_y}{(t(x-u,y-v)-\overline{t})}^2}},$$ (1)

where f(x, y) denotes the grayscale intensity value at the point (x, y) in the target image f of size M_x × M_y, x ∈ {1, …, M_x}, y ∈ {1, …, M_y}, t(x, y) denotes the grayscale intensity value at the point (x, y) in the template image t of size N_x × N_y, x ∈ {1, …, N_x}, y ∈ {1, …, N_y}, and (u, v) is the shift of the template in the x and y directions, respectively.

${\overline{f}}_{u,v}$ denotes the mean value of f(x, y) within the area of the template t when it is shifted to (u, v), and it is calculated as

$${\overline{f}}_{u,v}=\frac{1}{N_x{N}_y}{\sum }_{x=u+1}^{u+N_x}{\sum }_{y=v+1}^{v+N_y}f\left(x,y\right).$$ (2)

Similarly, $\overline{t}$, which is the mean value of the template t, is represented as

$$\overline{t}=\frac{1}{N_x{N}_y}{\sum }_{x=1}^{N_x}{\sum }_{y=1}^{N_y}t\left(x,y\right).$$ (3)

The normalization ensures that γ(u, v) is independent of changes in brightness or contrast of the image. These changes are related to the mean and standard deviation of the image intensity value.

For each patient, the minimum enclosing box determined by the radiation oncologist on the first frame was used as the template of the tumor to estimate the tumor positions on all subsequent frames with template matching (Fig. 2, the box labeled with “m”). In order to match the image resolution during manual localization, both the template image and the target frames were upsampled by a factor of 2 during the search. As noted previously by Cai et al., the upsampling will also improve the performance of template matching.²² The template matching algorithm was implemented using an inhouse code developed in MATLAB and specifically uti-lized the MATLAB intrinsic function normxcorr2. During the search, the template was allowed to move 7 pixels (or 14 pixels in the upsampled images) in each direction relative to the tumor position on the previous frame, enabling 27.3 mm of tumor movement in the anterior-posterior (AP) and superior-inferior (SI) directions, respectively. This range of motion far exceeds the maximum tumor movement observed in all patients between two consecutive frames. The position that corresponded to the maximum normalized cross-correlation value between the template and the “search area” on the target image was selected as the position of the tumor (${{\mathbf{x}}^{\rightharpoonup }}_{auto}$). In this study, 99.98% of the time the maximum normalized cross-correlation value obtained was greater than 0.7, the threshold used by Cervino et al.¹⁴ to define a successful match.

Usually, tumors on the MR images are sufficiently distinctive, and do not need the help from additional internal surrogates to achieve reliable matches in the search area. However, for extremely small tumors that may appear similar to the vascular structures or other tissues on an MR image, the performance of template matching was improved by using a slightly enlarged template (additional 2 pixels in each direction) as suggested by Cervino et al.¹⁴ These similar tissues would provide multiple competing maxima and the use of a larger template rendered the search more deterministic. The underlying assumption in allowing such an expansion of the template is the lack of relative movement between the tumor and its immediate surroundings. This, however, holds true only when dealing with immediate surroundings. Hence, we chose to expand the template by only 2 pixels. Larger expansions may result in violating this assumption and may lead to poor performance. Such an expansion was used only sparingly in this study and was applied only in one patient (denoted by footnote c in Table 1).

Data analysis

Tracking error for the template matching technique was estimated as the absolute difference between the tumor position determined using the automated (auto) template matching algorithm and the ground truth (man1) established by the radiation oncologist for each frame, as shown by

$$\Delta \stackrel{\rightharpoonup }{\mathbf{x}}=abs\left({\stackrel{\rightharpoonup }{\mathbf{x}}}_{auto}-{\stackrel{\rightharpoonup }{\mathbf{x}}}_{man1}\right),$$ (4)

where each vector contains two components as

$$\stackrel{\rightharpoonup }{\mathbf{x}}=x_{\mathrm{AP}}{\stackrel{\rightharpoonup }{i}}_{\mathrm{AP}}+x_{\mathrm{SI}}{\stackrel{\rightharpoonup }{i}}_{\mathrm{SI}}.$$ (5)

The tracking error was compared to the interoperator variability as estimated for each frame by

$$\Delta {\stackrel{\rightharpoonup }{\mathbf{x}}}_{\mathrm{IOV}}=\frac{abs\left({{\mathbf{x}}^{\rightharpoonup }}_{man1}-{{\mathbf{x}}^{\rightharpoonup }}_{man2}\right)+abs\left({{\mathbf{x}}^{\rightharpoonup }}_{man2}-{{\mathbf{x}}^{\rightharpoonup }}_{man3}\right)+abs\left({{\mathbf{x}}^{\rightharpoonup }}_{man3}-{{\mathbf{x}}^{\rightharpoonup }}_{man1}\right)}{3}.$$ (6)

Similar to Eq. 4, all vectors in Eq. 6 contain the AP and SI components as illustrated in Eq. 5.

One concern with the use of trained nonphysician reviewers is whether this introduces systematic errors, thereby artificially increasing the interoperator variability. To specifically address this, data from all patients were used to calculate the localization differences between the radiation oncologist and the two trained reviewers (${{\mathbf{x}}^{\rightharpoonup }}_{man2}-{{\mathbf{x}}^{\rightharpoonup }}_{man1}$ and ${{\mathbf{x}}^{\rightharpoonup }}_{man3}-{{\mathbf{x}}^{\rightharpoonup }}_{man1}$). Data from two patients with relatively large tracking errors were further analyzed to calculate the localization differences between two independent radiation oncologists (for Patient 1) as well as the differences between two sessions (for Patient 12) separated in time by 3 months by the same radiation oncologist.

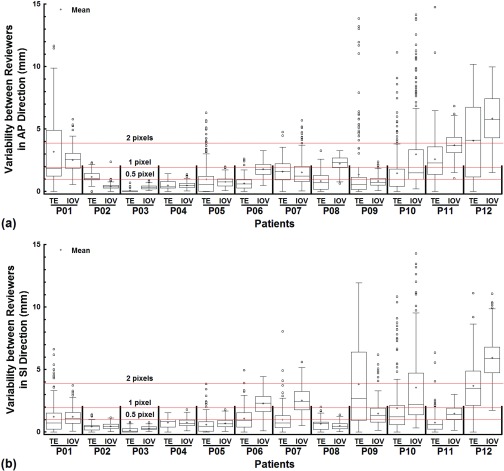
Box-and-Whisker plots were used to illustrate the tracking error ($\Delta {\mathbf{x}}^{\rightharpoonup })$ of template matching against the ground truth for all patients in the AP and SI directions, respectively. Similarly, Box-and-Whisker plots were also used to compare the tracking error ($\Delta {\mathbf{x}}^{\rightharpoonup })$ and the interoperator variability $\left(\Delta {{\mathbf{x}}^{\rightharpoonup }}_{\mathbf{IOV}}\right)$ for all patients in the AP and SI directions, respectively. Similar analysis was carried out to compare the localization differences for all patients in the AP and SI directions, respectively. On the Box-and-Whisker plot (Fig. 3), each box shows the first quartile (bottom edge, Q₁), the median, and the third quartile (top edge, Q₃). The bottom and top whiskers were calculated as Q₁ – 1.5 x IQR and Q₃ + 1.5 x IQR, respectively, where IQR = Q₃ – Q₁ is the interquartile range. Additionally, the mean value for each entity was also calculated (n = 200). To compare the tracking error ($\Delta {\mathbf{x}}^{\rightharpoonup }$) and interoperator variability $\left(\Delta {{\mathbf{x}}^{\rightharpoonup }}_{\mathit{IOV}}\right)$, linear regression was performed with KaleidaGraph 3.6 (Synergy Software, Reading, PA), and a p value of < 0.05 was considered statistically significant.

Figure 3.

The tracking error (TE) was compared to the interoperator variability (IOV) with Box-and-Whisker plots for all patients in the AP (a) and SI (b) directions, respectively. The mean value for each quantity for each patient was superimposed on the box plots. The lines marking the 0.5, 1, and 2 pixels positions were provided to facilitate comparisons.

RESULTS

The tracking error $\left(\Delta {\mathbf{x}}^{\rightharpoonup }\right)$ of the template matching algorithm when compared to the ground truth is shown in Fig. 3 for all 12 patients in the study. In ten out of the 12 patients, the median tracking error was less than one pixel (= 1.95 mm) and less than half a pixel (= 0.975 mm) in seven out of the 12 patients along the AP direction. In ten out of the 12 patients, the median tracking error was less than one pixel (= 1.95 mm) and less than half a pixel (= 0.975 mm) in nine out of the 12 patients along the SI direction. The largest median tracking error (along the AP direction for Patient 12) was 4.12 mm, slightly more than 2 pixels (= 3.90 mm). The median tracking error was positively related to the magnitude of the tumor motion, showing a modest correlation in the AP direction (R = 0.55, p = 0.06) and a strong correlation in the SI direction (R = 0.67, p = 0.02).

The failure rate of tumor tracking with template matching, defined as the percentage of tracking mismatches greater than 5 mm, was calculated and listed in Table 2 for each patient in the AP and SI directions, respectively. Seven patients had 0 or negligible failure rate in both directions. Two patients had a failure rate of <10% in both directions. Patient 1 (AP), Patient 9 (SI), and Patient 12 (AP and SI) experienced a failure rate of >20%.

Table 2.

The failure rate of tumor tracking with template matching for each patient in the AP and SI directions, respectively.

	AP (%)	SI (%)
Patient 1	24.0	3.0
Patient 2	0.0	0.0
Patient 3	0.0	0.0
Patient 4	0.0	0.0
Patient 5	2.5	0.0
Patient 6	0.0	0.0
Patient 7	0.0	0.5
Patient 8	0.0	0.0
Patient 9	8.0	36.5
Patient 10	5.0	9.0
Patient 11	8.0	1.0
Patient 12	39.0	23.5

Using the original template, the median tracking error for Patient 9 in the AP and SI directions was 6.23 mm and 18.67 mm, i.e., ∼3.0 pixels and ∼9.5 pixels, respectively. Using an enlarged template (additional 2 pixels along each direction) substantially decreased the median tracking error to 0.57 mm and 2.69 mm in the AP and SI directions, respectively.

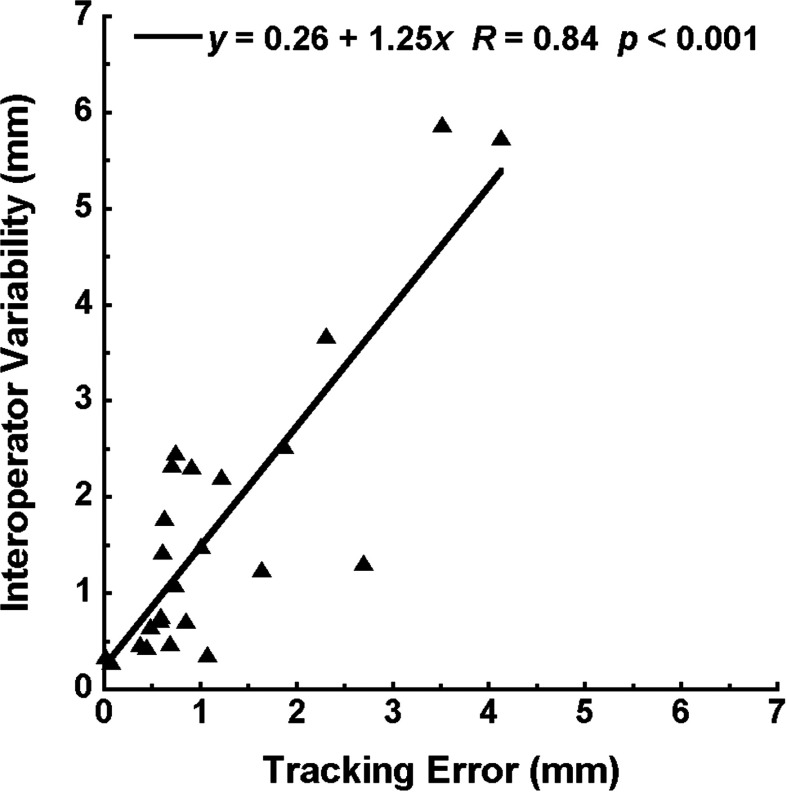
Figure 3 also shows the comparison between the performance of template matching and the interoperator variability $\left(\Delta {{\mathbf{x}}^{\rightharpoonup }}_{\mathbf{IOV}}\right)$. For almost all patients in both the AP and SI directions, either the median tracking error and median interoperator variability were of the same magnitude or the former was smaller. When the median tracking error was correlated with the median interoperator variability, a strong correlation was observed and the interoperator variability was higher (Fig. 4, y = 0.26 + 1.25x, R = 0.84, p < 0.001).

Figure 4.

A strong correlation was found between the interoperator variability and the tracking error.

Furthermore, the differences between the median tracking error and median interoperator variability are listed in Table 3 for all 12 patients. For Patient 2 in the AP direction and Patient 9 in the SI direction, the median tracking error was larger than the median interoperator variability by 0.36 and 0.70 pixels, respectively. For the rest, either the median interoperator variability was larger than the median tracking error or their differences were within a quarter of a pixel.

Table 3.

Differences between the median tracking error and median interoperator variability (positive values indicate larger tracking errors) for all patients in the AP and SI directions, respectively. Positive values larger than a quarter of a pixel were emphasized with bold font.

	AP		SI
	mm	pixel	mm	pixel
Patient 1	−0.67	−0.34	−0.37	−0.19
Patient 2	0.70	0.36	−0.01	−0.01
Patient 3	−0.34	−0.17	−0.22	−0.11
Patient 4	−0.11	−0.06	0.13	0.07
Patient 5	−0.19	−0.10	−0.18	−0.09
Patient 6	−1.17	−0.60	−1.41	−0.72
Patient 7	0.37	0.19	−1.73	−0.89
Patient 8	−1.64	−0.84	0.19	0.10
Patient 9	−0.16	−0.08	1.37	0.70
Patient 10	−0.50	−0.26	−1.00	−0.51
Patient 11	−1.39	−0.71	−0.84	−0.43
Patient 12	−1.63	−0.84	−2.37	−1.22

A small percentage of outliers were observed due to artifacts that affected the performance of template matching in tracking tumors. For tracking error (Fig. 3), the percentage of outliers for Patient 1 (SI), Patient 5 (AP), Patient 9 (AP), and Patient 10 (AP and SI) ranged from 9.5% to 13.0% out of the 200 time points. For the rest, it was no more than 5.5%. As for the interoperator variability (Fig. 3), the percentage of outiers for Patient 10 (AP) was 15.5%, and was in fact larger than the percentage of outliers for the tracking error. For the rest, the percentage was no more than 7.5%. A weak negative relationship was found between the percentage of outliers and the tumor dimension in the AP direction (R = −0.58, p = 0.05), but not in the SI direction (R = −0.04, p = 0.90).

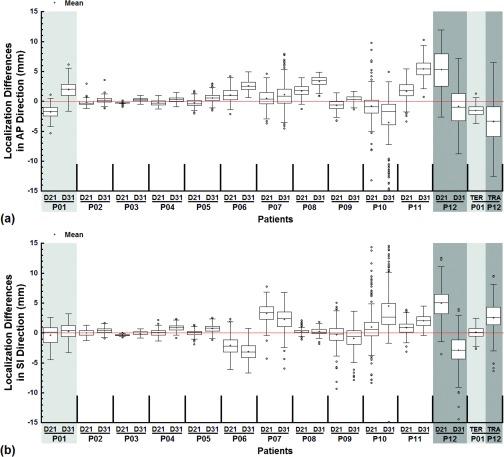
The localization differences show that for most cases the median differences were close to zero and the variations were the same for the two trained reviewers (Fig. 5). However, for larger tumors with abutting surrounding tissues and/or indistinguishable boundaries with the chest wall (Fig. 1), significant disagreement or systemic difference between the radiation oncologist and trained reviewers as well as between the two radiation oncologists or even between the two different sessions by the same radiation oncologist was observed.

Figure 5.

The tumor localization differences between the radiation oncologist and trained nonphysician reviewers were illustrated with Box-and-Whisker plots for all patients in the AP (a) and SI (b) directions, respectively. D21 and D31 denote ${{\mathbf{x}}^{\rightharpoonup }}_{man2}-{{\mathbf{x}}^{\rightharpoonup }}_{man1}$ and ${{\mathbf{x}}^{\rightharpoonup }}_{man3}-{{\mathbf{x}}^{\rightharpoonup }}_{man1}$, respectively. For comparison, one example of interoperator (TER, Patient 1) and intraoperator (TRA, Patient 12) localization differences for radiation oncologists were juxtaposed to the right of each plot. The time interval between the two sessions of tumor localization by the same radiation oncologist was 3 months for the intraoperator differences. The mean value for each quantity was superimposed on the box plots. The line marking 0 differences was provided to facilitate comparisons.

DISCUSSION

Successful treatment of mobile tumors in the thorax with radiotherapy often relies on the ability to accurately track their movement if breathing control is not an option. The use of template matching on thoracic cine-MR images was demonstrated by Cervino et al. by successfully tracking the vascular structures in the lung of healthy volunteers.¹⁴ In this work, we applied this technique to track thoracic tumors on cine-MR images and studied its performance by comparing tumor positions determined with template matching to those provided by a radiation oncologist. Since interoperator variability exists for manual tumor localization, the tracking error of template matching was further compared to the interoperator variability of three human reviewers. Results from this study showed that the performance of template matching is comparable with or better than the labor intensive manual determination of tumor positions.

Largely, the median tracking error of template matching in both the AP and SI directions was less than 1 pixel. Furthermore, for more than half of the patients studied, the median tracking error was less than half a pixel. The strong correlation between the tracking error and the interoperator variability (Fig. 4) indicates that if the template matching algorithm has a difficult time to determine the tumor position, it will also be difficult for human reviewers to reach a clear agreement, or vice versa. The slope of 1.25 and the positive intercept further confirm that the performance of the automated observer is no worse than that of human observers.

Tracking error also has a positive relationship with the magnitude of tumor motion in both the AP and SI directions. This result seems intuitive as the probability of failure with an automated algorithm is likely to increase when the tumor moves too far away from the origin. In terms of a relationship between tracking error and tumor size, mathematically we may be able to establish a correlation between tracking error and tumor size in the AP direction (R = 0.66, p = 0.02), but not in the SI direction (R = 0.34, p = 0.28). However, if we dig a little deeper into each individual patient it is apparent that the relationship is misleading. For example, the median tracking error is <1 pixel for Patient 7 and the failure rate using 5 mm as the threshold is almost 0 in both the AP and SI directions; however, it is the largest tumor in the datasets. We believe that the tracking error is related more to tumor deformation, rotation, and/or out-of-plane motion, which are difficult to capture in a simple mathematical parameter such as size. The other factor that seems to be related to tracking error and failure rate is the proximity of the tumor to other tissue structures with similar appearance (size, intensity, and contrast) on MR images, as can be seen for Patient 9 (Fig. 1).

In this study, the template matching algorithm was not optimized to handle large out-of-plane motion, deformation, and/or rotation of tumors.³⁰ Therefore, whenever these artifacts were not negligible, the template matching algorithm underperformed (Fig. 6). Fortunately, most thoracic tumors are stiff relative to the surrounding lung tissues^{31, 32} and are rarely deformed or pushed to rotate or move medially/laterally. However, once they are close to stiff structures like the chest wall or moving structures like the diaphragm and heart, these artifacts become significant, such as in Patient 1 (Fig. 6). The outliers in other patients were mostly due to occasional occurrences of these artifacts. In Patient 10, the out-of-plane motion was so big that the tumor disappeared in some slices. To deal with these artifacts, Cui et al. suggested the use of multiple templates that can be collected throughout one respiratory cycle.³ This, however, will significantly increase the computational time associated with this technique as one would need to compute normalized cross-correlation for each additional template.

Figure 6.

Representative slices illustrating successful tumor localization with template matching (a) and inaccurate tracking due to a combination of out-of-plane motion, deformation, and/or rotation (b) of the tumor in Patient 1.

While 2D lung tumor tracking using MR images was demonstrated in this study, it is potentially possible to extend this technique to 3D tracking. Pseudo 3D tracking can be achieved by taking interleaved orthogonal scans, since MR images can be conveniently acquired in any plane.^{26, 33} True 3D tumor tracking is possible but will need significant improvement in the temporal resolution of 4D-MRI. Since clinically relevant movements are mainly observed along the AP and SI directions,³⁰ a 2D tracking in the sagittal plane should suffice in most cases.

Current implementation of the template matching technique on cine-MRI datasets often results in significant processing time for each frame (∼10–15 s) on a computer with Intel Xeon CPUs of 2.40 GHz and 12 GB memory. Moving away from an interpreted platform such as MATLAB to a compiled C++ code will significantly shorten the processing time. During automated tracking, all frames were upsampled by a factor of 2 to match the image scaling used for manual localization, which increased the processing time by a factor of ∼10 with marginal increase of the tracking accuracy compared to the original images (data not shown). Therefore, significant efficiency improvement can be achieved using the original images without much deterioration of the tracking error. The calculation of cross-correlation can also be parallelized to speed up the processing. With sufficient modifications, the processing speed of this algorithm can be sufficiently fast to integrate the technique on hybrid MRI-Linac systems for real-time tracking by designing a dedicated FPGA/GPU system.³⁴

The combination of MRI and template matching circumvents three significant disadvantages during conventional motion management practices—low soft tissue contrast, the additional radiation dose of fluoroscopic kV imaging,¹ and the invasive nature of fiducial markers.³⁵ Tumor motion management has been a hot topic for radiation treatment of mobile cancerous lesions. This study serves as a preliminary investigation towards motion management with the newer hybrid MRI-Linac systems. As a byproduct, the template matching algorithm can also be used to replace the labor intensive manual determination as the ground truth when testing other motion management techniques.