Unknown Unknowns: the Challenge of Systematic and Statistical Error in Molecular Dynamics Simulations

In this issue, Neale et al. (1) present a calculation of the free energy to bind an antimicrobial peptide to a lipid bilayer using molecular dynamics simulations. This in itself is not unusual: many groups have used simulations to explore similar systems, and several have attempted to derive the binding thermodynamics. What is exceptional (and disturbing) about this article is the sheer computational effort required to get a good answer. Although Neale et al. (2) use a state-of-the-art Hamiltonian replica exchange technique, their results show that equilibration requires an astonishing 4 μs per simulation window. Worse yet, the results show that the error is not randomly distributed. Rather, the estimated free energy of binding becomes systematically more favorable as the runs are extended, suggesting that what we are seeing is an elongated relaxation process as opposed to simple improvements in statistical accuracy.

These last two concepts are often conflated, but long relaxation times can cause quite different symptoms in a simulation from simple statistical error. This is best understood by considering the expected value of some property A〈y〉 computed from the simulation. If the main concern is simple statistical uncertainty, then we know two things:

• 1.As simulation time increases, 〈A〉 → A_o, where A_o is the true value (given the force field and simulation conditions); and
• 2.We can expect that if we run multiple trajectories, the values of the 〈A〉 value computed from the trajectory will be distributed randomly about A_o, with a variance that drops roughly as $1/\sqrt{T_{\text{sim}}}$, where T_sim is the length of the simulations.

By contrast, systems with slow relaxations built in may not behave in this manner. For example, consider the system described by Fig. 1, which has two pairs of energy minima; each pair is separated by a small barrier in y, but a large barrier in x. If the quantity we are interested in is primarily a function of y (e.g. A(y)), the system will appear to make many transitions and 〈A〉 will appear to converge rapidly. However, if in building the system we consistently start on the left side of the x barrier, 〈A〉 will initially not converge to A_o. Rather, it will converge toward some different value A′_o, representing averaging over the left-hand side of the conformation space. Moreover, the standard tools developed for examining a scalar time series, like autocorrelation analysis and block averaging (3), will fail to detect the problem, because the kinetics of y appear fast. Even more sophisticated global sampling assessment methods (4–6) may struggle to recognize the problem, particularly if no slow transitions occur at all; none of these methods can tell you what has not yet been seen. As a result, they are quite good at identifying mediocre to poor sampling, but less effective when the sampling is truly awful.

Figure 1.

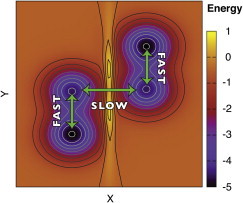
Energy surface with fast and slow relaxing degrees of freedom. Although the kinetics in the y dimension appear fast, correct averaging of y will depend on sampling the x dimension as well, which contains a larger barrier that will cause slow sampling. To see this figure in color, go online.

Systems with slow relaxation will also behave differently as the simulation time T_sim is increased. Initially, the apparent uncertainty in A(y) will drop, but at longer times the variance will increase again, as the systems run long enough to occasionally cross the barrier in x; it is only when a large number of barrier crossings (and their reverse) have occurred that the 〈A〉 will converge to A_o.

Ordinarily, the gold standard for quantifying error is to repeat the whole calculation using a different starting structure, but this too can fail if the construction procedure systematically produces one of the two states (e.g., you always start on the left side). Such circumstances are easily imaginable; for example, a crystal structure might capture one of two possible protein conformations. The case described by Neale et al. (1)—a peptide interacting with the membrane-water interface—represents another. It may sound like better system construction protocols will resolve these problems, and in principle they could. However, in practice, the fact is that the information needed to make optimal choices when building the system is generally not available, because that information is precisely what we hope to learn from the simulation.

That molecular dynamics runs into serious challenges trying to obtain adequate sampling is hardly surprising—the biomolecular simulation field has a long history of undue optimism with respect to the timescales needed to get reliably interpretable results. What makes the work of Neale et al. (1) so impressive is that instead of running from the problem, they embraced it, and applied overwhelming computational effort to carefully characterize just how hard it is. It appears that there is no substitute for the investigators’ chemical intuition and sense of caution to identify in advance the likely timescales for structural transitions in the system. The publication of this work is a cautionary lesson to the rest of the simulation community about just how challenging this class of calculation is, and the kind of computational investment likely required to solve it.