Stable Polyglutamine Dimers Can Contain β-Hairpins with Interdigitated Side Chains—But Not α-Helices, β-Nanotubes, β-Pseudohelices, or Steric Zippers

Abstract

A common thread connecting nine fatal neurodegenerative protein aggregation diseases is an abnormally expanded polyglutamine tract found in the respective proteins. Although the structure of this tract in the large mature aggregates is increasingly well described, its structure in the small early aggregates remains largely unknown. As experimental evidence suggests that the most toxic species along the aggregation pathway are the small early ones, developing strategies to alleviate disease pathology calls for understanding the structure of polyglutamine peptides in the early stages of aggregation. Here, we present a criterion, grounded in available experimental data, that allows for using kinetic stability of dimers to assess whether a given polyglutamine conformer can be on the aggregation path. We then demonstrate that this criterion can be assessed using present-day molecular dynamics simulations. We find that although the α-helical conformer of polyglutamine is very stable, dimers of α-helices lack the kinetic stability necessary to support further oligomerization. Dimers of steric zipper, β-nanotube, and β-pseudohelix conformers are also too short-lived to initiate aggregation. The β-hairpin-containing conformers, instead, invariably form very stable dimers when their side chains are interdigitated. Combining these findings with the implications of recent solid-state NMR data on mature fibrils, we propose a possible pathway for the initial stages of polyglutamine aggregation, in which β-hairpin-containing conformers act as templates for fibril formation.

Introduction

Protein misfolding and aggregation is connected to many devastating neurodegenerative diseases. One particularly interesting subset of these pathologies comprises the polyglutamine (polyQ) disorders, including Huntington’s disease and several ataxias (1). In these dominantly inherited diseases, the aggregating protein contains a polyQ sequence that has expanded beyond a certain threshold (typically between 30 and 40 consecutive glutamines), conferring pathogenicity and triggering the aggregation of the protein in question (1,2). The sequences flanking the polyQ stretch vary among the proteins, leading to differences in the exact threshold length, age of disease onset, and the course of neurodegeneration (3,4). However, as the expanded polyQ stretch is the only common feature among the disease-causing polyQ proteins, understanding its structure and properties seems to be key to understanding their shared pathological behavior.

The mature fibrillar aggregates of different polyQ proteins appear to have β-rich secondary structure with a core that has been shown to be dominated by the polyQ stretch (5–7). Using model peptides focused on the polyQ stretch, the principal details of the core structure have emerged: most likely the β-strands run perpendicular to the fibril axis, antiparallel β-sheets form along the axis, and the β-sheets stack such that their side chains interdigitate (8–10). Mounting evidence suggests, however, that these mature aggregates are not toxic enough to be the main culprits of neuronal death (11–19). On the other hand, some small soluble species occurring in the initial stages of aggregation are probably highly toxic (20–27), but here the structural details are largely missing. Revealing the polyQ conformers that occur during the initial stages of aggregation would, therefore, be beneficial for developing strategies that aim to alleviate disease pathology by targeting the toxic species.

Until now, it has not been experimentally possible to obtain high-resolution structural information on the aggregation-initiating conformation of polyQ peptides. A number of widely different structural models have been proposed. These include the water-filled β-nanotube (based on low-resolution x-ray diffraction on mature fibrils (28)); the dry-core β-pseudohelix (molecular simulations (29,30)); the β-sheet (mutational analysis (31) and solid-state NMR on fibrils (32)); the β-sheetstack (aggregation kinetics (33)); the steric zipper (first speculated based on a model for another peptide (34), recently supported by solid-state NMR on fibrils (10)); and the α-helix (bioinformatics analysis of interaction partners of polyQ proteins, circular dichroism, and chemical cross-linking (35)). However, the different models have never been systematically compared with a view to feasibility, possibly due to the lack of criteria for the assessment.

Here, we present a criterion for assessing the feasibility of different structural models of polyQ being found on the aggregation path. The criterion is deduced from a mechanistic model regularly used to analyze polyQ aggregation kinetics, and it is based on experimental data. We then use this criterion to assess the likelihood of different aggregation pathways via molecular docking calculations and atomistic molecular dynamics (MD) simulations. We find that most of the models proposed in the literature cannot form the long-lived dimers required in the early stages of aggregation. We also show that among the different models tested, the most stable dimer conformers always contain β-hairpins with interdigitated side chains, indicating that the formation of this motif could be crucial in the initial stages of polyQ aggregation.

Methods

Nucleated growth polymerization model

As a starting point for our analysis, we used the model sketched in Fig. 1. The model was initially proposed based on in vitro aggregation kinetics of polyQ peptides (36), and it has since been regularly applied in this context (for a recent review see Wetzel (37)).

Figure 1.

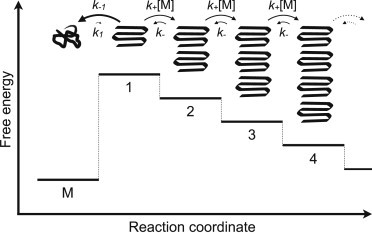
Initiation of polyQ aggregation according to the nucleated growth polymerization model suggested by Wetzel et al. (36,37,62). The model considers that the nonaggregating monomer ensemble M is in preequilibrium with the free-energetically most unfavorable state along the aggregation pathway (state 1), in which monomers are found in a conformation capable of initiating aggregation (36). For pathological-length polyQ, the population ratio between the states M and 1 is estimated to be of the order of 1,000,000,000:1 (63). Notably, due to asymmetric exit rates (k₋₁ > k₊[M], indicated by the length and thickness of arrows), a peptide in state 1 would still be much more likely to go to state M than to state 2 (37). From state n ≥ 2, the state n + 1 is more likely than state n – 1. As the monomer concentration [M] is initially effectively constant, we depict all the reactions as first-order, with the (second-order) growth reaction taking place with a pseudo-first-order reaction rate k₊[M].

The model considers only homogeneous (primary) nucleation, and it excludes any secondary pathways, on which aggregates would spawn new aggregates via processes such as fibril fragmentation (38) or surface-catalyzed nucleation (39). This choice agrees with the experimental finding (36) that the early-time rise in spontaneous aggregation kinetics profiles does not show the exponential signature of a secondary nucleation mechanism, but is polynomial (∼t²), suggesting that primary nucleation is dominant (40). The finding that seeding turns the sigmoidal profile concave (41) also signals primary nucleation (40).

In the nonaggregating monomer ensemble M (Fig. 1) the model considers, based on circular dichroism (42) and fluorescence correlation spectroscopy (43), polyQ to be intrinsically disordered and to resemble a polymer collapsed in poor solvent. Furthermore, as the mild concentration dependence of the early-time kinetics (of pathological length polyQ, Q_N>25 (33)) translates into a nucleus size of 1 in a nucleated polymerization theory analysis, the model considers that the ensemble M is in preequilibrium with the free-energetically most unfavorable state along the aggregation pathway, state 1, in which monomers have a particular folded form capable of triggering aggregation (36). Formation of a dimer, state 2, is the first step down the free energy landscape; from there on, an on-pathway state n has a higher likelihood of elongating (into state n + 1) than of dissociating (into state n − 1). Aggregate growth by monomer addition is suggested by the finding that the early polymerization rate is directly proportional to both monomer and aggregate concentrations (40,44,45).

Monomeric conformers

We used PyMol (The PyMOL Molecular Graphics System, Version 1.2r3pre, Schrödinger, Portland, OR), VMD (46), and published structures to generate six polyglutamine conformers described in the literature: the steric zipper (10,34), the β-nanotube (28), the β-pseudohelix (29,30), the β-sheet (31,32), the β-sheetstack (33), and the α-helix (35). All peptides consisted of 40 glutamine residues (Q₄₀), with NH₂/COOH termini. Their stability as monomers has been studied previously (47).

Docking

Docking calculations allow the generation of dimer structures and their ranking according to an estimate of their binding affinity. For each of the six Q₄₀ conformers, we docked two identical copies of the peptide on each other using Autodock 4.2 with its default force field parameters (48). A Lamarckian genetic algorithm was used for searching molecular conformations and a grid-based approach was used for energy calculations. The size of the grid was fixed at 0.05 nm. Each docking set comprised 140 copies, and the number of searches in each copy was 25 million. For each set, the 140 docked conformations were clustered based on their mutual root mean-square deviation (RMSD), each group thus representing a binding mode.

First, both monomers were treated as rigid bodies. To further optimize the docked conformations, rigid docking was followed by semiflexible docking. Docked structures from rigid docking were examined, and the side chains at the monomer-monomer interface were made flexible, i.e., the C_α-C_β bonds of side chains were allowed to rotate. If the number of side chains at the interface exceeded 10, they were divided into two groups, one rigid and the other flexible, and two separate sets of docking calculations were performed. Using semiflexible docking, structural particularities of the monomer constructs appeared not to prevent representative dimerization of the conformers, but highly compatible (especially for steric zippers and β-sheets), as well as intuitive, dimer structures emerged.

Note that as the entropy loss cannot be estimated, the docking scores do not represent free energies of binding. However, high scores indicate high dimerization propensity, and allow the selection of probable dimer structures to be used for the kinetic stability analysis in atomistic MD simulations.

Molecular dynamics

To assess the kinetic stability of nine high-scoring dimers obtained via docking, we performed extensive MD simulations.

Two identical sets of atomistic simulations were performed using GROMACS (49), version 4.5.3, one set with the united-atom GROMOS 43a1 (50) and one set with the all-atom CHARMM27 (51,52) force field. Before starting the simulations, the structures obtained via the docking were relaxed through two energy minimizations (using the steepest-descent algorithm) with the respective force fields, first without and then with constraints. Water was then added and, with the dimer position-restrained, was relaxed via short MD simulations. In CHARMM27, this was done with 5000 steps of 0.2 fs followed by 50,000 steps of 2 fs, in GROMOS 43a1 with 25,000 steps of 4 fs. Finally, 10 identical copies of each of the 18 systems were given new uncorrelated particle velocities from a Maxwell-Boltzmann distribution at 310 K.

In the GROMOS 43a1 simulations, we used the simple point charge water model (53), heavy hydrogens (54), reaction field electrostatics (ϵ_rf = 54), and a 4 fs time step. The van der Waals and Coulomb interactions were cut off at 1.4 nm, and the neighbor lists (r = 1.4 nm) were updated every step. In the CHARMM27 simulations, the TIP4P water model (55), particle-mesh Ewald (56,57) electrostatics and a 2 fs time step were used. For particle-mesh Ewald, we used fourth-order interpolation, a 1.3 nm real-space cutoff, a relative error of 10⁻⁵ in the direct and the reciprocal space, and size-optimized fast Fourier transform parameters (grid spacing of roughly 0.12 nm). The neighbor lists (r = 1.3 nm) were updated every 10 steps, with van der Waals interactions switched off between 1.0 and 1.2 nm.

All 180 simulations had periodic dodecahedron boundary conditions (initial distance from the dimer atoms to the face of the unit cell ≥1.2 nm). Pressure was kept at 1 bar using an isotropically coupled (τ = 1.0 ps) Parrinello-Rahman barostat (58). Temperature was maintained at 310 K using the velocity rescale thermostat (59), separately coupled to the peptides and water (τ = 0.1 ps in GROMOS 43a1 and 1.0 ps in CHARMM27). Covalent bonds were constrained to their equilibrium lengths by (fourth-order single-iteration) parallel linear constraint solver (P-LINCS) (60) in the peptides and by SETTLE (61) in water. All 180 simulations were carried out for 100 ns, for a total simulation time of 18 μs.

Results

Lifetime criterion for on-pathway dimers

The mechanistic model that we considered is suggested by kinetic experiments on polyQ peptides (36). In the model (see Fig. 1 and Methods), polyQ aggregation is nucleated by an alternatively folded monomer (state 1 in Fig. 1), and the formation of an on-pathway dimer (state 2) is the first step downhill in the free energy landscape (36,37,62).

Notably, the on-pathway dimer has a higher likelihood of elongating than of disintegrating (37), which gives a means to assess whether a given dimer structure can be on the aggregation path: The disintegration time of the on-pathway dimer will exceed the time required for its elongation into the on-pathway trimer (state 3).

In fact, for the diffusion along the reaction coordinate to drive the system toward the fibrillar state, for all on-pathway states n ≥2, the probability of entering the state n + 1 must exceed 50%. That is, going from the state n to state n + 1 must be more likely than exiting the state n through any disintegrative route. In terms of rate constants, this condition reads as k₊[M] > k₋ + k_−n. Here, k₊[M] and k₋ are as shown in Fig. 1; k_−n is the exit rate to any disintegrated state other than n − 1, which is considered to be vanishingly small for on-pathway states, and is thus not drawn in Fig. 1.

Thus, a necessary condition for a given dimer structure to be on the aggregation pathway is that its characteristic disintegration time τ_dis = 1/(k₋ + k₋₂), in other words, the time over which the dimer structure stays unchanged, exceeds the characteristic time τ_fwd = 1/k₊[M] needed for the elongation step to occur. Hence, for aggregation to proceed, the dimer must fulfill the following stability condition:

$${\tau }_{\text{dis}}>{\tau }_{\text{fwd}}=\frac{1}{k_{+}\left[\text{M}\right]}=\frac{1}{\left(2\times {10}^4{\text{s}}^{-1}{\text{M}}^{-1}\right)\times \left(50\times {10}^{-6}\text{M}\right)}=1\text{s}.$$ (1)

Here, we used the conservative estimates k₊ = 2 × 10⁴ s⁻¹ M⁻¹ and [M] = 50 μM (the elongation constant k₊ has been measured to be 1.14 × 10⁴ s⁻¹ M⁻¹ for K₂Q₄₇K₂ (63), and typical initial concentrations in experiments are 5–200 μM; see, for example, studies by Wetzel and colleagues (33,36,63)).

Hence, if the average lifetime of a dimer is not at least 1 s, the dimer in question cannot be on the aggregation pathway. In particular, for a given dimer structure to be on pathway, it must show extreme kinetic stability on the timescale of the hundreds of nanoseconds that is typical for MD simulations. For the on-pathway dimer, the likelihood of disintegration during 100 ns is 1 − exp(−100 × 10⁻⁹) ≈ 10⁻⁷, that is, 1 in 10 million dimers is expected to disintegrate during 100 ns. The kinetic stability of peptide dimers is thus a useful criterion for assessing candidate structures for the initial stages of polyQ aggregation.

A defining feature of the lifetime criterion is that it is, per construction, a tool of exclusion, not inclusion. It can eliminate unfeasible structures but never fully prove that a given structure is on pathway. This logic holds independent of the simulation length; even stability beyond the time limit of Eq. 1 does not provide an exact proof that a structure is on-pathway—only that it could be. With confidence, however, all structures failing to reach this time limit can be removed from the list of possible on-pathway candidates.

Construction of polyQ dimers with peptide-peptide docking

We generated dimers comprising two Q₄₀ peptides using semirigid peptide-peptide docking calculations on six different conformers: β-sheet, β-sheetstack, steric zipper, β-nanotube, β-pseudohelix, and α-helix. When using the docking approach, one makes the implicit assumption that no major monomer restructuring occurs upon dimerization; here, this assumption appears plausible, as the highest free energy state is known to be a structured monomer (Fig. 1). The initial monomer structures for the conformers were the same as in our previous study (47). The docking scores acquired from the calculations provided qualitative information on the stability of dimers (under the assumption of static conformers) and allowed for a rough comparison of their elongation potentials.

The highest docking score (49, given in −kcal/mol by Autodock (48)) occurred for two exactly aligned steric zipper peptides (Fig. 2). The high score reflected the large number of interpeptide hydrogen bonds, indicating that this conformer possesses a high elongation potential along this mode of binding. A high score (30) was also obtained when one of the monomers was rotated 180° in the plane of its backbone. For this orientation, however, the semirigid docking did not result in a perfect alignment of the β-strands, and no β-sheets were formed (Fig. 2).

Figure 2.

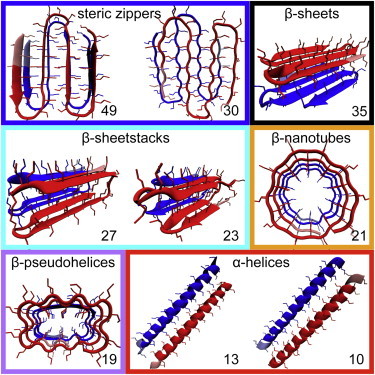
The highest-scoring polyQ dimer structures obtained with peptide-peptide docking are shown as snapshots. One monomer is colored red, the other blue; three N-terminal residues are represented with a lighter shade of the same colors. The numbers indicate the docking scores (given by Autodock in −kcal/mol) of the modes of binding. The color coding of the frames corresponds to that of the lines in Fig. 3. To see this figure in color, go online.

The second highest score (35) was obtained for a β-sheet dimer that had the β-sheets stacked on top of one another, with their side chains interdigitated (Fig. 2). No interpeptide hydrogen bonding occurred, and the peptide-peptide interactions were mostly dispersion interactions, as the tight-fitting interdigitation provided many close contacts between the side chains.

The high-scoring β-sheet dimer was similar to the two high-scoring configurations found for the β-sheetstack dimer (23 and 27; Fig. 2). As the side chains were already interdigitated in the β-sheetstack monomer, the dimerization took place by establishing backbone-backbone and side-chain-side-chain hydrogen bonds between the two polyQ peptides.

The tubelike conformers (β-nanotube and β-pseudohelix) were barely distinguishable in their scores (21 and 19), reflecting the high similarity in their modes of binding (along the tube axis; see Fig. 2). Interestingly, the polyQ in α-helical conformation showed the lowest docking scores (13 for the parallel and 10 for the antiparallel orientation), indicating a low elongation potential.

Assessment of dimer kinetic stability with MD simulations

The dimers obtained for each conformer via docking gave good initial configurations that were used for studying the kinetic stability of dimers by atomistic MD simulations. For each of the nine high-scoring dimeric structures (Fig. 2), 10 + 10 independent MD simulations (180 simulations in total) of 100 ns were performed using two different force fields, CHARMM27 (51,52) and GROMOS 43a1 (50), with an explicit solvent. We emphasize that because different MD force fields can differ in their ability to describe some features of peptides (64–66), we repeated all our MD simulations with two different atomistic force fields. This gives us a good control over possible systematic errors and allows verification of the significance of our observations.

The kinetic stability of the conformers was estimated by monitoring their lifetimes, which were obtained by visual inspection of the trajectories and analysis of the RMSD of dimer backbone atom distances (signaling conformational changes of the dimer), and the peptide-peptide center-of-mass distance (signaling separation of the monomers). Details of the analysis are available in the Supporting Material.

Comparison of the kinetic stabilities revealed that the β-hairpin-containing dimers (β-sheet and β-sheetstack dimers) displayed unwavering stability, maintaining their secondary structure (Figs. S1 and S3 in the Supporting Material) and a short intermolecular distance (Fig. S2) in all 60 replicas throughout the 100 ns simulation (Fig. 3).

Figure 3.

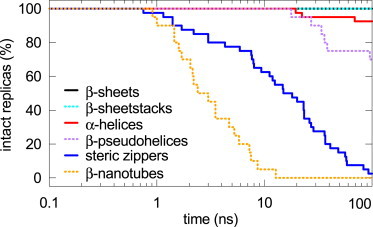
The percentage of intact dimers (whose monomers retain their initial conformation and remain associated) as a function of MD simulation time. All replicas are grouped under the conformer of the monomer, irrespective of the relative orientation of the peptides and the force field used. The color-coding is as in Fig. 2. To see this figure in color, go online.

The α-helix dimers also showed rather high stability, but disintegration events occurred in 3 of the 40 replicas: twice via monomer separation and once through a structural collapse of the dimer (Fig. S4). Note that the latter was the only replica in which either of the α-helix monomers lost its conformation.

Dimers of the other three conformers (β-nanotube, β-pseudohelix, and steric zipper) showed low stability, with all β-nanotube replicas and all but one steric zipper replica disintegrating before 100 ns (Fig. 3). The β-nanotube was the only conformer in addition to the α-helix that experienced a separation of monomers (Fig. S5).

Discussion

In this study, we pointed out that according to a mechanistic model regularly used to analyze polyQ aggregation kinetics (Fig. 1), the lifetime of an on-pathway polyQ dimer must exceed by more than six orders of magnitude the typical (100 ns) timescale of present-day MD simulations. Therefore, should an on-pathway dimer be simulated via MD, it should demonstrate extreme kinetic stability. We then created a set of nine polyQ dimers (of six different conformers; see Fig. 2) and performed extensive (180 × 100 ns) MD simulations on them. We found that the α-helical, β-nanotube, β-pseudohelix, and steric zipper dimers were not stable enough to be on the polyQ aggregation pathway. Instead, the extreme stability of dimers comprising β-hairpins stacked such that their side chains interdigitate (the β-sheet and β-sheetstack dimers) indicated that the on-pathway dimers could include this motive.

Characteristic lifetime

Based on the initial growth rate of on-pathway states, k₊[M], we deduced that the characteristic lifetime of an on-pathway dimer must exceed 1 s (Eq. 1). This estimate is still rather conservative, as can be gauged from the rate of the dissociation reaction, k₋, at the long-time limit. When fibril formation reaches equilibrium, it holds that k₋ = k₊[M]_c. Here, [M]_c is the characteristic final monomer concentration; it is equivalent to the critical initial monomer concentration, below which spontaneous fibril formation does not occur. The value of [M]_c has been measured experimentally and is known to decrease as polyQ length increases: [M]_c ≈ 30 μM for K₂Q₁₅K₂ (41), ≈3 μM for K₂Q₂₃K₂ (33), ≤1 μM for K₂Q₂₈K₂ (67), and is still less for longer polyQ sequences (37,41). Using the estimates [M]_c = 1 μM and k₊ = 1.14 × 10⁴ s⁻¹ M⁻¹ (still conservative for Q₄₀) gives k₋ = 1.14 × 10⁻² s⁻¹ and a characteristic lifetime for on-pathway states of 1/k₋ ≈ 90 s. Should a species have the ability to trigger neuronal death (68,69), this could be enough time to execute the toxic mission.

Kinetic stabilities of dimers

For the on-pathway dimer, no disintegration events should occur during the 100 ns MD simulations we performed here. Of the structures studied, only the β-sheet and β-sheetstack dimers achieved this (Fig. 3).

Dimers of Q₄₀ were built by docking monomeric structures proposed in the literature. We had previously explored their kinetic stabilities as monomers and shown that both α-helical and β-hairpin-containing monomers have average lifetimes exceeding 100 ns (47). With the exception of the α-helix, all the conformers gained kinetic stability upon dimerization.

The α-helical dimers did not demonstrate (Fig. 3) the extreme kinetic stability required for the on-pathway dimer (Eq. 1). In fact, as predicted by the low docking scores (Fig. 2), the α-helical monomers did not bind to one another very strongly, but in 5% of the MD simulations the α-helix dimers were observed breaking into monomers. As expected based on their robustness as monomers (47), the monomers retained their α-helical conformations in these events. Thus, although the polyQ stretch may populate the α-helical conformation as a monomer (35), the elongation into fibrils would only be feasible after a conformational conversion (70). We conclude that the α-helical assemblies are most likely off pathway with regard to polyQ aggregation.

The low kinetic stabilities observed here for the β-nanotube and the β-pseudohelix are consistent with other atomistic MD studies showing that (based on backbone RMSDs) dimers of tube-like conformers have short (10–50 ns) lifetimes (71,72).

The excellent compatibility of the steric zippers (signaled by their high docking scores in Fig. 2) led to a considerable stabilization upon dimerization: The average lifetime increased by two orders of magnitude from the subnanosecond times reported for monomers (47). Interestingly, however, this stabilization was still not enough to make the dimers last beyond 100 ns (Fig. 3). In contrast, the β-hairpin-containing dimers (i.e., the β-sheet and β-sheetstack) showed very high kinetic stability: none of the β-hairpin-containing dimers broke during the entire simulation time (60 × 0.1 μs). The stabilizing effect of β-hairpins has been demonstrated previously, as a dimer created by joining two Q₁₅ hairpins in the same plane, forming a four-strand β-sheet, was not stable over 10 ns (73), but a monomeric (Q₄₀) four-strand β-sheet had an average lifetime exceeding 100 ns (47). Our simulations are consistent with these results and with the high stabilities reported for large collections of extended β-strands (Q₆ and Q₁₅) organized into interdigitated β-sheets (74). Taken together, all these findings indicate that the β-hairpin motif alone is not sufficient to obtain an extremely stable structure, but that side chain interdigitation, characteristic of the steric zipper conformer, is also required. It appears that three to four strands in the β-sheet direction and two strands in the steric-zipper direction is enough for creating a highly stable system. The high stability is particularly interesting in light of reports indicating that the very toxic soluble species contain β-hairpins (23,75,76).

Possible pathway

It is noteworthy that the three conformers we found to have the highest docking scores (steric zipper, β-sheet, and β-sheetstack) differ only in their turn regions (Fig. 2). The turns are sharp hairpins in the β-sheet and rather gentle arches in the steric zipper (77). The β-sheetstack includes both turn types and thus demonstrates the compatibility of the β-sheet and steric-zipper conformers. Notably, all three could, in principle, fit the tight packing of β-strands found in the final fibrils.

The steric-zipper-based fibril was recently supported by Schneider et al. (10). They report their solid-state NMR results to be most compatible with peptides in a steric-zipper-like conformation, and not with a conformation containing β-hairpins. The high docking scores we obtained for the steric zipper (Fig. 2) are consistent with the results of Schneider et al. However, as is evident from the lack of kinetic stability of the steric-zipper dimer (Fig. 3), a docking event of this kind is feasible only if a robust, steric-zipper-compatible fibril already exists.

Support for the β-hairpin-containing fibrils, then, came from Kar et al. (32). The authors used solid-state NMR to show that certain β-hairpin-enhancing mutations in polyQ peptides do not change the resulting fibril structure. The formation rates of fibrils, however, increase greatly. They thus argue that β-hairpin-containing structures are the ones most likely to be found in the nucleus and in the final fibril. Our main finding that only the β-hairpin-containing dimers are long-lived enough to be on pathway (Fig. 3) is consistent with the results of Kar et al. However, fibril elongation can evidently not occur via β-sheet stacking (which was the arrangement found by the docking algorithm for the β-sheet dimer; see Fig. 2), as the fibril axis should be aligned with (and not perpendicular to) the plane of the β-sheets forming it (9,78).

In short, it seems that in the nucleation event, β-hairpin-containing conformers are required (32), whereas steric zippers better fit the final fibril (10). Based on our findings, we suggest that a possible explanation to this apparent contradiction lies in the inherent compatibility of the two conformers. As we demonstrated, the steric zipper dimers are too unstable to be on the aggregation path. In the initial stages of aggregation, the β-hairpin motif thus appears crucial. We also demonstrated that for unwavering stability the side chains of the β-hairpins should be interdigitated. This, notably, creates a surface that is compatible with the steric zipper conformer. We therefore suggest that in the initial stages, β-hairpin-containing peptides come together, creating a robust surface, on which further peptides then deposit themselves in the steric-zipper conformation.

This pathway agrees with the findings that the final fibrils contain predominantly steric zippers (10), and that enhancing the ability of β-hairpin formation will enhance the rate of fibril formation (32). Furthermore, it explains the finding of Kar et al. that although the nucleation of fibril formation is greatly facilitated by the β-hairpin-enhancing insertion, the elongation phase is actually somewhat retarded by it (32). Evidently, a preference for β-hairpins would speed up the initial steps on our suggested path, but would slow down the later steps, in which archlike turns, characteristic of the steric-zipper conformer, need to form.

The possible implications of this pathway for medicine would be related to the relatively benign effects of the mature aggregates (11–19) versus the high toxicity of early soluble species (20–27). Therapeutic strategies could be designed to encourage steric-zipper-like conformers (and thus aggregate maturation) while discouraging β-hairpin formation (and thus aggregate emergence).