Observation of Small Cluster Formation in Concentrated Monoclonal Antibody Solutions and Its Implications to Solution Viscosity

Abstract

Monoclonal antibodies (mAbs) are a major class of biopharmaceuticals. It is hypothesized that some concentrated mAb solutions exhibit formation of a solution phase consisting of reversibly self-associated aggregates (or reversible clusters), which is speculated to be responsible for their distinct solution properties. Here, we report direct observation of reversible clusters in concentrated solutions of mAbs using neutron spin echo. Specifically, a stable mAb solution is studied across a transition from dispersed monomers in dilute solution to clustered states at more concentrated conditions, where clusters of a preferred size are observed. Once mAb clusters have formed, their size, in contrast to that observed in typical globular protein solutions, is observed to remain nearly constant over a wide range of concentrations. Our results not only conclusively establish a clear relationship between the undesirable high viscosity of some mAb solutions and the formation of reversible clusters with extended open structures, but also directly observe self-assembled mAb protein clusters of preferred small finite size similar to that in micelle formation that dominate the properties of concentrated mAb solutions.

Introduction

The development of human therapeutics based on monoclonal antibodies (mAbs) and related products have evolved rapidly since the late 1980s, with an almost exponential growth in market value (1–4). Since antibody-based drugs have a high selectivity, few side effects, and good reproducibility, they have been applied in a broad number of clinical settings, including cancer treatment, chronic inflammatory diseases, transplantation, infectious diseases, and cardiovascular medicine (1,2,4,5).

The importance of mAb-based drugs in treating a wide range of diseases has motivated fundamental research into problems related to their manufacturability and ease of clinical use. One important industrial challenge is to minimize the viscosity of highly concentrated mAb protein solutions (2). A high viscosity can hinder large-scale production, purification, and delivery of these drugs at high concentrations. In particular, viscosities exceeding ∼50 mPa⋅S make it difficult to deliver drugs via subcutaneous (SC) injection (2,3). For some mAbs, this viscosity can be easily exceeded at the high protein concentrations (100–200 mg/mL) typically required for SC delivery. Another situation where the viscosity and diffusivity in dense environments is important is in the concentrated regions of endogenous proteins in intracellular environments. Thus, the understanding of the relationship between protein concentration and viscosity has broad implications in both scientific and technological applications.

It is hypothesized that the formation of reversibly self-associated aggregates (or reversible, nonpermanent clusters) at relatively high protein concentrations (>100 mg/mL) causes the high viscosities observed for some mAb solutions (2,6–8). One important characteristic of these clusters is that the clustering is reversible, i.e., clusters form at high concentrations and dissociate into monomers at sufficiently low concentrations. However, to date, it has been difficult to directly observe these mAb clusters and quantitatively characterize their microstructure in crowded environments. Therefore, the properties of mAb clusters are not clearly understood, and the relationship between the properties of clusters and high viscosity remains unclear. In addition to its relevance to the biopharmaceutical industry, protein clustering is of general interest in globular protein solutions and is a significant topic of current debate (9–13). The characterization of reversible cluster formation in mAb proteins can also provide new information that adds to our general physical understanding of clustering phenomena (14–19).

The novelty of our approach is that we combine the methods of small-angle neutron/x-ray scattering (SANS/SAXS), neutron spin echo (NSE), and computer simulations to conclusively identify the formation of reversible clusters and the morphology of clusters in highly concentrated and viscous mAb solutions. In particular, NSE makes it possible to estimate the hydrodynamic radius and characterize the dynamic properties in concentrated solutions. Our results provide conclusive evidence of the connection between the formation of reversible clusters with high excluded volume and the undesirable high viscosity of some mAb solutions.

Experimental Details

Materials and Methods

Two full-length humanized mAbs with markedly different solution viscosities, denoted mAb1 and mAb2, are used as model systems. Both mAbs are constructed with the same human IgG1 framework and thus have nearly the same molecular mass (≈150 kDa) and primary structure, with small sequence differences confined to the complementarity-determining region. The samples are purified so that the number of irreversible dimers is <3.2% for mAb1 and <0.5% for mAb2 (20). The structural properties of the solutions are dominated by monomers or reversibly associated aggregates. Detailed descriptions of these two mAbs can be found in the literature (7,20,21).

Lyophilized forms of these mAbs are reconstituted into D₂O-based buffers to reduce the incoherent background during neutron-scattering experiments. All of the formulations in this study are in 32 mM histidine/histidine-HCl buffer with 360 mM sucrose and 0.6 mg/mL polysorbate-20 (P-20) at pD ≈6.4 in D₂O. The theoretical net charges are +17 for mAb1 and +27 for mAb2 (21).

All rotational shear data were acquired on a stress-rate-controlled rheometer (Physica MCR 501, Anton Paar, Graz, Austria) using a 50 mm 0.490° anodized aluminum cone geometry with the temperature set at 20 ± 0.1°C for all experiments. A flow sweep, ascending and descending from 1 s⁻¹ to 2000 s⁻¹, was performed to check for hysteresis and sample degradation. mAb1 and mAb2 were measured at 5, 10, 20, 50, 100, and 150 mg/mL in their D₂O buffers. All samples were stable and reversible, with negligible hysteresis.

The SANS data were collected on the NG3 and NG7 beamlines at the NIST Center for Neutron Research (NCNR, Gaithersburg, MD). NSE experiments were performed on the NG5 at NCNR and on IN15 at Institut Laue-Langevin (ILL, Grenoble, France). The raw data were reduced and analyzed with the Igor Pro NCNR SANS software according to standard methods (23). The SAXS data were collected at the F2 beamline of the Cornell High Energy Synchrotron Source (CHESS). (It should be noted that reference in this document to certain commercial equipment, instruments, or materials does not imply recommendation or endorsement by the National Institute of Standards and Technology, nor does it imply that the products identified are necessarily the best available for the purpose.)

Theory for SANS/SAXS and NSE

When a particle is not spherical, as is the case for many nonglobular proteins, the measured SANS/SAXS intensity, I(Q), can be estimated, using the decoupling approximation (24,25), as

$$I\left(Q\right)=\varphi V_p{\left(\Delta \rho \right)}^{2}P\left(Q\right)\tilde{S}\left(Q\right)+B,$$ (1)

where B is the background, $V_p$ and $\varphi$ are the volume of one individual particle and the sample volume fraction, and $\Delta \rho$ is the scattering-length density difference between a particle and the solvent. Q = $(4\pi /\lambda )\sin (\theta /2)$, where θ is the scattering angle and λ is the neutron/x-ray wavelength. P(Q) is the angular averaged form factor, and $\tilde{S}\left(Q\right)$ is the apparent interparticle structure factor, which is linked to the true interparticle structure factor, S(Q), using the decoupling approximation (24,26):

$$\begin{array}{c}\tilde{S}\left(Q\right)=1+\beta \left(Q\right)\left(S\left(Q\right)-1\right)\\ \beta \left(Q\right)=\frac{{\left|\langle F\left(Q\right)\rangle \right|}^2}{\langle {\left|F\left(Q\right)\right|}^2\rangle }\end{array},$$ (2)

where F(Q) is the Fourier transformation of the density distribution of an individual particle. The angled brackets indicate the angular average of all possible orientations of a particle. Note that <|F(Q)|²> is equal to P(Q).

NSE measures the intermediate scattering function, I(Q,t)/I(Q), which can be fitted by a diffusion model to extract the apparent diffusion coefficient, D(Q). The latter contains the information of both internal dynamics and translational motion of particles in solution. We show later that in our experiments, the internal dynamics can be ignored such that the apparent diffusion coefficient is a good approximation of the translational diffusion coefficient.

In a colloidal system, solvent dynamics are typically very fast relative to those of colloidal particles. The relaxation time, τ_B, of a colloidal particle after it is perturbed by solvent molecules is typically very small (27). When the measurement time, t, is much larger than τ_B, colloidal particles are observed to execute Brownian motion. When a colloidal particle diffuses for a sufficiently long time, it will collide with other particles and diffusion will be hindered. This time is called the structural relaxation time, τ_I. Generally, when τ_B ≪ t ≪ τ_I, a colloidal particle is considered to diffuse in the short-time limit (13,27). τ_I can be expressed as

$${\tau }_I=\frac{R_0^2}{D_0},$$ (3)

where R₀ is the radius and D₀ the diffusion coefficient of the colloidal particle at infinite dilution (27). In the short-time limit, the intermediate scattering function, I(Q,t), can be expressed as

$$I\left(Q,t\right)/I\left(Q\right)=e^{-Q^2{D}_c\left(Q\right)t},$$ (4)

where $D_c\left(Q\right)=D_0\left(H\left(Q\right)/S\left(Q\right)\right)$ is the collective diffusion coefficient (27–29), and H(Q) is the hydrodynamic function, indicating how the particle diffusion is affected by complicated solvent flow patterns created by motions of the colloidal particles themselves. In the large Q limit, D_c(Q) = D_s, where D_s is the self-diffusion coefficient at the short-time limit. Given the size of a mAb protein, NSE measures the short-time dynamics of mAb proteins.

Computer simulations

Computer simulations are carried out to investigate the solution morphology of mAb dimers. We construct mAb dimers by associating two mAbs in various configurations, calculating the radius of gyration, and then comparing these calculations to experimental results. To survey potential relative positions of two mAb molecules in solution, we implemented a grid-based fast Fourier transform (FFT) docking algorithm based on shape complementarity, which was determined using Fourier correlation (30). A sufficiently large 3-dimensional grid was built around a single mAb molecule, and the grid spacing was set at 0.7 Å. A single target mAb molecule was centered and fixed on the grid, whereas a second ligand mAb molecule experienced stepwise Euler rotation. The radius parameter to construct the real-space map was set to be 1.8 Å, the surface layer thickness was set to be 2.5 Å, and the interior parameters (ρ and δ) of the target and ligand mAb molecules were set to be −15 and 1, respectively. The relative orientation of the ligand mAb with respect to the target mAb was sampled at a fixed interval of 5° along each Euler angle, yielding 23,328 structures that were evaluated using the FFT docking algorithm for surface complementarity. Sampling, FFT docking, and small-angle scattering calculations were carried out using SASSIE (31).

Results and Discussion

Fig. 1 a shows the solution viscosity (η) as a function of concentration, C, at 25°C, for mAb1 and mAb2. Note that mAb1 has an anomalously large viscosity of 310 mPa⋅S at 150 mg/mL, as compared to many other mAbs that have much lower viscosity at this concentration. For example, η for mAb2 is only 18 mPa⋅S at 150 mg/mL (Fig. 1 a). Even though η of mAb1 is not high compared to that of many other soft materials, such as polymer blends and colloidal glass/gel systems (32), it is sufficiently high to limit the allowable concentration for bulk manufacturing, as well as SC delivery. Interestingly, adding electrolyte (NaCl) significantly reduces the viscosity of concentrated mAb1 solutions, whereas it has a negligible effect for mAb2 (Fig. 1 b). The viscosity dependence on concentration and salt exhibits the same trends observed using water-based buffer, as reported in the literature (7). Fig. 1 c further compares the SANS patterns of the two mAb solutions at 150 mg/mL without added electrolyte. The scattering intensity for mAb2 shows a strong correlation peak due to the strong electrostatic repulsion between nearest neighbors. In contrast, mAb1 solutions show significantly less structure due to their anisotropic interaction potential, as discussed previously (21). With the addition of 150 mM NaCl, the electrostatic repulsion between mAb2 in solution is partly screened, as shown by the increase in scattering intensity at low Q (Fig. 1 d). Similar changes in the scattering patterns for mAb1 solutions are observed where I(Q) shows a significant increase in forward-scattering intensity when salts are added.

Figure 1.

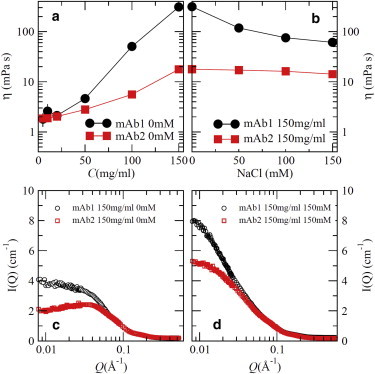
(a) Viscosity of mAb1 (solid circles) and mAb2 (solid squares) samples without added salts. (b) Viscosity of mAb1 and mAb2 samples at 150 mg/mL as a function of added salt concentration in buffers. (c and d) SANS patterns of mAbs at 150 mg/mL with (c) 0 mM NaC and (d) 150 mM NaCl. All measurements were performed at 25°C. Vertical lines indicate error bars with one standard deviation. Most error bars are smaller than the symbols. To see this figure in color, go online.

To identify cluster formation, some insights can be gained initially from examining the SAXS patterns of low-concentration solutions. The SAXS results for mAb1 and mAb2 at 5 mg/mL are shown in Fig. 2 a. The coherent scattering intensity, I(Q), can be expressed by Eq. 1. At very low concentrations, $\tilde{S}\left(Q\right)$ ≈ 1 and the apparent radius of gyration, R_G, can be estimated by Guinier analysis, as shown in Fig. 2 b. At 1 mg/mL, the apparent R_G is the same for both mAbs and corresponds to that of dispersed monomers in solution. However, when C increases, the apparent R_G for mAb2 decreases slightly due to the long-range electrostatic repulsion between the mAb2 proteins. In contrast, the apparent R_G of mAb1 increases from 5 nm at 1 mg/mL to 6.9 nm at 10 mg/mL, which is reversible upon dilution. Unlike mAb2, which remains dispersed as a monomer up to 10 mg/mL, a reversible clustering is apparent in mAb1 solutions. The cluster formation in mAb1 is further confirmed by dynamic-light-scattering (DLS) measurements of the collective diffusion coefficient, D_c(Q). Using DLS, an approximate hydrodynamic radius, R_H, can be estimated from the Stokes-Einstein-Sutherland equation, as shown in Fig. 2 c (29). (Although the structure factor, S(Q), can affect the estimated hydrodynamic radius, the estimated error from S(Q) is minor and does not affect our conclusions.) The apparent R_H for mAb2 remains constant at ≈5.4 nm when C ≤ 10 mg/mL, whereas the R_H for mAb1 is the same as that of mAb2 at 1 mg/mL and increases to 8.5 nm at 10 mg/mL. Again, it should be noted that this microstructure formation in mAb1 solutions is fully reversible upon dilution. Hence, the microstructure in mAb1 solutions consists of reversible clusters in equilibrium with monomers.

Figure 2.

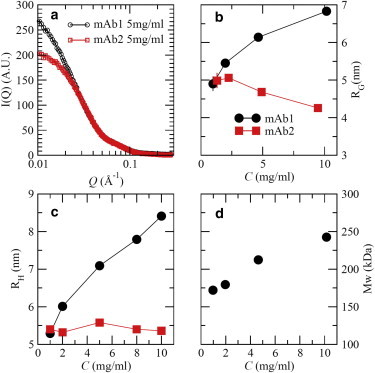
(a) SAXS patterns at 5 mg/mL without added salts. (b and c) The radius of gyration (b) and hydrodynamic radius (c) of both mAbs are shown. (d) Apparent Mw of mAb1, obtained from SAXS data. Vertical lines indicate error bars with one standard deviation. Most error bars are smaller than the symbols. To see this figure in color, go online.

The average apparent molecular mass, Mw, of the mAb1 clusters is further estimated using I(Q = 0). Assuming that $\tilde{S}\left(Q=0\right)\approx 1$, I(0) ≈ $\left(C{V}_p\Delta {\rho }^2/{\rho }_m^2{N}_A\right)Mw$, where ${\rho }_m$ is the mass density of an mAb protein, Mw is the average molecular mass of monomer or clusters in solutions, and $N_A$ is the Avogadro constant. The prefactor for Mw is independent of mAb protein structure at a given concentration and as such can be calculated using the scattering intensity and known Mw (≈150 kDa) of mAb2. Using the estimated prefactor value based on mAb2, the Mw of reversible clusters of mAb1 is estimated as a function of concentration (Fig. 2 d). It approaches ≈250 kDa at 10 mg/mL, consistent with previous static-light-scattering measurements at low concentrations (34). Note that ignoring $\tilde{S}\left(Q\right)$ may underestimate Mw by ≈20% at 10 mg/mL. (See the Supporting Material for details.) Therefore, the average molecular mass of formed clusters of mAb1 is close to that of an mAb dimer (Mw ≈ 300 kDa). Hence, the microstructure of mAb1 in solution progresses from dispersed monomers to an increasing proportion of clusters as the concentration increases from 1 to 10 mg/mL. The formation of clusters at low concentrations (<10 mg/mL) in mAb1 suggests that cluster size needs to be determined at higher concentrations, where the solutions exhibit an anomalously large viscosity (Fig. 1 a).

To extract a quantitatively accurate cluster size in the highly concentrated protein solution region, we use NSE to measure the short-time self-diffusion coefficient, D_s, of protein and to determine the hydrodynamic radius of the diffusing species. From I(Q,t)/I(Q), we can extract the apparent collective diffusion coefficient, D_c(Q), whose asymptotic value at the high Q limit is the short-time self-diffusion coefficient, D_s. The details of this method and analysis can be found in the literature (11–13,27,28,35–37). The D_c(Q) (Fig. 3 a) is extracted by fitting the data with a single exponential function for the correlation time of <50 ns. (One sample fitting of I(Q,t)/I(Q) is shown in the Supporting Material.) Using the method reported in the literature, we can estimate D_s by averaging values at Q > 0.15 Å⁻¹ (11). Note that within our Q range and time window, the contribution of any possible internal dynamics and rotational motions to the apparent diffusion coefficient is negligible. D_c(Q) in Fig. 3, a and b, remains almost constant at relatively large Q values (Q > 0.1 Å⁻¹). However, if internal and rotational dynamics are dominant contributions, they should produce a large increase in apparent D_c(Q) at the Q range whose corresponding length scale is commensurate with rotational and internal motions (38). Even for proteins with known strong internal motions studied by NSE, where D_c(Q) shows enhanced dynamics at large Q values, the relaxation time at high Q is dominated by translational motions, as the internal motions in those studies only contribute a small portion of the apparent D_c(Q) (39,40). Hence, the large difference we observe in D_c(Q) between mAb1 and mAb2 is mainly due to the change of translational motions.

Figure 3.

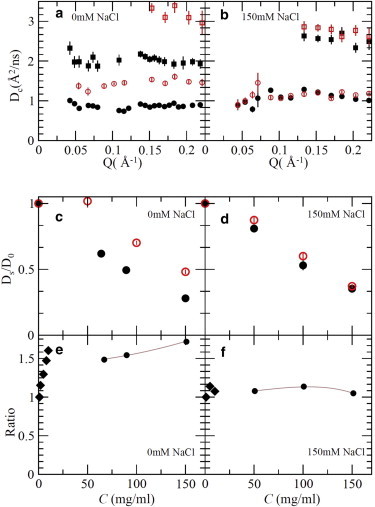
(a) D_c(Q) of mAb1 at 64 and 150 mg/mL (black solid squares and circles, respectively) and of mAb2 at 50 and 150 mg/mL (red open squares and circles, respectively) without added electrolyte. (b) D_c(Q) at 50 and 150 mg/mL with 150 mM NaCl added to the buffer. Solid and open symbols are for mAb1 and mAb2, respectively. (c and d) D_s/D₀ values for mAb1 (black solid circles) and mAb2 (red open circles) without (c) and with (d) added electrolyte. (e and f) Ratio of the 1/D_s of mAb1 to that of mAb2 for samples without (e) and with (f) 150 mM NaCl. Vertical lines indicate error bars with one standard deviation. Most error bars are smaller than the symbols. To see this figure in color, go online.

Clearly, D_s for mAb1 is much smaller than that for mAb2 at the same concentration, indicating that mAb1 still forms clusters at high concentrations. The normalized self-diffusion coefficients, D_s/D₀, of mAb1 (solid circles) and mAb2 (open circles) without added electrolyte are shown as a function of C in Fig. 3 c. At very low concentrations, D_s/D₀ = 1, as D_s is equal to the free diffusion coefficient of a monomer, D₀. The mAb2 proteins remain monomeric in solution up to ∼50 mg/mL. as D_s/D₀ ≈ 1. This is consistent with previous simulations and experimental results indicating that mAb2 remains dispersed as monomers up to at least 150 mg/mL without added salts (8,21,34). The decrease of D_s/D₀ is due to the hydrodynamic interaction effects with further increases in concentration (11,28).

Because R_H $\propto$ 1/D_s, the ratio of 1/D_s for mAb1 to that for mAb2 is an estimate of the average size of the diffusing objects in mAb1 solutions relative to the corresponding value in mAb2. (The hydrodynamic effect may slightly change the estimated R_H, but the effect is expected to be small, since hydrodynamic function at large Q limit is not very sensitive to interactions between colloidal particles if there is no cluster formation.) As mAb2 retains its monomer structure within our studied concentration range, this ratio can be viewed as approximately the relative size of reversible clusters in mAb1 solutions. Fig. 3 e shows the ratio of 1/D_s for mAb1 to that for mAb2 as a function of C. Note that when C ≤ 10 mg/mL (Fig. 3 e, solid diamonds), D_s is obtained by DLS, whereas at higher concentrations, D_s is obtained from NSE. The diffusivity results confirm that at ≤1 mg/mL, both mAb1 and mAb2 disperse predominantly as monomers in solution. However, by 10 mg/mL, the ratio of 1/D_s for mAb1 to that for mAb2 reaches ∼1.6. It is striking to observe that this ratio does not change substantially with further increases in concentration up to 150 mg/mL. This suggests that once mAb1 protein clusters form at relatively low concentrations (≈10 mg/mL), their average size remains relatively constant up to relatively large concentrations. This behavior is akin to that of self-assembled micellization in surfactant solutions, where above a critical micelle concentration all additional surfactants added to the system form micelles. The NSE diffusivity results therefore suggest that the critical monomer concentration for mAb1 is ∼10 mg/mL. Hence, at high concentrations, such as 150 mg/mL, the dominating fraction of mAb1 species is small reversible clusters with a preferred size.

The presence of these reversible clusters correlates with a high solution viscosity, which indicates that controlling the formation of clusters should adjust the viscosity of the system accordingly. Fig. 3 b shows the D_c(Q) of mAb1 and mAb2 solutions at 50 and 150 mg/mL with 150 mM NaCl added. The SANS patterns at 150 mg/mL with 150 mM NaCl are shown in Fig. 1 e. Because the electrostatic repulsion is screened by added salt, SANS patterns of both proteins show a strong low-Q intensity that could be mistakenly interpreted as an increase in cluster size. Conversely, Fig. 3 d clearly indicates that for mAb1 (black solid circles), D_s/D₀ increases when electrolyte is added, signifying that the average size of the reversible clusters becomes smaller. The decrease in average cluster size is due to the decrease in mAb1 protein-protein attraction. Our previous SANS study indicated that the attraction between mAb1 proteins is anisotropic and is due to the nonuniform charge distribution on mAb protein surfaces, which can subsequently be screened by increasing salt concentration (21). This decrease in average cluster size is associated with a commensurate decrease in solution viscosity for mAb1 (Fig. 1 b); for example, the viscosity of mAb1 at 150 mg/mL is reduced by 80% upon salt addition. This provides strong evidence that the presence of small reversible clusters is responsible for the increased viscosity of mAb1 solutions before salts are added.

The viscosity of mAb1 (Fig. 1 b, black solid circles) is still quantitatively larger than that of mAb2 (Fig. 1 b, red solid squares) despite the large decrease in the viscosity of mAb1 after addition of 150 mM NaCl. To understand the physical basis for the difference, we further compared the D_s/D₀ for mAb1 and mAb2 solutions with added salts (Fig. 3 d, black solid circles and red open circles, respectively). We found that after adding 150 mM NaCl, the D_s/D₀ becomes nearly identical for mAb1 and mAb2 at 150 mg/mL, indicating that the average size of the moving units becomes almost equal if we assume that the hydrodynamic interactions are similar. However, the structure formed in mAb1 solution has a larger length scale compared to that formed in the corresponding mAb2 solution, as indicated by the larger low-Q SANS intensity in the mAb1 pattern (Fig. 1 d). This difference in scattering and, correspondingly, in viscosity, is due to the small difference between mAb1 interactions and mAb2 interactions in solution. Although the attraction between mAb1 proteins is much weaker with added salts in solution, it is still slightly stronger than that between mAb2 proteins, as also observed previously at similar ionic strength (34). Thus, the formation of a large-length-scale network of loosely interacting monomers in mAb1 results in the slightly higher viscosity for this solution compared to similar solutions of mAb2. In the absence of added electrolyte, no mAb1 network will form, as can be seen from the suppressed intensity of SANS patterns in Fig. 1 c. Therefore, the dominant reason for the increased viscosity of mAb1 solution without added salts is mainly due to the formation of small protein clusters.

The size of reversible clusters in concentrated mAb1 solutions without added salts is similar to that at 10 mg/mL, at which concentration the apparent Mw of mAb1 clusters is approximately that of a dimer. Hence, it is likely that dimers dominate the solution at 10 mg/mL. It is thus useful to consider computer models of mAb1 dimeric clusters as the probable moving units. Dimers consisting of two identical mAbs using the crystal structure were generated by randomly associating two proteins. Although in general the solution structure of a mAb protein may differ from its crystal structure, we find that the R_G of the crystal structure (∼52 Å) agrees well with the R_G of the monomer protein in solution, obtained by SAXS measurements at 1 mg/mL. Therefore, we feel that the estimated R_G of dimers constructed using the crystal structure should be very helpful in qualitatively identifying the dimer structure. The R_G values for randomly associated dimers are shown in Fig. 4. (Note that we did not show individual results for all 23,328 configurations in Fig. 4, but the selected points are representative of all configurations.) As shown in Fig. 2 b, the mAb1 clusters have an experimental R_G of ≈6.9 nm at 10 mg/mL. Only a few of the representative configurations shown in Fig. 4 have an R_G around 7.0 nm. These configurations have an extended structure. Hence, it is likely that the clusters at high concentration also maintain an extended, open structure. This larger effective volume of open-structured clusters is consistent with an increase in solution viscosity. In contrast, the opposite effect has been reported for a densely packed cluster (42). Such relatively extended configurations (e.g., with Fab-Fab and Fab-Fc interactions) are also seen in molecular dynamics simulations of concentrated mAb1 solutions that use a coarse-grained charge distribution to approximate mAb1 charge heterogeneity (8). The simulations also suggest that Fab-Fab interactions are much more prevalent in mAb1 than in mAb2.

Figure 4.

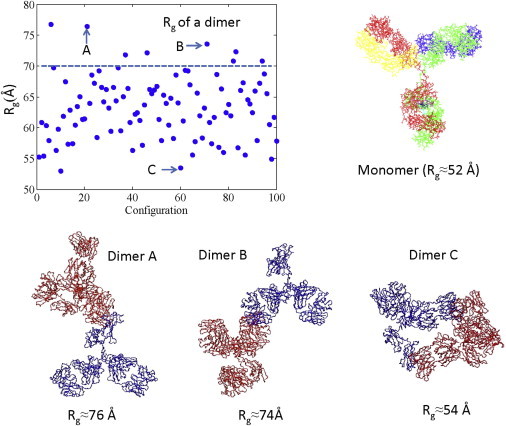
Estimates of the R_G values of dimers in different configurations. The representative dimers A–C correspond to the configurations indicated in the plot at upper left. To see this figure in color, go online.

It is also important to note that cluster formation in mAb1 solutions is qualitatively different from that observed in globular protein solutions such as lysozyme, where clusters only form at relatively high concentrations (>100 mg/mL) and the average size increases with the increase in volume fraction (11,13). Cluster formation in mAb1 solutions first appears at much lower concentrations (<10 mg/mL), and the size of clusters does not change over a wide concentration range. In other words, the mAb1 proteins form clusters with a preferred size over a relatively broad range of concentrations, which is a solution behavior similar to that observed in simple micellization (43). Here, we attribute this behavior to the very site-specific, anisotropic attraction between mAb1 proteins observed previously using SANS (21) and molecular modeling (8). Thus, in contrast to models for homogeneous spherical colloids, where cluster formation is a consequence of short-range attraction and long-range repulsion (17), the formation of protein clusters in our mAb solutions is driven by very specific, anisotropic interactions between mAbs in solution. The SANS and DLS experimental results (21,44), together with the coarse-grained computer simulation (8), support the idea that this specific interaction is due to the electric dipole effect, whose interaction strength is very sensitive to the ionic strength. This is also consistent with the observed decrease in the average size of clusters when salt is added to solutions, as the added salts can weaken the dipole attraction.

Conclusion

In conclusion, using NSE and SANS/SAXS to measure diffusivity and probe the microstructure of two model mAb proteins in solution over a broad concentration range with and without salt, we conclusively demonstrate that the formation of a reversible cluster phase for mAb1 in solution is consistent with the observed increase in viscosity of mAb solutions. We attribute this to the increased effective volume of clusters, as they have more extended structure. Interestingly, the average cluster size for mAb1 is that of a dimer, and it remains nearly identical over a wide range of concentrations. This unique mAb solution behavior has similarities to classical, idealized micelle formation. This suggests a unique method for control of protein clusters and solution viscosity by controlling these specific, anisotropic interactions through engineering the primary structure of mAbs. Not only do the insights obtained here regarding mAb clustering have important implications for the development of mAbs and their formulations with desired solution properties, but they also have a significant impact on our fundamental understanding of protein clustering observed in a wide range of solutions.