Attraction of Rotors to the Pulmonary Veins in Paroxysmal Atrial Fibrillation: A Modeling Study

Abstract

Maintenance of paroxysmal atrial fibrillation (AF) by fast rotors in the left atrium (LA) or at the pulmonary veins (PVs) is not fully understood. To gain insight into this dynamic and complex process, we studied the role of the heterogeneous distribution of transmembrane currents in the PVs and LA junction (PV-LAJ) in the localization of rotors in the PVs. We also investigated whether simple pacing protocols could be used to predict rotor drift in the PV-LAJ. Experimentally observed heterogeneities in I_K1, I_Ks, I_Kr, I_to, and I_CaL in the PV-LAJ were incorporated into two- and pseudo three-dimensional models of Courtemanche-Ramirez-Nattel-Kneller human atrial kinetics to simulate various conditions and investigate rotor drifting mechanisms. Spatial gradients in the currents resulted in shorter action potential duration, minimum diastolic potential that was less negative, and slower upstroke and conduction velocity for rotors in the PV region than in the LA. Rotors under such conditions drifted toward the PV and stabilized at the shortest action potential duration and less-excitable region, consistent with drift direction under intercellular coupling heterogeneities and regardless of the geometrical constraint in the PVs. Simulations with various I_K1 gradient conditions and current-voltage relationships substantiated its major role in the rotor drift. In our 1:1 pacing protocol, we found that among various action potential properties, only the minimum diastolic potential gradient was a rate-independent predictor of rotor drift direction. Consistent with experimental and clinical AF studies, simulations in an electrophysiologically heterogeneous model of the PV-LAJ showed rotor attraction toward the PV. Our simulations suggest that I_K1 heterogeneity is dominant compared to other currents in determining the drift direction through its impact on the excitability gradient. These results provide a believed novel framework for understanding the complex dynamics of rotors in AF.

Introduction

The mechanisms of atrial fibrillation (AF), the most common cardiac arrhythmia in the clinical practice, are not fully understood. Acute AF in normal isolated sheep hearts has been found to often depend on fast rotors localized mainly to the posterior wall of the left atrium (LA) and the pulmonary-veins (PVs) junction (PV-LAJ) with fibrillatory conduction toward the rest of the atria (1). Recent clinical data also point to rotors in various atrial sites as a mechanism driving paroxysmal AF (2–4). Previous simulations have already demonstrated that rotors can occur in the PV-LAJ, provided the PV size is adequate and that nonuniform coupling conditions exist (5). However, how the rotors form or drift in the PV-LAJ, as well as the underlying ionic mechanisms, have not been investigated systematically (6,7).

Earlier studies using simplified cardiac models have shown a causal link between rotor drift and spatial heterogeneity in the action potential (AP) properties (8). Rotors drifted toward regions with prolonged action potential duration (APD) or reduced excitability (9), which were mainly due to heterogeneities in multiple ion channels (10). In particular, the role of K⁺ currents I_K1 (inward rectifier potassium current) and I_Kr (rapid delayed rectifier potassium current) may be important, because they are known to be heterogeneously distributed in the heart (11), and have also been shown to influence rotor dynamics by affecting both the membrane APD and excitability (12–14). However, the complex heterogeneity in the expression of these channels at the PV-LAJ, such as in dogs, which show a larger current density of I_Kr and a smaller density of I_K1 in the PV compared to LA (15,16), in conjunction with structural discontinuities (i.e., narrow PV sleeves compared to the larger LA), precludes a simple prediction of the rotor dynamics at the PV-LAJ.

Our study aims to elucidate ionic mechanisms of rotor drifting at the PV-LAJ. We construct two- and pseudo three-dimensional models of the PV-LAJ to investigate the hypothesis that the characteristic heterogeneous dispersion of transmembrane currents during paroxysmal AF, in absence of remodeling, is a determinant of rotor drift. Our numerical simulations demonstrate I_K1 dominance in conveying a preferential rotor drift direction toward the PVs. We further demonstrate the cycle-by-cycle mechanism by which regions with longer refractoriness and lower excitability tend to attract rotors, and propose a set of measures to confirm our mechanistic proposition linking the ionic properties of the atrial substrate and the predisposition of the PVs, or any other region, to attract or repel rotor activity during AF (17–19).

Methods

Numerical models

Numerical simulations were performed on three models of the junction between the LA and the PV (see Fig. 1 and the Supporting Material) with increasingly realistic anatomical descriptions, as follows:

• 1.A 50 × 50 mm² regular two-dimensional square mesh model was implemented and subjected to no-flux boundary conditions;
• 2.A pseudo-three-dimensional cylindrical surface model was constructed by applying no-flux boundary conditions at the LA and PV edges, and periodic boundary conditions on the other two edges of a regular two-dimensional mesh; and
• 3.A pseudo-three-dimensional funnel-shaped surface was constructed with near-equilateral triangulated mesh with no-flux boundary conditions on the wide (LA) and narrow (PV) edges.

Figure 1.

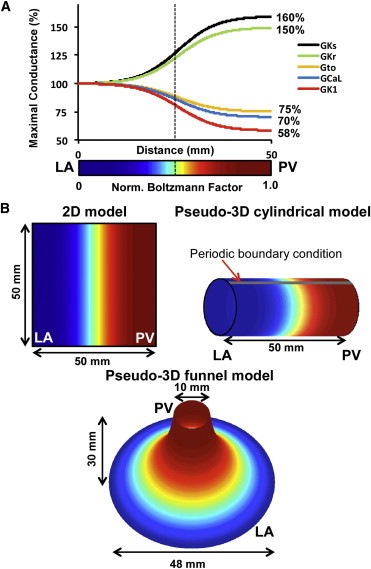
The PV-LAJ models. (A) Conductances for I_CaL, I_kr, I_ks, I_to, and I_K1 follow a Boltzmann function (x_1/2 = 25 mm, vertical dashed line; Δx = 5 mm) from LA to PV. (Color bar) Normalized Boltzmann factor across the junction. (B) Simulations were performed on 1), two-dimensional model of 50 × 50 mm²; 2), cylindrical pseudo three-dimensional model generated by a periodic boundary condition in the two-dimensional model; and 3), a funnel-shaped pseudo three-dimensional model. Colors represent the Boltzmann factor values. (Cyan-yellow) Steepest gradient region in the PV-LAJ.

The transmembrane potential was based on the Courtemanche-Ramirez-Nattel and Kneller (CRN-K) model of human atrial cell kinetics in the presence of 0.0015 μM acetylcholine (20–22). Electrical activity was computed using a mono-domain and numerically stable Euler forward scheme with 100-μm internodal distance, 0.005-ms time step, and isotropic diffusion coefficient of 0.062 mm²/ms adjusted for conduction velocity of 48 cm/s. Initial conditions were the steady-state membrane variables after pacing a single cell at 1 Hz for 10 s.

Heterogeneous ionic conditions were implemented by assigning a spatial Boltzmann distribution of conductance for I_K1, I_Ks (slow delayed rectifier potassium current), I_Kr, I_to (outward transient potassium current), and I_CaL (L-type calcium current) values between the LA and the PV based on data from dogs (16). This is described in Fig. 1 A, where maximum conductance for I_Kr and I_ks were increased by 50 and 60%, respectively, whereas I_K1, I_to, and I_CaL were diminished by 42, 25, and 30%, respectively. Three conditions of ionic heterogeneity were modeled, as follows:

• Condition I—all currents varied spatially according to their corresponding Boltzmann function;

• Condition II—all currents, except I_K1, varied; and

• Condition III—only I_K1 varied in space.

Additional conditions of heterogeneous intercellular coupling coefficient and distribution of I_Na (sodium current) are described and studied in the Supporting Material. Reentrant excitation patterns were induced by S1-S2 cross-field stimulation protocols and their pivoting points were identified as a singularity point (SP) and tracked in the phase domain (see Fig. S1 and Movie S1 in the Supporting Material).

Effective refractory period (ERP) was defined as the shortest interval of premature excitation for various basic cycle length trains after reaching steady state (see the Supporting Material). Spatial profiles of APD and peak sodium channels availability (h×j)_peak were obtained by averaging those parameters in time for every pixel across the model in the last two 5-s simulations. Measurements of minimum diastolic potential (MDP) and maximum upstroke velocity (dV/dt_max) followed a similar procedure.

Results

Ionic gradients and rotor attraction toward the PV

As a demonstration of dependence of rotor drift in the PV-LAJ on the specific ionic current heterogeneity, we generated rotors in the three conditions implemented in the cylindrical and flat model and tracked the spontaneous trajectory of their SP. Fig. 2 demonstrates that the rotor in the heterogeneous PV-LAJ region is unstable and its drift direction is a direct consequence of the particular ionic dispersion.

Figure 2.

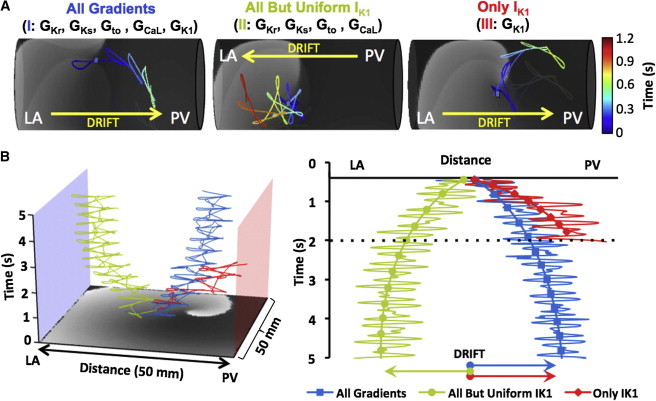
Simulations of rotor drift in the PV-LAJ and I_K1 role. (A) Rotor dynamics on the cylindrical model using the CRN-K kinetics under three conditions: 1), all currents varied spatially; 2), all currents varied spatially, except I_K1; 3), only I_K1 varied spatially. (Color-coded traces) SP trajectory of rotors initiated at the middle of the models (blue dots). Rotors under Conditions I and III drifted toward the PV edge. Drift direction was reversed when I_K1 heterogeneity was excluded in Condition II. (B) Time-space plots (and arrows) show rotor drift for the three conditions in a flat two-dimensional model.

In Condition I, i.e., heterogeneity in the currents I_K1, I_Ks, I_Kr, I_to, and I_CaL as characterized at the PV-LAJ in dog (16), the drift is toward the PV edge of the model. However, when all the currents except I_K1 are set to be heterogeneous, and I_K1 density is maintained homogenously, and is equal to the LA region value (Condition II), the drift reverses toward the LA (note that when the I_K1 is homogeneously equal to the PV region—which is not shown here—the drift is also toward the LA). On the other hand, when all the currents are set uniform (either with the LA or the PV values) and only I_K1 is set to disperse as in the dog (Condition III), the drift is again toward the PV, but with a faster rate as compared with the drift in Condition I. This set of three scenarios in cylindrical as well as in the flat models, shown in Fig. 2, clearly points to the strong effect of I_K1 on the direction of the rotor drift in the LA-PV junction area.

As controls, we simulated rotors in two-dimensional models with uniform ionic properties of either the LA or the PV that revealed nondrifting rotors. The rotors in the model with uniform LA properties were slightly faster than those in the model with the uniform PV properties (7.7 vs. 7 Hz, respectively; other properties of the rotors did not vary by >∼10%; see Fig. S2). We further tested the effect of all individual and pairwise currents on drift by switching them from heterogeneous to uniform (see Fig. S3) and concluded again that the I_K1 heterogeneity is the primary ionic factor that determines the direction of the drift toward the PV. To better understand the mechanisms leading to the attraction of the rotor toward the PV region, we quantified electrophysiological properties of the action potential and its propagation across the PV-LAJ.

Heterogeneous excitability and rotor drift in the PV-LAJ

Ionic heterogeneity is imposing nonuniform excitability properties and a rotor drift toward a predictable direction (9). In Fig. 3, we analyze the role of tissue excitability in rotor drifts by quantifying the spatio-temporal distribution of the product of membrane model parameters h and j (h×j, the fraction of sodium channels available for activation), which determines the I_Na availability during rotor pivoting (22). Fig. 3 A illustrates the drift trajectory of a rotor in a two-dimensional model under Condition I and shows a time-space plot of h×j along the line of the drift. A closer look at the time-space plot near the pivoting location during a single cycle shows higher values of h×j at the left side (LA) of the drift than at the right side (PV). Thus, a progressive shift of the pivoting point toward the PV is always toward a region with lower h×j values.

Figure 3.

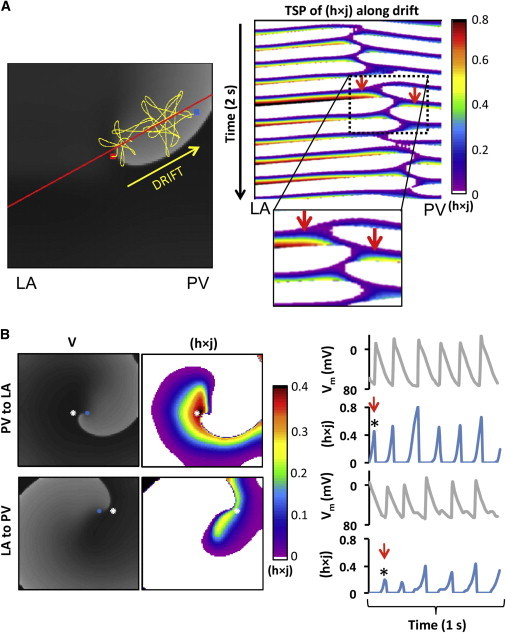
Heterogeneous sodium availability during rotor drift. (A) (Left) Voltage snapshot (gray scale) with superimposed trajectory of rotor SP (yellow tracing) drifting from the center of the model (red dot) toward its final location at the PV edge (blue dot). (Right) Color-coded time-space plot for h×j along the rotor drift direction (red solid line in voltage snapshot). (Inset) Magnified view showing close to the rotor core h×j is larger on the LA side than on the PV side (red arrows). (B) (Left) Snapshots of voltage (gray scale) and h×j (color-coded) maps at two instances; when the rotor wave-front near the core is directed from PV to LA (top); and approximately a half-cycle later, when it is directed from LA to PV (bottom). (Blue dots) Tip of the rotor; (white dots) 4 mm from tip, toward LA (top) and toward PV (bottom). (Right) Single-pixel time-series showing simultaneous voltage and h×j (white dots). (Red arrows) Times of the voltage and h×j snapshots on the left side of the panel.

Fig. 3 B shows snapshots of the voltage and h×j at a moment when the wavefront near the rotor tip is propagating toward the LA (top) and a half-cycle later, when that wavefront is propagating toward the PV (bottom). The h×j snapshots clearly demonstrate that the wave propagating toward the LA is facing a higher h×j (red) as compared with the wave propagating toward the PV. The h×j gradient during the drift is further confirmed by plotting the time-course of the voltage and h×j at 2 pixels flanking momentarily the SP of the rotor: one on the LA side and the other on the PV side, 4 mm away from the tip. Those plots show that the peak h×j for each cycle at the LA side is always >0.4 and at the PV side is always <0.4. As illustrated in greater detail in Fig. S4, the alternating SP drift is larger during propagation toward the PV (low h×j) than during its propagation toward the LA (high h×j). The result is a net drift toward the lower h×j (i.e., less excitable) region. Importantly, it is noticeable that a presence of heterogeneity at the core area is critical for the rotor drift; in absence of heterogeneity at the core, a rotor may be stable (see Fig. S5).

Fig. 4 summarizes the relationship between rotor drift and spatial distribution of excitability factors during reentry in the three conditions simulated. Fig. 4 A shows, for illustration purposes, a map with the distribution of the time-averaged h×j_peak for the model with greatest excitability gradient (Condition III) and shows that those values are approximately twofold larger in the LA edge compared with those at the PV edge (0.8 and 0.4, respectively). The graph in Fig. 4 A presents the spatial profiles of the h×j and the drift direction for the three conditions. It is seen that the two conditions with lowest density of I_K1 at the PV edge (blue and red) have profiles with reduced h×j at that edge as well, in contrast to the condition without the I_K1 gradient, where h×j is maximal at the PV edge. Overall, the directionality of the drift in the three conditions as indicated by the superimposed arrows is fully consistent with the rotor attraction by any region with lowest h×j values.

Figure 4.

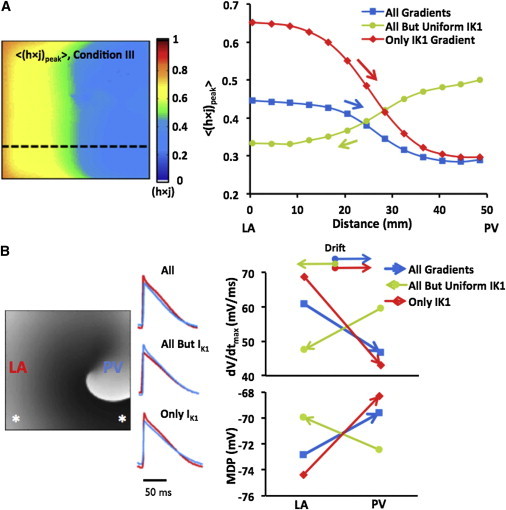
Gradients of sodium availability and AP measurements during rotor drift predict drift direction. (A) (Left) Map of averaged (h×j)_peak (〈(h×j)_peak〉) during rotor activity under Condition III; only I_K1 is showing an LA-to-PV decrease. (A) (Right) PV-LAJ spatial profiles of 〈(h×j)_peak〉 for the three conditions modeled. (Superimposed arrows) Direction of rotor drift for each condition, consistently toward the region of lowest 〈(h×j)_peak〉 (lowest sodium availability). (B) AP measurements of excitability during reentry. (Left) A voltage snapshot and APs from the LA (red) and PV (blue) edges (asterisks on map) for the three conditions simulated. (Right) Upstroke velocity (dV/dt_max) and MDP at the LA and PV region with direction of drift (arrows) for the three conditions. Drift is consistently toward lowest upstroke velocity and most positive MDP regions.

Next, Fig. 4 B quantifies metrics associated with the AP measurements of excitability: we focus on the dV/dt_max and MDP, which plays a role in determining the availability of I_Na during the membrane depolarization. On the left side, we present samples of aligned pairs of action potentials recorded in locations (asterisks) near the LA (red) and PV (blue) edges during reentry in the three conditions. As can be appreciated, each condition presents a distinct heterogeneity in its action potentials as quantified on the right side of the panel. For the three conditions, the drift direction is toward the regions with lowest excitability, as determined by the slowest dV/dt_max and most positive MDP (22).

Pacing predictors of rotor drift in the PV-LAJ

We investigated pacing protocols that could be used to predict drift direction. In Fig. 5, we demonstrate APD profiles consequential of a steady pacing at the center of the junction where rotors were initiated and radial propagation. Fig. 5 A, illustrates the steady-state APD₈₀ profiles at 2 Hz pacing for the three conditions along with an indication of drift direction. The APD profiles show different gradients for each particular condition of ionic gradients. Correlating the APD profiles with the reentry simulations we find that rotors initiated in Condition I drifted toward the PV (Fig. 2 B) and stabilized at the shortest APD region. When the I_K1 gradient is excluded (Condition II), the APD difference across the transition is maintained, but the drift direction reversed. In Condition III, the spatial APD difference is reversed. Yet, the rotor drifts from the LA to the PV, and does it even faster (Fig. 2 B) because there are no ionic effects opposing the I_K1 effect. Fig. 2 B presents ERP and dV/dt_max determined at 2 Hz pacing at the LA and PV edges. It is demonstrated that while ERP is, like APD₈₀, inconsistent with drift toward either longer or shorter periods, the drift is consistently toward the highest dV/dt_max for the three conditions.

Figure 5.

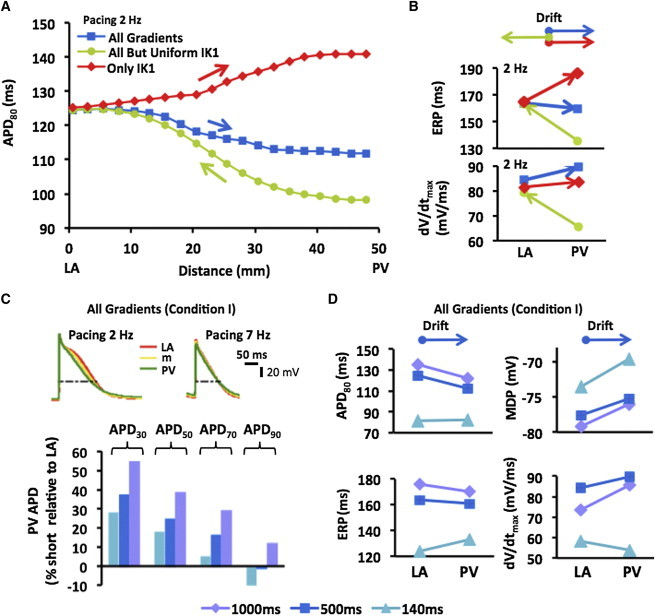
Pacing predictors for drift direction. (A) APD₈₀ profiles resulting from pacing at 2 Hz in the middle of the model show inconsistent drift (arrows) toward either short or long APD regions for the three simulated conditions. (B) ERP and dV/dt_max measured at LA and PV at 2 Hz pacing for the three conditions show inconsistent drift direction. (C) Frequency-dependence of APDs. (Top) Single pixels APs in three locations across the PV-LAJ at 2- and 7-Hz pacing. (Bottom) APDs in the PV relative to those in the LA. Notably, at all pacing rates slower than 140 ms (7.14 Hz, close to the rotation frequencies in the LA and PV; see Fig. S1), the APD in the PV is shorter than in the LA (except APD₉₀ at 140 and 500 ms). (D) APD₈₀, ERP, MDP, and dV/dt_max in the LA and PV as measured at 1000, 500, and 140 ms pacing rate. Drift direction is also indicated (arrows on top). To see this figure in color, go online.

Noticeably, the LA-PV dV/dt_max gradient directions (measured at 2 Hz pacing) in Fig. 5 B are contrasting the dV/dt_max gradient directions in Fig. 4 B (measured during reentry at ∼7 Hz), leading us to further assess the dependency of AP properties on pacing frequency. The traces at the top of Fig. 5 C show that APs in Condition I display distinct variation of duration at different repolarization levels during increasing pacing rate from 2 to 7 Hz. The bar-graph at the bottom of Fig. 5 C compares APD values across Condition I for 1000, 500, and 140 ms cycle lengths (respectively, 1, 2, and 7.14 Hz pacing rates). It shows that at 1 Hz pacing, the PV APD is shorter than the LA at all repolarization levels; and that at 2 Hz, and even more so at 7 Hz (close to the rotor frequency), APD₉₀ at the PV edge is longer than in the LA. Fig. 5 D shows that APD₈₀, dV/dt_max, and ERP across the model with Condition I heterogeneity measured only at a cycle lengths of 140 ms (7.14 Hz) resulted in gradient directions consistent with the previous prediction of the drift toward longer APD and lower excitability (9,23,24). However, the LA-PV dispersion of MDP displayed a rate-independent correlation with the drift direction. Regardless of the pacing rate, though, the drift was found consistently toward the region with the most positive MDP (also for Conditions II and III, not shown).

The I_K1 and rotor drift direction

Fig. 2 and Fig. S3 demonstrated the important role of I_K1 in determining the direction of the rotor drift in the PV-LAJ. Here we study the effect of various relevant current-voltage relationships of I_K1 on such drift direction. Fig. 6 A shows four relationships between the current density and transmembrane voltage (I/V relationship) for different I_K1 levels, including up- and downregulation, as well as their corresponding APs showing different APDs and MDPs. The four I/V relationships were incorporated in a PV-LAJ model with Condition I, and rotor activity as well as AP parameters were tracked. As can be observed from Fig. 6 B, increasing or decreasing the I_K1, increases or decreases the average rotor frequency, respectively. Fig. 6 C demonstrates that h×j profiles across the PV-LAJ vary both in levels and gradient directions as a consequence of altering the I/V relationships. In particular, it is noticeable that the rotor drifts toward the PV for a broad range of I_K1 levels whereas a reversal in the drift and h×j gradient direction occurs only at a 75% reduction in I_K1 (a behavior similar to that of a uniform I_K1 shown under Condition II in Fig. 2).

Figure 6.

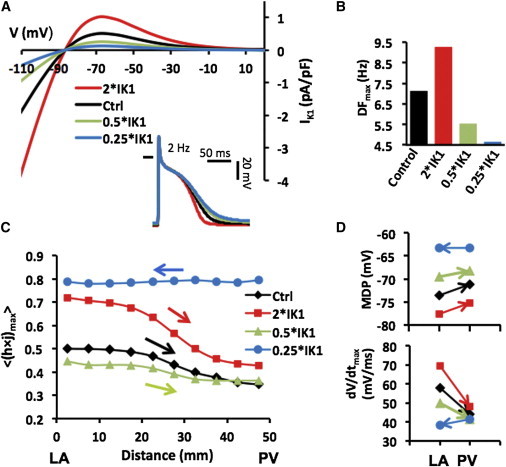
I_K1 levels and drift direction. (A) I_K1 I/V curves for normal (control) and other levels of I_K1 density. Steady-state APs induced at 2 Hz are illustrated. (B) Rotation frequency in LA homogenous model for each I_K1 density level. (C) Average peak I_Na availability profiles show drift toward lower excitability (arrows) in a model with Condition I. (D) Analysis of MDP and dV/dt_max for each profile at single pixels in the LA and PV (4 mm from boundaries) under Condition I. To see this figure in color, go online.

Up- and downregulation of I_K1 also hyperpolarize and depolarize MDP as well as increase and decrease upstroke speed, respectively (Fig. 2 D), with consistent drifts toward higher MDP and lower upstroke velocity. Overall, the consequences of altering the I/V properties of I_K1 in the heterogeneous models on, MDP and upstroke velocity shown in Fig. 2, C and D, are complex and suggest a nonmonotonic dependency. Nevertheless, further alterations in extracellular potassium concentration in the range of 4–7 mM, as well as alteration in the I/V profile to resemble closely those of Kir_2.1 or Kir_2.3 (25), affect excitability and rotation frequency, but do not alter direction of h×j gradients and drift directions toward the PV (see Fig. S6).

Comparative effects of ionic, passive, and geometrical gradients on rotor drift

A gradient in membrane currents is just one of the factors that may affect rotor drift. For example, the PV-LAJ is known to have a heterogeneous intercellular coupling that is also known to affect rotor drifts. Based on a 25% lower density of gap junctions and connexins relative to the rest of the atria (26), the intercellular coupling in the PVs’ region of the LA is speculated to be lower than that of the LA. As expected, the gradient in the passive properties of the tissue (24,27) attracted the rotor toward the PV, where the coupling coefficient is the lowest (see Fig. S7) and in a direction similar to that of the ionic gradients. Interestingly, our simulations suggest that the I_K1 heterogeneity is still a major factor determining the drift direction in the presence of the heterogeneous intercellular coupling.

In addition to the ionic heterogeneity, a prominent geometrical feature of the LA-PV junction, namely its funnel-shaped walls, may also affect functional rotor dynamics by spatial confinement in the PV and asymmetric source-sink relationships with the LA (5). In contrast to the gradient in the coupling, the effect of the geometrical confinement of the PVs on drift is not clear. Accordingly, we constructed a control homogeneous model with a uniform level of ionic currents and another model with heterogeneous distribution of the ionic currents (Figs. 1 and 2). A single functional rotor was initiated in both models close to the LA edge (see Fig. S1) and its spontaneous meandering and drift were tracked by the trajectory of its SP. In Fig. 7 we show that the ionic gradients play an important role in the drift of a rotor toward the PV even in the presence of a constraint imposed by the narrowing space near the PV. Panel A shows phase snapshots and the trajectory of the rotor superimposed on a homogeneous (left) and heterogeneous (right) funnel models. Panel B is a bull-eye presentation of the rotor trajectory in the homogeneous (left) and heterogeneous (right) funnel models. Panel C of Fig. 7 shows that the SP trajectory over a period of 5 s after onset in the heterogeneous versus the homogeneous model is characterized by a drift toward the PV, with gradual shortening of the distance between the pivoting point and the PV edge of the funnel model. Thus, we conclude that a generic funnel shape of a realistic dimension of the LA-PV junction does not eliminate the rotor attraction of the PV that is induced by the dispersion of ionic currents across that region.

Figure 7.

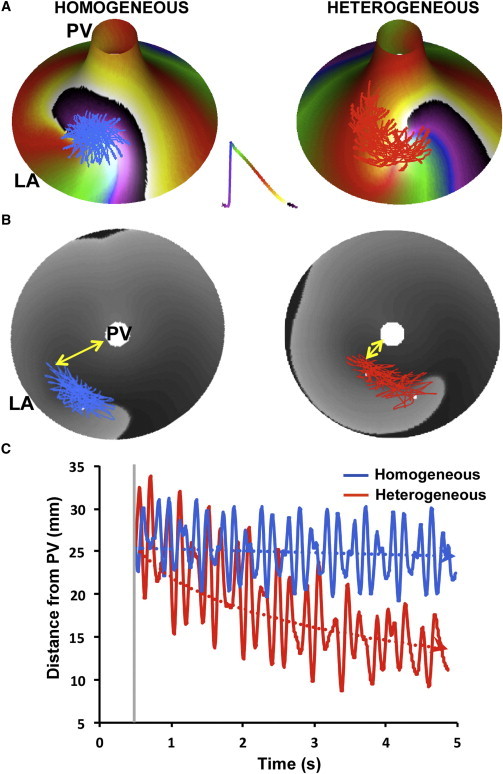
Geometry and drift. (A) Funnel-shaped PV-LAJ models with homogeneous (left) and heterogeneous (right, Condition I, see Fig. 1). Phase color-coded snapshot activity (see inset) and SP trajectory are superimposed on the model. (B) Bull-eye view of the models in panel A with voltage snapshot (gray levels) and SP trajectories. (Yellow arrows) Sample distance between the SP and the PV. (C) The decreasing distance between the SP and the PV edge demonstrates a PV attraction in the heterogeneous (red) versus the homogeneous (blue) model.

Discussion

The main findings of our study are as follows:

• 1.The heterogeneous distribution of transmembrane currents in the PV-LAJ plays a major role in the preferential localization of rotors near or at the PVs, and that the spatial dispersion of I_K1 is particularly important in determining such attraction.
• 2.Rotor drift in the PV-LAJ can be attributed to an excitability (maximum I_Na availability) gradient near the rotor pivoting point.
• 3.In dissecting tissue properties that can explain rotor drift by conducting simple 1:1 pacing protocols, the MDP variable is a reliable predictor, independent of frequency of pacing (that is, more-positive MDP attracts rotors). And finally,
• 4.The generic funnel-shaped geometry and the intercellular coupling dispersion in the PV-LAJ do not alter the ionic-induced attraction of rotors toward the PV, and further suggests that the particular dispersion of transmembrane currents present in the PLA during paroxysmal AF contributes to the important role of the PVs in maintaining the arrhythmia.

Mechanisms of AF and rotor dynamics

Our understanding of AF in individual patients would benefit from knowledge of how driving rotors form and then become stable or unstable, under the conditions of multifactorial substrate heterogeneity (28,29). Paroxysmal AF in patients and in isolated normal sheep hearts has been found often to depend on fast rotors localized to the posterior wall of the LA and the PVs’ region, with fibrillatory conduction toward the rest of the atria (1,2). However, the ionic properties underlying those rotors’ formation and drift remain unclear (7,30). Moreover, recent studies have indicated that, in some patients, rotors that drive the AF may reside outside of the PV area (4). Our simulations demonstrate, for the first time to our knowledge, that the spatial distribution of ionic currents found in the canine PV-LAJ are conducive to attracting rotors to the PV region.

In addition, we also demonstrate that this attraction toward the LA can be reversed or arrested, if certain ionic currents are altered, which in turn may explain the variability in the location of rotors found in different patients. AF, however, may involve several coexisting rotors at any given moment. In these cases, in addition to the drift imposed by the underlying substrate, the faster rotors can also exert an overriding influence on the slower rotors (31), and the combination of these two factors on rotor dynamics warrants further investigation.

Substrate heterogeneity and rotor drift

In addition to the role of restitution characteristics of cells in rotor stability (32), simulations with gradient of excitability showed spiral-wave drifting in the direction of the region exhibiting lower excitability and velocity, with an additional perpendicular component depending on the rotor chirality (8) as well as excitability and repolarization (9), regardless of the details of the initial conditions (33). Simulations using more biophysically detailed ionic models found that for a fixed gradient in APD imposed by linearly varying potassium currents, the velocity of the drift of a rotor is a function of the magnitude of the gradient (24) and a steep gradient in APD can lead to conduction block of premature beats (34).

Our results here are in agreement with all those previous studies, but refine the previous prediction that rotors would drift toward regions with longer APD (9,23,25) to only >80% repolarization measured at frequencies close to the rotor frequency. Our simulations (Fig. 5) also show drift predictability of various measures of excitability that include ERP, dV/dt_max, and h×j (I_Na availability); only MDP is able to predict drift direction, regardless of the pacing rate at which it is assessed. We also show, for the first time to our knowledge, that the attraction induced by the ionic heterogeneity is stronger than the constriction imposed by the small area in the distant PV sleeve produced by the curved geometry (Fig. 7). The homogeneous ionic condition simulation in the funnel model of the PV induces a stable, nondrifting rotor, and suggests that the smaller PV-versus-LA area increases safety for propagation toward the PV.

I_K1, I_Kr, and rotor dynamics during fibrillation

I_K1 and I_Kr density gradients in the dog PV-LAJ are found to be opposing each other (16). Because recent studies have shown these two currents to be important in rotor dynamics and AF (12–14,35–37), the ionic mechanisms leading to the propensity of the PV region to favor rotor activity (17–19) became complex. We show, for the first time to our knowledge, a clear propensity of the currents distribution in the PV-LAJ to attract rotors to the PVs and the dominant role for the I_K1 dispersion over all currents, and in particular, I_Kr in determining the localization of a rotor in that area. This opens the possibility that interplay between I_K1 and I_Kr may be important for the differential localization of rotors in AF.

Comparing with other studies, the drift toward low I_K1 in our study is fully consistent with the simulations by Kneller et al (21), who studied the effect of artificial heterogeneity in the inward rectifier I_K,ACh (acetylcholine-modulated inward rectifier potassium current) on AF dynamics. Although not explicitly analyzed, their simulations also suggest that while rotors accelerate their rotation frequency with increasing I_K,ACh (30), the low I_K,ACh regions are the ones that attracts rotors (21). On the other hand, a relatively recent study by Sekar et al. (38) in circular monolayers with overexpression of I_K1 either in a central circular island, or in its periphery, showed that rotors stably pivot around the island regardless of the relative level of I_K1. In that study, however, the gradient was very sharp relative to the size of the rotor core, and the preparation was highly symmetrical—which may explain why that study did not show a preferential anchoring of rotors to either low or high inward rectifying K⁺ current levels as observed in this and other studies (21,39).

Finally, in a recent study in cardiomyocytes monolayers with heterogeneous I_Kr expression, stable rotors localized to the region with the highest expression of I_Kr (35). Those stable rotors did not drift as in our simulations because they reside in a relatively uniform large region, in accordance with our simulations presented in Fig. S5.

Limitations

We study a specific set of membrane kinetic models (CRN-K) with a Boltzmann distribution of the current densities across the PV-LAJ; kinetic models preferred because of extensive validation of propagation properties (22,40) over a more recent and detailed model requiring adjustments (41,42). Experimental or clinical data on ionic properties and dispersion in the atria are scarce; we focused on the effect of reported ionic currents data for the dog. However, attraction or repulsion of rotors by the PVs at the PVLAJ may be affected by factors other than those studied here. For example, the heterogeneity in the intrinsic cellular properties may have different effective heterogeneity in refractoriness and excitability (33) depending on structural intercellular coupling (43), fibrosis (44), or the size of the medium (34,45–47). Further, the drift of rotors may be further influenced by accumulations or intra- or extracellular ions, as has been shown to occur in AF (48).

In our study, we ruled-out that PV funnel-like anatomy reverses the ionic-induced attraction to the PVs. However, additional anatomical factors such as wall thickness (49,50), the fiber bundles (51), or fibrosis (7) may also regulate the drift of rotors, possibly even counteracting the drift trend caused by the ionic gradients. To mitigate these limitations, we focused in our study on conditions relevant only to paroxysmal AF before any remodeling and fibrosis, and incorporated various possible I/V relationships to substantiate our conclusions regarding the I_K1 dominance and drift prediction (Fig. 6 and also Fig. S6, Fig. S7, and Fig. S8). Our study nevertheless should be considered only as a first step in elucidating the concept of heterogeneity-induced drift, and needs to be tested in future experimental studies.

Conclusions

Consistent with experimental and clinical studies on paroxysmal AF, simulations in an ionically heterogeneous model of the PV-LAJ showed rotor attraction toward the PVs, consistent with reduced coupling and despite spatial constriction in the PV region. Our simulations suggest that I_K1 heterogeneity across the PV-LAJ is dominant compared to other currents in conveying drift direction through its effect on refractoriness and excitability. Our simulations also suggest that measuring with high-resolution refractoriness, excitability, and diastolic potentials during pacing could provide a mechanistic guidance for the unstable components of rotors that are believed to underlie AF.