Measuring Microtubule Polarity in Spindles with Second-Harmonic Generation

Abstract

The spatial organization of microtubule polarity, and the interplay between microtubule polarity and protein localization, is thought to be crucial for spindle assembly, anaphase, and cytokinesis, but these phenomena remain poorly understood, in part due to the difficulty of measuring microtubule polarity in spindles. We develop and implement a method to nonperturbatively and quantitatively measure microtubule polarity throughout spindles using a combination of second-harmonic generation and two-photon fluorescence. We validate this method using computer simulations and by comparison to structural data on spindles obtained from electron tomography and laser ablation. This method should provide a powerful tool for studying spindle organization and function, and may be applicable for investigating microtubule polarity in other systems.

Introduction

Microtubules are crystalline lattices of α- and β-tubulin heterodimers, and since the two ends of the tubulin subunits are different, microtubules are intrinsically polar polymers. The polarity of microtubules has important biological consequences. The two microtubule ends polymerize with different dynamics (1) and the intrinsic directionality of the microtubule lattice allows molecular motors to move along them in a directed fashion (2,3). Microtubules are often organized into arrays in vivo (4–8), and the polarity of such a collection of microtubules can be defined as the vector sum of the normalized polarity of all the constituent microtubules. A bundle of parallel microtubules all oriented in the same direction has a polarity of magnitude 1, whereas a bundle of antiparallel microtubules has a polarity of zero and is thus a nonpolar structure. The polarity of microtubule arrays is thought to be crucial for the organization and function of many cell types (4), including neurons (5), epidermal cells (6), egg chambers in Drosophila (7), and shoot apical meristem cells (8).

The spindle, which segregates chromosomes during cell division, is a microtubule array with spatially varying polarity: microtubules in the center of the spindle are antiparallel, whereas microtubules near the spindle poles are predominantly parallel. The polarity of microtubules has long been thought to play a key role in spindle assembly (9–14). Proteins that localize to the antiparallel microtubules in the center of the spindle are believed to drive the elongation of the spindle in anaphase and to direct the location of the cleavage plan in cytokinesis (15–22). However, the interplay between protein localization, microtubule polarity, and spindle behavior remain poorly understood, largely because of the difficulty of measuring microtubule polarity in spindles.

Several methods have been used to study microtubule polarity. Electron microscopy can directly visualize the polarity of microtubules, but this technique requires the sample to be fixed and is highly labor intensive (23,24). Microtubule polarity can be estimated in live cells by imaging fluorescence-labeled plus-end tracking, but this method does not provide information on shrinking microtubules or stabilized microtubules (25). Laser ablation can also be used to infer microtubule polarity, but this technique is perturbative (26). Kwan et al. recently demonstrated that the polarity of microtubule arrays in dendrites and axons can be measured with second-harmonic-generation (SHG) microscopy (27). As SHG is a noninvasive optical technique, it is a promising method for studying microtubule polarity in other structures, such as spindles.

SHG is a nonlinear optical process in which highly polarizable, noncentrosymmetric materials emit photons with half the wavelength of incident light (28). The resulting emitted light is the coherent sum of the electromagnetic fields generated by the SHG emitters, and thus constructive and destructive interference between emitters can occur, depending on their positions and orientations. Few biological molecules produce detectable SHG signals (29–33). Individual microtubules are very weak SHG emitters, but the constructive interference between aligned microtubules in arrays produces appreciable signals that have been used to visualize microtubules in mitotic spindles (28,31,34–40), neurons (27,40–45), cilia (40), axonemes (46), and astroglial filaments in spinal tissues (47).

Kwan et al. used experiments and simulations to demonstrate that the polarity of microtubules in highly ordered arrays can be determined by measuring the ratio of forward propagating and backward propagating SHG signals (27). We found that for larger, more disordered microtubule arrays, as are found in spindles, the method of Kwan et al. cannot be used to reliably determine microtubule polarity. In this article, we present an alternative technique for measuring microtubule polarity in spindles with SHG. Our approach is based on the combined imaging of forward-propagating SHG and two-photon microscopy (TP) of fluorescently labeled microtubules. We first used numerical simulations to investigate the expected SHG signal from microtubule arrays with disorder similar to that found in spindles. These simulations, validated by comparison to electron-tomography reconstructions and SHG images of spindles, led us to propose a method for combining the SHG and TP signals to measure microtubule polarity throughout spindles. We confirmed that the polarity in meiotic spindles in Xenopus laevis egg extracts measured with this technique agrees with the polarity in these spindles previously determined by laser ablation (26). Finally, we used this method to measure microtubule polarity throughout the first mitotic spindle in Caenorhabditis elegans embryos, a spindle whose polarity has not previously been studied.

Materials and Methods

Microscopy

Our microscope system was constructed around an inverted microscope (Eclipse Ti, Nikon, Tokyo, Japan), with a Ti:sapphire pulsed laser (Mai-Tai, Spectra-Physics, Mountain View, CA) for excitation (850 nm wavelength, 80 MHz repetition rate, ∼70 fs pulse width), a commercial scanning system (DCS-120, Becker & Hickl, Berlin, Germany), and hybrid detectors (HPM-100-40, Becker & Hickl). The maximum scan rate of the DCS-120 is ∼2 frames/s for a 512 × 512 image. The excitation laser was collimated by a telescope to avoid power loss at the XY galvanometric mirror scanner and to fill the back aperture of a water-immersion objective (CFI Apo 40× WI, NA 1.25, Nikon). A half-wave plate (AHWP05M-980) and a quarter-wave plate (AQWP05M-980) were used in combination to achieve circular polarization at the focal plane, resulting in equal SHG of all orientations of microtubules in the plane, unbiased by the global rotation of the spindle, the spatial variation in the angle of the microtubules, and the local angular disorder of microtubules. Although the use of linearly polarized light would produce a greater maximum signal, the resulting measurement would depend on the orientation of microtubules relative to the plane of polarization. The rapid rotation of the C. elegans spindle during anaphase (see Movie S1 in the Supporting Material) would make it challenging to continually change the orientation of the polarization to match the spindle axis. We calibrated the circular polarization of our system according to the procedure reported by Chen et al. (48), and we restricted our scanning region to within the central ∼1.6% of the viewing area to minimize polarization distortions.

Two-photon fluorescence was imaged with a non-descanned detection scheme with an emission filter appropriate for either green-fluorescent-protein (GFP)-labeled tubulin in C. elegans (FF01-510/42-25, Semrock, Rochester, NY) or Atto565-labeled tubulin in Xenopus laevis egg extract (FF01-607/36-25, Semrock). Forward-propagating SHG was collected through an oil-immersion condenser (1.4, Nikon) with a 425/30 nm filter (FF01-425/30-25, Semrock). Both pathways contained short-pass filters (FF01-650/SP-25, Semrock) to block the fundamental laser wavelength. Image analysis was performed with MATLAB (The MathWorks, Natick MA), ImageJ (National Institutes of Health, Bethesda, MD), and Origin 8 (OriginLab, Northampton, MA).

Sample Preparation

CSF-arrested egg extracts were prepared from Xenopus laevis female oocytes as described previously (49). Briefly, demembranated sperm and calcium where added to extracts. Nuclei formed after 45–90 min. The reactions were driven into metaphase by addition of CSF-arrested extract, and spindles formed after 1 h at 20°C.

Strain JU1212 was used for a wild-type, unlabeled C. elegans sample. Strain AZ244 (unc-119(ed3) III; ruIs57[unc-119(+) pie-1::GFP::tubulin]) was used as a GFP-labeled tubulin C. elegans sample. Both strains were cultured at 24°C and fed on OP50 bacteria on nematode growth medium plates. Gravid C. elegans hermaphrodites were cut in half, and the released embryos were transferred onto a 4% agarose pad between a slide and a coverslip for imaging (50).

Numerical simulation of SHG

SHG arises from the nonlinear polarization of molecules by light, given in general by

$$\mathbf{P}={\mathbf{P}}_{\mathbf{0}}+\alpha \times \mathbf{E}+\beta \times \mathbf{E}\times \mathbf{E}+\gamma \times \mathbf{E}\times \mathbf{E}\times \mathbf{E}+\dots ,$$ (1)

where the dipole moment P is the permanent dipole moment, P₀, plus an induced polarization given by a Taylor expansion in powers of the electric field. α is the linear polarizability, and β and γ are the second- and third-order electric susceptibility tensors. E is the total electric field, but this value will be approximated as the field from laser excitation only, because even linear polarization is very small compared to the very intense laser pulses used in biological nonlinear microscopy. For SHG from a cylindrically symmetrical source such as a microtubule, the number of independent, nonzero elements of the second-order polarizability, β_ijk, is greatly reduced. Further assuming that the nonlinear polarization of tubulin arises from individual molecular bonds polarized along only a single axis, only two elements remain: β_zzz = n and β_zxx = β_zyy = β_xxz = β_xzx = β_yyz = β_yzy = m (51). The ratio n/m has been measured by polarization analysis of SHG from microtubules in both axonemes (46) and primary cortical neurons (44), and is here set at n/m = 4, intermediate between the two measurements. Considered in the coordinate frame of the microtubule shown in Fig. 1 (from here on, given by x′, y′, and z′), this gives a second-order polarization of

$$\begin{array}{l}{P}_{x^{\text{'}}}^{\left(2\right)}=2m{E}_{x^{\text{'}}}{E}_{z^{\text{'}}}\hfill \\ P_{y^{\text{'}}}^{\left(2\right)}=2m{E}_{y^{\text{'}}}{E}_{z^{\text{'}}}\hfill \\ P_{z^{\text{'}}}^{\left(2\right)}=n{E}_{z^{\text{'}}}^2+m\left(E_{x^{\text{'}}}^2+E_{y^{\text{'}}}^2\right).\hfill \end{array}$$ (2)

We model the light as being circularly polarized, as in experiments, and we assume that the polarization distortion introduced by the high NA objective is negligible in either the lateral direction or the axial direction. Kang et al. have reported that the maximum polarization distortion induced by a high-NA objective (we use an NA 1.25 objective) is <1% in the lateral direction of the focal volume and ∼15% in the axial direction (52). These levels of distortion occur in the very periphery of the point-spread function, where the nonlinear SHG excitation efficiency is extremely weak. In addition, any axial component of the electric field will be largely perpendicular to spindle microtubules, which are observed, via electron microscopy (53) and birefringence measurements (54), to be closely parallel to the spindle pole-to-pole axis. As a result, there is negligible SHG contribution from the axial component of the electric field.

Figure 1.

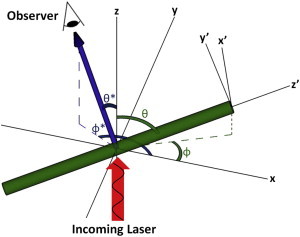
A schematic of the simulation of SHG, showing one MT and one possible direction of collected SHG. The amplitude and phase of the applied electric field depend on the lab coordinates (x, y, z), whereas the polarization of each MT is calculated in its coordinate frame (x′, y′, z′) and transformed back to lab coordinates for summation. The phasor addition of SHG emission from different points in the sample depends on the path difference, a function of the direction of observation (θ^∗, φ^∗). To see this figure in color, go online.

For the sake of clarity, we treat only a single frequency component, ω, of the incident laser, though in practice a pulsed laser is required to obtain sufficient peak power for nonlinear microscopy. Therefore, the electric field in lab coordinates is

$$\begin{array}{l}{E}_x=E_0\left(x,y,z\right)\cos \left(\omega t-\delta \left(z\right)\right)\hfill \\ E_y=E_0\left(x,y,z\right)\sin \left(\omega t-\delta \left(z\right)\right),\hfill \\ E_z=0\hfill \end{array}$$ (3)

where E₀(x, y, z) is the amplitude distribution of the laser and δ(z) is the spatial component of the phase (for example, E₀(x, y, z) is constant and δ(z) = kz for a plane wave). For a microtubule with its axis of symmetry, z′, at inclination θ from the z axis and azimuth ϕ in the xy plane, we may arbitrarily choose the x′ axis purely in the xy plane and, transforming the electric field, obtain

$$\begin{array}{l}{E}_{x^{\text{'}}}=E_0\left(x,y,z\right)\sin \left(\omega t-\phi -\delta \left(z\right)\right)\hfill \\ E_{y^{\text{'}}}=-E_0\left(x,y,z\right)\cos \theta \cos \left(\omega t-\phi -\delta \left(z\right)\right)\hfill \\ E_{z^{\text{'}}}=E_0\left(x,y,z\right)\sin \theta \cos \left(\omega t-\phi -\delta \left(z\right)\right)\hfill \end{array}.$$ (4)

Substituting this into Eq. 2 gives the polarization for the microtubule:

$$\begin{array}{l}{P}_{x^{\text{'}}}^{\left(2\right)}=m{E}_0^2\left(x,y,z\right)\sin \theta \sin \left(2\omega t-2\phi -2\delta \left(z\right)\right)\hfill \\ P_{y^{\text{'}}}^{\left(2\right)}=-\frac{1}{2}m{E}_0^2\left(x,y,z\right)\sin 2\theta \cos \left(2\omega t-2\phi -2\delta \left(z\right)\right)-\frac{1}{2}m{E}_0^2\left(x,y,z\right)\sin 2\theta \hfill \\ P_{z^{\text{'}}}^{\left(2\right)}=\frac{1}{2}\left(n-m\right)E_0^2\left(x,y,z\right){\sin }^2\theta \cos \left(2\omega t-2\phi -2\delta \left(z\right)\right)-\frac{1}{2}\left(n-m\right)E_0^2\left(x,y,z\right){\cos }^2\theta +\frac{1}{2}\left(n+m\right)E_0^2\left(x,y,z\right).\hfill \end{array}$$ (5)

Only the time-dependent terms in Eq. 5 produce radiation, so the constant terms (representing optical rectification) can be dropped for consideration of SHG.

Now turning to the problem of the total SHG signal emitted from many dipoles, we take advantage of the fact that radiation is collected and observed very far from the sample compared to the size of the focal volume. Differences in position within the sample will affect the phase of the radiated electric field but not the amplitude or the direction of radiation for a given orientation of dipole. As a result, we can treat the sample as a single effective dipole, with the amplitude determined by the superposition of dipoles using phasor addition rather than simple addition. However, the relative phase radiated from each dipole depends on the differences in path length to a specific point of detection, so the phasor addition must be performed for each direction at which radiation could be observed. The difference in path length relative to a dipole at the origin is given by

$$\Delta r\left({\theta }^{\ast },{\phi }^{\ast }\right)=x\cos \left({\phi }^{\ast }\right)\sin \left({\theta }^{\ast }\right)+y\sin \left({\phi }^{\ast }\right)\sin \left({\theta }^{\ast }\right)+z\cos \left({\theta }^{\ast }\right),$$ (6)

where x, y, and z are the coordinates of the microtubule and θ^∗ and ϕ^∗ are the inclination from z and the azimuth in the xy plane of the far-field point of observation.

The previous equations could apply to circularly polarized incident light with any amplitude or phase distribution, but following previous simulations of SHG (55), we use a 3D Gaussian approximation for the amplitude of the electric field from a tightly focused laser, with the phase differing from a plane wave by the Gouy phase shift, representing the loss of axial momentum due to focusing (56). Thus, the laser electric field is given by

$$E_0\left(x,y,z\right)=E_I\times \exp \left[-\frac{x^2+y^2}{w_{xy}^2}-\frac{z^2}{w_z^2}\right],\delta \left(z\right)=k_{\omega }z-\arctan \left(\frac{z}{z_R}\right),$$ (7)

where E_I is the peak magnitude of the electric field, ω is the angular frequency of the laser light (850 nm in all simulations), k_ω = 2πn_ω/λ is the wave vector of the fundamental in a sample with refractive index n_ω (chosen as 1.36 for cells), z_R = 1/2k_ωw_xy² is the Rayleigh length of the focused beam, and w_xy and w_z are the 1/e lateral and axial beam waists. Values of w_xy and w_z were determined empirically by two-photon fluorescence correlation spectroscopy of Alexa 488 dye (Invitrogen, Carlsbad, CA), according to a published calibration protocol (57).

Simulations of SHG signal from microtubules were carried out in MATLAB. For each simulated microtubule configuration, microtubules were broken up into individual harmonophores, each representing a single ring of tubulin dimers. This length scale is a coarse-graining with minimal loss of accuracy, as a ring of tubulin dimers is 8 nm long and 25 nm in diameter, small enough compared to the SHG wavelength of 425 nm to be considered an approximate point source. This choice follows Kwan et al., who compared this approximation to simulations with a separate point harmonophore for each tubulin dimer in a ring and found no significant difference (27). The amplitude and phase of each component of polarization was calculated in the microtubule coordinate frame according to Eq. 5, then transformed into the lab frame. Each lab frame component of the total polarization was summed using phasor addition for each angle collected by the condenser, and the total power radiated at each point, with the final SHG signal determined by integrating over all collected angles, which can be chosen to simulate microscope condensers of varying NA. Combining all these results, the time-averaged total collected power of SHG is

$$SHG=\sum _{{\theta }^{\ast }}\sum _{{\phi }^{\ast }}\Delta {\theta }^{\ast }\times \Delta {\phi }^{\ast }\times \sin \left({\theta }^{\ast }\right)\times \frac{{\left(2\omega \right)}^4}{{\left(4\pi {\epsilon }_0{c}^2\right)}^2}\times {\left|\sum _i{\mathbf{R}}_{\mathbf{i}}\left({\theta }_i,{\phi }_i\right){\mathbf{P}}_{\mathbf{i}}^{\left(\mathbf{2}\right)}\left(x_i,y_i,z_i,{\theta }_i,{\phi }_i,{\theta }^{\ast },{\phi }^{\ast }\right)\right|}^2\times {\sin }^2\left(\psi \right),$$ (8)

where θ^∗ and ϕ^∗ are the coordinates of a solid angle in the lab space, discretized over all those collected by the condenser, the sum over i is over all microtubule harmonophores, ${\mathbf{R}}_{\mathbf{i}}$ is the rotation matrix from microtubule to lab coordinates for the dipole i, ${\mathbf{P}}_{\mathbf{i}}^{\mathbf{(}\mathbf{2}\mathbf{)}}$ is the polarization of harmonophore i in the microtubule coordinate frame, and ψ is the angle between the summed lab-frame vector ${\sum }_i{\mathbf{R}}_{\mathbf{i}}{\mathbf{P}}_{\mathbf{i}}^{\mathbf{(}\mathbf{2}\mathbf{)}}$ and the direction (θ^∗, ϕ^∗). Incorporating the phase shifts due to microtubule rotation, the phase of the laser at an individual harmonophore’s position, and the path difference in the direction (θ^∗, ϕ^∗), we have

$${\mathbf{P}}_{\mathbf{i}}^{\mathbf{(}\mathbf{2}\mathbf{)}}\left(x{}_i,y_i,z_i,{\theta }_i,{\phi }_i,{\phi }^{\ast },{\theta }^{\ast }\right)=E_I^2\times \exp \left[-\frac{2x_i^2+2y_i^2}{w_{xy}^2}-\frac{2z_i^2}{w_z^2}\right]\times \left(\begin{array}{c}m\sin \left({\theta }_i\right)\sin \left[2\omega t-k_{2\omega }\Delta r\left(x{}_i,y_i,z_i,{\phi }^{\ast },{\theta }^{\ast }\right)-2{\phi }_i-2k_w{z}_i+2\arctan \left(\frac{z}{z_R}\right)\right]\\ -\frac{1}{2}m\sin \left(2{\theta }_i\right)\cos \left[2\omega t-k_{2\omega }\Delta r\left(x{}_i,y_i,z_i,{\phi }^{\ast },{\theta }^{\ast }\right)-2{\phi }_i-2k_w{z}_i+2\arctan \left(\frac{z}{z_R}\right)\right]\\ \frac{1}{2}\left(n-m\right){\sin }^2\left({\theta }_i\right)\cos \left[2\omega t-k_{2\omega }\Delta r\left(x{}_i,y_i,z_i,{\phi }^{\ast },{\theta }^{\ast }\right)-2{\phi }_i-2k_w{z}_i+2\arctan \left(\frac{z}{z_R}\right)\right]\end{array}\right)$$ (9)

and

$${\mathbf{R}}_{\mathbf{i}}\left({\theta }_i,{\phi }_i\right)=\left(\begin{array}{ccc}-\sin {\phi }_i& -\cos {\theta }_i\cos {\phi }_i& \sin {\theta }_i\cos {\phi }_i\\ \cos {\phi }_i& -\cos {\theta }_i\sin {\phi }_i& \sin {\theta }_i\sin {\phi }_i\\ 0& \sin {\theta }_i& \cos {\theta }_i\end{array}\right).$$ (10)

Results and Discussion

SHG imaging of spindles

We imaged the first mitotic division of C. elegans embryos with SHG and were able to visualize the spindle (Fig. 2). The middle of the spindle appears dark, as previously observed by Campagnola et al. (31). Such a dark region could result from a low density of microtubules, an antiparallel alignment of microtubules, or a combination of both of these effects, but SHG alone cannot distinguish between these possibilities. Campagnola et al. (31) sought to resolve this ambiguity by simultaneously imaging spindles with SHG and TP of GFP tubulin. As the TP image provides a measure of the density of microtubules, it may be possible to use this signal to correct the SHG signal for spatial variations in microtubule density, and thus obtain a measure of microtubule polarity throughout spindles. To apply this procedure, it is necessary to have an understanding of how the SHG signal depends on microtubule density, polarity, and other parameters.

Figure 2.

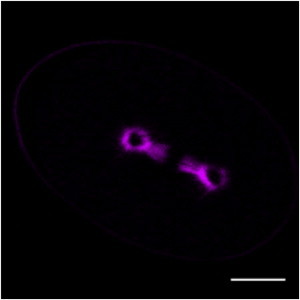
An SHG image of the first mitotic division of a C. elegans embryo. The mitotic spindle is clearly visible and displays a dark region in the middle where the MTs are predominantly antiparallel. Scale bar, 10 μm. To see this figure in color, go online.

The simplest approximation is to assume that all microtubules produce equal scattering, with no phase shift due to their relative positions, resulting in an SHG signal proportional to the square of the vector sum of all the constituent microtubules. If the microtubules only point in either the +x (ϕ = 0) or −x (ϕ = π) direction, then, in this approximation, Eq. 8 reduces to

$$\begin{array}{l}SHG={\left(N_{+}-N_{-}\right)}^2{\left|P_i^{\left(2\right)}\right|}^2\sum _{{\theta }^{\ast }}\sum _{{\phi }^{\ast }}\Delta {\theta }^{\ast }\times \Delta {\phi }^{\ast }\times \sin \left({\theta }^{\ast }\right)\times \frac{{\left(2\omega \right)}^4}{{\left(4\pi {\epsilon }_0{c}^2\right)}^2}\times {\sin }^2\left(\psi \right)\hfill \\ SHG\propto {\left(N_{+}-N_{-}\right)}^2\hfill \\ SHG\propto {\left(D_{MT}\times P_{MT}\right)}^2,\hfill \end{array}$$ (11)

where N₊ is the number of microtubules (MTs) with plus ends pointing in the +x direction and N₋ is the number of MTs with plus ends pointing in the −x direction. $D_{MT}=N_{+}+N_{-}$ is the density of MTs, and $P_{MT}$ is the polarity of microtubules, defined by$P_{MT}=(N_{+}-N_{-})/(N_{+}+N_{-})$. If this model were valid, the polarity could be measured, up to a multiplicative factor, by taking the square root of the SHG signal (which would be proportional to MT density × MT polarity) and dividing by the TP signal (which is proportional to the density of MTs). Kwan et al. performed simulations of ordered arrays of MTs and found that this simple quadratic relationship with polarity did fit the forward SHG signal quite well (27). However, it is not clear whether Eq. 11 will be valid for more disordered arrays of MTs, as found in spindles, since SHG is a coherent process, so in general, the generated signal depends on the detailed position and orientation of MTs, not just their average density and polarity. We performed a series of simulations of the expected SHG signal from arrays of MTs in configurations similar to those found in the spindle to better address this issue.

Simulation of SHG

Previous work has relied on simulation of SHG for interpreting SHG microscopy of membrane-embedded dyes (55), collagen (58), and neuronal MT bundles (27). We adopted similar methods to analyze spindle MTs, with some extension to account for dipoles with any possible orientation in three dimensions (see Materials and Methods). By providing the simulation with different possibilities for the exact position of every MT, we can determine how the confounding variables of MT spacing and orientation affect the SHG signal and how polarity information can be extracted from images of real spindles where the underlying MT configurations are unknown.

We first considered bundles of MTs randomly positioned in the xy plane, with their plus ends oriented parallel or antiparallel to the x axis. This model represents an upper bound on the possible effect of positional disorder on the SHG signal. For a fixed MT density, our simulations of these positionally disordered arrays show an increase in SHG signal with increasing MT polarity, but the simulated SHG does not go to zero when the polarity is zero, even though the MTs are antiparallel (Fig. 3 A). The nonnegligible SHG signal from antiparallel MTs shows that Eq. 11 is not applicable for disordered arrays of MTs.

Figure 3.

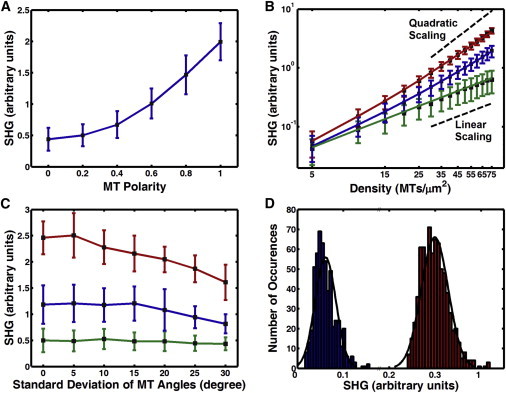
Computer simulation of SHG from arrays of MTs. (A) SHG dependence on polarity at a density of 50 MTs/μm². Mean SHG increases quadratically with polarity, but with large variance. (B) SHG dependence on density, on a log-log scale, for MTs with antiparallel (green), parallel (red), and intermediate polarity (blue). Lines are simultaneous fits to the model given in Eq. 13. (C) SHG signal from MTs with the angular deviation from parallel drawn to a half-normal distribution, for MTs with antiparallel (green), parallel (red), and intermediate polarity (blue). SHG decreases at very high skew but is minimally affected at the level of angular disorder found in the spindle. Error bars in A–C show the standard deviation. (D) Histograms of simulated SHG at low (blue) and high (red) polarity. Distributions have positive skew but are close to Gaussian, more so at higher SHG signal. To see this figure in color, go online.

To better understand why the simulations show deviations from Eq. 11, we performed simulations over a broad range of polarities and MT densities. Although the average SHG signal from parallel MTs approaches quadratic scaling with density at high density, SHG from antiparallel MT arrays scales only linearly with MT density (Fig. 3 B). This result suggests that there is a polarity-independent component of SHG that is linear with MT density, in addition to the expected polarity-dependent component, which scales quadratically with both density and polarity.

In these simulations, the breakdown of Eq. 11 results from the positional disorder of MTs giving rise to significant local fluctuations in MT density and polarity due to the random positioning of MTs and the small effective focal volume, chosen to represent a nonlinear microscope. We were able to construct the following simple theory to explain these simulation results. We assume that Eq. 11 holds for any given configuration of MTs on the length scale of a single microscope focal volume, a micron-scale region with a particular density and polarity. Then, the average SHG generated from a collection of focal volumes with a particular average MT density and polarity will be a weighted average of Eq. 11 over the different focal volumes. Equation 11 shows that the SHG signal is proportional to the square of the number of excess parallel MTs, but the average of the squared number of excess parallel MTs is not simply the square of the average of the excess parallel MTs. Thus, the result of averaging Eq. 11 cannot be obtained by substituting the average MT polarity and density into Eq. 11. Rather,

$$\langle SHG\rangle \propto \langle {\left(N_{+}-N_{-}\right)}^2\rangle ={\langle N_{+}-N_{-}\rangle }^2+\text{Var}\left(N_{+}-N_{-}\right)={\left(D_{MT}\times P_{MT}\right)}^2+\text{Var}\left[D_{MT}\times P_{MT}\right],$$ (12)

where the first term after the final equality results because the average number of excess parallel MTs is equal to the density of MTs × the polarity. The variance term depends on the distribution of +x- and −x-facing MTs, but in general Var(N₊ – N₋) = Var(N₊) + Var(N₋) − 2Cov(N₊, N₋). Since antiparallel MTs will be growing from minus ends located in different parts of the spindle, it is reasonable to assume that their distributions in a given focal volume will be independent and that the covariance term can be dropped. Assuming that each MT is positioned approximately independently, the distribution of effective N₊ and N₋ in each focal volume is the sum over the effective contribution from each MT to the focal volume, so Var(N₊) and Var(N₋) will scale with N₊ and N₋, respectively. Therefore, Var(N₊ – N₋) ≈ D_MT(1 + P_MT)/2 + D_MT (1 − P_MT)/2 = D_MT, and we arrive at a contribution to the SHG signal that depends linearly on the density of MTs alone, independent of polarity. Substituting into Eq. 12 gives

$$\langle SHG\rangle =A{\langle D_{MT}\rangle }^2{\langle P_{MT}\rangle }^2+B\langle D_{MT}\rangle ,$$ (13)

where A and B are proportionality constants. The solid lines in Fig. 3 B are fits of Eq. 13, showing excellent agreement for parallel, antiparallel, and mixed-polarity MT arrays. As an alternate perspective on this model, consider that in Eq. 11, we approximated the inner sum of Eq. 8 as $D_{MT}\times P_{MT}$. In Eq. 13, we alter the approximation to $D_{MT}\times P_{MT}+\sqrt{D_{MT}}$, making a reasonable assumption, confirmed by our simulation results, that the deviations from perfect cancellation of antiparallel MTs are likely to scale with the square root of MT density.

MTs in spindles are not arranged in perfectly parallel or antiparallel arrays but have some degree of angular disorder. To test whether this will be significant in interpreting SHG microscopy, we simulated MT bundles with varying degrees of angular disorder (Fig. 3 C). Simulated SHG does decrease with increasing angular disorder, but the effect is small except with levels of disorder far greater than those found in spindles (based on electron microscopy (53) and birefringence measurements (54)). Thus, angular disorder of MTs in spindles is not expected to have a significant effect on SHG measurements.

In all of our simulations, there is considerable variance around the average SHG signal at a given density and polarity due to the many different configurations of MTs that are consistent with a particular average polarity and density, as well as the sensitive dependence of SHG on MT spacing. The distributions of simulated SHG are close to normal (Fig. 3 D), suggesting that if the signals from multiple locations are averaged together, the uncertainty in polarity will be close to the standard error of the mean, assuming that each location is sampled from the same underlying normal distribution. In the spindle, we are primarily interested in how polarity varies along the axis between the two poles, and we can thus calculate a profile of SHG at each position using an average over a line of pixels perpendicular to this pole-to-pole spindle axis.

Analysis of spindles

Our simulations of SHG from MT arrays involved a number of simplifications and approximations, so we sought to test whether they were realistic enough to apply to the analysis of experimental results by comparing the predicted to the measured SHG signals from MT arrays of known structure. To this end, we studied centrosomes from the first mitotic spindle in C. elegans embryos as a model system. We measured the density, orientation, and location of MTs emanating from these centrosomes in electron tomography reconstructions (provided by Thomas Müller-Reichert (59)) and simulated SHG signals from MTs with these distributions. Experimentally obtained SHG images of these centrosomes appear to be quite similar to the simulated versions (compare Fig. 4, A and B). The close agreement between the average measured radial SHG profile and the simulated radial profile (Fig. 4 C) demonstrates that the simulations accurately describe SHG from MTs in spindles. This suggests that the SHG signal generated from MTs in spindles should be described by Eq. 13.

Figure 4.

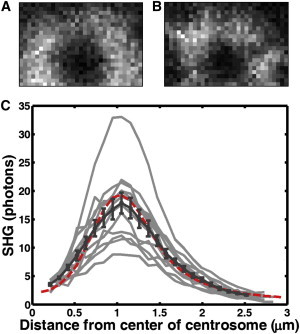
Comparison of experimental and simulated SHG from C. elegans centrosomes at the first mitosis. (A) An example of experimental SHG images of C. elegans centrosomes. (B) Simulated SHG signals based on a C. elegans centrosome in electron tomography reconstructions provided by Thomas Müller-Reichert (59). Image size is 3.3 × 2.3 μm. (C) Profile of SHG signal as a function of distance from the center of imaged and simulated centrosomes. Profiles from individual imaged centrosomes are in light gray, with the mean ± SD in dark gray and the scaled simulated SHG profile in red. To see this figure in color, go online.

Equation 13 relates the SHG signal to the density and polarity of MTs. TP microscopy of fluorescently labeled tubulin should produce a signal in the spindle that is proportional to the density of MTs (after background subtraction). Using the proportionality between TP fluorescence and MT density with Eq. 13 gives a formula for polarity, P_MT:

$$P_{MT}=\pm \sqrt{\frac{\left(\langle SHG\rangle -\beta \langle TP\rangle \right)}{\alpha {\langle TP\rangle }^2}},$$ (14)

where α and β are constants that depend on the statistics of MT spacing, the level of tubulin labeling, laser power, and other factors. Predicting α and β is not feasible, but they can be experimentally measured in one image of a spindle if the polarity is known at two locations. The polarity in the middle of spindles is zero, so if other methods can be used to establish polarity at another location, then α and β can be measured and the magnitude of polarity at all other locations can be determined using Eq. 14. There is also ambiguity in the sign of the measured polarity, but we can take advantage of the a priori knowledge that the spindle is bipolar, with plus ends pointing predominantly from the poles toward the equator and a plane of reflection symmetry in the middle. Therefore, the physically correct choice is the positive square root between the lefthand pole and the center of the spindle, and the negative square root on the other side.

Next, we tested this procedure for measuring polarity in spindles by applying it to meiotic spindles in Xenopus laevis egg extracts, whose polarity has previously been measured with laser ablation (26). Simultaneously acquired SHG images (Fig. 5 A) and TP images (Fig. 5 B) of these spindles were background subtracted and analyzed in a direction parallel to the spindle axis by averaging perpendicularly in a region of interest. The lowest value of SHG intensity, SHG_mid, was found near the middle of the SHG profile, where the two-photon intensity, TP_mid, was recorded as well. As the polarity in the center of the spindle is zero, Eq. 14 gives β = SHG_mid/TP_mid. We determined α using the Brugues et al. measurement of MT polarity (26) at a distance of ∼14 μm from the spindle center. With values for α and β established, we used Eq. 14 in conjunction with the SHG and TP data to determine how polarity varies along the spindle (Fig. 5 C). The agreement of the polarity profile measured from SHG and TP with the one determined from laser ablation argues for the validity of the proposed procedure.

Figure 5.

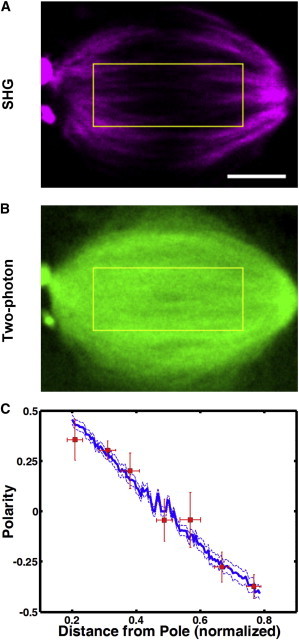
Analysis of MT polarity of a spindle assembled in Xenopus laevis egg extracts. SHG (A) and TP (B) images of the spindle. The yellow rectangle specifies the region of interest. Scale bar, 10 μm. (C) Polarity pattern extracted from SHG and TP images based on our proposed model in blue (mean ± SE). The polarity pattern previously measured by laser ablation is in red (mean ± SE) (26). To see this figure in color, go online.

Having verified our analysis method, we next thought to apply this approach to study a spindle whose polarity has not been previously characterized. We studied the first mitotic division of C. elegans, a widely used model system for cell division. We acquired simultaneous SHG and TP images of the first mitotic spindle in a C. elegans embryo (Fig. 6, A and B, respectively). We determined the value of β from the intensity of the SHG and TP signals in the middle of the spindle as described above. To determine a value for α, we need to know the polarity at another location in the spindle. We used electron tomography reconstructions of centrosomes in these spindles (59) to calculate a polarity of 0.95 near the pole. We calculated the profile of polarity through the spindle using the measured values of α and β (Fig. 6 C). The observed MT polarity pattern varies nearly linearly from pole to pole in metaphase. This system can record successive images in a single embryo (Movie S1), showing the potential to measure the temporal evolution of MT polarity in spindles throughout the course of cell division.

Figure 6.

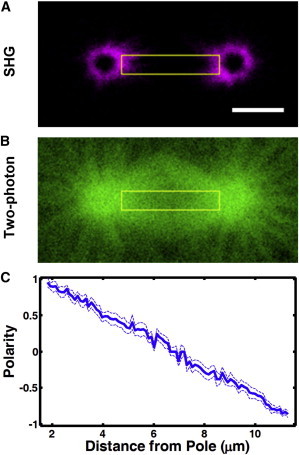
Analysis of MT polarity in the first mitotic spindle in a C. elegans embryo. SHG (A) and TP (B) images of the spindle. The yellow rectangle specifies the region of interest. Scale bar, 5 μm. (C) Polarity profile extracted from SHG and TP images based on the proposed model in blue (mean ± SE). To see this figure in color, go online.

This procedure for measuring MT polarity from SHG and TP imaging requires an independent measure of MT polarity in the spindle. Although this is not a serious limitation for the many model systems that have already been studied with electron microscopy, if such information is not known, it is possible to use an alternative approach to measure MT polarity with SHG and TP. This alternative approach requires independent calibrations of the SHG and TP signals. In Eq. 13, the constants A and B depend on the intrinsic SHG emission of MTs and details of the experimental setup such as the excitation laser conditions, optical layout, and detector sensitivity. These constants can be measured for a particular optical system using a sample with a known polarity and density of MTs. The C. elegans spindle provides one such possibility (Fig. 4), and in vitro arrays of MTs are another option. TP measurements can be calibrated by 1), measuring the molecular brightness of labeled proteins with fluorescence correlation spectroscopy (57); and 2), measuring the fraction of labeled tubulin molecules with Western blot or other techniques. Once both SHG and TP are calibrated, a TP image of a spindle can be converted into a measure of MT density, and Eq. 13 can be used to measure MT polarity. We used this procedure on spindles in HeLa cells expressing GFP tubulin, and found MT densities similar to that reported by electron microscopy (60) and polarity ranging continuously from near −1 to 1 at the poles (data not shown). This result demonstrated the feasibility of this alternative approach, but it is technically more challenging than the previously described method, introduces more uncertainty due to possible experimental errors during calibration, and requires a new calibration when changing the excitation laser power, the laser pulse-width, the laser wavelength, the optics configuration, or any other aspect of the experimental setup.

Conclusion

In this work, we have shown that the combination of SHG and TP microscopy can be used to quantitatively measure the polarity of MTs throughout spindles. It has been proposed that the polarity of MTs in the spindle is involved in spindle assembly, protein localization, force generation, and cleavage-furrow positioning, but it has been challenging to rigorously test these models due to the difficulty of measuring MT polarity in situ. Our method should greatly enhance the study of these phenomena by allowing real-time measurement of polarity under genetic, biochemical, and physical perturbation.

SHG and TP microscopy can be directly combined to measure spatial variations in MT polarity in spindles, up to an unknown constant of proportionality. Here, we describe two related approaches to determine this constant of proportionality and thus provide absolute measurements of MT polarity throughout spindles. The first approach requires independent measurements of MT polarity at two locations. As all spindles that have been examined have a polarity of zero at their center, it is necessary to determine polarity at only one additional location. This information can be obtained from either laser ablation (26) or electron microscopy (59). If the polarity at a second location cannot be determined, then the alternative, second approach can be used, in which SHG and TP are independently calibrated.

It will be interesting to explore the extent to which our approach can be adopted to measure MT polarity in other systems, such as neuronal processes (5,61), epidermal cells (6), egg chambers in Drosophila (7), and shoot apical meristem cells (8). A promising future direction would be to extend our setup to include dual-color, TP imaging, allowing simultaneous visualization of MT polarity and protein localization. Such a system would be a powerful tool for testing the proposed role of antiparallel MTs in recruiting proteins that are thought to drive central spindle assembly, anaphase B, and midbody formation. Another potential modification would be to measure MT density with quantitative polarized light microscopy (62) instead of fluorescence microscopy. With that modification, the system could provide a label-free method of measuring MT density and polarity, which could be applied to study nonmodel organisms, or in medical imaging.