Nucleotide Regulation of the Structure and Dynamics of G-Actin

Abstract

Actin, a highly conserved cytoskeletal protein found in all eukaryotic cells, facilitates cell motility and membrane remodeling via a directional polymerization cycle referred to as treadmilling. The nucleotide bound at the core of each actin subunit regulates this process. Although the biochemical kinetics of treadmilling has been well characterized, the atomistic details of how the nucleotide affects polymerization remain to be definitively determined. There is increasing evidence that the nucleotide regulation (and other characteristics) of actin cannot be fully described from the minimum energy structure, but rather depends on a dynamic equilibrium between conformations. In this work we explore the conformational mobility of the actin monomer (G-actin) in a coarse-grained subspace using umbrella sampling to bias all-atom molecular-dynamics simulations along the variables of interest. The results reveal that ADP-bound actin subunits are more conformationally mobile than ATP-bound subunits. We used a multiscale analysis method involving coarse-grained and atomistic representations of these simulations to characterize how the nucleotide affects the low-energy states of these systems. The interface between subdomains SD2–SD4, which is important for polymerization, is stabilized in an actin filament-like (F-actin) conformation in ATP-bound G-actin. Additionally, the nucleotide modulates the conformation of the SD1-SD3 interface, a region involved in the binding of several actin-binding proteins.

Introduction

Actin is a highly abundant protein found in all eukaryotic cells. As a central component of the cytoskeleton, it facilitates cell motility, cell division, and cellular transport (1) by the dynamic polymerization of its subunits (2). This polymerization in turn is affected by the nucleotide bound at the cleft of each actin subunit (3,4).

Functionally, ATP and ADP-bound subunits behave very differently: they polymerize at different rates (5) and have different affinities for various actin-binding proteins (6). During treadmilling, ATP facilitates the addition of actin monomers onto the barbed end of the filament. The affinity of ATP-bound actin for the barbed end is ∼10 times that of ADP-bound subunits and the association rate is ∼5 times faster (5). ADP-bound subunits are believed to interact more weakly with one another in the actin filament, increasing filament flexibility and facilitating depolymerization at the pointed end (7). Additionally, ADP-bound filaments have a higher affinity for the actin-severing protein cofilin than do ATP-bound filaments. The nucleotide also modulates the affinity of actin monomers for actin-binding proteins, including profilin and ADF/cofilin (8).

In crystal structures, however, ATP and ADP-bound actin monomers appear very similar (8–11). Several conformational differences between them have been observed, but none of these are generally accepted. The current picture (reviewed in Kudryashov and Reisler (12)) is that there are multiple regions in actin that exist in dynamic equilibria, and the nucleotide alters the relative stabilities of each conformation. Of these alterations, the most global structural change is the opening of the nucleotide-binding cleft of actin (see Fig. 1). Other proteins within the actin superfamily, including hexokinase, Arp2, Arp3 (13), and ParM (14), have been shown to have an open cleft when there is no nucleotide bound. Biochemical experiments have suggested that in actin, the cleft may at least transiently open and the open state is more frequently populated in the ADP-bound state (12,15–18). The structure of an open state of actin was determined in two separate studies, but in both cases the actin was cocrystallized with profilin (19,20). Molecular-dynamics (MD) simulations in which this structure was simulated after removal of the profilin molecule showed that the cleft closes, which suggests that the open cleft is not a low-energy conformation (21). Additional MD simulations confirmed the findings that the nucleotide does not significantly contribute to the extreme opening of the cleft (22,23).

Figure 1.

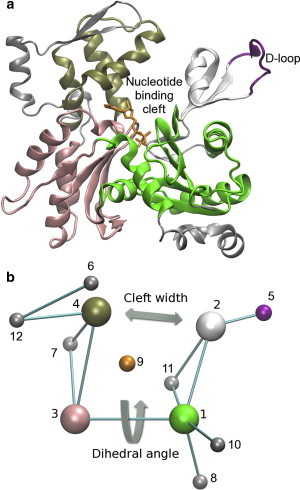
The 12-site CG model contains four main sites, representing the cores of the subdomains of actin, and eight minor sites, representing regions that are highly conformationally mobile, functionally important, or solvent exposed. Mapping from the all-atom (a) to CG (b) representation is shown, along with the two collective variables that are biased during US: the dihedral twist and the cleft width. To see this figure in color, go online.

Several conformational changes involving only local regions have also been identified. The S-loop (residues 70–79) is believed to coordinate with the γ-phosphate of ATP, acting as the nucleotide-sensing switch (24). The nucleotide state has also been correlated with two more distant conformational changes: the folding of the D-loop (residues 40–51) and the conformation of the W-loop (residues 165–172). The folding of the D-loop has been proposed as a mechanism for nucleotide-dependent regulation of filament dynamics, based on crystallographic and MD data (10,25–27). This is in agreement with experiments that showed a change in the signal from the fluorescently labeled D-loop region in G-actin when ATP was switched for ADP (28,29). The role of the D-loop remains controversial, however. Some MD studies indicated that switching nucleotides had no effect on the D-loop (23). Further, a discrete switching between states is unlikely, since this region has also been shown to be highly conformationally mobile in both ATP and ADP-bound F-actin (30). However, the relative populations of folded and unfolded D-loops may depend on the state of the nucleotide and represent a complex free-energy landscape with multiple local minima, as shown by biased MD simulations (26). Finally, the conformation of the W-loop has been shown to correlate with the state of the bound nucleotide (27) and is believed to mediate the opening of the cleft region in concert with profilin binding (20).

In addition to the lack of consensus about how the nucleotide can affect the conformation of a subunit, very few details are known about how these changes regulate the rate of and affinity for polymerization. In one experiment, addition of Mg²⁺ to ATP-bound 1,5-IAEDANS-labeled actin (Cys-374) led to a slow 25–35% change in fluorescence (t^1/2 ∼10–15 s), suggesting a change in the hydrophobic cleft region that was interpreted as activation for polymerization (31). This change was absent in ADP-bound actin. Actin polymerization is dependent on the addition of a divalent cation, and the lack of a strong change in fluorescence upon addition of Mg²⁺ in ADP-bound actin has been interpreted as evidence that G-actin does not adopt an activated state unless ATP is bound.

Since filament formation is known to require the flattening of the subunit (32), we hypothesize that the relative free energy of this motion is affected by the bound nucleotide, and that ATP stabilizes flattened conformations that are more likely to polymerize. This was suggested in the original Oda model for the filament, proposed by Oda et al. (32); however, it was unclear from that work whether the flattened conformation was possible in the monomeric environment or whether flattening was uniquely enabled by intersubunit contacts. A superclosed monomeric actin conformation was observed in MD simulations (23). However, as we noted in a previous publication, we only observe this superclosed conformation in simulations in which we do not explicitly place water molecules in the locations observed in the crystal structure (33). Furthermore, the timescale of transition between the G-actin and superclosed states (within 4 ns) seems to be too fast, since polymerization is likely to occur on the order of microseconds in the cell (k_on = 11.6 μM⁻¹s⁻¹ (5); G-actin concentration = 100 μM (34)). To accelerate sampling and characterize the nucleotide-dependent energetics of actin subunit flattening, we therefore performed umbrella sampling (US) MD simulations of ATP and ADP bound starting from both a flattened F-actin (Oda model) conformation of monomeric actin that was gradually twisted and the native G-actin monomer conformation that was gradually flattened.

Materials and Methods

System setup

For each nucleotide state, two sets of monomeric actin structures were generated starting from either the G-actin crystal structures (Protein Data Bank (PDB) ID: 1NWK for ATP-bound (10) and 1J6Z for ADP-bound (11)) or the Oda model for F-actin (PDB ID: 2ZWH for both ADP and ATP (32), referred to here as O-ADP and O-ATP, respectively). To eliminate variability due to the conformation of the D-loop, in all systems the D-loop was replaced by the unfolded loop from the PDB 1ATN structure. The crystal structures were solvated, ionized, and equilibrated, and all-atom MD simulations were run for 50 ns as described previously (33).

1D US simulations

The actin monomer simulations that started in the Oda conformation spontaneously twisted to a G-like conformation during the equilibrium simulation, and snapshots from this trajectory with the correct propeller twist for each US window were selected. Since the monomer simulations starting from the G-actin conformations did not show this flattening, the propeller twist dihedral angle was incrementally biased to create appropriate starting structures starting at −21.25° and with each window generated after preequilibration of the previous window. The range of propeller twists sampled was −36.25° to −1.25° for G-actin and −28.75 to −1.25 for the Oda conformations, with 2.5° between windows. A force constant of 0.598 kcal mol⁻¹ degree⁻² (chosen based on fluctuations in unbiased simulation) was used to restrain the propeller twist to the target value. Each window was preequilibrated for 200 ps, followed by 4 ns of sampling. All simulations were performed using NAMD (35) in the constant NPT ensemble at 310 K and 1 atm of pressure, using Langevin dynamics to thermostat the system and the Nosé-Hoover Langevin barostat. Free-energy plots were generated using the weighted histogram analysis method (WHAM) to combine sampling windows (36).

Coarse-grained model

The all-atom MD simulation trajectories were mapped into a 12-site coarse-grained (CG) representation as described previously (37) (Fig. 1 a). Details about which parts of the protein were mapped to specific CG sites are provided in Table S1 in the Supporting Material.

To consistently align actin subunits, we designed an internal reference frame. The origin was set at CG site 3 (the core of SD3). The x axis was chosen to lie along the vector connecting CG site 1 (the core of SD1) and CG site 3, and the y axis was chosen to be perpendicular to the x axis and the vector connecting CG site 3 and CG site 4 (the core of SD4). All structures were shifted and rotated to align their internal reference frames before calculating the principal components of motion in the CG coordinates.

Path refinement using a CG double-well model

We applied the finite-temperature string method with swarms (38) to the G-actin to Oda-actin transition in an ADP-bound actin monomer using a two-state elastic network model (with crystal structures 1J6Z and 2ZWH as endpoints). The absolute coordinates of a 13-site CG model of actin were chosen as the collective variable space for the string. The 13 sites were sites 1–4, 6–8, 11, and 12 of the current model, and four sites within the D-loop region (residues 40–43, 44–45, 46–47, and 48–51). This was done to increase the resolution of the CG sites on the D-loop conformation beyond just a single site. Since the N-terminus is not resolved in the 1J6Z structure and the model was based on the C_α atoms in the protein, the CG sites representing the nucleotide (site 9) and the N-terminus (site 10) were omitted.

2D US simulations

The starting structures for each two-dimensional (2D) simulation system were based on the crystal structures specified above. These structures were solvated, minimized, heated, and preequilibrated as described in the Supporting Material. For each system, we initialized the four closest windows to this starting point. The windows were constrained with a force constant of 0.6 kcal/mol degree² and 3.75 kcal/mol Ų for the dihedral angle and cleft width, respectively. The systems were equilibrated for 2 ns, and then 4 ns of production sampling was performed. WHAM (36) was used to combine the sampling windows. New windows were initialized using the self-learning US algorithm (39). The free-energy surface was progressively better defined with an energy cutoff increasing from 2 to 6 kcal/mol in 1 kcal/mol increments. The final energy landscapes were obtained after eight iterations using a bin size of 0.2 Å for the cleft width variable and 0.5° for the twist angle.

Calculating the area explored by each simulation

To obtain a normalized area measure, the free-energy surfaces (ranging from 16.1 to 30.9 in cleft width and from −39.75 to 7.25 in twist angle) were scaled such that each side had a dimensionless length of one and the surface had a total area of one. Probability levels were set by determining the minimum energy cutoff at which the given percentage of conformations, as determined by the Boltzmann distribution, would have an energy less than or equal to the cutoff.

Results and Discussion

The output of 1D US simulations depends on both the initial configuration and the bound nucleotide

We started our investigation by attempting to characterize a simple 1D free-energy pathway for the flattening of the actin subunit, a motion that is associated with filament formation. Since ATP-bound actin subunits polymerize significantly faster than ADP-bound subunits, we anticipated that ATP would stabilize flattened configurations of actin. To test this hypothesis, we performed US simulations using a collective variable description of the flatness of the subunit, CG dihedral angle 2-1-3-4 (shown in Fig. 1; see Materials and Methods for details).

We initialized these simulations in two ways: by twisting the F-actin configuration (Oda model) and by flattening the G-actin configuration. We independently determined the 1D free-energy curve (not shown) for each set of configurations and observed a strong dependence on the starting conformation, suggesting that there are differences between the G-actin and Oda conformations that are not fully sampled by 1D free-energy calculations. We interpret this to mean that the underlying complexity of the molecular interactions and the limit of finite MD sampling prevent the convergence of the 1D free-energy curves.

Although the subunit twist collective variable is a good first approximation to the global conformational rearrangement between the G-actin structure and the Oda model, the lack of convergence between the 1D US simulations suggests that other collective motions or local high-energy transitions (such as the breaking of an electrostatic bridge or the rotation of a backbone dihedral angle) may be involved. It is advantageous to identify these factors, both to improve our understanding of the G- to F-actin transition and to verify whether they are realistic or instead represent artifacts of the structural refinement procedure.

Principal component analysis reveals that the major difference between the Oda- and G-actin simulations is the distance between CG sites 2 and 4

To facilitate analysis, we projected the all-atom simulation results onto a reduced space of CG sites and concatenated the CG representations of the G-actin and Oda windows representing equivalent twist angles. Since the first half of the trajectory was from the G-actin simulations and the second half was from the F-actin simulations, the slowest mode identified by principal component analysis represents the difference between the two. It should be noted that since this is an artificially constructed trajectory of selected frames from different simulations we expect that only the first mode can be meaningfully interpreted. We validated this by comparing the mode values obtained for each of the top four modes for the G-actin and Oda conformations. As shown in Fig. S1 C, only the first mode differentiates between the two conformations. This mode corresponds to a change in the distance between CG sites 2 and 4, as illustrated by the strong correlation between the value of the first mode and the 2-4 distance (Fig. S1, A and B) for both ADP and ATP-bound actin subunits at a variety of dihedral angle values. Although there were other changes in this first mode, the 2-4 distance was most consistently observed across windows to separate the Oda- and G-actin simulations.

Complex coupling between the twist and cleft width is preserved in a simplified double-well representation

To qualitatively evaluate the coupling between the subunit twist and the cleft width, we projected the minimum free-energy path obtained using the finite-temperature string method with swarms (38) onto these two CG variables. As shown by the black line in Fig. 2 c, there is a complex coupling of these two degrees of freedom even in this simplified representation of actin. Furthermore, the pathway determined by this method shows reasonable agreement with the free-energy landscape obtained using US, as described in the next section. These results suggest that the change in cleft width observed in our simulations is encoded in the structure of actin and is not likely to be an artifact of either the simulation or the structural refinement procedures.

Figure 2.

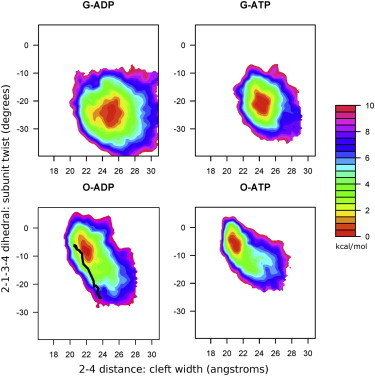
The 2D free-energy surface of the actin monomer as a function of both the dihedral twist and the nucleotide cleft width reveals that both collective variables are affected by the bound nucleotide, and that ADP-bound actin is more conformationally mobile in both the Oda and G-actin conformations. The line in the Oda-ADP panel indicates the transition path between G-actin and Oda structures, as identified using the string method with a double-well CG potential. To see this figure in color, go online.

Self-learning adaptive 2D US results in distinct energy minima with clear nucleotide dependence

To allow the system to move more naturally through a 2D free-energy space defined by the CG dihedral and cleft width variables (cf. Fig. 1 b), we applied the recently developed self-learning US algorithm (39). Unlike traditional US, this adaptive method starts only with a small set of simulation windows very close to the initial structure. These windows are fully sampled and used to generate neighboring windows. In this way, the system is minimally perturbed and windows that are far from the starting structure are generated and equilibrated in a stepwise manner. Rather than predefining a sampling range, the method generates only windows below a given free-energy cutoff, thereby reducing the cost of the simulation by exploring only physically relevant regions and naturally defining the range of sampling.

We have previously noted that the solvation of the active site is critical for determining the stability of the actin subunit, and have taken steps to ensure appropriate solvation of this region (33). However, when sampling the opening of the cleft, the solvation of the electrostatic residues bridging SD2 and SD4 may also affect the free-energy landscape. To address this concern, we included the waters observed in the crystal structures that were within 5 Å of the protein for the G-actin simulations. We also placed these waters around the Oda model, aligning each domain independently, and removed waters with obvious clashes. We constrained the entire protein subunit to its starting position during minimization and preequilibration to allow the water molecules to fully penetrate the protein.

Fig. 2 shows the 2D potential of mean force (PMF) results obtained after self-learning adaptive US was performed for an actin monomer in the G-actin and Oda configurations when bound to either ADP or ATP. Here again, there is a dependence of the results on the initial monomer conformation, so the 2D PMF results cannot be fully converged. It should be noted that this finding differs fundamentally from the behavior observed by Splettstoesser et al. (23), who reported multiple transitions from the G-actin state to a superclosed state in a series of unbiased MD simulations 4 ns in length. (For a more in-depth discussion about the differences between our simulations and the superclosed state reported by Splettstoesser et al. (23), see Supporting Material.) In contrast to the 1D PMF results, we now observe clearly distinct local energy minima in the collective variable space that are well defined, locally converged within each simulation, and well separated between simulations. This allows us to define locally stable free-energy minima that can be contrasted to better elucidate the nucleotide-dependent differences in each state and to identify additional collective variables that may be used in the future to study the G- to F-actin transition. Thus, although we do not observe a transition between the open and closed states or between the ADP and ATP-bound states, it is still informative to compare the locally stable endpoints of these two slow processes.

A comparison of the ADP- and ATP-bound states reveals that ADP-bound subunits are more twisted and have a somewhat more open cleft than ATP-bound subunits in the lowest-energy state accessed from each of the two starting configurations. In addition, the nucleotide changes the area of conformational space that is accessible, particularly at higher-energy level contour lines.

The fact that these results are still not converged despite the slow stepwise application of a bias up to 6 kcal/mol suggests that even in monomeric actin, the Oda-like conformation represents a locally stable conformation. To verify that the simulations were locally equilibrated, we plotted the trajectory of the lowest-energy window in each of the states onto the two collective variables that we biased. As shown in Fig. S2, in each case the trajectory reversibly crosses into regions overlapping neighboring windows many times, indicating that the simulations are locally equilibrated.

To quantify the difference in structure, we determined the minimum energy point in each landscape (see Table S2). When starting from the G-actin conformation, the lowest-energy state becomes 3.5° more twisted when ADP is bound than when ATP is bound (−26.25° vs. −22.75°). Starting from the Oda configuration, this difference is decreased to 2° (−8.25° vs. −6.25°). The cleft width also shows some dependence on the nucleotide: ADP-bound actin subunits have a more open cleft than ATP-bound subunits. Interestingly, in the G-actin simulations, the subunit twist appears to be independent of the cleft width, particularly in the ADP-bound case. In contrast, the Oda simulations reveal a strong correlation between twisting and the opening of the cleft. The contacts between SD2 and SD4 (described in more detail below) may modulate the energetics of flattening and couple twisting and cleft opening.

To quantitatively compare the area of configurational space explored by each system, we calculated the area of the polygon enclosed by a contour line for a range of different energies. These levels were chosen to represent specific probability cutoffs as explained in the Materials and Methods section. In addition, the CG coordinates along which we performed US were rescaled such that the plot area shown in Fig. 2 was square and equal to one. In Fig. S3 we plot the area explored as a function of probability cutoff. The nucleotide-dependent difference in conformational mobility is masked when we look at only the half of the landscape that is lowest in energy (e.g., 50% level, 0.43 kcal/mol). However, with a cutoff encompassing 75% of the potential configurations (0.85 kcal/mol), ADP-bound G-actin is clearly more conformationally mobile than ATP-bound G-actin, and with a 90% cutoff (1.4 kcal/mol) this difference is seen for both G-actin and Oda simulations. At a cutoff of 99.99% (5.7 kcal/mol), ADP-bound G-actin explores twice as much conformational space as does ATP-bound G-actin (0.21 vs. 0.11, where the entire area shown in Fig. 2 is normalized to one). The simulations that start in the Oda configurations show a similar trend (0.13 vs. 0.09). The increased mobility of ADP-bound actin was previously suggested based on biochemical experiments (12) and MD simulations (23); however, this mobility was related to the larger-scale switching between open and closed (or closed and superclosed) cleft states. In this study, we looked at the dynamics within each (noninterconverting) substate and found that even on this local scale, ADP-bound actin is more conformationally mobile than ATP-bound actin.

Root mean-square deviation analysis reveals that the internal structure of the CG sites does not change

We hypothesized that ATP-bound actin is less conformationally mobile than ADP-bound actin because its lowest-energy state is relatively more stable. To validate this supposition, we characterized the lowest-energy US window using a multiscale analysis method. Using a previously developed CG mapping method (37), we calculated the C_α root mean-square deviation (RMSD) for each of the four main CG sites to determine whether internal conformational changes could account for the differences in energetics between different nucleotides or between different configurations. As shown in Table S3, the fluctuation of the CG site within a trajectory is of the same order of magnitude as the difference when we compare the average structures of different nucleotide states given the same starting configuration. A comparison of the G-actin and Oda lowest-energy windows for the same nucleotide shows that in some cases, the RMSD is twice that observed in the simulation, but still well below the resolution of the starting structures. We conclude that neither the nucleotide nor the G-actin to Oda transformation significantly alters the backbone morphology of the main CG sites.

The main CG sites reorient in response to both the nucleotide and the G-actin to Oda conformational change

We next determined whether there were any significant changes in the inter-CG site distances for the main CG sites in the lowest-energy windows for each US simulation system. Because each CG site represents a (relatively) rigid body rather than a point mass, it is also useful to understand how the relative positions of pairs of CG sites change. To that end, we assigned each CG site an internal frame of reference corresponding to the moments of inertia calculated using only the C_α atoms. We designated one of the CG sites in each pair as the reference site (first CG site in each pair in Table S4). In the all-atom representation, the reference site was aligned for all frames and for both configurations in the comparison. We could then directly compare the relative position of the center of mass of the comparison site and the orientation of its principal axes between systems. Changes in the center-of-mass position reflect translations of the comparison site relative to the reference CG site, and changes in the third moment of inertia (the long axis of the CG site) reflect rotations of the comparison site relative to the reference CG site.

The first two columns of Table S4 characterize the nucleotide-dependent differences in the G-actin and Oda conformations, respectively. The largest change is in the distance between CG sites 2 and 4, but this difference is not very big (∼1 Å for both conformations). Treating the CG sites as 3D bodies rather than just as points reveals more interesting changes. In G-actin, the nucleotide primarily changes the relative positions of SD2 and SD4, whereas in the Oda conformation the nucleotide primarily changes the orientation of SD2.

The third and fourth columns of Table S4 show the differences between the G-actin and Oda conformations for ADP and ATP-bound actin, respectively. If the G-actin to Oda transition were composed of a simple rotation of the actin subunit, we would expect to see a change in the distance and the relative position between CG sites 2 and 4, and a change in the relative orientation between CG sites 1 and 3 and CG sites 2 and 4. We see the expected change in distance between CG sites 2 and 4, but the relative positions and orientations reveal a more complex transition.

As expected, the largest change in relative position is seen for the CG site 2-4 pair. However, all of the other pairs of CG sites also show some degree of translation and reorientation between the G-actin and Oda conformations. CG sites 3 and 4 shift and rotate more relative to one another in the G-actin to Oda transition when ADP is bound, and CG sites 1 and 2 shift and rotate more relative to one another in the G-actin to Oda transition when ATP is bound. CG sites 3 and 1 should rotate relative to one another during flattening. In ATP-bound actin, these two sites reorient relative to one another much more than in ADP-bound actin, but in both cases they do so less than expected. ATP thus couples the flattening of the subunit with twisting of the nucleotide-binding cleft, whereas in ADP the flattening appears to happen mostly as a result of the reorientation of SD2.

These differences help explain why the simulations that started in different conformations did not converge: there appear to be additional reorientations of the subdomains required to facilitate subdomain flattening that are not fully sampled in these simulations. To better understand the nature of these reorganizations, we looked at the interfaces between CG sites on an atomistic level.

Reorientation of the CG sites correlates with atomistic-scale differences in inter-CG-site contacts

In Fig. 3 we show the average protein backbone structure over the lowest-energy sampling window for each of the simulation systems after aligning the internal reference frame for SD4. Consistent with the CG analysis, the position and orientation of SD2 relative to SD4 depends on the bound nucleotide in G-actin. The position of SD2 in ATP-bound G-actin is more similar to the Oda conformation than would be expected based on the dihedral twist in the minimum energy window. These changes in relative position correlate with changes in the side-chain interactions that hold SD2 and SD4 together. Important residues are depicted in Fig. 3, and detailed distance information and SEs are provided in Table S5. In ADP-bound G-actin, the top of the cleft is held together by the relatively weak interaction between Thr-203 and Arg-62 (Fig. 3 d). In ATP-bound G-actin, the translation and reorientation of SD2 relative to SD4 allows Arg-62 to form a salt bridge with Glu-207 (Fig. 3 b), as well as to interact with Thr-203. The weaker interaction between SD4 and SD2 in ADP-bound actin may account for the increased conformational space that ADP-bound G-actin is able to explore.

Figure 3.

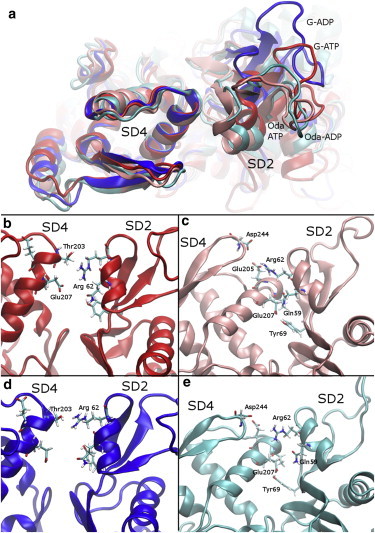
The interface between SD2 and SD4 is affected by both the nucleotide and the starting configuration. (a) Backbone structure of the average structure from the lowest-energy US window for each system after aligning the internal reference frame of SD4. (b–e) Contacts between SD2 and SD4 in G-ATP, Oda-ATP, G-ADP, and Oda-ADP, respectively. To see this figure in color, go online.

In the Oda conformation, nucleotide-dependent changes in the relative orientation of the SD2 to SD4 conformation alter the interactions that stabilize this region. In ADP-bound Oda actin, a single stable contact is formed between SD2 and SD4 in the average structure of the lowest-energy window, i.e., that between Glu-207 and Tyr-69 (Fig. 3 e). This contact is also observed in ATP-bound actin, but in addition Glu-207 intermittently forms a salt bridge with Gln-59 (see Fig. 5 c). Arg-62 also forms a salt bridge with Glu-205, further stabilizing the minimum energy conformation in ATP-bound Oda actin, whereas in ADP-bound actin, Arg-62 intermittently interacts with Asp-244.

Figure 5.

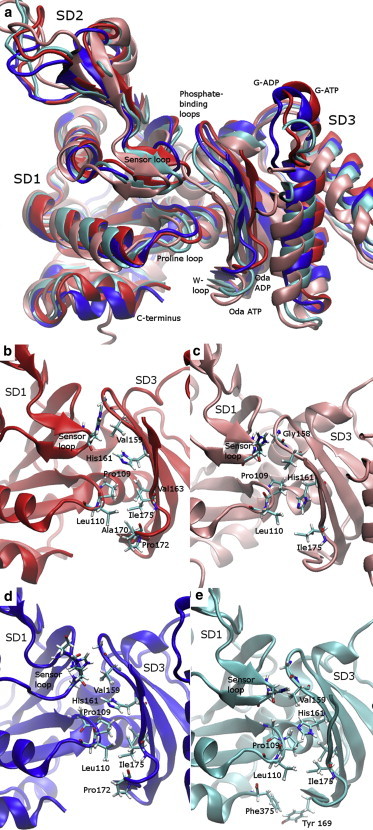
The hydrophobic region between SD1 and SD3 adapts to a range of different twists. (a) The backbone structures of the average position of the lowest-energy sampling window for each system after aligning the internal reference frame for SD1, with SD4 removed for clarity. (b–e) Contacts between SD1 and SD3 in G-ATP, Oda-ATP, G-ADP, and Oda-ADP, respectively. To see this figure in color, go online.

The reorientation of SD2 relative to SD4 may also affect the stabilization of the D-loop, a region that was previously implicated as potentially contributing to nucleotide-dependent differences in actin polymerization. All of the simulations that we performed started with the D-loop in an unfolded configuration. Our simulations did not show a significant difference in the flexibility of the D-loop (as measured by the internal RMSD during the low-energy window simulations) based on changing either the nucleotide or the conformation. This is not surprising given that we did not accelerate sampling in the D-loop region, and all of the D-loops remained in an unfolded conformation. It was previously shown that D-loop rearrangement is a slow event with significant energy barriers along the transition path (26). However, within this unfolded ensemble, the contacts between the helix in SD2 and the D-loop appear to be modulated by the conformation of the actin subunit. There are more contacts between residues 52–66 and the D-loop in G-actin (54.1 ± 0.7 for G-ADP; 51.0 ± 0.7 for G-ATP) than in the Oda conformation (36.4 ± 0.5 for Oda ADP; 38.8 ± 0.5 for Oda ATP). In addition, the nucleotide appears to affect the backbone conformation of the D-loop, specifically the hydrogen-bond formation between residues 44 and 48. We speculate that these collective variables may represent early differences in D-loop behavior that led to the differences reported by Pfaendtner et al. (26). The role of the interaction between the D-loop and the helix in SD2 in mediating D-loop behavior is supported by very recent combined MD and experimental data that suggest that a magnesium cation at this interface may modulate the stiffness of actin filaments (40). The presence and solvation of this cation is likely to be important in the future for accurate simulations of the dynamics of the D-loop.

In the Oda conformation, the nucleotide affects the position of SD4 relative to SD3. This is clear from the backbone structures shown in Fig. 4 (with SD2 removed for clarity), where the internal reference frames of SD3 are aligned for all structures. SD4 shifts toward the nucleotide cleft and rotates toward SD1. This clamping motion explains why the relative position and rotation of SD3 relative to SD4 in the G-actin to Oda comparison is larger in ADP-bound actin than in ATP-bound actin.

Figure 4.

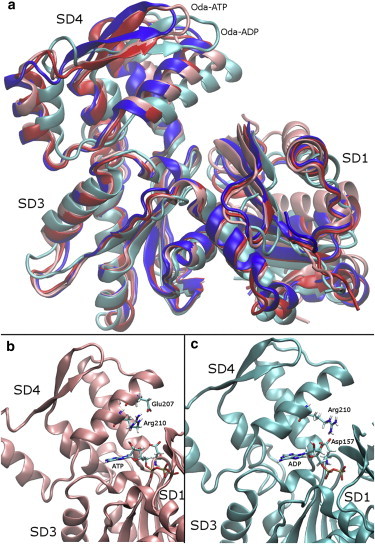
The relative position of SD4 changes significantly in the Oda ADP-bound actin system compared with the other systems simulated. (a) Backbone structure of the average position of the lowest-energy US window for each system after aligning the internal reference frame for SD3, with SD2 removed for clarity. (b and c) Contacts between SD3 and SD4 for Oda ATP and Oda ADP, respectively. To see this figure in color, go online.

At the side-chain level, this is reflected in the interactions of Arg-210 (see Tables S5 and S6 for quantitation). In the ADP-bound Oda minimum-energy window Arg-210 associates with Asp-157 in SD3, whereas in all the other minimum-energy windows Arg-210 interacts with Glu-207 in SD4. Arg-210 also interacts with the ATP’s ribose ring in the Oda system. This interaction is broken when Arg-210 moves to interact with Asp-157, potentially destabilizing ADP binding in the Oda conformation.

The relative positions of SD1 and SD3 also appear to be regulated by the nucleotide. As can be seen in Fig. 5, there are significant differences in the positions of the phosphate-binding loops (residues 14–16 and 156–159), the sensor loop (residues 70–78), the proline loop (residues 108–111), the W-loop (residues 165–172), and the C-terminus. Analysis of the side-chain contacts reveals that even though the phosphate-binding loops shift position, their contacts remain more or less the same (data not shown). There are, however, other nucleotide-dependent changes in the hydrophobic clusters between SD1 and SD3 formed by the sensor loop, the proline loop, and the W-loop (see Table S5 for values and SEs). The orientation of the sensor loop and its coordination with residues 158 and 159 changes with both the nucleotide and the conformation. In G-actin, the nucleotide changes the interactions between residues 72 and 73 in the sensor loop and residues 158 and 159 at the end of the second phosphate-binding loop. In ADP-bound G-actin, the sensor loop is relatively disordered and residue 72 contacts residue 158 near the phosphate-binding loop of CG site 3, mostly through its carbonyl oxygen. In ATP-bound actin and in the Oda conformations, the sensor loop is ordered into a β turn. The carbonyl oxygen of residue 73 hydrogen bonds with the backbone nitrogen of residue 75. This shifts the sensor loop down and orients MeHis toward the phosphate-binding loop of CG site 3. In the Oda conformation, an additional close contact is formed between residue 74 and the phosphate loop that is not present in either of the G-actin conformations. The sensor loop was previously implicated as being important for sensing the nucleotide (10). Results from previous MD simulations of this phenomenon have not been consistent, with some simulations showing an effect on this loop (27) and others revealing no effect (22). We suspect that these differences are due to differences in how the active site is solvated, an issue we return to in Conclusions.

The position of the proline loop is also affected by the nucleotide. Comparing ATP-bound actin with ADP-bound actin, residue 109 in the proline loop is farther from residue 161 in G-actin and farther from residue 163 in Oda actin. These changes may play a role in modulating the conformation of the W-loop (discussed below) in response to the identity of the nucleotide. The interactions between the proline loop and the W-loop are also affected by the conformational state of actin: residue 110 makes closer contacts with residues 172 and 175 in the W-loop in G-actin than in Oda actin. The proline loop was previously implicated in modulating the polymerization of actin and its ATPase activity (41).

A final nucleotide-dependent difference that may alter the accessibility of the hydrophobic cleft at the bottom of actin is observed in the Oda simulations: in ATP-bound actin the C-terminus is fully solvent exposed, whereas in the ADP-bound system (and in the G-actin systems) it is tucked into the cleft. In ADP-bound Oda actin this association is particularly strong: Phe-375 interacts directly with Tyr-169. This difference in the positioning of the C-terminus is interesting in light of the experimental observation of a slow change in the fluorescence of C-terminal labeled ATP-bound actin upon the addition of magnesium, which is believed to be associated with the activation of the subunit for polymerization (31). However, given the limited timescales of the simulations, this difference should not be overinterpreted.

The W-loop (residues 165–172) has been implicated as a nucleotide sensor (4,12,27). The nucleotide appears to modulate the solvent accessibility of this region by changing the hydrophobic interactions mentioned above. To quantitate this effect, we calculated the solvent-accessible surface area of the W-loop in the average structure of the lowest-energy window for each system. The W-loop in ADP-bound G-actin was significantly more solvent exposed than in ATP-bound actin (537 Å² compared with 475 Å² in G-ATP bound actin). The Oda conformations had a very similar W-loop accessibility (510 Å² in ATP-bound vs. 502 Å² for ADP-bound), but showed a significant difference in the region just above the W-loop (residues 172–175) which was significantly more solvent accessible in ATP-bound Oda actin (263 Å²) than in ADP-bound Oda actin (234 Å²).

Nucleotide- and conformation-dependent differences in interactions between the nucleotide and the protein

The nucleotide-dependent long-range changes in inter-CG site contacts described above must in some way be mediated by interactions between the nucleotide and the local protein environment. Additionally, since actin subunit flattening is believed to facilitate ATP hydrolysis, we expect there to be conformation-dependent changes in these interactions. In Table S6 we summarize some of these key distances for residues previously identified as interacting with the nucleotide, including the phosphate-binding loops (13–17 and 156–159), the sensor loop (71–74), the magnesium-coordinating residues (11 and 154), and a residue at the back of the nucleotide-binding cleft (301).

Ser-14, in the first phosphate-binding loop, has been implicated as being important for sensing the state of the nucleotide and modulating the conformation of the sensor loop in response (10). Our simulations show additional nucleotide-dependent differences in the contacts between the phosphate-binding loops and the nucleotide. In G-actin, ATP makes closer contacts with residues 14–16 in the first phosphate-binding loop, and with residues 156, 158, and 159 in the second phosphate-binding loop than does ADP. In the Oda conformation, both ATP and ADP form close contacts with the first phosphate loop, whereas the second phosphate loop shows the same nucleotide dependence as in G-actin.

The sensor loop also interacts differently with ATP compared with ADP. In both conformations, residues 71, 73, and 74 are closer to ATP than to ADP. This differential stabilization of the sensor loop is not a direct interaction—in all cases the closest contact is >4 Å. As discussed above, the response of the sensor loop to changes in the nucleotide has not been consistent among MD simulations. The indirect nature of these interactions is consistent with the explanation that this inconsistency is caused by inadequate solvation of the nucleotide-binding cleft.

Two acidic residues at the base of the nucleotide cleft (11 and 54) coordinate the first solvation shell of waters around the nucleotide-bound magnesium. Table S6 shows the average closest distance between the magnesium and these residues. It is perhaps surprising that ADP-bound magnesium is more closely coordinated to these residues in G-actin. It is likely that this occurs because the γ-phosphate of ATP holds the nucleotide tightly upward against the phosphate binding loops, whereas in ADP the phosphate tail can shift downward to facilitate this closer coordination. This downward motion of the phosphate tail is further reflected in the closer contact between the α-phosphate and residue 301 in ADP-bound actin. The flattened Oda conformation appears to accommodate close coordination with both the phosphate-binding loops and these acidic residues, but still shows a slight downward motion compared with ATP based on the contact with residue 301.

Conclusions

Based on the free-energy landscapes we determined in simulations and our multiscale analysis of the most energetically favorable window in those simulations, we conclude that there are significant differences between G-actin and Oda-actin that reflect the identity of the bound nucleotide. Here, we consider these differences in the context of the following questions: How does the nucleotide affect the rates of polymerization? How does the nucleotide alter the binding affinity of actin binding protein profilin? What local differences in conformation might prevent the interconversion of G-actin and Oda-actin conformations on the scale that we can simulate?

In both the G-actin and Oda conformations, ATP-bound actin is less conformationally mobile than ADP-bound actin. The additional conformations that ADP-bound actin explored are unfavorable to polymerization, since the cleft opened and the subunit became more twisted. Thus, one possible explanation for the increased rate of polymerization is an entropic one: ATP-bound actin subunits are more likely to be in a conformation that is favorable for polymerization because they explore a smaller conformational landscape. An alternative energetically based explanation for the increased rate of polymerization in ATP-bound actin can be found in the all-atom analysis of the interface between SD2 and SD4. ATP-bound actin preferentially polymerizes at the barbed end of actin, so the incoming subunit will interact with the filament via the SD2-SD4 interface. As shown in Fig. 4, the surface formed by SD2 and SD4 in the G-actin ATP-bound simulation (cleft width 24.5 Å, subunit twist −22.75°) is much more similar to that in the Oda structure than to that in the ADP-bound G-actin system, even without complete subunit flattening or cleft closure. ATP-bound actin may therefore polymerize more rapidly than ADP-bound actin due to the favorable arrangement of the SD2-SD4 surface. Finally, both the Oda and G-actin ATP-bound systems showed a salt bridge cross-linking SD2 and SD4, and in both cases this bridge involved Arg-62. This salt bridge may explain in part why the ATP-bound actin subunits are less conformationally mobile. Arg-62 is known to be important for polymerization: filament models show that it forms part of the intersubunit interface (43), and the R62D mutant of actin is nonpolymerizable (44).

Effect of nucleotide on the affinity of profilin for actin

Although the SD2-SD4 interface is likely responsible for the nucleotide’s effect on polymerization, actin-binding proteins such as profilin interact at the SD1-SD3 interface, and their affinities for actin are sensitive to the state of the nucleotide. The CG analysis described above showed changes in the relative positions and orientations of SD1 and SD3, and the associated all-atom analysis showed that the nucleotide affects the interactions of the W-loop with the proline loop. Profilin binds to the W-loop side of actin and interacts with Ala-170 and His-173, among others. As discussed in the atomistic analysis of the SD1-SD3 interface, the W-loop overall, including Ala-170, is more solvent exposed in ATP-bound G-actin, whereas in ATP-bound Oda-actin the region just above the W-loop, containing His-173, is significantly more solvent exposed. These changes to favor the exposure of residues involved in the profilin interface suggest a mechanism by which ATP can facilitate profilin binding, consistent with experimental data showing that profilin binds to ATP-bound G-actin with a higher affinity than it does to ADP-bound G-actin (1).

The G- to Oda-actin conformational change

Although we identified several interesting nucleotide effects on actin structure and dynamics that are consistent regardless of the starting configuration, we had hoped to see a full conversion between the G-actin and Oda (F-actin) states that would allow us to evaluate their relative energies and posit a mechanism for interconversion. However, even when we used self-adaptive sampling in a 2D CG collective variable space, the G-actin and Oda states did not converge within the timeframe that we could simulate. This is perhaps not surprising given the complex interactions that occur between CG sites that are not directly biased by these two collective variables. However, even without full convergence, the simulations are enlightening in that they suggest that the Oda configuration represents a local minimum even in a monomer simulation. However, this appears to be highly dependent on the solvating waters around actin, since in the initial equilibrium simulations in which the cleft was less rigorously solvated, the Oda configuration showed some degree of spontaneous twisting. The solvation of actin, both at the top of the nucleotide cleft and around the magnesium cation at the base of the cleft, appears to critically modulate the dynamics we observe. Undersolvation of active-site clefts (or unrealistic solvation in general) and its influence on simulations have long been known (45), and in the actin system may account for the significant differences in behavior reported from MD simulations in the literature.

CG analysis enabled us to identify local structural changes that may be important collective variables to sample in future simulations to facilitate convergence. Based on the last two columns of Table S4, it is clear that the subdomains of actin change in their relative position and orientation more than can be described by the two collective variables that we have chosen. However, even in the simplified CG representation that we have chosen, and focusing only on the main CG sites, these variables would account for an additional 24 degrees of freedom (4 pairs of CG sites × (3 rotational + 3 translational degrees of freedom). The multiscale path sampling algorithm that is currently being developed (Tempkin, Qi, Weare, Dinner, unpublished) should facilitate accelerated sampling in this collective variable space and enable a better understanding of the full G- actin to Oda conformational exchange in the future. The self-learning US algorithm could potentially also be used with a few additional dimensions to yield better convergence. Selecting some of the remaining differences between the G-actin and Oda models to bias may facilitate sampling of a full interconversion between states. Such ambitious US simulations will be attempted in the future. Most importantly, perhaps, our results illustrate quite clearly the inherent challenges in developing and applying accurate highly (or ultra) CG models such as the one shown in Fig. 1 b for G-actin. Underlying the simplified CG representation, in which numerous amino acid residues are grouped into each CG site, are a multitude of complex molecular interactions or states. In turn, this makes it very challenging to obtain a simple description of the interactions between the highly CG sites from a bottom-up perspective, pointing to the need for a new conceptual and methodological framework to represent ultra CG models such as the one we recently developed (46).