A Feature-based Developmental Model of the Infant Brain in Structural MRI

Abstract

In this paper, anatomical development is modeled as a collection of distinctive image patterns localized in space and time. A Bayesian posterior probability is defined over a random variable of subject age, conditioned on data in the form of scale-invariant image features. The model is automatically learned from a large set of images exhibiting significant variation, used to discover anatomical structure related to age and development, and fit to new images to predict age. The model is applied to a set of 230 infant structural MRIs of 92 subjects acquired at multiple sites over an age range of 8-590 days. Experiments demonstrate that the model can be used to identify age-related anatomical structure, and to predict the age of new subjects with an average error of 72 days.

1 Introduction

The human brain undergoes dramatic developmental changes in the first years of life. Structural MR imaging offers the potential to model these changes over time and across the human population, in order to understand normal growth patterns and assess potential disorders [1], for example neurodevelopmental disorders relating to pre-term birth [2, 3]. Anatomical development is closely tied to chronological age, and computational tasks of interest include automatically learning links between anatomical image structure and age, and predicting the age or developmental stage of new subjects.

A number of methods are used to analyze aging in structural MRI of the adult brain, e.g. group analysis via voxel-based morphometry (VBM) [4], growth patterns of dilation and contraction [5], discriminative classifiers [6–8]. These methods generally require accurate intensity-based segmentation and registration, tasks which remain research challenges in the context of the infant brain [9, 1] due to pronounced intensity changes over the course of development, e.g. the contrast inversion of white/grey matter during myelination [10]. Infant temporal atlases are thus often treated as templates constructed over relatively narrow age ranges via age-specific registration and segmentation methods [11, 12, 9], and quantitative analysis has been largely limited to measures of growth, e.g. tissue volume changes [2, 3, 13]. Modeling dynamic image measurements across the infant developmental age range remains a challenge.

This paper proposes modeling development as a collection of distinctive, conditionally independent image features, localized in space and time. Anatomical structure is modeled as persisting over limited spatial and temporal windows, and as potentially only occurring in subsets of subjects. This provides a natural means of describing phenomena such as the disappearance/emergence of structure, spatially varying developmental rates, natural inter-subject variability and pathology. The model is based on scale-invariant features [14, 15], distinctive image patterns that can be robustly extracted in the presence of global image deformations including scale changes, and that can therefore offer an information source complementary to typical growth measures such as volume change. Our model builds on the approach of [16], where local image features are used to construct a binary classifier for Alzheimer’s disease in T1 MRI data. Here, a posterior probability is defined over a continuous variable of age, conditioned on feature data. Anatomical structure is modeled as a latent variable conditioned on age, and hypothesis testing is used to identify features most informative regarding age. The model is trained from combined cross-sectional and longitudinal data, in order to identify age-informative anatomical structure, and age is predicted via maximum a-posteriori estimation.

Experiments demonstrate several important advancements on the state-ofthe-art. The model can be automatically trained from a large set of infant T1-weighted MRI data, acquired at multiple sites and scanners. Spatially-localized, age-related anatomical patterns are discovered across the infant age range, including white matter myelination. Cross-validation trials predict subject age with an average error of 72 days, which to our knowledge is the first published result for automatic infant age prediction from structural MRI data.

2 Feature-based Developmental Model

The proposed model hypothesizes the existence of anatomical features that can be localized in time and space, and used to represent development in structural MRI data. Scale-space theory provides a framework for identifying both the location and spatial extent of such features [14], and forms the basis for invariant feature detection methods widely adopted in the computer vision community [17, 15]. So-called scale-invariant features are spherical image regions characterizing the 3D location x and scale σ of distinctive image patterns. They can be automatically extracted from images via Gaussian derivative operators, for instance as extrema in the difference-of-Gaussian (DoG) scale space [15]:

$$\{x_i,{\sigma }_i\}=\underset{x,\sigma }{\text{local argmax}}\{\mid G(\sigma )\ast I(x)-G(\kappa \sigma )\ast I(x)\mid \},$$ (1)

where I(x) is the image, G(σ) is a Gaussian kernel of variance σ², and κ is a constant defining the multiplicative sampling rate in scale. The DoG is a computationally efficient approximation to the Laplacian-of-Gaussian operator, which is effective in identifying natural blob-like image structures. Once identified, image content within each region (x_i, σ_i) is cropped and rescaled to a fixed-size region, then encoded as an appearance descriptor for computing feature-to-feature correspondence. The gradient orientation histogram (GoH) descriptor has been shown to be among the most effective for image-to-image matching [17], here a 3D variant with 8 orientation and 8 spatial bins is computed from 11 × 11 × 11 normalized voxel regions. Due to spatial normalization, the scale-invariant feature representation is independent of isotropic image scaling, and is thus particularly useful in characterizing local anatomy independently from global growth or volume change.

2.1 Probabilistic Model

Let $\stackrel{‒}{I}=\left\{I_j\right\}$ represent a set of local features extracted in a subject image I, and let A represent a random variable of age. The posterior probability of A conditioned on data $\stackrel{‒}{I}$ can be expressed using Bayes rule as:

$$p(A\mid \stackrel{‒}{I})=p(\stackrel{‒}{I}\mid A)p\left(A\right)∕p\left(\stackrel{‒}{I}\right),$$ (2)

where $p(\stackrel{‒}{I}\mid A)$ is the likelihood of A associated with data $\stackrel{‒}{I}$, p(A) is the posterior probability of A, and $p\left(\stackrel{‒}{I}\right)$ is a constant as data $\stackrel{‒}{I}$ are fixed. Under the assumption of conditionally independent local feature measurements, the likelihood can be expressed as:

$$p(\stackrel{‒}{I}\mid A)=\prod _{j}p(I_j\mid A),$$ (3)

where p(I_j∣A) is the likelihood associated with an individual observed feature I_j and age A.

An image set is naturally described in terms of distinctive local structure shared across images, for instance the human brain can be described by corpus callosum, ventricles, etc. The model here adopts a description based on a code book of distinctive image features. Let F = {f_i} represent discrete random variable, where event f_i indicates a distinct mode of feature appearance and geometry. Applying marginalization and Bayes rule, the likelihood in Equation (3) is expressed as:

$$p(I_j\mid A)=\sum _{i\in F}p(I_j,f_i\mid A)=\sum _{i\in F}p(I_j\mid f_i,A)p(f_i\mid A).$$ (4)

In equation (4), p(I_j∣f_i, A) represents the likelihood of feature f_i and age A associated with I_j, which can generally be taken to be a unimodal Gaussian density over feature parameters of location, log scale and appearance descriptor elements. Factor p(f_i∣A) is the conditional probability of f_i given age A, and is modeled as a multinomial distribution.

2.2 Learning, Analysis, Fitting

The goal of model learning is to generate a code book F = {f_i} of model features characteristic of a training image set, and to estimate associated age-related factors p(I_j∣f_i, A) and p(f_i∣A). Prior to learning, training images are normalized to a common reference space via a global coordinate transformation to an atlas template, e.g. a similarity or affine transform. Scale-invariant features are then extracted from each image, and a code book F = {f_i} of model features representative of the image data is generated. A number of approaches could be used for this purpose, here we adopt a robust clustering strategy [16] similar to the mean-shift algorithm [18], which identifies clusters of features that are similar in terms of geometry and appearance across subjects. Each cluster f_i is characterized by a prototype feature, and cluster membership is defined by fixed thresholds on geometrical distance (location, log scale) and learned thresholds on appearance descriptor distance [16]. Note that this clustering procedure identifies a large, arbitrary number of clusters, and is capable of robustly grouping features despite imprecision in approximate inter-subject image alignment.

With model features defined, factors in Equation (4) are estimated from feature samples in clusters f_i. Age A is defined as a discrete random variable over K age categories. Gaussian mean and variance parameters of p(I_j∣f_i, A) are estimated via maximum likelihood for each age category, probability mass parameters of p(f_i∣A) are determined via maximum a-posteriori (MAP) estimation from co-occurrence counts of f_i, A and a Laplace prior. While f_i generally represents a distinctive anatomical structure, a special model feature f₀ is reserved for spurious features arising from background noise. As such features can vary arbitrarily in geometry and appearance, p(I_j∣f₀, A)p(f₀∣A) is taken to be uniform and constant.

Model fitting is used to interpret image data associated with a new subject in terms of the entire code book F, and to estimate the age or developmental stage. Fitting aims to identify the MAP age estimate A_MAP maximizing the posterior probability:

$$A_{MAP}=\underset{A}{\mathrm{argmax}}\left\{p\right(A\mid \stackrel{‒}{I}\left)\right\}.$$ (5)

As in learning, the image is first spatially normalized via subject-atlas alignment. Image features are then extracted and matched to model features, where a match occurs between image and model feature pair (I_j, f_i) if the Euclidean distance between their normalized geometry and appearance descriptors falls within geometry and appearance thresholds associated with f_i. Equation (5) is then evaluated via Equation (4) at each discrete age value to identify A_MAP.

3 Experiments

Experiments validate our model on infant brain development in T1-weighted MRI data from the data set of [19], consisting of 92 healthy subjects imaged from one to seven times over an age range of 8-590 days, for a total of 230 images. All subject images are robustly aligned to a single subject arbitrarily selected as an atlas via a similarity transform (rigid + isotropic scaling). Alignment correctness is validated by inspection of resampled images and alignment parameters. Scale-invariant features are extracted in individual aligned images, after which clustering is used to generate a code book F of model features for analysis. Finally, age-conditional factors p(I_j∣f_i, A) and p(f_i∣A) are trained based on F and subject age labels A, where A is discretized into 10 bins with equal image counts and approximately equal age ranges. The prior p(A) can be set according to expectations, here it is taken to be uniform.

3.1 Age-Related Structure

Distributions p(f_i∣A) quantify the probabilistic relationship between learned anatomical features and age. A variety of criteria could be used to quantify the informativeness of this relationship; we found that information-theoric measures such as entropy tend to overemphasize the importance of spurious, low entropy distributions generated from small numbers of data samples. Here, we consider a Fisher’s exact test computed from a 2x2 contingency table of the presence/absence of feature f_i within/without a 2-category (120-day) age window. The null hypothesis is that feature/age are statistically independent, in which case their co-occurrence follows a hypergeometric distribution, which effectively accounts for small sample sizes.

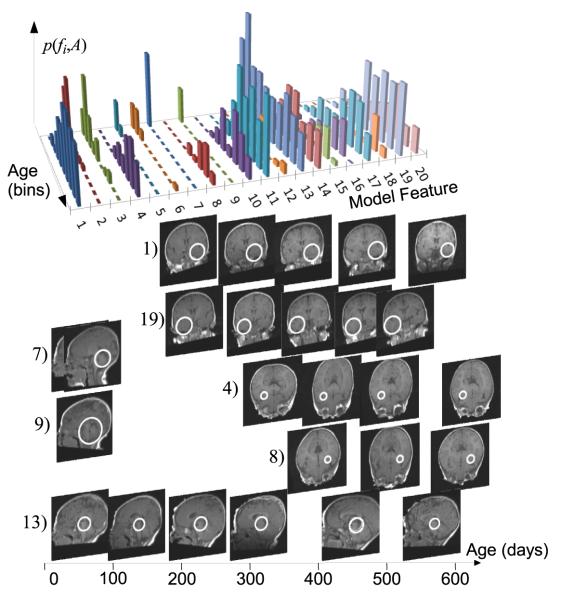
From a total of 6.5K learned model features, 36 are identified with a false discovery rate [20] of 0.05. Figure 1 illustrates the 20 features bearing the most significant relationship with age. Note that significant features show a high degree of symmetry, out of 20 features, eight represent homologous structure identified independently in opposite hemispheres with similar age distributions, another three represent midbrain structure.

Fig. 1.

Top: distribution p(f_i, A) for the 20 most significant age-related features over 10 age categories. Below: visual examples of features (white circles) in subject image slices over age. Pairs (4, 8) and (1,19) represent symmetric white matter patterns appearing at slightly different onsets. (7) and (9) represent distinct modes cerebellar anatomy linked with vermian development and occurring exclusively in early life. (13) occurs in the brain stem across the age range, more frequently in early life. Note the lack of visible white matter under 100 days, e.g. corpus callosum.

3.2 Age Prediction

Model fitting allows age prediction from individual subject images, which may be potentially useful assessing developmental stage. A five-fold cross validation paradigm is adopted, where subjects are randomly divided into 5 mutually exclusive subsets of approximately the same number of images. For each subset, age is predicted for all images based on a model trained on the remaining 4 subsets. Note that different images of the same subject are never present in both testing and training subsets.

The infant brain increases in size, particularly during early weeks, and thus an initial baseline for predicting age from structural MR would be based on volume or size measurements [13]. For comparison, a linear predictor of age based on isotropic subject scale relative to the atlas results in a mean error of 102 days, random guessing results in a mean error of 200 days. Figure 2 illustrates the result of MAP age prediction, which results in a mean error of 72 days. Although this is lower than baseline methods, it is non-negligible, and we hypothesize that error may be related to differences in developmental rates between different subjects. Curves in Figure 2 plot predicted age trajectories for 5 subjects, while a high degree of inter-subject variability is observed, 90% of sequential age predictions follow a monotonically increasing trend. Thus, it may be more accurate to interpret the predicted age as the stage of development with respect to the population, which may generally either lag or lead the actual chronological age; we intend to investigate this possibility in future work.

Fig. 2.

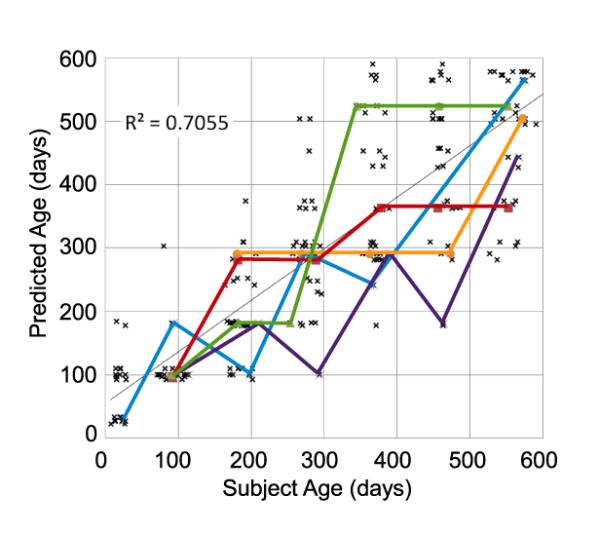
MAP predicted age vs. subject age across subjects. Thick colored lines illustrate age trajectories for five subjects with scans at 6 or more time points.

4 Discussion

This paper presents a novel model describing anatomical development as a collection of features localized over space and time. Validation on infant structural MRI data demonstrates statistically significant age-related features can be automatically discovered across the infant age range, and the first results of infant age prediction are presented. Numerous avenues for future investigation exist, including modeling longitudinal feature-time trajectories or dependencies between features, linking developmental changes other factors such as gender or disease, incorporating alternative image features such as affine invariant features, investigating alternative means of querying age-related model features. Modeling based on a fixed reference coordinate system here is sufficient for infant brains, an evolving coordinate system [21] will allow application of the modeling to prenatal, fetal and embryonic stages of development.