Abstract
The spinal cord is an essential and vulnerable component of the central nervous system. Differentiating and localizing the spinal cord internal structure (i.e., gray matter vs. white matter) is critical for assessment of therapeutic impacts and determining prognosis of relevant conditions. Fortunately, new magnetic resonance imaging (MRI) sequences enable clinical study of the in vivo spinal cord’s internal structure. Yet, low contrast-to-noise ratio, artifacts, and imaging distortions have limited the applicability of tissue segmentation techniques pioneered elsewhere in the central nervous system. Additionally, due to the inter-subject variability exhibited on cervical MRI, typical deformable volumetric registrations perform poorly, limiting the applicability of a typical multi-atlas segmentation framework. Thus, to date, no automated algorithms have been presented for the spinal cord’s internal structure. Herein, we present a novel slice-based groupwise registration framework for robustly segmenting cervical spinal cord MRI. Specifically, we provide a method for (1) pre-aligning the slice-based atlases into a groupwise-consistent space, (2) constructing a model of spinal cord variability, (3) projecting the target slice into the low-dimensional space using a model-specific registration cost function, and (4) estimating robust segmentations using geodesically appropriate atlas information. Moreover, the proposed framework provides a natural mechanism for performing atlas selection and initializing the free model parameters in an informed manner. In a cross-validation experiment using 67 MR volumes of the cervical spinal cord, we demonstrate sub-millimetric accuracy, significant quantitative and qualitative improvement over comparable multi-atlas frameworks, and provide insight into the sensitivity of the associated model parameters.
Keywords: Cervical Spinal Cord Segmentation, Groupwise Registration, Multi-Atlas Segmentation, Spinal Cord Internal Structure
Introduction
The spinal cord is an essential and vulnerable component of the central nervous system which can be significantly affected by numerous neurological conditions – e.g., amyotrophic lateral sclerosis, multiple sclerosis, and neuromyelitis optica (Bede et al., 2013; Bede et al., 2012; Dietz and Curt, 2006; Wingerchuk et al., 2007; Yiannakas et al., 2012). Differentiating and localizing pathology/degeneration of the gray matter (GM) and white matter (WM) plays a critical role in assessing the magnitude of tissue damage, therapeutic impacts and determining prognosis of these conditions (Gilmore et al., 2006; Jarius and Wildemann, 2010). While automated methods have been used to segment the spinal cord from the surrounding cerebrospinal fluid (CSF)(Carballido-Gamio et al., 2004; Chen et al., 2011; Huang et al., 2009; Ma et al., 2010; McIntosh and Hamarneh, 2006) and semi-automated methods have been used for more detailed parcellation of the individual spinal columns(Horsfield et al., 2010; Kaminsky et al., 2004), automated delineation of internal spinal cord structures (i.e., GM/WM) has not been reported for any imaging modalities. In fact, high-resolution MRI that can provide contrast among spinal cord internal structures has only recently become feasible in clinically acceptable scan times (Farrell et al., 2008; Ozturk et al., 2013; Smith et al., 2010; Yiannakas et al., 2012; Zackowski et al., 2009). Moreover, MRI of the cervical spinal cord is hindered by numerous technical challenges (Hinks and Quencer, 1988; Karpova et al., 2013; Mikulis et al., 1994) – including (1) the small dimensions (1-2 cm in diameter) with subsequent signal to noise limitations, (2) similarity between WM and GM T1 and T2 values resulting in poor intra-cord contrast (Smith et al., 2008), (3) involuntary/physiological patient motion, and (4) imaging in homogeneities and artifacts. Given the challenges associated with spinal anatomy, imaging data, and subsequent processing, developing a robust system to consistently and accurately overcome these challenges is essential. The goal of this manuscript is to provide an efficient and accurate segmentation framework specifically focused on segmenting the spinal cord’s internal structure and enabling future clinically relevant inference about the anatomy and its associated conditions.
Over the past decade, multi-atlas segmentation has come to represent the de facto standard segmentation framework for its ability to rapidly and accurately generalize structural information from labeled examples (i.e., atlases) (Heckemann et al., 2006; Rohlfing et al., 2004b). In multi-atlas segmentation, multiple atlases are registered to the target (Avants et al., 2008; Ourselin et al., 2001) and the resulting voxelwise label conflicts are resolved using label fusion (Artaechevarria et al., 2009; Asman and Landman, 2012c; Coupé et al., 2011; Sabuncu et al., 2010; Wang et al., 2012; Warfield et al., 2004). Since its inception, multi-atlas segmentation has exploded in popularity and has been used across a wide range of potential applications – including, but not limited to, whole-brain (Aljabar et al., 2009; Artaechevarria et al., 2009; Asman and Landman, 2011a; Asman and Landman, 2012b; Heckemann et al., 2006; Sabuncu et al., 2010; Wolz et al., 2010), hippocampus (Cardoso et al., 2013; Coupé et al., 2011; Wang et al., 2012), cardiac (Isgum et al., 2009), prostate (Langerak et al., 2010), and abdomen (Wolz et al., 2012).
The manner in which the atlas-target registrations are performed has a substantial impact on multi-atlas segmentation quality (Klein et al., 2009). In a typical multi-atlas framework, each atlas is non-rigidly registered to the target in a pairwise fashion (i.e., each atlas-target registration is computed independently). More recently, “groupwise” registration approaches (i.e., pre-alignment of the atlas information to a common groupwise space) have become increasingly popular (Balci et al., 2007; Bhatia et al., 2007; Cootes et al., 2001; Cootes et al., 1995; Depa et al., 2011; Jia et al., 2012; Wolz et al., 2010). Groupwise registrations have several benefits, primarily: (1) they reduce the computational burden by requiring only a single registration from the groupwise space to the target space, and (2) through projecting the co-registered atlas information into a low dimensional space (i.e., a “manifold”) (Cao et al., 2011; Jia et al., 2012; Wolz et al., 2010), they provide a natural framework for modeling the relationships between atlases – e.g., for atlas selection (Aljabar et al., 2009; Rohlfing et al., 2004).
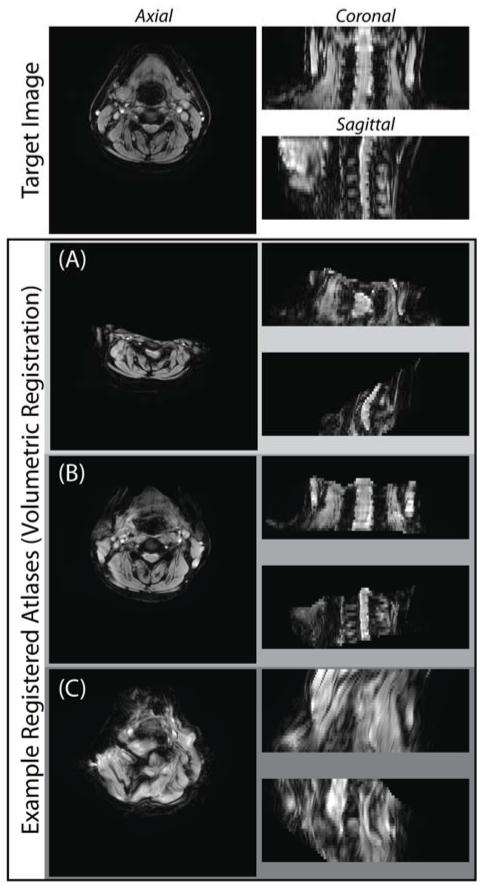
However, regardless of the registration framework, if consistent 3-D deformable registration between the atlases and the target cannot consistently and accurately find structurally-meaningful correspondence, then the applicability of multi-atlas segmentation is unlikely. Unfortunately, due to the extreme variability exhibited among cervical spinal cord 3-D MRI of individual subjects, deformable atlas-target registrations consistently suffer (Figure 1) from (a) poor global initialization, (b) undesired boundary conditions, and (c) dramatic over-smoothing due to lack of local correspondence. Comparatively speaking, when viewed from a 2-D axial cross-section within the acquisition plane (i.e., a slice), the inter-subject variability is notably lessened. As a result, when viewed from a slice-based perspective, robustly discovering structurally relevant homology becomes substantially easier. Additionally, a slice-based perspective on the segmentation of cervical MRI (1) enables the use of significantly more (slice-based) atlases, and (2) dramatically reduces the computational burden of individual atlas-target registrations.
Figure 1.
Problems associated with non-rigid volumetric registration of cervical spinal cord MRI. Non-rigid volumetric registration of cervical spinal cord MRI is challenging and may yield suboptimal results, including (A) poor global initialization, (B) undesired boundary conditions, and (C) overly smoothed deformations as a result of poor local correspondence.
Herein, we propose the first approach for fully automated segmentation of cervical spinal cord internal structure using a groupwise slice-based multi-atlas registration framework. Building on the seminal work on “eigenfaces” (Turk and Pentland, 1991) and active shape/appearance models (Cootes et al., 2001; Cootes et al., 1995), we provide a method for (1) pre-aligning the slice-based atlas information into a common, groupwise-consistent coordinate system, (2) constructing a model describing spinal cord variability (i.e., “eigenspines”), (3) registering the target image slice to the model space using a simultaneous intensity- and model-driven cost function, and (4) estimating a final segmentation by fusing the provided atlas information. Additionally, the proposed framework provides a natural mechanism for selecting geodesically appropriate atlases (i.e., atlas selection) and initializing the free model parameters in an informed model-specific context. This presentation is a reformulation of a recently published conference paper (Asman et al., 2013) in which we provide a completely rederived groupwise registration framework to provide substantial improvements in overall robustness and accuracy.
In this manuscript, we begin by deriving the theoretical framework governing our proposed slice-based groupwise registration framework. Next, we perform a cross-validation experiment (using 67 subjects) in which we demonstrate significant quantitative and qualitative improvement over comparable volumetric and slice-based pairwise registration frameworks (in terms of GM and WM segmentation accuracy). Lastly, the sensitivity of the proposed model is addressed with respect to the free model parameters.
Theory
Problem Definition
Consider a target gray-level image represented as a vector, , where N is the number of voxels in the image. Let T ∈ LN×1 be the latent representation of the true target segmentation, where L = {0, …, L − 1} is the set of possible labels that can be assigned to a given voxel. Consider a collection of J atlases with associated intensity values, , and label decisions, D ∈ LN×J. The index variables i, j, and l will be used to iterate over the voxels, atlases, and labels, respectively. To summarize, the goal of the proposed approach is to:
Rigidly register all of the atlas information, {A, D}, to a common groupwise space. In other words, we need to construct , where NM < N is the number of voxels that are consistent among the atlases in the common model space (i.e., the relevant subset cropped from each slice).
Construct the appearance model using the groupwise-consistent atlas representations. The appearance model consists of (1) the mean image, (2) the orthogonal eigenvectors (“eigenspines”)describing the modes of variation, , (3) the associated eigenvalues, , and (4) the weights associated with each atlas when projected into the model space, . Note, V < J << NM represents the number of modes of variation that are used in the model.
Find the optimal rigid transformation, R, that maps the target image, I, to the groupwise model space, IM = R ∘ I, by minimizing a model-driven cost function. Project IM into the low-dimensional model space, described by .
Using ω and ωM, select the geodesically-closest K≤J atlases to use. Label fusion is then used to fuse the selected K atlases resulting in a segmentation estimate of ,.
Transform to , an estimate of the desired segmentation in the original target space.
Note, as the model we are constructing describes a 2-D (slice-based) representation of the spinal cord, all rigid transformations described in this manuscript are 2-D three degree-of-freedom transformations. In other words, a given transformation matrix, R, can be described by {tx, ty, θ}, where {tx, ty} represent a two-dimensional translation, and θ represents a rotation angle. We will use the notation, R ∘ X, to denote the application of transformation matrixR to imageX.
Creation of a Groupwise Consistent Atlas Representation
The first step in constructing the appearance model describing the slice-based representations of the spinal cord is to register the atlas information,{A, D}, to a common groupwise space (i.e., a space in which all atlas slices are co-aligned).Here, we use an iterative process to construct the groupwise consistent representation of the atlases.
Let χ(k) ∈ LNM×1 represent the “mean” segmentation image (herein, via majority vote–see eq. 2) at the kth iteration of the described procedure. Then, for each individual atlas, {Aj, Dj} the goal is to optimize the following label-based cost function:
| (1) |
where is the rigid transformation that minimizes the L0 norm (i.e., the discretemetric) between the current estimate of the groupwise mean segmentation, χ(k), and the jth atlas segmentation transformed into the current model space, .
After the optimized rigid transformations are computed for each individual atlas, the mean segmentation estimate can be updated using majority vote fusion:
| (2) |
where δ(·,·) is the Kronecker delta function. The process defined by (1) and (2) is then iterated until the mean segmentation estimate converges to a consistent segmentation (i.e., no change in the L0 norm between successive iterations: ||χ(k−1) − χ(k)||0 = 0). In practice, convergence typically occurred in fewer than 5 iterations. Note, an alternative approach could be to use Expectation-Maximization (EM) to fuse the initial registered atlases for construction of the groupwise consistent mean (e.g., (Weisenfeld and Warfield, 2009)); however, unlike the proposed method, this type of framework would largely rely on the success of the initial registrations. Lastly, the groupwise consistent representation of the atlases (i.e., ) is then constructed using the final transformations, , after the iterative registration procedure has converged:
| (3) |
Appearance Model Construction
Now that we have all of the atlas information in a groupwise consistent representation, {AM, DM}, it is possible to construct an appearance model. The first step is to find the mean atlas image, using the aligned atlas image information
| (4) |
Next, we find the eigen vectors (referred to as “eigenspines”), , and eigenvalues, using principal component analysis (PCA) (Jolliffe, 1986). As a result, for the vth eigenspine/eigenvalue pair, uv is chosen such that the following function is maximized
| (5) |
subject to the constraint that all eigenspines are unit vectors (i.e., |uv| = 1) and orthogonal (i.e., ). Note that the number of eigenspine/eigenvalue pairs that are constructed is a function of the desired fraction of the total variance that the model should explain, k. This number, V, is chosen as the minimum value for which
| (6) |
Finally, we compute the projection weights for each of the atlases that were used in constructing the model. These weights, , where each element, is found through a vector projection:
| (7) |
Thus, be directly interpreted as the relative amount of variance explained by each of the V available modes of variation, for a given atlas j.
As an important aside, in standard practical applications, the creation of the groupwise consistent atlas representation (eqs. 1-3) and the construction of the appearance model (eqs. 4-7) would be performed entirely “offline” (i.e., a new model would not need to be constructed for each desired target volume).
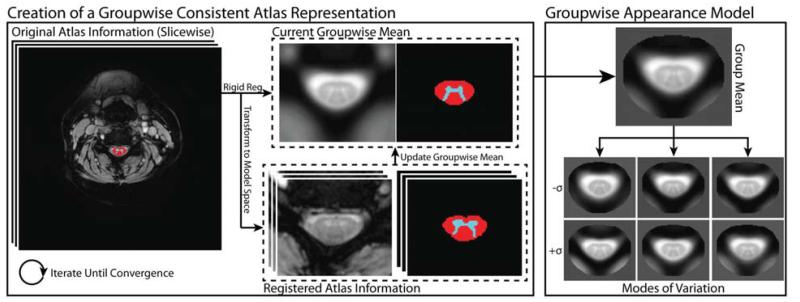
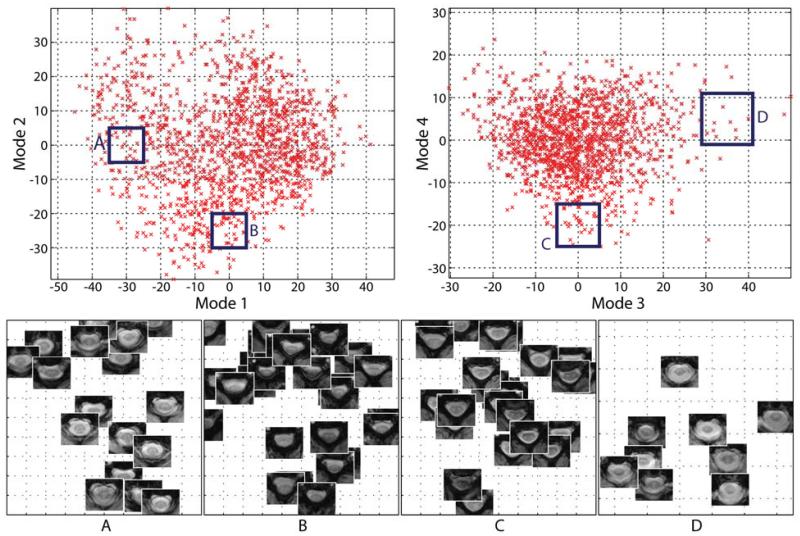
Figure 2 provides a visual representation of the theoretically described process of both creating the groupwise-consistent atlas representations and, subsequently, understanding the resulting appearance model. Figure 3 visualizes local relationships between the atlases when they are projected into the low-dimensional appearance model space, and demonstrates that the low dimensional representation maintains the relationships between the visually expected atlas similarities.
Figure 2.
Flowchart describing the construction of the groupwise consistent atlas representation and the resulting groupwise appearance model. In an iterative procedure, all of the atlases registered to the current estimate of the mean, which is then updated. Using the co-registered atlas data, the groupwise appearance model is constructed using principal component analysis.
Figure 3.
Example local atlas image content with respect to the primary modes of variation constructed in the model. The geodesic distance between co-registered atlases (i.e., the distance in the low-dimensional model) visually corresponds to anatomical similarity.
Groupwise Registration and Segmentation using the Appearance Model
Once the appearance model for the atlases has been constructed, the primary remaining challenge is to find the rigid transformation, R, that maps each target image, I, into the model space – represented by IM. We define a cost function that is a function of both (1) how well the model represents IM, and (2) the image similarity between IM and a weighted average representation of the atlases, . Thus, for a given transformation, R, the projection weights for the target image, can be found similarly to (7) as
| (8) |
We can then define the model similarity between all of the individual atlases and the projected target image, , using the current estimate of the desired transformation matrix, R. Let βj (i.e., the similarity between the jth atlas and the projected target image)be defined as
| (9) |
where Z is the partition function which enforces the constraint that Σj βj = 1, and τ is a model weighting parameter indicating the decay constant associated with the geodesic distance between a given atlas and the projected target image in model space. Using these similarity weights, we construct (1) the weighted mean of the atlas projection weights, (2) the weighted standard deviation of the projection weights , and (3) the weighted image representation of the projected target image from the atlases, , where
| (10) |
| (11) |
| (12) |
Using (10)-(12), we define the registration cost function for aligning the target image to the model space, R, to be
| (13) |
where the first term, , represents the squared L2 norm between the projected target image and the weighted average representation of the projected target image (i.e., using the model weights and the atlas image information), and the second term, approximates the Gaussian log-likelihood of the observed weights of the projected target image, ω, given the provided appearance model.
Given the optimal rigid registration, R, that maps the target image into the appearance model space, it is possible to estimate the underlying target segmentation using label fusion. The geodesic distance-based similarity weights, β provide a natural and straightforward mechanism for performing informed atlas selection (Aljabar et al., 2009; Rohlfing et al., 2004a) – a claim qualitatively supported in Figure 3. Here, we select the set of all atlases for which βj is greater than some arbitrary constant, ε. Let {,} be the set of selected atlases, where K = {k|βk > ε}. Thus, the segmentation estimate of the target image in model space, , is
| (14) |
where can be approximated using a pre-defined label fusion framework – e.g., (Asman and Landman, 2012b; Asman and Landman, 2012c; Heckemann et al., 2006; Sabuncu et al., 2010; Wang et al., 2012; Warfield et al., 2004).
Finally, the last remaining step is to transfer the segmentation estimate from model space, , to the original space defined by the target image . This can be easily accomplished using the inverse of the optimal rigid transformation found in (13).
| (15) |
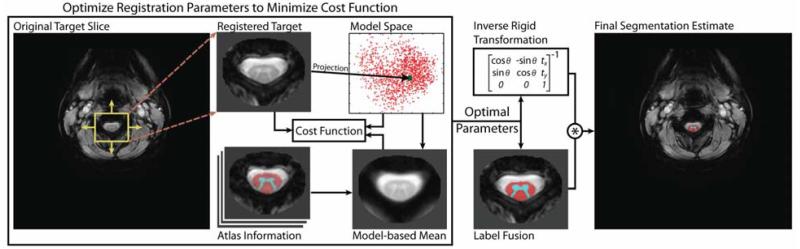
Figure 4 provides a visual representation of the described framework for both registering and projecting the target image into the low-dimensional model space, and constructing and transferring the label fusion estimate into the original target coordinate system.
Figure 4.
Flowchart describing the process of (1) registering the target image with the model space, and (2) constructing the final segmentation estimate. For a given rigid transform, the registered target is projected into the model space enable a model-informed cost function to be evaluated. This process is repeated until the optimal rigid transformation is found. Using the optimal parameters (i.e., the transform and the selected atlas content), the segmentation estimate is constructed through label fusion and, finally, transferred back to the original target coordinate system.
Model Parameters and Initialization
The proposed model has three primary parameters:
The fraction of the explained model variance to use, κ, and, thus, the number of modes of variation to use, V (eq. 6).
The weighting parameter indicating the decay constant associated with the geodesic distance between a given atlas and the projected target image in model space, τ (eq. 9).
The threshold for determining which atlases to keep when performing the label fusion step, ε(eq. 14).
First, the fraction of the explained model variance to use, κ, and, thus, the number of modes of variation to use, V, plays a critical role in both registration and segmentation accuracy. Sub-optimal values for this parameter can have adverse effects on the quality of the registration and segmentation. A value that is too small (i.e., using too few modes of variation) can result in an inability to accurately represent the variability exhibited within the target image. As a result, the projection of the registered target image could indicate erroneous relationships with the provided atlases. Alternatively, values that are too large (i.e., using too many modes of variation) could lead to the inclusion of modes of variation that are simply noise (i.e., modes that do not provide meaningful information on the variability of the cervical spinal cord).
Second, the weighting parameter, τ (eq. 9), provides a mechanism for converting the geodesic distance between each individual atlas and the projected target image into relative weights for each atlas. This parameter can be viewed as a proxy for determining the influence of geodesic distance within the low-dimensional model space. To illustrate, for values of τ that are too small, the influence of atlases that are faraway from the projected target image will be given too much influence on the registration/segmentation framework. Alternatively, for values of τ that are too large, only the closest atlases to the projected target image will be given any substantial influence, resulting in a representation of the target image that is too sparse. Fortunately, the estimated model provides a natural mechanism for a priori estimation of this parameter. For ease of representation, let represent the collection of atlases that would be chosen for atlas j given the model parameters {τ, ε}. For a fixed ε, the optimal value for τ can be approximated as:
| (16) |
where is an estimate (via a majority vote) of the jth atlas segmentation of voxel i using a given parameter value, τ, and the remaining J − 1 atlas segmentations. In other words, we choose τest such that the resulting estimated atlas segmentations are closest to the original, known, atlas segmentations.
Lastly, observe that the threshold for determining which atlases to keep when performing the label fusion step, ε, is very tightly related to the value chosen for the weighting parameter, τ. In eq. 16, we fixed the value of ε in order to directly optimize τ. Empirically, we found that for a given change in ε, the optimal value for τ would change accordingly (i.e., an increase/decrease in ε would cause a corresponding increase/decrease in τ) without affecting the resulting segmentation accuracy. As a result of this direct relationship, we use a constant value of ε = 10−3 for all subsequent experiments.
Methods and Results
Data
Herein, we study a dataset consisting of 67 MR volumes of the cervical spinal cord. All data were acquired axially on a 3T Philips Achieva scanner (Philips Medical Systems, Best, The Netherlands) using a single channel body coil for transmission and a 16-channel neurovascular coil for signal reception. The center of the imaging volume was aligned to the space between the 3rd and 4th cervical vertebrae. T2*-weighted data were obtained using a 3D gradient echo (TR/TE/a = 121/12ms/9°) with a multi-shot EPI (EPI factor = 3) covering a field of view of 190 × 224 × 90 mm3 with nominal resolution of 0.6 × 0.6 × 3 mm3. Fat saturation was implemented using a 1331 binomial water excitation (ProSet), 2 signal averages, and a SENSE factor of 2.
The “gold standard” manual labels were constructed by an experienced rater who is familiar with MR images of the cervical spinal cord. The labeling process was performed using the Medical Image Processing, Analysis and Visualization (MIPAV) software (McAuliffe et al., 2001). For each slice, two labels were considered: the white matter (WM) and the gray matter (GM) (often referred to as the gray matter horns).Due to imaging artifacts and lack of reasonable contrast, not all slices on each volume were labeled (in total, a collection of 1538 slices were labeled). As a result, all volumetric accuracy measurements were constructed using only the slices that were labeled by the experienced rater and all un-labeled slices were ignored.
Implementation of Proposed Framework
All computations for the proposed groupwise registration framework were performed using MATLAB (Mathworks, Natick, MA) on a 64-bit quad-core 3.07 GHz desktop computer with 13GB of RAM, running Ubuntu 12.04. The minimization/maximization procedures found in eqs. 1, 13 and 16 were coarsely initialized using aline search and finely optimized using the Neider-Mead simplex direct search algorithm (Lagarias et al., 1998). Additionally, for registering the target image to model space (eq. 13), the rigid transformations were initialized such that they aligned the center of mass of the target image with the model space. To eliminate undue impact of uninformative voxels, all image representations in the derived model space were cropped to include all voxels that were within 10mm of the final mean segmentation of the groupwise-consistent slice-based atlases (forming Nm in eq. 2) obtained from the model (see Figure 2). While this value could certainly be considered an additional model parameter, we empirically found that, as long as we ignored most of the background information, the exact amount of cropping did not noticeably impact registration/segmentation accuracy. Lastly, to simplify the direct comparison of image intensities (e.g., eq. 13), the registered target image and all of the atlas images were normalized to a unit Gaussian distribution within the region-of-interest specified by the defined model space.
Baseline Approaches
Registration
To assess the accuracy of the proposed framework we consider three registration procedures: (1) a pairwise volumetric non-rigid registration framework, (2) a pairwise slice-based rigid registration framework, and, (3) the proposed groupwise slice-based rigid registration framework – as described above. The procedures for the baseline pairwise volumetric and slice-based registration frameworks are described below.
For the pairwise volumetric non-rigid registration, we used the SyN non-rigid registration algorithm (Avants et al., 2008) (as part of the Advanced Normalization Tools [ANTs] toolkit, http://stnava.github.io/ANTs/). In recent comparisons (Klein et al., 2009; Landman et al., 2012), the SyN registration algorithm has been consistently shown to be the premier registration algorithm for multi-atlas segmentation. For all presented results, we used the default parameters for large deformation mapping described in (Avants et al., 2009).
For the pairwise slice-based rigid registration, we used the symmetric rigid registration algorithm based on (Ourselin et al., 2001) (available as “reg_aladin” in the “NiftyReg” registration package -- http://sourceforge.net/projects/niftyreg/). Due to the symmetric constraint on the resulting registration, we have empirically found this method to consistently result in fewer failures when compared to alternative unidirectional rigid registration approaches – e.g., (Jenkinson and Smith, 2001). The default parameters provided by the NiftyReg software package were used for all presented results. Note, for fairness of comparison, atlas images in the slice-based pairwise registration procedure were cropped in the same manner as the described groupwise registration framework to minimize failures due to the inclusion of uninformative background information.
Label Fusion
As we are interested in multi-atlas segmentation, the label fusion technique used to combine (or “fuse”) the resulting registered atlases plays a critical role in segmentation accuracy. Herein, we consider a variety of label fusion algorithms that represent the gamut of the state-of-the-art label fusion approaches. The label fusion approaches we consider are: (1) majority vote (MV) (Heckemann et al., 2006; Sabuncu et al., 2010), (2) locally weighted vote (LWV) (Artaechevarria et al., 2009; Isgum et al., 2009; Sabuncu et al., 2010; Wang et al., 2012), (3) patch-based segmentation (PBS) (Coupé et al., 2011), (4) Simultaneous Truth and Performance Level Estimation (STAPLE) (Rohlfing et al., 2004b; Warfield et al., 2004), and (5) Non-Local STAPLE (NLS) (Asman and Landman, 2012b; Asman and Landman, 2012c).
For MV and LWV, the results were obtained using the exact same approach as described in (Sabuncu et al., 2010). For STAPLE, convergence of the Expectation-Maximization (EM) (Dempster et al., 1977) framework was detected when the average change in the trace of the performance-level parameters fell below 10−4, “consensus voxels” (i.e., voxels where all raters agree) were ignored in the estimation process, and a voxelwise label prior (governed by the result of a probabilistic majority vote) was used. For PBS, a 1mm isotropic search neighborhood and 2mm isotropic patch neighborhood were used. The remaining parameters were chosen in exactly the same manner as described in (Coupé et al., 2011). Finally, where applicable, NLS used the same initialization parameters as described above for STAPLE and the same non-local correspondence parameters as described for PBS. Additionally, for NLS, the locally normalized correlation coefficient (LNCC)(Artaechevarria et al., 2009; Cardoso et al., 2013) was used for the weighting in the non-local correspondence model–see (Asman et al., 2013) for details.
The implementation of all label fusion algorithms presented in this manuscript are available as part of the Java Image Science Toolkit (JIST, www.nitrc.org/projects/jist)(Lucas et al., 2010).
Experimental Methods
Herein, we present two experiments to demonstrate the benefits of the proposed slice-based groupwise registration framework.
Leave-One-Out Cross-Validation
For the first experiment, we perform a leave-one-out cross-validation (LOOCV) to demonstrate the effects of (1) the three considered registration frameworks, and (2) label fusion accuracy for each registration framework. For the pairwise volumetric registration, we non-rigidly registered all 66 non-target volumes to the target volume independently. For the pairwise slice-based registration, due to practical limitations in registering over 1500 slices to each target slice, we chose the 85 slice atlases (excluding the slices from the target) that exhibited the largest GM/WM contrast (difference in intensity profiles) – measured using the Kullback-Leibler divergence (Amari et al., 1996) between kernel density estimates of the intensity values associated with each structure. Note, increasing the number of slice atlases beyond 85 had little to no effect on segmentation accuracy. Finally, for the proposed groupwise slice-based registration framework, the groupwise appearance model was constructed uniquely for each target volume (i.e., the slices in the target volume were not used in the construction of the model).Note, for standard use (i.e., situations with a well-defined labeled training set and an unlabeled testing set), the model would beidentical for all target volumes in the testing set and, thus, could be computed entirely offline. For all presented experiments, the fraction of explained model variance, κ, was set to 0.99, the model weighting parameter, τ, was set to τest (see Eq. 16), and the atlas selection threshold, ε, was set to 10−3. For reference, using these values for {τ,ε} resulted in the use of, on average, 460 modes of variation and 25 atlases per target image slice.
For each registration framework, the accuracy of the resulting segmentations are presented both quantitatively (Figure 5) and qualitatively (Figures 6 and 7). For the quantitative results, the volumetric accuracy of the resulting segmentations when compared to the manual labels for both gray matter and white matter are considered using: (1) the Dice similarity coefficient (DSC)(Dice, 1945), (2) the symmetric (or bi-directional) mean surface distance error (MSDE), and (3) the symmetric (or bi-directional) Hausdorff distance error (HDE} (Huttenlocher et al., 1993). For the qualitative results, we show representative example segmentations from both a slice-based perspective (Figure 6) and volumetric perspective (Figure 7). Due to the consistently poor performance of the typical pairwise volumetric registration framework (e.g., Figure 1), only the results of a majority vote are considered in the quantitative results (Figure 5). Additionally, this approach is excluded in the qualitative comparison (Figures 6 and 7) to simplify the visual comparison.
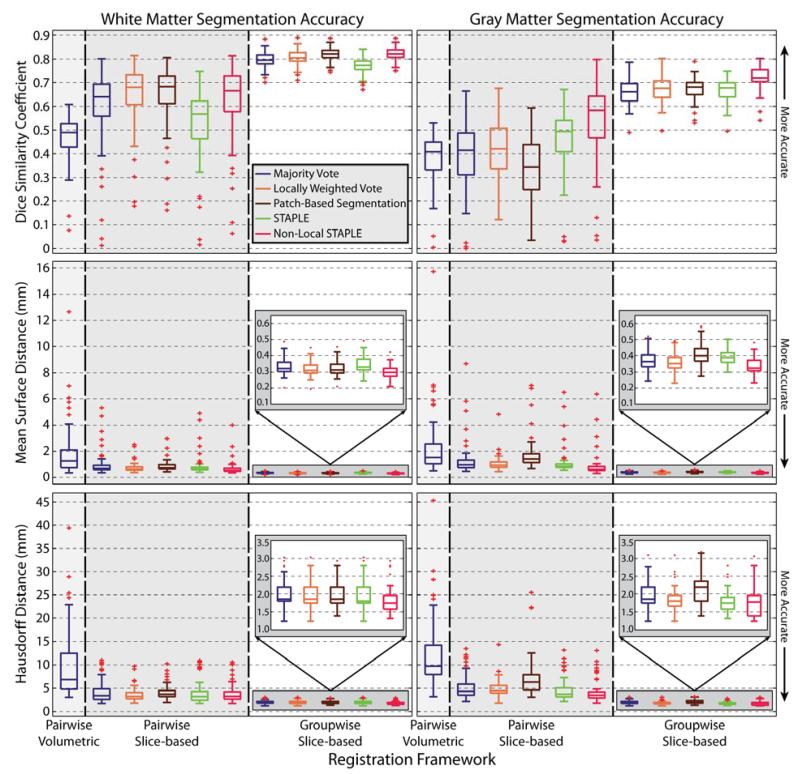
Figure 5.
Quantitative comparison of the considered registration frameworks and label fusion approaches for the accuracy of both gray matter and white matter segmentation. For both structures, the accuracy is measured in terms of the Dice similarity coefficient, mean surface distance error, and Hausdorff distance error. The proposed groupwise slice-based registration framework provides consistent improvement across both structures and by all of the considered metrics.
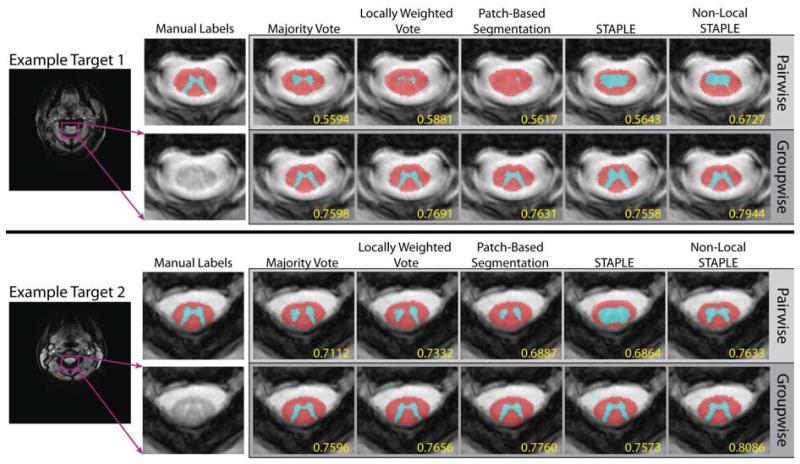
Figure 6.
Slice-based qualitative comparison of a pairwise slice-based registration framework and the proposed groupwise slice-based registration framework. For both examples, the proposed framework provides significantly more accurate segmentations and is able to maintain the complex structure of the GM horn.
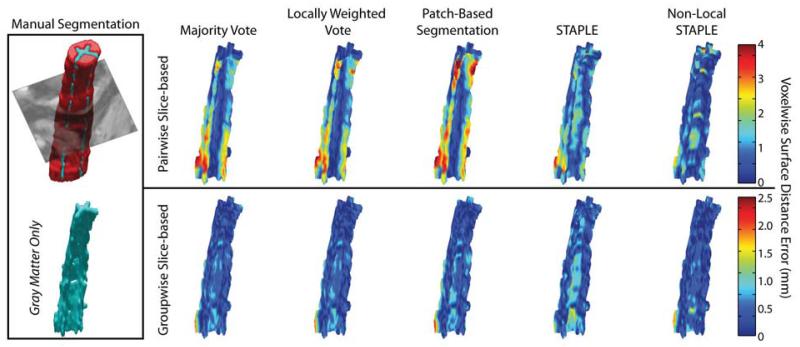
Figure 7.
Volumetric qualitative comparison of the accuracy of the segmented gray matter for the pairwise slice-based framework, and the proposed groupwise slice-based framework. The proposed registration framework consistently estimates the complex shape of the GM horn more accurately than its pairwise counterpart. Note the different axes for the two different registration frameworks.
Sensitivity to Model Parameters
For the second experiment, we assess the accuracy of the proposed groupwise slice-based registration framework with respect to the free model parameters. As discussed above, there are two primary parameters that need to be assessed: (1) the fraction of the explained model variance to use, κ, and, thus, the number of modes of variation to use, V (see eq. 6) and (2) the weighting parameter indicating the decay constant associated with the geodesic distance between a given atlas and the projected target image in model space, τ (see eq. 9). For κ, eightunique values are considered ranging from κ = 0.7 to κ = 0.9999, while holding the weighting parameter constant, τ = τest (Figure 8A). For τ, 21 unique values are considered in reference to the estimated parameter value τest (Eq. 16) ranging from τ − τest = −0.2to τ − τest = 0.2, while holding the explained model variance constant, κ = 0.99, (Figure 8B). For both parameters, the accuracy of the resulting segmentations is assessed using the mean DSC across both labels. Lastly, in order to isolate the impact of the considered parameter, the results are assessed using a simple majority vote fusion – alternative fusion approaches would obfuscate the impact of the considered parameter with the impact of the more sophisticated fusion approaches.
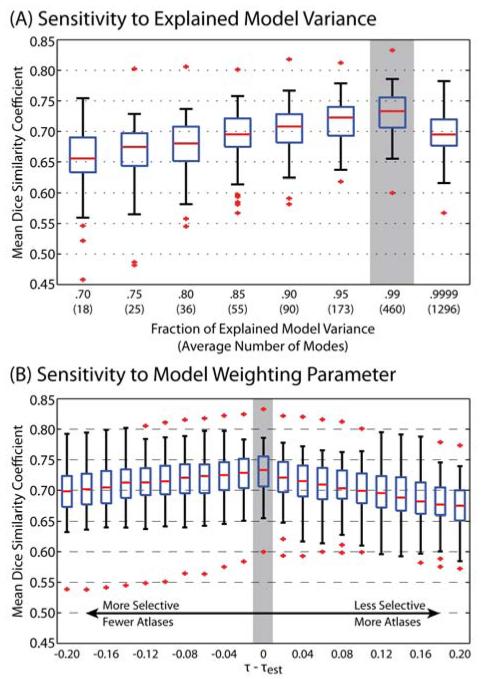
Figure 8.
Quantitative analysis of the sensitivity of the proposed registration framework to the free model parameters. For the fraction of explained variance, (A), the inclusion of a significant portion of the modes of variation provides valuable benefits in terms of segmentation accuracy (i.e., up to κ = 0.99). However, inclusion of too many modes (i.e., κ = 0.9999) results in sub-optimal performance. For the model weighting parameter, (B), the estimated parameter value inferred from the model appears to be the near-optimal parameter value across the considered targets. For both parameters, the gray bar indicates the value used in the other presented experiments. Note, for (A) and (B) the accuracy measures are the result of a majority vote so that the effect of the parameter is not obfuscated by more sophisticated fusion algorithms.
Experimental Results
Leave-One-Out Cross-Validation
The quantitative results of the LOOCV experiment (Figure 5) demonstrate consistent improvement in overall segmentation accuracy for each of the considered metrics. First, due to the inherent limitations of the traditional pairwise volumetric registration framework when applied to the spinal cord, it is immediately evident that the volumetric approach is consistently outperformed by both of the slice-based approaches for both WM and GM across all of the considered metrics. In particular, due to the poor initialization and the resulting boundary errors, the volumetric approach performs considerably worse than the slice-based approaches in terms of the resulting HDE (the median H DE is approximately 5mm worse than the pairwise slice-based registration and close to 8mm worse than the proposed groupwise registration).
Second, the proposed groupwise slice-based registration framework provides substantial improvement in terms of both robustness and accuracy over the pairwise slice-based registration framework. For a given label fusion algorithm, the segmentations using the groupwise framework significantly outperformed its pairwise counterpart (paired t-test, p < 0.01) for both GM and WM across each of the considered accuracy metrics. In particular, the distance-based metrics demonstrate substantial improvements in terms of overall robustness provided by the proposed approach. For the worst case, the groupwise framework provides an improvement of approximately 5mm and 8.5mm in MSDE for the GM and WM, respectively, and an improvement of approximately 7mm and 10mm in HDE error for the GM and WM, respectively.
As expected, the label fusion approach significantly impacts overall segmentation accuracy. However, perhaps surprisingly, no label fusion algorithm was statistically significantly better across all metrics and anatomy considered. NLS appears to be the most consistent performer as it results in statistically significant improvement (paired t-test, p < 0.01) over the other considered fusion algorithms in terms of 4 of the 6 metrics – DSC and MSDE for GM, and MSDE and HDE for WM.
Both the slice-based (Figure 6) and volumetric (Figure 7) qualitative analysis corroborate the quantitative improvement provided by the proposed registration framework. In Figure 6, two representative slices are presented for both the proposed groupwise and the baseline pairwise slice-based registration frameworks. The first example (top of Figure 6) provides an example where inconsistencies in the pairwise registrations result in highly inaccurate and inconsistent segmentation results. To contrast, the corresponding groupwise results are substantially closer to the manual labels despite the lack of contrast on the corresponding target image. The second example (bottom of Figure 6) shows one of the best-case scenarios for the slice-based pairwise registration framework. Nevertheless, the proposed groupwise framework is consistently more accurate in its ability to maintain the shape of the GM structure and, thus, results in substantially more accurate segmentation estimates. Likewise, the representative volumetric example (Figure 7) illustrates consistent improvement in terms of voxelwise surface distance error for the estimation of the GM horn. In particular, it is evident that all of the fusion algorithms are capable of consistently estimating the complex shape of the GM structure throughout the volume, given the proposed groupwise registration framework. Note the different scale on the axes for the two registration frameworks, which was used to provide finer detail on the voxelwise accuracy of the GM segmentations.
Sensitivity to Model Parameters
The accuracy of the proposed registration framework is not particularly sensitive to either of the considered model parameters (Figure 8). In terms of sensitivity to the fraction of explained model variance (Figure 8A), it is clear that, in general, increasing the number of modes of variation provides valuable benefits in terms of segmentation accuracy. Thus, it can be inferred that the complex appearance of the spinal cord requires the use of a significant fraction of the explained variance in order to accurately approximate the relationships between the projected target and the groupwise representation of the atlases. However, utilizing too many modes of variation (e.g., κ = 0.9999) results in sub-optimal performance as these additional modes are modeling the noise in the atlases, as opposed to structurally-meaningful spinal cord variability.
In terms of the sensitivity to the model weighting parameter, τ, it is evident that the estimated parameter value (τest in eq. 16) properly scales the geodesic relationships between the projected model image and the projected atlas information (Figure 8B). As a result, when τ − τest > 0, the approach is more selective, and inaccurately discards the impact of atlases that are relatively close in the low-dimensional model space. Alternatively, when τ − τest < 0, the impact of unrepresentative atlases is disproportionately large in the registration and segmentation results, resulting in sub-optimal segmentation accuracy. Interestingly, inclusion of fewer atlases (i.e., τ − τest > 0) is more detrimental to segmentation accuracy than the inclusion of extra atlases (i.e., τ − τest < 0). As a result, it can be inferred that the inclusion of extra atlases in the fusion process provides valuable improvement in segmentation accuracy – a strong indicator for the complexity and variability of the human cervical spinal cord.
Discussion
We propose a groupwise slice-based registration framework through the construction of an appearance model representation of the cervical spinal cord (Figures 2-4). The proposed framework provides a powerful mechanism for: (1) modeling the variability exhibited within the cervical spinal cord population (Figure 2), (2) naturally and rapidly registering a target slice to the modeled spinal cord population (Figure 4), and (3) selecting a collection of geodesically appropriate atlases for segmenting the target image (Figures 3 and 4). While none of the individual components of the proposed framework are fully unique to this work, together, these techniques enable the first fully-automated framework for robust and accurate segmentation of the cervical spinal cord’s internal structure. We have demonstrated superior performance over typical pairwise (volumetric and slice-based) multi-atlas registration frameworks. Quantitatively, we demonstrate significant segmentation accuracy improvements for both GM and WM segmentation across five different fusion approaches and three different accuracy metrics (Figure 5). Additionally, qualitative segmentation assessment supports the quantitative improvement in both slice-based (Figure 6) and volumetric (Figure 7) representations.
The sensitivity of the proposed model-based groupwise representation of the spinal cord was assessed with respect to the primary model parameters. The results of this sensitivity analysis (Figure 8) demonstrate that the proposed approach is not particularly sensitive to (1) the fraction of explained variance (Figure 8A) or (2) the weighting parameter for determining the optimal collection of representative atlases (Figure 8B). The results of this analysis provide several important insights into the robustness of the proposed framework. First, modeling the complex inter-subject variability in the spinal cord requires a significant fraction (i.e., κ = 0.99) of the explained model variance to be utilized. However, not surprisingly, the inclusion of nearly all of the modes of variation (i.e., κ = 0.9999) has a detrimental impact on registration/segmentation accuracy. Secondly, the inclusion of extra atlases by means of a larger model weighting parameter, τ, is less detrimental than the inclusion of fewer atlases, which strongly implies the utility of selecting appropriate and sufficient atlases when modeling the complexity and variability of the human cervical spinal cord.
Although label fusion is certainly not the focus of this manuscript, it is worth noting the fact that none of the fusion algorithms used in this manuscript reported superior performance across all of the considered metrics (Figure 5). While NLS was the most consistent performer, resulting in statistically significant improvement in 4 of the 6 considered metrics, the lack of a consistently superior fusion algorithm is problematic. Thus, investigation into label fusion optimality (e.g., through re-formulating rater models (Asman and Landman, 2011b; Asman and Landman, 2012a; Commowick et al., 2012a; Commowick and Warfield, 2010) or corrective learning (Ledig et al., 2012; Wang et al., 2011)) remains an open problem and certainly warrants continued investigation.
Despite the promise of the proposed framework, there are several areas for future investigation that could provide increased applicability to new problem spaces. First, all of the registrations performed in this manuscript were simple, 2-D (three degree-of-freedom) rigid transformations. Additional degrees of freedom (e.g., scale, skew) and/or deformable registration techniques would enable a more compact representation (i.e., fewer modes of variation) of the cervical spinal cord variability. However, this more compact representation would come at the cost of more complex parameter optimization, and, thus, increased likelihood in converging to an undesired local minimum. In our experiments, the three degree-of-freedom approach was found to (1) succinctly model observed spinal cord variability, and (2) quickly and robustly find inter-subject correspondence. Second, the proposed framework was performed entirely on the 2-D cross-section of the spinal cord, without regard for introducing or enforcing 3-D consistency. Consistency throughout the image volume could theoretically be maintained through the use of (1) Markov Random Fields (Van Leemput et al., 1999; Zhang, 1992), or (2) constraints on the slice-based rigid transformations (Pitiot et al., 2006). Due to the consistent performance provided by the proposed framework and concerns with the degree of anterior-posterior image distortion, we did not feel that this was necessary at this time. Lastly, and probably most obviously, further investigation into modeling complex 3-D structures (as opposed to the 2-D approach presented here) would increase the applicability of the proposed groupwise approach.
Finally, given the known anatomical context of the spinal canal and the vast research that has gone into the optimality and design of non-rigid registration algorithms, there is no doubt that 3-D volumetric registrations could be more successful than the results presented in this manuscript (Figures 1 and 5). However, one of the primary motivations for this work was to demonstrate that typical approaches, which are often highly successful on oft-studied structures (e.g., the brain), are problematic when applied to new, highly difficult structures (i.e., structures exhibiting large imaging and anatomical variability). As a result, reasonable segmentation of the spinal cord’s internal structures through 3-D deformable registrations often require (1) a priori structural information, (2) a highly-tuned application-specific registration framework – e.g.,(Commowick et al., 2012b), or (3) a multi-contrast cost function (e.g., using Tl- and T2*-weighted images). Additionally, and potentially most importantly, pairwise 3-D non-rigid registration algorithms can often take upwards of an hour to perform each individual registration on a modern cpu. For the LOOCV presented above, estimating a complete 3-D segmentation took almost threedays of cpu time per target. Given offline construction of the appearance model, the framework presented in this manuscript took approximately one minute per target slice, resulting in a complete 3-D segmentation in approximately 30 minutes – less than the time it would take to perform a single atlas-target non-rigid registration.
Highlights.
Provide a simple method for pre-aligning slice-based atlases into a groupwise consistent space.
Demonstrate a technique for constructing a model of spinal cord variability.
Develop a model-specific registration cost function for aligning the target with the model.
Provide a natural framework for selecting geodesically-appropriate atlas information.
Demonstrate superior performance over state-of-the-art approaches.
Acknowledgements
This research was supported by in part by NIH 1R21NS064534, NIH 1R03EB012461, NIH 2R01EB006136, NIH R01EB006193, NIH IT32EB014841, the NIH/NINDS Intramural Research Program, and the National Multiple Sclerosis Society (Peter Calabresi). The authors are grateful to Zhoubing Xu for the provided manual labels.
Grant Support
NIH 1R21NS064534 (Prince/Landman), NIH 2R01EB006136 (Dawant), NIH R01EB006193 (Dawant), NIH 1R03EB012461 (Landman), NIH IT32EB014841 (Gore), NIH K01EB009120 (Smith)
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- Aljabar P, Heckemann R, Hammers A, Hajnal J, Rueckert D. Multi-atlas based segmentation of brain images: Atlas selection and its effect on accuracy. Neuroimage. 2009;46:726–738. doi: 10.1016/j.neuroimage.2009.02.018. [DOI] [PubMed] [Google Scholar]
- Amari S, Cichocki A, Yang HH. A new learning algorithm for blind signal separation. Advances in neural information processing systems. 1996:757–763. [Google Scholar]
- Artaechevarria X, Muñoz-Barrutia A, Ortiz-de-Solorzano C. Combination strategies in multi-atlas image segmentation: Application to brain MR data. IEEE Trans. Med. Imaging. 2009;28:1266–1277. doi: 10.1109/TMI.2009.2014372. [DOI] [PubMed] [Google Scholar]
- Asman A, Landman B. Characterizing spatially varying performance to improve multi-atlas multi-label segmentation, Information Processing in Medical Imaging (IPMI) Vol. 6801. Springer; 2011a. pp. 85–96. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Asman A, Landman B. Robust Statistical Label Fusion through Consensus Level, Labeler Accuracy and Truth Estimation (COLLATE) IEEE Trans. Med. Imaging. 2011b;30:1779–1794. doi: 10.1109/TMI.2011.2147795. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Asman AJ, Landman BA. Formulating Spatially Varying Performance in the Statistical Fusion Framework. IEEE Transactions on Medical Imaging. 2012a;31:1326–1336. doi: 10.1109/TMI.2012.2190992. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Asman AJ, Landman BA. Non-Local STAPLE: An Intensity-Driven Multi-Atlas Rater Model, Medical Image Computing and Computer-Assisted Intervention (MICCAI) Springer; Nice, France: 2012b. pp. 417–424. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Asman AJ, Landman BA. Non-Local Statistical Label Fusion for Multi-Atlas Segmentation. Medical Image Analysis. 2012c;17:194–208. doi: 10.1016/j.media.2012.10.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Asman AJ, Smith SA, Reich DS, Landman BA. Robust GM/WM Segmentation of the Spinal Cord with Iterative Non-Local Statistical Fusion, Medical Image Computing and Computer-Assisted Intervention (MICCAI) Springer; Nagoya, Japan: 2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Avants B, Epstein C, Grossman M, Gee J. Symmetric diffeomorphic image registration with cross-correlation: Evaluating automated labeling of elderly and neurodegenerative brain. Medical Image Analysis. 2008;12:26–41. doi: 10.1016/j.media.2007.06.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Avants BB, Tustison N, Song G. Advanced Normalization Tools (ANTS) Insight Journal. 2009 [Google Scholar]
- Balci SK, Golland P, Shenton M, Wells WM. Free-Form B-spline Deformation Model for Groupwise Registration. Med Image Comput Comput Assist Interv. 2007;10:23–30. [Google Scholar]
- Bede P, Bokde A, Elamin M, Byrne S, McLaughlin RL, Jordan N, Hampel H, Gallagher L, Lynch C, Fagan AJ, Pender N, Hardiman O. Grey matter correlates of clinical variables in amyotrophic lateral sclerosis (ALS): a neuroimaging study of ALS motor phenotype heterogeneity and cortical focality. Journal of neurology, neurosurgery, and psychiatry. 2013;84:766–773. doi: 10.1136/jnnp-2012-302674. [DOI] [PubMed] [Google Scholar]
- Bede P, Bokde AL, Byrne S, Elamin M, Fagan AJ, Hardiman O. Spinal cord markers in ALS: diagnostic and biomarker considerations. Amyotroph Lateral Scler. 2012;13:407–415. doi: 10.3109/17482968.2011.649760. [DOI] [PubMed] [Google Scholar]
- Bhatia KK, Hajnal J, Hammers A, Rueckert D. Similarity metrics for groupwise non-rigid registration. Med Image Comput Comput Assist Interv. 2007;10:544–552. doi: 10.1007/978-3-540-75759-7_66. [DOI] [PubMed] [Google Scholar]
- Cao V, Vuan V, Li X, Turkbey B, Choyke PL, Van P. Segmenting images by combining selected atlases on manifold. Med Image Comput Comput Assist Interv. 2011;14:272–279. doi: 10.1007/978-3-642-23626-6_34. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Carballido-Gamio J, Belongie SJ, Majumdar S. Normalized cuts in 3-D for spinal MRI segmentation. IEEE transactions on medical imaging. 2004;23:36–44. doi: 10.1109/TMI.2003.819929. [DOI] [PubMed] [Google Scholar]
- Cardoso MJ, Leung K, Modat M, Keihaninejad S, Cash D, Barnes J, Fox NC, Ourselin S. STEPS: Similarity and Truth Estimation for Propagated Segmentations and its application to hippocampal segmentation and brain parcelation. Medical Image Analysis. 2013;17:671–684. doi: 10.1016/j.media.2013.02.006. [DOI] [PubMed] [Google Scholar]
- Chen M, Carass A, Cuzzocreo J, Bazin P-L, Reich DS, Prince JL. Topology preserving automatic segmentation of the spinal cord in magnetic resonance images, Biomedical Imaging: From Nano to Macro; 2011 IEEE International Symposium on. IEEE; 2011; pp. 1737–1740. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Commowick O, Akhondi-Asl A, Warfield SK. Estimating A Reference Standard Segmentation with Spatially Varying Performance Parameters: Local MAP STAPLE. IEEE transactions on medical imaging. 2012a;31:1593–1606. doi: 10.1109/TMI.2012.2197406. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Commowick O, Warfield S. Incorporating priors on expert performance parameters for segmentation validation and label fusion: a maximum a posteriori STAPLE. Medical Image Computing and Computer-Assisted Intervention–MICCAI. 2010;2010:25–32. doi: 10.1007/978-3-642-15711-0_4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Commowick O, Wiest-Daesslé N, Prima S. Automated diffeomorphic registration of anatomical structures with rigid parts: Application to dynamic cervical MRI. Medical Image Computing and Computer-Assisted Intervention–MICCAI. 2012b;2012:163–170. doi: 10.1007/978-3-642-33418-4_21. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cootes TF, Edwards GJ, Taylor CJ. Active appearance models. Pattern Analysis and Machine Intelligence. IEEE Transactions on. 2001;23:681–685. [Google Scholar]
- Cootes TF, Taylor CJ, Cooper DH, Graham J. Active shape models-their training and application. Computer vision and image understanding. 1995;61:38–59. [Google Scholar]
- Coupé P, Manjkn JV, Fonov V, Pruessner J, Robles M, Collins DL. Patch-based segmentation using expert priors: Application to hippocampus and ventricle segmentation. Neuroimage. 2011;54:940–954. doi: 10.1016/j.neuroimage.2010.09.018. [DOI] [PubMed] [Google Scholar]
- Dempster AP, Laird NM, Rubin DB. Maximum likelihood from incomplete data via the EM algorithm. Journal of the Royal Statistical Society. Series B (Methodological) 1977:1–38. [Google Scholar]
- Depa M, Holmvang G, Schmidt EJ, Golland P, Sabuncu MR. Towards efficient label fusion by pre-alignment of training data; Proc. MICCAI Workshop on Multi-atlas Labeling and Statistical Fusion; 2011; pp. 38–46. [PMC free article] [PubMed] [Google Scholar]
- Dice LR. Measures of the amount of ecologic association between species. Ecology. 1945;26:297–302. [Google Scholar]
- Dietz V, Curt A. Neurological aspects of spinal-cord repair: promises and challenges. The Lancet Neurology. 2006;5:688–694. doi: 10.1016/S1474-4422(06)70522-1. [DOI] [PubMed] [Google Scholar]
- Farrell JA, Smith SA, Gordon-Lipkin EM, Reich DS, Calabresi PA, van Zijl PC. High b-value q-space diffusion-weighted MRI of the human cervical spinal cord in vivo: feasibility and application to multiple sclerosis. Magnetic resonance in medicine: official journal of the Society of Magnetic Resonance in Medicine / Society of Magnetic Resonance in Medicine. 2008;59:1079–1089. doi: 10.1002/mrm.21563. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gilmore CP, Bö L, Owens T, Lowe J, Esiri MM, Evangelou N. Spinal cord gray matter demyelination in multiple sclerosis–a novel pattern of residual plaque morphology. Brain Pathol. 2006;16:202–208. doi: 10.1111/j.1750-3639.2006.00018.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Heckemann RA, Hajnal JV, Aljabar P, Rueckert D, Hammers A. Automatic anatomical brain MRI segmentation combining label propagation and decision fusion. Neuroimage. 2006;33:115–126. doi: 10.1016/j.neuroimage.2006.05.061. [DOI] [PubMed] [Google Scholar]
- Hinks RS, Quencer RM. Motion artifacts in brain and spine MR. Radiol. Clin. North Am. 1988;26:737–753. [PubMed] [Google Scholar]
- Horsfield MA, Sala S, Neema M, Absinta M, Bakshi A, Sormani MP, Rocca MA, Bakshi R, Filippi M. Rapid semi-automatic segmentation of the spinal cord from magnetic resonance images: Application in multiple sclerosis. Neuroimage. 2010;50:446–455. doi: 10.1016/j.neuroimage.2009.12.121. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Huang SH, Chu VH, Lai SH, Novak CL. Learning-based vertebra detection and iterative normalized-cut segmentation for spinal MRI. IEEE transactions on medical imaging. 2009;28:1595–1605. doi: 10.1109/TMI.2009.2023362. [DOI] [PubMed] [Google Scholar]
- Huttenlocher DP, Klanderman GA, Rucklidge WJ. Comparing images using the Hausdorff distance. Pattern Analysis and Machine Intelligence. IEEE Transactions on. 1993;15:850–863. [Google Scholar]
- Isgum I, Staring M, Rutten A, Prokop M, Viergever MA, van Ginneken B. Multi-atlas-based segmentation with local decision fusion–Application to cardiac and aortic segmentation in CT scans. IEEE Trans. Med. Imaging. 2009;28:1000–1010. doi: 10.1109/TMI.2008.2011480. [DOI] [PubMed] [Google Scholar]
- Jarius S, Wildemann B. AQP4 antibodies in neuromyelitis optica: diagnostic and pathogenetic relevance. Nature Reviews Neurology. 2010;6:383–392. doi: 10.1038/nrneurol.2010.72. [DOI] [PubMed] [Google Scholar]
- Jenkinson M, Smith S. A global optimisation method for robust affine registration of brain images. Medical Image Analysis. 2001;5:143–156. doi: 10.1016/s1361-8415(01)00036-6. [DOI] [PubMed] [Google Scholar]
- Jia H, Vap P-T, Shen D. Iterative multi-atlas-based multi-image segmentation with tree-based registration. Neuroimage. 2012;59:422–430. doi: 10.1016/j.neuroimage.2011.07.036. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jolliffe IT. Principal component analysis. Springer-Verlag; New Vork: 1986. [Google Scholar]
- Kaminsky J, Klinge P, Rodt T, Bokemeyer M, Luedemann W, Samii M. Specially adapted interactive tools for an improved 3D-segmentation of the spine. Computerized medical imaging and graphics: the official journal of the Computerized Medical Imaging Society. 2004;28:119–127. doi: 10.1016/j.compmedimag.2003.12.001. [DOI] [PubMed] [Google Scholar]
- Karpova A, Arun R, Davis AM, Kulkarni AV, Mikulis DJ, Sooyong C, Rabin D, Craciunas S, Smith SR, Hansen MA, George J, Fehlings MG. Reliability of quantitative magnetic resonance imaging methods in the assessment of spinal canal stenosis and cord compression in cervical myelopathy. Spine. 2013;38:245–252. doi: 10.1097/BRS.0b013e3182672307. [DOI] [PubMed] [Google Scholar]
- Klein A, Andersson J, Ardekani BA, Ashburner J, Avants B, Chiang MC, Christensen GE, Collins DL, Gee J, Hellier P. Evaluation of 14 nonlinear deformation algorithms applied to human brain MRI registration. Neuroimage. 2009;46:786–802. doi: 10.1016/j.neuroimage.2008.12.037. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lagarias JC, Reeds JA, Wright MH, Wright PE. Convergence properties of the Nelder--Mead simplex method in low dimensions. SIAM Journal on Optimization. 1998;9:112–147. [Google Scholar]
- Landman BA, Ribbens A, Lucas B, Davatzikos C, Avants B, Ledig C, Ma D, Rueckert D, Vandermeulen D, Maes F, Erus G, Wang J, Holmes H, Wang H, Doshi J, Kornegay J, Manjon J, Hammers A, Akhondi-Asl A, Asman AJ, Warfield SK. MICCAI 2012 Workshop on Multi-Atlas Labeling. Create Space Independent Publishing Platform; 2012. [Google Scholar]
- Langerak TR, van der Heide UA, Kotte ANTJ, Viergever MA, van Vulpen M, Pluim JPW. Label fusion in atlas-based segmentation using a selective and iterative method for performance level estimation (SIMPLE) IEEE Trans. Med. Imaging. 2010;29:2000–2008. doi: 10.1109/TMI.2010.2057442. [DOI] [PubMed] [Google Scholar]
- Ledig c., Wolz R, Aljabar P, Lotjonen J, Heckemann RA, Hammers A, Rueckert D. Multi-class brain segmentation using atlas propagation and EM-based refinement, Biomedical Imaging (ISBI); 2012 9th IEEE International Symposium on. IEEE.2012. pp. 896–899. [Google Scholar]
- Lucas BC, Bogovic JA, Carass A, Bazin P-L, Prince JL, Pham DL, Landman BA. The Java Image Science Toolkit (JIST) for rapid prototyping and publishing of neuroimaging software. Neuroinformatics. 2010;8:5–17. doi: 10.1007/s12021-009-9061-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ma J, Lu L, Zhan V, Zhou X, Salganicoff M, Krishnan A. Hierarchical segmentation and identification of thoracic vertebra using learning-based edge detection and coarse-to-fine deformable model. Med Image Comput Comput Assist Interv. 2010;13:19–27. doi: 10.1007/978-3-642-15705-9_3. [DOI] [PubMed] [Google Scholar]
- McAuliffe MJ, Lalonde FM, McGarry D, Gandler W, Csaky K, Trus BL. Medical image processing, analysis and visualization in clinical research, Computer-Based Medical Systems, 2001. CBMS 2001; Proceedings. 14th IEEE Symposium on. IEEE; 2001.pp. 381–386. [Google Scholar]
- Mcintosh C, Hamarneh G. Spinal crawlers: deformable organisms for spinal cord segmentation and analysis. Med Image Com put Comput Assist Interv. 2006;9:808–815. doi: 10.1007/11866565_99. [DOI] [PubMed] [Google Scholar]
- Mikulis DJ, Wood ML, Zerdoner OA, Poncelet BP. Oscillatory motion of the normal cervical spinal cord. Radiology. 1994;192:117–121. doi: 10.1148/radiology.192.1.8208922. [DOI] [PubMed] [Google Scholar]
- Ourselin S, Roche A, Subsol G, Pennec X, Ayache N. Reconstructing a 3D structure from serial histological sections. Image and vision computing. 2001;19:25–31. [Google Scholar]
- Ozturk A, Aygun N, Smith SA, Caffo B, Calabresi PA, Reich DS. Axial 3D gradient-echo imaging for improved multiple sclerosis lesion detection in the cervical spinal cord at 3T. Neuroradiology. 2013;55:431–439. doi: 10.1007/s00234-012-1118-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pitiot A, Bardinet E, Thompson PM, Malandain G. Piecewise affine registration of biological images for volume reconstruction. Medical Image Analysis. 2006;10:465–483. doi: 10.1016/j.media.2005.03.008. [DOI] [PubMed] [Google Scholar]
- Rohlfing T, Brandt R, Menzel R, Maurer CR. Evaluation of atlas selection strategies for atlas-based image segmentation with application to confocal microscopy images of bee brains. Neuroimage. 2004a;21:1428–1442. doi: 10.1016/j.neuroimage.2003.11.010. [DOI] [PubMed] [Google Scholar]
- Rohlfing T, Russakoff DB, Maurer CR. Performance-based classifier combination in atlas-based image segmentation using expectation-maximization parameter estimation. IEEE Transactions on Medical Imaging. 2004b;23:983–994. doi: 10.1109/TMI.2004.830803. [DOI] [PubMed] [Google Scholar]
- Sabuncu MR, Yeo BTT, Van Leemput K, Fischl B, Golland P. A generative model for image segmentation based on label fusion. IEEE Transactions on Medical Imaging. 2010;29:1714–1729. doi: 10.1109/TMI.2010.2050897. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Smith SA, Edden RA, Farrell JA, Barker PB, Van Zijl PC. Measurement of T1 and T2 in the cervical spinal cord at 3 tesla. Magnetic resonance in medicine: official journal of the Society of Magnetic Resonance in Medicine / Society of Magnetic Resonance in Medicine. 2008;60:213–219. doi: 10.1002/mrm.21596. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Smith SA, Jones CK, Gifford A, Belegu V, Chodkowski B, Farrell JA, Landman BA, Reich DS, Calabresi PA, McDonald JW, van Zijl PC. Reproducibility of tract-specific magnetization transfer and diffusion tensor imaging in the cervical spinal cord at 3 tesla. NMR in Biomedicine. 2010;23:207–217. doi: 10.1002/nbm.1447. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Turk M, Pentland A. Eigenfaces for recognition. Journal of Cognitive Neuroscience. 1991;3:71–86. doi: 10.1162/jocn.1991.3.1.71. [DOI] [PubMed] [Google Scholar]
- Van Leemput K, Maes F, Vandermeulen D, Suetens P. Automated model-based tissue classification of MR images of the brain. IEEE Trans. Med. Imaging. 1999;18:897–908. doi: 10.1109/42.811270. [DOI] [PubMed] [Google Scholar]
- Wang H, Das SR, Suh JW, Altinay M, Pluta J, Craige C, Avants B, Yushkevich PA. A learning-based wrapper method to correct systematic errors in automatic image segmentation: consistently improved performance in hippocampus, cortex and brain segmentation. Neuroimage. 2011;55:968–985. doi: 10.1016/j.neuroimage.2011.01.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang H, Suh JW, Das SR, Pluta J, Craige C, Yushkevich PA. Multi-Atlas Segmentation with Joint Label Fusion. IEEE Transactions on Pattern Analysis and Machine Intelligence. 2012;35:611–623. doi: 10.1109/TPAMI.2012.143. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Warfield SK, Zou KH, Wells WM. Simultaneous truth and performance level estimation (STAPLE): an algorithm for the validation of image segmentation. IEEE Transactions on Medical Imaging. 2004;23:903–921. doi: 10.1109/TMI.2004.828354. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Weisenfeld NI, Warfield SK. Automatic segmentation of newborn brain MRI. Neuroimage. 2009;47:564–572. doi: 10.1016/j.neuroimage.2009.04.068. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wingerchuk DM, Lennon VA, Lucchinetti CF, Pittock SJ, Weinshenker BG. The spectrum of neuromyelitis optica. Lancet Neurol. 2007;6:805–815. doi: 10.1016/S1474-4422(07)70216-8. [DOI] [PubMed] [Google Scholar]
- Wolz R, Aljabar P, Hajnal JV, Hammers A, Rueckert D. LEAP: Learning embeddings for atlas propagation. Neuroimage. 2010;49:1316–1325. doi: 10.1016/j.neuroimage.2009.09.069. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wolz R, Chu C, Misawa K, Mori K, Rueckert D. Multi-organ Abdominal CT Segmentation Using Hierarchically Weighted Subject-Specific Atlases. Medical Image Computing and Computer-Assisted Intervention–MICCAI. 2012:10–17. doi: 10.1007/978-3-642-33415-3_2. 2012. [DOI] [PubMed] [Google Scholar]
- Yiannakas M, Kearney H, Samson R, Chard D, Ciccarelli O, Miller D, Wheeler-Kingshott C. Feasibility of Grey Matter and White Matter Segmentation of the Upper Cervical Cord In Vivo: A pilot study with application to Magnetisation Transfer Measurements. Neuroimage. 2012;63:1054–1059. doi: 10.1016/j.neuroimage.2012.07.048. [DOI] [PubMed] [Google Scholar]
- Zackowski KM, Smith SA, Reich DS, Gordon-Lipkin E, Chodkowski BA, Sambandan DR, Shteyman M, Bastian AJ, van Zijl PC, Calabresi PA. Sensorimotor dysfunction in multiple sclerosis and column-specific magnetization transfer-imaging abnormalities in the spinal cord. Brain: a journal of neurology. 2009;132:1200–1209. doi: 10.1093/brain/awp032. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang J. The mean field theory in EM procedures for Markov random fields. Signal Processing, IEEE Transactions on. 1992;40:2570–2583. doi: 10.1109/83.210863. [DOI] [PubMed] [Google Scholar]