Genome Scale Modeling in Systems Biology: Algorithms and Resources

Abstract

In recent years, in silico studies and trial simulations have complemented experimental procedures. A model is a description of a system, and a system is any collection of interrelated objects; an object, moreover, is some elemental unit upon which observations can be made but whose internal structure either does not exist or is ignored. Therefore, any network analysis approach is critical for successful quantitative modeling of biological systems. This review highlights some of most popular and important modeling algorithms, tools, and emerging standards for representing, simulating and analyzing cellular networks in five sections. Also, we try to show these concepts by means of simple example and proper images and graphs. Overall, systems biology aims for a holistic description and understanding of biological processes by an integration of analytical experimental approaches along with synthetic computational models. In fact, biological networks have been developed as a platform for integrating information from high to low-throughput experiments for the analysis of biological systems. We provide an overview of all processes used in modeling and simulating biological networks in such a way that they can become easily understandable for researchers with both biological and mathematical backgrounds. Consequently, given the complexity of generated experimental data and cellular networks, it is no surprise that researchers have turned to computer simulation and the development of more theory-based approaches to augment and assist in the development of a fully quantitative understanding of cellular dynamics.

1. INTRODUCTION

System approaches are hardly new, but the foundations of “Systems Biology” have only been achieved now at the beginning of the 21^st century [1] with the support of the two main international journals “Science” and “Nature”. The content of Kitano’s papers is not new by itself, but they were written at the right time. The first reason for the renewed interest nowadays for a system-level approach is linked to the progress in molecular biology experiments (such as genome sequencing), high-throughput generated data (microarray data), biosensors, and nano-biotechnology [2]. This progress enables scientists to collect comprehensive data sets on system performance and to gain biological information on the properties, structures and functions of biomolecules [2, 3].

Present-day systems biology approaches aim to understand biological systems, such as cells or tissues, and also how their functions arise from the interplay of their components. They involve examination of the structure and dynamics of molecule interactions as a whole, rather than isolated parts of a cell. According to Westerhoff and Palsson, two lines of investigation led to contemporary systems biology. One of them starts from identification of individual molecules and aims at up-scaling to a simultaneous view on all molecules and their interactions. But the other line originates from non-equilibrium thermodynamics and focuses on the formal analysis of new functional states arising from molecule interactions aiming at the discovery of general principles rather than being descriptive [4].

Based on these two aspects of systems biology, two different approaches exist as well: bottom-up (from the parts to the whole) and top-down (from the whole to the parts) approaches (Fig. 1). Bottom-up systems biology starts with the parts of the system, formulating the behavior of each component and integrating these formulations usually as mechanistic models to predict system behavior. In contrast, top-down systems biology is characterized by the use of potentially complete that is large, genome-wide data sets for identification of network interaction structures or modules, employing phenomenological models.

Fig. (1).

A scheme showing the relationship between the two main approaches to modeling biological systems, the top-down approach that works from the whole to the parts of a system, and the bottom-up approach, going from the parts to the whole.

A second major reason for a renewed interest for a system-level understanding is the failure of classical philosophy used in molecular biology, namely the “reductionist” approach. Now, it is becoming clear that everything in physiology and pathology will not be explained by one or a few genes/proteins in a cell or an organism. On the other hand, many common diseases are polygenic and are characterized to be complex at the clinical, cellular, and molecular levels.

Innovative “omics” technologies such as genomics, transcriptomics, proteomics, and metabolomics facilitate a strategy towards the simultaneous analysis of the large number of genes, transcripts, proteins, and metabolites in many laboratories. Therefore, a huge volume of data has been generated about the make-up of cells and their behavior at various cellular levels and different environmental conditions, which enables us to reconstruct genome scale biomolecular networks (e.g., transcriptional regulatory networks, interactomic networks, metabolic networks, protein-protein interaction networks) to perform deeper biological analyses. Furthermore, along with omic data generation, in order to compile the biomolecular networks, analytical platforms are being developed that can mathematically process raw data, integrate and curate various data types in a biologically meaningful way and finally interpret them in a system’s context to properly describe cellular functions and behaviors [5].

As a result of these recent technological advances, the view of molecular biology has been changed, so we consider each component as a part of a complex network not as a single entity. Moreover, to have a more accurate look at the cell’s biology, it has been recommended to integrate omic data (e.g., genome sequence, transcriptome, proteome, and metabolome) and gain a global insight into cellular behavior because it results from the action and interplay between the distinct networks in a complex web of hierarchical, multi-leveled and regulated dynamic processes [6], according to Linus Pauling’s statement “Life is a relationship among molecules and not a property of any molecule”.

The most important resources for such information are the scientific literature and human expertise deposited in public databases. In particular, for the development of mathematical models, standardized resources that provide their data in a computational amenable and reusable manner are a preferable resource.

The paper is organized as follows: in the first section, we define graph theory we use, its applications in systems biology, and four types of networks that represent molecular interactions. Section two is the main section of the paper, where static and dynamic modeling algorithms commonly used in systems biology are reviewed using examples that generated from experimental data. Section three presents resources and databases, such as gene and protein sequence and annotation databases, biological network resources, and biomodel repositories. In section four, we discuss the software tools that were developed for biological modeling and simulation. In section five, standards and programming languages for the representation of molecular pathway are described. Finally, in conclusion of the paper, we give an overview of all processes in modeling and simulating biological networks.

2. GRAPH THEORY AND BIOLOGICAL NETWORKS

The theoretical underpinnings for the analysis of networks come from mathematics (in particular graph theory and computer science), probability theory, and statistics. We describe networks in terms of (static) graphs. Mathematically, a graph G = (V, E) is a pair of sets, where V is a set of n vertices or nodes and E is a set of m links or edges which connect pairs of nodes [8].

Some properties of graphs, such as node degree, directed vs. undirected, loops, paths, cyclic vs. acyclic, simple vs. multigraph, completeness, connectedness, and bipartiteness, are important and widely used in the topological analysis of biological networks. One of the most important properties of biological networks is scale-freeness, i.e., these networks have a node degree that follows a power law distribution (Barabasi-paper, Jeong-Nature-paper).

Topological analysis of a biological network identifies the global qualitative properties of the system. Network topology is used to provide the significance of a node in communicating with other nodes. Scale-free networks share two important functional characteristics. First, they are differently sensitive to damage. So if a small, peripheral node stops functioning, the network is very likely to continue working without problem. By contrast, if a hub is damaged, the functionality of the entire network is likely to be jeopardized. These topological characteristics are seen in biological networks. In other words, if a hub node is closed, most of the nodes and edges will be affected. Degree distribution of a scale-free network having k connections to other nodes satisfies the following relation:

P(k) ~ k^γ

where γ is power-law parameter. The “betweenness” centrality Cb(n) of a node n is computed as follows:

Cb(n) = ∑_s≠n≠t (σ_st (n) /σ_st),

where s and t are nodes in the network different from n, σ_st denotes the number of shortest paths from s to t, and σ_st (n) is the number of shortest paths from s to t that n lies on.

In comparison to random networks, scale-free networks exhibit a few nodes with higher degrees, the hubs, and a lot of nodes with low degree. In systems biology, we consider the following three types of graphs.

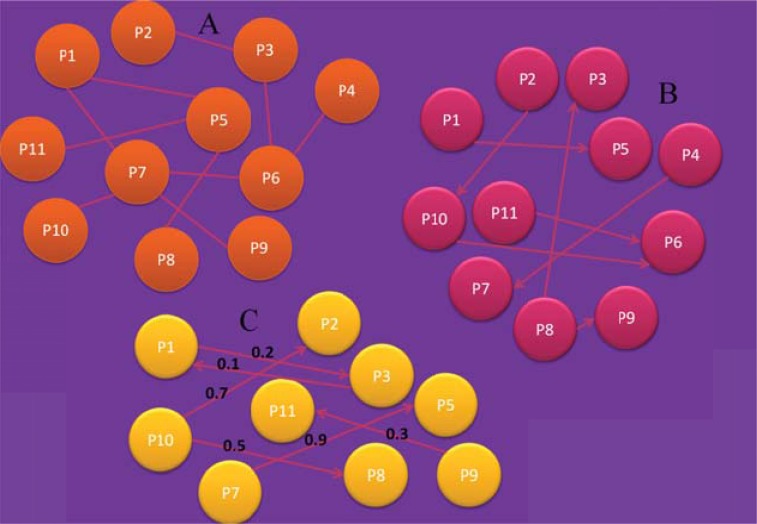
Undirected graph: As indicated by the name, the edges are undirected, i.e. one edge can be considered as a multi-edge of two edges of opposite direction. A multi-edge connection consists of two or more edges that have the same endpoints (Fig. 3A). Such multi-edges are especially important for biological networks in which two nodes can be linked by more than one connection. In such networks, each edge indicates a different type of information [9]. This is an important feature, since there are networks, such as protein-protein interaction (PPI) networks in which two proteins might be evolutionary related, co-occur in the literature, or are co-expressed in some experiments, resulting by this way in three different connections, each one with a different meaning [10].

Fig. (3).

A) Undirected graph. B) Directed graph. C) Weighted directed graph.

Directed graph: A directed graph is defined as an ordered triple G = (V, E, f), where f is a function that maps each element in E to an ordered pair of nodes in V. The ordered pairs of nodes are called directed edges, arcs, or arrows. An edge E = (i, j) is considered to have a direction from i to j (Fig. 3B).

Directed graphs are most suitable for the representation of schemes, describing biological pathways or procedures which show the sequential interaction of elements at one or multiple time points and the flow of information throughout the network. These are mainly signal transduction, metabolic, and gene regulatory networks [9, 11].

These graphs are often bipartite graphs, meaning that the edges connect only nodes of different types, such that edges divide the node set into two different disjoint sets. In biology, the two types of nodes describe the reactions and biochemical species, respectively.

Weighted graph: A weighted graph is defined as a graph G = (V, E), where V is a set of nodes and E is a set of edges between the vertices, E = ((u, v) | u, v ∈ V), associated with a weight function w: E→R, where R denotes the set of all real numbers (Fig. 2C). Most of the times, the weight w_ij of an edge between nodes i and j represents the relevance of the connection. Typically, a larger weight corresponds to higher reliability of a connection. Currently, weighted graphs are the most widely used network description throughout the field of molecular biology, bioinformatics and systems biology. As an example, relations whose importance varies are frequently assigned to biological data to capture the relevance of co-occurrences, identified by literature and text mining, sequence homology or structural similarities between proteins or co-expression of genes in microarray experiments [9, 12].

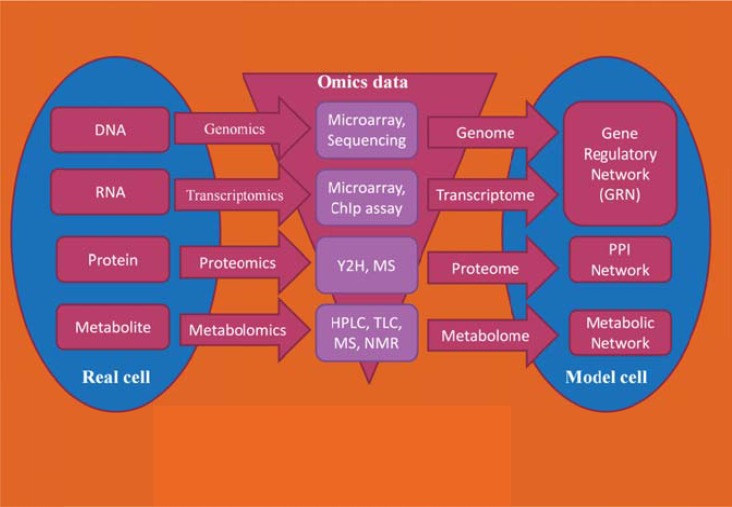
Fig. (2).

Schematic representation of developing a model cell from a real cell using high-throughput omics technologies.

In all multi-cellular organisms, especially in human, most cellular components exert their functions through interactions with other cellular components. The totality of these interactions represents the human interactome. The potential complexity of this network is daunting with approximately 22,000 protein-encoding genes, about a thousand of metabolites, and as yet undefined number of distinct proteins (alternatively spliced and more than 300 different post-translationally modified forms) and non-coding functional RNA molecules (especially miRNA). The individual cellular components that serve as the nodes of the interactome easily exceed one hundred thousand. The number of functionally relevant interactions between the components, representing the links of the interactome, is expected to be much larger and until now, remains largely unknown [13].

Networks of molecular interactions are widely studied to reveal the complex roles played by genes, gene products, controlling elements, and the cellular environments in biological processes. In these networks, the nodes represent genes or gene products and the edges specific interactions. In gene regulatory networks such as a protein–DNA network, an edge may represent the binding of a transcription factor to a promoter region of the DNA sequence, while in a protein–protein physical interaction network; it might characterize a recorded evidence of co-immunoprecipitation or a two-hybrid interaction. The nodes of the network are usually associated with additional information about the genes (or gene products), such as their Gene Ontology (GO) classification, or positions in the chromosome (or localization sites) [14]. We can distinguish between four types of molecular biology networks:

Metabolic networks (MN): These networks aim to describe the basic biochemistry in a living cell. Biologically, important reactions have been described in terms of reaction pathways catalyzed by enzymes, and metabolic networks are systematic collections of such biochemical data. Cellular metabolism (anabolism and catabolism) covers extensively studied processes that are essential to the survival of any free-living organism. The cellular metabolic process can be characterized as a set of biochemical transformations, each of which involves the consumption as well as the production of one or more metabolites. Subject to the law of mass conservation, the net sum of metabolites and electrical charge is conserved in each reaction and thus in the network as a whole [15]. For metabolic networks, often the stoichiometry is known, also are known the metabolite concentrations in many cases, and even the reaction rates and / or reaction constants for some special networks.

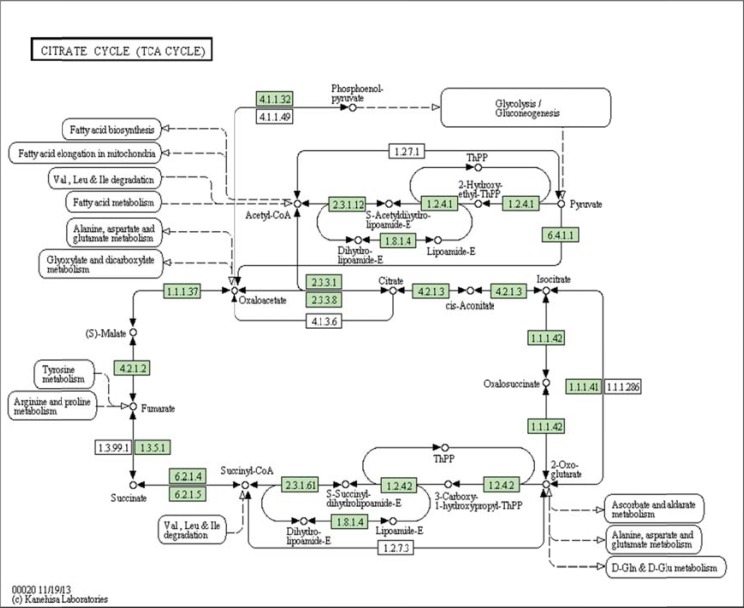
(Fig. 4) depicts a typical metabolic network in KEGG representation. Networks are represented as directed, bipartite graph, where the vertices (circles) are the metabolites, and the edges the reactions indicated by the corresponding enzyme number surrounded by a rectangle.

Fig. (4).

Citrate cycle (TCA cycle) from KEGG (map 00020). Metabolites are represented as circles and reactions as rectangles labeled by the EC number of the enzyme that catalyzes the reaction. The directed edges exist only between metabolites and reactions. The dashed edges lead to or come from other pathways.

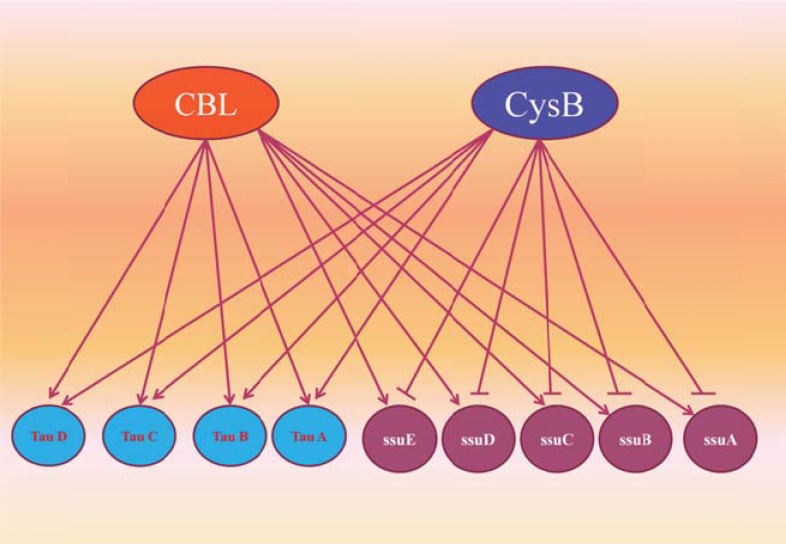
Gene Regulatory Networks (GRNs): GRNs are represented as directed graphs. They consist of genes connected by directed edges, if one gene regulates the transcription of the other gene (Fig. 5). However, interactions within these networks are very subtle, intricate, and ill understood. While GRN sections of a few tens to a few hundreds of genes are known in details for several organisms, the quality of the data drops dramatically as the network size grows. Nevertheless, GRNs are currently considered among the most important frontiers of biological sciences and are at the center of tremendous research efforts for the biological community. The increase of quantity and quality of the data generated in the field, fostered by modern high-throughput technologies such as microarray, is bound to follow the same exponential trend as the gene sequencing did in its time. In the meantime, however, it is possible, and useful, to abstract many details of the individual GRNs in the cell and focus on the system-level properties of the whole network dynamics [16].

Fig. (5).

Example from part of E. coli GRN in which the nodes Cbl and CysB are transcription factors which regulate other genes.

Protein-Protein Interaction Networks (PPINs): PPINs are represented as undirected graphs. In such networks, an undirected edge is drawn between each pair of proteins for which there is evidence of a physical or biochemical interaction (Fig. 6). A PPIN mainly holds information on how different proteins as functional macromolecule within the cell, operate in coordination with others to enable the biological processes. Despite the fact that for the majority of proteins the complete sequence is already known, their molecular function and interaction are not yet fully determined. Determining and predicting protein structure and function are still a bottleneck in computational biology research. So, many experimental and computational techniques have been developed in order to infer protein function from interactions with other biomolecules [8, 9].

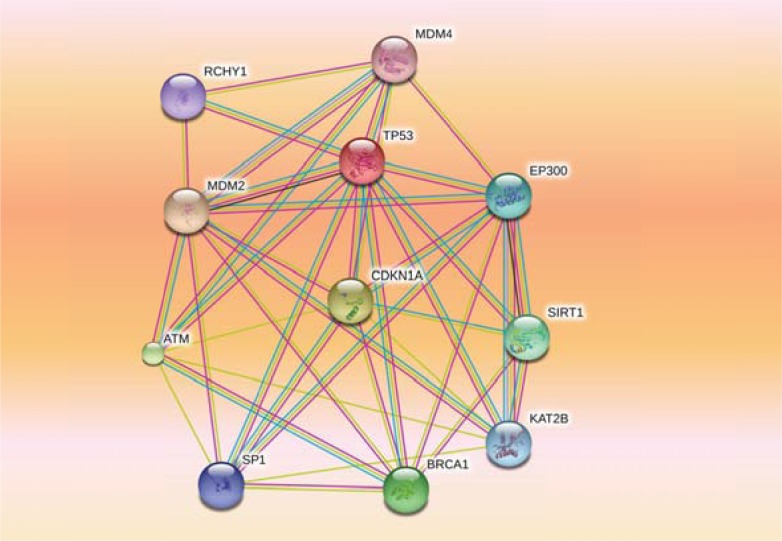
Fig. (6).

Protein-protein interaction network for human TP53 produced from STRING database. The nodes represent genes and the edges interactions. Thicker lines indicate a stronger association.

Making these distinctions and simplifications must necessarily neglect details of the biological processes. In fact, the PPINs will be highly and intricately interconnected, so factorizing them into distinct networks will ultimately underestimate the biological complexity [17].

Signal Transduction Networks (STNs): STNs are mainly represented as bipartite graphs, similar to MN. Here, reactions mainly describe complex formation, phosphorylation, dephosphorylation, activation, deactivation and other. These networks exhibit various properties and regulatory patterns. These include the ability to process the signals to functions such as switches and oscillations. The processes underlying this complex system involve many interacting molecules and cannot be understood by reductionism approach alone. In reality, signal transduction networks act as a bridge between extracellular environment and intracellular response. The integration of computational models with experimental results provides valuable insight into system-level understanding of cellular signal transduction networks.

Several experimental techniques were used to measure the dynamics of STNs, such as flow cytometry, immunofluorescence microscopy, protein arrays, and mass spectrometry. These techniques generate large amounts of data that require systems biology approaches.

3. FORMALISMS FOR MODELING MOLECULAR INTERACTIONS

Modeling of biological processes helps to incorporate existing knowledge about molecule interactions. Knowing the interaction structure of a set of functionally related cellular components, computational or mathematical models can be constructed. The model representation can then be used to simulate and predict the system’s behavior. Several modeling algorithms for describing properties of pathways as a system, taking also into account the interactions between components, differ in their ability to represent the temporal and stochastic behavior as well as in their level of granularity [19].

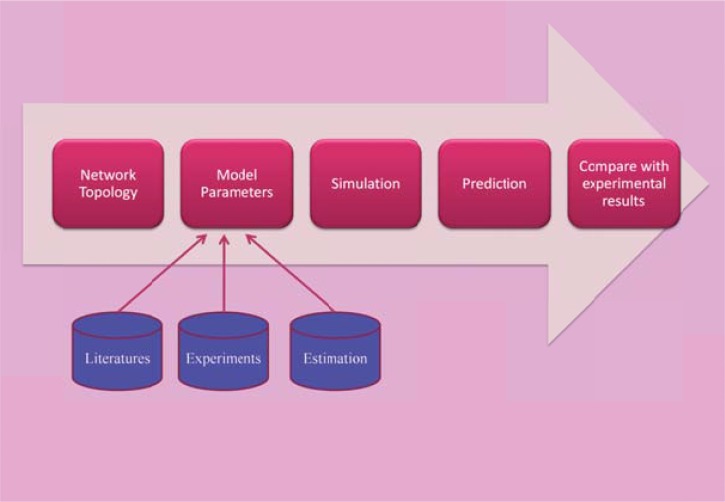
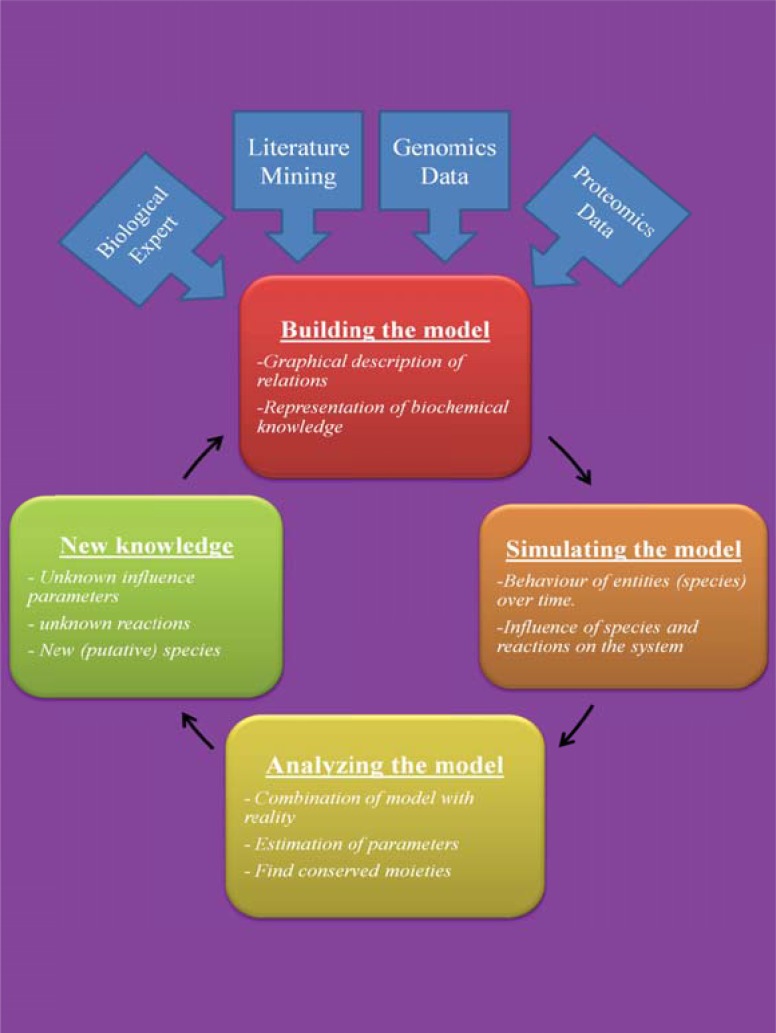
Since the properties of biological systems are not similar to the properties of their components and interactions, it is essential to consider the strength of interactions and dynamic behaviors [20]. The dynamics of the system are its behavior over time, such as an oscillatory behavior. The system structure includes the system components, interactions between components, and processes regulation of these interactions. The dynamics of system controls by processes are based on the design principles of its structure, such as feedback control. The interactions between different parts of a system refer to a protocol. The properties that arise from the structure of a system and the interactions between parts of the system (protocols) are called emergent properties [20]. The factors, such as the concentrations of the molecules or the reaction rates are defined on the component interactions in terms of system parameters or state variables. Mathematical equations use parameters for discovery of universal properties and dynamic behavior of a system [21]. This procedure is called model building. The models produce hypotheses that guide the experimental design, while experimental results are used to develop the mathematical models. Model development is an iterative process with the aim of further improvement of the model to reflect known system properties and the experimental observations. The parameter estimation can be done by comparing modeling and experimental results to estimate unknown parameters [22]. The final model can be subjected to various conditions and may be allowed to evolve in time - a step typically referred to as simulation [23]. The general goal of simulation is to model complex systems, which often behave in a nonlinear (the nonlinearity between stimulus and response) and adaptive (modification to response more appropriately) way. The attributes of a good model are clear structure and relations, nearly realistic results, should be as simple as possible, and applicable to many different objects (generality) [24].

3.1. Static Modeling of Biological Network (Graph Representation)

A simple and intuitive way to represent knowledge about molecules and their interaction structure is a graph consisting of nodes and edges. Nodes correspond to molecules and edges refer to interactions among the molecules. Graphs enable the analysis of the interaction structure by graph theoretic approaches. In that way, topological features like connectivity of compounds or network motifs can be revealed [25]. This kind of modeling approach lacks the temporal aspect of molecular interactions, and therefore cannot reflect the detailed dynamic behavior of network, but can often give insight into possible pathways. However, a graph representation is often the starting point for further study of a biological network.

Network and Pathway inference or static modeling of networks has become a very active area of research. So, reconstruction and disruption of biological networks and pathways, including metabolic pathways, protein-protein interaction networks (PPI), signal transduction pathways, and gene regulatory networks (GRN), have been some of the valuable tools in the abstraction of biological concepts. Therefore, network and pathway analyses and their changes in different conditions achieve valuable knowledges for diagnosis, treatment, and further experimental designs. Numerous methods for network and pathway analysis have been proposed that among them SafeExpress [26] (a R package) is useful for gene expression mapping and statistics analyses of biological networks and pathways.

3.2. Dynamic Modeling of Biological Networks

In the past few years, there has been a considerable effort in the computer science community to develop languages and software tools for modeling and analyzing biological systems. Among the challenges which must be addressed in this regard, are: the definition of languages powerful enough to express all the relevant features of biochemical systems, the development of efficient algorithms to analyze models and interpret the results, and the implementation of modeling platforms which are usable by non-programmers. Computational and mathematical modeling, in conjunction with the use of formal intuitive modeling languages, enables biologists to define models, using a notation very similar to the informal descriptions they commonly use, but formal and, hence, automatically executable. Discrete, computational models are suitable for pathway modeling if precise quantitative relationships or parameters are unknown [27].

4. MODELING ALGORITHMS

Biological networks and pathways are inherently complex. To understand the functioning of these pathways, we not only need to identify the constituent elements (gene, protein, and metabolite) and their interactions, but also we need to know how their dynamics evolve over the time [28].

(Table 1) shows a different type of models and their uses. A general system consists of an input (E), a system object (S), and an output (R). The modeling algorithm is selected based on the type of the problem or goals of modeling and data requirements.

Table 1.

Type of models used in biological modelling.

Type of Problem	Given	To Find	Uses of Models
Synthesis	E and R	S	Understand
Analysis	E and S	R	Predict
Instrumentation	S and R	E	Control

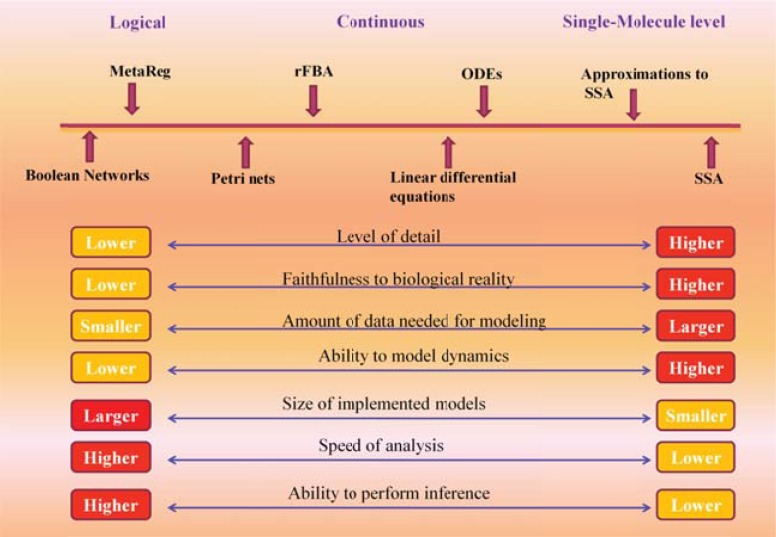
These days, several different algorithms and tools have been developed for the modeling and simulation of extracellular and intracellular signaling pathways, metabolic pathways, and gene regulatory networks. (Fig. 8) illustrates some of these methods classified according to their properties.

Fig. (8).

A comparison between modeling algorithms and their ability in modeling of biological processes.

In systems biology, different modeling and simulation techniques are used, such as the systems of ODEs (Ordinary Differential Equations), stochastic methods, Petri nets, π-calculus, PDEs (Partial Differential Equations), cellular automata methods, agent-base systems, and hybrid approaches. In this survey, we consider ODEs, Petri nets, Boolean networks, cellular automata, and agent-base as some of the most important of these algorithms.

4.1. ODE Modeling

One of the most commonly applied methods for modeling biological systems is based on ODEs. A differential equation is known as an equation indicating the relationship between a function and some of the derivatives of it. Basically, a differential equation designates how a variable, such as [Substrate], i.e. the concentration of Substrate, changes by the passing of time. This is done through inter-relating the rates of changes regarding the concurrent concentrations [30].

In the study of GRNs, analytical approaches represent the more realistic end of the model spectrum. Such models comprise nonlinear systems of ordinary differential equations (ODEs), where each variable denotes the concentration of a different gene product [31].

As an example, suppose the following reaction in which product P₁ produced:

$\varnothing \stackrel{ k1 }{\to }P1 \left(1\right)$

This is an ordinary reaction without any catalyst which can be modeled by means of mass action kinetics. Mass action explains the behavior of reactants and products in an elementary chemical reaction. Mass action kinetics describe such a behavior by an equation in which the rate of a chemical reaction is directly proportional to the concentration of the reactants, where k₁ represents the reaction rate constant. Reaction (1) is called a zero-order reaction. (Fig. 9A) demonstrates a zero-order reaction kinetics in the condition that k₁ is 1 micromole/s.

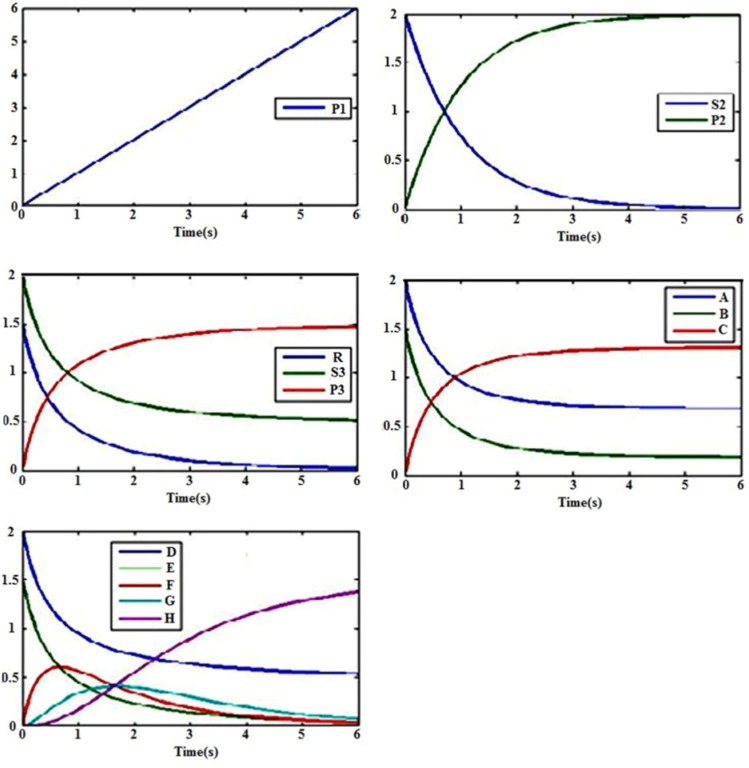
Fig. (9).

Computational simulation of reaction rates with mass action kinetics. A) Zero-order reaction kinetics. B) First-order reaction kinetics. C) Second-order reaction kinetics. D) Reversible reaction kinetics. E) Consecutive reaction kinetics. The unit of vertical coordinate is micromol/liter.

With a first-order reaction, the reaction rates correlate with the concentration of one reactant, here S₂. As an instance, assume the following reaction in which the substrate S₂ is converted into the product P₂:

$S2 \stackrel{ k2 }{\to }P2.$

The reaction rate goes on as below:

$v=k2\left[S2\right]$

It is clear that the reaction rate (v) is directly dependent on some factors S₂, namely, the more the concentration of the S₂, the higher the reaction rate. Hence, the faster S₂ is consumed the faster P₂ is produced. According to the above equation, it would not be difficult to introduce differential equations defining the rate of change in [S₂] and [P₂]:

$\frac{d\left[S2\right]}{dt}= -K2 \left[S2\right];$

$\frac{d\left[P2\right]}{dt}= K2 \left[S2\right];$

For modeling and simulating reactions, it is necessary to know substrate’s and product’s initial concentrations. (Fig. 9B) shows the first-order reaction kinetics in the condition that the initial concentration of S₂ is 2 micromole/liter and k₁ is 1 s^-1.

On the other hand, a second-order reaction is correlated with the square of the concentrations of an individual reactant or both reactants:

$S3+R \stackrel{ k3 }{\to }P3 \left(2\right),$

Where the reaction rate is:

$v=k3\left[S3\right]\left[R\right]$

(Fig. 9C) indicates a second-order reaction kinetics in the condition with the initial concentrations of S₃ and R as much as 2 micromole/liter and 1.5 micromole/liter, respectively, and k₃ as 1 µM^-1S^-1.

It is feasible to model reversible reactions by two distinct reactions or by one reaction. For example:

$A+ B<\frac{ k4 }{kr4}>C$

The reaction rate by which C is produced is:

$v=k4 \left[A\right]\left[B\right]- kr4 \left[C\right]$,

Where k₄ is the rate constant of the forward direction and kr₄ is for the reverse one. (Fig. 9D) shows the above reversible reaction kinetics in the condition that initial concentrations A and B are 2 and 1.5 micromol/liter, respectively, and k₄ and kr₄ are 1 µM^-1S^-1 and 0.1 S^-1, respectively.

The consecutive reaction is an example of the complex reactions in which several biochemical reactions are done consecutively

$D+ E<\frac{ k5 }{kr5}>F \stackrel{ k6 }{\to }G\stackrel{ k7 }{\to }H$

(Fig. 9E) shows the consecutive reaction kinetics above for which the initial concentrations of E and D are presumed 2 micromol/liter and 1.5 micromol/liter, respectively. Also, k₇, k₆, and k₅ are 1 µM^-1S^-1 and kr₅ is considered to be 0.1 S^-1.

According to what mentioned above, consider the enzymatic reaction below

$E+ S<\frac{ k1 }{kr1}>ES \stackrel{ k2 }{\to } E+P$

Basically, enzymes (E) and substrates (S) bind together to form complexes (ES). The enzyme facilitates circumventing activation barrier by accelerating the chemical change of the substrate into the product (P). Then enzymes and the products are separated to form E and P. ES formation is explained by a second order (in units of µM^-1 s^-1) forward rate constant (k1), a reversal rate constant (kr1; in s^-1) of the first order, and a first order catalytic rate constant (k2; in s^-1) as well. The enzymatic reaction rate above, regarding Michaelis-Menten equation is:

$V=\frac{\text{Vmax }\left[\text{S}\right]}{\text{Km}+\left[\text{S}\right]}.$

Here, [S] presents the concentration of substrate, Vmax is the maximum rate. The Michaelis constant Km is the substrate concentration at which the reaction rate is half of the Vmax.

$Km\left(Michaelis constant\right)= \frac{k2+Kr1}{k1}$

with Vmax = k2 [E_t], where [E_t] (the total amount of enzyme)= [E] + [ES], Where k2 is rate limiting and as below:

$V=\frac{\text{k}2\left[\text{Et}\right]\left[\text{S}\right]}{\text{Km}+\left[\text{S}\right]}.$

Types of models which have been used in the literatures can be classified mathematically as: ordinary differential equations (ODEs) [32], delayed differential equations (DDEs), partial differential equations (PDES), Fredholm integral equations (FIES) (in the estimation of parameter problem), stochastic differential equations (SDEs), and integro-differential equations (IDEs). Different software packages can be used for different types of models for numerical analysis and simulations [33].

4.2. Petri Nets

Petri nets represent a refinement of monopartite graph models to bipartite, directed graphs that are used to model concurrent, causal systems. Also they have been used successfully in many areas; in biology, for example, to simulate metabolic networks [34], but also signal transduction pathways [35] and gene regulatory systems [36].

Petri nets (PN) have been named after Carl Adam Petri who developed the basic definitions in his PhD thesis in 1962 [37]. The main ideas are the consequent distinction between active and passive nodes and the use of discrete movable objects to express system’s dynamics. The set of nodes consists of places for the passive part, representing biochemical species, and transitions as the active part, representing chemical reactions. The movable objects are called tokens. They are associated with each place and correspond to discrete amounts of the biochemical species, for example, number or a mole of molecules. The directed, weighted arcs connect places with transitions and divide the places into intput places or pre-places, representing reactants or substrates, and pre-conditions, and output places or post-places, representing the products of a reaction and post-conditions. The arc weights indicate the minimal number of tokens that are necessary for firing a transition, i.e., taking place of a reaction, and the number of tokens that will be produced on the output places, respectively. In metabolic networks, these arc weights exactly correspond to the stoichiometric coefficients of the underlying chemical reaction.

By firing rules, tokens are transferred through the PN from one place to another, simulating a flux, for example, of substances or information, through the network. Originally, PN were restricted to qualitative simulation with discrete time steps. However, advanced PN are able to mimic Boolean, timed-discrete [38], Bayesian, Fuzzy [39], stochastic [40], continuous systems of ordinary differential equations [41], and even hybrid systems [42]. Note that in case of stochastic modeling, the same concepts and algorithms are then used as known in classical systems biology since the 70ies [43]. The same holds for continuous PN that solve exactly the same systems of differential equations as known, for example, from Metabolic Control Analysis [44]. The necessary kinetics can be found in each biochemical text book.

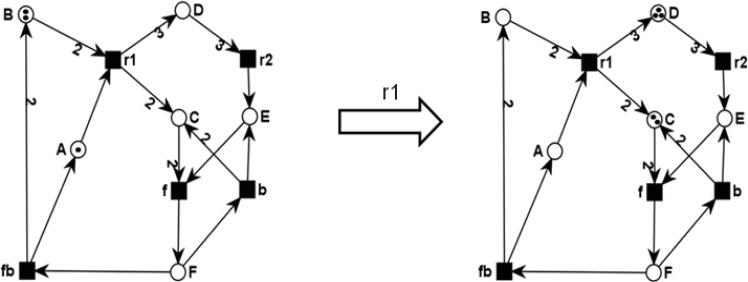
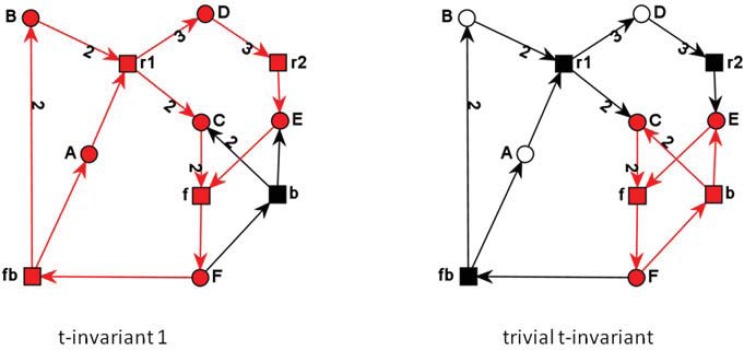
(Fig. 10) illustrates the PN model of the chemical equations

Fig. (10).

PN model of the chemical equation system: (1) r1: A + 2 B ® 2 C + 3 D, (2) r2: 3 D ® E, (3) f (forward) and b (backward): 2 C + E « F, and (4) fb (feedback): F ® A + 2B in the initial marking (1,2,0,0,0,0), giving the token distribution on all places (A,B,C,D,E,F) and in the marking after firing of r1, resulting in the system state (0,0,2,3,0,0). The figures were drawn using MonaLisa.

(1) r1: A + 2 B → 2 C + 3 D,

(2) r2: 3 D → E

(3) f (forward) and b (backward): 2 C + E ↔ F, and

(4) fb (feedback): F → A + 2B.

In the initial marking (A=1,B=2,C=0,D=0,E=0,F=0), giving the token distribution on all places (A,B,C,D.E,F), only the transition r1 is enabled and can therefore fire, reaching the new system state (0,0,2,3,0,0) defined by the token distribution over all places. Evolving the dynamics of the PN in (Fig. 10), five different system states can be reached. These states can be compiled in the reachability graph, where the nodes represent the system states and the arcs the corresponding transformations of one state into another one. The directed arcs are labeled by the transition that has then to fire. The reachability graph of the PN in (Fig. 10) is depicted in (Fig. 11).

Fig. (11).

The reachability graph RG of the PN in Fig. 10. Each node represents a system state and the arcs the corresponding transformations of one state into another one labeled by the transition that has then to fire.

PN provide methods for analysis as well as for simulation. For example, system’s invariants can be defined. Invariants define important analysis methods to describe the overall dynamic behavior of the system. Based on the incidence matrix place-invariants (p-invariants) and transition-invariants (t-invariants) can be defined. The incidence matric C of a PN is an n x m matrix, where n is the number of places and m the number of transitions. Each matrix entry c_ij indicates the change in the token number on place p_i by firing of transition t_j. Then, a t-invariant is a semi-positive integer vector that fulfills C ● x = 0 and a p-invariant a semi-positive integer vector that fulfills C^T ● y = 0.

A p-invariant defines a set of places whose weighted sum of tokens always remains constant, representing a substance conservation rule. A t-invariant is a multi-set of transitions whose (multiple) firing leads to the initial marking M₀. Always, non-trivial and minimal solutions are considered. The complete set of these minimal t-invariants describes the basic dynamics of a system under steady-state conditions, if each transition is part of at least one t-invariant. The importance of these system’s invariants is well-known in systems biology; they are called elementary modes there [46]. Using that concept, new possible pathways have been predicted, which were experimentally confirmed, e.g., the phosphoenolpyruvate glyoxylate pathway in hungry E. coli bacteria [47].

(Table 2) shows the incidence matrix for the PN in (Fig. 11). The resulting linear algebraic equation systems are then for t-invariants (A) and for p-invariants (B):

Table 2.

The incidence matrix of the PN in Firgure 11, indicating the change in the token number of each place when a transition fires. The columns are the transitions and the rows the places.

Incidence Matrix	r1	r2	f	b	fb
A	–1	0	0	0	+2
B	–2	0	0	0	+2
C	+2	0	–2	+2	0
D	+3	–3	0	0	0
E	0	+1	–1	+1	0
F	0	0	+1	–1	–1

$\begin{array}{ll}\left(A\right)\hfill & \left(B\right)\hfill \\ -x_1+2x_5=0\hfill & -y_1–2y_2+2y_3+3y_4=0\hfill \\ –2x_2+2x_5=0\hfill & –3y_4+y_5=0\hfill \\ 2x_1–2x_3+2x_4=0\hfill & –2y_3–y_5+y_6=0\hfill \\ 3x_1–3x_{2 }=0\hfill & 2y_3+y_5–y_6=0\hfill \\ x_2–x_3+x_{4 }=0\hfill & 2y_1+2y_2–y_6=0\hfill \\ x_3–x_4–x_5=0\hfill & \hfill \end{array}$

The t-invariants for the PN in (Fig. 11) are illustrated in (Fig. 12). The second t-invariant is called as trivial, because it just represents a reversible reaction, consisting of a forward and a backward transition.

Fig. (12).

The two t-invariants of the PN of Fig. 10 each colored in red. The second t-invariant (right side) is trivial t-invariant, it represents just a reversible reaction, consisting of a forward and a backward reaction.

The computation of all t-invariants is NP-hard [48]. Many algorithms have been developed to improve existing implementations (for an overview and study see Ackermann & Koch, 2011). Nevertheless, if even all t-invariants can be computed, their number grows exponentially with increasing complexity and size of the network. Thus, an exhaustive analysis becomes not only time-consuming, but also not manageable anymore. Therefore, further network decomposition methods have been developed. These methods are based on t-invariants and try to find a structure within a set of them. One possibility is to summarize the common parts of the support of the solution vectors, i.e., all its non-zero elements, in such a way that only transitions are grouped together which exclusively belong to the same t-invariants [35]. The resulting transition sets called maximal common transitions sets (MCTS or MCT-sets) are disjunctive. In contrast to t-invariants, MCT-sets must not necessarily be connected.

As this decomposition criterion does not allow that a transition is a member of two MCT-sets, clustering methods have been applied, allowing overlapping transition sets. Support-based methods resulting in t-clusters were developed [49] and also methods that consider the complete solution vector, for example, as aggregations around common motifs [50]. Another decomposition that is also based on the support vectors of t-invariants has been proposed as minimal cut sets [51], which cover a minimal set of those transitions whose knockout would inhibit a special biological function defined by a transition set in the model.

There are many further benefits in using PN. PN have a firm mathematical foundation that allows analysis of performance measures and analysis of properties. The following properties are relevant also for biochemical systems.

1. Liveness, meaning that all transitions (biological processes and reactions) are live, i.e., each transition can always fire again and again. This property depends on the initial marking. Liveness should hold for biochemical systems, because a deadlock would mean an interruption of the metabolism, signal transduction or gene regulation.

2. K-boundedness, meaning that in every place, the number of tokens is always less than an integer number k. That could be important if, for example, the toxic accumulation of metabolites should be avoided. Another advantage is that the number of states could be enumerated and used in model checking techniques to verify the model.

3. Soundness, represents a combination of liveness and boundedness that ensures a proper termination in the simulation. If we add a source place with one token and one sink place without any token to the model, then, the procedure terminates and there will be a token in the sink place and all other places would be empty. In addition, there would be no dead transitions (i.e., activities that never happen). In terms of biochemical systems, soundness ensures that all biochemical processes and reactions could be carried out while the system executes.

4. Reachability, meaning that, given a certain system state (marking), M, another state, M’, can be reached from M. The reachability graph, RG, compiles all possible system states, the vertices in RG, with the transformations between the states, the edges in RG labeled by the firing transition, see also (Fig. 11). For unbounded models, i.e., having places with an infinite number of tokens, the RG becomes infinite and cannot be explored for all states. Then, those questions as the following cannot be answered: If we block the immune system, can we still reach a state where the parasite is cleared from the blood system?

PN have been applied to very different biological systems and problems, such as in medical sciences for modeling iron homeostasis in human [52] and processes in the Duchenne Muscle Dystrophy in human [36a], complex assembly processes of the spliceosome [53], and many other processes [54]. Also new PN editing and analysis tools have been developed for the application to biology, for example Cell Illustrator [55] or MonaLisa [45]. For more detailed PN theory, Reisig 1985 and David & Alla 2005 can be considered.

4.3. Boolean Models

The simplest dynamic models – synchronous Boolean network models – were used as a model for gene regulatory networks already in the 1960s by Stuart Kauffman. Boolean dynamic models assign values of 1 or 0 to each node, which reflects a molecule’s state in terms of on/off or active/inactive. A Boolean function (AND, OR, NOT and combinations of these) or logic rule takes into account the state of the variables at a certain time-point in order to get an evaluation for the next time point. In that way, Boolean models enable the study of the causal and temporal relationships on a coarse grained modeling level [56].

Boolean network modeling as a qualitative approach has been wildely used wherein the knowledge of mechanistic details and kinetic parameters is scarce [57]. The fundamental steps of Boolean modeling of biological regulatory networks can be found in [58].

Actually, the Boolean models are a kind of graph: G(V, F)

V is a set of nodes (genes or proteins) as x₁ , x₂, …, x_n

F is a list of Boolean functions f(x₁ , x₂, …, x_n)

4.4. Bayesian Network

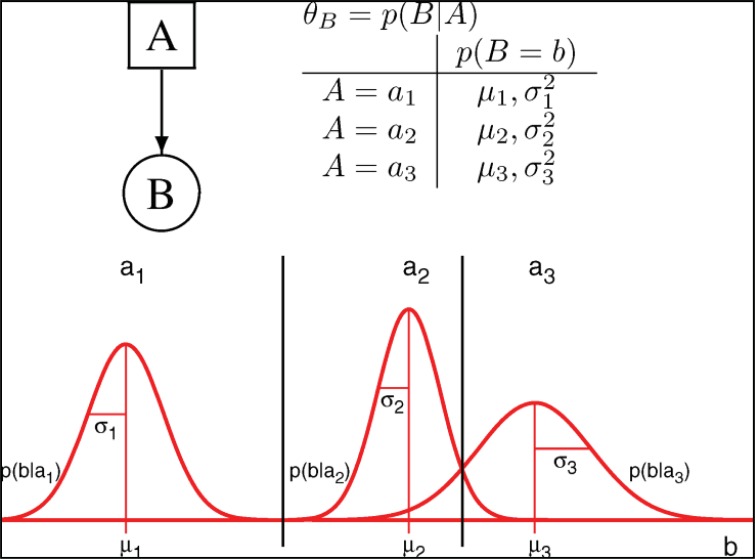
Another computational method for modeling, based on a graph representation, is Bayesian Networks (BNs). Bayesian modeling is valuable modeling approach because its biology is complex and biological data are noisy. BNs models illustrate the effects of pathway components (nodes) upon each other in the form of an influence diagram. The Bayesian formalism can handle discrete and continuous values, while Boolean networks can only handle discrete values. In Bayesian Network, a node represents a random variable for the conditional probability distribution of each pathway component. Bayesian modeling offers the ability to describe stochastic processes and to deal with uncertainty, incomplete knowledge and also noisy observations. In this network, limitations are the static and the acyclic nature of Bayesian networks [59].

In BNs, the relationships between variables (e.g., gene or protein) are encoded by conditional probability distributions (CPDs) of the form p(G2|G1)—the probability of G2 given G1. For discrete variables, probability distributions are expressed as conditional probability tables (CPTs) containing probabilities that are the model parameters. For BNs, which use continuous variables, conditional probability densities are used in a similar way to CPTs [60].

There are several attractive properties of BNs for the inference of signaling pathways from biological datasets. They can represent complex stochastic nonlinear relationships among multiple interacting molecules, and their probabilistic nature can accommodate noise inherent to biologically derived data. They can describe direct molecular interactions as well as indirect influences that proceed through additional, unobserved components – including crosstalk between pathways. They can also incorporate prior biological knowledge when available, by assigning increased or decreased likelihoods to particular inter-molecular connections.

Although not directly focused on signaling pathways, the pioneering works of Pe’er and Friedman [61], and Hartemink et al. [62], were some of the first efforts to learn biological regulatory pathways directly from high-throughput data.

4.5. Cellular Automata and Dynamic Cellular Automata

Cellular Automata (CA) is a discrete dynamical system, it means space, time, and the states of the system are discrete. Each point in a regular spatial lattice, called a cell, could have any one of a finite number of states. The states of the cells in the lattice are updated according to a local rule. That is, the state of a cell at a given time depends only on its own state and the states of its nearby neighbors at the previous time step. All cells on the lattice are updated synchronously. Thus the state of the entire lattice advances in discrete time steps. The theory of CA is immensely rich, with simple rules and structures being capable of producing a great variety of unexpected behaviors. Von-Neumann was one of the first people to consider such a model, and incorporated CA into his "universal constructor" [63]. Comprehensive studies of CA have been performed by S. Wolfram starting in the 1980s [64].

The CA approach has been widely used in some complex systems studies, such as biological systems, traffic issues, economic systems, environmental problems, engineering methods, social networks, and complex industrial systems, and has produced many meaningful results.

Application of CA in biology mainly shows itself in the subject of systems biology such as shape space simulations of the immune system [65], development of an artificial brain [66], a study of morphogenesis in simple cellular systems [67], modeling the competitive growth of two underwater species C. aspera and P. Pectinatus [68], a model of an enzymatic reaction [69], and especially in the study of excitable media [70]. Recently, CA has been widely used in the Center for the Study of Biological Complexity at VCU in Richmond, Virginia as a modeling approach for simulation biological problems [71].

We consider two simple examples of simulation biological networks using CA. The first example is a model used by Kier and Cheng [69] in setting up modeling of enzyme activity. The enzymatic reaction mechanism is assumed to start with an interaction between the substrate (S) and enzyme (E), which form a SE complex. The complex is rearranged to a complex PE and this will go to the enzyme E and the product P, which are then separated and the enzyme molecule E is free to take part in another interaction. Here is the summary of such reaction:

$$S+E\to SE\to PE\to P+E$$ (1)

This system can be described by some rate law, usually in the form of a Michaelis-Menten (MM) law:

$$\frac{d[S]}{dt}=\frac{V_{\max }[E][S]}{K_m+[S]}$$ (2)

in which Vmax is the maximum conversion rate and Km is the Michaelis-Menten coefficient.

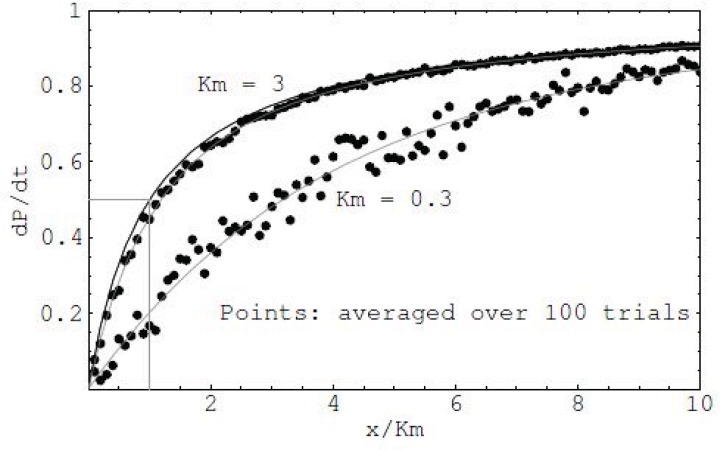
The quasi-steady state of the system has been reached after many iterations, rather than on the temporal changes. Hence, the model is a spatial one. A network to be studied is consisted of different cell groups, each group including one of the network species: enzymes, substrates, or products. The number of cells in each group reflects the relative concentrations of each network species. Each group of cells moves freely in the lattice. When an encounter between a specific substrate and a specific enzyme occurs, an enzyme-substrate complex is formed. The formed complex has an assigned probability of changing to a new complex which is the enzymatic product. Following this, another probability is assigned for separation of the product from the enzyme. The movement probability determines extent of any movement. Thus, zero probability for an enzyme cell would designate a stationary state. All cells compute their states at the same time. All three types of probabilities were assumed equal to unity. This means all cells may interact, join, and break apart with equal probability. Therefore the collection of rules associated with a network species represents a profile of the species structure and its relationship with other species. One could obtain the influences of different species at the final profile of the network by systematically varying the rules. The output of the system is shown in (Fig. 15).

Fig. (15).

Comparison of the MM reaction simulation using CA (dots) in two different K_m values (3.0 and 0.3) with the analytical result (two gray curves) (V_max = 1).

In another example, we present evidence that the CA method is capable of providing an insight on the dynamics of a signaling pathway. In modeling the dynamics of a signaling pathway, the first goal is to show whether the model reproduces the amplification of the signal through the pathway. The next goal is to test the pathway sensitivity to a variety of initial conditions, and to reproduce experimentally patterns found on substrate and product variations.

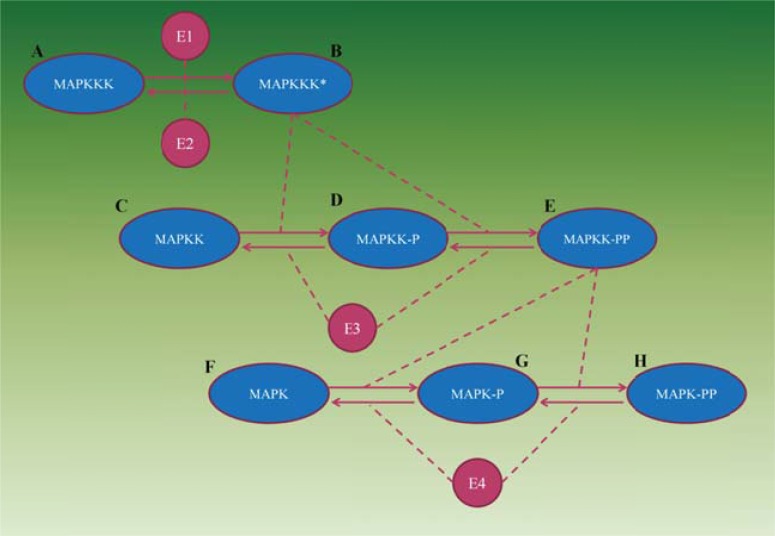
Here, we demonstrate a CA approach to the mitogen-activated protein kinase (MAPK) signaling pathway transmits signals from the plasma membrane to targets in the cytoplasm and nucleus. This pathway plays an important role in intracellular signaling related to different diseases such as Parkinson and cancer [73]. It contains three levels of phosphorylations, i.e., posttranslational protein modification reactions which are catalyzed by E1–E4 enzymes (Fig. 16).

Fig. (16).

The MAPK signaling cascade. Dashed lines indicate catalyst action.

The CA approach for the system has been obtained using a two-dimensional lattice with the size of 100×100. Similar to the previous example, the cells obeyed probabilistic rules for moving, joining and breaking away (for details of the rules see [71b].).

The complete list of elementary steps is shown below:

$$\begin{array}{l}A+E1\to AE1\to BE1\to B+E1\hfill \\ B+E2\to BE2\to AE2\to A+E2\hfill \\ C+B\to CB\to DB\to D+B\hfill \\ D+B\to DB\to EB\to E+B\hfill \\ D+E3\to DE3\to CE3\to C+E3\hfill \\ E+E3\to EE3\to DE3\to D+E3\hfill \\ F+E\to FE\to GE\to G+E\hfill \\ G+E\to GE\to HE\to H+E\hfill \\ G+E4\to GE4\to FE4\to F+E4\hfill \end{array}H+E4\to HE4\to GE4\to G+E4$$ (3)

in which A=MAPKKK, B=MAPKKK*, C=MAPKK, D=MAPKK-P, E=MAPKK-PP, F=MAPK, G=MAPK-P, H=MAPK-PP, E3=MAPKK-protease, E4=MAPK-protease, and E1 and E2 are the hypothetical enzymes.

First, the CA simulation produces temporal plots, which include changes in substrates and product concentrations from the beginning of the reaction till reaching a steady state. Then, this information is used to construct spatial models of concentration depending on the enzyme propensity and other variables of the process. The inhibitory control of enzyme activities is also simulated by CA for the entire probability range of 0–1. A CA simulation example of the concentration profile of the MAPK cascade versus the propensity of enzyme E3 is shown in (Fig. 17). The figure demonstrates the potential of CA modeling to produce stable patterns of the pathway (network) ingredient concentrations, and to define optimal parameter ranges for obtaining certain goals.

Fig. (17).

A spatial model of the eight MAPK molecules’ concentration dependence on the propensity of enzyme E3.

There is also another type of CA called Dynamic CA (DCA) which differs from conventional CA in that the DCA model attempts to simulate real motions via Brownian dynamics. In other words, motions of particles are intended to mimic motions observed in real macromolecules. Therefore, random objects cannot be taken up and randomly scattered over the lattice in each time step as they are in most CA models. Rather, DCA requires that regular time steps be taken in which the lattice size and time steps could be sufficiently small to be consistent with physical laws or experimentally measured parameters (i.e. diffusion rates).

Finally, it should be considered that CA models have a relative validity and need experimental calibration and validation. At present, applying CA to large-scale networks including thousands of genes, proteins and metabolites may be out of reach, because of the extremely high computational price. A reasonable strategy to deal with seems to be in obtaining stable dynamic patterns in small networks, and then extrapolation these patterns under specific conditions.

4.6. Agent-based Modeling

In the following, the characteristics of multi-agent systems and the Adequacy of Multi-Agent Systems (MAS) for Modeling and Simulating Biological Systems are described. Then, the advantages of Multi-Agent Systems compared to Non-Agent-Based approaches are studied and finally, in order to illustrate the multi-agent system approach applicability, different literatures that are exemplar applications of modeling and simulation of biological systems are referred.

In computational science, an agent is an interactive computer system that is situated in some environment and that is capable of autonomous action in this environment in order to meet its design objectives. Multi-agent systems are a set of agents interacting in a given dynamic environment. A good introduction to MAS can be found in [74].

In order to apply multi-agent systems for modeling and simulating biological systems, it is necessary to understand how the characteristics of multi-agent systems contribute to the field.

We identified the characteristics that make multi-agent systems an appropriate tool to tackle biological systems modeling and simulation problems through the following claims:

• Agents are autonomous entities: an agent is capable of acting without direct external intervention;

• Agents are interactive entities: an agent communicates with the environment and other agents;

• Agents are pro-active entities: an agent is goal-oriented, i.e., it does not simply react to the environment;

• Agents and multi-agents systems have the capacity for adaptation: an agent is capable of responding to other agents and/or its environment to some degree, and a multi-agent system might adapt itself to a specific state through the learning processes;

• Agents can have the capability of learning: an agent is able to modify its behavior based on its experience;

• Agents can be rational: an agent is able to choose an action based on internal goals;

• Agents can be mobile: an agent is able to transport itself from one environment to another.

• Multi-agent systems can handle the complexity of solutions through decomposition, modeling and organizing the interrelationships between components [75].

• Multi-agent systems provide abstractions that allow decomposing a biological system to a set of agents;

• Multi-agent systems provide flexibility for modeling more sophisticated, globally emergent behavior;

• Multi-agent systems by their nature are powerful tools for modeling complex systems [75]. Modeling complex systems implies a deep understanding of the system both in terms of its structure and its behavior and multi-agent systems allows this specification.

• Software agents embody distribution and heterogeneity and, thus, they are indicated as the new abstraction for the engineering of complex distributed systems;

• Multi-agent systems are capable of being open systems: agents may enter and leave the environment at their will, and the systems have no single point of control.

• Multi-agent systems are capable of being self-organized: agents could be organized in a structure that might evolve into a different structure according to the agents’ behavior, performance, and others.

• Multi-agent systems can produce the emergent behavior: the global effect resulting from the interaction of the individuals is often unpredictable and non-deterministic.

• Finally, the locality is an intrinsic feature of an agent: the agents’ decisions are taken considering only the local environment and not the global average.

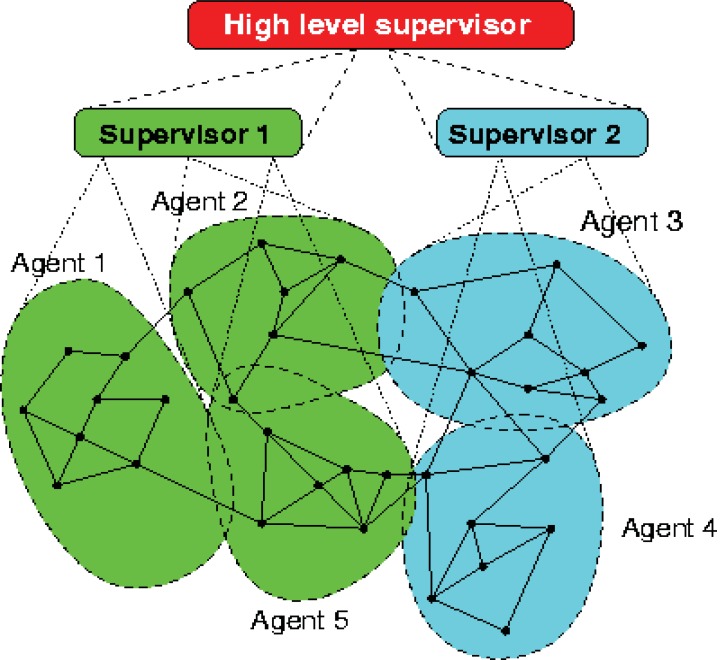
Considering the nature of the biological systems, all of these characteristics make the multi-agent system a suitable paradigm for modeling and simulating these complex systems. The complex system biology problems can be modeled as hybrid systems, i.e., systems with both continuous and discrete dynamics. In the (Fig. 18), a multi-level control structure with local control agents at the lowest level, and one with higher supervisory control levels are shown.

Fig. (18).

A schematic representation of a hierarchical multi-agent framework (http://www.negenborn.net/rudy/phd).

None of the mathematical models used for describing biological systems allows expression of partial information about a system, i.e. to formally describe open systems. Moreover, depending on the system’s complexity, there would be an explosion of differential equations; for example, to model it with more than 50 equations to model a subsystem. Another drawback is the absence of an abstraction for the models. Physicians must deeply understand mathematical methods in order to model the system, while multi-agent systems can provide the right level of abstraction for that [76].

Compared to the Monte Carlo methods, multi-agent systems are not just probabilistic. More than reproducing the emergent behavior, they can provide advanced mechanisms existent in biological systems, such as learning and adaptation that, as far as we know, are not possible to implement through Monte Carlo simulation. Those mechanisms not only make the model more complete but also allow the optimization of self-organization, for instance.

Considering the cellular automata approach, the multi-agent system approach for modeling and simulating biological systems might be more suitable since it provides an easier way of representing the interactions between entities through the agents’ interactions. Moreover, the software engineering for multi-agent systems can provide powerful techniques, methods and tools for the engineering of modeling and simulation of biological systems. For instance, self-organization of biological systems could be modeled through the self-organization modeling techniques existing in agent-oriented methodologies that accomplish this purpose [77].

Addressing the Petri Nets approach for modeling biological systems, they are not suitable for studying systems exhibiting continuous dynamic behavior that: (1) cannot be described by a set of discrete states, (2) cannot be broken down to atomic processes, or (3) are dependent on spatial properties [54b]. Examples include fluid dynamics and protein folding. And multi-agent systems could address all of these different kinds of behaviors.

The MAS model is a powerful tool used to describe local behavior and leaves the system free to simulate all events just by interactions between agents. However, the goal here is not to prove that multi-agent systems simulation is better or not than the non-agent-based related work cited. They are all powerful ways of modeling and simulating biological systems and have been proven to work. Instead, it is important to understand how multi-agent systems complement these approaches in nature and behavior. Some exemplar applications of Multi-Agent Systems for modeling and simulating biological systems are surveyed:

In order to give an overview of modeling and simulation of biological systems using multi-agent systems, different literatures that are exemplar applications of modeling and simulation of biological systems are referred through the following claims:

• Agent Based Modeling of Cancer and Tumor Biology [78].

• Agent Based Modeling of Vascular Biology [79].

  In this paper uses a Starlogo model to simulate the effect of growth factors on angiogenesis. It is a good example of the use of the spatial characteristics of ABM in the validation process.

• Agent Based Modeling of Intracellular Signalling and Metabolic Processes [80]. The paper presents the formation of cell membrane structures based on relatively simple interaction rules drawn from classical flocking models. This project is related to the ongoing CyberCell project.

5. STRUCTURAL MODELING

Structural modeling has a further advantage and needs less information to build the model than kinetic modeling. Structural modeling consists of two distinct analyses; topological analysis and Flux Balance Analysis (FBA), as stated in (Fig. 19). For topological analysis of metabolic networks, we need a branch of discrete mathematics named graph theory, in which a metabolic network model is represented as a graph. In these graphs, vertices and edges represent the metabolites and enzymatic reaction, respectively. Many computational tools are available for analyzing global and local properties of this network such as; finding the essential nodes of a network. All information we need in this modeling is a list of biochemical reactions.

Fig. (19).

Different kinds of analyses of reconstructed metabolic models and their applications.

Genome scale metabolic models have emerged as a valuable tool for illustrating whole cell function, based on a complete set of reactions of biochemical networks. These models are used for the prediction of organism's behavior. All information we need in this modeling is a list of biochemical reactions and their stoichiometry [81].

6. RESOURCES AND DATABASES

Today different database systems for molecular structures (genes and proteins) and biological networks and pathways are available. The most important resources for such information include the scientific literatures and human expertise curated in public databases. In particular, for the development of mathematical models standardized resources that provide their data in a computerized amenable and reusable manner are a preferable resource.

6.1. Primary Data Resources

The National Center for Biotechnology Information (NCBI), the European Bioinformatics Institute (EMBL-EBI) and the DNA Database of Japan (DDBJ) (http:// www.ddbj.nig.ac.jp) provide several primary databases that are widely used in biological research, offering information about nucleotide and protein sequences, genes, genomes, molecular structures and gene expression that are generated in worldwide laboratories. Similarly to nucleotide sequence databases, UniProt (www.uniprot.org), provides information on protein sequences and their annotations and Protein Data Bank (PDB) focuses on protein structures (www.rcsb.org). These databases are primary database. Moreover, there are many databases for protein families, domains and functional groups; such as InterPro, PFAM, CATH, SCOP and many other secondary databases. Recently, also non-coding RNAs (ncRNAs) and microRNAs have been revealed to be highly important in the control of cellular systems, giving rise to the implementation of related databases, like RNAdb or miRBase, with the objective of gathering current information.

Microarray data provide a valuable resource in the interpretation of the transcriptome levels of genes. Large repositories store these data from multiple studies such as the Gene Expression Omnibus (GEO) at NCBI and the ArrayExpress at EMBL-EBI. These databases provide free distribution and shared access to comprehensive gene expression datasets. Data includes single and dual channel microarray based on experiments measuring the abundance of mRNA (gene expression array), genomic DNA (CGH array, SNP array) and protein molecules (protein array). Also SAGE and mass spectrometry peptide profiling Data have been archived.

6.2. Pathway and Interaction Databases

Pathway and network databases are particularly interesting for modeling approaches since they offer a straightforward way of building networks topologies by the annotated reaction systems. These databases provide integrated representations of functional knowledge of the different components of a biological system and constitute a basis for the topology of mathematical models. The on-line resource center Pathguides (see http://www.pathguide.org/) contains information and clasification about 325 biological pathway resources. These databases have been grouped into four major, slightly overlapping categories: protein interactions, metabolic pathways, signaling pathways, and transcription factors/gene regulatory networks. It also has a specific category called Pathway Diagrams. The databases Kyoto Encyclopedia of Genes and Genomes (KEGG), Reactome and BioCyc as pioneer of interaction databases contain metabolic reactions and signal transduction pathways. KEGG is a reference knowledge-base offering information about genes and proteins, biochemical compounds, reactions and pathways. It provides many reference pathways that are linked to genes and reactions of over 38 eukaryotes and many microorganisms. It can be accessed via the web, FTP and web services. Also, Recon database [82] is a comprehensive metabolic resource that contains metabolic reaction of human metabolism in health and disease. The total number of reactions in Recon2 (latest version) is 7,440 and total number of metabolites is 5,063. Reactome has been managed as a collaboration of the Cold Spring Harbor Laboratory, the EBI and the Gene Ontology Consortium. It uses a very precise specification (ontology) of components and interactions and comprises details on stoichiometry, localization, references to external databases, etc. This covers also processes like complex formation events or translocations of molecules. A further pathway database with a similar scope is BioCyc that covers pathway data on Escherichia coli (EcoCyc), and predicts metabolic pathways of other microorganisms (MetaCyc) and human (HumanCyc) as well. STRING (functional protein association networks) is an important PPI database that takes into account the different types of interactions between proteins in human and other model organisms.

Databases with a specific focus on signaling events are BioCarta, Spike, Transpath, STKE, NetPath and the Pathway Interaction Database (PID). An inherent aspect of the pathway concept is protein–protein interaction subject of the databases IntAct or database of interacting proteins (DIP). Gene regulation processes and gene regulatory networks are not yet covered in as much detail as metabolic processes or signaling. However, there are some databases that store information on transcription factor binding sites; such as RegulonDB, TRED and Transfac databases. The lack of uniform data models and data access methods of the existing almost 325 interactions and pathway databases make data integration very difficult. The figure illustrates the overlap of several of these pathway resources.

Besides topological information about cellular reaction networks, kinetic data, such as kinetic laws and kinetic constants, are of particular interest in the generation of mathematical models. Two databases that are concerned with such data are BRENDA and SABIO-RK.

6.3. Systems Biology Model Repositories

Systems have been made available to the scientific community in the form of publications, often depicting a diagram of the reaction system or a list of the reaction equations, along with a mathematical description (e.g. as a differential equation system), and lists of kinetic parameters and concentrations of specific states. Recently, model databases have been installed such as the BioModels database (www. ebi.ac.uk/biomodels) or JWS (jjj.biochem.sun.ac.za/data base). Both are public, centralized databases of curated, published, quantitative kinetic models of biochemical and cellular systems. For instance, the BioModels database currently provides 409 curated and 420 non- curated models.

6.4. Species-specific Databases

Whereas most of the above-mentioned databases are fairly general, there are multiple databases with a specific focus. For instance, there are databases that focus on a certain species, for example MGD for moose, Flybase for Drosophila melanogaster, wormbase for Caenorhabditis elegans or SGD for yeast, either they contain information on specific diseases, such as cancer (e.g. COSMIC) and diabetes (e.g. T1DBase), or they hold information on a specific subject, such as chemical compounds found in biological systems (ChEBI, the Human metabolome database, PRIDE, Lipid-Maps, and the Human serum metabolome project).

In conclusion, mining literature for systems biology, the integration of literature information is highly important. Literature is accessed in a derived form such as the concepts represented by the Gene Ontologies (GO) and Medical Subject Headings (MeSH). A further approach that has been recently applied for building systems biology resources is text mining [84]. Text mining (manual or with the program) can either be used for pre-selection of appropriate literature or be used for the automatic extraction of data from literature. In particular, systems biology can benefit significantly from the extraction of data on molecular interactions of cellular components and related information about the kinetics of the interactions [85]. However, text mining of scientific literature is still in its early phase and the precision of its results, as given by false-positive and false-negative rates, has to be improved. For further review of literature mining see [86].

7. SYSTEMS BIOLOGY TOOLS

The first question one might ask is why developing specialized software to model biochemical networks? Given the availability of both generic commercial and freely available tools for numerical analysis, one might ask if there is such a need? There are probably at least two reasons why researchers develop their own specialized tools for modeling biochemical systems. The first is that specialized tools reduce the errors that occur while transcribing a reaction scheme (that is, a biological representation) into the mathematical formalism ready for simulation. Deriving the math equations by hand is often a source of error (especially in published papers), particularly in large models. The second important reason is that developing software offers an opportunity to codify and build up new numerical algorithms or new theoretical approaches that are specific to problems found in systems biology [87]. Today Researchers make use of a large number of different tools for modeling, analysis, visualization and data manipulation.

7.1. Visualization Tools

Tools that allow users to draw pathways on a screen and turn them into simulatable models seem to be fairly rare. We confine your attention here to tools that are specifically designed to assist in simulation, rather than pathway annotation. Examples of the latter include the Edinburgh Pathway Editor [88], Cytoscape [89], BioUML [90], geWorkbench [91], Medusa [92], VANTED [93], and BioTapestry [94]; and many others also exist.

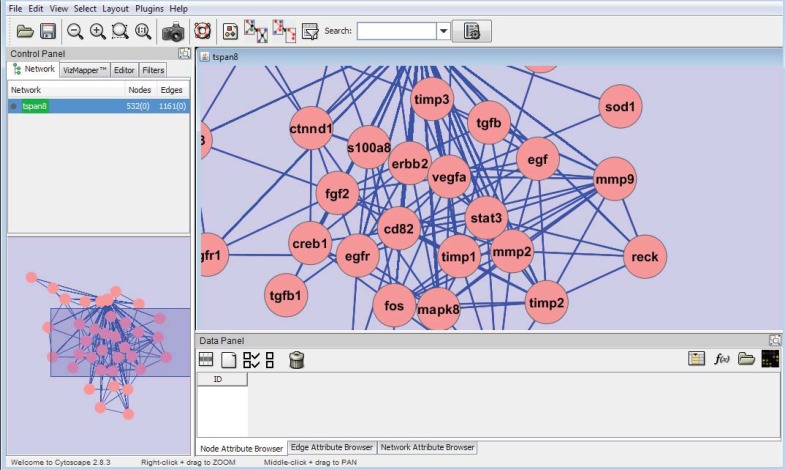
Cytoscape, is an open source bioinformatics software platform and has become a standard tool for integrated analysis and visualization of biological networks. Its central organizing principle is a network graph, with biological entities (e.g. genes, proteins, cells, patients), represented as nodes and biological interactions represented as edges between nodes. Data is integrated with the network using attributes, which map nodes or edges to specific data values such as gene expression levels or protein functions. Attribute values can be used to control visual aspects of nodes and edges (e.g. shape, color, size) as well as to perform complex network searches, filtering operations and other analysis.

The latest Version of Cytoscape (2-8-3) has introduced two significant new features that improve its ability to integrate and visualize complex datasets. The first feature allows non-programmers to map graphical images onto nodes, which greatly increases the power and flexibility with which integrated data can be visualized. The second feature is the introduction of spreadsheet-like equations into Cytoscape's Attribute Browser to enable the advanced transformation and combination of datasets directly within Cytoscape. Separately, each of these features provides useful new capabilities to Cytoscape. Taken together, however, these features provide a mechanism for expressing relationships between sets of data while simultaneously visualizing the integrated results [95]. For various kinds of network manipulations, there are a lot of Cytoscape plugins. BiNoM is a Cytoscape plugin, developed to facilitate the manipulation of biological networks represented in standard systems biology formats (SBML, SBGN, BioPAX) and to carry out studies on the network structure.

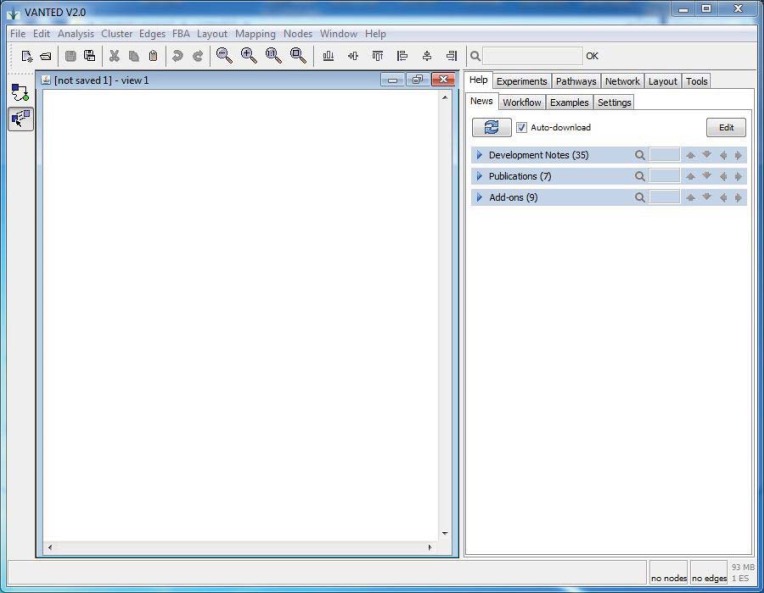
VANTED (Visualization and Analysis of Networks containing Experimental Data) is a Java-based software which has been developed by an IPK group in order to create and analyze biological networks [93, 96]. A user could load and edit biological pathways or functional hierarchies in a graph representation. One could do some steady-state analysis such as Flux balance analysis (FBA), Knock-out analysis, Robustness analysis, and Flux variability analysis. It could also map experimental datasets onto the graph elements and could visualize time series data, data of different genotypes, or environmental conditions in the context of biological processes. More information is available through software tutorial which additionally contains example pathways and measurement datasets.

VANTED contains some Add-ons for demonstration and analysis of biological networks in which we will describe them in the summary.

FBA-SimVis: The constraint-based analysis of metabolic models.

FluxMap: advanced visualization of simulated or measured flux data in biological networks.

PetriNet: handle discrete and continuous place-transition nets of varying complexity.

DBE2 (Database of Biological Experiments): an extension of the original DBE system in which experimental data can be easily shared and combined.

MetaCrop: enable browsing the content of the handcurated Metacrop database.

HIVE (Handy Integration and Visualization of multimodal Experimental Data): combines network-focused Systems Biology approaches with spatio-temporal information.

SBGN-ED: Editing, Translating and Validating of Systems Biology Graphical Notation (SBGN) Maps, an emerging standard for graphical representations of biochemical and cellular processes studied in systems biology.

CentiLib: computation and investigation of weighted and unweighted centralities in biological networks.

GLIEP (Glyph-based Link Exploration of Pathways): navigation and exploration process of interconnected pathway visualization as well as providing insight into the overall interconnectivity.

Using VANTED requires Java runtime version 6 or later and it has been tested on Windows, Mac OS X, Ubuntu Linux, and Sun Solaris platforms. At the time of writing this review, the latest version is 2.1.0.

7.2. Modeling and Annotation Tools

Once the model topology is designed, a mathematical model can be created. If this is, for example, a kinetic model, further data on the kinetic laws and kinetic parameters have to be identified or appropriate assumptions have to be made. For this purpose, diverse software tools have been developed. One can use commercial tools like Mathematica or Matlab that are well elaborated and offer broad spectra of functionalities. One disadvantage of using these programs is that the differential equation system of the mathematical model has to be formulated explicitly by the user. Overviews of current software platforms and projects that face up this as well as an overview about computational requirements for this purpose hav been given. Common systems among others for this purpose are Gepasi, COPASI, E-Cell, ProMoT/Diva, Virtual Cell or the Systems Biology Workbench (SBW) and its add-ons. Some of these tools are shown in (Table 4).

Table 4.

Partial list of computational systems biology simulation tools.

Name	Category	Model Representation	Function	URL
MATLAB, with SimBiologyToolbox	Continuous and stochastic	Mathematical (e.g.ODE)	General-purpose mathematical environments, simulation and analysis	www.mathworks.com
XPPAut	Continuous and stochastic	ODE	General purpose; simulation, analysis	www.math.pitt.edu/_bard/xpp/xpp.html
Copasi	Continuous and stochastic	ODE	Simulation and analysis	www.copasi.org
Virtual Cell	Continuous and stochastic	ODE-based, PDE	Simulation and parameter sensitivity analysis	www.nrcam.uchc.edu
Systems Biology Workbench, including Jarnac and JDesigner	Discrete, continuous and stochastic	ODE/SBML	Data-exchange framework for Data-exchange framework for modeling, simulation and analysis	sbw.kgi.edu
Narrator	Continuous and stochastic	Graphical,ODE-based	Modeling and simulation	www.narrator-tool.org
STOCHSIM	Stochastic	Probabilistic	General-purpose biochemical Simulator	www.pdn.cam.ac.uk/groups/comp-cell/ StochSim.html
E-CELL	Continuous	Object-oriented	Modeling and simulation	www.e-cell.org
SPiM	Stochastic	calculus	Simulation	http://www.doc.ic.ac.uk/_anp/spim/
BioSigNet	Discrete	Graphical	Reasoning, hypothesis testing	www.public.asu.edu/_cbaral/biosignet
BIOCHAM	Discrete and continuous	Logical + kinetic models	Simulation and analysis	contraintes.inria.fr/BIOCHAM
PRISM	Discrete	Stochastic process algebra	General purpose; Analysis((model checking))	www.cs.bham.ac.uk/_dxp/prism
PEPAWorkbench	Discrete	Stochastic process algebra	General purpose; Analysis	www.dcs.ed.ac.uk/pepa/tools

A comprehensive list of modeling and simulation tools is also given which reports the results of an online survey of systems biology standards. This report identified CellDesigner as the most popular stand-alone application in respect to its graphical functionalities [97].

Example by CellDesigner: (Fig. 23) illustrates the Ras / Erk pathway that is activated by EGF. These pathways are activated by EGF attachment to EGFR. After the interaction of EGF with the EGFR, the receptors undergo homo- or heterodimerization that causes auto phosphorylation of certain tyrosine residues in the cytoplasmic end. After phosphorylation, the Shc adaptor binds its site and Grb2 attaches to Shc, and then SOS (GTP exchange protein for Ras) is employed by Grb2 [98]. Also, Grb2 directly binds its receptor, accordingly SOS binds Grb2. [99]. In the next step SOS converts Ras-GDP into Ras-GTP which is the activated form of Ras [98]. Activated Ras induces Raf phosphorylation and activation. Raf is a kind of Serin/Threonine kinase that phosphorylates and activates the MEK (MAP kinase kinase). The activated MEK, phosphoralates and activates ERK (extracellular signal-regulated kinase) [100]. ERK or MAPK (mitogen activated protein kinase) phosphorylate a variety of the proteins that leads to cell growth and proliferation [101]. Also, receptor internalization from the cell surface and receptor degradation were done by Cbl factor.

Fig. (23).

A) A simple pathway created by VANTED. B) Flux balance analysis of the pathway A using VANTED.

Gepasi and COPASI come up with user-friendly interfaces for the simulation and analysis of bio- chemical systems. They support the definition of compartments. Common kinetic types as well as user-defined kinetic types are available. They provide time-course simulation and steady-state calculation and also the ability to explore the behavior of the model over a wide range of parameter values, using a parameter to scan that runs one simulation for each parameter combination. Gepasi and COPASI can characterize steady states, using metabolic control analysis (MCA) and linear stability analysis and they are capable of performing parameter estimation with experimental data and optimization [102].

SQUAD (standardized qualitative dynamical systems) program was introduced for the dynamic simulation of biological signaling networks [103]. SQUAD uses the standardized qualitative dynamical systems and a binary decision diagram to identify the steady states of the signaling system. SQUAD can be used for perturbing networks in a manner similar to what is performed in knock out experiments. The network translates into a discrete dynamical system by:

$x_i\left(t+1\right)=\{\begin{array}{c}(xa1(t)\vee xa2(t)\dots \vee xan(t))\wedge \neg (xi1(t)\vee xi2(t)\dots \vee xim(t))\\ xa1(t)\vee xa2(t)\dots \vee xan(t)\\ \neg (xi1(t)\vee xi2(t)\dots \vee xim(t))\end{array}\vee ,\wedge ,\text{and }\neg \text{ are the logical operators OR},\text{ AND},\text{ and NOT xi}\in [0,1]$

Generalized Logical Analysis (GLA) is used to locate steady states, which is based on the analysis of the all the loops that constitute the network. Also, reduced Order Binary Decision Diagram (ROBDD) algorithm has been implemented in SQUAD for the analysis of networks containing only binary nodes.

SQUAD aims at simulating and predicting the behavior of a regulatory network when subject to stimuli, such as drugs, or determines the role of specific components within the network. SQUAD provides a graphical interface, for the fast nonparametric simulation of large biological networks (Fig. 25). A good example of SQUAD application is that a study used it for simulation of apoptosis in liver cell signaling network, and its modifications in response to viral infection were investigated [104].

Fig. (25).

Graphical interface of SQUAD program. The output of SQUAD program describes the identified steady states of T-helper cell network. The network is loaded into SQUAD using an SBML file. State1: all the nodes inactive, State2: Active IFNγ, and State3: Active IL-4.

E-Cell is based on the modeling theory of the object-oriented Substance–Reactor Model. Models are constructed with three object classes, substance, reactor and system. Substances represent state variables, reactors describe operations on state variables and systems represent logical or physical compartments. The time - course calculation is done by the use of a simulation engine. Numerical integration is supported by first-order Euler or fourth-order Runge–Kutta method.

ProMoT/Diva consists of the modeling tool, ProMoT, and the simulation environment Diva. The workbench deals with modular models and can handle Differential Algebraic Equation (DAE) systems. Modeling is supported with a graphical user interface and a modeling language. The modeling tool provides the possibility to use existing modeling entities out of knowledge bases.

Virtual Cell (URL: www.nrcam.uchc.edu) is a web based tool that uses a user interface to input the data needed for the modeling [105]. Virtual Cell can be used to model different ranges of signaling mechanisms, including diffusion, flow, membrane & lateral membrane transport, and reaction kinetics. The necessary parameters involved are topology of network, respective kinetic parameters in reactions, and sub cellular localizations of each component of the network. For each model Virtual Cell automatically generates the mathematical framework for running a simulation, and generate the appropriate program code. The model and its components can be reused and published using the Virtual Cell database. The output of data is in different formats including spreadsheets, images that represent the system state over time, and QuickTime movies (Fig. 26). Import/export of models is possible via of SBML, CellML, and MatLab formats.

Fig. (26).

Simulation results of Virtual Cell program. The virtual Cell model used to model of an enzymatic reaction over ten stochastic trajectories at t = 4.0 obtained from 1000 trials. The reactions and network topology imported into Virtual Cell from the KEGG database automatically.

NSIN (Nonparametric Simulator of Signal Transduction Networks) tool is a computational framework to describe the general profile of a process evolving and the time course of the proportion of active form of molecules in signal transduction networks [106]. This continuous model, does not require biochemical or kinetic parameters in order to capture the system dynamics. The activity of nodes will change step by step acceding to the specific functions. During iteration nodes are updated to their new values in a semi-synchronous manner. Also the possibility of perturbation experiments on the model is incorporated.

To analyze a signal transduction network, the program requires specification of network in terms of its source, target, and type of interaction matrices. An input is a directed graph in which the nodes represent the elements (e.g. proteins), and the edges represent interactions (e.g. phosphorylation) between two types of elements. The program needs the two input files. The first input simply identifies the source and target of each interaction and the second identifies the type of interaction including activator or inhibitor. The simulation starts from signal receptors, and iteratively traverses the whole network, and updates the state of every node. At each time point the state of a node is determined by the previous state, and the states of its upstream neighbors via a combination of two processes including the weighting edges, and simulation of signal flow from the initial(s) node(s). The simulator provides both single and set running modes. In single mode, users can specify the input node activity, and the activities of the nodes will change in the iteration. A set-mode run consists of multiple inputs, each with different activities. The output includes continuing values for level of activation of giving molecule (proportion of active molecules) at discrete time-steps, at final time-steps, and the weight of edges in the network. The NSIN program is freely available at http://lbb.ut.ac.ir/Download/LBBsoft/NSIN.

The SBW provides a server that acts as a broker between different modeling and simulation tools (clients) via a common interface. These clients (add-ons) cover graphical tools for model population, deterministic and stochastic simulators and also analysis tools like the integration of MetaTool. Closely related to the SBW is the development of SBML that is used for communication by SBW.

7.2.1. Model Parameters

Once the topology of network has been set up, the next step is to collect the parameters for each of the interactions (Fig. 27) [20]. An example of available databases for parameter selection and development of models is DOQCS (URL: docqcs.ncbs.res.in). If for under consideration model parameters are incomplete, it is possible to create nonparametric models [21]. This approach can fill the model variable gap by experimentally verified assumptions and estimations [22].

Fig. (27).

Flow chart of the steps involved in the preparation of a computational model. Initially, the model is defined as the network. Once the interactions between components are set up, parameters are collected from the different sources. The simulation results and predictions can be compared with the experimental results or use of experimental design.

8. STANDARDS USED IN SYSTEMS BIOLOGY

An important part of systems biology is data integration. Although data integration itself cannot explain the dynamical behavior of biological systems, it is useful for increasing the information content of the individual experimental observation, enhancing the quality of the data and identifying relevant components in the model as a new pathway or network. On the basic level of complexity, data integration consists of the integration of heterogeneous data resources and databases with the aim of parsing data from these databases, query for information and to make it usable for modeling. Technically, database integration requires the definition of data-exchange protocols, languages and the development of parsers that interconnect the databases to a data layer that is able to display the heterogeneous data sources in a unified way.

A standard for representation, storage and exchange of data is a convention about the information items necessary to describe the experiment and the encoding of this information (e.g. expression data of microarray experiments or information about the relations between components and interactions of a pathway). The standard has to enable an unambiguous transfer and interpretation of the data and information. Developing a standard involves four steps: an informal design of a conceptual model, a formalization, the development of a data exchange format and finally the implementation of supporting tools [107].

8.1. Conceptual Design

The first step, the conceptual model design, gives an informal description of the related domain and specifies its delimitation. The description should address the minimal number of most informative parameters but should still provide a common ground for all related applications. For instance, for the microarray domain a conceptualization is provided with Minimum Information about a Micro- array Experiment (MIAME) [108] and Minimum Information about a Proteomics Experiment (MIAPE) [109] which gives guidelines for the standardized collection, integration, storage and dissemination of proteomics data. Like specifications for experimental data also concepts for the description of mathematical models such as Minimum Information Requested in the Annotation of Biochemical Models (MIRIAM) [110] have been elaborated.

8.2. Data Representation Formalisms and Languages

The description of a given domain can be represented in any format, but the use of common representation formalisms and languages makes it easier to compare and interpret data from similar domains and it also facilitates the integration, computational processing and comprehensive interpretation of that data.

Controlled vocabularies are a prerequisite for a consistent data description. They contain sets of words or phrases representing particular entities, processes or abstract concepts. Within a particular controlled vocabulary, individual terms are usually associated with a unique identifier, an unambiguous definition and occasionally also synonymous to prevent misinterpretations.

Furthermore, ontologies are used for the conceptualization of a knowledge domain. An Ontology defines terms and relations along with a vocabulary of a topic area and thus, provides a common terminology over a certain domain. Relations are, for example, ‘is-a’ relations that describe a generalization, forming a term hierarchy. An example is the GO that builds the basis for a generalized functional annotation of genes and their products. The naming of genes and gene products is not necessarily systematic and genes having identical functions are given different names in different organisms or the verbal description of location and function might be different. To address this problem, the GO was initiated as a collaborative effort (www.geneontology.org). GO terms have a parent– child relationship. GO defines three top-level categories, ‘molecular function’, ‘biological process’ and ‘cellular component’ it organizes all keywords in a hierarchical graph-like structure. The terms, defined in GO, form a directed acyclic graph. The power of the GO project lies in the fact that many applications have been developed that use GO terms to validate other data for functional information.

8.3. Data Exchange Formats

During the last years, the eXtensible Markup Language (XML) has been proofed to be a flexible tool for the definition of standard formats not only for applications in different fields of information technology, but also for the management of data from diverse experimental platforms. One example designed for data from microarray experiments is MAGE-ML [111]. Others are, for instance, those dealing with pathway data and mathematical models. SBML, CellML and BioPAX have enough potential to become de facto standards for their respective application area [112].

With the surge in the number of incompatible simulation tools since the year 2000, it was realized by at least two communities that some forms of standardization for model exchange were necessary. CellML and SBML are the two standards that emerged. CellML is primarily a notation for representing biochemical models in a strict mathematical form; as a result it is, in principle, completely general. In contrast, SBML uses a biologically inspired notation to represent networks from which a mathematical model can be generated. Each one has its strengths and weaknesses, but SBML has a simpler structure than CellML and as a result there is more software support for SBML. Most software tools at the present time support import and export of SBML. Both standards have very active communities, intracellular models, being primarily the domain of SBML and physiological models for CellML [113].

BioPAX [114] is defined by the BioPAX working group and is designed for handling information on the pathways and topologies of biochemical reaction networks. The Systems Biology Markup Language (SBML) is a format for describing dynamic models, common to research in many areas of computational biology, including metabolic pathways, cell signaling pathways, gene regulatory network and other biological networks and pathways. Major releases of the SBML standard are called levels, where level 2 is the most recent. SBML defines a list of species (entities of the model), compartments, parameters and reactions, among others. SBML is widely used—it is supported by over 200 software systems [115].

A comparison of SBML and BioPAX comes to the conclusion that, while the main structures of these formats are similar, SBML is tuned towards simulation models of molecular pathways. BioPAX turns out to be the most general and expressive format, even if it is lacking definitions for the representation of dynamic data such as kinetic laws and parameters [116].

It is argued that the syntactic and document- centric XML cannot achieve the level of interoperability required by the highly dynamic and integrated bioinformatics applications. Therefore, semantic web technology like resource-descrip- tion framework (RDF) and the web ontology language (OWL) have been proposed as alternatives to current XML technology [117].

Using standards brings several advantages, e.g. Ontology along with a defined vocabulary is used to promote an accurate description of the data and provides a software-independent common representation of the data. One of the most important general problems in building standards in biology is that our understanding of living systems is not static but rather constantly developing what necessitates a regular update of these standards.

9. CONCLUSION AND PERSPECTIVES

Quantitative modeling methods are still in their infancy for the analysis of biological networks. While describing biological processes at the system level (e.g. a cell), it is important to remember that the biological data is often very noisy, and the processes are highly complex: biomolecular concentrations and interactions change over time and in response to internal or external stimuli as well as to dynamical intrasystem processes. Todays, the graph theory and its properties (static modeling) applied to describe biological networks may reach its limits when the contingency and conditionality of interactions need to be considered. Computational systems biology and predicting methods have seen tremendous advances during this decade. In the past few years, research in computational systems biology has moved beyond interaction networks, based simply on clustering and correlation. Simple Petri nets modeling and boolean networks can reveal important topological network properties, but are too crude to explain some important aspects of network dynamics. While, ODEs allow more detailed descriptions of network dynamics, by explicitly modeling the concentration changes of molecules over time. In the biological systems both continuous and discrete aspects are present. Therefore, Hybrid models have been developed in an attempt to describe both, discrete and continuous aspects in one model and such models have therefore been proposed for biological systems modeling.

In surveying the development of software in systems biology, we see a vibrant and sometimes innovative community with a very wide range of tools to satisfy all manners of users. There are still some areas that are lacking, most notably bifurcation analysis and model composition.

Fig. (7).

A static model of cell cycle created by CellDesigner (http://www.pantherdb.org).

Fig. (13).

A simple representation of Boolean network model and their regulation functions.

Fig. (14).

A simple Bayesian network with two nodes.

Fig. (20).

Overlap between important network and pathway databases and their interaction.

Fig. (21).

An overview of Cytoscape start window.

Fig. (22).

An overview of VANTED start window.

Fig. (24).

An output of CellDesigner.

Fig. (28).

Modeling workflow processes.

Table 3.

Selected data resources and databases for systems biology research.

Data Resource	URL
Pathway Database
KEGG	http://www.genome.jp/kegg/
Reactome	http://www.reactome.org
Recon X	http://humanmetabolism.org/
BioCyc	http://biocyc.org/
Pathway interaction database (PID)	http://pid.nci.nih.gov/
BioCarta	http://www.biocarta.com/
IntAct	http://www.ebi.ac.uk/intact/
Database of Interacting Protein (DIP)	http://dip.doe-mbi.ucla.edu/dip/Main.cgi
Kinetics Database
BRENDA	http://www.brenda-enzymes.org
UMBBD	http://umbbd.msi.umn.edu
SABIO-RK	http://sabio.villa-bosch.de/
Expression Data Resource
Gene Expression omnibus (GEO)	http://www.ncbi.nlm.nih.gov/geo
ArrayExpress	http://www.ebi.ac.uk/arrayexpress/
Ontology
Gene Ontology	http://www.geneontology.org
Systems Biology Repositories
Biomodels	http://www.ebi.ac.uk/biomodels-main/
CellML	http://www.cellml.org/
JWS	http://jjj.biochem.sun.ac.za/index.html

CONFLICT OF INTEREST

The author(s) confirm that this article content has no conflicts of interest.