A Brief Review: The Z-curve Theory and its Application in Genome Analysis

Abstract

In theoretical physics, there exist two basic mathematical approaches, algebraic and geometrical methods, which, in most cases, are complementary. In the area of genome sequence analysis, however, algebraic approaches have been widely used, while geometrical approaches have been less explored for a long time. The Z-curve theory is a geometrical approach to genome analysis. The Z-curve is a three-dimensional curve that represents a given DNA sequence in the sense that each can be uniquely reconstructed given the other. The Z-curve, therefore, contains all the information that the corresponding DNA sequence carries. The analysis of a DNA sequence can then be performed through studying the corresponding Z-curve. The Z-curve method has found applications in a wide range of areas in the past two decades, including the identifications of protein-coding genes, replication origins, horizontally-transferred genomic islands, promoters, translational start sides and isochores, as well as studies on phylogenetics, genome visualization and comparative genomics. Here, we review the progress of Z-curve studies from aspects of both theory and applications in genome analysis.

1. INTRODUCTION

In theoretical physics, there exist two basic mathematical approaches, algebraic and geometrical methods, which, in most cases, are complementary. In the area of genome studies, however, algebraic approaches, such as Markov chain models and hidden Markov chain models, have been widely used, while geometrical approaches have been less explored for a long time. The Z-curve theory is a geometric approach to genome analysis.

The Z-curve is a 3-dimensional curve that represents a given DNA sequence in the sense that each can be uniquely reconstructed given the other [1-3]. The Z-curve, therefore, contains all the information that the corresponding DNA sequence carries. The analysis of a DNA sequence can then be performed through studying the corresponding Z-curve.

Historically, various methods for the graphical representation of DNA sequences were proposed, such as the H curve [4] and the 2-dimensional DNA walk [5]. It has been shown that most of these methods are, in fact, special cases of the Z-curve, and an extensive comparison between the Z-curve and other representations was detailed in reference [2]. One of the advantages of the Z-curve is its intuitiveness, enabling global and local compositional features of genomes to be grasped quickly in a perceivable form. The methodology of

the Z-curve is a suitable platform on which other methods, such as statistics, can be integrated to address bioinformatics questions. The Z-curve method [1, 2] has found many applications in genome analysis since its initiation two decades ago. Here, we review the progress of the Z-curve studies from aspects of both theory and applications in genome research.

2. PART-1: THEORY OF THE Z-CURVE

2.1. Symmetry of Four DNA Bases and its Geometric Representation

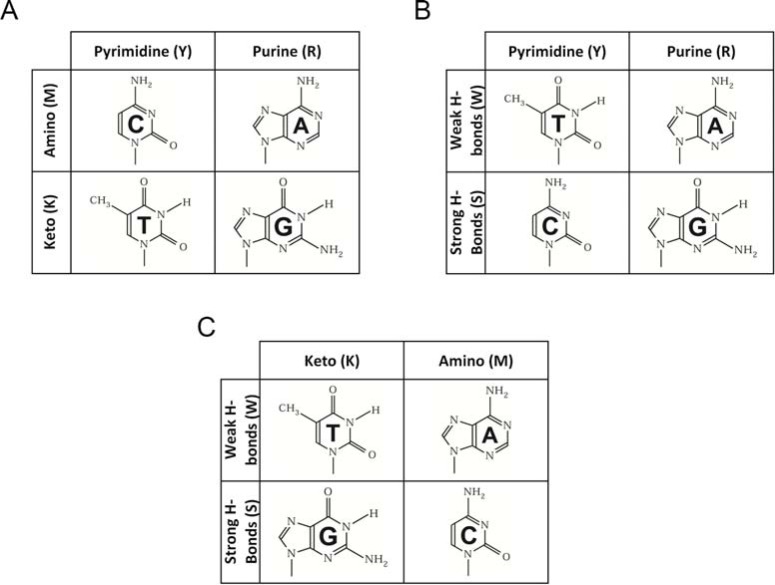
The DNA sequence is composed of 4 kinds of nucleotides, adenine, cytosine, guanine and thymine, denoted by A, C, G and T, respectively. The number of possible combinations when taking 2 bases at a time from 4 bases is 6. The 6 combinations are: R (A/G) and Y (C/T); M (A/C) and K (G/T); W (A/T) and S (G/C), where R, Y, M, K, W and S represent the bases of puRine, pYrimidine, aMino, Keto, Weak hydrogen bonds and Strong hydrogen bonds, respectively, according to the NC-IUB recommendation [6]. The chemical structures of the four bases are shown in (Fig. 1), illustrating the symmetry among the four bases. According to different criteria, the four bases can be classified into two categories.

Fig. (1).

Chemical structures of four DNA bases, displaying the basic symmetry.

(i) Criterion 1, according to the chemical structure of having single or double rings

$\text{Bases}\{\begin{array}{l}\text{Purine, R=A, G,}\\ \text{Pyrimidine, Y=C, T.}\end{array}$

(ii) Criterion 2, according to the chemical structure of having an amino or keto group

$\text{Bases}\{\begin{array}{l}\text{Amino,}\begin{array}{c}\end{array}\text{M}=\text{A,}\begin{array}{c}\end{array}\text{C,}\\ \text{Keto,}\begin{array}{c}\end{array}\text{K}=\text{G},\begin{array}{c}\end{array}\text{T}.\end{array}$

(iii) Criterion 3, according to the structure of the double helix forming two or three hydrogen bonds in the Watson-Crick pair

$\text{Bases}\{\begin{array}{l}\text{Weak,}\begin{array}{ccc}& & \end{array}\text{W}=\text{A,}\begin{array}{c}\end{array}\text{T,}\\ \text{Strong,}\begin{array}{c}\end{array}\begin{array}{c}\end{array}\begin{array}{c}\end{array}\begin{array}{c}\end{array}\begin{array}{c}\end{array}\begin{array}{c}\end{array}\text{S}=\text{G},\begin{array}{c}\end{array}\text{C}.\end{array}$

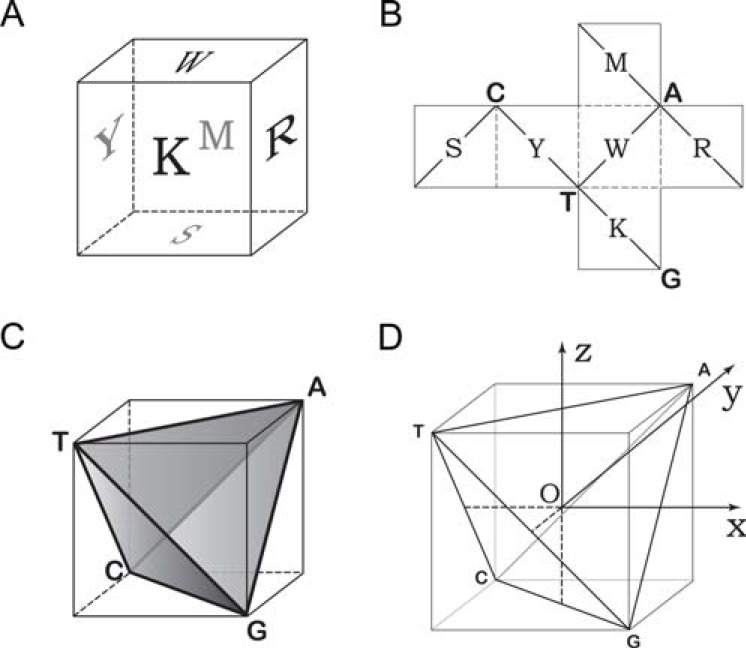
We seek to find some geometrical representation for the above symmetry. If a 2-dimensional (plane) graph is adopted, we find that the symmetry can be represented by (Fig. 1A-C). If a 3-dimensional graph is adopted, the regular cube, as shown in (Fig. 2A), seems to be the unique choice to represent the symmetry. Each face of the cube is assigned to one, and only one, of the six characters: R, Y, M, K, W and S, thereby keeping the rule that R and Y, M and K, as well as W and S are on opposite sides. To prepare (Fig. 2A), readers may cut (Fig. 2B) and fold it along the dashed lines. Diagonals of the regular cube form a regular tetrahedron ACGT, as shown in (Fig. 2C). Assigning one of A, C, G and T to each vertex of the tetrahedron as shown in (Fig. 2C) is not arbitrary. Note that the vertex A of the tetrahedron is also the vertex of the cube, at which three faces of the cube, R, M and W, are crossed. The intersection base of R (A/G), M (A/C) and W(A/T) is A. Similar assignments can be applied to the vertices C, G and T, as shown in (Fig. 2C and D).

Fig. (2).

The coordinate system based on the regular tetrahedron. A) a cube displaying the basic symmetry: R/Y, M/K and S/W symmetry; B) an extended plot for the cube. C) a cube and its inscribed tetrahedron; D) a coordinate system is set up to establish the Z-curve theory.

To further the study, a coordinate system needs to be established (Fig. 2D). The line connecting the middle point of an edge and that of the opposite edge of the tetrahedron is called the middle line. There are a total of three middle lines in a tetrahedron, crossing at the center O, and they are perpendicular to each other. A Cartesian coordinate system OXYZ can be set up by using the three middle lines, as shown in (Fig. 2D).

Thus, the cube-tetrahedron geometric entity established here correctly reflects the symmetry of the four DNA bases.

2.2. The DNA Group

A regular tetrahedron is a geometric entity of high symmetry. All possible rotational motions which keep the tetrahedron fixed in the space form a group, called a tetrahedron group or T-group. As shown in (Fig. 2D), a tetrahedron group consists of 12 operational elements, which are described below.

I, i.e., the identity operation;

R_x, R_y and R_z, i.e., the 180° rotation along x, y and z axes, respectively;

R_A, R_C, R_G and R_T, i.e., the 120° rotation along AO, CO, GO and TO axes, respectively;

R²_A, R²_C, R²_G and R²_T, i.e., the 240° rotation along AO, CO, GO and TO axes, respectively.

A point with coordinates x, y and z will be transformed accordingly under the operational elements of the T-group. For example,

$\begin{array}{l}I:x\iff x,y\iff y,z\iff z;\\ R_x:x\iff x,y\iff -y,z\iff -z;\\ R_y:x\iff -x,y\iff y,z\iff -z;\\ R_z:x\iff -x,y\iff -y,z\iff z;\end{array}$

The transforms of x, y and z under the 12 operations of the T-group are listed in (Table 1). The four elements I, R_x, R_y and R_z form an invariant subgroup of the T-group, which is isomorphic to the Klein-4 group, or K4 group. The K4 group and its cosets exhaust the T-group. Therefore, all the 12 elements of the T-group can be divided into four classes, which are (I), (R_x,R_y, R_z), (R_A, R_C, R_G, R_T) and (R²_A, R²_C, R²_G, R²_T).

Table 1.

Twelve Elements of the DNA Group (A4 Group or the Tetrahedron Group).

Element	A4 Group	Tetrahedron Group
I	A     C     G     T	x        y        z
Rx	G     T     A     C	x       -y       -z
Ry	C     A     T     G	-x        y       -z
Rz	T     G     C     A	-x       -y        z
RA	A     T     C     G	z       x         y
RC	G     C     T     A	z      -x        -y
RG	T     A     G     C	-z       -x        y
RT	C     G     A     T	-z        x       -y
R2A	A     G     T     C	y       z        x
R2C	T     C     A     G	-y       -z        x
R2G	C     T     G     A	-y        z       -x
R2T	G     A     C     T	y       -z       -x

On the other hand, the set of all possible permutations of four objects forms a symmetric group, denoted by S₄. Among the 24 elements of the symmetric group S₄, the set of all 12 even permutations forms an invariant subgroup of S₄, referred to as the alternative group of order 4, denoted by A₄. The DNA group is defined as a particular A₄ group, in which the permuted objects are the four DNA bases A, C, G and T. According to the group theory, the T-group and A₄ group are isomorphic with each other. From the perspective of the abstract group, the T-group and the A₄ group are the same group, because they have the same group structure and matrix representation. The four bases A, C, G and T are assigned to the four vertices of the tetrahedron, as shown in (Fig. 2D).

The four characters A, C, G and T will be transformed accordingly under the 12 operational elements of the DNA group or the A₄ group. For example,

$\begin{array}{l}I:\text{A}\iff \text{A},\text{C}\iff \text{C},\text{G}\iff \text{G},\text{T}\iff \text{T};\\ R_x:\text{A}\iff \text{G},\text{C}\iff \text{T};\\ R_y:\text{A}\iff \text{C},\text{G}\iff T;\\ R_z:\text{A}\iff \text{T},\text{G}\iff \text{C}.\end{array}$

Biologically, the transform R_x is called transition, whereas the transform R_y and R_z are called transversion. Here R_z is termed as the complementary transform.

We have previously established that the T-group and the A₄ group are the same group [3], and thus their elements should have one-to-one corresponding relations, as shown in (Table 1). Both the A₄ group and the T-group are called the DNA group, which forms the basis of the Z-curve theory.

2.3. The Z-transform Formulas

Let the occurrence frequencies of the four bases, A, C, G and T in a DNA sequence be denoted by a, c, g and t, respectively. The normalized condition reads

$$a+c+g+t=1,$$ (1)

indicating that among the four real numbers a, c, g and t, only three of them are independent.

Suppose that X, Y and Z are the coordinates of a point P in the coordinate system shown in (Fig. 2D), which can be expressed by a linear combination of the four frequencies a, c, g and t, as follows

$$\{\begin{array}{l}X=a_{11}a+a_{12}c+a_{13}g+a_{14}t,\\ Y=b_{11}a+b_{12}c+b_{13}g+b_{14}t,\\ Z=c_{11}a+c_{12}c+c_{13}g+c_{14}t,\end{array}$$ (2)

where a₁₁, a₁₂, …, c₁₃, c₁₄ are real coefficients. Eqs. (2) can be re-written as a matrix form

$$\left(\begin{array}{l}X\\ Y\\ Z\end{array}\right)=\left(\begin{array}{l}{a}_{11}\begin{array}{c}\end{array}{a}_{12}\begin{array}{c}\end{array}\begin{array}{c}{a}_{13}\begin{array}{c}\end{array}{a}_{14}\end{array}\\ b_{11}\begin{array}{c}\end{array}{b}_{12}\begin{array}{c}\end{array}\begin{array}{c}{b}_{13}\begin{array}{c}\end{array}{b}_{14}\end{array}\\ c_{11}\begin{array}{c}\end{array}{c}_{12}\begin{array}{c}\end{array}\begin{array}{c}{c}_{13}\begin{array}{c}\end{array}{c}_{14}\end{array}\end{array}\right)\times \left(\begin{array}{l}a\\ c\\ g\\ t\end{array}\right)$$ (3)

The coordinates of the four vertices of the regular tetrahedron A, C, G and T are already known, and shown in (Table 2). Based on the 12 numbers in (Table 2), the 12 coefficients can be uniquely determined, and eqs. (3) becomes

Table 2.

Coordinates of the 4 Vertices of the Regular Tetrahe-dron ACGTa.

Coordinates	Vertices
	A	C	G	T
X		-		-
Y			-	-
Z		-	-

^aRefer to Fig. 2 (d) for the original coordinate system, where the height of the tetrahe-dron is 1. Consequently, the edge length of the tetrahedron is $\sqrt{6}/2$, and the edge length of the cube is $\sqrt{3}/2$.

$$\left(\begin{array}{l}X\\ Y\\ Z\end{array}\right)=\frac{\sqrt{3}}{4}\left(\begin{array}{l}1\begin{array}{c}\end{array}-1\begin{array}{c}\end{array}\begin{array}{c}\end{array}1\begin{array}{c}\end{array}-1\\ 1\begin{array}{c}\end{array}\begin{array}{c}\end{array}1\begin{array}{c}\end{array}-1\begin{array}{c}\end{array}-1\\ 1\begin{array}{c}\end{array}-1\begin{array}{c}\end{array}-1\begin{array}{c}\end{array}\begin{array}{c}\end{array}1\end{array}\right)\times \left(\begin{array}{l}a\\ c\\ g\\ t\end{array}\right).$$ (4a)

Equivalently, eqs. (4) may be re-written as

$$\{\begin{array}{l}X=\frac{\sqrt{3}}{4}\left[(a+g)-(c+t)\right],\\ Y=\frac{\sqrt{3}}{4}\left[(a+c)-(g+t)\right],\begin{array}{c}\end{array}X,\begin{array}{c}\end{array}Y,\begin{array}{c}\end{array}Z\in [-\frac{\sqrt{3}}{4}\\ Z=\frac{\sqrt{3}}{4}\left[(a+t)-(g+c)\right].\end{array},\begin{array}{c}\end{array}\frac{\sqrt{3}}{4}]$$ (4b)

Eqs. (4) are called the Z-transform formulas, which were first derived in 1991 by a totally different way [1]. The Z-transform formulas transform the four base frequencies into three coordinates of a point (called a mapping point) in a three-dimensional space. As previously indicated [1], for convenience, we introduced the reduced coordinate system x, y and z

$$\{\begin{array}{l}X=\frac{\sqrt{3}}{4}x,\\ Y=\frac{\sqrt{3}}{4}y,\\ Z=\frac{\sqrt{3}}{4}z,\end{array}$$ (5)

such that

$$\{\begin{array}{l}x=(a+g)-(c+t),\\ y=(a+c)-(g+t),\\ z=(a+t)-(g+c).\end{array}\begin{array}{c}\end{array}x,\begin{array}{c}\end{array}y,\begin{array}{c}\end{array}z\in [-1,\begin{array}{c}\end{array}1].$$ (6a)

In what follows, we always use the Z-transform formulas based on the reduced coordinate system eqs. (6), unless otherwise indicated. Equivalently, eqs. (6a) can be also re-written as a matrix form

$$\left(\begin{array}{l}x\\ y\\ z\end{array}\right)=\left(\begin{array}{l}1\begin{array}{c}\end{array}-1\begin{array}{c}\end{array}\begin{array}{c}\end{array}1\begin{array}{c}\end{array}-1\\ 1\begin{array}{c}\end{array}\begin{array}{c}\end{array}1\begin{array}{c}\end{array}-1\begin{array}{c}\end{array}-1\\ 1\begin{array}{c}\end{array}-1\begin{array}{c}\end{array}-1\begin{array}{c}\end{array}\begin{array}{c}\end{array}1\end{array}\right)\times \left(\begin{array}{l}a\\ c\\ g\\ t\end{array}\right).$$ (6b)

Letting

$$U=\left(\begin{array}{l}x\\ y\\ z\end{array}\right),\begin{array}{c}\end{array}V=\left(\begin{array}{l}a\\ c\\ g\\ t\end{array}\right),$$ (7)

and

$$Z=\left(\begin{array}{l}1\begin{array}{c}\end{array}-1\begin{array}{c}\end{array}\begin{array}{c}\end{array}1\begin{array}{c}\end{array}-1\\ 1\begin{array}{c}\end{array}\begin{array}{c}\end{array}1\begin{array}{c}\end{array}-1\begin{array}{c}\end{array}-1\\ 1\begin{array}{c}\end{array}-1\begin{array}{c}\end{array}-1\begin{array}{c}\end{array}\begin{array}{c}\end{array}1\end{array}\right),$$ (8a)

Equivalently, eqs. (6b) may be re-written with a simplified form

$$U=Z\times V.$$ (9)

The reverse equation of eqs. (6) is

$$\left(\begin{array}{l}a\\ c\\ g\\ t\end{array}\right)=\frac{1}{4}\times \left(\begin{array}{l}1\\ 1\\ 1\\ 1\end{array}\right)+\frac{1}{4}\times \left(\begin{array}{c}\begin{array}{l}\begin{array}{c}\end{array}1\begin{array}{c}\end{array}\begin{array}{c}\end{array}\begin{array}{c}1\end{array}\begin{array}{c}\end{array}\begin{array}{c}\end{array}1\\ -1\begin{array}{c}\end{array}\begin{array}{c}\end{array}1\begin{array}{c}\end{array}-1\\ \begin{array}{c}\end{array}1\begin{array}{c}\end{array}-1\begin{array}{c}\end{array}-1\\ -1\begin{array}{c}\end{array}-1\begin{array}{c}\end{array}\begin{array}{c}\end{array}1\end{array}\end{array}\right)\times \left(\begin{array}{l}x\\ y\\ z\end{array}\right)$$ (10)

It is shown that regardless of the values of x, y and z,$a+c+g+t\equiv 1$. In fact, it was shown in 1991 that the mapping point P (x, y, z), corresponding to a, c, g and t, is always situated within the tetrahedron ACGT shown in (Fig. 2D) [1].

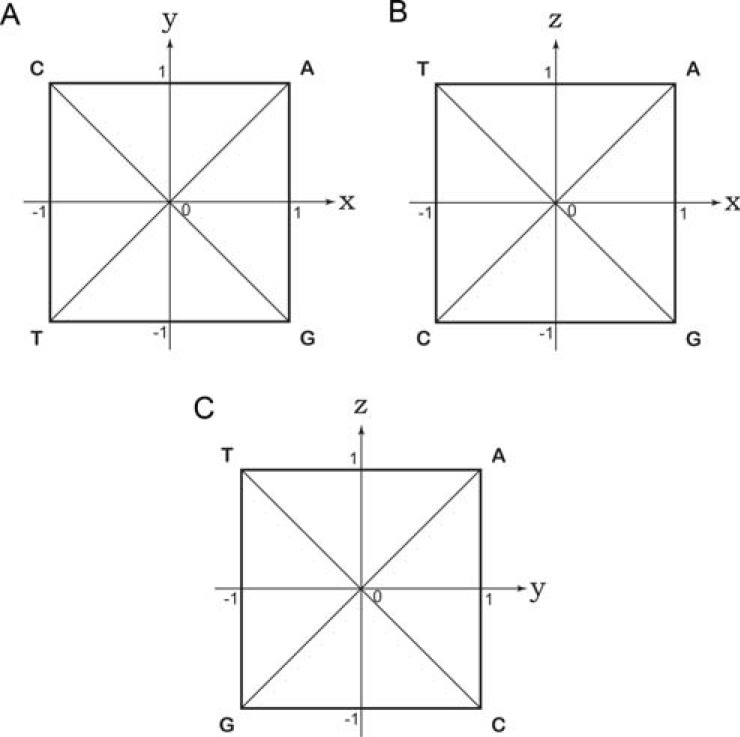
To provide a clear visualization, the tetrahedron and the mapping points within it are projected onto some coordinate planes. Referring to (Fig. 2C and D), note that the tetrahedron ACGT has 4 vertices A, C, G and T, and six edges AC, AG, AT, CG, CT and GT. Interestingly, the projection of six edges onto any coordinate plane forms a regular square and two diagonal lines within the square, where the projection of four vertices of the tetrahedron forms four vertices of the square, as shown in (Fig. 3A, B and C), for the x-y, x-z and y-z planes, respectively. Note that (Fig. 3A, B and C) are in accordance with (Fig. 1A, B and C), respectively. It should be noted that A, C, G and T are sometimes used to denote DNA bases, while the same symbols can represent vertices of the tetrahedron or squares. Refer to (Fig. 3A) first. Projections of four edges AG, AC, CT and GT form the four sides of the square, whereas those of AT and GC form the two diagonal lines of the square. Based on the Z-transform formulas eqs. (6), the base composition of a DNA sequence, i.e., the values of a, c, g and t, can be visualized by observing the position of the mapping point in the square. For example, if the DNA sequence has only one kind of base, say, A, then a = 1, c = g = t = 0. The corresponding mapping point is situated at the vertex A in (Fig. 2A). Similar results for (Fig. 3A) are summarized as follows.

Fig. (3).

Projection of the 3-D coordinates onto planes. The projection of the 3-D coordinate system onto the A) x-y, B) x-z and C) y-z planes.

$\begin{array}{l}VertexA:a=1,\begin{array}{c}\end{array}c=g=t=0; VertexC:c=1,\begin{array}{c}\end{array}a=g=t=0;\\ VertexG:g=1,\begin{array}{c}\end{array}a=c=t=0; VertexT:t=1,\begin{array}{c}\end{array}a=c=g=0;\\ SideAG:a+g=1,\begin{array}{c}\end{array}c=t=0; SideGT:g+t=1,\begin{array}{c}\end{array}a=c=0;\\ SideTC: c+t=1,\begin{array}{c}\end{array}a=g=0;SideCA:a+c=1,\begin{array}{c}\end{array}g=t=0;\\ x>0,\begin{array}{c}\end{array}a+g>1/2;x=0,\begin{array}{c}\end{array}a+g=1/2;x<0,\begin{array}{c}\end{array}a+g<1/2;\\ y>0,\begin{array}{c}\end{array}a+c>1/2;y=0,\begin{array}{c}\end{array}a+c=1/2;y<0,\begin{array}{c}\end{array}a+c<1/2;\\ Firstquadrant:a+g>1/2\begin{array}{c}\end{array}\text{and}\begin{array}{c}\end{array}a+c>1/2;\\ Secondquadrant:c+t>1/2\begin{array}{c}\end{array}\text{and}\begin{array}{c}\end{array}a+c>1/2;\\ Thirdquadrant:c+t>1/2\begin{array}{c}\end{array}\text{and}\begin{array}{c}\end{array}g+t>1/2;\\ Fourthquadrant:a+g>1/2\begin{array}{c}\end{array}\text{and}\begin{array}{c}\end{array}g+t>1/2;\\ DiagonalAOT: g=c;\Delta \text{AGT:}\begin{array}{c}\end{array}g>c;\Delta \text{ATC:}\begin{array}{c}\end{array}c>g;\\ DiagonalCOG: a=t; \Delta AGC: a >t; \Delta \text{CTG:}\begin{array}{c}\end{array}t>a;\\ \Delta \text{AOG:}\begin{array}{c}\end{array}a>t\begin{array}{c}\end{array}\text{and}\begin{array}{c}\end{array}g>c;\Delta \text{AOC:}\begin{array}{c}\end{array}a>t\begin{array}{c}\end{array}\text{and}\begin{array}{c}\end{array}c>g;\\ \Delta \text{COT:}\begin{array}{c}\end{array}t>a\begin{array}{c}\end{array}\text{and}\begin{array}{c}\end{array}c>g;\Delta \text{GOT:}\begin{array}{c}\end{array}t>a\begin{array}{c}\end{array}\text{and}\begin{array}{c}\end{array}g>c;\\ OriginO:a=c=g=t=1/4.\end{array}$

Similar deductions for the annotation of (Fig. 3B and C) are left out for readers who might be interested in doing so.

2.4. Linear Representation of the DNA Group

Based on the reduced coordinate system, the coordinates of the four vertices A, C, G and T can be represented by

$$(A)=\left(\begin{array}{l}1\\ 1\\ 1\end{array}\right),\begin{array}{c}\end{array}\begin{array}{c}C=\end{array}\left(\begin{array}{l}-1\\ \begin{array}{c}\end{array}1\\ -1\end{array}\right),\begin{array}{c}\end{array}(G)=\left(\begin{array}{l}\begin{array}{c}\end{array}1\\ -1\\ -1\end{array}\right),\begin{array}{c}\end{array}T=\left(\begin{array}{l}-1\\ -1\\ \begin{array}{c}\end{array}1\end{array}\right)$$ (11)

We previously established the linear representation of the DNA group, i.e., the tetrahedron group or the alternative group A₄ in 1997 [3]. For readers’ convenience, here we re-write the result (see eqs. (6) in [3] as follows:

$$\begin{array}{l}I=\left(\begin{array}{l}1\begin{array}{c}\end{array}\begin{array}{c}\end{array}0\begin{array}{c}\end{array}\begin{array}{c}\end{array}0\\ 0\begin{array}{c}\end{array}\begin{array}{c}\end{array}1\begin{array}{c}\end{array}\begin{array}{c}\end{array}0\\ 0\begin{array}{c}\end{array}\begin{array}{c}\end{array}0\begin{array}{c}\end{array}\begin{array}{c}\end{array}1\end{array}\right),R_x=\left(\begin{array}{l}1\begin{array}{c}\end{array}\begin{array}{c}\end{array}0\begin{array}{c}\end{array}\begin{array}{c}\end{array}0\\ 0\begin{array}{c}\end{array}-1\begin{array}{c}\end{array}\begin{array}{c}\end{array}0\\ 0\begin{array}{c}\end{array}\begin{array}{c}\end{array}0\begin{array}{c}\end{array}\begin{array}{c}-\end{array}1\end{array}\right),R_y=\left(\begin{array}{l}-1\begin{array}{c}\end{array}0\begin{array}{c}\end{array}\begin{array}{c}\end{array}0\\ 0\begin{array}{c}\end{array}\begin{array}{c}\end{array}1\begin{array}{c}\end{array}\begin{array}{c}\end{array}0\\ 0\begin{array}{c}\end{array}\begin{array}{c}\end{array}0\begin{array}{c}\end{array}\begin{array}{c}-\end{array}1\end{array}\right),R_z=\left(\begin{array}{l}-1\begin{array}{c}\end{array}\begin{array}{c}\end{array}0\begin{array}{c}\end{array}\begin{array}{c}\end{array}0\\ \begin{array}{c}\end{array}0\begin{array}{c}\end{array}-1\begin{array}{c}\end{array}\begin{array}{c}\end{array}0\\ \begin{array}{c}\end{array}0\begin{array}{c}\end{array}\begin{array}{c}\end{array}0\begin{array}{c}\end{array}\begin{array}{c}\end{array}1\end{array}\right)\\ R_A=\left(\begin{array}{l}0\begin{array}{c}\end{array}\begin{array}{c}\end{array}0\begin{array}{c}\end{array}\begin{array}{c}\end{array}1\\ 1\begin{array}{c}\end{array}\begin{array}{c}\end{array}0\begin{array}{c}\end{array}\begin{array}{c}\end{array}0\\ 0\begin{array}{c}\end{array}\begin{array}{c}\end{array}1\begin{array}{c}\end{array}\begin{array}{c}\end{array}0\end{array}\right),R_C=\left(\begin{array}{l}\begin{array}{c}\end{array}0\begin{array}{c}\end{array}\begin{array}{c}\end{array}0\begin{array}{c}\end{array}\begin{array}{c}\end{array}1\\ -\begin{array}{c}1\end{array}\begin{array}{c}\end{array}\begin{array}{c}\end{array}0\begin{array}{c}\end{array}\begin{array}{c}\end{array}0\\ \begin{array}{c}\end{array}0\begin{array}{c}\end{array}\begin{array}{c}-\end{array}1\begin{array}{c}\end{array}\begin{array}{c}\begin{array}{c}\end{array}\end{array}0\end{array}\right),R_G=\left(\begin{array}{l}\begin{array}{c}\end{array}0\begin{array}{c}\end{array}\begin{array}{c}\end{array}0\begin{array}{c}\end{array}\begin{array}{c}-\end{array}1\\ \begin{array}{c}-\end{array}1\begin{array}{c}\end{array}\begin{array}{c}\end{array}0\begin{array}{c}\end{array}\begin{array}{c}\end{array}0\\ \begin{array}{c}\end{array}\begin{array}{c}0\begin{array}{c}\end{array}\end{array}\begin{array}{c}\end{array}\begin{array}{c}1\end{array}\begin{array}{c}\end{array}\begin{array}{c}\end{array}0\end{array}\right),R_T=\left(\begin{array}{l}0\begin{array}{c}\end{array}\begin{array}{c}\end{array}0\begin{array}{c}\end{array}\begin{array}{c}-\end{array}1\\ \begin{array}{c}1\end{array}\begin{array}{c}\end{array}\begin{array}{c}\end{array}\begin{array}{c}0\end{array}\begin{array}{c}\end{array}\begin{array}{c}\end{array}0\\ 0\begin{array}{c}\end{array}\begin{array}{c}-\end{array}1\begin{array}{c}\end{array}\begin{array}{c}\end{array}0\end{array}\right)\\ R_A^2=\left(\begin{array}{l}0\begin{array}{c}\end{array}\begin{array}{c}\end{array}1\begin{array}{c}\end{array}\begin{array}{c}\end{array}0\\ 0\begin{array}{c}\end{array}\begin{array}{c}\end{array}0\begin{array}{c}\end{array}\begin{array}{c}\end{array}1\\ 1\begin{array}{c}\end{array}\begin{array}{c}\end{array}0\begin{array}{c}\end{array}\begin{array}{c}\end{array}0\end{array}\right),R_C^2=\left(\begin{array}{l}0\begin{array}{c}\end{array}\begin{array}{c}-\end{array}1\begin{array}{c}\end{array}\begin{array}{c}\end{array}0\\ 0\begin{array}{c}\end{array}\begin{array}{c}\end{array}0\begin{array}{c}\end{array}\begin{array}{c}-\end{array}1\\ 1\begin{array}{c}\end{array}\begin{array}{c}\end{array}0\begin{array}{c}\end{array}\begin{array}{c}\end{array}0\end{array}\right),R_G^2=\left(\begin{array}{l}\begin{array}{c}\end{array}0\begin{array}{c}\end{array}-1\begin{array}{c}\end{array}\begin{array}{c}\end{array}0\\ \begin{array}{c}\end{array}0\begin{array}{c}\end{array}\begin{array}{c}\end{array}0\begin{array}{c}\end{array}\begin{array}{c}\end{array}1\\ -\begin{array}{c}1\end{array}\begin{array}{c}\end{array}\begin{array}{c}\end{array}0\begin{array}{c}\end{array}\begin{array}{c}\end{array}0\end{array}\right),R_T^2=\left(\begin{array}{l}\begin{array}{c}\end{array}\begin{array}{c}0\end{array}\begin{array}{c}\end{array}\begin{array}{c}\end{array}1\begin{array}{c}\end{array}\begin{array}{c}\end{array}0\\ \begin{array}{c}\end{array}0\begin{array}{c}\end{array}\begin{array}{c}\end{array}0\begin{array}{c}\end{array}\begin{array}{c}-\end{array}1\\ \begin{array}{c}-\end{array}1\begin{array}{c}\end{array}\begin{array}{c}\end{array}0\begin{array}{c}\end{array}\begin{array}{c}\end{array}0\end{array}\right)\end{array}$$ (12)

This matrix representation depicts correct relationships among the 12 elements of the DNA group. For example, a rotation of 180° along the x-axis in (Fig. 2D), followed by another similar rotation, leads to the original state, i.e.,

$$R_x\times R_x=I\begin{array}{c}\end{array}\iff \left(\begin{array}{l}1\begin{array}{c}\end{array}\begin{array}{c}\end{array}0\begin{array}{c}\end{array}\begin{array}{c}\end{array}0\\ 0\begin{array}{c}\end{array}-1\begin{array}{c}\end{array}\begin{array}{c}\end{array}0\\ 0\begin{array}{c}\end{array}\begin{array}{c}\end{array}0\begin{array}{c}\end{array}\begin{array}{c}-\end{array}1\end{array}\right)\times \left(\begin{array}{l}1\begin{array}{c}\end{array}\begin{array}{c}\end{array}0\begin{array}{c}\end{array}\begin{array}{c}\end{array}0\\ 0\begin{array}{c}\end{array}-1\begin{array}{c}\end{array}\begin{array}{c}\end{array}0\\ 0\begin{array}{c}\end{array}\begin{array}{c}\end{array}0\begin{array}{c}\end{array}\begin{array}{c}-\end{array}1\end{array}\right)=\left(\begin{array}{l}1\begin{array}{c}\end{array}\begin{array}{c}\end{array}0\begin{array}{c}\end{array}\begin{array}{c}\end{array}0\\ 0\begin{array}{c}\end{array}\begin{array}{c}\end{array}1\begin{array}{c}\end{array}\begin{array}{c}\end{array}0\\ 0\begin{array}{c}\end{array}\begin{array}{c}\end{array}0\begin{array}{c}\end{array}\begin{array}{c}\end{array}1\end{array}\right)=I$$ (13)

That is to say, the matrix representation not only results in a one-to-one correspondence among elements of the DNA group, but also correctly reflects their relations based on the multiplication of matrices.

In the following, we show that the transform matrix (3x4) eq. (8a) and its variants also constitute a one-to-one representation to each element of the DNA group. For this purpose, eq. (8a) can be re-written as

$$Z=\left(\begin{array}{l}1\begin{array}{c}\end{array}-1\begin{array}{c}\end{array}\begin{array}{c}\end{array}1\begin{array}{c}\end{array}-1\\ 1\begin{array}{c}\end{array}\begin{array}{c}\end{array}1\begin{array}{c}\end{array}-1\begin{array}{c}\end{array}-1\\ 1\begin{array}{c}\end{array}-1\begin{array}{c}\end{array}-1\begin{array}{c}\end{array}\begin{array}{c}\end{array}1\end{array}\right)=\left(\begin{array}{l}\\ (A)\begin{array}{c}\end{array}(C)\begin{array}{c}\end{array}(G)\begin{array}{c}\end{array}(T)\\ \end{array}\right),$$ (8b)

where (A), (C), (G) and (T) are denoted by eqs. (11). Referring to (Table 2), we find that the order of the four nucleotides above correspond to the element I of the A₄ group. Similarly, its 11 variants can be derived, and are listed as follows

$$\begin{array}{l}{Z}_I=\left(\begin{array}{l}1\begin{array}{c}\end{array}-1\begin{array}{c}\end{array}\begin{array}{c}\end{array}1\begin{array}{c}\end{array}-1\\ 1\begin{array}{c}\end{array}\begin{array}{c}\end{array}1\begin{array}{c}\end{array}-1\begin{array}{c}\end{array}-1\\ 1\begin{array}{c}\end{array}-1\begin{array}{c}\end{array}-1\begin{array}{c}\end{array}\begin{array}{c}\end{array}1\end{array}\right),Z_x=\left(\begin{array}{l}\begin{array}{c}\end{array}1\begin{array}{c}\end{array}-1\begin{array}{c}\end{array}\begin{array}{c}\end{array}1\begin{array}{c}\end{array}-1\\ -1\begin{array}{c}\end{array}\begin{array}{c}-\end{array}1\begin{array}{c}\begin{array}{c}\end{array}\begin{array}{c}\end{array}\end{array}1\begin{array}{c}\end{array}\begin{array}{c}\end{array}1\\ -1\begin{array}{c}\end{array}\begin{array}{c}\end{array}1\begin{array}{c}\end{array}\begin{array}{c}\end{array}1\begin{array}{c}\end{array}\begin{array}{c}-\end{array}1\end{array}\right),Z_y=\left(\begin{array}{l}-1\begin{array}{c}\end{array}\begin{array}{c}\end{array}1\begin{array}{c}\end{array}\begin{array}{c}-\end{array}1\begin{array}{c}\end{array}\begin{array}{c}\end{array}1\\ \begin{array}{c}\end{array}1\begin{array}{c}\end{array}\begin{array}{c}\end{array}1\begin{array}{c}\end{array}-1\begin{array}{c}\end{array}-1\\ -1\begin{array}{c}\end{array}\begin{array}{c}\end{array}1\begin{array}{c}\end{array}\begin{array}{c}\end{array}1\begin{array}{c}\end{array}\begin{array}{c}-\end{array}1\end{array}\right),\\ Z_z=\left(\begin{array}{l}-1\begin{array}{c}\end{array}\begin{array}{c}\end{array}1\begin{array}{c}\end{array}-1\begin{array}{c}\end{array}\begin{array}{c}\end{array}1\\ -1\begin{array}{c}\end{array}\begin{array}{c}-\end{array}1\begin{array}{c}\end{array}\begin{array}{c}\end{array}1\begin{array}{c}\end{array}\begin{array}{c}\end{array}1\\ \begin{array}{c}\end{array}1\begin{array}{c}\end{array}-1\begin{array}{c}\end{array}-1\begin{array}{c}\end{array}\begin{array}{c}\end{array}1\end{array}\right),Z_A=\left(\begin{array}{l}1\begin{array}{c}\end{array}-1\begin{array}{c}\end{array}\begin{array}{c}-\end{array}1\begin{array}{c}\end{array}\begin{array}{c}\end{array}1\\ 1\begin{array}{c}\end{array}\begin{array}{c}-\end{array}1\begin{array}{c}\end{array}\begin{array}{c}\end{array}1\begin{array}{c}\end{array}-1\\ 1\begin{array}{c}\end{array}\begin{array}{c}\end{array}1\begin{array}{c}\end{array}-1\begin{array}{c}\end{array}\begin{array}{c}-\end{array}1\end{array}\right),Z_C=\left(\begin{array}{l}\begin{array}{c}\end{array}1\begin{array}{c}\end{array}-1\begin{array}{c}\end{array}\begin{array}{c}-\end{array}1\begin{array}{c}\end{array}\begin{array}{c}\end{array}1\\ \begin{array}{c}-\end{array}1\begin{array}{c}\end{array}\begin{array}{c}\end{array}1\begin{array}{c}\begin{array}{c}\end{array}\begin{array}{c}-\end{array}\end{array}1\begin{array}{c}\end{array}\begin{array}{c}\end{array}1\\ \begin{array}{c}-\end{array}1\begin{array}{c}\end{array}\begin{array}{c}-\end{array}1\begin{array}{c}\end{array}\begin{array}{c}\end{array}1\begin{array}{c}\end{array}\begin{array}{c}\end{array}1\end{array}\right),\\ Z_G=\left(\begin{array}{l}-1\begin{array}{c}\end{array}\begin{array}{c}\end{array}1\begin{array}{c}\end{array}\begin{array}{c}\end{array}1\begin{array}{c}\end{array}\begin{array}{c}-\end{array}1\\ -1\begin{array}{c}\end{array}\begin{array}{c}\begin{array}{c}\end{array}\end{array}1\begin{array}{c}\end{array}\begin{array}{c}-\end{array}1\begin{array}{c}\end{array}\begin{array}{c}\end{array}1\\ \begin{array}{c}\end{array}1\begin{array}{c}\end{array}\begin{array}{c}\end{array}1\begin{array}{c}\end{array}-1\begin{array}{c}\end{array}\begin{array}{c}-\end{array}1\end{array}\right),Z_T=\left(\begin{array}{l}-1\begin{array}{c}\end{array}\begin{array}{c}\end{array}1\begin{array}{c}\end{array}\begin{array}{c}\end{array}1\begin{array}{c}\end{array}\begin{array}{c}-\end{array}1\\ \begin{array}{c}\end{array}1\begin{array}{c}\end{array}\begin{array}{c}-\end{array}1\begin{array}{c}\end{array}\begin{array}{c}\end{array}1\begin{array}{c}\end{array}-1\\ -1\begin{array}{c}\end{array}\begin{array}{c}-\end{array}1\begin{array}{c}\end{array}\begin{array}{c}\end{array}1\begin{array}{c}\end{array}\begin{array}{c}\end{array}1\end{array}\right),Z_A^2=\left(\begin{array}{l}1\begin{array}{c}\end{array}\begin{array}{c}\end{array}1\begin{array}{c}\end{array}\begin{array}{c}-\end{array}1\begin{array}{c}\end{array}-1\\ 1\begin{array}{c}\end{array}\begin{array}{c}-\end{array}1\begin{array}{c}\end{array}-1\begin{array}{c}\end{array}\begin{array}{c}\end{array}1\\ 1\begin{array}{c}\end{array}-1\begin{array}{c}\end{array}\begin{array}{c}\end{array}1\begin{array}{c}\end{array}\begin{array}{c}-\end{array}1\end{array}\right),\\ Z_C^2=\left(\begin{array}{l}-1\begin{array}{c}\end{array}\begin{array}{c}-\end{array}1\begin{array}{c}\end{array}\begin{array}{c}\end{array}1\begin{array}{c}\end{array}\begin{array}{c}\end{array}1\\ -1\begin{array}{c}\end{array}\begin{array}{c}\end{array}1\begin{array}{c}\end{array}\begin{array}{c}\end{array}1\begin{array}{c}\end{array}\begin{array}{c}-\end{array}1\\ \begin{array}{c}\end{array}1\begin{array}{c}\end{array}-1\begin{array}{c}\end{array}\begin{array}{c}\end{array}1\begin{array}{c}\end{array}\begin{array}{c}-\end{array}1\end{array}\right),Z_G^2=\left(\begin{array}{l}-1\begin{array}{c}\end{array}\begin{array}{c}-\end{array}1\begin{array}{c}\end{array}\begin{array}{c}\end{array}1\begin{array}{c}\end{array}\begin{array}{c}\end{array}1\\ \begin{array}{c}\end{array}1\begin{array}{c}\end{array}\begin{array}{c}-\end{array}1\begin{array}{c}\end{array}\begin{array}{c}-\end{array}1\begin{array}{c}\end{array}\begin{array}{c}\end{array}1\\ -1\begin{array}{c}\end{array}\begin{array}{c}\end{array}1\begin{array}{c}\end{array}\begin{array}{c}-\end{array}1\begin{array}{c}\end{array}\begin{array}{c}\end{array}1\end{array}\right),Z_T^2=\left(\begin{array}{l}\begin{array}{c}\end{array}1\begin{array}{c}\end{array}\begin{array}{c}\end{array}1\begin{array}{c}\end{array}\begin{array}{c}-\end{array}1\begin{array}{c}\end{array}-1\\ -1\begin{array}{c}\end{array}\begin{array}{c}\end{array}1\begin{array}{c}\begin{array}{c}\end{array}\begin{array}{c}\end{array}\end{array}1\begin{array}{c}\end{array}\begin{array}{c}-\end{array}1\\ -1\begin{array}{c}\end{array}\begin{array}{c}\end{array}1\begin{array}{c}\end{array}\begin{array}{c}-\end{array}1\begin{array}{c}\end{array}\begin{array}{c}\end{array}1\end{array}\right),\end{array}$$ (14)

where Z_I = Z. Based on the 12 Z matrices, we have

$$Z_i\times V=R_i\times U,\begin{array}{cc}& \end{array}i=I,\begin{array}{c}\end{array}x,\begin{array}{c}\end{array}y,\begin{array}{c}\end{array}z,\begin{array}{c}\end{array}A,\begin{array}{c}\end{array}C,\begin{array}{c}\end{array}G,\begin{array}{c}\end{array}T,\begin{array}{c}\end{array}{A}^2,\begin{array}{c}\end{array}{C}^2,\begin{array}{c}\end{array}{G}^2,\begin{array}{c}\end{array}{T}^2.$$ (15)

Note that each Z_i corresponds to each R_i by a way of one-to-one correspondence. Therefore, the Z matrix also constitutes a representation of the DNA group in this sense. However, it is not an ordinary representation of the DNA group, because the similar multiplication relation such as eq. (13) does not exist among the Z matrices.

It should also be noted that the Z-transform formulas eqs. (6), which transform the nucleotide frequencies into the coordinates of a point in a three-dimensional space, are unique and invariant under the operations of the DNA group. The Z-transform formulas shown in eqs. (6) represent the unique set of equations which reflect the inherent features of the DNA group. The Z-transform formulas are the core of the Z-curve theory.

2.5. The Z-transform Formulas for Studying Correlations of Multiple Nucleotides

To extract features of a given DNA sequence, in addition to considering occurrence frequencies of a single nucleotide, correlations of multiple nucleotides should also be considered. Therefore, the Z-transform formulas should be extended to consider the correlations of multiple nucleotides.

The case of a single nucleotide

$$\left(\begin{array}{l}x\\ y\\ z\end{array}\right)=Z\times \left(\begin{array}{l}p(A)\\ p(C)\\ p(G)\\ p(T)\end{array}\right),\begin{array}{c}\end{array}a=p(A),\begin{array}{c}\end{array}c=p(C),\begin{array}{c}\end{array}g=p(G),\begin{array}{c}\end{array}t=p(T).$$ (16)

Eqs. (16) are equivalent to eqs. (9). Here we have 3 (= 3x4°) parameters.

The case of di-nucleotides

$$\left(\begin{array}{l}{x}_H\\ y_H\\ z_H\end{array}\right)=Z\times \left(\begin{array}{l}p(HA)\\ p(HC)\\ p(HG)\\ p(HT)\end{array}\right),\begin{array}{c}\end{array}H=A,\begin{array}{c}\end{array}C,\begin{array}{c}\end{array}G,\begin{array}{c}\end{array}T,$$ (17)

where p(HA) represents occurrence frequencies of the di-nucleotide HA, and so forth. Here we have 12 (=3x4¹)parameters.

The case of tri-nucleotides

$$\left(\begin{array}{l}{x}_{HI}\\ y_{HI}\\ z_{HI}\end{array}\right)=Z\times \left(\begin{array}{l}p(HIA)\\ p(HIC)\\ p(HIG)\\ p(HIT)\end{array}\right),H,I=A,\begin{array}{c}\end{array}C,\begin{array}{c}\end{array}G,\begin{array}{c}\end{array}T,$$ (18)

where p(HIA) represents occurrence frequencies of the tri-nucleotide HIA, and so forth. Here we have 48 (=3x4²) parameters.

The case of tetra-nucleotides

$$\left(\begin{array}{l}{x}_{HIJ}\\ y_{HIJ}\\ z_{HIJ}\end{array}\right)=Z\times \left(\begin{array}{l}p(HIJA)\\ p(HIJC)\\ p(HIJG)\\ p(HIJT)\end{array}\right),\begin{array}{c}\end{array}H,I,J=A,\begin{array}{c}\end{array}C,\begin{array}{c}\end{array}G,\begin{array}{c}\end{array}T,$$ (19)

where p(HIJA) represents occurrence frequencies of the four-nucleotide HIJA, and so forth. Here we have 192 (=3x4³) parameters.

The case of penta-nucleotides

$$\left(\begin{array}{l}{x}_{HIJK}\\ y_{HIJK}\\ z_{HIJK}\end{array}\right)=Z\times \left(\begin{array}{l}p(HIJKA)\\ p(HIJKC)\\ p(HIJKG)\\ p(HIJKT)\end{array}\right),\begin{array}{c}\end{array}H,I,J,K=A,\begin{array}{c}\end{array}C,\begin{array}{c}\end{array}G,\begin{array}{c}\end{array}T,$$ (20)

where p(HIJKA) represents occurrence frequencies of the five-nucleotide HIJKA, and so forth. Here we have 768 (=3x4⁴) parameters.

The case of hexa-nucleotides

$$\left(\begin{array}{l}{x}_{HIJKL}\\ y_{HIJKL}\\ z_{HJIKL}\end{array}\right)=Z\times \left(\begin{array}{l}p(HIJKLA)\\ p(HIJKLC)\\ p(HIJKLG)\\ p(HIJKLT)\end{array}\right),\begin{array}{c}\end{array}H,I,J,K,L=A,\begin{array}{c}\end{array}C,\begin{array}{c}\end{array}G,\begin{array}{c}\end{array}T,$$ (21)

where p(HIJKLA) represents occurrence frequencies of the six-nucleotide HIJKLA, and so forth. Here we have 3072 (=3x4⁵) parameters.

To calculate the occurrence frequencies of multiple nucleotides for a given DNA sequence, we use a moving window with size = 1, 2, 3, 4, 5 and 6. Starting from the first nucleotide or base, move the sliding window rightward one base at a time, and then the frequencies can be calculated. Substitute the frequencies into eqs. (16) to (21), and then the Z-curve parameters can be obtained. For some applications, eq. (16), i.e., 3 parameters are sufficient. However, in some cases, more parameters are needed. The space spanned by the 3 parameters is denoted by V₁, and similarly we have V₂, V₃, V₄, V₅ and V₆, respectively, corresponding to eqs. (16) to (21). Usually, the direct sum among different spaces is needed. For most applications, there are six possible choices

$$\text{V}=\left(\begin{array}{l}{\text{V}}_{\text{1}},\\ {\text{V}}_{\text{1}}\oplus {\text{V}}_{\text{2}},\\ {\text{V}}_{\text{1}}\oplus {\text{V}}_{\text{2}}\oplus {\text{V}}_{\text{3}},\\ {\text{V}}_{\text{1}}\oplus {\text{V}}_{\text{2}}\oplus {\text{V}}_{\text{3}}\oplus {\text{V}}_{\text{4}},\\ {\text{V}}_{\text{1}}\oplus {\text{V}}_{\text{2}}\oplus {\text{V}}_{\text{3}}\oplus {\text{V}}_{\text{4}}\oplus {\text{V}}_{\text{5}},\\ {\text{V}}_{\text{1}}\oplus {\text{V}}_{\text{2}}\oplus {\text{V}}_{\text{3}}\oplus {\text{V}}_{\text{4}}\oplus {\text{V}}_{\text{5}}\oplus {\text{V}}_{\text{6}},\end{array}\right)$$ (22)

where the symbol ⊕ represents the direct sum of two spaces. The dimensions of the spaces V₁ to V₆ are 3, 15 (= 3+12), 63 (= 15+48), 255 (= 63+192), 1023 (= 255+768) and 4095 (= 1023+3072), respectively. Generally, for the space$\text{V}={\text{V}}_{\text{1}}\oplus {\text{V}}_{\text{2}}\oplus \mathrm{...}\oplus {\text{V}}_{\text{m}}$, the dimension is

2.6. Quadratic Form of x, y and z

Starting from eq. (9)

$$U=Z\times V,$$ (9)

We have

$$U^T=V^T\times Z^T$$ (23)

where “T” means the transpose operation of a matrix. Furthermore, we find

$$U^T\times U=V^T\times Z^T\times Z\times V.$$ (24)

Simple derivation shows that

$$x^2+y^2+z^2=4S-1,$$ (25)

where S is defined by

$$S=a^2+c^2+g^2+t^2.$$ (26)

S, named as “genome order index” [7], is useful for designing a fast genome segmentation algorithm [8, 9]. We also observed that for most genomes

$$S<1/3$$ (27)

Eq. (27) has a clear geometrical explanation. The surface of the inscribed sphere is described by the equation

$$x^2+y^2+z^2={\left(\frac{1}{\sqrt{3}}\right)}^2=\frac{1}{3}.$$ (28)

Therefore, S<1/3 implies that the mapping point is within the inscribed sphere [7].

2.7. The Z-curve

One of the most important applications of the Z-transform formulas is to derive the equation of the Z-curve. Consider a DNA sequence with N bases that are inspected one base at a time. From the first base to the n^th base, compute accumulative numbers of the bases A, C, G and T, denoted by A_n, C_n, G_n and T_n, respectively. Based on the Z-transform formulas eqs (6), we find

$$\left(\begin{array}{l}x(n)\\ y(n)\\ z(n)\end{array}\right)=Z\times \left(\begin{array}{l}{A}_n/n\\ C_n/n\\ G_n/n\\ T_n/n\end{array}\right).$$ (29)

Multiplied by n to both hands of eq. (29), and letting

$$x_n=n\times x(n),\begin{array}{c}\end{array}{y}_n=n\times y(n),\begin{array}{c}\end{array}{z}_n=n\times z(n),$$ (30)

we have

$$\left(\begin{array}{l}{x}_n\\ y_n\\ z_n\end{array}\right)=Z\times \left(\begin{array}{l}{A}_n\\ C_n\\ G_n\\ T_n\end{array}\right)$$ (31a)

or equivalently

$$\{\begin{array}{l}{x}_n=(A_n+G_n)-(C_n+T_n),\\ y_n=(A_n+C_n)-(G_n+T_n),\\ z_n=(A_n+T_n)-(G_n+C_n),\end{array}n=0,\begin{array}{c}\end{array}1,\begin{array}{c}\end{array}2,\begin{array}{c}\end{array}3,\mathrm{....},\begin{array}{c}\end{array}N,\begin{array}{c}\end{array}{x}_x,y_n,z_n\in [-N,N],$$ (31b)

which was first derived in 1994 by an entirely different method [2]. It should be noted that A_n, C_n, G_n and T_n are the cumulative occurrence numbers of A, C, G and T, respectively, in the sub-sequence from the 1^st base to the nth base in the sequence with length N. We define A₀=C₀=G₀=T₀=0, therefore, x₀ = y₀ = z₀ = 0. The Z-curve is defined as the connection of the nodes P₀ (x₀, y₀, z₀), , P₂ (x₂, y₂, z₂), …, P_N(x_N, y_N, z_N) one by one sequentially with straight lines. The connection results in a curve with a zigzag shape, hence the name Z-curve. Note that the Z-curve always starts from the origin of the three-dimensional coordinate system. Once the coordinates x_n, y_n and z_n (n = 1, 2, …, N) of a Z-curve are given, the corresponding DNA sequence can be reconstructed uniquely from the so-called inverse Z-transform formulas

$$\left(\begin{array}{c}{A}_n\\ C_n\\ G_n\\ T_n\end{array}\right)=\frac{n}{4}\times \left(\begin{array}{c}1\\ 1\\ 1\\ 1\end{array}\right)+\frac{1}{4}\times \left(\begin{array}{ccc}1& 1& 1\\ -1& 1& -1\\ 1& -1& -1\\ -1& -1& 1\end{array}\right)\times \left(\begin{array}{c}{x}_n\\ y_n\\ z_n\end{array}\right),\begin{array}{c}\end{array}n=1,\begin{array}{c}\end{array}2,\begin{array}{c}\end{array}\mathrm{...},\begin{array}{c}\end{array}N,$$ (32)

where the normalized relation of A_n + C_n + G_n + T_n = n is used.

The three components of the Z-curve, x_n, y_n and z_n, represent three independent distributions, that is, those of purine/pyrimidine (R/Y), amino/keto (M/K) and strong-H bond/weak-H bond (S/W) bases, respectively, and they completely describe the DNA sequence being studied. In the subsequence constituted from the 1^st base to the nth bases of the sequence, when purine bases (A/G) are in excess of pyrimidine bases (C/T), x_n > 0, otherwise, x_n < 0, and when the numbers of purine (A/G) and pyrimidine bases (C/T) are identical, x_n = 0. Similarly, when amino bases (A/C) are in excess of keto bases (G/T), y_n > 0, otherwise, y_n < 0, and when the numbers of amino (A/C) and keto bases (G/T) are identical, y_n = 0. Finally, when weak H-bond bases (A/T) are in excess of strong H-bond bases (G/C), z_n > 0, otherwise, z_n < 0, and when the numbers of (A/T) and (G/C) bases are identical, z_n = 0. The x_n and y_n components are termed RY and MK disparity curves, respectively. Similarly, the AT and GC disparity curves are defined by (x_n + y_n)/2 and (x_n-y_n)/2, which shows the excess of A over T and G over C, along the genome. The RY and MK disparity curves, as well as AT and GC disparity curves, can be used to predict replication origins of various genomes.

2.8. The GC Profile

For most genome sequences, Chargaff Parity Rule II holds, i.e.,$A_N\cong T_{N}and{C}_N\cong G_N$, where N is the length of a genome or a chromosome. According to eqs (31), we find

$$x_n\cong 0,y_n\cong 0,z_n>>1,\text{for}\begin{array}{c}\end{array}n>>1$$ (33)

Therefore, the curves of z_n ~ n are roughly straight lines in this case. To amplify the variations of the straight-line-like curve, the curve of z_n ~ n is firstly fitted by a straight line using the least square technique,

$$z=kn,$$ (34)

where (z, n) is the coordinate of a point on the fitted straight line and k is its slope. We define the z’ curve, where

$${z^{\prime }}_n=z_n-kn.$$ (35)

Therefore, the variations of z_n ~ n curve deviated from the straight line, which corresponds to a constant G+C content (see eq. (36) below), are protruded by the z’ curve. One may also use the average slope of the z_n ~ n curve to compute k, k = z_N / N, where z_N is the terminal coordinate of the z_n ~ n curve and N is the sequence length. The essence of the z’ curve is to display the variations of the G+C content along a genome or chromosome based on the cumulative count of G and C bases. Let $\overline{G+C}$ denote the average G+C content within a region Δn in a sequence, it was shown that [10].

$$\overline{\text{G}+\text{C}}=\frac{1}{2}(1-k-\frac{\Delta {z^{\prime }}_n}{\Delta n})\equiv \frac{1}{2}(1-k-k^{\prime }),$$ (36)

where is the average slope of the z’ curve within the region Δn. Both quantities of $\Delta {z^{\prime }}_n$ and Δn can be calculated by using the z’ curve. It is clear to see from eq. (36) that a jump in the z’ curve, i.e., $k\text{'}>0$, indicates a decrease of G+C content or an increase of A+T content, whereas a drop in the z’ curve, i.e., $k\text{'}<0$, indicates an increase of G+C content or a decrease of A+T content. The region Δn is usually chosen to be a fragment of a DNA sequence. The above method to calculate G+C content is called the windowless technique [10].

The GC profile is defined as$-{z^{\prime }}_{}$, because it is more intuitive in the sense that a jump denotes an increase in GC content. We emphasize the importance of the GC profile for genome studies, because it represents a windowless technique to calculate the G+C content along genome sequences.

2.9. A Segmentation Algorithm Based on the Z-transform

Let n be a point within a DNA sequence of length N$(2\le n\le N-1)$, which divides the whole sequence into two parts: the right and left sub-sequences, and then denote frequencies of bases in the right sub-sequence and left sub-sequence by (a_r, c_r, g_r, t_r) and (a_l, c₁, g₁, t₁), respectively. The frequencies are mapped onto two points, P_R (x_r, y_r, z_r) and P_L(x_l, y_l, z_l), in a 3-D space, where

$$\left(\begin{array}{l}{x}_i\\ y_i\\ z_i\end{array}\right)=\left(\begin{array}{l}1\begin{array}{c}\end{array}-1\begin{array}{c}\end{array}\begin{array}{c}\end{array}1\begin{array}{c}\end{array}-1\\ 1\begin{array}{c}\end{array}\begin{array}{c}\end{array}1\begin{array}{c}\end{array}-1\begin{array}{c}\end{array}-1\\ 1\begin{array}{c}\end{array}-1\begin{array}{c}\end{array}-1\begin{array}{c}\end{array}\begin{array}{c}\end{array}1\end{array}\right)\times \left(\begin{array}{l}{a}_i\\ c_i\\ g_i\\ t_i\end{array}\right),\begin{array}{cc}& \end{array}i=r,l.$$ (37)

The square of Euclidean distance between the two points is denoted by D, where

$$D(n)={(x_r-x_l)}^2+{(y_r-y_l)}^2+{(z_r-z_l)}^2$$ (38)

Substituting eqs. (37) into eq. (38), we have

$$D(n)=C\times [{(a_r-a_l)}^2+{(c_r-c_l)}^2+{(g_r-g_l)}^2+{(t_r-t_l)}^2]$$ (39)

where C is a constant. Note that D is a function of n. Suppose that when $n=n^{*}(2\le n^{*}\le N-1)D(n^{*})=\text{Maximun}$ Then the point $n^{*}$ is called a compositional segmentation point [8]. The segmentation algorithm is recursive, i.e., after n* is determined, the same procedure is applied to both the left and right sub-sequences recursively, until D(n) is less than a given threshold. For more details refer to [8].

Eq. (39) can be extended to the case of a binary sequence. For example, by replacing the bases G and C with S, and bases A and T with W, a DNA sequence can be transformed into a binary sequence of S and W. In this case, the algorithm results in compositional segmentation points according to GC content. A software, called GC-Profile, was developed to implement the algorithm for genome segmentation [9].

3. PART-2: APPLICATIONS IN GENOME ANALYSIS

The Z-curve theory has been successfully applied in many different research areas in analyzing genomes of bacteria, archaea, eukaryotes and viruses. The applications include, to name a few, the identifications of protein-coding genes, replication origins, horizontally-transferred genomic islands, isochore structures, genome segmentation points, promoters and translational start sites, as well as studies on nucleosome positioning, DNA curvature profiles, phylogenetics and comparative genomics, in various organisms (Table 3). It is not practical to cover all these areas in detail in a single review, and thus we will only highlight some studies.

Table 3.

A Partial List of Z-curve Applications in Genome Analysis.

Research areas	Involved Z-Curve Components	Algorithm, Software or Database	Life Domains or Virus	Species
Protein-coding gene recognition a	x, y, z, S	Z-curve algorithm [1, 2], Zcurve [12]	Bacteria	Acinetobacter baumannii [17], Variovorax paradoxus [18], Amycolatopsis mediterranei [19], Bacillus thuringiensis [20], Streptomyces tendae [21], Phaeobacter gallaeciensis [22], Desulfobacterium autotrophicum [23], Mycobacterium tuberculosis [24], Magnetospirillum gryphiswaldense [25], Beggiatoa [26]
			Phage, plasmid	Fosmids of marine Planctomycetes [127], plasmids in the human gut [128], phage Rtp [129]
			Archaea	Archaea of the ANME-1 group [27]
			Eukaryotes	Leptospira interrogans [130], Yeast [11], Short human protein-coding genes [56, 131], Drosophila [55]
		Zcurve_V [14], Zcurve_CoV [15]	Virus, Coronavirus, phages	Prophage [33], Me Tri virus [28], novel human coronaviruses NL63 and HKU1 [34], novel bat coronaviruses [35], bat coronaviruses 1A, 1B and HKU8 [36], novel human coronavirus [37]
			SARS_CoV	Various strains of SARS_CoV [38-53]
Replication origin identification	AT, GC, MK and RY disparity b	Ori-finder [78], DoriC [132, 133]	Archaea	Methanosarcina mazei[69], Halobacterium species NRC-1[63], Methanocaldococcus jannaschii [68], Sulfolobus acidocaldarius [72], Haloferax volcanii [73], Desulfurococcus kamchatkensis [74], Thermococcus sibiricus [75], Sulfolobus islandicus [76]
			Bacteria	Moraxella catarrhalis [79], Sorangium cellulosum [80],  Microcystis aeruginosa [80], Cyanothece [81], Cupriavidus metallidurans [82], Azolla filiculoides [83], Variovorax paradoxus [18], Corynebacterium pseudotuberculosis [84], [85], Orientia tsutsugamushi [86], Propionibacterium freudenreichii [87], Laribacter hongkongensis [88], Legionella pneumophila [89], Ehrlichia canis [90]
			Phage, plasmid	Streptococcus pneumoniae Virulent Phage Dp-1 [134], R-plasmid pPRS3a from Bacillus cereus [135]
Genomic island identification	z’	GC profile [9, 10]	Bacteria	Corynebacterium efficiens [105], Rhodopseudomonas palustris [106], Corynebacterium glutamicum [104], Vibrio vulnificus and Bacillus cereus [103], Agrobacterium tumefaciens, Rolstonia solanacearum, Xanthomonas axonopodis, Xanthomonas campestris, Xylella fastidiosa and Pseudomonas syringae [107], Streptomyces lividans [108], Parachlamydiaceae UWE25 [109], epsilon proteobacteria Sulfurovum and Nitratiruptor [110], Acinetobacter oleivorans [111], Silicibacter pomeroyi [112]
			Archaea	Haloquadratum walsbyi [136]
GC content variation,	z’, S	GC profile [9, 10]	Eukaryotes	Human genome: isochores [94, 98, 137] and replication time zones [138]; Isochores for chicken [97], Arabidopsis thaliana [96], mice [95] and pig [99]; DNA curvature profile for Aspergillus fumigatus [100]
isochore, genome segmentation			Bacteria	Bifidobacterium longum [139], Streptomyces avermitilis [140], Erwinia amylovora [141], Ralstonia pickettii [142]
Promoter, translational start sites, nucleosome positioning	x, y, z	Z-curve algorithm [11, 12], GS-finder [113]	Bacteria	Translational start sites [113] and promoters [115] of Escherichia coli and Bacillus subtilis
			Eukaryotes	Human Pol II promoter [114], Yeast genome for stable and dynamic nucleosome positioning [116]
Comparative genomics, genome visualization	x, y, z, z’	Z-curve database [117]	Bacteria, archaea, eukaryotes and viruses	Bacillus cereus [103], Bacillus cereus ATCC 10987 [119], Coronavirus [118], human immunodeficiency virus [120], human [121, 143], E. coli [122], Seven GC-rich bacteria [126], 90 species [1], Aeropyrum pernix K1 [124], Streptomyces coelicolor [125]

3.1. Identification of Protein-coding Genes

One of the most important applications of the Z-curve theory is gene-finding in various genomes. The principle in using the Z-curve theory to identify protein-coding genes is straightforward. Based on the Z-transform formulas, the occurrence frequencies of 4 bases in a DNA sequence are mapped onto a point in a 3-dimensional (3-D) or 15-, 63-, 255-, 1023- and 4095-D space, depending on the number of correlated bases under consideration (eqs. (16) to (22)). The first application was for gene recognition in the budding yeast genome, where a 3-D space (eqs. (16)) was adopted [11]. However, since the protein coding sequence has 3 phases, the 3 Z-curve parameters are expanded to 9 (3x3 phases) parameters. Adding the genome order index S (eq. (26)) into the set of 9 Z-curve parameters, a 10-D space is spanned by the 10 parameters. It was observed that the mapping points of protein coding sequences and non-coding sequences are distributed in two distinct regions in the 10-D space, although there is minor overlapping [12]. Therefore, the two kinds of points can be discriminated by the Fisher discriminant method, or other classifiers, such as support vector machines.

The Z-curve algorithm was first applied to recognize protein coding genes in the budding yeast (Saccharomyces cerevisiae) genome with an accuracy better than 95%, where the accuracy is defined as the average of sensitivity and specificity [11]. The same algorithm achieved an accuracy rate over 98% in the Vibrio cholerae genome, based on 9 parameters only [13]. The success of the above studies led to the development of a series of ab initio gene-finding software for various species with different numbers of Z-curve parameters.

3.1.1. Gene-finding in Bacterial, Archaeal, Phage and Virus Genomes

Based on 33 Z-curve parameters, we developed ZCURVE 1.0, which is an ab initio gene-finding software for bacterial and archaeal genomes [12]. Based on the 9 Z-curve parameters, ZCURVE_V was developed for identifying protein-coding genes in viral and phage genomes [14]. We also developed the software, ZCURVE_CoV, for gene-finding in coronavirus genomes, with special applications for SARS-coronavirus genomes [15, 16].

The above set of gene-finding software has been widely used in various laboratories worldwide. For example, ZCURVE 1.0 has been used for annotating protein-coding genes in many newly sequenced bacterial genomes, such as those of Acinetobacter baumannii [17], Variovorax paradoxus [18], Amycolatopsis mediterranei [19], Bacillus thuringiensis [20], Streptomyces tendae [21], Phaeobacter gallaeciensis [22], Desulfobacterium autotrophicum [23], Mycobacterium tuberculosis [24], Magnetospirillum gryphiswaldense [25] and Beggiatoa [26]. ZCURVE 1.0 was also used for annotating archaeal genomes, e.g., archaea of the ANME-1 group [27] (Table 3).

For some genomes, e.g., those of the bacterium Mycobacterium tuberculosis H37Ra [24] and Me Tri virus [28], ZCURVE 1.0 was the only software used for genome annotation, more frequently, however, results of ZCURVE 1.0 were combined with those of others, such as Glimmer [29] and Genmark [30]. For instance, ZCURVE 1.0 is integrated into meta-gene-finding tool YACOP [31] and GARSA [32]. It is noteworthy that ZCURVE 1.0 is especially suitable for genomes with high GC contents, e.g., GC content > 56% [12]. Likewise, ZCURVE_V and ZCURVE_CoV have been widely used for annotating protein-coding genes in newly sequenced genomes of viruses, coronaviruses [28, 33-37] and SARS coronaviruses [38-53].

3.1.2. Gene-finding in Eukaryotic Genomes

Algorithms based on the Z-curve theory have been used for recognizing protein coding genes in a number of eukaryotic genomes, e.g., the budding yeast genome [11], Leptospira interrogans genome [54] and Drosophila genomes [55]. The Z-curve algorithm has also been used in recognizing short coding sequences of human genes [56]. The algorithm based on the 189 Z-curve parameters was shown to be the most accurate among those tested for a given database, with the second one being an algorithm based on the Markov chain of order five [56], and the result was later confirmed by an independent study [57]. Recognition of exons and introns of human genes was also studied by using the Z-curve method [58].

3.1.3. Gene-finding Using the Fast Fourier Transform (FFT) Technique

The standard genetic code defines a mapping between a codon and an amino acid. According to this mapping, protein coding regions are divided into a series of tri-nucleotides (codon or triplet), resulting in a period-3 property in coding regions. Therefore, it is possible to find coding regions by exploring the 3-periodicity of DNA sequences. Consequently, the first step is to transform the DNA sequence into a digital sequence or signal, and the Z-curve is especially suitable for this purpose.

According to eqs. (31), $\Delta x_n=x_{n+1}-x_n=\pm 1,\Delta y_n=y_{n+1}-y_n=\pm 1and\Delta z_n=z_{n+1}-z_n=\pm 1$ . Applying the FFT to $\Delta x,\Delta yand\Delta z$, respectively, we are able to detect the 3-periodicity in the FFT power spectrum for each of the three numerical sequences. To increase the sensitivity, a lengthen-shuffle FFT algorithm was proposed for finding protein coding regions [59]. For example, the method was used to detect introns in the C. elegance chromosome III [60], and was later improved by using an adaptive filter to predict the exons in DNA sequences [61]. The relationship between the Z-curve and the Fourier transform for DNA sequence classification was studied in details [62].

3.2. Prediction of Replication Origins

3.2.1. Prediction of Replication Origins of Archaeal Genomes

Bacterial and eukaryotic genomes contain single and multiple replication origins, respectively. It was once a mystery whether archaea could have multiple oriCs.

Using the Z-curve method, we firstly predicted three oriCs as well as their precise locations for Sulfolobus solfataricus [63], and the prediction was consistent with later experimental evidence [64-67].

The archaeon Methanococcus jannaschii was the first to have its genome sequenced, however, its oriCs were notoriously difficult to locate by both theoretical and experimental methods. The Z-curve method predicted 2 oriCs [68] that were supported by later experimental evidence [66]. Similarly, we predicted a single oriC in the genome of Methanosarcina mazei [69] and 2 oriCs in the genome of A. pernix [70], which were also supported by experimental evidence [71]. The Z-curve method has been commonly used for annotating newly sequenced archaeal genomes, such as those of Sulfolobus acidocaldarius [72], Haloferax volcanii [73], Desulfurococcus kamchatkensis [74], Thermococcus sibiricus [75], and Sulfolobus islandicus [76].

3.2.2. Prediction of Replication Origins in Bacterial Genomes

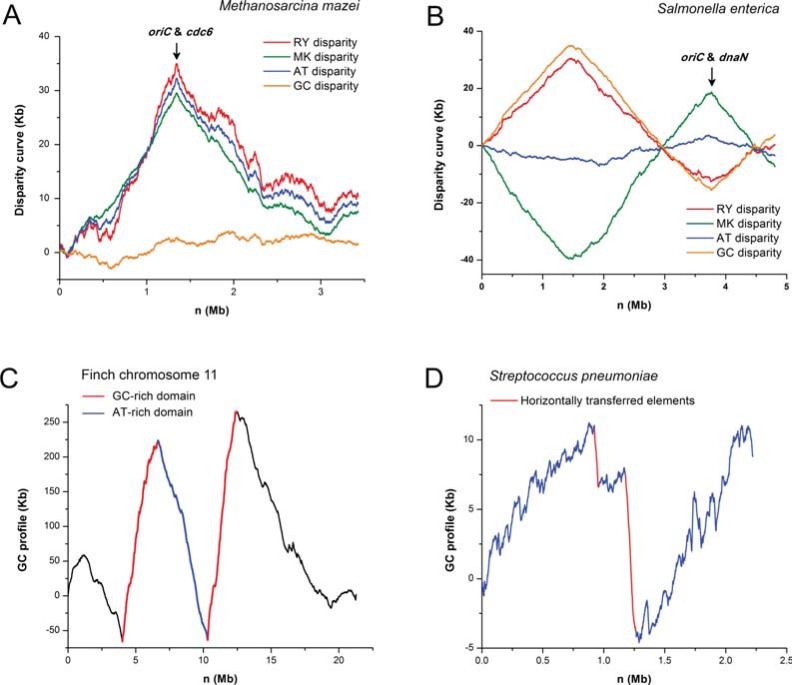
The Z-curve method is an effective technique that detects the asymmetrical nucleotide distribution around replication origins. The Z-curve contains all the information of its corresponding DNA sequence, and therefore the GC-skew [77] is a special case of the Z-curve. Thus the Z-curve can reveal nucleotide asymmetry that is not detectable by GC skew [70]. For instance, RY, MK and AT disparity curves show an oriC in the archaeon Methanosarcina mazei Tuc01 (Fig. 4A), while RY, MK, and GC disparity curves show an oriC in the bacterium Salmonella enterica tr. CT18 (Fig. 4B).

Fig. (4).

The Z-curve reveals features of archaeal, bacterial and eukaryotic genomes. The Z-curve shows replication origins in genomes of A) the archaeon Methanosarcina mazei Tuc01 and B) the bacterium Salmonella enterica subsp. Typhi str. CT18. The Z-curve shows C) the domain structure in chromosome 11 of finch, and D) horizontally-transferred genomic elements in the genome of Streptococcus pneumoniae ATCC 700669.

Ori-Finder, an integrated in silico method to predict oriC regions of bacterial genomes, has been developed, based on the Z-curve method, along with distributions of DnaA box patterns, indicator genes, and phylogenetic relationships [78]. Ori-finder has become a commonly used annotation tool for identifying oriCs in newly sequenced archaeal and bacterial genomes, e.g., those of Moraxella catarrhalis [79], Sorangium cellulosum [80], Microcystis aeruginosa [80], Cyanothece [81], Cupriavidus metallidurans [82], Azolla filiculoides [83], Variovorax paradoxus [18], Corynebacterium pseudotuberculosis [84, 85], Orientia tsutsugamushi [86], Propionibacterium freudenreichii [87], Laribacter hongkongensis [88], Legionella pneumophila [89], and Ehrlichia canis [90] (Table 3).

3.3. Studies of Genome Domain Structures

G+C content is an important characteristic of genome sequences. In the human genome, based on density gradient ultra-centrifugation experiments, it was found that long domains of relatively homogenous G+C content exist, and these domains are referred to as isochores [91, 92]. Traditionally, the G+C content along the genome is calculated using an overlapping or non-overlapping sliding window technique, based on which, however, isochores are hard to identify [93]. We developed a windowless technique in G+C content calculation, the GC profile [9, 10], which was used to study isochore structures in genomes of human [94], mouse [95], Arabidopsis thaliana [96] and chicken [97]. Based on the GC profile, the technique of wavelet multi-resolution analysis was used to identify isochore boundaries in the human genome [98]. For instance, a clear domain structure is revealed by the GC profile in chromosome 11 of finch (Fig. 4C). Other groups also used GC-Profile to study isochores in the pig genome [99] and to assess DNA curvature profiles for Aspergillus fumigatus [100].

3.4. Identification of Horizontally-transferred Genomic Islands in Bacterial Genomes

It is generally accepted that horizontal gene transfer (HGT) plays an important role throughout the genome evolution of prokaryotes, because HGT alters the genotype of a bacterium, and could potentially lead to new traits [101]. Genomic islands (GIs) contain clusters of horizontally transferred genes and therefore, identification of horizontally-transferred GIs is an important biological issue. Because the GC profile is sensitive to changes in GC content, it is a powerful tool in identifying GIs [102].

Based on the method of GC profile, GIs in many bacteria have been identified, e.g., Bacillus cereus [103], Corynebacterium glutamicum [104], Corynebacterium efficiens [105], Vibrio vulnificus CMCP6 [104], and Rhodopseudomonas palustris [106]. For instance, it was once believed that R. palustris does not have GIs, but analysis based on the GC profile identified 3 GIs that help explain how this bacterium survives in a versatile environment [106]. Corynebacterium efficiens can grow and produce glutamate at temperature above 40°C; unexpectedly, however, an aspartate kinase is less thermostable. This kinase gene is located in a GI that we identified, and this result suggests an explanation for its being less thermostable, i.e., the adaptive mutations have not occurred extensively due to the recent HGT [105]. For instance, horizontally transferred elements in Streptococcus pneumoniae ATCC 700669 can be clearly shown by the GC profile (Fig. 4D). The GC profile method has also been used for identification of GIs in other genomes, e.g., those of plant pathogens [107], Streptomyces lividans [108], Parachlamydiaceae UWE25 [109], epsilon proteobacteria Sulfurovum and Nitratiruptor [110], Acinetobacter oleivorans [111], and Silicibacter pomeroyi [112].

3.5. Identification of Promoters, Translation Start Sites and Nucleosome Positioning

Based on the behavior of the Z-curve near the bacterial gene translation start sites (TSS), a self-training method was proposed to find TSS with high accuracy [113]. It is likely that methods based on the same principle can also be used to recognize TSS in archaea and eukaryotes as well. Indeed, the Z-curve method was used to recognize human Pol II promoters [114] and promoters for bacterial genomes [115]. The positioning of nucleosomes, an elementary structural unit in eukaryotic chromatin, is pivotal in regulating many cellular processes, such as gene transcription. The Z-curve algorithm has been used to construct a genome-wide dynamic nucleosome positioning map for the budding yeast [116].

3.6. Visualization of DNA Sequences, Comparative Genomics and the Z-curve Database

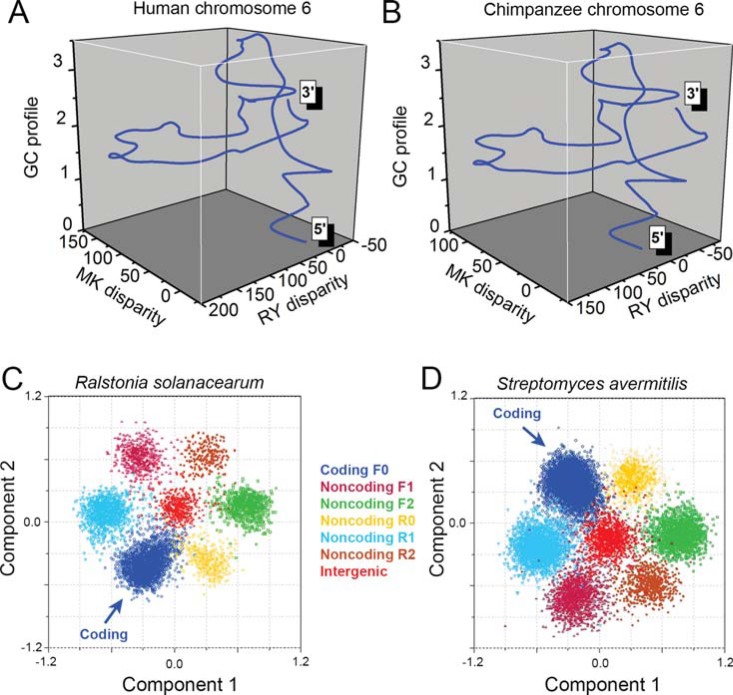
One of the aims for developing the Z-curve theory is to visualize DNA sequences. By using the Z-curve, features of related DNA sequences can be grasped quickly in a perceivable form [1, 2]. Therefore, we constructed the Z-curve database (www.zcurve.net), which contains Z-curves for currently available genomes, online Z-curve drawing tools and other Z-curve related software [117]. For instance, human chromosome 6 and chimpanzee chromosome 6 are homologous, and they apparently have similar Z-curve patterns (Fig. 5A and B). A typical example is the visualization of the genomes of related SARS-coronaviruses. Based on the 3-D coordinates of the corresponding Z-curves, the phylogenetic tree was constructed and was found to be in agreement with that based on sequence alignment [118]. Comparative genomics based on the GC profile was used to identify genomic islands [103, 119].

Fig. (5).

Genomic nucleotide composition features revealed by the Z-curve method. 3-D Z-curves for human chromosome 6 (A) and chimpanzee chromosome 6 (B). The 2 homologous chromosomes show similar Z-curves. To show global nucleotide composition patterns, Z-curves have been smoothed for 50,000 times by using the B-spline function. An ORF-flower phenomenon is revealed by the Z-curve method in genomes with high GC content. All open reading frames are mapped onto a 9-dimensional space using the Z-curve method, and protein-coding ORFs are located in a distinct region, compared with non-coding ORFs and intergenic sequences. Shown are principal component analysis for the genomes of Ralstonia solanacearum GMI1000 (C) and Streptomyces avermitilis MA 4680 (D). F0, F1, F2, R0, R1, and R2 stand for reading frames of protein-coding, forward 1, forward 2, non-coding reverse 0, reverse 1 and reverse 2, respectively.

According to eqs. (6), the base composition of a DNA sequence can be represented by a point in a 3-D space, thus providing an intuitive method to display base compositions. This method was used to study the codon usage in the genomes of AIDS virus [120], human [121], E. coli [122], Vibrio cholerae [123], Aeropyrum pernix K1 [124], Streptomyces coelicolor A3(2) [125] and seven GC-rich bacteria [126]. In prokaryotic genomes with high-GC content, coding ORFs and non-coding ORFs are located in distinct regions in a 9-dimensional space revealed by the Z-curve method, forming a flower-like pattern (Fig. 5C and D).

4. SUMMARY

The three components of the Z-curve, x, y and z, which display distributions of purine/pyrimidine (R/Y), amino/keto (M/K) and strong-H bond/weak-H bond (S/W) bases, respectively, are independent, and completely describe the DNA sequence. The x and y components are related to the disparities of RY, MK, AT and GC bases, and can therefore be used to identify oriC regions in prokaryotic and eukaryotic genomes. The component z is related to G+C content, and can therefore be used to identify domain structures of eukaryotic genomes and genomic islands of prokaryotic genomes. The set of all three components can be used in identifications of protein-coding genes, promoters, translational start sites or in other bioinformatics issues. Generally, further applications are expected to benefit from the use of functions based on the three components, i.e., f (x, y, z), with potential integration of other parameters.

In conclusion, the methodology of the Z-curve provides a geometrical approach to analyzing genomic DNA sequences. Considerable progress in applying the Z-curve method has been achieved, and the Z-curve theory provides a solid basis for future developments.

CONFLICT OF INTEREST

The authors confirm that this article content has no conflicts of interest.