Single molecule fluorescence probes dynamics of barrier crossing

Abstract

Kramers developed the theory on how chemical reaction rates are influenced by the viscosity of the medium^1,2. At the viscosity of water, the kinetics of unimolecular reactions are described by diffusion of a Brownian particle over a free-energy barrier separating reactants and products. For reactions in solution this famous theory extended Eyring's transition state theory, and is widely applied in physics, chemistry, and biology, including reactions as complex as protein folding^3,4. Because the diffusion coefficient of Kramers theory is determined by the dynamics in the sparsely-populated region of the barrier top, its properties have not been directly measured for any molecular system. Here we show that the Kramers diffusion coefficient and free energy barrier can be characterized by measuring the temperature- and viscosity-dependence of the transition path time for protein folding. The transition path is the small fraction of an equilibrium trajectory for a single molecule when the free-energy barrier separating two states is actually crossed (Fig. 1a). Its duration, the transition path time, can now be determined from photon trajectories for single protein molecules undergoing folding/unfolding transitions⁵. Our finding of a long transition path time with an unusually small solvent viscosity-dependence suggests that internal friction as well as solvent friction determine the Kramers diffusion coefficient for α-helical proteins, as opposed to a breakdown of his theory that occurs for many small-molecule reactions². It is noteworthy that the new and fundamental information concerning Kramers theory and the dynamics of barrier crossings obtained here come from experiments on a protein rather than a much simpler chemical or physical system.

The molecule studied in this work is the all-α-helical 73 residue, designed protein, α₃D (Fig. 1b, Extended Data Fig. 1). In single-molecule experiments⁶, as well as in all-atom molecular dynamics simulations⁷, α₃D is a two-state protein (Fig. 1a) at neutral pH (Extended Data Figs. 3,4), i.e. only two states are observable at equilibrium and at all times in kinetic experiments. In the single molecule studies reported here we use the maximum likelihood method of Gopich and Szabo⁸ in a photon-by-photon analysis of the fluorescence trajectories to obtain both the average transition path time (t_TP) and, from the mean residence time in the unfolded state, the folding time (t_f) (the reciprocal of the folding rate coefficient)^6,9,10. The basic idea of their method is to determine the most likely parameters of an assumed model that are most consistent with a collection of photon trajectories for which the color and interval between each photon are known. For diffusive barrier crossings the times, t_f and t_TP, are given by the following two equations,

Figure 1.

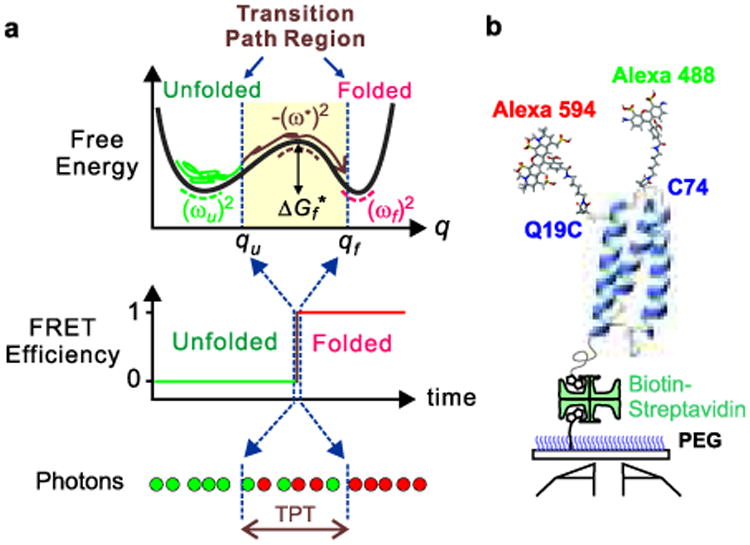
Schematics of α₃D structure and a one-dimensional free energy surface for a two-state protein. a, Free energy as a function of reaction coordinate (q), a segment of a FRET efficiency trajectory, and a segment of a photon trajectory (red: acceptor; green: donor) indicating the transition path time (TPT) in the idealized case where there is no noise in the FRET efficiency in either the unfolded or folded states because they are exactly 0 and 1, respectively. In the folding reaction, the vast majority of the time is spent exploring the configurations of the unfolded well (called the waiting or residence time) with numerous unsuccessful attempts at crossing the free energy barrier to the folded state. The diagram indicates that the “jump” in the FRET efficiency corresponds to the transition path. The brown trajectory on a transition path is one that leaves the unfolded well, crosses the position q_u on the reaction coordinate, and reaches q_f on the other side of the barrier without re-crossing q_u. b, Dye-labeled α₃D molecules are immobilized on a polyethylene glycol-coated glass surface via a biotin-streptavidin-biotin linkage.

Extended Data Figure 1.

Amino acid sequences of polypeptides containing protein α₃D. Dyes were attached to the cysteine residues (red) and a biotin molecule was attached to the lysine residue (blue) in the AviTag sequence.

Extended Data Figure 3.

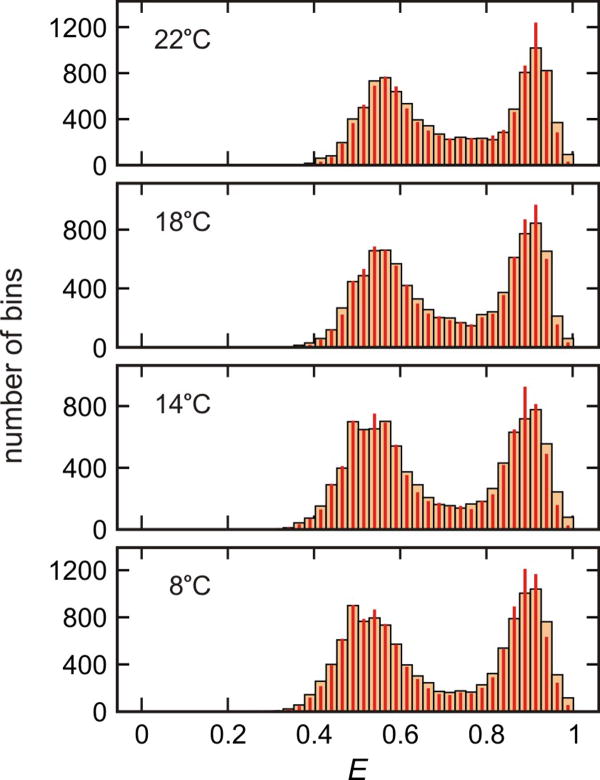
FRET efficiency histograms of α₃D in 2.25 M GdmCl solution at different temperatures. The FRET efficiency histograms were constructed from 1 ms bins in the trajectories with the mean photon count rate > 40 ms^-1. Wide and narrow bars are the experimental histograms and the histograms constructed from recolored photon trajectories using the parameters obtained from the maximum likelihood method with the two-state model (Extended Data Table 1), respectively. The agreement between the two histograms validates the description of α₃D as a two-state folder⁸. The similar ratio of the integral of the folded (high FRET) and the unfolded (low FRET) distributions indicates that the equilibrium constant is unchanged over the temperature range of the measurement, as shown more precisely in the maximum likelihood analysis. At high temperature and low pH, where the 11 glutamates and 1 aspartate are protonated, more than two states are observed^36,37.

Extended Data Figure 4.

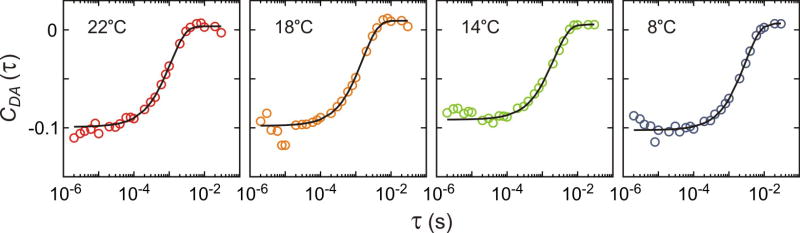
Donor–acceptor cross-correlation functions at different temperatures. Black solid lines are exponential functions that best fit the data. The fitting parameters are listed in Extended Data Table 1.

$$t_f=\frac{2\pi }{\beta D^{\ast }{\omega }^{\ast }{\omega }_u}exp\left(\beta \mathrm{\Delta }{G}_f^{\ast }\right)$$ (1)

$$t_{\mathit{\text{TP}}}\approx \frac{1}{\beta D^{\ast }{\left({\omega }^{\ast }\right)}^2}ln\left(2e^{\gamma }\beta \mathrm{\Delta }{G}_f^{\ast }\right)$$ (2)

where D* is the diffusion coefficient at the free energy barrier top, (ω*)² and (ω_u)² are the curvatures of the free energy surface at the barrier top and the unfolded well, respectively, and ΔG_f* is the free energy barrier height (Fig. 1b). β = 1/k_BT, where k_B is the Boltzmann constant, T is the absolute temperature, and γ is Euler’s constant (= 0.577…). Equation (1) is from Kramers¹ and equation (2) from Szabo^9,11, which makes the same assumptions and approximations as Kramers concerning the underlying physics. (The major difference between Kramers and transition state theory is that the pre-exponential factor of the latter does not contain a diffusion coefficient, and is simply 2π/ω_u¹.) D* (= k_BT/ζ*, the Einstein relation) is determined by the friction, ζ*, that damps the motion across the barrier top, which in the simplest case is due entirely to solvent viscosity. Two critical assumptions in these equations are that a one-dimensional free energy surface is sufficient to accurately describe the dynamics and that the dynamics are Brownian. That a one-dimensional free-energy surface is adequate has been validated for protein folding by lattice simulations¹², off-lattice simulations^13,14, and by the agreement of experiment and predictions of theoretical models^3,4.

An important property of equation (2) for the following development is that the transition path time is predicted to be insensitive to the barrier height, in contrast to the folding time, which is greatly affected by a small change of the barrier height that may be caused by viscogens and/or chemical denaturants even when the equilibrium population is unchanged¹⁵. This insensitivity of the transition path time to barrier height has very recently been observed in our single molecule fluorescence experiments for two proteins with folding times that differ by ∼10⁴ -fold⁵. Consequently, the properties of the transition path time are expected to be determined by D*(ω*)².

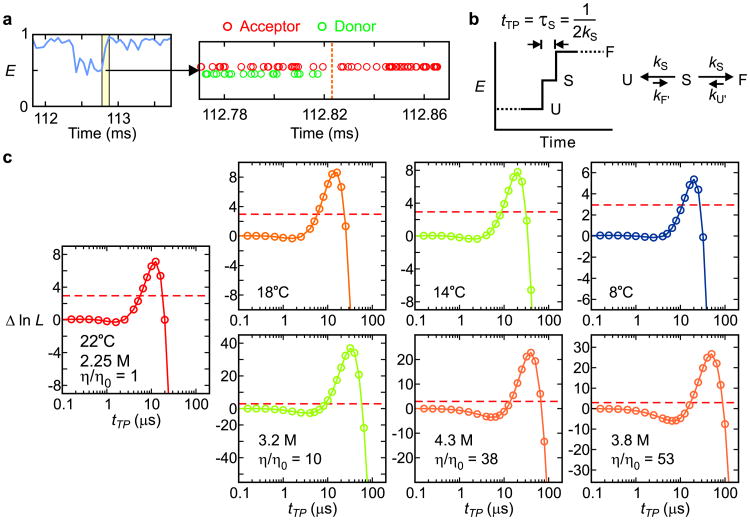
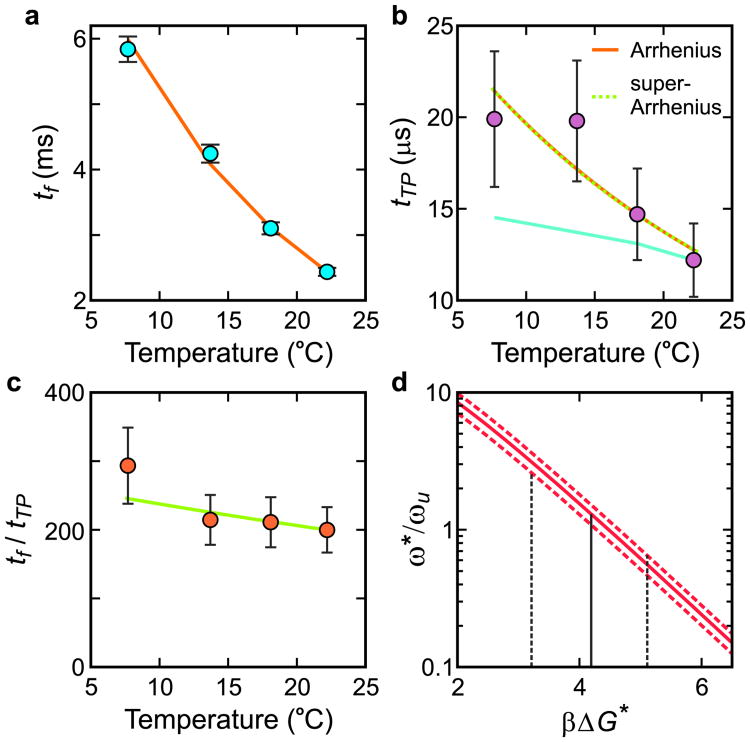
Figure 2 shows how the transition path times are determined using the Gopich-Szabo maximum likelihood method (see also Methods); Figures 3 and 4 show how the transition path and folding times depend on temperature and viscosity. One immediate result from these experiments is that the height of the free energy barrier can be simply obtained from the ratio of the folding time to the transition path time, t_f/t_TP (equations (1) and (2)), if ω*/ω_u is known. (Although energy barrier heights for reactions are routinely determined from the temperature dependence of the rate, albeit most often without consideration of the temperature-dependence of the pre-exponential factor (equation (1)), the free energy barrier height is much more difficult to determine). ω*/ω_u cannot be obtained from our experiments. We therefore use the value of 1.3 calculated from the potential of mean force in all-atom molecular dynamics simulations by Shaw and coworkers⁷ for α₃D, which together with our measurements of t_f/t_TP yields a ΔG_f* of 4.2 ± 1.0 k_BT at 22°C (Fig. 3d and Methods). With a barrier height of 4.2 k_BT, the pre-exponential factor (equation (1)) is ∼ 40 μs, significantly larger than previous estimates of ∼ 1 μs¹⁶. However, the larger pre-exponential factor is consistent with the longer transition path time of 10-20 μs for this protein compared with our previously-measured transition path times for an all- β (2 μs) and an α/β (< 10 μs) protein⁵.

Figure 2.

Determination of transition path times. a, A FRET efficiency trajectory (50 μs bin time) with photon trajectory of the yellow segment. b, Schematic of a FRET efficiency trajectory using a one-step model to describe the transition path from unfolded (U) to folded (F) states for a two-state protein. The average transition-path time, t_TP, is equal to the lifetime of a virtual intermediate state S (τ_S = (2k_S)^-1). c, The difference of the log likelihood, Δln L = ln L(t_TP) − ln L(0), plotted as a function of t_TP for folding and unfolding transitions at different temperatures (upper row, 2.25 M guanidinium hydrochloride, GdmCl) and at different solvent viscosities at 22°C (lower row). L(0) is the likelihood for a two-state model with instantaneous folding and unfolding transitions. Therefore, Δln L quantifies how much better or worse the one-step model with a finite transition path time in (b) describes the photon trajectory than a two-state model with an instantaneous transition (Extended Data Fig. 2b). The maximum values of Δln L of all data are much greater than the 95% confidence limit (horizontal dashed line at Δln L = 3), which indicates that the transition-path times determined by the maximum of Δln L (Extended Data Table 1 and 2) are highly statistically significant. The number of transitions analyzed were 522 (22°C), 355 (18°C), 265 (14°C), 284 (8°C), 699 (η/η₀ = 10), 541 (η/η₀ = 38), and 423 (η/η₀ = 53).

Figure 3.

Temperature dependence of folding and transition path times at 2.25 M GdmCl. a, Folding time. The points are the data, and the solid curve is the fit with an Arrhenius law. b, Transition path time. The points are the data, and the orange solid and green dashed curves are the fits with an Arrhenius and a super Arrrhenius law (see text), which are indistinguishable over this small temperature range. The cyan line is the predicted transition path time scaled to the transition path time at 22°C using equation (2) if the solvent were the only source of friction affecting the diffusion coefficient, D*. c, Ratio of folding to transition path times vs temperature. The points are the data and the solid curve is the temperature dependence with ΔG * = 4.2 k_BT at 22°C obtained in (d). d, Determining βΔG_f* at 22°C. The value of ω*/ω_u is evaluated for the measured t_f/t_TP, 200 (continuous red curve), including its error, i.e. 233 (upper red dashed curve), and 167 (lower red dashed curve). The most probable value of ω*/ω_u obtained from the MD simulations⁷ is 1.3, corresponding to βΔG_f* = 4.2. (See Methods)

Figure 4.

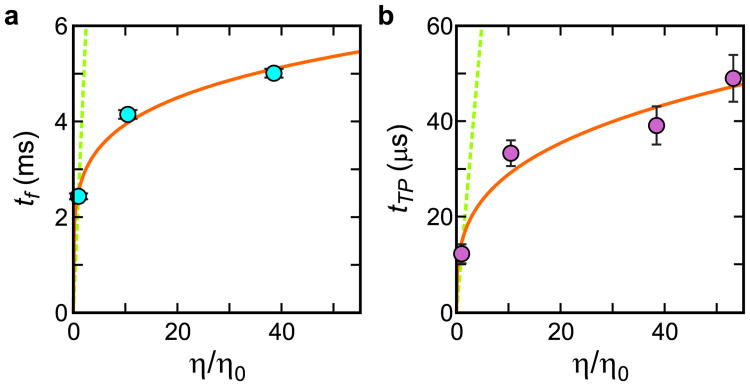
Viscosity dependence of folding and transition path times. The solid curve is a fit to the power-law function A(η/η₀)^α, with A = 2.5 ± 0.1 ms and α = 0.19 ± 0.01 for the folding time (a) and A = 15 ± 2 μs and α = 0.30 ± 0.03 for the transition path time (b). The green dashed lines show the dependence expected when the folding or transition path times are linearly proportional to the solvent viscosity (see Extended Data Fig. 5 and 6 and Extended Data Table 2)

For very low free-energy barriers (≲ 2 k_BT), heights have previously been estimated from ensemble kinetic experiments by Gruebele and coworkers. In this case there is a significant population of partially folded molecules at the barrier top. ΔG_f* was then obtained from an approximate relation: t_f/t_m = exp(βΔG_f*), where t_m is a relaxation time corresponding to a “molecular phase”, interpreted as resulting from a change in population at the barrier top produced by a temperature-jump¹⁷. Barrier heights have also been estimated from single-molecule force experiments¹⁸, and, for very low barriers, from calorimetric measurements of the excess heat capacity¹⁹. One caveat to our measurements is that FRET measures the transition path time for compaction of the polypeptide chain, which would underestimate the transition path time if collapse and folding are not simultaneous. For example, a twice-longer transition path time that could result from additional time for side-chain annealing within a compact structure would lower the barrier by only 0.7 k_BT.

Since the transition path time is insensitive to the barrier height, the more interesting result is that our measurements characterize D*(ω*)², the pre-logarithmic factor in equation (2). The temperature-dependent data suggest that the variation of the transition path time results from variation of D* and not from ω*. First, within the errors of our experiment, the small variation of the ratio t_f/t_TP, which does not depend on D*, is consistent with both a constant ΔG_f* and ω*/ω_u over this temperature range (Fig. 3c). Furthermore, the equilibrium constant does not change with temperature (Extended Data Fig. 3 and Extended Data Table 1), suggesting that the curvatures in neither the unfolded, (ω_u)², nor folded, (ω_f)², wells have changed. The invariance of the free energy surface in this temperature range is not surprising, since the protein unfolds at both lower (cold denaturation) and higher temperatures.

Extended Data Table 1.

Temperature dependence of the kinetic parameters obtained from the two-state maximum likelihood analysis, the relaxation rate obtained from the donor-acceptor cross-correlation analysis, and the transition path times.

Temprature (°C)	22.2	18.1	13.7	7.7
Viscosity (η/η0)	1	1.07	1.12	1.19
EF	0.91 (0.0005)	0.90 (0.0006)	0.89 (0.0006)	0.89 (0.0006)
EU	0.55 (0.0007)	0.54 (0.0008)	0.52 (0.0008)	0.52 (0.0008)
k (ms-1)	0.85 (0.02)	0.66 (0.02)	0.52 (0.01)	0.37 (0.01)
pF	0.48 (0.008)	0.49 (0.009)	0.46 (0.010)	0.47 (0.010)
Donor-acceptor cross correlation, k (ms-1)	0.92 (0.04)	0.64 (0.02)	0.47 (0.02)	0.34 (0.01)
Transition path time (μs)	12.2 (2.0)	14.7 (2.5)	19.8 (3.3)	19.9 (3.7)

Errors are standard deviations obtained from the diagonal elements of the covariance matrix calculated from the likelihood function. [GdmCl] = 2.25 M.

In the simplest case, when all of the friction (ζ*) opposing the motion over the barrier top is due to the solvent viscosity, η, 1/D* ∝ η. However, we find a much smaller viscosity dependence, i.e. 1/D*; ∝ η^α, with an α of only 0.3 (Fig. 4b). One might interpret this result as a breakdown of Kramers theory in which the Brownian assumption fails and causes a reduced viscosity dependence². However, given the extremely weak viscosity dependence, the more likely possibility is that there is an additional source of friction from intra-molecular interactions^20-22. This so-called internal friction has been previously used to explain the decreased viscosity dependence observed for the relaxation rate of a protein conformational change²³ and the folding time of an α-helical protein under conditions where the viscogen does not perturb the equilibrium constant, and therefore is presumed not to alter the free energy surface¹⁵. A clear example of internal friction influencing protein dynamics can be found in the studies of Schuler and coworkers on the reconfiguration time of unfolded proteins and intrinsically disordered proteins, where the viscosity dependence is reduced as the polypeptide becomes more compact at the lower denaturant concentrations and increased intra-molecular interactions slow the motion of the chain²⁴.

Additional evidence for internal friction comes from the much greater temperature dependence of the transition path time than predicted by the temperature dependence of the solvent viscosity (in the absence of added viscogen) (Fig. 3b). Using the Arrhenius law, the activation energy for D* is 11 (± 4) k_BT. However, for protein folding Bryngelson and Wolynes²⁵ showed that D* should exhibit super-Arrhenius behavior, i.e. D* ∝ exp[−(ΔE/k_BT)²], which fits the data equally well (Fig. 3b), where ΔE² is the local mean-squared fluctuation in energy and is a measure of the underlying “landscape roughness.” With this temperature dependence ΔE = 2.3 (± 0.4) k_BT. Interestingly, our predicted transition path time at 370 K, the temperature of the molecular dynamics simulations⁷, is 1.7 μs using the Arrhenius law and 2.3 μs using the super-Arrhenius equation. Both are in excellent agreement with the observed value of 0.9 μs in the MD simulations. The agreement is even better if a viscosity correction were applied to the MD value⁵, because the TIP3P water used in the simulations is 3-fold less viscous than real water.

Assuming that the total friction is a simple sum of the internal friction and the friction from the solvent (ζ = ζ_solvent + ζ_internal) and that the internal friction is independent of solvent composition and viscosity^20,23, one might have expected that the transition path time would be linear in viscosity with a non-zero intercept (Fig. 4b), as found for the myoglobin relaxation²³ and atomistic folding simulations where the friction of the implicit solvent was varied²⁶. However, at the highest concentrations of viscogen (Table S2), the solvent is largely non-aqueous (at η/η₀ = 53 the solvent is only ∼7% water by weight), and our assumptions of solvent-independent internal friction, two stateness, and unchanged curvatures of the free energy surface may no longer hold.

An obviously important remaining issue is the detailed structural origin of internal friction in protein folding. What are the dominant contributions of these microscopic dynamics that give rise to internal friction and thereby slow the diffusive motion along the reaction coordinate? For dynamics involving buried residues and therefore presumably less influenced by solvent viscosity, what is the relative importance, for example, of making and breaking inter-residue contacts compared to dihedral angle flips²³? How much of the internal friction results from the increased frustration caused by local non-native contacts that is more likely for a designed protein such as α₃D than a naturally occurring protein²⁷? Do non-Markovian effects contribute to the reduced viscosity dependence^20,21? Why is much larger apparent internal friction observed in folding all α-helical proteins^15,28,29 compared to all-β or α/β proteins (see review by Hagen³⁰)? The answers to these fundamental questions about protein folding dynamics will require transition path time measurements on proteins of different sequences and folds in combination with further investigations by theory and simulations.

Methods

Materials

The preparation and purification of dye-labeled α₃D has been described previously⁶.

Single molecule spectroscopy

Single molecule FRET experiments were performed using a confocal microscope system (MicroTime200, Picoquant). The CW mode of a dual mode (CW/pulsed) 485 nm diode laser (LDH-D-C-485, PicoQuant) was used to excite donor dyes through an oil-immersion objective (PlanApo, NA 1.4, ×100, Olympus). Donor and acceptor fluorescence was collected by the same objective, split into two channels, and focused through optical filters (ET525/50m for the donor and E600LP for the acceptor, Chroma Technology) onto photon-counting avalanche photodiodes (SPCM-AQR-15, PerkinElmer Optoelectronics). Additional details for the optical setup and single molecule experiments can be found elsewhere^9,31.

Protein molecules were immobilized on a biotin-embedded, polyethyleneglycol-coated glass coverslip (Bio_01, Microsurfaces Inc.) via a biotin (surface)-streptavidin-biotin (protein) linkage. To reduce dye bleaching and blinking, 1 – 2 mM of l-ascorbic acid (A92902, Sigma) and methyl viologen (856117, Sigma) were added to the 50 mM Hepes buffer (pH 7.6) solution³² for the temperature-dependence experiment. For the experiments in 50% and >50% glycerol, higher concentrations of 10 mM and 40 mM ascorbic acid/methyl viologen were used, respectively, to increase the bimolecular rates that reduce blinking and bleaching.

To collect a large number of trajectories, we used an automated data collection scheme as described in ref. ⁵.

Temperature control and measurement

Temperature was controlled by flowing dry nitrogen cooled by liquid nitrogen into a chamber surrounding the microscope objective and sample with a fixed flow rate. The temperature was varied by changing the flow rate and was measured at the confocal spot using the fluorescence lifetime of rhodamine B³³, excited by a 485 nm laser in the pulsed mode, using the calibration equation:

$${\tau }_{\mathit{\text{life}}}(\text{ns})=2.64-0.0572T+4.63\times {10}^{-4}{T}^2-1.34\times {10}^{-6}{T}^3.$$

with T in °C.

Measurement of relative viscosities

The relative viscosities (η/η₀) of the solutions were obtained from the absolute temperature (T in K) and the translational diffusion times (τ) using the relationship η ∝ τT. The translational diffusion times were measured by fluorescence correlation spectroscopy (FCS) experiments on an Alexa Fluor 488- and Alexa Fluor 594-labeled rigid rod molecule, 20-residue poly-proline, as described previously⁵.

Calculation of donor and acceptor cross-correlation

To further test the assumption of a two-state model in our data analysis using the maximum likelihood method (see below), we calculated the donor-acceptor cross-correlation function, as C_DA(τ) = -A exp(kτ), as shown in Extended Data Fig. 4 and compared its decay rate with the sum of the rate coefficients determined by the maximum likelihood method (Extended Data Table 1). To obtain the timescale of the unfolded state dynamics at high viscosity, the donor-acceptor cross-correlation function was calculated (Extended Data Fig. 6) for the photon trajectories in the unfolded segments that were extracted using Viterbi algorithm^6,34,35.

Extended Data Figure 6.

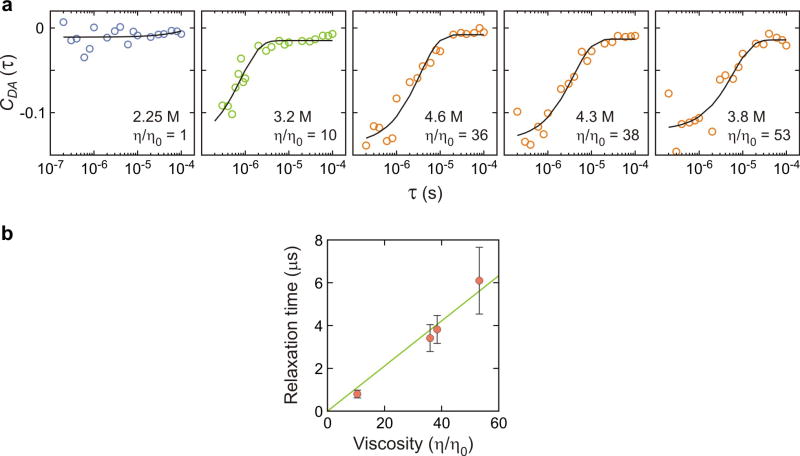
Donor–acceptor cross-correlation of the segments of the fluorescence trajectories corresponding to the unfolded state²⁴. a, Black solid lines are exponential functions that best fit the data. The fitting parameters are listed in Extended Data Table 2. b, The unfolded state dynamics are slowed approximately linearly by the solvent viscosity as previously observed at high denaturant concentrations²⁴. The relaxation time at η/η₀ = 1 (aqueous solution) is too fast to be measured by this method.

Calculation of likelihood functions

To determine parameters for the two-state kinetics, we used the Gopich-Szabo maximum likelihood method and analyzed the photon trajectories without time binning. This method yields the most likely parameters of an assumed model that can reproduce the observed photon trajectories. The likelihood function for the j^th photon trajectory is⁸.

$$L_j={\mathbf{1}}^{\mathrm{T}}\prod _{i=2}^{N_j}[\mathbf{F}(c_i)exp(\mathbf{K}{\tau }_i)]\mathbf{F}(c_1){\mathbf{p}}_{\mathit{\text{eq}}},$$ (S1)

where N_j is the number of photons in a trajectory, c_i is the color of the i^th photon (donor or acceptor), and τ_i is a time interval between the i^th and (i-1)^th photons (Extended Data Fig. 2a). The photon color matrix F depends on the color of a photon as F(acceptor) = E and F(donor) = I − E, where E is a diagonal matrix with elements that are FRET efficiencies of the individual states. I is the identity matrix, p_eq is a vector consisting of the equilibrium population of each state, and 1^T is a row vector with elements of 1. The calculation of likelihood values was performed using the diagonalization of the matrix exponential in equation (S1) as described in ref.⁸. Practically, the log likelihood function was calculated and the total log likelihood function of all trajectories was calculated by summing individual log likelihood functions as $lnL=\sum _{j}ln{L}_j$. For a two-state system, there are four independent parameters - the apparent FRET efficiencies and the rate coefficients of the folded and unfolded states (E_F, E_U, k_F, k_U). In analyzing the data, instead of varying the two rate coefficients, it is more convenient to vary the sum of the rate coefficients (k = k_F + k_U) and the fractional population of folded molecules (p_F = k_F/[k_F + k_U]). For the two-state kinetic model (Extended Data Fig. 2b), the rate matrix is given by

Extended Data Figure 2.

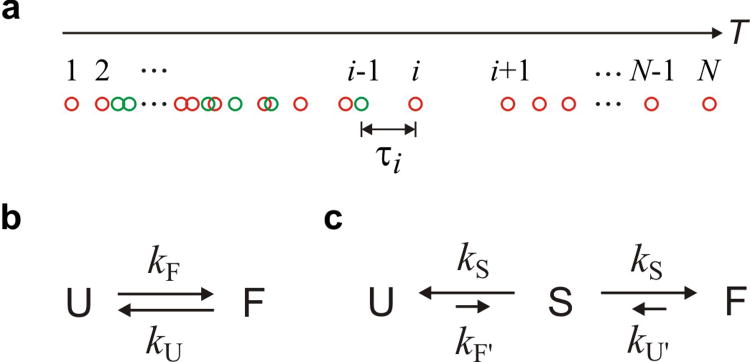
Photon trajectory and kinetics models. a, The definition of photon indices and time interval of a photon trajectory with a folding transition. Photon trajectories were analyzed using (b) the two-state model to determine kinetics parameters or (c) the three-state model to determine the average transition path times (t_TP = 1/2k_S).

$$\mathbf{K}=\left(\begin{array}{cc}-k_U& k_F\\ k_U& -k_F\end{array}\right).$$ (S2)

The 4 parameters (E_F, E_U, k_F, k_U) can be obtained by maximizing the log likelihood ln L.

In the measurement of the average transition-path time, t_TP, molecules were illuminated at 10 – 15 times higher laser intensity (20 – 30 kW/cm²) than the intensity used for the determination of two-state kinetics parameters above to collect photons at high photon count rates of 550 – 710 ms^-1. This high photon count rate permitted clear resolution of transitions by collecting photons in 50-100 μs bins. The photon trajectory in the short segment near the transition (∼ 1 ms) was then analyzed using the likelihood function. We adopted a three state model with a virtual intermediate (“step”) state S in addition to the folded (F) and unfolded (U) states, which is the simplest discrete representation of how the FRET efficiency changes along the transition path. In this model, the FRET efficiency of S is midway between the folded and unfolded states (E_S = (E_F + E_U)/2) and the lifetime of S (τ_S) corresponds to the average transition-path time, t_TP. The rate matrix of this kinetics scheme (Extended Data Fig. 2c) is

$$\mathbf{K}=\left(\begin{array}{ccc}-k_{{\mathrm{U}}^{\prime }}& k_{\mathrm{S}}& 0\\ k_{{\mathrm{U}}^{\prime }}& -2k_{\mathrm{S}}& k_{{\mathrm{F}}^{\prime }}\\ 0& k_{\mathrm{S}}& -k_{{\mathrm{F}}^{\prime }}\end{array}\right).$$ (S3)

F′ and U′ are used for the folded and unfolded states to distinguish these from those in the two state model with an instantaneous transition. In this analysis t_TP = τ_S = 1/2k_S, and t_TP is the same for folding and unfolding transitions, which is also the case for the real transition path in Fig. 1(b) regardless of the relative stability of the folded and unfolded states as long as q_u and q_f are the same for the two paths. The likelihood function of this model for the j^th photon trajectory with a single transition is ⁵

$$L_j={{\mathbf{v}}_{\mathit{\text{fin}}}}^T\prod _{i=2}^{N_j}[\mathbf{F}(c_i)exp(\mathbf{K}{\tau }_i)]\mathbf{F}(c_1){\mathbf{v}}_{\mathit{\text{ini}}},$$ (S4)

where v_ini and v_fin are state vectors at the beginning and the end of the trajectory. For the case of a folding transition in Extended Data Fig. 2a, v_ini = (0 0 1)^T and v_fin = (1 0 0)^T. In the analysis, the folded and unfolded segments were assigned using the Viterbi algorithm^34,35, adapted for photon trajectories⁶, and k_F and k_U were obtained from the low intensity measurements (Extended Data Table 1). When there are multiple transitions in a trajectory, each pair of segments with a single folding or unfolding transition was analyzed separately. In the calculation of the likelihood function in equation (S4) for these segments, we reduced the rate coefficients by a factor of 1000 to effectively eliminate the possibility of multiple transitions that are not resolvable, i.e. k_U′ (= k_U/1000) and k_F′ (= k_F/1000). This treatment is valid since we use the difference of the log likelihood values (Δln L) in this paper.

The reader is referred to previous publications for an in-depth understanding of the Gopich-Szabo maximum likelihood method⁸ and its experimental application to a two-state protein system⁶ and for the transition path analysis⁵.

Determination of the free energy barrier height

The free energy barrier height at 22°C was determined (in Fig. 3d) using the ratio of the folding time to the transition path time t_f/t_TP, and the ratio of the curvatures at the barrier top and the bottom of the unfolded state (ω*/ω_u)². The value of ω*/ω_u was evaluated for the measured t_f/t_TP, 200 (continuous red curve), including its error, i.e. 233 (upper red dashed curve), and 167 (lower red dashed curve). The most probable value of ω*/ω_u obtained from the MD simulations⁷ is 1.3, the average of 0.94 (using the fraction of native contacts as the reaction coordinate (R. B. Best., G. Hummer, and W.A. Eaton, under review by Proc. Natl. Acd. Sci. USA) and 1.6 (using an optimized reaction coordinate⁷), corresponding to βΔG_f * = 4.2. Assuming an uncertainty of a factor of 2 for ω*/ω_u, the possible range of βΔG_f * becomes 3.2 to 5.1 for ω*/ω_u between 0.65 and 2.6. Using the reported times from the MD simulations of t_f = 27 ± 8 μs, and t_TP = 0.9 ± 0.2 μs, and ω*/ω_u = 1.6 from the one-dimensional free energy surface constructed with an optimized reaction coordinate, the ratio of equations (1) and (2) yields a barrier height of 1.7 ± 0.6 k_BT, which is close to the 2.1 k_BT (no error reported) barrier height for this surface⁷. Using the fraction of native contacts as the reaction coordinate for all 3 quantities, the corresponding times are t_f= 26.4 ± 8.8 μs, t_TP = 0.83 ± 0.17 μs (boundaries for the transition path are the two well minima), and ω*/ω_u = 0.94 ± 0.18, the calculated barrier height is 2.5 ± 0.6 k_BT, compared to the barrier height of 2.4 ± 0.3 k_BT (R.B. Best, unpublished results).

Extended Data Figure 5.

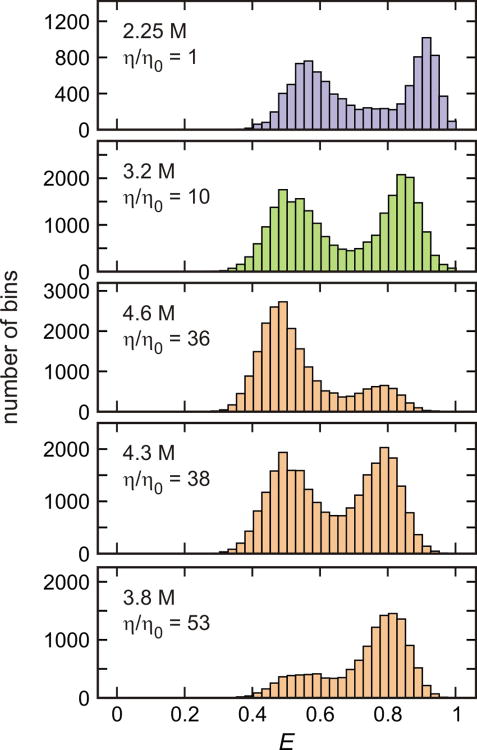
FRET efficiency histograms of α₃D at various solvent viscosities. The FRET efficiency histograms were constructed from 1 ms bins in the trajectories with the mean photon count rate > 50 ms^-1 for 2.25 M and 3.2 M GdmCl and from 2 ms bins in the trajectories with the mean photon count rate > 30 ms^-1 for 4.6 M, 4.3 M, and 3.8 M GdmCl concentrations. At the relative viscosity (η/η₀) 1, 10, and 38, the higher concentration of GdmCl was used to counteract the stabilization of proteins by glycerol to maintain the ratio of folded to unfolded molecules as close to unity as practically possible. The similar ratio of the integral of the folded (high FRET) and the unfolded (low FRET) distributions indicates that the equilibrium constant is unchanged at these conditions, as shown more precisely in the maximum likelihood analysis.

Extended Data Table 2.

Viscosity dependence of the kinetic parameters obtained from the two-state maximum likelihood analysis, the transition path time, and the correlation time of the unfolded state dynamics obtained from the donor-acceptor cross-correlation at 22°C.

Gdmcl (M)	2.25	3.2	4.6	4.3	3.8
Glycerol (%)	0	50	55	58	61
Viscosity (η/η0)	1	10	36	38	53
EF	0.91 (0.0005)	0.84 (0.0004)	0.79 (0.0007)	0.79 (0.0004)	0.81 (0.0005)
EU	0.55 (0.0007)	0.50 (0.0005)	0.47 (0.0004)	0.49 (0.0005)	0.52 (0.0011)
k (ms-1)	0.85 (0.02)	0.48 (0.01)	0.46 (0.01)	0.40 (0.01)	0.56 (0.01)
pF	0.48 (0.008)	0.50 (0.006)	0.23 (0.004)	0.50 (0.005)	0.72 (0.005)
Transition path time (μs)	12.2 (2.0)	33.3 (2.7)	NA	39.1 (4.0)	49.0 (4.9)
Donor-acceptor cross correlation time in the unfolded state, 1/k (μs)	NA	0.80 (0.18)	3.4 (0.6)	3.8 (0.7)	6.1 (1.6)

Errors are standard deviations obtained from the diagonal elements of the covariance matrix calculated from the likelihood function.