Efficient Calculation of Empirical P-values for Genome-Wide Linkage Analysis Through Weighted Permutation

Abstract

Linkage analysis in multivariate or longitudinal context presents both statistical and computational challenges. The permutation test can be used to avoid some of the statistical challenges, but it substantially adds to the computational burden. Utilizing the distributional dependencies between π̂ (defined as the proportion of alleles at a locus that are identical by descent (IBD) for a pairs of relatives, at a given locus) and the permutation test we report a new method of efficient permutation. In summary, the distribution of π̂ for a sample of relatives at locus x is estimated as a weighted mixture of π̂ drawn from a pool of ‘representative’ π̂ distributions observed at other loci. This weighting scheme is then used to sample from the distribution of the permutation tests at the representative loci to obtain an empirical P-value at locus x (which is asymptotically distributed as the permutation test at loci x). This weighted mixture approach greatly reduces the number of permutation tests required for genome-wide scanning, making it suitable for use in multivariate and other computationally intensive linkage analyses. In addition, because the distribution of π̂ is a property of the genotypic data for a given sample and is independent of the phenotypic data, the weighting scheme can be applied to any phenotype (or combination of phenotypes) collected from that sample. We demonstrate the validity of this approach through simulation.

Despite the recent development of association methods in general, and genome-wide association in particular (Neale and Sham 2004), linkage analysis remains a useful technique in the identification of genomic regions that may harbor quantitative or qualitative trait loci. Linkage analysis is robust to population stratification, and is expected to yield signals when multiple variants give rise to phenotypic variation (allelic heterogeneity). Multivariate linkage analyses of correlated or longitudinal data can increase the power and interpretability of results. At the same time, certain statistical problems and computational limitations that are inherent in linkage analysis of complex traits hinder its application. The vast majority of multivariate linkage analyses have been conducted using extensions of the univariate variance components (MVC) model (Amos 1994; Wang and Elston 2007). However, a major limitation of the MVC approach arises from parameters estimates at the boundaries of the parameter space, which leads to asymptotic distributions characterized by complex mixtures of χ² distributions with different degrees of freedom which are influenced by the covariance between variables and the specific hypotheses tested (Amos et al. 2001; Visscher 2006).

The calculation of empirical P-values provides the most general solution to this problem. Currently the two most popular methods for obtaining empirical P-values for linkage analyses involve using ‘gene-dropping’ simulations or permutation to randomize the relationship between genotypic and phenotypic data. Both methods produce asymptotically unbiased estimates of significance (Churchill and Doerge 1994; Ott 1989). Gene-dropping requires the simulation of unlinked genotypic data that preserve the information content, allele frequency and patterns of missing data that are observed within the ‘true’ genotypic data. Alternatively, permutation can be used to randomize either the coefficient of genotypic sharing π̂, or the phenotypes, across relative pairs. Essentially, the connection between the genotypic and the phenotypic data is deliberately disrupted and the linkage analysis is repeated over a large number of permutations in order to obtain an empirical distribution of test statistics for which the null hypothesis is true. The test statistic obtained from the original, un-permuted dataset is then compared with this empirical distribution to assess significance. This approach has an attractive simplicity, but it does require that the permutations are performed across pedigrees with the same family structure by first permuting across families of the same size and then permuting within families. However, while empirical P-values offer robustness against violation of the assumptions of statistical methods (Churchill and Doerge 1994; Ott 1989), they remain computationally intensive for multivariate analyses.

In a genome scan, linkage analysis is conducted at a large number of loci (typically 500–3,500) across the autosomes. Ideally, simulation and permutation methods should be employed at each locus in the genome scan. The computational time required to obtain empirical significance based on k replicates is k times that required for the initial analyses. For example, if we chose to examine evidence for linkage at 1 cM intervals, resulting in ~3,500 analyses that each take ~1 min, running 5,000 permutations or stimulations would require to 291,667 h (or just over 33 years) of computation time to generate the null distribution, with additional processing time required to extract the empirical P-values from the distribution. Thus, the time required to obtain empirical P-values multivariate analyses especially when using large samples and complex pedigree structures, can be prohibitive.

Several solutions have been proposed to overcome this computational burden. Sequential stopping (or adaptive permutation) strategies, adjust the number of simulations or permutations conducted at each locus so that fewer simulations are performed for less significant loci (Besag and Clifford 1991). While in the replicate pool method a small number of simulations or permutations are conducted at each loci, the per-family LOD score contributions are saved and resampled (Song et al. 2004; Terwilliger and Ott 1992; Wigginton and Abecasis 2006; Zou et al. 2004). These two methods have also been combined (Song et al. 2004).

Duffy has implemented the sequential stopping rule for a range of univariate analyses in SIBPAIR (http://www.qimr.edu.au/davidD/#sib-pair), and Wigginton and Abecasis (2006) have implemented the replicate pool in PSEUDO for use with the Kong and Cox NPL test (Kong and Cox 1997) conducted by MERLIN (Abecasis et al. 2002). However, while PSEUDO can examine convergent linkage peaks from univariate analyses of correlated traits there are currently no applications that implement either method for use with multivariate linkage analyses.

Here we propose a new efficient permutation method for calculating point-wise empirical P-values designed for use with uni- or multivariate variance components linkage analyses, which uses weighted mixtures to reduce the number of loci at which permutation must be conducted.

Methods

Background

Using permutation to obtain empirical P-values in the context of linkage analysis has been described previously (Iturria et al. 1999; Wan et al. 1997). In brief, consider a variance components linkage analysis of in a sample of full sibling pairs. Note that while we use the likelihood ratio χ² test to illustrate the method, in principle other test statistics may be employed. For each family at a given locus the data under analysis will consist of the phenotypes, any covariates and the coefficient of genotypic sharing at the loci (π̂). Assuming an alternate hypothesis of linkage (i.e., ${\sigma }_{\mathrm{QTL}}^2>0$), and a null hypothesis of no linkage ( ${\sigma }_{\mathrm{QTL}}^2=0$), the significance of linkage can be assessed using a permutation test which randomizes the relationship between the phenotypes and π̂ while preserving the covariation among the phenotypes and the relationship between the phenotypes and the covariates. The linkage analysis is then conducted using the randomized data, yielding a new χ² statistic, and the process is repeated m times to obtain a set of ${\widehat{\chi }}_i^2\left(P\right)$, i = 1…m. Finally, χ̂², the statistic computed with the observed data, is compared to the empirical distribution of χ̂² (P) under the null hypothesis. It is important to note that an empirical P-value derived in this way is point-wise in nature, that is it does not control the experiment- or family-wise type one error associated with testing many hundreds or thousands of loci across the genome. A false discovery rate procedure could be used after point-wise empirical P-values have been obtained.

As the phenotype and covariate information remain constant for all loci across the genome it follows that for any given locus from a genome-wide linkage scan, the results of a series of m permutation tests will depend on the distribution of the probabilities that a pair of relatives share zero, one or two alleles identical by descent (IBD) at that locus. In effect, any two loci at which the distributions of π̂ (which is computed as P(IBD = 2) + 0.5P(IBD = 1)) are identical will yield identical empirical P-values (if m is sufficiently large).

Consider a linkage analysis conducted at i regular intervals across the autosomes using a multipoint algorithm to compute IBD. In the absence of genotype based selection, and assuming that the sample remains constant across loci, the distribution of π̂ at each locus under analysis does not vary markedly (Visscher et al. 2006). For example, given a sample of full sib-pairs the distribution of π̂ will be polymodal with the primary mode approached 0.5 and secondary modes at 0 and 1.

Given the relatively low variation in the distribution of π̂, we hypothesized that it would be possible to approximate the distribution of π̂ at a given locus x by creating a weighted mixture of l loci. If this were so, then a weighted bootstrap of permutation results from each of the l loci would closely approximate the actual empirical significance that would have been obtained by permutation at loci x. In this article, we use simulation to explore the feasibility and applicability of obtaining empirical P-values with this weighted permutation method.

Thus, we illustrate the use of this technique for both univariate and multivariate variance components analyses. In addition we examined the robustness of the method to non-normality, selection, and ordinal phenotypes. To this end, approximate P-values obtained from the proposed weighted permutation approach were compared to empirical P-values derived from the standard permutation approach (described above). The proposed weighted permutation method, simulation and analysis of data are described below.

Weighted permutation method for obtaining approximate P-values

A five part process was used to estimate empirical P-values via the weighted permutation approach. R and Mx scripts that implement the method are available from http://www.vipbg.vcu.edu/~sarahme/permute.html.

Distribution binning

At each of the i loci under analysis, π̂ is first binned into a number of equidistant bins by multiplying π̂ by 50 and rounding to the nearest integer. Bin frequency is then tabulated yielding i vectors, each containing the bin frequencies at a particular locus.

Identification of representative loci

Many methods might be used to identify a pool of l loci that could be weighted to derive empirical P-values and the ideal value of l to maximize specificity and sensitivity of estimate P-values. We have experimented with both random selection (not shown) and a ‘representative loci’ approach, which we will describe here, and with l values of 50, 20, and 10. Based on the assumption that among the distributions of π̂ observed there may be groups of loci that more closely reflect each other (perhaps due to phenotypic selection or sampling biases) we attempted to identify a series of ‘typical’ or ‘representative’ loci from which weighted mixtures might be obtained that would accurately capture the distribution of π̂ at other loci. To obtain these representative loci we utilized an existing R: Bioconductor package Genefinder, which is designed to identify similar patterns of gene expression in microarray data (Gentry and Kagen 2006, http://rss.acs.unt.edu/Rdoc/library/genefilter/html/genefinder.html). We entered bin frequencies into Genefinder analyses, to obtain for each of the i loci, the five loci with the closest (Euclidean distance) bin frequencies. The loci were then ranked by the frequency with which they had been identified in the Genefinder analysis, and the top l loci were selected to form a pool of representative loci.

Obtaining mixture weights

Mixture weights were obtained in a simplified multivariate regression procedure. For each locus in turn, a vector of linear weights was estimated, producing the linear combination of the representative π̂ distributions that best approximated the locus under analysis. Thus, at each locus in turn the approximate probability densities in each bin were estimated by multiple regression using the L representative loci as predictors. Formally, the regression model may be written as, f_i = β₁f₁ + β₂f₂ … β_Lf_L, where f_i is the vector of π̂ bin frequencies at locus i, subject to the constraints that 0 ≤ β_l ≤ 1for all l = 1…L, and $\sum _{l=1}^L{\beta }_l=1$. This constrained regression analysis was implemented in Mx (Neale et al. 2006b) using a script available from http://www.vipbg.vcu.edu/~sarahme/permute.html.

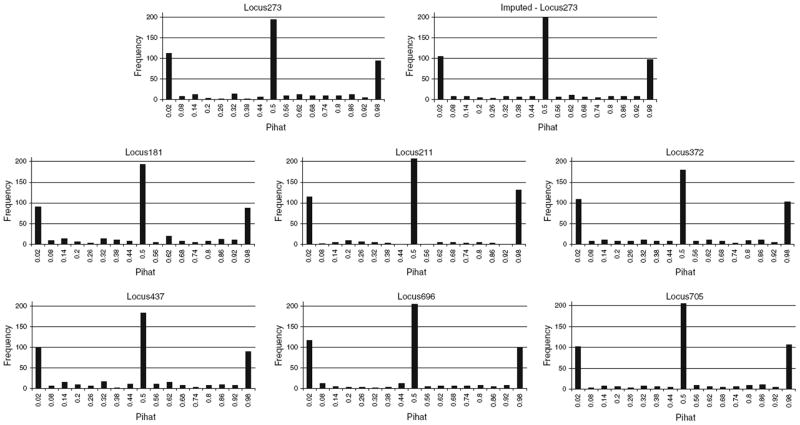
Figure 1 shows the observed and estimated distributions for an example locus with the representative loci that were used to obtain this estimate.

Fig. 1.

The observed (top left) and imputed (top right) distributions for an example locus with the representative loci (lower six graphs) that were used to obtain this estimate. The following regression equation was used to impute the data Locus 273 imputed = 0.28 * Locus181 + 0.01 * Locus211 + 0.10 * Locus372 + 0.06 * Locus437 + 0.37 * Locus696 + 0.18 * Lo-cus705 + 0 * Locus491 + 0 * Locus215 + 0 * Locus152 + 0 * Locus504. The four representative loci with zero weights are not shown here

Permutation of the representative loci

Following the identification of the l representative loci permutation is used to obtain a χ̂²(P) distribution at each l locus. As the permutation test requires that the randomized data be analyzed using the same analytic method as the observed data the implementation of the permutations depend in part on the program used to conduct the initial linkage analysis.

The simulated examples used Mx to conduct the linkage analysis. In Mx linkage analysis the data is supplied in a flat file, with each family’s data entered on a separate record. Each record contains the phenotypes and π̂ which is pre-computed using IBD estimates from MERLIN. Given this format permutation can be conducted with a simple awk command which separates the column(s) containing the π̂ data from the phenotypes, randomizes these columns and then merges the randomized data with the phenotypes. In the simulated examples we used permutation to create 5,000 null replicates for each of the l representative loci.

However, if the analysis were conducted using a program which used a pedigree file format such as SOLAR the IBD estimates could be saved at each of the representative loci, these could than be separated from the identifiers, randomized, and read back in to obtain a χ̂²(P) distribution.

Bootstrapping of the representative distributions

Once the χ̂²(P)distributions had been obtained we compiled composite test statistic distributions for each of the i loci under analysis. For each loci under analysis we multiplied the vector of weights by the number of permutations or length L which was used to perform a weighted draw from the l χ̂²(P). For example given the situation shown in Fig. 1 where Locus 273 was imputed from Loci 181, 211, 372, 437, 696, 705, 491, 215, 152, and 504 using the weights 0.28, 0.01, 0.10, 0.06, 0.37, 0.18, 0, 0, 0, and 0 we would draw at random 1,400 χ̂² statistics from the χ̂²(P) distribution of Locus 181, 50 from the distribution of Locus 211, and so on. A point-wise P-value would then be calculated for each locus by comparing the observed test score to the composite test distribution. In the simulated examples this bootstrapping step was repeated 100 times for each locus and the resultant point-wise P-values were averaged to yield an approximate weighted permutation P-value.

Simulation and data analysis

To assess performance of the proposed method, genotypic and phenotypic data were simulated under six conditions:

1. Normally distributed quantitative trait

2. Highly skewed non-normal quantitative trait (described further below)

3. Normally distributed quantitative trait where an extremely discordant and concordant (EDAC) sampling strategy had been applied

4. Binary trait with 20% prevalence

5. Bivariate normally distributed quantitative trait

6. Bivariate skewed quantitative trait

For all simulations genotypic data were produced using TWINSIM (http://www2.qimr.edu.au/davidD/twinsim.html). Inter-marker distances and marker coverage were based on the genotypic data of the Irish Affected Sib-Pair Study of Alcohol Dependence study (Kuo et al. 2007, 2006; Prescott et al. 2006) with six alleles present at each marker (allele frequencies 0.1, 0.5, 0.2, 0.1, 0.05, 0.05) yielding data for 1,020 autosomal markers at an average inter-marker distance of 4 cM. Data were simulated for 500 nuclear families each composed of a pair of parents with two offspring. For simulations 1–4, phenotypes with unit variance were simulated such that: 20%, 10% and 5% of the variation was due to additive QTLs on chromosomes 10, 4, and 12; 40% was due to a residual additive genetic effects; and the remaining 25% due to non-shared environmental sources. A Fisher-Cornish expansion (1938) was applied to the data in simulation 2 to yield a data set in which was both skewed (S = 2) and kurtotic (K = 6). In simulation 3, a post hoc selection strategy was applied so that families were ascertained only if the phenotypes of both offspring fell in the top or bottom 20% of the distribution (the 500 ascertained families were drawn from an initial pool of 30,000 simulated families). The phenotypes in simulation 4 were recoded as affected when they fell in the top 20% of the distribution, and as unaffected otherwise. The simulation of the bivariate data sets is summarized in Table 1 below. A Fisher-Cornish expansion was applied to one set of simulations to yield a skewed bivariate data set, with skewed cross-trait and cross-sibling distributions.

Table 1.

Simulation parameters for the bivariate data sets

	Normally distributed bivariate data		Skewed bivariate data
	Trait 1	Trait 2	Trait 1	Trait 2
QTL effects (proportions of variance)
Ch 4	5	0	25	0
Ch 10	30	20	15	20
Ch 12	0	15	15	15
Additive genetic effects (proportions of variance)
A1	5	15	5	15
A2	20	0	0	0
Non-shared environmental effects (proportions of variance)
E1	40	0	40	0
E2	0	50	0	50
Skew following transformation			−1	−2
Kurtosis following transformation			1	4.5

Application

Multipoint identity by decent was estimated using MERLIN at 5 cM intervals across the genome, yielding 735 locations for analysis. IBD estimates were transformed to π̂, and standard sib-pair variance components linkage analyses were conducted in Mx ( $H_0:{\sigma }_{\mathrm{Total}}^2={\sigma }_{\mathrm{Add}.\mathrm{Gen}.}^2+{\sigma }_{\mathrm{Non–sharedEnv}.}^2$; $H_1:{\sigma }_{\mathrm{Total}}^2={\sigma }_{\mathrm{QTL}}^2+{\sigma }_{\mathrm{Add}.\mathrm{Gen}.}^2+{\sigma }_{\mathrm{Non–sharedEnv}.}^2$). For the bivariate case, a fully pleiotropic QTL was modeled (the path coefficients were specified as a 2 × 1 vector). While there are many linkage tests that may be employed for the analysis of univariate data, VC linkage analysis is suitable for a wide range of analytic situations, including univariate and multivariate analyses, qualitative and quantitative data, and selected samples (with the incorporation of ascertainment corrections for non-symmetric ascertainment schemes). Although univariate VC linkage analyses with skewed phenotypes show an increase type one error when the asymptotic null distribution of ${\chi }_{0.1}^2$ is assumed, this can be corrected through the calculation of empirical P-values through gene-dropping or permutation (Li et al. 2006) or the use of an corrected test statistic (Li et al. 2006; Peng and Siegmund 2006). Thus, as the primary aim of the current simulations was not to assess the efficiency or accuracy of the QLT statistics per-se but rather to examine the convergence between P-values obtained using the weighted permutation approach and P-values using a standard permutation approach (in which a set number of permutations are performed at each and every loci) we used VC linkage analyses for all simulations.

To summarize, to generate a ‘true’ empirical P-value to which the approximate weighted permutation P-value could be compared, π̂ as randomized across the 500 sib-pairs and the analysis was rerun recording the observed minus twice log-likelihood. This process was repeated 5,000 times. The observed test statistic was then compared to this series of permutation results to obtain a ‘true’ point-wise empirical P-value. The empirical P-values from the mixture distribution approach were then compared against this ‘true’ point-wise empirical P-value. Preliminary analyses revealed no difference in the performance of the method as the size of the representative pool was decreased from 50 to 20 then to 10 loci. Thus, the results from a representative pool size of 10 loci are described here.

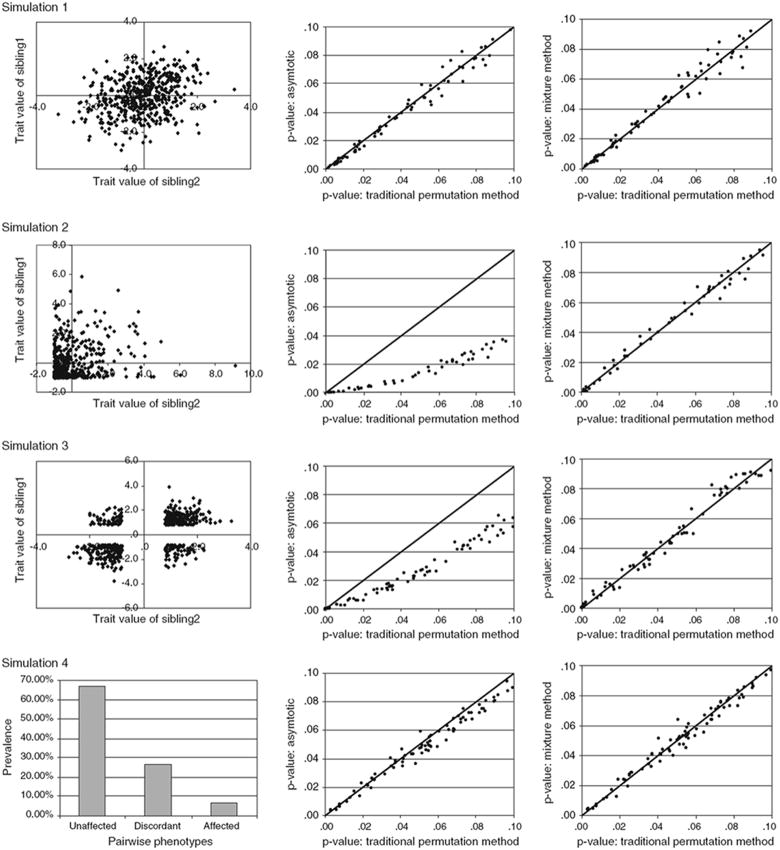
Graphical summaries of analyses of the univariate normally distributed data are given in Fig. 2. The bivariate distribution of the sibling phenotypes is shown in the first column. The second column shows the relationship between the asymptotic P-values (calculated as ${\chi }_{0.1}^2$, a 50:50 mixture of a point mass of zero and ${\chi }_1^2$) and the empirical P-values obtained using the standard permutation method, and has been truncated to show only those loci with an empirical P-value of 0.1 or less. As these figures show when the assumptions of multivariate normality are met (as in simulations 1 and 4) there is close agreement between the asymptotic and empirical P-values, however, in the face of obvious violation (simulations 2 and 3) the use of asymptotic P-values would result in an increase in type one errors as has previously been demonstrated. The third column shows the relationship between the empirical P-values obtained using the standard permutation method, and those derived from the weighted permutation method. In all cases, the approximate weighted permutation P-values agree closely with the empirical P-values. However, while there is little discrepancy between the P-values obtained from the standard and weighted permutation approaches there is a large difference in the efficiency of these two methods; 3,675,000 linkage analyses using null replicated were conducted to obtain the empirical P-values (735 loci each permuted 5,000 times), in contrast the approximate P-values were obtained from only 50,000 analyses of null replicates (10 loci each permuted 5,000 times). At an average time of 1 s per analysis for simulation 4 the weighted permutation method could produce point-wise P-values on a single processor for all loci in 14 h, as compared to the 1,021 h (43 days) required for the standard permutation method.

Fig. 2.

Graphical summary of the analyses of the univariate data sets. Rows: 1st results from a normally distributed continuous variable, 2nd a highly skewed continuous variable resulting from threshold based ascertainment, 3rd a normally distributed continuous variable with EDAC sampling, 4th a binary variable with a 20% prevalence. Columns (left to right): The bivariate distribution of the phenotypic values (the trait value of sibling 1 is shown on the y axis while sibling 2 is shown on the x axis, a pair-wise prevalence graph is given for the binary data); for P-values <0.1 asymptotic P-values graphed against empirical P-values from 5,000 permutations/locus (with x = y reference line); for P-values <0.1 mixture distribution P-values graphed against empirical P-values from 5,000 permutations/locus (with x = y reference line)

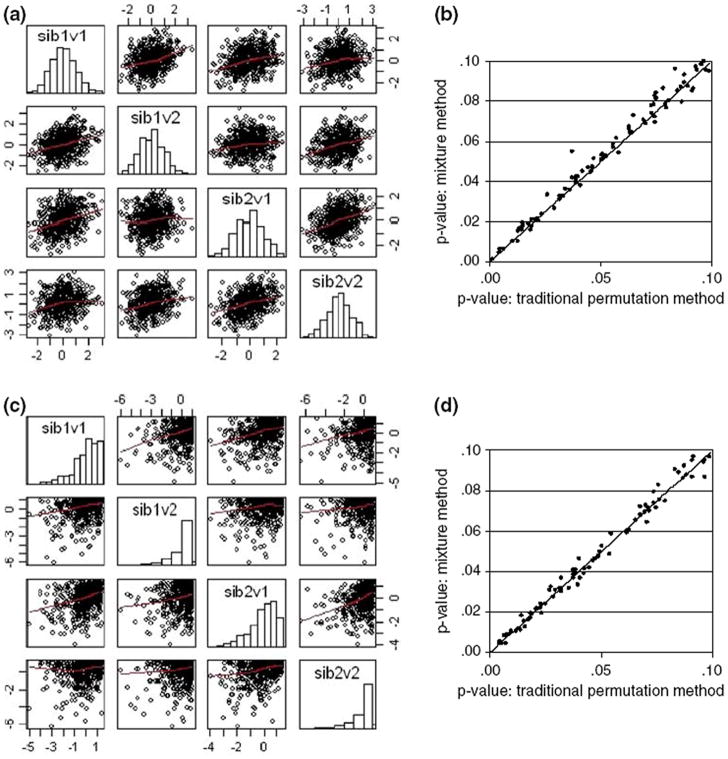
Given that the distribution of π̂ and the calculation of weights is not influenced by the number or phenotypes under analysis the results from the bivariate simulations shown in Fig. 3 are very similar. Here the left column summarizes the multivariate distribution of the phenotypes while the comparison of the weighted permutation and empirical P-values is shown in the right hand columns. Thus, neither the number nor the distribution of traits influences the ability of the proposed method to recover the empirical P-values derived from permutation. The mean and variance of the absolute deviation between the empirical P-values derived from traditional permutation methods and the weighted mixture P-value for both the univariate and bivariate simulations are given in Table 2.

Fig. 3.

Graphical summary of the analyses of the bivariate data sets. Rows: (graphs a and b) 1st results from two normally distributed continuous variables, (graphs c and d) 2nd two highly skewed continuous variables. Columns: left (graphs a and c) The bivariate distribution of the phenotypic values, univariate distributions of each of the phenotypes are summarized using histograms on the diagonal while scatterplots give the bivariate distributions for each pair of traits; (graphs b and d) for P-values <0.1 mixture distribution P-values graphed against empirical P-values from 5,000 permutations/locus (with x = y reference line)

Table 2.

Mean and variance of the absolute deviation, and correlations between the P-values. The absolute deviation is calculated as the absolute difference between empirical P-values derived from traditional permutation methods and the weighted mixture P-values. Spearman’ rank correlations of the empirical P-values derived from traditional permutation methods and the weighted mixture P-values are given

	Mean absolute deviation	Variance	Spearman’s correlation
Univariates
Normal	0.0112	1.119E-04	0.986
Skew	0.0075	3.586E-05	0.984
EDAC	0.0079	3.863E-05	0.991
Binary	0.0081	4.182E-05	0.983
Bivariates
Normal	0.0059	2.217E-05	0.988
Skew	0.0065	8.317E-05	0.992

Discussion

Using the distributional dependencies between π̂ and the permutation test, we have reported a new method, which can be used to obtain empirical P-values efficiently. Because the method depends on the distribution of π̂, its performance is a function of the sample’s genotype data rather than its phenotypic distribution. The method is theoretically robust to sample selection and distributional properties of the phenotype. Additional simulations (not described here) suggest that the method is also robust to the dimensionality that arises from larger sibships. This robustness is in part due to the analysis of bin frequency data rather than the continuous distribution, and also the stability of the average amount of genetic sharing across loci. Thus, although more work is needed, the results presented here suggest that the method is robust to phenotypic distributions and could be used with larger pedigrees and potentially with other linkage statistics.

Ordinarily, obtaining empirical P-values for a genome-wide scan is computationally intensive, requiring tens or hundreds of thousands of permutation runs at each of thousands of locations across the human genome. The new weighted permutation approach described here offers a highly efficient alternative which greatly reduces the number of permutation analyses performed. Our results suggest that accurate approximations may be obtained with as few as 10 representative loci. In the case of a genome-wide scan performed at 1 cM intervals, it would require only 10 sets of permutation tests as opposed to approximately 3,500 or to provide a more concrete example, if each analysis took approximately 10 s and we ran 5,000 permutations at each locus, the new method would require 139 h of computation as compared to 48,611 h. Given that complex multivariate analyses can take many minutes per analysis the proposed method could potentially save weeks or months of computation time. The current method also requires fewer analyses than current efficient techniques. The proposed technique would require 50,000 analyses to derive empirical significance estimates for a 1 cM linkage scan. In contrast, the replicate pool method would require approximately 350,000 analyses (assuming 100 replicates at each locus). While the number of analyses required using the sequential stopping rules are situation specific and can not be calculated a priori, it is likely to be more than would be required by the replicate pool method.

A particularly valuable aspect of this development is that it makes multivariate analyses practical. Such analyses are frequently computationally intensive, requiring optimization across a large number of parameters. Evaluation of the likelihood function in such analyses may involve inversion of large covariance matrices in the case of continuous measures, or the numerical estimation of multidimensional integrals when the data are ordinal or binary. This latter case is of particular relevance in the study of complex phenotypes, particularly those that involve behavioral or psychological measures (e.g., psychiatric disorders, substance abuse), because the assessments rarely involve truly quantitative measures made on an interval scale (Neale et al. 2006a; Neale et al. 2005). In such situations, data analysis should ideally proceed using the symptoms, signs or questionnaire responses at the item level of measurement, rather than by their aggregation into a scale score which may possess undesirable properties such as different measurement error at different points on the distribution. Multivariate analyses often generate statistics that do not conform to simple distributional assumptions (Self and Liang 1987) and are therefore excellent candidates for permutation tests.

Although the five-step process we describe may seem complex, it can be simplified when it is to be applied multiple times to the same dataset. The distribution of π̂ is a property of the genotypic data for a given sample and is independent of the phenotypic data. Therefore, the weighting scheme to construct the distribution of π̂ at the target loci need only be obtained once. While a new set of permutations will be needed at the representative loci, their mixing proportions remain invariant and can be applied to any phenotype (or combination of phenotypes) collected from that sample. Application of this reduced step procedure assumes that only small amounts of data are missing and that they are missing completely at random.

An inherent limitation of the proposed method is that the standard error of the approximate P-values will vary across loci as function of the number and weighting of representative loci contributing to the composite distribution of test statistics at each locus. However, this is also a limitation of the sequential stopping rule technique and further investigation is required to determine the extent and impact that this may have on the accuracy of approximate P-values. While the standard error is expected to fluctuate across loci (due to varying information content of the markers), obtaining the approximate P-value from the mean of a series of bootstraps will yield approximate P-values that are asymptotically distributed as empirical P-values. The second potential disadvantage is that permutation testing in arbitrary pedigrees is inherently complex when the sample size of any particular pedigree structure is small. Thus the method may be difficult to implement in samples in which permutation testing is inherently complex. In addition, this method is unsuitable for use in any situation where obtaining an empirical P-value via permutation is untenable such as an analysis of affection status in a sample of affected sib-pairs.

In conclusion, we have implemented a new computationally efficient method for obtaining approximate empirical P-values for genome scans. Further work is planned to examine the robustness of the method, the optimum number of permutations, representative loci and bootstraps to maximize selectively and specificity.