Informational Requirements for Transcriptional Regulation

Abstract

Transcription factors (TFs) regulate transcription by binding to specific sites in promoter regions. Information theory provides a useful mathematical framework to analyze the binding motifs associated with TFs but imposes several assumptions that limit their applicability to specific regulatory scenarios. Explicit simulations of the co-evolution of TFs and their binding motifs allow the study of the evolution of regulatory networks with a high degree of realism. In this work we analyze the impact of differential regulatory demands on the information content of TF-binding motifs by means of evolutionary simulations. We generalize a predictive index based on information theory, and we validate its applicability to regulatory scenarios in which the TF binds significantly to the genomic background. Our results show a logarithmic dependence of the evolved information content on the occupancy of target sites and indicate that TFs may actively exploit pseudo-sites to modulate their occupancy of target sites. In regulatory networks with differentially regulated targets, we observe that information content in TF-binding motifs is dictated primarily by the fraction of total probability mass that the TF assigns to its target sites, and we provide a predictive index to estimate the amount of information associated with arbitrarily complex regulatory systems. We observe that complex regulatory patterns can exert additional demands on evolved information content, but, given a total occupancy for target sites, we do not find conclusive evidence that this effect is because of the range of required binding affinities.

1. Introduction

Regulation of gene expression is a central process in living systems that is addressed primarily through the regulation of transcription (Ptashne, 2005). At its most fundamental level, transcriptional regulation is implemented by the binding of a class of proteins, known as transcription factors (TF), to specific sites in the promoter regions of regulated genes (Huang et al., 1999; Orphanides and Reinberg, 2002). Binding of a TF to these sites can either facilitate or hinder binding of the RNA–polymerase holoenzyme at the promoter, resulting in activation or repression of transcription (Ptashne, 2005; Minchin and Busby, 2009). TF-binding sites are typically short (6–20 bp) and fixed-length and often degenerate DNA sequences that are efficiently located and bound by the TF through recognition of specific patterns or motifs. Information theory provides a robust theoretical framework to analyze the interaction between TF and their binding sites (Schneider et al., 1986). Given a collection of aligned TF-binding sites (i.e., a TF-binding motif), one can compute the amount of information present in the TF-binding motif as the difference in uncertainty about which base occupies each position of the motif when compared with an equivalent number of unaligned genome subsequences of the same length. More formally, the information R_sequence(i) of the ith position in the TF-binding motif is defined as the difference between the entropies of the unaligned and aligned sequences:

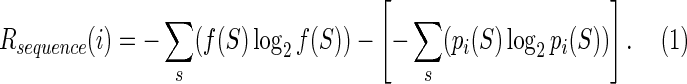At any given position, the frequencies of each base in an unaligned collection of sites will follow the genomic background frequencies f (S) for each base S, whereas the collection of aligned TF-binding sites will display position-specific frequencies p_i(S) for the ith position. Assuming positional independence, the total amount of information embedded in the motif is

where the sum ranges over all positions i of the motif up to its length L.

The formula for R_sequence forms the basis of sequence logos, the standard graphical representation of TF-binding motifs, and has become the most extended model for TF-binding motifs (Schneider and Stephens, 1990). As defined, R_sequence can be interpreted formally as the amount of information embedded by evolution in a set of TF-binding sites, and it follows naturally that this value should be linked to the amount of information required to locate those sites in the genome. Given a genome of size G, the information required to locate M sites is given by

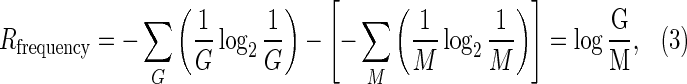which corresponds to the difference between the entropy of a system with an unspecific TF that binds with equal affinity at all genome positions and that of a system with a specific TF capable of binding with equal affinity to M target sites and nowhere else in the genome. R_frequency therefore provides a lower bound on the information required to identify M target sites in a genome of size G.

It has been shown for several bacterial TFs operating on unbiased genomes that R_frequency provides a good approximation to the observed R_sequence (Schneider et al., 1986), and the approximate equality R_sequence≈R_frequency has come to be seen as a fundamental result of the application of information theory to TFs and their binding sites. Several analytical models of TF-binding site evolution have been developed (Gerland and Hwa, 2002; Berg et al., 2004; Mustonen and Lassig, 2005; Stewart et al., 2012) and even applied to the study of the relationship between R_sequence and R_frequency (Kim et al., 2003), but for tractability these models require strong assumptions for the binding model and genomic background, and thus do not capture the full dynamics of the evolution of mutual information between TFs and their cognate-binding sites. In previous work, the relationship between R_sequence and R_frequency has been further substantiated by explicit evolutionary simulations (Schneider, 2000). Synthetic genomes encoding a simulated TF (or recognizer) and predefined locations for target sites were evolved using a genetic algorithm framework. The system modeled the TF as a linear classifier with an evolvable threshold capable of designating each position of the genome as bound or unbound. The fitness of an organism was evaluated as the inverse of the total amount of errors made by the recognizer: binding at nontarget locations (false positives) and failing to bind at predefined targets (false negatives). Using this model, it was shown that the observed R_sequence at predefined targets evolves to closely match the predicted R_frequency (Schneider, 2000).

Most experimental techniques used traditionally in the identification of TF-binding sites provide a qualitative description of potential sites as bound or not bound by the protein. As a consequence, most theoretical models of the interaction between TFs and their binding sites have traditionally aimed at matching a binary representation of TF-binding sites. Nonetheless, as ChIP-seq and other high-throughput quantitative protein–DNA binding assays have made manifest, TFs often display a broad range of affinities for target sites and these distinct affinities lead in vivo to different occupancies that can have relevant physiological effects (Browning and Busby, 2004; Maerkl and Quake, 2007; Mardis, 2007). These findings have recently led to the emergence of computational methods capable of harnessing high-throughput data to capture the quantitative nature of TF activity (Roider et al., 2007; Badis et al., 2009; Zhao and Stormo, 2011). Hence, an important theoretical question in the analysis of TF-binding motifs concerns the impact of regulatory demands on the observed information content (R_sequence). The effect of regulatory demands on the information content of TF-binding motifs is not obvious. For instance, motifs harboring sites with lower than average occupancies might require less information because such sites need not be recognized as precisely by the TF. On the other hand, in such a situation the TF must ensure that different groups of sites be bound at distinct occupancies, which might require additional information (Erill and O'Neill, 2009). Predictive estimators of R_sequence, like R_frequency, are based on a binary definition of TF-binding sites and cannot be generalized trivially to systems with differential regulation of sites. In this work we develop and validate a platform to simulate the co-evolution of TFs and their binding motifs, and we use it to explore the impact of regulatory requirements in TF-binding motifs. We generalize R_frequency to deal with realistic evolutionary scenarios, and we validate this generalization using evolutionary simulations. Our results reveal a logarithmic dependence of the evolved information content on the fraction of total probability mass associated with target sites. Further, we observe that evolved systems can effectively exploit the genomic background to enact their regulatory roles. Finally, simulations on arbitrary regulatory patterns reveal that the evolved information content is predicted by total target occupancy and is invariant with respect to the complexity of the site-wise arrangement of target occupancies.

2. Results and Discussion

2.1. In silico evolution of transcriptional regulatory networks

The evolution of simple transcriptional regulatory networks has been studied before by means of explicit simulation of TFs and their binding sites, leading to fundamental insights into the informational constraints faced by such networks (Schneider, 2000). In this work we generalize this approach by developing an evolutionary simulator that incorporates biophysical modeling and addresses several caveats of previous attempts. Evolutionary simulator of transcriptional regulatory motifs (ESTReMo) uses a genetic algorithm backbone to simulate the evolution of transcriptional regulatory networks using a modular approach (Fig. 1). In ESTReMo, each organism contains two evolvable components: a TF model and a set of promoter regions for target genes. The TF is modeled as a feed-forward artificial neural network that operates on the set of target promoter regions and on a fixed genomic background. In each generation, the TF model is used to compute the free energy of binding for all positions in target promoter regions and in a randomly sampled subset of the genomic background. The occupancy of each promoter position is computed according to a statistical mechanical distribution on an effective background generated by scaling up the randomly drawn samples. These occupancies are then used to determine the expression level for each target gene following a given expression model. Finally, organism fitness is evaluated as the sum of cost–benefit differences for each target gene and its desired expression level using an empirical fitness model.

FIG. 1.

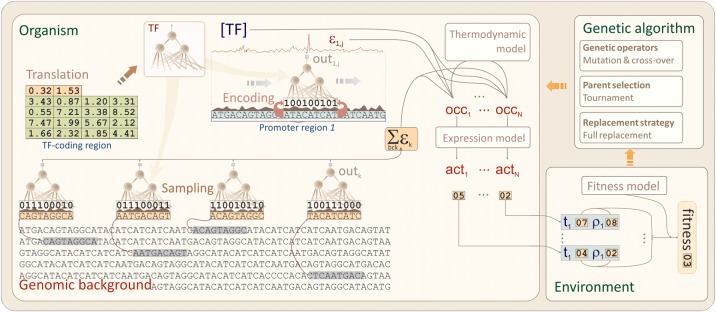
Schematic representation of the evolutionary simulator of transcriptional regulatory motifs (ESTReMo). Diagram summarizes the internal organization of an individual organism and its connection with the fitness model. TF, transcription factor.

The combination of thermodynamic and empirical fitness models with a modular approach taken in ESTReMo has several advantages. The interpretation of neural network outputs as binding energies permits their incorporation into a well-described biophysical framework that can explicitly model nonspecific binding and physical distributions of site occupancy, and makes the results of the simulation directly comparable with real biological systems (Stormo and Fields, 1998; Djordjevic et al., 2003). This also enables us to couple predicted expression levels with a fitness model anchored on empirical data that take into account the effects of both under- and over-regulation of target genes (Dekel and Alon, 2005). The use of continuous energy, occupancy, and expression levels in conjunction with a continuous fitness function ensures that a fitness gradient is always available for the evolutionary process. This makes it possible to evolve regulatory systems on large genomic backgrounds, which is otherwise infeasible with threshold-based approaches. Furthermore, the use of a fixed genomic background, as opposed to an evolvable one, prevents the system from actively pruning pseudo-sites and allows us to run simulations on real genome sequences.

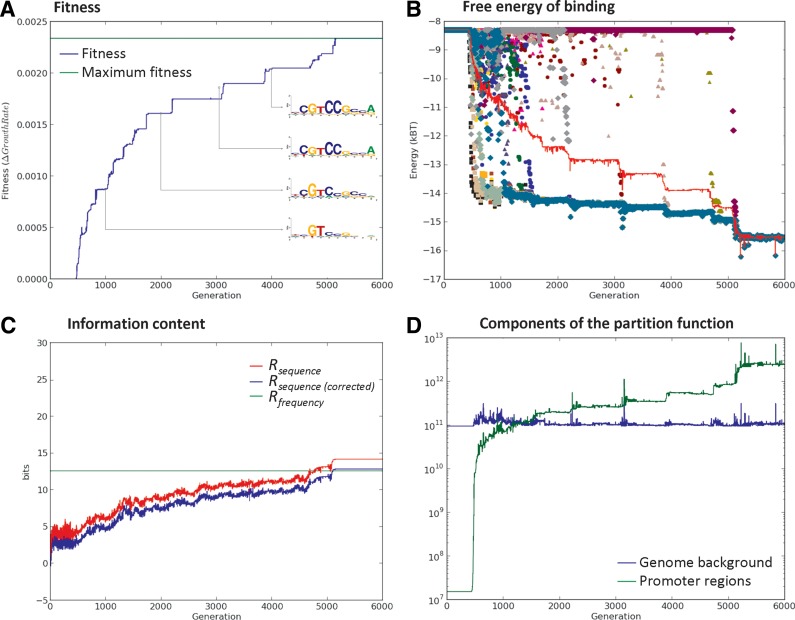
As illustrated in Figure 2, ESTReMo simulations are characterized by a period of rapid increase in fitness (Fig. 2A), in which the TF evolves to associate strong affinities (low energy values) to a primordial core of target sites, while maintaining the background at energies close to nonspecific binding. Thereafter, the simulation displays a step-wise increase in fitness that results from a progressive refinement of the recognizer and the gradual incorporation of additional sites. This behavior can also be traced by changes in the individual binding energies of sites (Fig. 2B) and by changes to the information content (R_sequence) of the associated TF-binding motif (Fig. 2C), and ultimately results in the TF assigning the preset fraction of probability mass to its target sites and the remainder to the background (Fig. 2D).

FIG. 2.

Trace indicators for a complete evolutionary simulation. All values correspond to the fittest organism in the population at any given generation. (A) Organism fitness. Sequence logos illustrate the step-wise evolution of the associated TF-binding motif as new sites are recognized. (B) Free energy of binding for each site in the motif. (C) Information content R_sequence (corrected and uncorrected for small-sample error) of the evolved TF-binding motif. The predicted R_frequency for the system is superimposed. (D) Contributions to the partition function from the sampled background (blue) and the promoter regions (green).

2.2. Evolutionary strategies for modulating regulatory activity

An important caveat of R_frequency as a predictor of evolved information content for the purposes of evolutionary simulations is that it assumes a scenario that cannot be evolved in a realistic framework for a single-molecule model. The posterior entropy in R_frequency assumes that all M sites targeted by the TF are bound with equal probability and that no other sites in the genome are bound, thereby assigning all the probability mass to M sites. Whereas these conditions can be approximated in nature by systems with multiple molecules of the TF, in a realistic simulation for the single-molecule case this ideal can never be achieved. In ESTReMo, where nonspecific binding is taken into account and where pseudo-sites cannot be completely eradicated by selection, the assumptions in R_frequency result in the uninformative evolution of systems targeting motifs as close to the consensus as possible. To circumvent this problem, we sought to evolve systems in which only a fraction (α) of the total probability mass is assigned to target sites. This led us to explore possible generalizations of R_frequency to this general case. Such an extension is bound by two opposing scenarios. If we assume that a fraction α of the total probability mass is assigned uniformly to M sites, the remaining (1−α) fraction can be distributed evenly over the genomic background (by extension of the maximum entropy assumption in R_frequency):

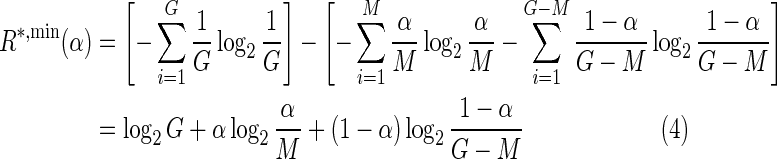or it can be concentrated at a single genomic position:

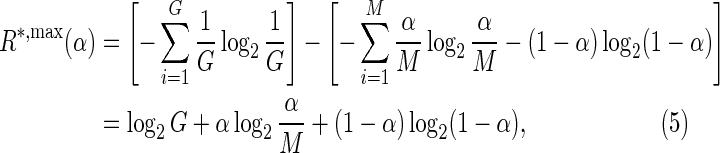leading to a lower bound (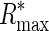) and an upper bound (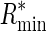) on the information content of a system capable of assigning a fraction α of its total probability mass uniformly among M sites.

In between these two bounds, a theoretical optimum may be defined as follows. On a uniform genomic background of size G, a classifier operating on R bits of information will recognize 2^−R · G positives in expectation. The fraction α of its probability mass assigned to the M target sites is therefore:

which leads directly to

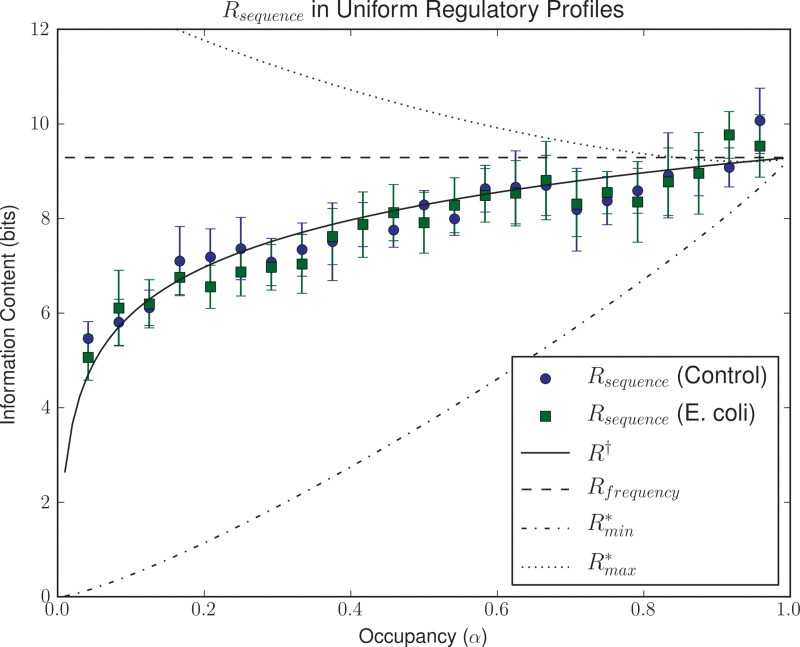
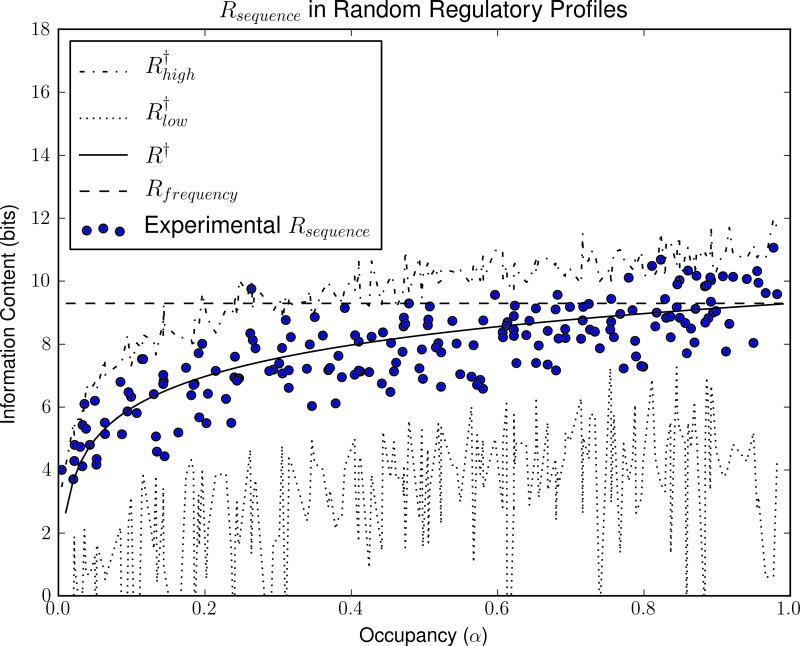
For any given α, the formula for R^† is therefore equivalent to R_frequency for a TF targeting M/α sites, suggesting that the optimal strategy for adjusting the occupancy of target sites in a TF consists in exploiting a proportional number of pseudo-sites with similar affinity to the target sites. To analyze the general applicability of this principle, we ran simulations to evolve TFs capable of recognizing sixteen 16-bp-long binding sites on an effective background of 10,000 bp sampled from either the Escherichia coli K-12 or a randomly generated genome of equal length. Specifically, we monitored the evolved R_sequence for evolutionary runs in ESTReMo under increasing α values. The results (Fig. 3) reveal that R^† is a robust predictor of the evolved R_sequence (R² = 0.59, p < 0.001), validating this particular generalization of R_frequency. We observe similar R_sequence values for simulations operating on E. coli and randomly generated uniform backgrounds (Mann–Whitney U-test p > 0.05). Despite this, TFs operating on real, larger genomic backgrounds may be able to exploit imbalances in the distribution of L-mers, already known to be targeted by restriction enzymes, to effectively decrease the informational demands of their associated TF-binding motifs (Gelfand and Koonin, 1997; Hahn et al., 2003).

FIG. 3.

Evolution of uniform regulatory systems. Plot shows evolved R_sequence values for simulations on randomly generated backgrounds (solid circles) and on the Escherichia coli genome (squares) as a function of the fraction of total probability mass (α) assigned to target sites. Error bars depict the 95% confidence interval for the mean. Corresponding values of R_frequency, 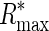, , 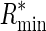and R^† are shown.

The regulatory properties of a TF are a function of its binding affinity for its target sites, the genome it operates on, and the number of TF molecules present in the cell. Even though the formal derivation of R^† and the experimental results presented here apply only to the single-molecule case, they have obvious implications for the general case of multiple copy number. The binding of TFs to sites that do not directly regulate the expression of genes (i.e., pseudo-sites) has been traditionally interpreted as genetic noise faced by the TF and assumed to be indiscriminate following the random occurrence of pseudo-sites in large genomes (Berg and von Hippel, 1987; Robison et al., 1998). The evolutionary principle behind R^†, however, suggests that TFs may be able to actively exploit pseudo-sites to modulate the effective occupancy of target regulatory sites, and that they may do so by relying on a small set of low-binding-energy pseudo-sites rather than on generic genome-wide sequestration by a full range of weak binding sequences. Hence, these results indicate that strong pseudo-sites may be considered functional and could be actively selected for by evolution.

2.3. Evolution of complex regulatory motifs

Transcriptional regulation of gene expression involves the precise tuning of both expression levels and temporal patterns of activation through the modulation of interactions between TFs, RNA–polymerase, and their respective binding sites (Browning and Busby, 2004; Friedman et al., 2005; Alon, 2007). Unfortunately, the precise effects of regulatory demands on the information content of evolved TF-binding motifs are hard to anticipate. Furthermore, the generalization of conventional approaches to predict information content in TF-binding motifs, such as R_frequency, leads to counterintuitive results. The formula for R_frequency in Equation 3 can be generalized to incorporate the entropy of a specific system that binds differentially to its target sites (as opposed to uniformly):

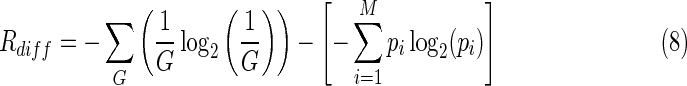Because the posterior entropy is now smaller than in the standard R_frequency case, the predicted information content must be higher. For instance, in a system targeting 16 sites on a 10,000 bp background, R_frequency predicts that a recognizer needs 9.29 bits of information to correctly locate its sites. For a recognizer that binds 75% of its time to 4 of its 16 sites and only 25% of the time to the remaining 12, however, the generalized R_diff indicates that 10.8 bits are necessary. This same reasoning applies to R^† and other generalizations of R_frequency and suggests that differential regulation imposes additional informational demands on TFs. It has been suggested that these informational requirements could be linked to guaranteeing accurate regulation throughout an extended regulatory range (Erill and O'Neill, 2009). Nonetheless, sites with decreased affinity for the TF should be more degenerate, from which it follows that a motif containing a significant number of “weak” sites should display lower information content (R_sequence).

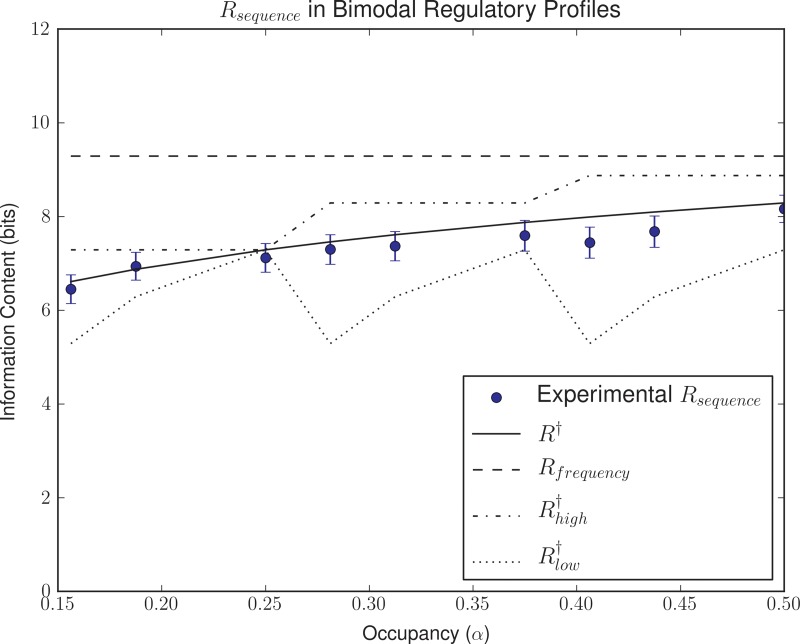
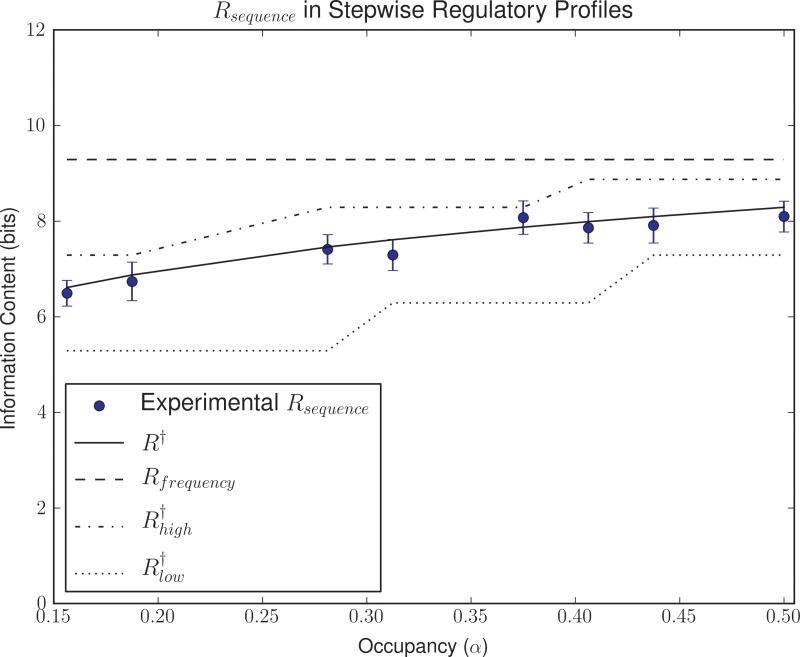
We analyzed the effect of regulatory constraints on the evolution of TFs and their binding motifs by simulating the evolution of two illustrative types of regulatory systems targeting 16 sites on a 10,000 bp effective background. In bimodal systems, one half of the 16 sites required higher occupancy (α_high) than the other half (α_low). In stepwise regulatory ladders, each of the 16 sites was set to evolve a value of occupancy (α_i) that increased gradually from α_low to α_high. In both cases, we defined a reference value for total probability mass α = 0.5, and we assigned sequential fractional values to α_low and α_high (α/4, α/8, and α/16 for α_low and α·3/4, α/2, and α/4 for α_high). The results (Figs. 4 and 5) reveal that the evolved information content (R_sequence) traces R^† for the effective α (α_eff), defined as the total amount of probability mass assigned to all 16 sites in each setting (R² = 0.23, p < 0.01 for Fig. 4 and R² = 0.22, p < 0.001 for Fig. 5).

FIG. 4.

Evolution of bimodal regulatory systems. The plot shows evolved R_sequence values for different evolutionary simulation scenarios with half of the sites set to higher occupancy (α_high) than the other half (α_low). Error bars depict the 95% confidence interval for the mean. For each R_sequence value, the corresponding R^† values for α_high, α_low, and α_eff values are shown.

FIG. 5.

Evolution of stepwise regulatory ladders. The plot shows evolved R_sequence values for different evolutionary simulation scenarios with sites gradually increasing from low (α_low) to high (α_high) occupancy. Error bars depict the 95% confidence interval for the mean. For each R_sequence value, the corresponding R^† values for α_high, α_low, and α_eff values are shown.

The results of bimodal and stepwise ladder systems strongly suggest that the information requirements of the system are dictated primarily by the effective fraction of total probability mass (α_eff) that the TF needs to assign to its target sites. In essence, the fraction of total probability mass assigned to target sites dictates the specificity of the TF, which imposes constraints on the required information content (R_sequence) of the TF-binding motif. As a result, the information content of a TF-binding motif for a system implementing an arbitrarily complex regulatory pattern can be estimated to first order by R^†(α_eff). To analyze the possible role of other contributing factors, such as the regulatory range that the TF needs to target, we conducted a series of simulations in which the regulatory targets for sixteen sites were sampled uniformly at random from the set of possible regulatory profiles. The results shown in Figure 6 reveal that the information content of evolved TF-binding motifs meeting these regulatory demands correlates with R^†(α_eff) (R² = 0.66, p < 0.01), and is effectively bound by R^† computed for 1 site at α_high and for 1 site at α_low (permutation test, p < 0.01). We detected no relationship, however, between information content and the coefficient of variation of the target occupancies (R² = 0.004, p > 0.05), suggesting that the dispersion of the regulatory targets is not explanatory after correction for mean occupancy. These results therefore support the previously stated hypothesis that the effective fraction of total probability mass is the major factor dictating the evolution of information content in TF-binding motifs. Furthermore, they show that for a given effective occupancy the span of required occupancies does not exact additional informational requirements on TF-binding motifs.

FIG. 6.

Evolution of randomized regulatory scenarios. The plot shows 198 evolved R_sequence values for different evolutionary simulation scenarios. The full dataset is shown instead of summary statistics because of the uniqueness of α values. For each R_sequence value, the corresponding R^† values for α_high and α_low are shown.

3. Conclusions

The informational requirements for transcriptional systems with complex regulatory demands are not obvious. By generalizing R_frequency into R^† as a predictive indicator for the evolved information content in TF-binding motifs and assessing its accuracy by means of evolutionary simulations, here we show that the informational requirements of arbitrarily complex regulatory patterns are dictated primarily by the effective fraction of probability mass assigned to target sites. We find that the presence of a large number of low-occupancy sites in a regulatory system can decrease the expected information content, but this effect is weak in comparison to the influence of the effective fraction of probability mass. As a result, the amount of information in TF-binding motifs for systems with complex regulatory demands can be effectively estimated to first order by R^†.

4. Methods

4.1. Evolutionary simulator

The evolutionary simulator used in this work, ESTReMo, has been developed integrally in C++ as an open-source project and is available for download online. ESTReMo implements a genetic algorithm with fixed population size, generational replacement, mutation, and k-tournament selection (Eiben and Smith, 2007). The genetic algorithm evolves a simulated TF (recognizer) and a set of promoter regions wherein TF-binding sites are expected to evolve. Promoter sequences are stored as DNA strings and encoded using a BIN4 notation for processing by the recognizer (Wu and McLarty, 2000). The recognizer is encoded as a set of weights that are instantiated into a predefined neural network architecture. We use a single-layer feed-forward network with linear activation function, which effectively maps to a position-specific weight-matrix model (Workman and Stormo, 2000). Independent mutation rates and operators are used for the recognizer and for the promoter regions. Mutations in promoter regions change the base at a given position following predefined nucleotide frequencies. Recognizer weights are mutated by adding or subtracting a factor (Δw) that is distributed as the cube of a standard uniform random variable. The output of the recognizer for the ith site S_i is interpreted as the change in free-energy (ɛ_i) associated with binding in units of K_BT, where K_B is the Boltzmann constant and T the absolute temperature. Occupancies for all positions in all promoter sequences are computed by assuming a Boltzmann distribution (Stormo and Fields, 1998):

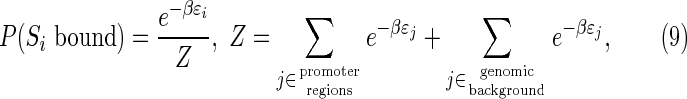where β = 1/K_BT is inverse temperature and j is the genome coordinate. The genomic component Z_G of the partition function Z for the Boltzmann distribution is approximated by taking S contiguous samples (indexed by U_j) uniformly at random from a genome sequence and scaling their energy contributions to the desired effective genome size (G). The scaled partition function is then given by

where ɛ_Uj is the energy associated with a given random sample U_j and S is the number of samples. For any given promoter sequence, expression of the associated gene is evaluated as the maximum occupancy for any site within the promoter sequence. Expression is assumed to encompass transcription and translation, resulting in a value of enzyme concentration within the cell. Target expression levels are defined as desired intracellular concentrations. The relationship between target expression level and fitness is assumed to follow the experimentally fitted cost–benefit function reported for LacZ (Dekel and Alon, 2005):

where E is the enzyme (LacZ) concentration, L is the amount of lactose present in the medium (mM), K_Y is the Michaelis constant of LacY (mM), M_E is the maximum enzyme concentration, and δ and η are dimensionless tuning parameters for benefit and cost, respectively. Equation 11 is defined in terms of wild-type concentrations for the enzyme (E, M_E). In practice, we assume an enzyme wild-type concentration of 1 μM (Lu et al., 2007; Flamholz et al., 2013). Values for all parameters in the fitness model are reported in Table 1.

Table 1.

Summary of Standard Parameters for the Simulations Reported in This Work

Category	Parameter	Valuea
Genetic algorithm	Tournament size	2
	Promoter region mutation rate (μp)	0.001 mutations/bp/generation
	Recognizer mutation rate (μr)	0.005 mutations/weight/generation
	Population size	500
	Maximum number of generations	15,000
	Stopping criteria	Max generation & optimal fitness
	Recognizer weight initialization	0
	Promoter region base initialization	Uniform
Regulatory network	Promoter regions	16
	Size of promoter regions	32 bp
	Length of binding sites	16 bp
Genome	Size	10,000 bp
	Sequence	Random 50% GC/E. coli
Fitness model	Wild-type enzyme concentration	1 μM
	Benefit parameter (δ)	0.17
	Cost parameter (η)	0.02
	Maximum enzyme concentration (M)	1.8
	Michaelis constant of LacY (KY)	0.4 mM
Occupancy model	Distribution of transcription factor	Boltzmann
	Temperature	30°C
	Nonspecific binding	−8 kcal/mol
	Expression function	Max occupancy in promoter

^aVariations to these parameters are explicitly noted in the text.

Native ESTReMo C++ code can be compiled to run serially or in conjunction with a CUDA extension that offloads the estimation of the partition function to a General Purpose Graphical Processing Unit (GPGPU).

4.2. Evolutionary simulations

All simulations reported in this work targeted the evolution of a simulated TF capable of regulating sixteen 16-bp-long sites while facing a background genome with an effective size of 10,000 bp sampled from either the E. coli K-12 (NC_000913) or uniform random sequences of equivalent size. Only the forward strand was considered for the effects of the simulation. The mutation rate for promoter regions was set at 10⁻³ mutations per base per generation following previous work (Schneider, 2000), effectively setting the system slightly below the one mutation per genome per generation limit. The per-weight mutation rate for the recognizer then was adjusted empirically to a conservative rate below the limit at which simulations failed to converge. A complete list of parameters for the simulations is provided in Table 1. Simulations were run on a 2.80 GHz × 8 core Intel X58 system with 12 Gb of RAM and an NVidia 580 GPU unit, and on the University of Maryland Baltimore County (UMBC) High Performance Computing Facility Tara cluster. All simulations were run for 15,000 generations, and only simulations that attained a fitness value within 1% of the predicted maximum fitness were kept for analysis.

4.3. Data analysis

The ability of R^† to approximate the R_sequence values generated by the evolutionary simulation scenarios was assessed by computing the Pearson correlation coefficient of determination (R²) and its associated p-value. Statistical support for the difference in R_sequence values evolved in real and randomly generated genomic backgrounds was assessed using a Mann–Whitney U-test. Support for bounds on evolved R_sequence values based on R^† computed at minimum (α_low) and maximum (α_high) occupancy values was assessed by a permutation test. All statistical tests were performed using the Python Scipy library. All code used to perform the data analysis may be found online at http://sourceforge.net/projects/estremo/.

Acknowledgments

The authors would like to thank Joseph P. Cornish and Matthias K. Gobbert for contributions to the development of precursors to the ESTReMo platform. This work was supported by NSF Grant MCB-1158056. The UMBC High Performance Computing Facility is supported by the NSF MRI (CNS-0821258 and CNS-1228778) and SCREMS (DMS-0821311) programs and by the UMBC. We would also like to thank the four anonymous reviewers, whose insightful comments improved this article.

Author Disclosure Statement

No competing financial interests exist.