Elucidating Influenza Inhibition Pathways via Network Reconstruction

Abstract

Viruses evade detection by the host immune system through the suppression of antiviral pathways. These pathways are thus obscured when measuring the host response to viral infection and cannot be inferred by current network reconstruction methodology. Here we aim to close this gap by providing a novel computational framework for the inference of such inhibited pathways as well as the proteins targeted by the virus to achieve this inhibition. We demonstrate the power of our method by testing it on the response to influenza infection in humans, with and without the viral inhibitory protein NS1, revealing its direct targets and their inhibitory effects.

1. Introduction

Many viruses use the host's cellular machinery to replicate themselves. On the other hand, hosts contain mechanisms for sensing the presence of viruses, for example, via viral DNA/RNA sensors. These mechanisms trigger the activation of immune signaling pathways that lead to attacking the pathogen and to warning nearby cells (Takeuchi and Akira, 2009).

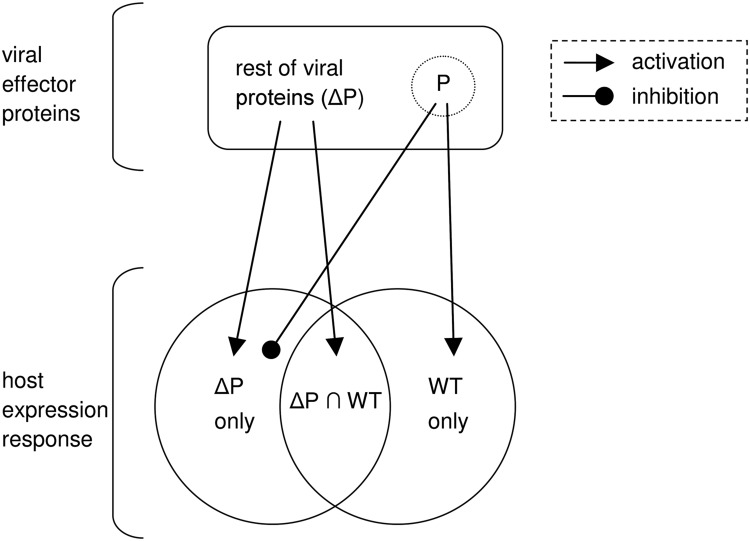
In order to evade detection, some viruses subvert these defense mechanisms by suppressing essential proteins or protein–protein interactions along antiviral pathways. This pattern of manipulation is sometimes driven by a particular viral protein that inhibits antiviral pathways in the host that would otherwise be induced by the other viral components. Therefore, this framework has the following key factors: a wild-type (WT) virus; some protein P of the virus carrying out an inhibitory role; and the rest of the viral components, denoted ΔP. Consequently, relevant host pathways can be divided into three categories: pathways that are induced by the presence of the ΔP components; out of these, pathways that are inhibited by the WT owing to the presence of the suppressing protein P; and finally, pathways that show up only in the WT scenario, supposedly triggered by that same protein P. This general framework is illustrated in Figure 1.

FIG. 1.

A schematic overview of the inhibition framework. (Top) Viral effector proteins, including the inhibitory protein P (e.g., NS1) and the remaining viral proteins ΔP. (Bottom) Host transcriptional response; genes are divided into three categories: genes that are expressed in the presence of the ΔP mutant virus but not in the WT, and vice versa, and genes that are expressed in both conditions. As the WT virus includes all ΔP proteins, we would expect the differentially expressed response for the ΔP virus to be fully contained by the response to the WT virus. However, this is not the case because of the role that P plays in the inhibition of pathways that are activated by the other viral proteins.

In this article, we aim to elucidate these different types of pathways, focusing on the pathways that are inhibited by the special protein P. Many viruses are known to fit to this framework (Brzózka et al., 2006; Reid et al., 2007; Ronco et al., 1998). Here we focus on the influenza A virus, whose NS1 protein is known as an antiviral signaling inhibitor (Gack et al., 2009; Li et al., 2006; Pichlmair et al., 2006), and for which human gene expression data are available, describing the response to both the WT virus and its ΔNS1 mutant.

The reconstruction of signaling pathways for a given response is based upon defining some source (aka anchor) proteins mediating the process, and on a genome-wide screen yielding terminal proteins that are affected by it. These are used to infer a compact protein–protein interaction (PPI) subnetwork connecting the anchors to the terminals (Lan et al., 2011; Yosef et al., 2011). However, the setting of the current article differs from previous ones in that the target pathway is inhibited rather than active in the studied condition, and to reveal it one should contrast the normal response to the pathogen with the response resulting from knocking out the inhibitor gene.

Our contribution in this article is twofold: (i) we provide a general computational framework for the inference of host pathways that are inhibited by a virus during an infection process; and (ii) we apply our framework to study influenza infection in humans, predicting the involvement of several human genes in the inhibition process—specifically, out of 19 inferred proteins, 7 are known to be directly inhibited by the NS1 protein and another 9 predictions are supported by evidence from other influenza proteins or from other viruses.

2. Preliminaries

Let G = (V, E) be a directed graph representing a PPI network with vertex set V and edge set E. Let T₂ ⊂ T₁ ⊂ V be two sets of terminals representing the response to the ΔP mutant (T₁) and the response that is common to the WT virus and its ΔP form (T₂). We relate to these sets as the two conditions. Let 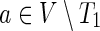be an anchor node (either a single protein or an auxiliary node representing several proteins). We seek a compact subtree H = (U, F) of G that will explain the data; that is, H should span the terminals in T₁ and provide a parsimonious explanation for the inhibition of the terminals in T₁\T₂.

We assume that the virus inhibitory protein works by inhibiting specific interactions in the host through binding to one of their end points (Gack et al., 2009; Reid et al., 2007). For a vertex , let H(v) denote the subtree rooted at v. If (u, v) is a candidate inhibited (directed) edge in H, then we assume that H(v) is inhibited and, hence, all the terminals within it should be in T₁\T₂. Thus, we seek a small subset I ⊆ F of inhibited edges that “cover” all terminals in T₁\T₂ while minimizing the number of “false positive” terminals in T₂. We may require some minimal distance from the anchor to both endpoints of an edge for classifying that edge as inhibited—for example, if the anchor node represents all viral proteins, then a minimum distance of one reflects the reasonable assumption that only host-host interactions can be inhibited. We call the arising problem of finding a subnetwork and an associated set of inhibited edges inhibited pathway reconstruction (IPR). Its precise objective is defined in the next section.

3. The Algorithm

We devised an algorithm for solving the IPR problem based on an integer linear programming (ILP) approach. The algorithm uses a flow-based technique in order to connect an anchor to a set of terminals T_i by pushing |T_i| units of flow out of the anchor and collecting them at the terminals. The amount of flow per edge 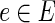and condition 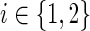is denoted by the variable x_e,i. The algorithm uses binary variables q_e to mark the inhibited edges and uses auxiliary binary variables r_e to propagate inhibition downstream, thus ensuring that no two edges on the same path from the anchor could be classified as inhibited. The variables p_e assist in counting false positive terminals of T₂. Finally, variables of the form z_e indicate for every edge 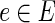whether it participates in the solution subnetwork H.

Denote by R ⊂ E the subset of edges touching a node that, according to prior knowledge, is able to form a physical interaction with the virus inhibitory protein. The goal is to minimize a weighted combination of: the number of edges in H; the number of inhibited edges from R; the number of inhibited edges not in R; and the number of false positive terminals of T₂. In our formulation we denote by In(v) (Out(v)) the set of incoming (outgoing) edges of a node 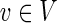respectively; 1_A(x) denotes the indicator function. The ILP formulation is given below. For clarity, we omitted the constraints on variable ranges.

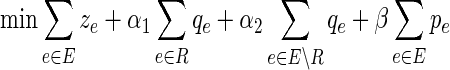s.t.:

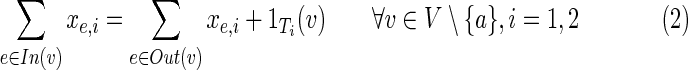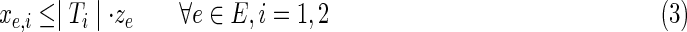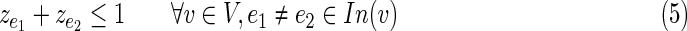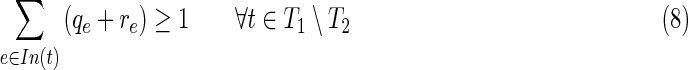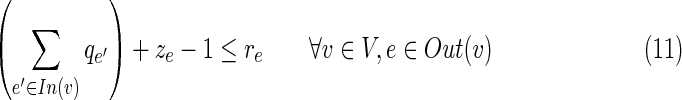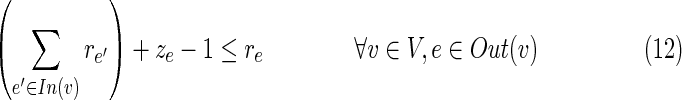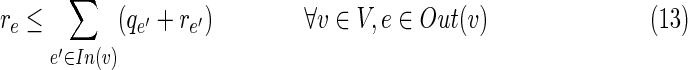We now explain in detail the constraints of the program:

• • The first two constraints ensure that each of the terminals is reached from the anchor in each of the conditions in which it is expressed: for each condition 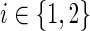, the anchor releases flow equal to the number of terminals observed in T_i; a terminal collects a single unit of flow and passes on the rest; a nonterminal passes all of its incoming flow downstream.

• • Constraint (3) ensures that edges with nonzero flow take part in the solution.

• • Constraint (4) requires that terminals in T₁\T₂ not receive flow of type i = 2, reflecting our biological assumption that genes expressed only in the ΔP condition do not receive an incoming signal from the anchor in the WT condition.

• • Constraint (5) ensures that the resulting subnetwork forms a tree.

• • The next two constraints set p_e as the number of terminals falsely located under an inhibited edge e. That is, p_e = x_e,2 if q_e = 1, otherwise p_e = 0.

• • Constraint (8) requires that all terminals in T₁\T₂ be inhibited, directly or indirectly.

• • The last five constraints define the interrelations between q, r, and z. The variable q_e is set to 1 if and only if the edge e is inhibited directly by the virus. In this case, r_e is set to 0 and the inhibition propagates to downstream neighboring edges in the solution by turning on their r variable. Formally, if q_e = 1 then r_e = 0; and if q_u,v = 1 or r_u,v = 1 then for every edge (v, w) for which z_v,w = 1, also r_v,w = 1.

The program can be solved efficiently by noting that it is sufficient to restrict z and q to integer (binary) values; in this case, the other variable types (x, p, and r) are naturally assigned integer values in any optimal solution, as shown in the Appendix.

3.1. Implementation details

Implementation platform. We implemented the algorithm in Java, using the commercial IBM ILOG CPLEX optimizer to solve the ILP.

ILP performance settings. As solving the ILP is time consuming, we filtered the PPI network using a heuristic data reduction method that aims to retain those edges that are more likely to participate in the optimal solution (Mazza et al., 2013). This method selects edges that lie on a near-shortest path (in our setting up to one edge longer than a shortest path) between the anchor and any of the terminals. Further, we instructed the ILP solver to accept approximate solutions that deviate by at most 20% from the optimum and set a time limit of 3 hours for an execution. Instead of returning one arbitrary solution that fulfils the approximation ratio, we instructed the algorithm to return a solution pool of size at most 20.

Selection of parameter values. Our algorithm depends on three types of parameters. The first parameter is the bias, which reflects the difference of weights α₂−α₁, set in the range 0–4, which we referred to as unbiased (0) and biased (1–4) experiments. For each bias we tested different combinations of the other two parameters: (i) the exact number of allowed inhibitions: either 3, 4, or 5 (added to the ILP by restricting the sum of all q_e-s to this value), and (ii) the false positive penalty (β): either 2, 4, or 8.

Analyzing multiple solutions. In order to cope with multiple solutions (either multiple approximate solutions to the same instance or solutions to different selections of parameters), all of our analyses were based on aggregate statistics rather than on a single instance. For example, to predict nodes that are likely to be located under inhibited edges, we computed per node the percent of solutions in which it is found under some inhibited edge and defined a corresponding score.

4. Experimental Results

4.1. Data preparation

We tested our method on data from Shapira et al. (2009) concerning infection of primary human bronchial epithelial cells by the influenza virus. The data consisted of two mRNA expression profiles showing gene activity in human cells in the presence of the influenza virus: one in its wild-type form and another with the NS1 gene deleted (ΔNS1 mutant). Additionally, the data contained information on physical interactions between influenza proteins and human proteins, tested using the Y2H method. We applied our algorithm to reconstruct PPI subnetworks anchored at the ΔNS1 proteins through which we infer signaling pathways that are likely to be inhibited by the influenza NS1 protein.

As the background network for the application, we used the network of Yosef et al. (2011), which contains 44,738 bidirectional PPIs over 10,169 proteins. We added the ΔNS1 proteins (NS2, PA, PB1, PB2, M1, M2, HA, NA, NP) along with their 124 interactions with human proteins as reported in Shapira et al. (2009). We further added manually curated interactions between the viral RNA and 16 human proteins, 5 of them having specific interactions with viral RNA (Allen et al., 2009; Diebold et al., 2004; Guillot et al., 2005; Pichlmair et al., 2006; Sabbah et al., 2009; Wu et al., 2011), and the remaining 11 interact with Poly I:C, a viral-RNA-like component (collected from the RNA-protein network of Ingenuity^® Systems IPA). Finally, we connected all virus-related nodes to an artificial node that represents the ΔNS1 mutant, serving as the anchor for the application. We allowed inhibitions () only for edges whose both endpoints are at distances of at least two from the artificial anchor (that is, only host–host interactions).

The terminal sets for the two conditions were selected as all genes at time point t = 8h, whose differential expression score in the corresponding profile was above a cutoff of 0.67 (Shapira et al., 2009). We selected t = 8 since earlier time points had too few differentially expressed genes and later time points induced an order of magnitude more genes that might be associated with secondary responses. The first terminal set included all 62 differentially expressed genes from the ΔNS1 profile, while the second set included 28 genes that were expressed in both profiles. We aimed to study how NS1 suppresses the expression of the 34 genes that belong to the first profile only. (In this study, we ignored genes in PR8\ΔNS1; one possible explanation for their expression is an activation signal stemming from NS1).

We first applied the heuristic filtering, yielding 9684 directed interactions over 1666 genes. With this background, we tested all combinations of parameters, analyzed separately per bias. Every resulting solution consisted of a subnetwork and a set of inhibited edges.

4.2. Biological results

We used the output produced by our algorithm to provide two types of predictions. First, we sought to divide the revealed pathways into two subsets, pathways that are inhibited by NS1 (henceforth, the inhibited set) and pathways that are not (the non-inhibited set). Second, we looked for genes that are likely to play an explicit role in the NS1 inhibition process.

In the following subsections, we discuss the analyses made to achieve our predictions and describe the validation methods. In both analyses we focused on the group of experiments with bias = 4, in order to best exploit our prior knowledge on the interactions that NS1 is able to form.

4.2.1. Extracting the inhibited pathways

In order to distinguish between inhibited and noninhibited pathways, we counted for each of the 232 human non-terminal genes belonging to any solution subnetwork (163 total with bias = 4 and all 9 combinations of the other two parameters), the percentage of solutions in which it appears below some inhibited edge. We assumed that the higher the percentage, the more likely it is that a gene participates in an inhibited pathway. On the other hand, we have prior knowledge that the NS1 protein has strong inhibition effects on immune system–related pathways. Therefore, to select the threshold that best divides the list into two functionally coherent groups, we applied the GSEA method (Subramanian et al., 2005) to our ranked list (using classic weights) to compute the enrichment score and leading edge subset (i.e., the high-ranking genes) with respect to the comprehensive Gene Ontology (GO) category “cellular response to cytokine stimulus.” This analysis yielded an enrichment score of 0.28 (p < 0.02 over 1000 permutations of the ranked list), breaking the list into 93 genes in the inhibited set (corresponding to a threshold of 1.2%) and 139 in the non-inhibited set.

We compared the biological functions of the inhibited versus non-inhibited gene sets using the GO annotation. We computed the enrichments of the inhibited set with respect to five antiviral response–related GO categories, such as toll-like receptor (TLR) signaling and interferon production (Fig. 2). As depicted in Figure 3a, these p-values were more significant than the respective p-values attained for the non-inhibited set, indicating that our predicted inhibited pathways indeed have a unique immune-related role, which might explain why NS1 chooses to focus on their inhibition.

FIG. 2.

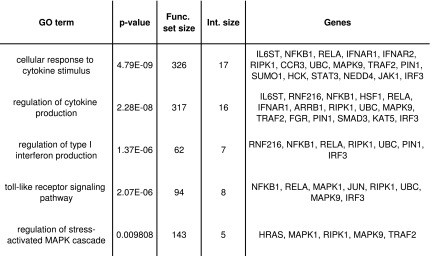
Functional enrichment analysis of the inhibited set. For every gene ontology (GO) category (left-most column), the following information is given (columns 2–5, respectively): hyper-geometric test p-value, calculated based on a background of 10194 genes that comprise the human PPI network that we used; total number of genes in the GO category; size of the intersection with the 93 genes in the inhibited set; and the intersecting gene names.

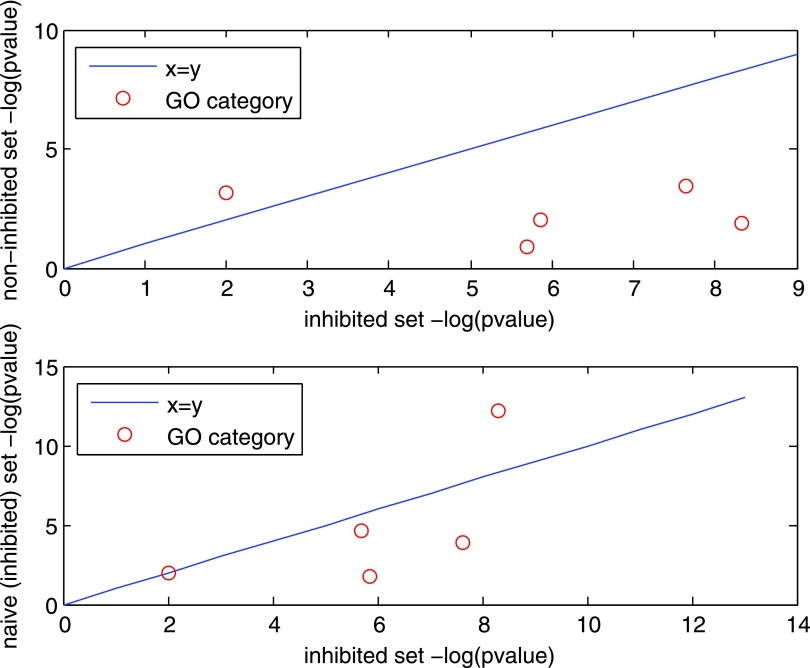
FIG. 3.

Performance of the Inhibited Pathway Reconstruction algorithm. The plots compare the −log p-value of the hyper-geometric enrichment test between the IPR predicted inhibited pathways (x-axis) and the IPR non-inhibited pathways (top), or the inhibited pathways produced by the naïve algorithm (bottom). The circles represent GO categories. IPR, inhibited pathway reconstruction.

Next, we compared the performance of our algorithm to that of a naïve approach, which predicts the inhibited pathways by reconstructing a minimum Steiner tree that spans the genes in ΔNS1\PR8 using NS1 as the anchor. This method is inherently biased as it uses knowledge on feasible virus–host PPIs of NS1. However, it is naïve in the sense that it is not aware of the information embodied in the ΔNS1 ∩ PR8 condition. We applied the same heuristic filtering and collected all suggested solutions within 20% of the optimum, amounting to 44 subnetworks with a total of 93 noninput genes in their union. The intersection of these genes with the inhibited set that was inferred by our algorithm (also of size 93) contained 43 genes, showing that the predictions are quite different. Figure 3b shows that the p-values attained for the inhibited set produced by our algorithm compare favorably to those attained by the naïve algorithm.

4.2.2. Inferring the inhibited genes

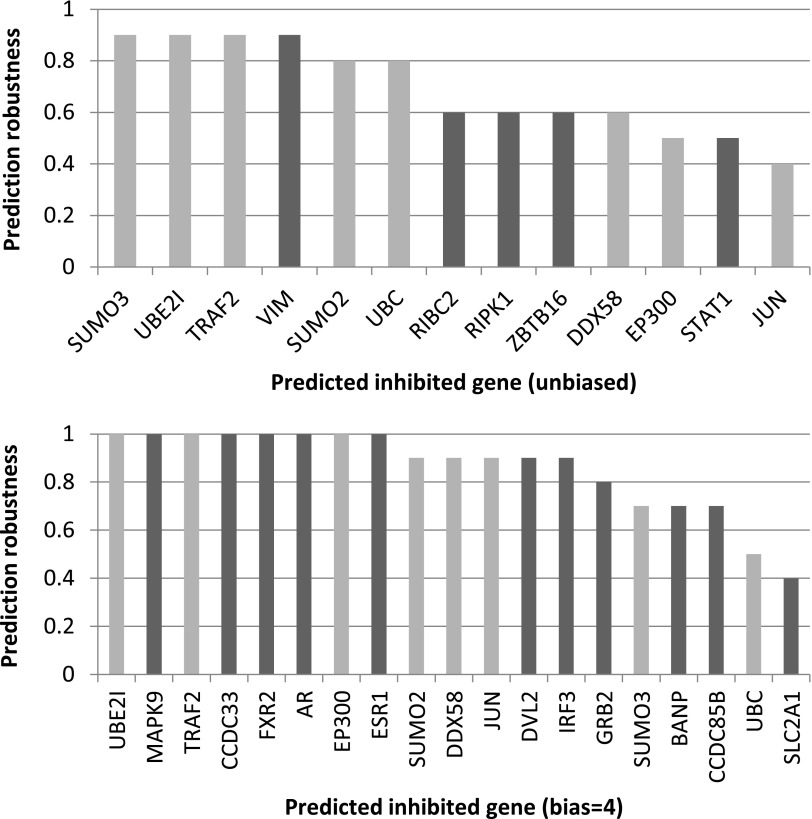
To predict genes that are directly manipulated by NS1 in the inhibition process, we performed the following steps. Per algorithm execution, we gathered the inhibited edges from all suggested solutions. For each gene touching an inhibited edge (and leading to at least two terminals), we predicted it as inhibited if it showed up for at least two of the nine parameter combinations when setting the bias to a fixed value. To evaluate the robustness of these predictions with respect to the gene expression measurements, we executed the above process 10 times, each time hiding 10% randomly chosen terminals (6 out of 62). The robustness scores of our predictions, defined as the fraction of executions in which they were raised, are summarized in Figure 4, for the unbiased (bias = 0) and biased (bias = 4) settings (we omitted three predictions whose robustness score was below 0.4). Interestingly, 8 predictions were shared between the unbiased and biased analyses out of 13 and 19 predictions in total, respectively. The predictions remained stable for a similar robustness analysis with respect to the input PPI network, performed by removing from the filtered network 5% randomly chosen interactions and adding 5% randomly chosen interactions.

FIG. 4.

Predicted direct inhibitions of NS1. The histograms display the prediction robustness of each gene, defined as the fraction of runs in which the gene was predicted when random 10% of the terminals were hidden. Separate histograms are shown for the unbiased and biased settings. Genes that were predicted in both settings appear in light gray.

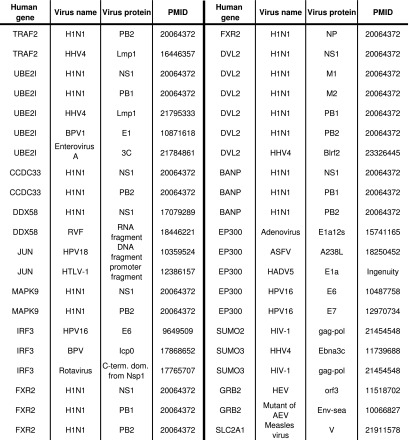
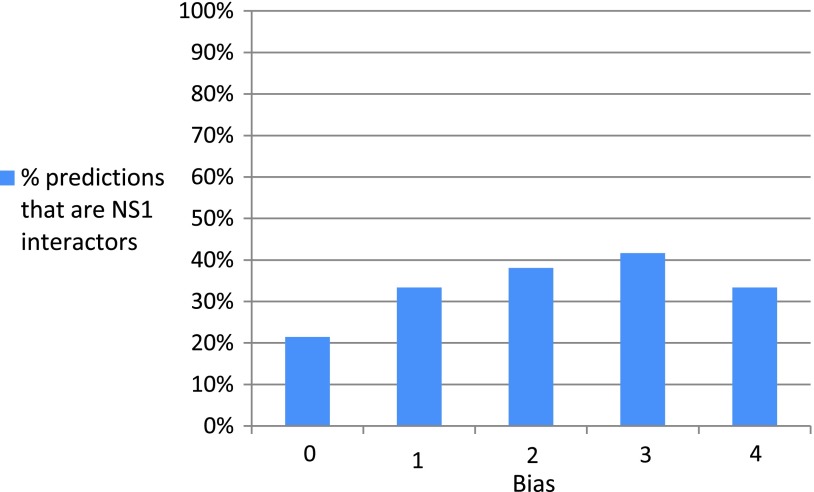
We evaluated the results of the biased analysis by looking for every predicted gene, whether it is involved in any known viral interactions. Notably, 16 out of 19 genes had strong support from the literature (Fig. 5). In particular, 7 are known to interact with NS1, including UBE2I, DVL2, CCDC33, DDX58, BANP, MAPK9, and FXR2 (Mibayashi et al., 2007; Shapira et al., 2009). Another gene, TRAF2, interacts with the influenza protein PB2 (Shapira et al., 2009). Interestingly, 8 additional genes are known to interact with proteins of other viruses. For example, IRF3 interacts with the E6 protein of the human papillomavirus (Ronco et al., 1998), and EP300 interacts with the A238L protein of the African swine fever virus (Granja et al., 2008). As another support, we found that 7 of the 8 proteins that were predicted by both the unbiased and biased configurations have known interactions with either influenza or other viruses (Figs. 5 and 6). The genes for which we did not find support are ESR1, CCDC85B, and UBC. This might be either because such interactions are unknown or because NS1 suppresses the corresponding interactions by operating on their neighbor. To conclude, Figure 7 shows for all bias values the percentage of the predictions that are also direct NS1 interactors. The high proportion of NS1 interactors for higher bias values indicates the utility of using prior knowledge for generating more accurate and biologically relevant reconstructions.

FIG. 5.

Literature support for predicted direct inhibitions of NS1. Every record shows the predicted gene, virus name, and protein name with which it interacts, as well as the Pubmed ID that reported this interaction.

FIG. 6.

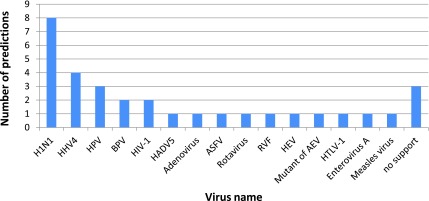
Viral interactors of predicted inhibited genes. This histogram shows for every virus the number of predicted inhibited genes that interact with at least one protein of that virus. Predicted genes that interact with more than one type of virus are counted for each of these viruses. Predicted genes for which no support for viral interaction was found appear under the column “no support”.

FIG. 7.

Biased prediction statistics. This histogram shows for every bias value the percentage of predictions that are NS1 interactors.

5. Conclusions

In this article we described a novel network reconstruction method that is able to infer interactions and pathways that are inhibited by viral proteins. This research opens the door for various future directions. One possible extension is to relax the tree assumption, thus enabling synergy interactions and alternative pathways to genes under normal versus inhibition conditions. Another future direction is to integrate prior knowledge on interaction types (activation versus inhibition) to achieve reconstructions that account for the direction of expression change. A final direction would be to explore multiple viruses simultaneously, where each virus activates different sets of differentially expressed genes while performing different inhibitions. Depending on the availability of such data, these suggested approaches may lead to new predictions and hypotheses that could be subjects for experimental validations.

6. Appendix

Lemma 1. In the ILP algorithm from Section 3, assume that 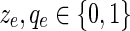for every 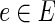. Then the rest of the variable types, constrained by the ranges 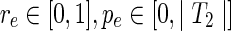, and 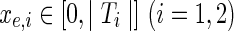, are assigned integer values in any optimal solution.

Proof. Let 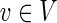. We first prove that for every 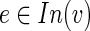and , x_e,i is an integer. From constraint (5) and the integrality of z, at most one of these edges can have z_e = 1, and thus, from constraint (3), at most one of them can have a positive value for x_e,i. Denote by S_i(v) the set of terminals reachable from v in condition i, and let 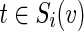. By applying the above argument for every node on the (single) path from v to t, we conclude that t can receive flow only from v, hence from constraint (2) we infer that 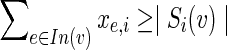. However, the other direction holds too since the flow (for condition i) that v sends can be collected only by terminals in S_i(v). Therefore, for every 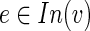, either x_e,i = 0 or x_e,i = |S_i(v)|, as required.

The integrality of r is proved by induction on the (tree) structure of an optimal subnetwork. [For an edge e not in the subnetwork r_e = 0 from constraint (9)]. Let 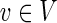and assume that for every 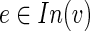, r_e is an integer. Let 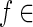Out(v) with z_f = 1. Now examine the expression 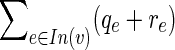, which appears in the last constraint. If it evaluates to 0 we are done. Otherwise, eithe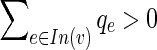r or 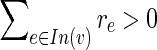. Combining with the integrality of q, the induction hypothesis and constraint (9), either of these must equal 1. From (11) or (12) it follows that r_f = 1.

Finally, the integrality of p follows immediately from the integrality of q and x.   ■

Acknowledgments

A.M. was supported in part by a fellowship from the Edmond J. Safra Center for Bioinformatics at Tel-Aviv University. I.G.-V. was supported by the Israeli Centers of Research Excellence (I-CORE) Gene Regulation in Complex Human Disease, Center No. 41/11. I.G.-V. is a faculty fellow of the Edmond J. Safra Center for Bioinformatics at Tel Aviv University as well as an Alon fellow. R.S. was supported by a research grant from the Israel Science Foundation (grant no. 241/11).

Author Disclosure Statement

No competing financial interests exist.