Common Intrinsic Connectivity States Among Posteromedial Cortex Subdivisions: Insights From Analysis of Temporal Dynamics

Abstract

Perspectives of human brain functional connectivity continue to evolve. Static representations of functional interactions between brain regions are rapidly giving way to dynamic perspectives, which emphasizes non-random temporal variations in intrinsic functional connectivity (iFC) patterns. Here, we bring this dynamic perspective to our understanding of iFC patterns for posteromedial cortex (PMC), a cortical hub known for its functional diversity. Previous work has consistently differentiated iFC patterns among PMC subregions, though assumed static iFC over time. Here, we assessed iFC as a function of time utilizing a sliding-window correlation approach, and applied hierarchical clustering to detect representative iFC states from the windowed iFC. Across subregions, five iFC states were detected over time. Although with differing frequencies, each subregion was associated with each of the states, suggesting that these iFC states are “common” to PMC subregions. Importantly, each subregion possessed a unique preferred state(s) and distinct transition patterns, explaining previously observed iFC differentiations. These results resonate with task-based fMRI studies suggesting that large-scale functional networks can be flexibly reconfigured in response to changing task-demands. Additionally, we used retest scans (~1 week later) to demonstrate the reproducibility of the iFC states identified, and establish moderate to high test-retest reliability for various metrics used to quantify switching behaviors. We also demonstrate the ability of dynamic properties in the visual PMC subregion to index inter-individual differences in a measure of concept formation and mental flexibility. These findings suggest functional relevance of dynamic iFC and its potential utility in biomarker identification over time, as d-iFC methodologies are refined and mature.

1. Introduction

Posteromedial cortex (PMC), a cortical hub commonly referred to as ‘posterior cingulate/precuneus’, is implicated in a diverse range of higher-order cognitive and affective functions (Cavanna and Trimble, 2006). Efforts to understand the heterogeneity of the roles ascribed to PMC have increasingly highlighted the presence of functionally differentiable subdivisions. Initially reliant on cytoarchitectonic (Brodmann, 1909; Vogt, 1911) and animal tract-tracing studies (Pandya and Seltzer, 1982; Parvizi et al., 2006), models positing PMC subregions have gained support from resting-state fMRI (R-fMRI) studies of intrinsic functional connectivity (iFC). For example, seed-based correlation analysis of iFC differentiated the PMC into four distinct subregions (three in precuneus and one in posterior cingulate cortex) associated with unique functional systems (visual, cognitive, sensorimotor, and limbic) (Margulies et al., 2009). Recent data-driven approaches (e.g., cluster analysis), which avoid potential biases of a priori models, confirmed the presence of PMC subdivisions (Cauda et al., 2010; Zhang and Li, 2012; Zhang et al., 2012). However, in describing the connectivity of these subregions, prior studies have relied on a key assumption – namely, that iFC patterns are static during an R-fMRI scan.

Recent studies have questioned the temporal invariance of iFC patterns. Using a growing list of data-driven methods, investigators have found that the constituents of intrinsic connectivity networks (ICNs), as well as their within- and between-network connectivity vary over time (Chang and Glover, 2010; Handwerker et al., 2012; see Hutchison et al., In press, for a review; Kang et al., 2011; Kiviniemi et al., 2011; Smith et al., 2012). Rather than interpreting such variations as random noise, most posit that they reflect meaningful dynamic properties of iFC. In particular, Allen et al. (2012) found that iFC alternates among a finite number of states – each characterized by a highly structured and quasi-stable connectivity pattern that emerges and dissolves with periods of tens of seconds to minutes. Concerns about potential confounds such as motion were alleviated by finding iFC dynamics in anesthetized nonhuman primates (Hutchison et al., 2012) and rodents (Keilholz et al., 2013; Majeed et al., 2011). The validity of transient functional interactions is supported by neuronal (Popa et al., 2009) and neurophysiological (Chang et al., 2013; de Pasquale et al., 2012) approaches as well.

Here, we revisit previously established iFC differentiations among PMC subregions, now taking into account temporal dynamics. Specifically, we explore the possibility that PMC subregions have a common set of iFC states (i.e., highly structured and quasi-stable connectivity patterns), the existence of which would emphasize the flexibility of network associations and would resonate with task-based phenomena. To identify common iFC states, we: 1) used a sliding-window correlation approach to characterize iFC over time for each seed, 2) pooled iFC windows across seeds and participants, and 3) grouped them using hierarchical clustering. Temporal profiles for each subregion were then reconstructed from the cluster assignments and used to determine the extent to which iFC states are “common” to PMC subdivisions, and characterize potential differences in transition behaviors. Finally, we assessed the reproducibility and test-retest reliability of these state-related findings – properties commonly assumed, but not yet tested.

2. Methods

2.1 Dataset and data acquisition

The current study utilized the Nathan Kline Institute (NKI) test-retest (TRT) dataset publically available via the International Neuroimaging Data-Sharing Initiative (INDI: http://fcon_1000.projects.nitrc.org/indi/pro/eNKI_RS_TRT/FrontPage.html). Two participants were excluded from the original release due to either brain atrophy or a missing retest session, leaving a final sample of 22 participants (16 males, age range 19-60, mean = 33.45, SD = 12.53). An MPRAGE structural image and two ten-minute resting scans (at least one week apart) were collected for each participant in a Siemens Trio 3.0 T scanner. Participants were instructed to keep their eyes open and fixate on a central cross on the screen. The resting scans were collected using a multiband EPI sequence (TE = 30 ms, flip angle = 60°, slice thickness = 3.0 mm, field of view = 222 mm, matrix size = 74 × 74, TR = 645 ms; no gap, resolution = 3.0 × 3.0 × 3.0 mm³) (Moeller et al., 2010). In addition to these resting state scans, test-retest resting state scans using two different scanning protocols (2 × 2 × 2 mm resolution, TR = 1400ms; and 3 × 3 × 3 mm resolution, TR = 2500ms), and three non-repeated task scans (i.e. visual check-board stimulation, breath holding, eye movement calibration) following resting scans were acquired on these participants. These additional scans were not used in the current study.

As part of the NKI-Rockland protocol, phenotypic characterizations (http://fcon_1000.projects.nitrc.org/indi/pro/eNKI_RS_TRT/FrontPage.html) were obtained for 16 of the 22 participants. Psychiatric assessments using the Structured Clinical Interview for the DSM-IV (SCID-I/NP, First et al., 2002) detected that three of the participants met criteria for a current episode of major depressive disorder. We verified in our dynamic iFC (d-iFC) analyses and neuropsychological assessments that these individuals did not represent extreme outliers. For each of the state dynamic metrics, and each of neuropsychological scores, extreme outliers were identified using the corresponding three inter-quartile range. Results indicated that no depressive patients are outliers in any of the indices (see Inline Supplementary Table S2 for details). As such, they were included in all analyses to increase the statistical power for this exploratory study. All data were collected according to protocols approved by the institutional review board of the NKI. Informed consent was obtained from each participant prior to participation.

2.2 Imaging preprocessing

Data were preprocessed using the Data Processing Assistant for Resting-State fMRI (DPARSF, Yan and Zang, 2010, http://www.restfmri.net), which is based on Statistical Parametric Mapping (SPM8) (http://www.fil.ion.ucl.ac.uk/spm) and Resting-State fMRI Data Analysis Toolkit (REST, Song et al., 2011, http://www.restfmri.net). The first ten seconds of data were removed to allow data to reach T1 equilibrium, leaving a total of 884 volumes for final analysis. The time series were realigned to the first image and then to the mean of all functional images using a six-parameter (rigid body) linear transformation. After realignment, individual structural images (T1-weighted MPRAGE) were co-registered to the mean functional image using a 6 degrees-of-freedom linear transformation without re-sampling. The registered T1 images were segmented into gray matter (GM), white matter (WM) and cerebrospinal fluid (CSF) using the New Segment module (Ashburner and Friston, 2005) in SPM8.

The realigned data were regressed on 27 nuisance covariates (signals from WM, CSF, global signal, and Friston-24 motion parameters) to reduce the potential effects of physiological processes (e.g. respiration and cardiac processes) and motion. Linear and quadratic trends were removed to account for scanner drift. The Friston 24-parameter model (i.e., 6 head motion parameters, 6 head motion parameters one time point before, and the 12 corresponding squared items) (Friston et al., 1996) was used to regress out head motion based on recent reports demonstrating that higher-order models were more effective in removing head motion effects (Satterthwaite et al., 2012; Yan et al., 2013a). The individual 4D residual volume was spatially normalized to the Montreal Neurological Institute (MNI) space using Diffeomorphic Anatomical Registration Through Exponentiated Lie algebra (DARTEL) in SPM8 (Ashburner, 2007). The time series of each voxel were then standardized to zero mean and unit variance.

After preprocessing, normalized time series for 4 spherical seed regions (radius: 3mm) and 156 target regions of interests (ROIs) were extracted in MNI space. The seed locations were selected based on a previous study (Margulies et al., 2009) to represent one posterior cingulate cortex (PCC) subregion (retrosplenial region, seed 1, location: -2/-36/35) and three subdivisions of precuneus with different functional roles: sensorimotor anterior (seed2, location: -2/-47/58), cognitive/associative central (seed 3, location: -2/-64/45), and visual posterior precuneal region (seed 4, location: -1/-78/43). These four seeds correspond to seeds 4, 6, 14, and 17 in Margulies et al. (2009), respectively. They were previously determined to be representative of four distinct PMC subdivisions based upon their unique iFC patterns. The specific iFC patterns associated with these seeds corresponded to limbic (seed 4), motor (seed 6), cognitive (seed 14), and visual (seed 17) networks predicted from prior tract-tracing studies in the macaque monkey.

Target regions were defined using an atlas derived from the spatially constrained functional parcellation of an independent dataset (Craddock et al., 2012). Twenty-one ROIs corresponding to brain stem and cerebellum and 23 ROIs corresponding to PMC (i.e. precuneus and PCC) were removed from the atlas, leaving a total of 156 target ROIs for the analysis. Imaging of the brainstem and cerebellum is particularly susceptible to motion induced by physiological processes such as cardiac pulsation and respiration, and inconsistent slice coverage across individuals. Given the lack of physiological monitoring (e.g., respiration, cardiac cycle) in our acquisition, we removed these regions from the analysis to minimize potential confounds in the dynamic patterns revealed. PMC regions were also removed from the set of target regions to be conservative and avoid influences between PMC subregions with respect to their findings. Static and dynamic iFC analyses that specifically examined the connectivity between the four representative PMC seed regions are reported in Supplementary Materials (see Supporting Information, Inline Supplementary Table S1, and Fig. S1).

2.3 Static iFC analysis: replication of Margulies et al. 2009

To replicate previous static iFC (s-iFC) analysis results (Margulies et al., 2009), Pearson’s correlation coefficients were computed between each seed and 156 target ROIs at the individual level. The correlation coefficients were then Fisher Z-transformed. At the group level, one sample t-tests were performed to identify target ROIs that were significantly correlated with each seed. Results were False Discovery Rate (FDR) corrected at q = 0.05 (Genovese et al., 2002). For display purpose, the p values for s-iFC were negative log₁₀ transformed and plotted on a surface map (for the analysis flow, see Fig. 1).

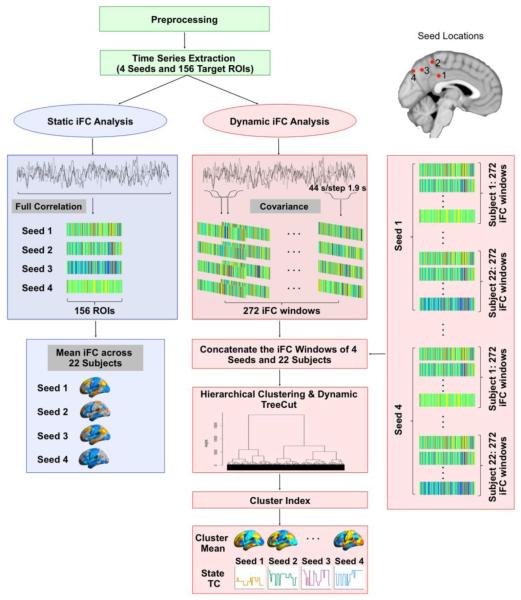
Figure 1. Data Analysis Overview.

After standard preprocessing, for each participant, the BOLD signal time series were extracted in MNI space for each of the four seeds and the 156 target ROIs. Seed locations were selected to represent the four subdivisions of posteromedial cortex (PMC) according to Margulies et al. (2009): limbic posterior cingulate cortex subregionn (Seed 1), sensorimotor (Seed 2), cognitive (Seed 3), and visual (Seed 4) precuneal region. The target ROIs were derived from the Craddock-200 functional atlas with brainstem, cerebellum, and PMC regions removed from the analysis. The time series were subjected to static and dynamic intrinsic functional connectivity (s-iFC and d-iFC) analysis. s-iFC was performed to replicate results of Margulies et al. (2009). d-iFC states were identified using a sliding-window correlation (window size = 44s, step = 1.9s) in combination with hierarchical clustering analysis. The optimal number of clusters was determined using a dynamic tree cut algorithm. The mean iFC of each cluster was calculated and thresholded as a representative pattern for a given state. The time course (TC) of state was reconstructed for each participant and each seed by temporally concatenating the cluster index.

2.4 Dynamic iFC analyses

2.4.1 Sliding-window correlation analysis

Dynamic iFC was characterized using sliding time-window correlation and hierarchical clustering analyses (see Fig. 1). Specifically, we constructed a tapered window by convolving a rectangular window (width = 44s / 69 TR)¹ with a Gaussian waveform (σ = 1.94s / 3 TR). This window was applied to the extracted time series in step of 3 TRs, resulting in 272 time windows per subject. Following previous work (Allen et al., 2012), the covariance matrix from the seed and target ROIs in each window was calculated using the graphical LASSO method (Friedman et al., 2008) in volume space. This method employs an L1 regularization on the inverse covariance matrix to reduce the noise induced by the limited number of data points available in a window (Varoquaux et al., 2010). The covariance is equivalent to the correlation matrix since we standardized the time series entering graphical LASSO. The regularization parameter lambda (λ) was optimized separately for each subject by maximizing the log-likelihood in a leave-one-out cross-validation framework. For each window, the correlations between each seed and 156 target ROIs were extracted, Fisher Z-transformed, and then standardized to unit variance and zero mean. This procedure resulted in 272 iFC windows per seed and 1088 (272 × 4 seeds) total windows per subject. Each iFC window is a 1 × 156 vector.

2.4.2 Hierarchical clustering analysis

Connectivity windows were concatenated across the four PMC seeds and 22 subjects, resulting in 23936 (1088 × 22) iFC windows. We concatenate the iFC windows of all seeds and subjects to estimate connectivity patterns common to PMC subdivisions and all subjects; this approach allows multiple connectivity states to co-occur at a given point in time (e.g. different seeds can have different states at a the same time point). This method has been used in recent studies using K-means clustering to detect representative connectivity patterns (Allen et al., 2012) and using Principle Component Analysis to identify elementary “building blocks” of dynamic iFC with time-dependent weights (Leonardi et al., 2013). The concatenated iFC windows were then submitted to hierarchical clustering analysis using the hclust package in R (Murtagh, 1985). We used hierarchical clustering because it is deterministic, doesn’t require prespecification of the number of clusters, and outputs a dendrogram to help visualize the structure of the data (Everitt, 1974). Clustering was based on the Euclidean Distance metric in combination with the Ward linkage method (Ward, 1963). Preliminary qualitative evaluations on a fraction of the dataset, suggested that Ward linkage, which is appropriate for Euclidean Distances only, provides the best separation. The optimal number of clusters was determined using the dynamic tree cut algorithm, which employs an iterative procedure to automatically identify clusters in complicated dendrograms (Langfelder et al., 2008)². The combination of hierarchical clustering with dynamic tree cut has been effective in finding gene modules in gene expression data (Langfelder et al., 2008) and detecting functional network modules in fMRI data (Mumford et al., 2010).

For each connectivity state identified by cluster analysis, a representative connectivity map was generated. This was accomplished by testing whether the mean connectivity strength (i.e., Fisher z-transformed correlation coefficient) calculated between a given seed ROI and each of the 156 target ROIs was non-zero across the iFC windows assigned to the state (one sample t-test). For visualization, the calculated p-values were then corrected for multiple comparisons using a FDR procedure (q<0.05). The cluster assignments of the iFC windows for each seed and subject form a time course of connectivity state transitions for that seed. Seven indices that we collectively refer to as the ‘state profile’ were calculated based on the state time courses to quantify different aspects of the seeds’ dynamic connectivity:

1. Seed Integration/Segregation Index: as the 4 seeds may share the same state at some time windows, and separate into 2, 3, or 4 different states at other time windows, this index was defined as the percent of time that the 4 seeds were in 1, 2, 3, or 4 states.

2. Seed Pair Overlap Index: this index measures the percent of time that each pair of the 4 seeds shared the same state.

3. Total Duration of a State in % frames: this index is defined as the percent of time that each seed spent in a given state.

4. Number of Spans for a give state: the number of times during a scan that a seed transitions into a given state.

5. Mean Duration of a State in % frames: defined as the percent of time a seed spends in a given state divided by the number of transitions into that state.

6. Number Of Transitions: defined as the number of switch from one state to another.

7. Transition Matrix: the probability of changing from one state to a different state, calculated as the number of transitions from a given state to a target state divided by the total number of transitions a given state to all other states.

2.5 Test-retest reproducibility and reliability

In order to have biomarker potential, a state not only needs to be reproducible over time, but also must possess properties that vary across individuals and can be reliably measured. In this regard, we performed two sets of analyses, one to evaluate the reproducibility of states across imaging sessions, and the other to quantify test-retest reliability for inter-individual differences in state profiles. Thus, our use of reproducibility refers to the ability of our analyses to generate the same states when applied to data collected from the same subjects at different time points (i.e., 1+ weeks apart). In order to measure reproducibility, we repeated our d-iFC analysis on session 2 (retest) data and calculated the spatial similarity (i.e., Pearson’s correlations) between states derived from sessions 1 and session 2.

Test-retest (TRT) reliability assesses the consistency of inter-individual differences in state measures from one scan session to the next. In this regard, it is important to compute dynamic profiles based on the same states. Thus, we ensure that the two sessions had identical state definitions by concatenating the data from the two sessions before deriving the states³. Then the same temporal metrics were computed based on these newly identified clusters for each session separately. Intra-class correlations (ICC) (Shrout and Fleiss, 1979), were calculated to evaluate the TRT reliability of these dynamic metrics using linear mixed models (see Zuo et al., 2013, for details).

2.6 Validation of windowed iFC measurements using time series randomization

Variations observed in iFC obtained during sliding window analysis may reflect meaningful temporal dynamics, or could be a by-product of the noise induced by the limited number of time points present in the windows. We evaluated this by comparing covariance values estimated from the actual data to those estimated from surrogate data generated by phase randomization. Although this method preserves the temporal autocorrelation present in the data, it destroys all spatial correlation (Theiler et al., 1992); our use is appropriate given that we are not incorporating spatial information into our comparison. Phase randomization techniques have been used in previous dynamic iFC studies to test the hypothesis that the observed correlation fluctuations or the identified iFC states in the original fMRI data are unlikely to come from merely random event timing and are more likely to represent meaningful neuronal connectivity changes (Allen et al., 2012; Handwerker et al., 2012). Modeling the underlying correlation structure of the time series in the time-domain was also used to detect significant BOLD activation (Marchini and Ripley, 2000). Depending on the specific questions examined, the phase of different measures (e.g. seed time series, target ROI time series, sliding-window correlation time series) can be randomized to generate the appropriate null distribution. In the present study, we tested the hypothesis that the dynamic iFC was dependent on the exact timing of the seed time series by randomizing the phase of the seed time series while keeping the target ROI time series intact.

For each subject, a frequency spectrum was calculated for the time series of each seed, using the Fourier transform. The resulting phases were randomly permutated 100 times³, and time series were reconstructed using the inverse Fourier transform, resulting in 100 surrogate time series per seed. The advantage of this approach is that the precise timing of the signal fluctuations was randomized but the amplitude and temporal autocorrelation were preserved. For each randomization, the regularized covariance matrix was estimated for each sliding window using the surrogate time series of the four seeds and the original time series of the 156 target ROIs. Using the randomization results, we created a null distribution, and evaluated whether the covariance of real data exceed these values in the null distribution.

2.7 Association with phenotypic characteristics

To illustrate the potential utility of d-iFC in mapping brain-behavior relationships, we tested for associations between dynamics metrics and a subset of the phenotypic data available for the participants (Nooner et al., 2012). Specifically, we tested for relationships with intelligence (scaled Full-Scale, Verbal, and Performance intelligence quotient [IQ] scores from Wechsler Abbreviated Scale of Intelligence [WASI]) and several key subcomponents of executive function (scaled design switching, verbal category switching, total weighted achievement, and color-word inhibition scores from Delis-Kaplan Executive Function System [D-KEFS]). We were particularly interested in executive function, as it is central to cognitive flexibility and efficiency. We have 7 different indices that describe the dynamic interactions among the four PMC seeds, from which we calculate 174 metrics (see Table 2). Of these, only 38 show reasonable (> 0.4) test-retest reliability (see the third and fourth columns of Table 2). The five metrics calculated from the transition matrix were additionally excluded because they include too few non-zero values across subjects. Partial correlation coefficients were computed between the remaining 33 metrics and each of the 7 phenotypic measures listed above, with mean framewise displacement (FD) (Power et al., 2012) added as a control variable to partial out the residual effect of motion; this resulted in a total of 231 tests (33 × 7 = 231) which are the total number of tests we corrected for. The correlation results were False Discovery Rate (FDR) corrected at q=0.05 to account for multiple testing. For significant correlations, the data distribution was checked for outliers using R bagplot, a bivariate boxplot.

Table 2.

Number of reliable metrics per dynamic index.

Dynamic Index	Number of Metrics / Index	Metrics with Moderate Test-retest Reliability (0.4 < ICC < 0.6)	Metrics with High Test-retest Reliability (ICC > 0.6)
Seed Integration/Segregation Index	4 a	1	0
Seed Pairs Overlap Index	6 b	3	1
Total Duration of a State	20 c	10	3
Number of Spans for a State	20 c	7	2
Mean Duration of a State	20 c	2	3
Number of Transitions	4 d	1	0
Transition Matrix	100 e	3	2
Total	174	27	11

^a4 = # of unique state(s)

^b6 = # of unique seed region pairings

^c20 = # of seed regions × # of iFC states

^d4 = # of seeds

^e100 = # of seed regions × (# of iFC states × # of iFC states)

3. Results

3.1 s-iFC analyses: replication of Margulies et al. (2009)

Prior to examining temporal dynamics for PMC, we repeated the static analyses of Margulies et al. (2009), finding a high degree of concordance between our results and those of the prior work (see Fig. 2A). In particular, we found that the ventral PMC (seed 1), which is based in PCC, exhibited strong iFC with the limbic regions, including the anterior cingulate (ACC), paracingulate, and medial prefrontal cortex (MPFC) including frontal pole, as well as the dorsolateral prefrontal cortex (DLPFC) and inferior parietal lobule (IPL). In contrast, the sensorimotor anterior precuneal region (seed 2) exhibited iFC with medial areas related to sensory and motor processing, such as paracentral lobule, supplementary motor area, cingulate motor cortex, lateral primary motor cortex and the postcentral gyri. The cognitive/associative central precuneal region (seed 3) was associated with DLPFC, multisensory posterior inferior parietal lobule (especially the angular gyrus), and frontal pole. Of note, while the iFC of the PCC subregion and cognitive precuneal subdivision were highly correlated (r = 0.89), these two subdivisions can be differentiated by more extensive and stronger connectivity with MPFC and medial temporal lobe for the PCC compared to cognitive precuneal subdivision (these findings are concordant with those of Margulies et al., 2009).

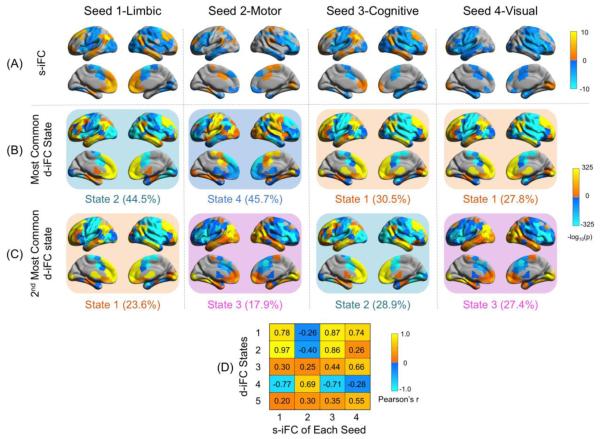
Figure 2. Relating static intrinsic functional connectivity (s-iFC) pattern and dynamic iFC (diFC) states.

The spatial pattern of the s-iFC for a given seed has the highest similarity to the state it spent the most time in (compare A and B for each seed; also see D for correlation coefficients). The state in which a seed spent the second longest time in was plotted in (C). The −log₁₀ transformed p map was plotted onto a surface map. The state number and the percent of time each seed spent in that state were listed below the state surface map.

Finally, the visual posterior precuneal region (seed 4) demonstrated iFC with the cuneus and lingual gyri, which are commonly associated with basic visual processing, along with higher order cognitive processes (e.g., inhibitory control, word processing). In addition to the regions consistent with previous study, we also observed connectivity to bilateral lateral temporal cortex for seed 1 and 3 and connectivity to left rostral DLPFC for seed 2. Importantly, the distinctive siFC patterns for PMC subregions described here replicated in session 2 as well (data not shown)⁴. Methodological differences may account for the subtle discrepancy between the results. The current scanning protocol is with better coverage (field of view = 222 mm vs. 192 mm), higher temporal resolution (TR = 645 ms vs. 2000 ms), and longer acquiring duration (10 min vs. 5 min), which may allow us to detect connectivity within the regions that are poorly covered in typical standard scan protocol such as lateral temporal lobe⁵. Of note, the connectivity to the lateral temporal lobes we observe here in seeds 1 and 3 is also consistent with the finds from the corresponding functional connectivity in the macaque monkey (Margulies et al., 2009).

3.2 d-iFC analyses

3.2.1 Detection of common states across PMC subdivisions

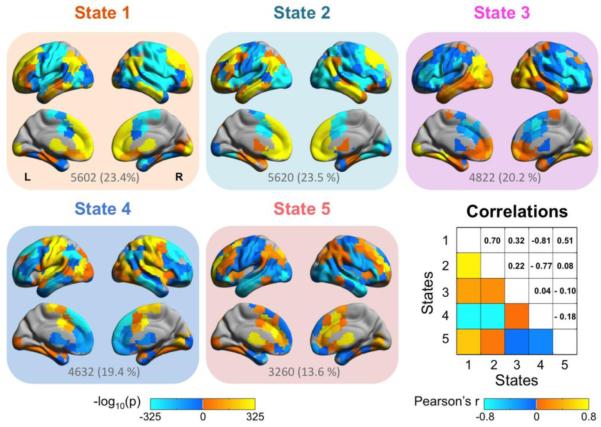
We next revisited the aforementioned s-iFC distinctions among PMC subregions, though now taking into account temporal dynamics. By combining sliding-window correlation with hierarchical cluster analysis, we detected five states among the four subdivisions (see Fig. 3). Although state 3 was highly distinct and showed low correlation with the others, the remaining four states showed a high degree of correlation with one another – either positive (e.g., state 1 and 2) or negative (e.g., states 2 and 4). The Fisher Z transformed correlation coefficients in these states exceed what can be expected by chance (Fig. S2). Figure 4 summarizes the composition of the iFC states identified, by depicting the percent overlap between each of the states and the 10 primary ICNs that Smith et al. (2009) previously identified and matched with “behavioral domains” using the BrainMap database (see Fig. 4). Each of the five states appeared to be a combination of these previously identified functional systems, rather than a reflection of a single system – possibly illustrating the higher order integration role commonly ascribed to PMC as a ‘hub’ region. Importantly, each subregion was associated with all of the states, though to varying degrees (from 6.7 – 45.7%; for example, seed 2 spent 11.8% of time in state 1, 7.8% in state 2, 17.9% in state 3, 45.7% in state 4, and 16.9% in state 5), suggesting that these iFC states are “common” to all four PMC subdivisions. Consistent with the suggestion of prior work (Allen et al., 2012), not all participants exhibited all connectivity states, though states 2 and 4 are common across all participants (see Fig. S3B).

Figure 3. Posteromedial cortex intrinsic functional connectivity (iFC) states.

Depicted are the five states identified by hierarchical clustering of iFC windows across seeds and participants over time. For display, the p values of the ROIs exhibiting significant connectivity were −log₁₀ transformed and plotted onto an MNI space surface map in lateral and medial view using BrainNet Viewer (http://www.nitrc.org/projects/bnv/) (L = left; R = right). The total number and percentage of iFC windows belong to each state was listed below each state.

Figure 4. Characterizing posteromedial cortex intrinsic connectivity states.

We summarize the anatomic location and functional components of the connectivity states using the 10 primary intrinsic connectivity networks (ICNs) identified by Smith et al. (2009). The sagittal (MNI X coordinates) slice presented in previous paper was shown here for each ICN thresholded at Z = 3 (shaded in light green). The behavioral domain corresponding most strongly to each ICN was listed below the sagittal slice. The percent overlap between each state and each ICN was plotted in a pie chart. The whole circle represents the total number of voxels in an ICN which can be divided into three parts: percentage overlap with positive connections in a state (% Positive: red), percentage overlap with negative connections in a state (% Negative: blue), and percentage non-overlap with a state (Non-overlap: white).

State 1, which mainly consists of iFC windows for the cognitive (30.5%), visual (27.8%), and limbic (23.6%) subregion, is primarily composed of components from the higher-order default and cognitive control networks, the visual networks, as well as subcortical regions such as thalamus, caudate, and putatmen. State 2 mainly consists of limbic (44.5%) and cognitive (28.6%) subregions and includes the core regions of default network (DN) such as MPFC, medial and lateral temporal lobe, lateral parietal cortices, and subcortical regions. This state exhibits a similar pattern to that of state 1 (r = 0.70). However, these states do not appear to be the result of over-clustering; important differences in direction and strength of connectivity were observed between these two states within DLPFC, ventrolateral prefrontal cortex (VLPFC), medial temporal lobe, lateral parietal lobe, visual cortex, and subcortical regions (paired sample t-tests, FDR corrected at q = 0.05). State 3 is more evenly associated with all 4 seeds and overlaps with the visual networks and DN. State 4 is predominantly contributed by sensorimotor subdivision (45.7%) and includes the core regions of “task-positive” network (TPN) such as motor cortex, frontal eye fields, anterior proportion of intraparietal sulcus, anterior insula, and extrastriate cortex. State 4 is highly anti-correlated with state 1 (r = −0.81) and 2 (r = −0.77) and exhibits opposite connectivity patterns in distributed regions within frontal, parietal, and temporal lobe, and subcortical regions to these states. State 5 overlaps with all ten ICNs and also includes subcortical regions. Furthermore, this state is evenly contributed by all four subdivisions. These suggest that this state may have high flexibility in being involved in different tasks.

Given that s-iFC represents the full correlation computed across all time points, one question is to what degree s-iFC patterns are reflective of specific d-iFC states. To examine this question, we computed Pearson’s correlations between the s-iFC pattern for each seed and each of the d-iFC states. We found that the s-iFC pattern of a given seed had the highest similarity to the state it spent the most time in (Fig. 2), indicating that the s-iFC is most reflective of that state. For example, the s-iFC of the limbic subregion (seed 1) was almost perfectly correlated with state 2 (r = 0.97), with both including common regions such as MPFC, ACC and paracingulate cortex, DLPFC, medial and lateral temporal lobe, and IPL.

3.2.2 PMC subregion state profiles

Figure 5A, B, and C present the state time courses for three representative participants. Rather than remaining in a single state, all seeds exhibited switching behavior across multiple states (Fig. 5, Seed 1 to 4) and overlapped with each other at different time windows (Fig. 5, All 4 Seeds). The State Integration/Segregation Index indicated that most of the time these four seeds were in either two or three unique states. This pattern holds at the group level (Fig. 6, left Panel A), when the percent of time for which the four subdivisions were in 1, 2, 3, or 4 states were averaged across participants, suggesting certain subdivisions overlapped with each other on the same state. To quantify the percent of time the two seed regions were associated with the same state simultaneously, a Seed Pair Overlap Index was computed. Results revealed that all pairs of seeds overlapped with each other to varying degrees, with seed 1 and 3 having the highest percentage of overlap (48.5%). The s-iFC patterns of these two seeds were highly similar, and they mainly overlapped when associated with state 1 and 2, the iFC states they spent most of their time in. The percentage overlap between seed 3 and seed 4 was also high (46.7%), and they mainly overlapped when associated with state 1 and 3. Seed 1 and 2 had the lowest percent of overlap, but it was still over 20% of time. These results suggested substantial functional integration across PMC subdivisions, which can not be appreciated by traditional s-iFC analysis.

Figure 5. State time courses for three representative participants (A, B, and C).

The state time courses were plotted for each seed separately (Seed 1-Limbic, Seed 2-Motor, Seed 3-Cognitive, and Seed 4-Visual), as well as all seeds together to highlight overlaps. Assigned states are plotted at the time point corresponding to the center of the sliding window in unit of TR. The seed Integration/Segregation Index (defined as the percent of time the four seeds possesses 1, 2, 3, or 4 unique state(s)) indicated that for most of the time, the four seeds were associated with either two or three unique states.

Figure 6. State profiles and their reliability.

State profile of session 1 (left panel) and state profile test-retest (TRT) reliability calculated using 2 sessions (right panel) were plotted. For the state profile, indices describing state integration and segregation (A) and Number of transitions (C) are depicted in boxplots. Outliers were indicated by an “o”. The Total Duration in % frame, # of Spans, and Mean Duration (Total Duration / # of Spans) were plotted for each seed and each state using its own scale (B). The Transition Matrix (C), the mean probability (Prob.) of changing from one state at time t (rows) to another state at time t+1 (columns) across all subjects, was plotted for each seed, separately. The diagonal value (changing within its own state) was removed. The corresponding TRT reliability estimates for these dynamic metrics were quantified using intra-class correlation (ICC) and plotted accordingly.

To test the hypothesis that each subdivision was associated with a unique state profile, we computed a set of dynamic metrics to quantify the time each seed spent in each state (i.e., duration of scan spent in a given state, number of times associated with a given state, mean time spent in a given state) and transition patterns (i.e., total number of state transitions, transition matrix) (see Table 1 and Fig. 6, left panel B and C). Importantly, as is evident in Figure 6, each subdivision was associated with a distinct state profile.

Table 1.

State profile summary information.

	Preferred State(s) (Total Duration in % frames)	State With Highest Frequency in Terms of Spans (# of spans)	State With Highest Mean Span (Mean Duration in % frames)	Number of Transitions	Most likely State Switch (Probability)
Seed 1- Limbic	2 (44.5%)	2 (3.1)	2 (15.7%)	7.9	5 to 2 (0.75)
Seed 2- Motor	4 (45.7%)	4 (3.0)	4 (17.1%)	8.0	2 to 4 (0.61)
Seed 3 - Cognitive	1 (30.5%) and 2 (28.9%)	1 (2.5) and 2 (2.5)	2 (13.7%)	9.0	1 to 2 (0.52)
Seed 4- Visual	1 (27.8%) and 3 (27.4%)	1 (2.9)	3 (11.8%)	10.3	5 to 1 (0.53)

Note: The summary measures for each seed are averages generated across participants. See figure 7 for more complete information regarding key indices.

3.2.3 Dependencies on GSR and the effect of motion

To determine the extent to which the iFC states detected depend on GSR, we repeated the same dynamic iFC analysis procedures using the data preprocessed without GSR. For session 1, four d-iFC states were detected and these states correlated well with four of the five states detected in our primary analysis with GSR (compare Fig. S4 A and B, left panel); state 5, which contained the least number of windows in our primary analyses with GSR, was not detected in session one. For session 2, four states were detected, three of which correlated well with states identified in primary analyses with GSR (states 1 and 5 from our primary analyses were not detected) (compare Fig. S4 A and C, left panel). Similar to our primary analysis, these states are associated with all four seeds in both sessions, although to varying proportion (Fig. S4 B and C, right panel), confirming that these states are common to the four PMC subregions. Overall, these results suggest the detection of iFC states is possible without GSR, though the reproducibility increases with GSR. Regarding the relationships noted in our primary analyses between the diFC metric for seed 4 (duration spent in state 4) and the DKEFS, we did not find a significant relationship in either session without GSR, once again suggesting a possible cleaning effect.

An obvious concern can arise despite the various procedures taken to minimize and/or account the effect of motion – namely that one or more states may be artifactually driven by motion. To provide further insights into this concern, we first examined potential associations between the occurrence of a state and that of large frame-wise displacements (FD > 0.2mm). Importantly, none of the states showed strong associations between their occurrence and that of a high motion (Fig. S5: A and B). State three did have a larger proportion of windows with high motion compared to the others, possibly suggesting a greater risk of motion when the brain shifts into that state. Given the global nature of motion, we looked for associations between the occurrence of large frame-wise displacements and increased overlap in the state associations for the 4 PMC seed regions (i.e., when a motion occurs, do they all shift to be associated with the same state); we found that this was not the case as the percent of time four seeds shifted into the same state is very low for all states (ranges from 0.38% to 2.26%), compared to the percent of windows with mean FD greater than 0.2mm (ranged from 8.84% to 34.03%) (compare Fig. S5B with C).

3.2.4 Test-retest reproducibility and reliability

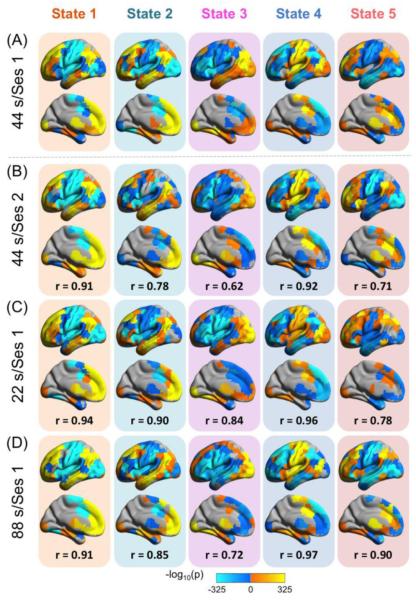
To examine the reproducibility of the d-iFC states, similar d-iFC analysis was performed on session 2 data. Six common states were detected in session 2 and five of them were significantly correlated with the states detected in session 1 (Fig. 7A and B: r ranged from 0.62 to 0.91, all significant at p < 0.0001 based on permutation testing [10,000 permutations]). Furthermore, the common iFC states were also highly correlated with five of the six states detected using a window size of 22s (Fig. 7C: r ranged from 0.78 to 0.96, all significant at p < 0.0001 based on permutation testing) and the five states detected using a window size of 88s (Fig. 7D: r ranged from 0.72 to 0.97, all significant at p < 0.0001 based on permutation testing), suggesting that these iFC patterns were highly reproducible and robust to window size selections.

Figure 7. Assessing iFC state reproducibility and robustness.

The states identified in session 1 (A) were significantly correlated with the states identified in session 2 (B) in the primary analysis with a window size of 44s (all correlations are significant after FDR corrected at q < 0.05). These states (A) were also significantly correlated with five of the states detected when we repeated our analyses using window sizes of 22s (C) and 88s (D) (all correlations are significant after FDR corrected at q < 0.05). r represents the Pearson’s correlations coefficient. Ses: session.

To assess the TRT reliability of the dynamic metrics, states common to the two sessions were first identified by clustering data concatenated from both sessions. Five states were identified and they were significantly correlated with the states detected in session 1 (r range from 0.65 to 0.97, all significant at p < 0.0001 based on permutation testing). Overall, we found that TRT reliability of the dynamic metrics varied from low to high across metrics, with the Seed Pair Overlap Index and Total Duration having the highest overall reliability (Fig. 6, right panel). For each of the dynamic indices depicted in Figure 6, Table 2 summarizes the total number of metrics (based upon the number of seeds, seed pairings, or states a given metric is applied to), and the number of times the index exhibits moderate or high ICC values.

3.2.5 Association between dynamic metrics and phenotypic characteristics

We found that Mean Duration seed 4 in state 4, a reliable metric (ICC = 0.65, see Fig. 8C), is negatively correlated with the total weighted achievement score (TWAS) assessed using the Twenty Question Test of the D-KEFS, a measure of concept formation and flexibility of thinking. This correlation is significant in both session 1 (r = −0.82, p = 0.00018) and session 2 (r = −0.79, p = 0.00042) after controlling for motion and correcting for multiple comparisons (Fig. 8 A and B). A false discovery rate correction for 231 simultaneous tests was performed for each session with q=0.05. The threshold detected after correction is 0.00018 and 0.00042 for session 1 and session 2, respectively. This negative correlation was unlikely to be confounded by age or sex, as neither is associated with dynamic metrics and neuropsychological (i.e. IQ and executive function) measures (all p > 0.20). The effect in session 2 was also not driven by the outlier as the correlation became even more significant after removing the circled outlier (r = −0.91, p ~= 0).

Figure 8. Relating d-IFC to inter-individual variation in executive function.

Mean Duration of seed 4 in state 4, a reliable measure (C: intra-class correlation [ICC] = 0.65), was negatively correlated with the total weighted achievement score (TWAS) assessed using the Twenty Question Test of the Delis-Kaplan Executive Function System (D-KEFS). This correlation was significant in session 1 (A) and 2 (B) (FDR corrected at q < 0.5), either with or without the circled outliers being removed. Note that the statistics reported here were with all data points included.

Furthermore, this negative correlation was confirmed when using different window sizes. Specifically, when the window size was 22s, the correlation was significant in both sessions (session 1: r = −0.64, p = 0.007; session 2: r = −0.54, p=0.024; one-tailed). When the window size was 88s, the correlation was significant in session 1 (r = −0.74, p = 0.001; one-tailed,) but was not significant in session 2 (p > 0.1, one-tailed). These correlations did not appear to be driven by those participants diagnosed with depression, as they were still significant for sessions 1 (Fig. S6C: r = −0.78, p = 0.001, one-tailed) and 2 (Fig. S6D: r = −0.66, p = 0.01, one-tailed) after excluding these subjects. The remaining brain-behavior correlations were only significant in one session or not significant in either session after FDR correction, and thus not discussed here.

4. Discussion

Our findings replicate and provide novel insights into previous observations of differentiable siFC patterns across PMC subregions. Specifically, we demonstrated a set of reproducible iFC states that were common to the PMC subregions, with each subregion possessing a unique state profile. As expected, s-iFC of each subregion was reflective of the state(s) it spent the most time in, suggesting that the observation of differentiable s-iFC networks results from differences in the specific iFC state for which each sub-region shows a preference. Several state profile metrics exhibited moderate to high test-retest reliability, suggesting their utility in indexing differences between individuals and populations; Total Duration and Seed Pair Overlap Index were particularly reliable. Interestingly, the mean duration of time seed 4 spent in state 4, a highly reliable metric, was able to predict individual differences in categorization ability and mental flexibility in both sessions, suggesting functional relevance of dynamic metrics. Overall, this work demonstrates the ability of d-iFC analyses to enrich our understanding of intrinsic brain function and characterize inter-individual variations.

Our work revisited the commonly reported negative relationships (i.e., anti-correlations) between the ‘default’ and ‘task-positive’ networks (Fox et al., 2005; Kelly et al., 2008), suggesting a more complex picture. Similar to prior dynamic studies (Allen et al., 2012; Chang and Glover, 2010; Majeed et al., 2011), our findings suggest that PMC subregions change their associations with the DN and TPN over time. While the PCC spent almost half of its time associated with the DN (state 2), its network associations changed at times to be more inclusive of the TPN (state 4) – suggesting that commonly cited segregations between the two networks are not hardwired. The emerging picture was further enriched by findings that several of the remaining states (e.g., 3 and 5) were actually mixtures of DN and TPN components.

The concept of changing network associations is not specific to R-fMRI. Electrophysiological studies of the mesoscale connectome have revealed transient interactions arising between distributed functional ensembles of neurons in response to changing task demands (Varela et al., 2001). At the macroscale, Spreng et al. (2010) divided the classic DN (Buckner, 2012) into a core DN (akin the hippocampal based sub-network of Andrews-Hanna et al., 2010) and a fronto-parietal network (FPN) based control system, finding that the associations of the FPN with the DN core vs. TPN change as a function of task demands. Recent work by Cole et al. (in press) further demonstrated the existence of flexible hubs within the FPN (i.e. lateral PFC and posterior parietal cortex); they argued that FPN’s role in adaptive control for a wide range of cognitive tasks is made possible by these hubs, which flexibly update their brain-wide iFC patterns according to task demands.

The state-related results in the current study are consistent with those of prior work using similar methods to detect discrete states at a larger scale based on whole-brain connectivity (Allen et al., 2012). Similar to our current findings, Allen et al (2012) found that the network membership and connectivity of PMC subregions (e.g., precuneus and PCC) with the rest of the brain change across states. Using a revised point-process method, Liu and Duyn (2013) reported that DMN can be decomposed into 8 PCC-related co-activation patterns (CAPs) and different proportion of PCC/precuneus are involved in different CAPs. While the whole-brain connectivity analysis revealed more information on how various brain regions interact, our results provided more detailed information regarding how subdivisions within posteromedial cortex interact with other regions and change over time. Our work demonstrates the feasibility of using sliding-window correlation to capture the functional integration and segregation of units within complex brain regions. The novel insights gained from the present work enriched our understanding of the functional organization of PMC and provided complementary information to other dynamic studies focusing on large-scale network transitions.

In attempting to understand the functional significance of temporally dynamic iFC patterns, we draw attention to two possible explanations. First, consistent with suggestions that the intrinsic architecture provides a representation of the dynamic repertoire of the brain’s responses (Mennes et al., 2013; Smith et al., 2009), the various states captured through d-iFC analysis may reflect the range of network configurations required to support flexible brain function. Alternatively, they may reflect transient cognitive events occurring during an R-fMRI scan, which may either, invoke, or result from different states. Experimental manipulations capable of perturbing temporal dynamic patterns can help to discern between these possibilities; examples include secondary tasks (Cole et al., in press), brain stimulation techniques (Fox et al., 2012), and real-time fMRI (Sulzer et al., 2013; Van De Ville et al., 2012). Note that consistent with prior work (Margulies et al., 2009), we labeled seed 1 as limbic seed and seed 3 as cognitive seed based on their s-iFC patterns. We did not attempt to label the d-iFC states, as their functional significance remains unclear and the spatial pattern of several states can not be easily interpreted, as they include distributed regions that span several of the previously identified intrinsic connectivity nextworks (ICNs). Future work is needed to understand the physiological origins of these states and how they are related to psychological functions.

Several recent studies have suggested that intrinsic phenomena may underlie critical aspects of cognition and behavior (Sadaghiani and Kleinschmidt, 2013). For example, simultaneous EEG-fMRI studies linking fluctuations in network connectivity to alpha power (Chang et al., 2013; Tagliazucchi et al., 2012) suggest that iFC dynamics may partly reflect states of arousal and vigilance. Perhaps most exciting, a recent study found that large-scale network interactions during the pre-stimulus interval can predict trial-to-trial variations in performance in a psychomotor vigilance task (Thompson et al., 2012). Adding to this growing literature, the current study demonstrated the ability of d-iFC feature to index executive function. Specifically, we found that those individuals whose visual subregion of the PMC spent a greater amount of time in state 4 (including key regions of TPN) for a given occurrence (i.e. Mean Duration) during rest, exhibited poorer concept formation and mental flexibility when performing the Twenty Question Test of the D-KEFS.

The association between the visual subregion of PMC and mental flexibility is of particular interest, as this subregion exhibited the largest number of transitions and was most equally associated with the five iFC states. Although speculative, greater time fixed on state 4 during R-fMRI may reflect a decreased tendency to flexibly reorganize brain circuitry to support task demands. The human brain’s unique capacity to rapidly reconfigure and flexibly adapt to different cognitive control demands has been demonstrated in rapid instructed task learning (Cole et al., 2013). Using methods similar to the current study, Damaraju et al. (2012) reported that the iFC states of schizophrenia patients switched less often than healthy controls, suggesting a relatively rigid connectivity. This association between reduced network flexibility and poorer cognitive task performance was confirmed with task-based fMRI (Spreng and Schacter, 2012). Of note, initial findings of precuneus abnormalities in adult ADHD (Castellanos et al., 2008; Uddin et al., 2009) included the visual subregion. Future work may benefit from increased focus on this portion of PMC and its associations with executive function.

Beyond delineating iFC states for PMC subregions, we presented various metrics for characterizing state transition behaviors, several of which exhibited high test-retest reliability. In particular, the Total Duration (% of time a given seed spends in a state) and Seed Pair Overlap Index (i.e., % of time two seeds are in the same state) have the highest reliability; the transition matrix had the lowest reliability. Findings of moderate to high reliability are promising for potential applications in characterizing inter-individual and group-differences; studies have already shown altered temporal dynamics in a number of clinical populations (Hamilton et al., 2011; Jones et al., 2012; Sakoglu et al., 2010). Importantly, while test-retest reliability is a key component of determining the appropriateness of a metric for clinical application, it is not the sole determinant (Castellanos et al., 2013). As recently noted for motion (Yan et al., 2013a), artifactual signals can either increase or decrease reliability. Future work combining electrophysiological and fMRI recordings, or interventional approaches, can increase confidence regarding accuracy. Furthermore, substantial work is required to appropriately validate and optimize d-iFC approaches before dynamic metrics can be confidently used as biomarkers of normal development and psychiatric diseases.

Several methodological considerations arise from usage of sliding-window analyses. In particular, concerns are about whether window-based temporal iFC fluctuations are meaningful, and whether the window size is optimal. We verified that our window-based measurements of iFC are meaningful by comparing correlations obtained with real data vs. those obtained following phase randomization procedure (Fig. S2). Additionally, we performed our analyses using a number of window sizes (22s, 44s, 88s), demonstrating the robustness of our findings. While the window size of 44s was selected based on previous work, a recent review noted that 30-60s tend to give robust findings (Hutchison et al., in press). Multiband imaging technologies afforded us 69 time points / window, as opposed to 22 time points when using the more common TR=2s, increasing our confidence in windowed iFC measurements. Following Allen et al. (2012), we also used graphical Lasso to improve the estimation of the covariance matrix, though found little difference relative to non-regularized coefficients; future work should explore such optimizations further. Finally, our usage of a test-retest dataset served to further increase confidence in our findings.

The process of developing and refining d-iFC analyses will undoubtedly require the field to revisit and rethink preprocessing strategies. In particular, the present work draws attention to global signal regression – a technique that is among the most commonly used and controversial in the R-fMRI field. Specifically, we found that while the detection of iFC states is possible without GSR, the approach does appear to increase detectability and reproducibility. Advocates of GSR in s-iFC analyses note that by removing global variance, GSR can increase the spatial specificity of correlation patterns, improve the correspondence between resting-state correlations and anatomy (Fox et al., 2009), enhance the neuronal-hemodynamic correspondence (Keller et al., 2013) and account for the effects of motion at the time series level (Yan et al., 2013a). Criticisms center around the potential for GSR to artifactually generate negative correlations (Murphy et al., 2009; Weissenbacher et al., 2009), alter interregional correlation patterns across participants (Gotts et al., 2013; Saad et al., 2012), and remove neural components along with artifactual (Yan et al., 2013b). Several authors have advocated alternative approaches that account for the impact of nuisance signals on inter-individuals differences at the group analysis stage (Saad et al., 2013; Yan et al., 2013b) – unfortunately, this is too late to facilitate the detection of d-iFC states. In contrast, principled approaches to nuisance signal correction at the time series level have also emerged (e.g., RETROICOR (Glover et al., 2000) and ANTICOR (Jo et al., 2010)) – though they are not likely to be able to account for the impact of motion as GSR does. As previously noted by Yan et al. (2013a), scrubbing is not appropriate for d-iFC analyses, as the method alters the temporal structure. In sum, despite its limitations and flaws, GSR may have potential utility in d-iFC analyses until more effective alternatives are solidly established. One promising alternative that is worth mention is the recent development of multi-echo MRI sequences capable of providing voxel-wise indices of physiologic and motion artifacts (Bright and Murphy, 2013; Kundu et al., 2012).

Some limitations of our work should be noted. First, the sample size was relative small (n=22), and included individuals with depression. While our results did not appear to be confounded by the patients, as their state profile and neuropsychological testing scores were within normal range, it is important to replicate our findings with a larger and homogenous sample. Second, it may not be an optimal approach to use previously demonstrated coordinate system for precuneus/PCC (Margulies et al., 2009). Defining the seed regions based on previous study or the current dataset is a trade-off between location accuracy and the variability introduced by data-driven methods (e.g., parameter selection). To reduce variability and avoid biases in findings introduced by using the same dataset, we used the pre-defined seeds and verified that these seeds actually represent four distinctive subregions. Future work directly compare these two approaches are warranted. Third, various parameters related to data acquisition (e.g., sampling rate, scan duration), data preprocessing (e.g., motion correction, global signal regression), and specific analysis approaches (e.g. window size, increasing step, clustering methods, determination on optimal number of clusters) can potentially influence findings. For example, data acquired with slower sampling rates will have fewer observations in the window, which in turn produces higher error in the estimated correlation coefficients. As such, one might anticipate that inter-individual differences would be less reliable than what is seen with fast TR (e.g., multiband) imaging approaches. Though, of note, slow TR data does have greater signal-to-noise ratio in each volume, which may provide an advantage. Thus, future work with slow TR data may benefit from similar examinations of test-retest reliability before proceeding with large-scale usage. Overall, systematic examination is merited in future works to attain a methodologically robust analysis pipeline readily applicable to developmental and clinical populations.

Fourth, through our clustering analysis, we did not see evidence of an ‘intermediate state’ that would co-occur between transitions from one major state to another. More fine-grained analyses explicitly examining the transition period for more subtle variations are warranted in future work to capture the evolving changes of the iFC patterns. Fifth, though being a robust partitioning algorithm, the hierarchical clustering algorithm has certain drawbacks such as inability to scale well (i.e. computationally demanding for large datasets) and no back-tracking capability (Rokach and Maimon, 2006). Future work examining the efficiency of other clustering algorithms or developing approaches other than clustering is necessary for a better understanding of temporal dynamics of functional connectivity.

While the present work focused on PMC, the insights gained will likely have ramifications for other structurally and functionally heterogeneous regions (e.g., anterior cingulate cortex, striatum, amygdala). Findings from prior works that used s-iFC to characterize functionally differentiable subdivisions within these regions (Di Martino et al., 2008; Margulies et al., 2007; Roy et al., 2009) can be enriched by reconsideration through the lens of temporal dynamics. More broadly, the field needs to address the challenges of replacing static accounts of functional interactions within the connectome with dynamic representations. Future work will benefit from expanding the scope of d-iFC investigations to include local measures (e.g. regional homogeneity, voxel-mirrored homotopic connectivity) and large-scale network properties (e.g. network centrality). Finally, temporal dynamics needs to be considered as another dimension by which phenotypic variables can be used to annotate the connectome and derive neurophenotypes (Craddock et al., 2013).

In conclusion, we demonstrated that PMC subregions alternate between a shared set of diFC states, with each possessing a preferred state(s); additionally, we established the reproducibility of d-iFC states and demonstrated moderate to high test-retest reliability for a subset of metrics used to quantify state switching behaviors. The present work brings the dynamic perspective to our understanding of the functional organization of PMC and draws attention to the need for an enhanced conceptualization of iFC in the brain.

Highlights.

• Temporal dynamics of posteromedial cortex (PMC) functional connectivity were examined.

• PMC subregions alternated between a common set of functional connectivity states at rest.

• Each PMC subregion possessed unique preferred state(s) and state transition patterns.

• Connectivity states were reproducible, and various state metrics appeared reliable.

• Inter-individual variation in state properties was related to cognitive flexibility.