Modeling of the RAG Reaction Mechanism

SUMMARY

The RAG complex in vertebrate V(D)J recombination must coordinate its catalytic steps with its binding to its two distant recombination sites in a manner that is still unclear. Here we test the ability of the plausible reaction schemes to fit observed time courses for RAG nicking and DNA hairpin formation inV(D)J recombination. The reaction schemes with the best fitting capability (a) strongly favor a RAG tetrameric complex ([RAG1₂:RAG2₂]) over a RAG octameric complex ([RAG1₄:RAG2₄]);(b) indicate that once a RAG complex brings two RSS sites into synapsis, the synaptic complex rarely disassembles (nearly irreversible); (c) predict that binding of both RSS sites (synapsis) occurs before catalysis (nicking); and (d) show that RAG binding properties permit strong distinction between RSS sites within active chromatin versus non-specific DNA or RSS sites within inactive chromatin, a point with evolutionary implications. The results provide insights for synapsis by nuclear proteins generally and testable predictions.

INTRODUCTION

Relating the biochemical behavior of nuclear proteins to their in vivo function is challenging. Accurate binding affinities for many nuclear proteins are not known or are known only for non-ideal conditions. For nuclear proteins that have enzymatic activity, one can determine the binding affinity specifically of the catalytically active fraction of a purified protein preparation. However, this has not been done for very many eukaryotic nuclear enzymes that stably bind to DNA sites.

For the function of RAG1 and RAG2 (the RAG complex) in V(D)J recombination, much is known about the sites of action in vivo, and outstanding work has demonstrated the regions of the genome at which the RAG complex is localized in early B cells (Chakraborty et al., 2007; Ji et al., 2010a; Ji et al., 2010b; Subrahmanyam et al., 2012). Although antigen receptor loci are among the best-defined genetic loci in eukaryotic biology, there are numerous unresolved biochemical questions about the function of the RAG complex that are central to its action in the cell (Schatz and Swanson, 2011). Among these questions, some are highlighted here. First, what is the stoichiometry of the RAG complex when it binds to one RSS? Second, what is the stoichiometry of the RAG complex when it brings two RSS sites together and carries out its nicking and hairpin formation reactions? Third, does the RAG complex bring two sites together (synapse a 12RSS and a 23RSS) before it carries out the first catalytic step, which is nicking, at each RSS? Fourth, is there a specific order in which the RSS sites are bound? Fifth, is the synaptic state reversible? All of these questions are important for both normal and pathologic conditions for V(D)J recombination.

Kinetic modeling can help rule in or out certain models for enzyme binding and catalysis. Application of such modeling to the RAG complex of V(D)J recombination has been very limited (Yu et al., 2004). Recently, we generated full-length RAG complexes that do not suffer from the truncations of RAG1 or 2 used previously. We have reported initial rate kinetic studies, which have provided insight into the function of the RAG complex at RSS sites (Shimazaki et al., 2012; Shimazaki et al., 2009).

Here we have formulated reaction schemes for most of the likely pathways by which the RAG complex can act on its target sites. Then we determine how well each scheme can fit experimental data for time courses of the nicking and hairpin reactions for full-length RAG complexes. Comparison of the goodness-of-fit between the reaction schemes permits determination of which schemes are most likely and which are incompatible with the data. Reliability of this approach is improved because we have measured values for rate constants and for equilibrium constants at some steps, and this markedly limits the process of arriving at best-fit values for the few steps for which we do not have measurements. This process allows insight into the function of the catalytically active fraction of the RAG proteins, which is not currently possible using other experimental approaches. Our findings provide insights that are relevant to RAG function in vivo, provide testable predictions, and provide an example of how biochemical information can be used to study the way in which nuclear proteins search for and bring together specific sites in the genome.

RESULTS AND ANALYSIS

Time Course of RAG Nicking and Hairpin Formation

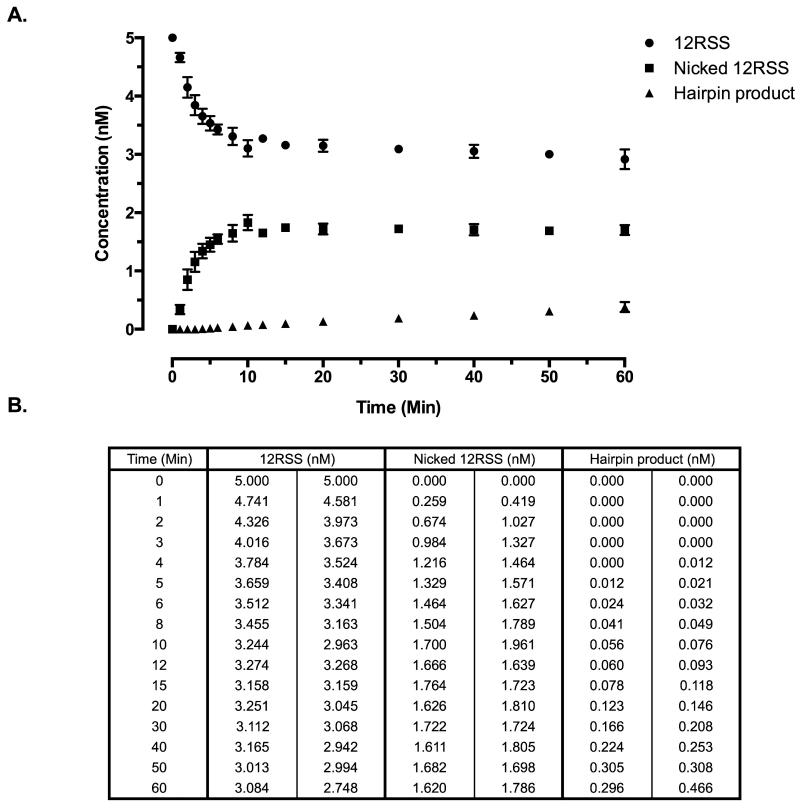
We measured RAG nicking and hairpin formation over a 60 min time course in order to provide data for comparing models for the reaction schemes. The amount of nicked and hairpin product at defined time points is determined by running the products on denaturing PAGE gels. The results show a hyperbolic time course (Fig. 1), as we have found previously (Shimazaki et al., 2012; Shimazaki et al., 2009; Yu and Lieber, 2000; Yu et al., 2004).The amount of substrate consumed plateaus at a point that reflects the amount of active RAG complex in the reaction. Addition of more RAG proteins can convert additional substrate to product(not shown).The plateau level of products formed is an equilibrium measure of the amount of active RAG complex. This measure matches the fraction of active RAG complex measured by an entirely different method, namely burst kinetics (Shimazaki et al., 2012). Although here we only show labeled 12RSS and cold 23RSS, previous studies on 23RSS have shown indistinguishable kinetic parameters from 12RSS(Shimazaki et al., 2012; Shimazaki et al., 2009; Yu and Lieber, 2000; Yu et al., 2004).

Figure 1. Kinetics of coupled cleavage assay with the full-length RAG complex.

(A) Time course of nicking at 12RSS, hairpinning at 12RSS, and undigested 12RSS substrate. Data points represent the average and error bars show the range. These experiments were repeated twice, and related time courses indicate that these time courses are quite representative. (B) The table shows numerical values of concentration in nM for 12RSS, nicked 12RSS and hairpin product over the time course of the reaction (see Experimental Procedures for details).

The RAG complex is known to remain bound to the signal ends after hairpin formation (Jones and Gellert, 2001), and it is not entirely clear how the RAGs become removed from the signal ends in vivo(Lin and Desiderio, 1993; Lin and Desiderio, 1994).

Reaction Schemes

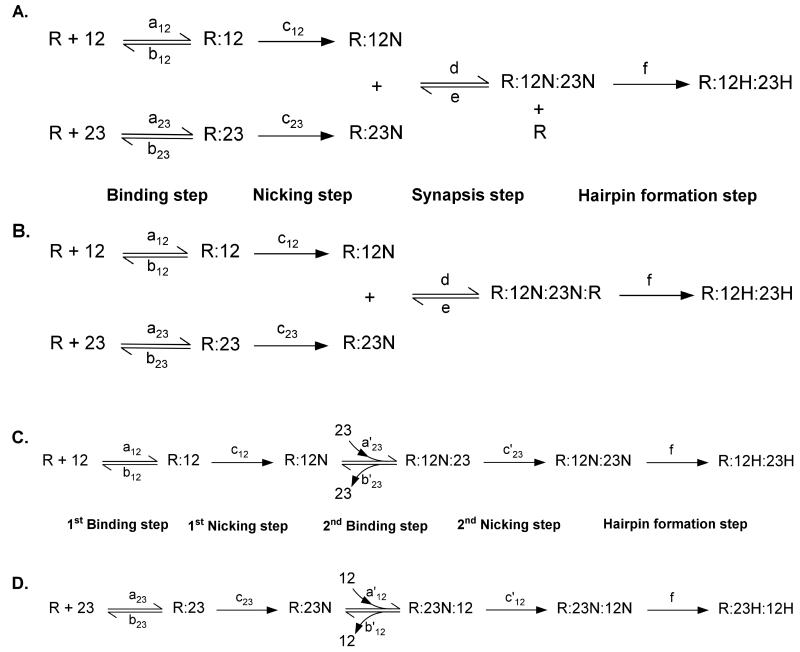
There are a limited number of plausible reaction schemes for binding, nicking and hairpinning by the RAG complex on its two substrates, the 12RSS and 23RSS (Fig. 2 and Fig. 3). Our analysis determined how well these reaction schemes can fit the data, within the constraints of our measured rate constants or ratios of rate constants (equilibrium constants). Model 1 is based on reaction scheme 1, and so forth. Modeling determines the value of unmeasured constants that yield the best fit to the observed data within the constraints of that model.

Figure 2. Schematics of the potential mechanisms of RAG nicking and hairpin formation.

The RAG catalytic complex can carry out nicking and hairpin formation in at least eight mechanistically distinguishable ways. Reaction schemes 1 to 4 are shown here. For other reaction schemes please see Figure 3. Catalytic rate constants are shown next to the corresponding reaction arrows by lowercase letters with subscripts. See text for details. R, RAG enzymatic complex; 12, 12RSS; 23, 23RSS; R:12, RAG bound to 12RSS; R:23, RAG bound to 23RSS; N, nicked; H, hairpin.

Figure 3. Schematics of the potential mechanisms of RAG nicking and hairpin formation.

The RAG catalytic complex can carry out nicking and hairpin formation in at least eight mechanistically distinguishable ways. Reaction schemes 5 to 8 are shown here. Catalytic rate constants are shown next to the corresponding reaction arrows by lowercase letters with subscripts. See text for details. R, RAG enzymatic complex; 12, 12RSS; 23, 23RSS; R:12, RAG bound to 12RSS; R:23, RAG bound to 23RSS; N, nicked; H, hairpin. See also Figure 2.

Modeling of Reaction Scheme 1:Parallel Binding and Nicking Prior to Synapsis

The modeling process is done as described in the Experimental Procedures. Basically we write out the differential equations for each kinetic step of the reaction schemes (Figs. S1 and S2 A-D). We then take our measured kinetic constants or ratios of constants (in the case of equilibrium constants) and assign these. We allow the remaining rate constants to float (i.e., meaning that they can assume any value over an unlimited range all the way up to diffusion limits).

The first model we considered assumes that each active RAG complex binds to and nicks one substrate before synaptic complexes are formed. As it is shown in its schematic representation (Fig. 2A), in this reaction, RAG complexes that are bound to nicked 12RSS and 23RSS come together to form a synaptic complex that only includes one RAG tetrameric complex. During the synapsis step, one RAG tetrameric complex is released and can be recycled. The release of one RAG tetrameric complex during the synapsis formation step is essential for this model, because without this [as is shown in reaction scheme 2 (Fig. 2B) and its model in Fig. S1.E], the modeling cannot fit the experimental data. The RAG complex which remains bound to the 12RSS and 23RSS can then catalyze the hairpin formation step.

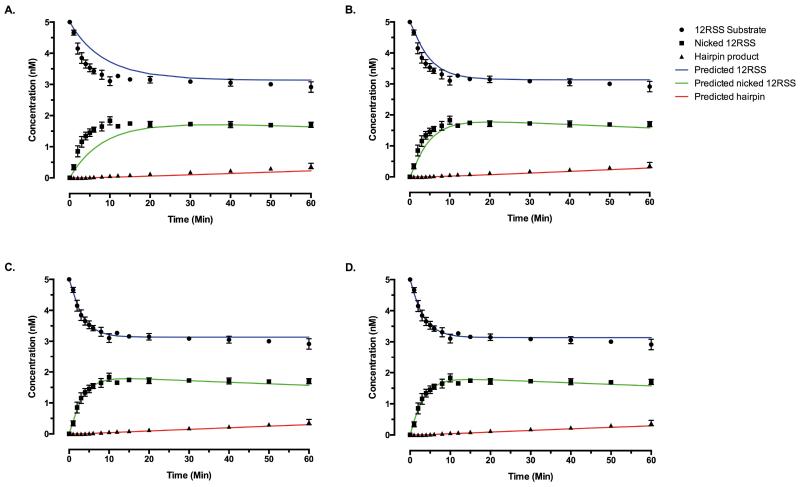
The squared 2-norm of the residual (deviation of the fit from the data) for the best fit was 5.446 (Fig. 4A). Even the best fit for this model cannot be considered to be a very strong fit, primarily because the residuals are not centered on zero (Figs. S3-4). There is a systematic positive error in the predicted values for the concentration of the 12RSS substrate, as well as systematic negative errors in the predicted values for the concentration of nicked product during early time points and hairpin product during late time points.

Figure 4. The outcome of curve fitting for Models 1, 5, 7, and 8.

Predicted concentrations of 12RSS substrate (blue), nicked 12RSS (green), and hairpin 12RSS (red) based on the best fit of (A) scheme 1, (B) scheme 5, (C) scheme 7, and (D) scheme 8 are shown in solid lines. Experimentally measured concentrations of 12RSS, nicked 12RSS, and hairpin 12RSS are shown in points with error bars as explained in Figure 1. See text for more information on conditions and assumptions of curve fitting. Schemes 7 and 8 provide similarly good fits for other RAG couple-cleavage time courses that start with different substrate concentrations (data not shown).

For all the fits that had resnorm values less than or equal to 6, the kinetic rate constant of hairpin formation step (designated as f in the figures) was between 3.14×10⁻⁵ and 9.99×10⁻⁵s⁻¹.Furthermore, the forward rate constant for the synapsis formation step was much larger than the reverse rate (at least two orders of magnitude), which means the synapsis and release of one RAG complex is a nearly irreversible step.

Modeling of Reaction Scheme 5:Sequential Binding/Nicking Before Second RSS is Bound

Reaction schemes 2, 3 and 4 did not provide very good fits to the observed data, and these are discussed in the supplement (Fig. S1.E-G). In scheme 5, a sequential reaction is proposed for nicking and hairpin formation by the RAG complex (Fig. 3A). Here we assume that each RAG complex first binds to one of its substrates (either the 12RSS or 23RSS), and nicks that substrate after binding. Then the RAG:RSS complex binds and nicks the other substrate, leading to formation of a complex composed of RAG, nicked 12RSS (12N), and nicked 23RSS (23N). A hairpin formation step follows the second nicking reaction and generates the final hairpin products.

The main difference between this reaction scheme and what is proposed in reaction scheme 1 (Fig. 2A) is that here, one RAG enzymatic complex undergoes two sequential binding and nicking steps. This is a different type of synapsis from scheme 1where two RAG complexes come together. The kinetic rate constants of the second binding and nicking steps (shown in Fig. 3A by a’₁₂, a’₂₃, b’₁₂, b’₂₃, c’₁₂, and c’₂₃) are not necessarily the same as those of the first binding and nicking steps (namely, a₁₂, a₂₃, b₁₂, b₂₃, c₁₂, and c₂₃).

The norm of the residual (resnorm) for the best fit of this model was 1.16, which is about 5-fold smaller than that of model 1 (compare Figs. 4A and B). There is also less systematic bias in the residuals compared to model 1.This shows that this model fits our experimental data better than model 1.However the residuals are still not normally distributed and the mean of the residuals is still significantly different from zero (Figs. S3-4). Nevertheless, for all the fits with resnorm values less than or equal to 2, the kinetic rate constant of the hairpin formation step was between 4.6×10⁻⁵ and 13.9×10⁻⁵s⁻¹, which is very similar to that of model 1.

An interesting point about the results of the modeling is that in all fits with resnorm values less than or equal to 2, the catalytic rate constant of the second nicking step of 12RSS (c’₁₂ in the Fig. 3A) is more than 0.01s⁻¹, while this constant for the first nicking step (k_cat or c₁₂ in the figure) is measured to be 0.0063s⁻¹.This implies that the nicking of 12RSS is about 1.6-fold faster when the RAG complex is already bound to a nicked 23RSS compared to when a free RAG complex binds to a 12RSS and catalyzes the nicking. Furthermore, the Michaelis-Menten constant, K_M, for 12RSS nicking reaction is less than 3.2nM when the 12RSS binds after the 23RSS, whereas it is measured to be 4.7nM when the reaction is done in the absence of the 23RSS(Shimazaki et al., 2012; Shimazaki et al., 2009; Yu and Lieber, 2000; Yu et al., 2004).As we showed previously for these reactions, K_M equals K_D (the dissociation constant, which is b/a) (Shimazaki et al., 2012).Therefore, the fact that K_M is smaller when the 12RSS binds to RAG after a 23RSS is already bound suggests that the second RSS binding is somewhat stronger than the first.

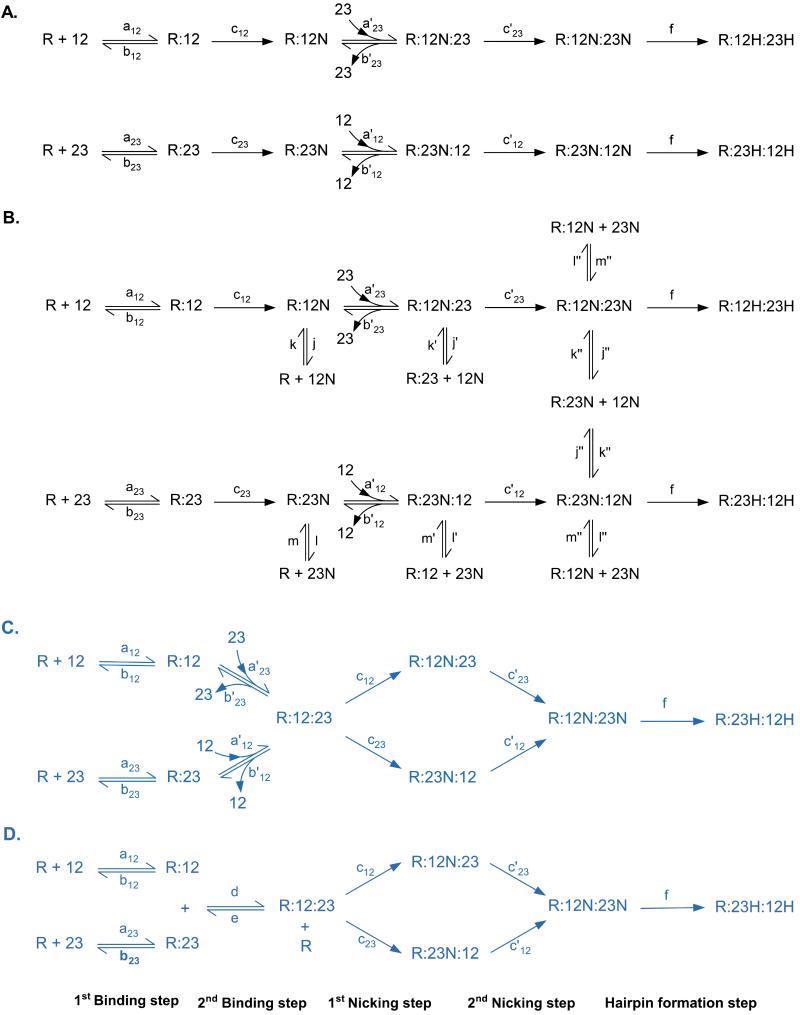
Modeling of Reaction Scheme 7:Sequential Binding and Then Nicking of Both RSS Sites

This reaction scheme proposes a sequential substrate binding (in either order) in which one RAG enzymatic complex sequentially binds to its two substrates (12RSS and 23RSS) prior to any catalysis, and then nicks both RSSs before moving forward to hairpin formation (Fig. 3C). The order of binding is not specified, which means that the RAG complex can bind to the 12RSS and then the 23RSS or vice versa. Similar to reaction scheme 5 (Fig. 3A), the kinetic rate constants of the second binding and nicking steps (a’₁₂, a’₂₃, b’₁₂, b’₂₃, c’₁₂, and c’₂₃) are allowed to be different from those of the first binding and nicking steps.

After curve fitting, the best fit for this model had a resnorm of 0.180, which is more than 30-fold smaller than for model 1 (Fig. 4C). Systematic negative bias that was evident in reaction scheme 1 is no longer present in this model, and the residuals are indeed normally distributed and centered on zero (Figs. S3-4). For all the fits with resnorm values less than or equal to 0.5, the range of values for the constants that were allowed to float are shown in Supplemental Table 1.The kinetic rate constant of hairpin formation step was in a very narrow range between 4.82×10⁻⁵ and 5.79×10⁻⁵ s⁻¹, providing useful insight, because direct formal kinetics on the hairpin step are very difficult to conduct.

Similar to what is shown in model 5, data from curve fitting of model 7 also suggest that the second RSS binding to the RAG complex is stronger than the first binding step. In all fits with resnorm<0.5, K_D for binding of the 12RSS in the second binding step is <0.6nM (<0.41nM for 23RSS), whereas this constant is measured to be 4.7nM for the first binding step (4.0nM for 23RSS). Therefore, binding of the second RSS is 8- to 11-fold tighter than the first RSS.

Modeling of Reaction Scheme 8:Parallel Binding Prior to Synapsis, Followed by Nicking

Another scheme that results in binding of both RSS sites prior to any catalysis is one in which two independent RAG complexes bind each RSS, followed by synapsis prior to any nicking or hairpinning (Fig. 3D). In contrast to reaction scheme 7 (Fig. 3C), here free RSS sites only bind to free RAG and not to a RAG complex that is already occupied by another RSS substrate. This reaction scheme is similar to scheme 1, except for the order in which nicking and synapsis formation happens.

Modeling of this scheme indicates that it also can fit the observed time courses extremely well (Fig. 4D). The best fit of this model has a resnorm value of0.188, which is nearly the same as the resnorm value for the best fit of model 7 (0.180). Similar to Model 7, and in contrast with Model 1 and 5, the residuals of Model 8 are also normally distributed with the mean of residuals being statistically not different from zero (Figs. S3-4). Therefore, modeling of kinetic time courses cannot distinguish between reaction schemes 7 and 8, and this modeling analysis provides the basis for directing future experimental work to distinguish these two schemes (see Discussion).

For all the fits with resnorm values less than 0.5, the kinetic rate constant of hairpin formation step was between 4.73×10⁻⁵ and 6.12×10⁻⁵s⁻¹.Hairpin rate constants in all the models, including models 7 and 8, are in an impressively narrow range, which suggests that only values in this narrow range can fit the experimental data. Furthermore, in all the fits with resnorm below 0.5, the value of parameter d is at least one order of magnitude larger than e. This suggests that the synapsis formation step in this model is an almost irreversible step, since the kinetic rate constant for its forward reaction is much larger that the reverse.

Stoichiometry of the RAG Complex

All of the reaction schemes that provided some level of fit assumed that the RAG complex was a tetramer [R1₂:R2₂]. The reaction schemes give only poor fits if we assumed that the RAG complex is an octamer[R1₂:R2₂]:[R1₂:R2₂], which is essentially a dimer of two tetramers. The reason why a RAG octamer is incompatible with our data is that the amount of active RAG enzyme is limiting. Since in an octameric RAG scenario, such as reaction scheme 2 (Fig. 2B), two RAG complexes remain bound to each hairpin product, concentration of available active RAG complexes in the reaction is depleted too quickly. Consequently the rate in which nicking and hairpin formation happens, as well as final concentration of nicked and hairpin products, cannot match the observed data.

Relevance of Equilibrium Aspects of RAG Binding to RSS Sites and to Chromatin

We wondered how the kinetic insights above on RAG binding and catalytic rates may relate to the distribution of RAG proteins observed in the genome of murine pro-B cells and pro-T cells, which is presumably near equilibrium. Experimentally, the K_D of active RAG complexes for 12 or 23RSS sites is 4.7 nM. The observed affinity of the RAG complex for H3K4me3 is 5 uM (Elkin et al., 2005; Liu et al., 2007; Matthews et al., 2007; Ramón-Maiques et al., 2007). We assume two RAG2 polypeptides are present in each RAG complex, and this allows for one or two interactions of the RAG complex, via the RAG2 PHD domain, with the histone octamers located at or adjacent to the RSS.

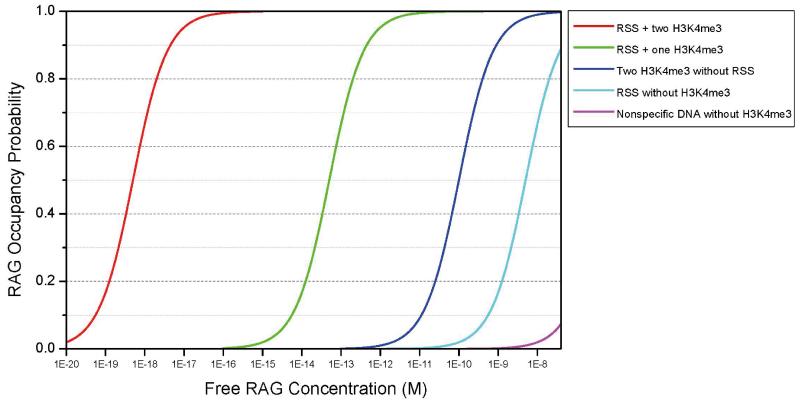
Given these observations, one can use equation 1 below (see Supplement for details) to plot the probability that the RAG complex will bind to sites with the following characteristics:(a) RSS with two H3K4me3 sites nearby;(b) RSS with one H3K4me3 site nearby;(c) no RSS site with two H3K4me3;(d) RSS with noH3K4me3; and (e) non-specific DNA with no H3K4me3.

$${\mathrm{P}}_{occ,X}={\left[\mathrm{R}\right]}_{\text{free}}∕({\mathrm{K}}_{\mathrm{D},\mathrm{X}}+{\left[\mathrm{R}\right]}_{\text{free}})$$ (Eq. 1)

Here P_{occ, X} is the probability of a given site, X, being occupied by RAG.[R]_free is the concentration of free RAG complex and K_D,X is the overall K_D for site X. We assume that bindings to the RSS site and each H3K4me3 are independent; meaning that binding to one of these sites does not affect the affinity of RAG complex toward other sites. Hence, overall K_D for a given site with both RSS and H3K4me3 is obtained by multiplying the observed K_D for RSS by K_D for H3K4me3 (see Supplement for details). We also assume that the K_D for RAG complex binding to the RSS is not affected by distortions of the DNA due to chromatin context.

In Figure 5, as the free RAG concentration is plotted across the x-axis over a 10¹³ range, one can observe the occupancy efficiency on the y-axis. As expected, the highest occupancy at low free RAG concentrations occurs for the case where the RAG complex makes both an RSS and two H3K4me3 contacts. Nonspecific DNA but within active (H3K4me3) chromatin is 9 logs weaker at achieving an equivalent probability of occupancy. An RSS located within inactive chromatin (no H3K4me3) is ~10 logs weaker in this respect. Nonspecific DNA in inactive chromatin is ~12 logs weaker.

Figure 5. Probability of RAG binding at RSS sites in active and inactive chromatin as a function of free RAG concentration.

The probability of RAG binding at any position in the genome depends on the presence or absence of H3K4me3 marks as well as RSS sites at that position. The likelihood of a non-specific DNA region, an RSS without H3K4me3 mark, a region with two H3K4me3 marks but without RSS sequence, and an RSS with one, or two H3K4me3 marks to be occupied by RAG complex are shown here as a function of free RAG concentration in the nucleus.

The total RAG concentration in the mammalian pro-B cell nucleus is not known, but 40 nM (~13,000 RAG1 molecules or ~6500 RAG tetrameric complexes per nucleus(Leu and Schatz, 1995)) is a within the range of reasonable estimates(40 nM is the right-hand margin of Fig. 5 graph).But the free RAG concentration is likely to be many logs below this. Importantly, we find that any free RAG concentration below 1 pM would permit highly specific RAG binding to RSS sites with either one or two H3K4me3 interactions; moreover, this would be associated with negligible binding at non-specific sites, whether these are in regions with or without H3K4me3.

DISCUSSION

The major findings of this study are (a) synapsis of two RSS sites must occur prior to any catalysis (nicking or hairpinning) and the binding for this can occur sequentially or in parallel;(b) the catalytic RAG complex cannot be an octamer and is consistent with a tetramer;(c) once a RAG complex brings two RSS sites into synapsis, the synaptic complex rarely disassembles (nearly irreversible); and (d) the binding properties of the RAG complex permit nearly complete distinction between RSS sites within active chromatin and all other sites [RSS sites within inactive chromatin and non-specific (non-RSS) sites regardless their chromatin].

Sequential versus Parallel Binding Models During Early Lymphoid Development

Both reaction schemes 7 and 8 can fit in vitro biochemical data well, and there are experimental methods by which these can be distinguished (see Testable Predictions). However, there are biological reasons why both schemes may be possible not only in vitro, but also in vivo. Model 7 may be most applicable when the J cluster is accessible earlier than other portions of a given antigen receptor locus -- a circumstance that is common because the J cluster is close to the enhancer for most loci(Chakraborty et al., 2007; Ji et al., 2010b; Subrahmanyam et al., 2012). Sequential binding may allow the RAG complex to bind at the J cluster while awaiting chromatin opening at the V or D segments. Indeed, genome-wide chromatin IPs indicate that the RAG complexes are detectable at the J cluster, but not elsewhere, even within active loci (Chakraborty et al., 2007; Ji et al., 2010b; Subrahmanyam et al., 2012).It is possible that action by the RAG complex at the first RSS, often the J segments, might then give the complex an advantage for binding and catalysis, based on the results we describe, which indicate that RAG binding at a second site (while bound to the first site) is more efficient.

For pro-B cell stages at which both RSS sites are located within active chromatin(Subrahmanyam et al., 2012), such as some of the IgHD_H to J_H joinings, the parallel binding model (scheme 8 in Fig. 3D) may be equally relevant in vivo as scheme 7.Parallel binding would permit the two RSS site searches to proceed simultaneously, which may be more efficient under the dilute RSS site concentrations in the nucleus.

Octameric RAG:RSS Complexes are Inconsistent with the Observed Kinetics

There is uncertainty about the stoichiometry of the RAG complex, in particular, whether the catalytic RAG complex is functionally a tetramer or an octamer(Grundy et al., 2009; Schatz and Ji, 2011; Shlyakhtenko et al., 2009).Our modeling results for all reaction schemes that we examined only fit the experimental data when we assume a RAG tetramer but not when we assume a RAG octamer.

While this means that the catalysis is done by a tetramer, we cannot exclude a non-catalytic role of a RAG octamer. For example, there is the possibility that a RAG octamer exists and serves a role in bringing two distant portions of DNA closer together at two specific RSS sites (regional synapsis), and this could create a high local DNA concentration for RSS recombination (Ji et al., 2010b; Schatz and Ji, 2011). Then other RAGs, existing as catalytically active RAG tetramers, could carry out nicking and hairpin formation at other RSS sites nearby the synapsed sites. Further experimental and kinetic modeling will be required to consider such a more complex possibility.

Evolutionary Implications of RAG Site-Selectivity

In the five situations that we assumed for equilibrium RAG binding, an RSS with one HeK4me3 and an RSS with no HeK4me3 have little chance of recruiting a RAG complex because they are 5 and 10 logs less preferable than an RSS with two HeK4me3.Nonspecific sites also have little chance to recruit a RAG complex because they are 12 logs less preferable, even though there are 6 × 10⁹ such sites. The only off-target site category that is borderline is H3K4me3-rich chromatin lacking an RSS.H3K4me3-rich regions are less than 3% of the genome, which means there are <10⁸ of them, and they are 9 logs less preferable. There is some small chance for them to recruit RAG complexes. However, the nicking rate constant for even moderate RSS sites is 15-fold lower than for optimal RSS sites, and nonspecific DNA is immeasurably low but at least 100-fold lower(Shimazaki et al., 2012).Moreover, the off-rate for the RAG complex (reflected in constant b) is much faster than the nicking rate (constant c) (Suppl. Tables 1 and 2).Hence, the RAG complex will fall off of the occasional nonspecific DNA to which they bind at rates that are 10,000 to 630,000-fold faster than they nick such sites. These magnitudes of such impressive site-selectivity are not obvious without determination of the relevant kinetic and equilibrium values, as done here.

The RSS sites of the vertebrate immune system and the RAG1 gene appear to have evolutionary origins in transposons in the genomes of Anopheles gambiae (mosquitoes) (Kapitonov and Jurka, 2005).However, there is no RAG2 in these organisms. Without the RAG2 PHD domain for H3K4me3 targeting, the site selectivity of the RAG complex may have been sufficient for random transposon movement in insects with short lifespans but would not have been sufficient to permit adequate targeting in long-lived organisms with a highly orchestrated gene assembly system such as V(D)J recombination. Mis-targeting by RAG complexes in mice that lack the RAG2 PHD domain may explain their impaired V(D)J recombination and genetic instability (Akamatsu et al., 2003; Curry and Schlissel, 2008; Deriano et al., 2011; Liang et al., 2002; Zhang et al., 2011).

Testable Predictions

Our analysis has value in making several predictions that are central to RAG function. First, our results predict that once two recombination sites are brought into synapsis, they rarely dissociate. This is testable using single molecule Forster (fluorescence) resonance energy transfer (sm-FRET) where one can monitor how long individual complexes remain in synapsis before dissociation. The physiologic significance of a nearly irreversible synapsis is that this would permit a longer time for the RAG complex to carry out the hairpin formation reaction, and again, this essentially drives the reaction forward, and past the truly irreversible hairpin formation step.

Second, our results predict synapsis prior to any catalytic nicking. Again sm-FRET could allow monitoring of release of a nicked fragment from single RSS/RAG complexes or 12RSS/23RSS/RAG complexes. Our results predict that the complete complexes are almost always formed before nicking. The physiologic value of this would be to minimize nicking of only one RSS by the RAG complex, which might otherwise cause deleterious recombination events.

Third, our results predict that the active RAG complex is a tetramer rather than an octamer. This can be tested experimentally when fluorescently labeled RAG complexes become available. Then one could create one preparation of RAG tetrameric complexes labeled with one fluor and another preparation with another fluor, and then mix with RSS target DNA and monitor FRET between the mixture of two types of tetrameric RAG complexes. When done with appropriate positive controls, the absence of FRET would indicate that no octameric RAG complex is formed on the target DNA.

From our analysis, synapsis precedes any catalysis, but either of two schemes can fit the time courses equally well (Fig. 3C and 3D). Distinction between these two schemes can be done use sm-FRET. The 12RSS-Cy3 can be tethered to a surface and then RAGs can be added to form a 12RSS:RAG complex (i.e., R:12 in the Fig. 2 and 3 mechanistic schemes).The unbound RAG complexes can be washed away in a flow arrangement. In a separate tube, RAG complexes can be bound to 23RSS-Cy5 DNA to form R:23 complexes. In the final step, the R:23 complexes are added. The sm-FRET in this arrangement can be compared to that seen when the 23RSS is added without pre-binding RAG complexes. The results will determine which of the two schemes most readily explains the observed time courses (Fig. 3C and 3D).

Relevance of Our Approach to a Broader Range of Nuclear Proteins

This study provides a formal analysis for how a protein complex can bring two sites in the nucleus together. The RAG complex carries out two DNA sequence searches and then executes two catalytic steps that lead to double-strand DNA breaks at these two distant locations in the genome. In contrast to simple DNA binding proteins, such as transcription factors, the catalytic steps have permitted a clearer assessment by in vivo and in vitro methods of how and where the RAG complexes bind to the DNA. The detailed on and off rates derived here may be useful in considering other protein-DNA interactions and cases of site-to-site synapsis.

EXPERIMENTAL PROCEDURES

RAG Nicking and Hairpin Time Courses

Preparations of full-length RAG1 and RAG2 complex, and HMGB1 protein were described previously (Shimazaki et al., 2012).Burst kinetic assays to determine the active fraction of the RAG complex and coupled cleavage assay with both 12- and 23RSS were done as previously described (Shimazaki et al., 2009).To determine the oligomerization status of RAG proteins, we have done gel filtration analysis on different versions of RAG complexes, including the core/core RAG complexes (core RAG1 plus core RAG2), as well as combinations of core and full-length versions of RAG1 and RAG2. The preparations of RAG complexes analyzed by gel filtration thus far are all consistent with tetrameric RAG complexes.

Briefly, the cleavage reaction contains 5 nM of 5′ end labeled 12RSS substrate, 5 nM unlabeled 23RSS substrate, 20 nM of the tetrameric RAG complex and 1 μM HMGB1(high-mobility group protein B1), 25 mM K-morphorinepropanesulfonic acid (MOPS)-KOH, pH 7.0, 30 mM potassium glutamate, 30 mM potassium chloride (KCl), 5 mM MgCl₂, 1 mM DTT, and 0.05 mg/ml BSA and is incubated at 37°C for 60 min. The reaction is stopped by adding 0.1% SDS and 20 mM EDTA, and then heat denatured. Products are separated on denaturing gels and visualized using a Molecular Image FX (Bio-Rad).The intensity of autoradiography is quantified using Quantity One (Bio-Rad).

Modeling

All modeling steps are done in MATLAB 7.12.0 (R2011a), and similar approaches have been successfully used previously for enzyme kinetic modeling (Yu et al., 2004).Eight reaction schemes are proposed as potential mechanisms for binding of RAG to its substrates (12RSS and 23RSS) and subsequent nicking and hairpin formation. For each reaction scheme, a system of differential equations is defined such that each equation in the system represents the rate of change in concentration of one biochemical species in the reaction scheme.

Systems of differential equations were then solved numerically as initial value problems by MATLAB ordinary differential equation solver, ode15s. The concentration of substrates (12RSS and 23RSS) and catalytically active fraction of RAG at the beginning of the reaction (t = 0min) were used as initial values.

For each reaction scheme, the lsqcurvefit utility of MATLAB was used to find kinetic rate constants that best fit the experimental data. K_m and k_cat values that we reported previously were used here to calculate related kinetic rate constants (Shimazaki et al., 2012).To perform an exhaustive search on the entire possible range of kinetic rates and also to ensure that local minima do not bias our results, we used a number of starting point values uniformly dispersed along the range of rate constants for each reaction scheme. Curve fitting was done for all combinations of these starting values, and the resulting fits were sorted based on their norm of residuals (resnorm). Details of the equations and the conditions under which they were solved are discussed in the Results and Analysis section and in the Supplemental Modeling Procedure.

HIGHLIGHTS.

• RAG kinetics indicate that RAG synapsis is nearly irreversible.

• Synapsis is favored prior to any RAG catalysis (nicking).

• A RAG octamer is inconsistent with RAG double-strand break formation kinetics.

• Sequence-specific RAG binding and chromatin contacts are both essential to achieve site specificity.