A Subject-Independent Method for Automatically Grading Electromyographic Features During a Fatiguing Contraction

Abstract

Many studies have attempted to monitor fatigue from electromyogram (EMG) signals. However, fatigue affects EMG in a subject-specific manner. We present here a subject-independent framework for monitoring the changes in EMG features that accompany muscle fatigue based on principal component analysis and factor analysis. The proposed framework is based on several time- and frequency-domain features, unlike most of the existing work, which is based on two to three features. Results show that latent factors obtained from factor analysis on these features provide a robust and unified framework. This framework learns a model from EMG signals of multiple subjects, that form a reference group, and monitors the changes in EMG features during a sustained submaximal contraction on a test subject on a scale from zero to one. The framework was tested on EMG signals collected from 12 muscles of eight healthy subjects. The distribution of factor scores of the test subject, when mapped onto the framework was similar for both the subject-specific and subject-independent cases.

I. INTRODUCTION

Activities of daily living often involve repetitive or sustained contractions. The result of such contractions is an increase in muscle fatigue, which is commonly defined as a reduction in the maximal force generating capability of the muscle [1]–[3]. Prolonged fatiguing contractions can result in damage to the involved muscles and is considered a major factor contributing to muscle pain and accidental falls [National Institute for Occupational Safety and Health, A Harvard medical school study (2004), U.S. Bureau of Labor Statistics (2002)]. Annual direct cost of occupational injuries due to slip and fall caused due to muscle fatigue is expected to exceed 43.8 billion by the year 2020 in the U.S. [Bureau of Labor Statistics (2004)].

These accidents have the potential to be avoided if individuals and clinicians could continuously monitor the progression of muscle fatigue. Unfortunately, it is impractical to repeatedly measure the reduction in maximal force generating capabilities of the muscle. Thus, in an effort to monitor the progression of muscle fatigue and minimize muscle fatigue-related injuries in a more practical fashion, researchers have attempted to track the changes in electromyographic (EMG) features of the involved muscles that can correlate with an increase in muscle fatigue [1], [4]–[7].

Typically, during a sustained submaximal fatiguing contraction, the mean amplitude of the EMG increases while the power spectrum of the EMG signal shifts to lower frequencies [8]. These changes are consistent with the recruitment of additional motor units and a decrease in the conduction velocity of action potentials along the muscle fibers [9], respectively. However, there is often a large amount of intersubject variability in such features [1], [3] and these phenomena can also be affected based on the type of contraction performed or electrode location [10]. These, generally, unpredictable variations across subjects make it difficult to develop a general framework that can grade several EMG features from a subject without prior data from that same subject. Such limitations make the application of systems to detect the progression of muscle fatigue in the workplace and clinical settings difficult and impractical. To overcome this limitation, we propose a general framework that can grade the changes in EMG features of a test subject during a fatiguing contraction without prior data from the same subject. We refer to this ability as a subject-independent method for grading EMG features. This framework is based on EMG data recorded from a reference group during a similar fatiguing contraction.

Because of the large intersubject variability in EMG features, it may not be possible to reduce myoelectric information into a single EMG parameter. Moreover, only EMG amplitude parameters may not be able to reliably track the myoelectric manifestations of fatigue [11]. However, it may be possible to track the myoelectric manifestations of fatigue by observing multiple EMG amplitude and spectral parameters, collectively. Hence, multiple EMG features were used to develop the subject-independent generalized framework. Many studies have only used two or three EMG features, namely, root mean square, mean frequency, and median frequency [3], [5], [6].

Although studies have attempted to track multiple features from the EMG signal during fatiguing contraction [12]–[14], these frameworks require baseline data from the test subject. Thus, these frameworks are not subject-independent. Others [15] have suggested to have developed a subject-independent fatigue estimating index [generalized mapping index (GMI)] based on a mapping function derived from multiple features. These claims are based on the fact that GMI has better signal-to-noise ratio, compared to commonly used estimators of fatigue such as mean frequency of EMG signals. In the proposed framework, the subject-based variability of the suggested measure was quantified and is shown to be an order less than the subject-based variability of the commonly used features such as mean frequency and median frequency. Moreover, GMI is based on four time-domain features, that are used to train an artificial neural network based on an assumption of linear relationship between muscle fatigue and time. Whereas, the proposed method derives its grading index based on both time- and frequency-domain features and do not assume any specific trend in progression of fatigue. However, to date, it has not been proven that multiple features can be used to track the progression of muscle fatigue, and therefore we are only attempting to determine when the muscles are approaching the point of task failure through the EMG features, in a subject-independent manner.

The proposed framework uses factor analysis to learn the relation between the EMG features during a fatiguing contraction, rather than learning the values of the features. Latent factors, obtained as a result of factor analysis on multiple features, represent the relation between the features. An analysis of the subject-based variability of each of the commonly used frequency and time-domain features and latent factors revealed that the latent factors are more robust across multiple subjects. Subject-based variability of these commonly used features has been provided in Section II-E and has been compared with the subject-based variability of the latent factors.

The purpose of this study was to develop a computer algorithm to automatically grade EMG features typically associated with muscle fatigue, during a fatiguing contraction, without the need to calibrate or train the system with baseline or subject-specific data, thus, forming a subject-independent framework. In this paper, we present a computer algorithm that quantifies a set of EMG parameters obtained during a fatiguing contraction on a scale from zero to one in real time. The scale is defined such that the zero denotes the beginning of the contraction and one denotes the point at which the subjects were unable to sustain the required contraction force as a result of muscle fatigue (task failure). However, the computer algorithm is not limited to tracking EMG features during sustained isometric contractions only. It is capable of tracking EMG parameters during dynamic contractions as well, as long as the reference data are also collected under similar exercise. A successful application of the proposed mapping index using SEMG signal from a repetitive gripping activity is presented in our earlier work [16], though in a subject-dependent manner.

II. METHODS

The proposed algorithm was applied to intramuscular EMG signals collected from 12 hand muscles during a sustained isometric fatiguing contraction and compared to the results from standard amplitude and spectral measures. The data are from a published report [17], which investigated the influence of fatigue on EMG–EMG coherence across hand muscles.

A. Subjects

Eight adults (five men, three women; 27 ± 6 years) participated in the study. Subjects reported being without any neurological disorders or musculoskeletal injuries of the hand and were right-handed. Subjects gave a written informed consent before participation in the study, and all experimental procedures were approved by the Institutional Review Board at Arizona State University.

B. Experimental Setup

Subjects sat in an adjustable chair facing a computer monitor. The right forearm was placed on a flat rigid platform with the wrist and hand in a semisupinated and neutral position, respectively. Movement of the forearm and wrist was prevented by rigid dowel restraints inserted into the platform around the forearm and wrist. The hand was positioned in a three-digit (thumb, index, and middle finger) grasp posture for the fatiguing contractions as shown in Fig. 1.

Fig. 1.

Experimental Setup: hand positioned in a three-digit grasp posture.

1) Force Measurement

The isometric force of each of the distal pads of thumb, index, and middle fingers was measured with 6-D force/torque transducers (ATI Nano-17/S1 Apex, NC) mounted on a manipulandum. They measure force in all three spatial dimensions and torque about all three spatial axes. The contact surfaces of the sensors for the index and middle fingers were 3 cm apart vertically (center-to-center), and 8 cm apart horizontally from the surface of the force/torque sensor for the thumb.

2) EMG Measurement

The intramuscular EMG was recorded with electrodes comprised of one 50 μm stainless steel wire insulated with Formvar (California Fine Wire, Grover Beach, CA) from 12 muscles of the hand. Insulation was removed from the recording tip and the opposite end of wire. One electrode was inserted into the belly of each muscle via a 27-gauge hypodermic needle. Once the electrode was inserted, the quality of the signal was optimized by changing the depth and angle of the needle. Electrode placement was further verified with electrical stimulation. The needle was then removed and the wire electrode remained in the muscle for the duration of the experiment. The muscles recorded and analyzed included six intrinsic and six extrinsic hand muscles (for details, see [17]).

The EMG recordings were amplified 2000× and band-pass filtered between 3 Hz and 1 kHZ (Neurodata Acquisition System model 12, Grass Instruments, Warwick, RI). A reference surface electrodes (gold-plated silver disc, Grass Instruments; West Warwick, RI) was placed on the skin over the radial styloid to serve as a reference electrode.

3) Data Acquisition

Force and EMG recordings were acquired and digitized at 2 kHZ with 12-bit A/D converter boards (PCI-6225, National Instruments, Austin, TX) displayed, and stored on a computer using LabView v 6.0, National Instruments.

C. Experimental Procedure

1) Maximal Voluntary Contractions (MVC)

Subjects increased digit isometric grasp force of all three fingers from rest (~1N) to maximum over a period of 3 s and then maintained the maximum force for 6 s. Subjects performed three MVC trials with a minimum of 3-min of rest between trials. The trial with the greatest total sum of digit forces was used as the reference value to compute the target force for the submaximal fatiguing contraction.

2) Submaximal Fatiguing Contraction

Subjects performed a sustained isometric contraction with the thumb, index, and middle fingers at a total force of 40% of MVC. Subjects began the task by increasing digit total force from rest (~1N) to the target force. Data collection began when the subject was able to maintain the target force for ≥3 s. Visual feedback of the target force was provided as a horizontal line on the computer for the duration of the contraction. The subject’s total digit force was also displayed as a red trace in real time. The contraction was ended when the subject could not maintain the total force within ±10% of the target force or they were unable to maintain the same hand and forearm posture despite strong verbal encouragement for 3 s. However, all subjects failed due to an inability to maintain the target force.

D. Data Analysis

A set of nine time- and frequency-domain features were extracted from the interference EMG, after downsampling to 1 kHz (see Table I). The linear envelope (LE) of the rectified EMG signal was obtained with the Butterworth low-pass filter of third-order with a cutoff frequency of 2.5 Hz. Features were derived from running windows of 1000 time samples with a 50% overlap, i.e., features were derived every 500 ms. The spectral components were obtained using a 1024 point DFT, yielding a spectral resolution of 0.97 Hz. We have used multiple time- and frequency-domain features to extract more information about the amplitude and spectral characteristics of the EMG signal. Mean and peak of LE, maximum peak amplitude, root mean square [3], [18], and spectral energy [21] provided information about the amplitude of the EMG signal, whereas zero crossing count [4], median frequency [18], [19], mean frequency [3], [5], [20], and spectral entropy [6] provided information about the frequency content of the EMG signal. A brief description of the features is as follows.

TABLE I.

Time- and Frequency-Domain Features Extracted From EMG Signal

	Time Domain Features
1	Mean of linear envelope (LE)
2	Peak of linear envelope (LE)
3	Zero crossing count [4]
4	Maximum peak amplitude
5	Root mean square (RMS) [3], [18]

	Frequency Domain Features
6	Median frequency [18], [19]
7	Mean frequency [3], [5], [20]
8	Spectral entropy [6]
9	Spectral energy [21]

Mean and peak of LE are mean and peak voltages, respectively, of the 2.5-Hz LE obtained as described before. Zero-crossing count is obtained by counting the number of times the EMG voltage changes sign in a window of 1000 time samples or 1 s. The maximum peak amplitude is the maximum voltage obtained in every window. Median frequency mf, which is a measure of skewness in power spectrum, is defined as the frequency that divides the power spectrum into two equal parts and was obtained as follows:

$$\sum _{i=1}^{\mathrm{m}\mathrm{f}}{I}_i=\sum _{i=\mathrm{m}\mathrm{f}+1}^n{I}_i.$$ (1)

where n is the number of frequency bins, which is equal to the bandwidth of the signal, i.e., 500, and I_i is the amplitude or intensity of spectrum at ith bin. Mean frequency defined as the normalized, first-order spectral moment was calculated as the sum of the product of the spectrogram amplitude and the frequency, divided by the total sum of spectrogram amplitude or intensity, as follows:

$$\text{Meanfrequency}=\frac{{\sum }_{i=1}^n{I}_i\times f_i}{{\sum }_{i=1}^n{I}_i}.$$ (2)

where f_i is the frequency of spectrum at ith bin of n frequency bins and the spectral energy was obtained as follows:

$$\text{Spectral}\text{energy}=\frac{1}{n}\sum _{i=1}^n{I}_i^2.$$ (3)

The spectral entropy, defining the entropy in the power spectrum was obtained as

$$\text{Spectral}\text{entropy}=-\sum _{i=1}^n{p}_i\times log(p_i)$$ (4)

where $p_i=\frac{I_i}{{\sum }_{j=1}^n{I}_j}$.

E. Model for Grading EMG Features Related to Fatigue

Even though EMG amplitude and spectral features vary differently across subjects during a contraction, the relation among the features tended to be subject-independent. Therefore, the framework was based on the relation between multiple features of the EMG signal. Principal component analysis on the nine features listed in Table I from all 12 muscles over eight subjects revealed that the first two components captured 98.71 ± 1.1% of the total variance, therefore, we performed factor analysis [22] on these nine features using two factors. Factor analysis was used to describe variability among the features to define a potentially lower number of variables, i.e., latent factors. These experiments revealed two latent factors, which were used for the analysis of the reference framework.

Because our aim was to develop a generalized subject-independent method for grading the changes in the EMG signal during a fatiguing contraction, we measured the variability of each feature and latent factor, between subjects, with an intra-class correlation (ICC) analysis. The ICC coefficient measures the fraction of the total variance that is due to between group variance (groups are values of a particular feature or latent factor over all twelve muscles belonging to different subjects) as follows:

$${\text{ICC}}^f=\frac{{\sigma }_{\text{sb}}^2(f)}{{\sigma }_{\text{sb}}^2(f)+{\sigma }_{\text{sw}}^2(f)}$$ (5)

where ${\sigma }_{\text{sb}}^2(f)$ is the variance in the feature or latent factor f between subjects and ${\sigma }_{\text{sw}}^2(f)$ is the variance within subjects. Between-subjects and within-subjects variances of each feature and latent factors were obtained using Kruskal–Wallis one-way analysis of variance [23] across multiple subjects.

Since ICC values capture the between-subject variance, with respect to the total variance in a feature, higher ICC values indicate greater variation across subjects. The individual EMG features had greater ICC values compared to the latent factors (see Table II). Despite the large variation in feature values across subjects, the relation between the features and the two latent factors did not differ significantly across subjects, as indicated by significantly lower ICC values of the latent factors, shown in bold in Table II.

Table II.

Subject-Based Variability for Features and Latent Factors

No.	Features/Latent factors	ICC based on subjects
1	Mean of LE	0.738
2	Peak of LE	0.716
3	Zero crossing count	0.929
4	Max peak value	0.839
5	Root mean square	0.714
6	Median Frequency	0.914
7	Mean Frequency	0.914
8	Spectral Entropy	0.775
9	Spectral Energy	0.737
10	Latent Factor 1	0.076
11	Latent Factor 2	0.098

The latent factors provide a reference model to monitor changes in the EMG signal of a subject with respect to a reference group of subjects in real time. Therefore, we used these latent factors to derive our automatic algorithm. Analysis of the relation of the EMG features with the two latent factors over all subjects and muscles revealed that features related to EMG amplitude were strongly correlated with latent factor 1 while the features related to frequency content of the EMG signal were strongly correlated with latent factor 2 (see Table III). Corresponding significant coefficients are in bold for reference.

Table III.

Correlation Coefficients: Features Versus Latent Factors (Bold Values Indicate Significant Correlation (P < 0.05) Coefficient)

Sl.no	Features	Latent Factor 1	Latent Factor 2
1.	Mean of LE	0.98	0.02
2.	Peak of LE	0.87	−.01
3.	Zero crossing count	−0.01	0.90
4.	Max peak value	0.81	0.09
5.	Root mean square	0.98	0.05
6.	Median Frequency	0.02	0.95
7.	Mean Frequency	0.01	0.96
8.	Spectral Entropy	−0.79	0.31
9.	Spectral Energy	0.97	−0.01

F. Subject-Independent Framework for Grading EMG Features Related to Fatigue

The main requirement of the subject-independent framework was to obtain a generalized or reference mapping of features extracted from the EMG signal, which could be used to map and quantify the progression of multiple features continually in real time, during a fatiguing exercise of a subject, without the need to calibrate the algorithm with subject-specific data.

The reference mapping, in the proposed framework, was obtained through the latent factors (latent factors 1 and 2). The mapping was then used to monitor the changes in EMG features on a continuous scale from zero to one of a test subject in real time. The state 0 represents the beginning of the contraction whereas the state 1 represents the estimated point of task failure with respect to the reference framework.

The proposed framework consisted of two major components: 1) developing the reference framework and 2) projecting a test subject’s features into the reference framework. The reference framework was developed with the EMG features from seven subjects and cross validated on the remaining eighth subject, known as test subject, following a leave-one-out strategy. As per this strategy, the reference data consisted of features from all seven subjects and the test data consisted of features from the remaining eighth subject referred to as the test subject. Details of the framework are provided in Fig. 2. Table IV defines notations used in Fig. 2.

Fig. 2.

Subject-independent framework for grading EMG features.

Table IV.

Notation I

Notation	Explanation
K	Number of subjects in reference set
Sk(t)	Input time series signal for a subject k in reference set
ST(t)	Input time series signal for test subject T
N	Total number of windows in signal
D	Feature dimension
F	Feature matrix
L	Reference factor loadings
FS	Factor scores

1) Development of the Reference Framework

A set of nine features (see Section II-D) were extracted from each window of 1000 time samples of the preprocessed EMG signal of a subject k, with 50% overlap. Preprocessing of the raw EMG signal involved denoising using a high-pass filter of 20 Hz. In step 2 of the framework, as shown in Fig. 2, features extracted from all K subjects were appended to form F_reference. Factor analysis was performed on F_reference, in step 3, to obtain the factor loadings L and the factor scores FS_reference. Factor analysis was performed with two principal components, using standard MATLAB function “factoran.” Factor loadings define the relation of each feature to the two latent factors (latent factors 1 and 2). Typical factor loadings obtained for a reference group of subjects is shown in Table III. This provides a reference mapping for grading EMG signal from a test subject.

2) Projecting a Test Subject’s Features Into the Reference Framework

The feature vectors extracted from EMG signal of a test subject in step 4 were mapped in the reference framework, using the equation defined in step 5 of Fig. 2. The factor scores FS_test obtained in step 5 map the test subject features in the reference framework using the reference factor loadings L. The latent factor 1 and latent factor 2 components of FS_test, i.e., P1 and P2, respectively, obtained in step 6, provided a composite view of the changes in the features of the EMG signal from the test subject. These values were normalized with respect to maximum and minimum values of the respective components of the reference factor scores FS_reference to generate a continuous grading in the range [0,1], in step 7. We inverted the grading on latent factor 2 to get an increasing value with a decrease in values of latent factor 2.

III. Results

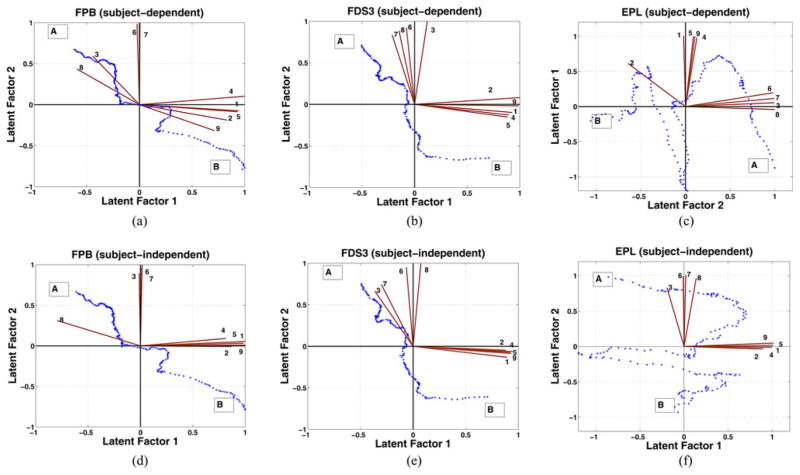
Fig. 3 shows typical trends of the extracted features from three different muscles, namely, 1) FPB, 2) FDS3, and 3) EPL for a representative subject (subject 1). For the flexor muscles, the values of amplitude-related features such as mean of LE, peak of LE, maximum peak amplitude, root mean square, and spectral energy increased throughout the contraction and the values of frequency-related features such as median frequency, mean frequency, spectral entropy, and zero-crossing count decreased as the power spectrum shifted toward lower frequencies. These trends are consistent with the recruitment of additional motor units and a decrease in the conduction velocity of action potentials along the muscle fibers as discussed in Section I. The features of the extensor muscles did not always follow the same trend as those of the flexors, especially for subject 1 shown in Fig. 3(c). However, the framework was still able to derive the factor score distributions for this muscle in a subject-independent manner as shown in Fig. 4(f).

Fig. 3.

Time- and frequency-domain features during the fatiguing contractions for muscles (a) FPB, (b) FDS3, and (c) EPL for a representative subject (subject 1).

Fig. 4.

Subject 1 factor scores with respect to own, i.e., subject-dependent framework and rest seven subjects features, i.e., subject-independent framework, from beginning to end of contractions (A to B) for the muscles FPB [(a) and (d)], FDS3 [(b) and (e)], and EPL (sub1) [(c) and (f)]. Feature axis numbered as per Table I. The angles between each feature axis and the two latent factors indicate the respective correlation between each feature and the latent factors. Smaller angle signifies higher correlation.

Fig. 4 shows the distribution of factor scores for the three muscles for a test subject (subject 1), obtained by the subject-dependent and subject-independent frameworks. Factor scores obtained by using factor analysis (standard MATLAB function “factoran”) solely on subjects’s own features are referred to as subject-dependent and the subject-independent factor scores are obtained based on the features of the other seven subjects, as per the algorithm described in Fig. 2. The angle between the axis representing a feature and the axis representing the specific latent factor indicates the correlation between the feature and the latent factor. A greater correlation corresponded to a smaller angle between the two axes.

The start of contraction is denoted as (A) and the end of contraction as (B). As mentioned earlier in Section II-E, the amplitude-related features correlated well with latent factor 1 and the frequency-related features correlated well with latent factor 2. This corresponded to a shift of factor scores toward higher values for latent factor 1 and lower values for latent factor 2, respectively, during the duration of the contractions. This is in accordance with the observation that as fatigue progresses the amplitude of the EMG signal typically increases while the frequency of the signal shifts to lower values. Consequently, the factor scores for most cases, started in the upper-left quadrant at (A) and ended in the fourth quadrant of the framework at the end of contractions (B).

To compare the factor scores obtained by the subject-dependent and subject-independent frameworks, a linear regression using degree 1 polynomial was performed on the two-factor score distributions. Table V shows the mean slope and intercept values obtained for both subject-dependent and subject-independent factor scores, for all the twelve muscles, averaged over eight subjects. Leave-one-out strategy, as explained in Section II-F, was used to obtain the subject-independent factor scores for each subject. The distribution of factor scores did not differ significantly whether the reference model was based on subject’s own features (subject-dependent framework) or on the features of other seven subjects (subject-independent framework). A multivariable analysis of variance revealed that the means of the slope and intercept values obtained using subject-dependent and subject-independent frameworks did not differ significantly (p > 0.05).

Table V.

Linear Regression Results on Factor Score Distributions for Subject-Dependent and Subject-Independent Frameworks

Muscle	subject_dependent		subject_independent
	slope	intercept	slope	intercept
First dorsal interosseus (FDI)	−0.68 ± 0.18	−0.00 ± 0.01	−0.67 ± 0.16	−0.00 ± 0.01
First palmar interosseus (FPI)	−0.31 ± 0.12	−0.01 ± 0.02	−0.29 ± 0.14	−0.01 ± 0.02
Second dorsal interosseus (SDI)	−0.64 ± 0.13	−0.00 ± 0.02	−0.67 ± 0.11	−0.00 ± 0.01
Second palmar interosseus (SPI)	−0.55 ± 0.36	−0.00 ± 0.05	−0.51 ± 0.31	−0.00 ± 0.02
Abductor pollicis breves (APB)	−0.86 ± 0.46	−0.18 ± 0.51	−0.85 ± 0.57	−0.19 ± 0.53
Flexor pollicis breves (FPB)	−0.84 ± 0.10	−0.01 ± 0.09	−0.85 ± 0.12	−0.04 ± 0.09
Extensor digitorum 2 (ED2)	−0.49 ± 0.01	−0.00 ± 0.00	−0.51 ± 0.00	−0.00 ± 0.00
Extensor digitorum 3 (ED3)	−0.75 ± 0.12	−0.01 ± 0.12	−0.77 ± 0.31	−0.01 ± 0.11
Extensor pollicis longus (EPL)	−0.62 ± 0.24	−0.00 ± 0.00	−0.59 ± 0.25	−0.00 ± 0.00
Flexor digitorum superficialis 2 (FDS2)	−0.82 ± 0.31	−0.00 ± 0.00	−0.83 ± 0.28	−0.00 ± 0.00
Flexor digitorum superficialis 3 (FDS3)	−0.74 ± 0.14	−0.00 ± 0.01	−0.73 ± 0.11	−0.00 ± 0.02
Flexor pollicis longus (FPL)	−0.72 ± 0.13	−0.02 ± 0.01	−0.74 ± 0.12	−0.02 ± 0.01

Note that for each of the three different muscles, the factor loadings for the subject-dependent frameworks shown in Fig. 4(a)–(c) are very similar to the factor loadings of their respective subject-independent frameworks shown in Fig. 4(d)–(f), respectively. This is due to the low-subject-based variability of the factor loadings shown in Table II. Hence the distribution of the factor scores obtained by the subject-independent framework is similar to the distribution in the subject-dependent framework. This is also evident from the similarities in slope and intercept values in the two frameworks presented in Table V. Also, note that though the factor score distributions are different across the flexor (FPB and FDS3) and extensor muscle (EPL) but the factor loadings are very similar across both the muscle types.

Fig. 5(a)–(c) shows the gradings of the EMG features (associated with muscle fatigue) obtained as per the algorithm shown in Fig. 2, by projecting factor scores obtained in Fig. 4(d)–(f) on both the latent factors for the three muscles, flexor pollicis brevis (FPB), flexor digitorum superficialis 3 (FDS3), and extensor pollicis longus (EPL), respectively. The EMG feature gradings increased on a scale between zero and one from the start of contractions defined by (A) to end of the contractions (B), during the progression of the fatiguing exercise for all three muscles. Please note that for the extensor muscle EPL [see Fig. 5(c)], the P1_gradings which capture the EMG amplitude, did not increase with fatigue up to point B. However, the P2_gradings related to EMG spectral characteristics, increased from zero at the start of contractions (A) to one at the end of contractions (B), signifying the importance of capturing changes in both EMG amplitude and spectral characteristics for grading features related to fatigue.

Fig. 5.

Subject 1 EMG feature gradings with respect to reference framework for muscles (a) FPB, (b) FDS3, and (c) EPL obtained by projecting respective subject-independent factor scores (A–B) in Fig. 4 on both the latent factors.

IV. Discussion

The subject-independent framework presented here provides a practical way to track the changes in EMG features associated with muscle fatigue. The framework is based on hidden factors or latent factors derived from multiple EMG amplitude and spectral features. The goal of the proposed algorithm is to associate the beginning of the contraction and the time of task failure, in which there is a significant level of muscle fatigue, to the changes in the multiple EMG features, in a subject-independent manner. This was shown in two primary ways: first, the factor scores for most cases, started in the upper-left quadrant of the subject-independent framework and ended in the fourth quadrant of the framework (see Fig. 4), and second, the gradings of the EMG features obtained from the projections of the factor scores on the latent factors 1 and 2 (see Fig. 5) increased in a scale from zero to one with respect to the reference framework in either both or one of the latent factors. So far this analysis cannot measure the extent of muscle fatigue. However, the framework provides a method to identify in a subject-independent fashion when the muscles are approaching a level of fatigue that would result in task failure. Another advantage of this framework is that it operates in real time.

Although surface EMG is more practical for clinical purposes, its current ability to record from individual hand muscles is limited. Therefore, intramuscular electrodes were used in this study to record the EMG activity of small hand muscles due to its higher selectivity and reduced risk of crosstalk. Nevertheless, studies using surface EMG or intramuscular EMG during sustained submaximal isometric contractions have revealed similar changes in the signal features, such as an increase in EMG amplitude and a left shift in frequency content of the power spectra [8], [24]. Although our present study is based on data from eight subjects, we have collected EMG data from 12 muscles per subject, thus, increasing the number of muscles sampled. We have applied the proposed framework successfully to several extensor and flexor muscles. We observed that the performance of the algorithm was relatively not sensitive to the type of the muscle, indicating flexibility in the choice of muscles.

V. Conclusion

This study provides a generalized framework for grading several EMG features during a sustained submaximal fatiguing contraction. Despite the use of a constant isometric contraction, this algorithm provides the first step to developing similar systems that could potentially identify the time when the muscles are approaching a level of fatigue that may cause injury, on a subject-independent basis, from features extracted from the surface EMG. To this end, we have previously applied a similar algorithm that can extract latent factors from the surface EMG signals, but to date, this algorithm cannot be used to monitor fatigue on a subject-independent basis [16]. Furthermore, latent factor mapping should in future studies be associated with the drop in MVC force to ensure that the mapping is a reliable estimate of muscle fatigue.

Biographies

Rita Chattopadhyay received the B.E. degree in electrical engineering with a first class first position from Bengal Engineering College, Calcutta, India, in 1985, and the M.E. degree in system science and automation from the Indian Institute of Science, Bangalore, India, in 1996. She is currently working toward the Ph.D. degree from the Department of Computer Science and Engineering, Arizona State University, Tempe, expected graduation Spring 2013.

She has around 23 years of industry experience working in Siemens and GE research centers in the areas of design and development of embedded systems for signal and video processing. She has published in the renowned IEEE and ACM international conferences and journals. Her research interests include machine learning, data mining, and biomedical informatics.

Ms. Chattopadhyay has won the Knowledge Discovery in Databases best research paper nomination in 2011.

Mark Jesunathadas received the B.S. degree in mechanical engineering from California State Polytechnic University, Pomona, in 2003, and the Ph.D. degree in integrative physiology from the University of Colorado Boulder, Boulder, in 2009.

He has completed a Postdoctoral Fellowship from the Department of Biological and Health Systems Engineering, Arizona State University, Tempe, in 2012. His research focuses on the neural mechanisms involved in grasping and dexterous object manipulation.

Brach Poston received the Ph.D. degree in integrative physiology from the University of Colorado Boulder, Boulder.

He is currently a Project Scientist in the Department of Biomedical Engineering, Cleveland Clinic Lou Ruvo Center for Brain Health, Las Vegas, NV. He received the postdoctoral training at Arizona State University and the National Institutes of Health. His research interests include noninvasive brain stimulation, motor skill acquisition, strength training, neural control of the hand, and muscle fatigue.

Marco Santello received the Bachelor’s degree in movement sciences (Istituto Superiore di Educazione Fisica) from the University of L’Aquila, L’Aquila, Italy, in 1990, and the Doctoral degree from the University of Birmingham, Birmingham, U.K., in 1995.

After a Postdoctoral Fellowship in the Department of Physiology (now Neuroscience), University of Minnesota, he joined the Department of Kinesiology, Arizona State University (ASU), in 1999. Since 2010, he has been a Professor and Harrington Endowed Chair with the School of Biological and Health Systems Engineering, ASU. He has more than 60 publications on peer-reviewed journals, conference proceedings, and books. His main research interests are motor control, learning and biomechanics of object grasping and manipulation, neural control of hand muscles, multisensory integration, and robotics.

Dr. Santello received research awards from the National Institutes of Health, the National Science Foundation, the Whitaker Foundation, and ASU/Mayo Clinic. He is a member of the Society for Neuroscience, the Society of Neural Control of Movement, and the International Society of Motor Control.

Jieping Ye received the Ph.D. degree in computer science from the University of Minnesota, Twin Cities, in 2005.

He is currently an Associate Professor in the Department of Computer Science and Engineering, Arizona State University (ASU), Tempe. His research interests include machine learning, data mining, and biomedical informatics.

Dr. Ye won the outstanding Student Paper Award at the International Conference on Machine Learning in 2004, the SCI Young Investigator of the Year Award at ASU in 2007, the SCI Researcher of the Year Award at ASU in 2009, the National Science Foundation Career Award in 2010, the Knowledge Discovery in Databases (KDD) Best Research Paper Award honorable mention in 2010, and the KDD Best Research Paper Nomination in 2011.

Sethuraman Panchanathan (F’01) received the Bachelor’s degree in physics and electrical communication engineering from the University of Madras and Indian Institute of Science in 1981 and 1984, the Master’s degree in electrical engineering from the Indian Institute of Technology, Madras, in 1986, and the Ph.D. degree in electrical and computer engineering from the University of Ottawa, Ottawa, ON, Canada, in 1989.

He is currently the Senior Vice President of the Office of Knowledge Enterprise Development advancing research, innovation, enterprise and economic development. He is the Foundation Chair in Computing and Informatics and the Director of the Center for Cognitive Ubiquitous Computing (CUbiC), Arizona State University, Tempe. CUbiC’s flagship project iCARE for individuals who are blind and visually impaired won the Governor’s Innovator of the Year-Academia Award in November 2004. He has published more than 400 papers in refereed journals and conferences, and has mentored more than 100 graduate students. His research interests include the areas of human-centered multimedia computing, face/gait analysis and recognition, haptic user interfaces, medical image processing, media processor designs, and ubiquitous computing environments for enhancing quality of life for individuals with disabilities.

Dr. Panchanathan is a Fellow of the Society of Optical Engineering and a member of the Canadian Academy of Engineering.