Ion-Specific Induced Fluctuations and Free Energetics of Aqueous Protein Hydrophobic Interfaces: Toward Connecting to Specific-Ion Behaviors at Aqueous Liquid–Vapor Interfaces

Abstract

We explore anion-induced interface fluctuations near protein–water interfaces using coarse-grained representations of interfaces as proposed by Willard and Chandler (J. Phys. Chem. B 2010, 114, 1954−1958). We use umbrella sampling molecular dynamics to compute potentials of mean force along a reaction coordinate bridging the state where the anion is fully solvated and one where it is biased via harmonic restraints to remain at the protein–water interface. Specifically, we focus on fluctuations of an interface between water and a hydrophobic region of hydrophobin-II (HFBII), a 71 amino acid residue protein expressed by filamentous fungi and known for its ability to form hydrophobically mediated self-assemblies at interfaces such as a water/air interface. We consider the anions chloride and iodide that have been shown previously by simulations as displaying specific-ion behaviors at aqueous liquid–vapor interfaces. We find that as in the case of a pure liquid–vapor interface, at the hydrophobic protein–water interface, the larger, less charge-dense iodide anion displays a marginal interfacial stability compared with that of the smaller, more charge-dense chloride anion. Furthermore, consistent with the results at aqueous liquid–vapor interfaces, we find that iodide induces larger fluctuations of the protein–water interface than chloride.

I. Introduction

The fundamental nature of interactions between ions, cosolutes, and proteins in aqueous solutions continues to garner attention²⁻⁴ due to its importance in understanding protein denaturation, folding, protein–protein interactions to name a few examples. In the context of protein denaturation, Hofmeister effects or ion-specific effects, related to the modulation of surface tension and protein solubility by additive salts that influence the strength of direct and water-mediated interactions in solution have been intensely explored with the ultimate aim of extracting basic physical insights into the above-mentioned processes.⁵⁻⁸ At the heart of specific-ion effects as related to protein denaturation is the molecularly resolved interface between protein and aqueous solution; moreover, the nature of the differences in behavior of cations/anions at such interfaces (including both liquid–vapor interfaces and liquid-solute interfaces) weighs heavily on the interpretation and definition of these processes. Now amassed is a vast literature that discusses specific-ion effects as embodied in differential stabilities of halide ions at liquid–vapor interfaces.⁹⁻¹⁶ It has been widely shown that larger halide ions such as I^– and Br^– tend to bind to liquid–vapor interfaces more strongly and with lower transfer free energies than smaller, more charge-dense, and more strongly hydrated Cl^– and F^– anions. The microscopic origins and molecular mechanisms of these behaviors are concerned with several factors ranging from ion size, ion polarizability, and ion hydration properties to solvent polarizability.¹⁷ Recent studies¹⁸⁻²⁰ have begun to consider differential perturbations of liquid–vapor interface fluctuations by different anions. Ou et al. studied ion-specific effects at the aqueous liquid–vapor interface by exploring ion-induced interfacial fluctuations in the case of two chemically distinct anions Cl^– and I^–, which represent the neutral and chaotropic positions in the Hofmeister series, on distant liquid–vapor interface.^18,19 They observed that the more surface stable I^– anion (as observed elsewhere^12,16,20,21) induces larger interfacial fluctuations than the nonsurface active species Cl^–, thus demonstrating a strong correlation between induced interfacial fluctuations and anion surface stability as observed from molecular simulations. The authors trace these differences in induced interfacial fluctuations by Cl^– and I^– to the nature of the hydration environment around the anions; water molecules in the hydration shells of I^– are shown to be more dynamic and less persistent compared to those in proximity to Cl^–. When the liquid–vapor interface is approached, coupling of local solvent around anions with solvent further away and near an interface leads to different perturbations of the interface by the two anions, and thus different contributions to interface height fluctuations, and ultimately surface stability via contributions from interfacial entropy arising from surface fluctuation correlations.¹⁸⁻²⁰

This ion-specific effect is not necessarily restricted to the liquid–vapor interface; one might consider how the perturbation-inducing properties of the two anions may play out generally in the vicinity of hydrophobic interfaces. Heyda et al.²² examined systems of N-methylacetamide (NMA) in the presence of monovalent cations and anions in water. The larger anions, I^– and Br^–, demonstrated preferential spatial correlation with the hydrophobic methyl group, which supports earlier experiments addressing the importance of the nonpolar methyl groups for the halide ion–NMA interactions.²³ Horinek et al. investigated the potential of mean force (PMF) for Na⁺, Cl^–, Br^–, and I^– to transfer from bulk aqueous solution to a hydrophobic self-assembled monolayer-water interface in an infinite dilution.²⁴ Similarly, soft polarizable monovalent anions (I^– and Br^–) prefer to accumulate around the hydrophobic interface. In another contribution, Lund et al. probed the distribution of F^– and I^– around a spherical macromolecule.²⁵ They found that when the nanosphere is uncharged and considered as a hydrophobic particle, F^– ions are repelled whereas I^– ions are weakly attracted to it. In a recent molecular simulation study, Friedman et al.²⁶ analyzed extensive molecular dynamics simulations of three proteins in aqueous salt solutions. The authors concluded that binding of cations and anions to protein surfaces is heterogeneous, with the same amino residue demonstrating a wide range of binding probability to a particular ion. This heterogeneity stems from the heterogeneous environments found on protein surfaces. As pointed out by Giovambattista et al.²⁷ and others,^28,29 the local environment of any given amino acid residue is largely perturbed and defined by its neighboring residues. Jungwirth and co-workers have further provided volumes of data on the nature of differential, or ion-specific, binding of cations and anions to protein surfaces.³⁰⁻³² Specifically, using lysozyme as an example, they indicate that in the mixed aqueous solution of KCl and KI, I^– is preferential to be in close vicinity of the hydrophobic groups.^33,34 Furthermore, this specific-ion effect may play a crucial role in modulating protein–protein interaction in solution.³⁵

Because there is implied a connection of the behaviors of ions at aqueous liquid–vapor interfaces to those of possibly biochemical relevance (protein–water, bilayer–water, etc.),³⁶ we seek to begin to address connections with particular focus on hydrophobic regions of proteins (to use a model system that is a natural extension of the ideally hydrophobic aqueous liquid–vapor interface). We propose to consider how anions, in particular Cl^– and I^–, induce fluctuations at the interface of a molecularly “large” hydrophobic patch of a rigid protein in aqueous environment. We also seek to make connection of observed induced interfacial fluctuations to the free energetics (probabilities) of the two types of anions near the hydrophobic protein region. We anticipate that similar qualitative trends and behaviors should arise in the biomolecular context as observed for aqueous liquid–vapor interfaces. We note that unlike the liquid–vapor interface, the protein–water interfaces are more complicated because of their inherent chemical and topographical heterogeneity. The heterogeneities account for different effective hydrophobicity around protein surfaces, influencing the behavior of hydration water significantly.²⁷ With molecular dynamics simulations, Godawat et al.³⁷ found that water density near the surfaces of self-assembled monolayers (SAMs) with hydrophobic head groups (−CF₃, −CH₃) shows a poor distinction from that of SAMs with hydrophilic head groups (−OH, −CONH₂). However, differences arise when the fluctuations of water density near the two regions are considered. Enhanced fluctuations, reflected by the broad probability distributions of the water number density are observed around hydrophobic surfaces compared with the bulk solution and hydrophilic surfaces.^38,39 Moreover, the enhanced density fluctuations around hydrophobic surfaces could further be characterized by more compressible hydration shells and increased cavity formation,^40,41 indicating that the nature of hydration shells around hydrophobic surfaces are softer and more flickering than that of hydrophilic ones. Because the long-ranged ion-induced perturbations of aqueous protein interfaces involve the coupling of local hydration shells of the ions with distant hydration shells around protein surfaces, the nature of both would affect the extent of induced interfacial fluctuations. It would be interesting to compare the interface height fluctuations as Cl^–/I^– approaching the hydrophobic/hydrophilic protein regions. We note that the interface height fluctuations we are pursuing here are conceptually different from the density fluctuations, whereas both of them reflect the nature of hydration water around protein surfaces. Additionally, it has been reported that the ion-specific effects are dissimilar around hydrophobic and hydrophilic surfaces, with large I^– showing a stronger affinity than the smaller halide ions to the hydrophobic surfaces whereas the reverse trends of size-dependence of halide ions are realized at the hydrophilic surfaces.^25,35,42,43 We would like to further connect the affinity (probabilities) differences of Cl^–/I^– around protein patches with different hydrophobicity to their induced aqueous protein interfacial fluctuations correspondingly.

The particular protein we focus on in this study is hydrophobin-II (HFBII), which is a small protein with 71 amino acid residues expressed by filamentous fungi. The protein is known for its ability to form a hydrophobic coating on the surface of an object and it can self-assemble into a monolayer on hydrophobic/hydrophilic interfaces such as a water/air interface.⁴⁴ These functions are mainly determined by the amphiphilic structural characterization. Acharya et al.²⁸ mapped the effective hydrophobic regions and effective hydrophilic regions of HFBII by considering the density of small probe hydrophobic solutes around each region of the protein. Moreover, they selected three regions with different hydrophobicity on the basis of this and further monitor the density fluctuations in their vicinity. The calculations showed that around most hydrophobic region, they observe the largest density fluctuations whereas the least density fluctuations were detected around most hydrophilic region. Considering this, this protein is an ideal candidate to compare the characters between hydrophobic and hydrophilic interfaces.

The paper is organized as follows. In section II we discuss the simulation protocols and computational details of liquid–vapor interface and aqueous protein interfaces. Our results are presented in section III and are organized into four topics. We start the discussion by investigating the PMFs and interfacial fluctuations as a single Cl^–/I^– translocates across the aqueous liquid–vapor interface. We consider Cl^–/I^– density distributions around aqueous HFBII hydrophobic interface in 1.0 m solutions in the second part. We further investigate the PMFs and interfacial fluctuations as a single Cl^–/I^– approaches the aqueous protein hydrophobic interface, demonstrating the similarity between liquid–vapor interface and hydrophobic protein interface in terms of ion specific induced perturbations of the interface. We finish this section by examining a single Cl^–/I^– approaching another two regions with different hydrophobicity on the protein surface compared with the hydrophobic region we initially studied. We finish with our conclusions and general discussion in section IV.

II. METHOD

A. Simulation Details

Molecular dynamics simulations performed in this study include (1) umbrella sampling molecular dynamics simulations of translocation of a single Cl^–/I^– across the aqueous liquid–vapor interface, (2) molecular dynamics simulations of a single, fully rigid hydrophobin HFBII protein in 1.0 m concentration of KCl/KI aqueous solutions, and (3) potential of mean force calculations using molecular dynamics simulation trajectories of a single Cl^–/I^– approaching three different regions of the protein that are defined as hydrophobic, less hydrophobic and hydrophilic. Detailed simulation protocols are now discussed as follows.

1. Umbrella Sampling Potential of Mean Force Calculations: Ion Translocation Across Aqueous Liquid–Vapor Interface

Molecular dynamics simulations were performed using the CHARMM package.^45,46 Simulations of liquid–vapor interfaces were performed in the NVT ensemble. The temperature was maintained at T = 300 K using a Nosé–Hoover thermostat.⁴⁷ The simulation cell was rectangular with dimensions 24 Å × 24 Å × 100 Å, in which z is the direction normal to the liquid–vapor interface. A bulk slab consisting of 988 water molecules (represented by the nonpolarizable TIP3P model⁴⁸) and a single anion (Cl^–, I^–) was positioned in the center of the simulation cell, resulting in two liquid–vapor interfaces. We note that Lennard-Jones parameters for ions that are suitable with TIP3P were taken from Cheatham et al.⁴⁹ The parameters are listed in Table S1 Supporting Information along with the verification of these parameters. A rigid water geometry is enforced using SHAKE⁵⁰ constraints. Conditionally convergent long-range electrostatic interactions were treated using a particle mesh Ewald (PME)⁵¹ approach with a 30 × 30 × 128 point grid, sixth-order interpolation, and κ = 0.33. Dynamics were propagated using a Verlet leapfrog integrator with a 1.0 fs time step. Computational experiments measuring the reversible work (potential of mean force, PMF, further discussion in Supporting Information) for transferring single ions/molecules from bulk aqueous environment to the aqueous solution liquid–vapor interface have enjoyed a long history as a means to explore the origins of surface stability.^9,52 To determine the PMF, a reaction coordinate defining this pseudochemical reaction must be defined. Our reaction coordinate for PMF is the Cartesian z-component of the separation between the water slab center of mass and ion position. Along the z axis, to enhance sampling of the distribution of configurations where the reaction coordinate holds a particular value, the reaction coordinate was restrained within a certain narrow range (instead of its entire span). In this case, we constructed 26 continuous “windows” with width 1.0 Å. In each window, a single anion was restrained to z-positions from 10 to 35 Å relative to the water slab center of mass using a harmonic potential U_restraint(z;z_relative,ref) = (1/2)k_restraint(z – z_relative,ref)² with the force constant of 4 (kcal/mol)/Ų; this encompassed a range approximately 15 Å below the GDS to approximately 10 Å above it at 300 K. Though one could probe separations further into the bulk (toward the center of the system), this distance is sufficient to probe the differences of interest in this study. Total sampling time for each window was 30 ns; properties were calculated from all but the initial 1.0 ns, which was treated as equilibration.

2. Protein in KCl/KI Aqueous Solution

Simulations of a single hydrophobin in 1.0 m concentration of KCl/KI aqueous solution were performed with NAMD, version 2.9b3,^53,54 using the CHARMM 22 all-atom force field with CMAP backbone torsion correction term.⁵⁵ Identical parameters for water (TIP3P) and ions (Cl^–, I^–, and K⁺) were applied as the ones from liquid–vapor interface simulation. Isothermal–isobaric ensemble (NPT) simulations were performed using a cubic cell with a box size 60 Å × 60 Å × 60 Å. The NPT ensemble was used to eliminate the liquid–vapor interfaces, so only the protein–water interfaces were considered in the system. The initial structure of the protein was constructed using CHARMM-GUI.⁵⁶ The protein structure was based on the ultrahigh resolution structure at 0.75 Å of hydrophobin HFBII, with PDB code 2B97.⁵⁷ The original crystal structure was actually the dimerization complex of the protein. Only one monomer, composed of 70 residues, was modeled in this study. The protein was placed in the center of the box, with center of mass located at (x = 0 Å, y = 0 Å, z = 0 Å), the rest of the box was filled with 6481 water molecules, 116 K⁺ and 116 Cl⁺/I^–, resulting in a molal concentration of 1.0 m. Temperature was maintained by Langevin bath at 300 K, and the pressure was kept constant by Langevin pressure control at 1 atm. A switching distance of 10 Å, nonbonded real-space cutoff of 12 Å, and a pairlist generation distance of 14 Å were used for the van der Waals interactions, and the particle mesh Ewald (PME) method was employed for the calculation of conditionally convergent electrostatic interactions. The grid size of PME in the x dimension is 60, in the y dimension is 60, and in the z dimension is 60 (as close to a 1 Å grid point separation as possible). The SHAKE algorithm was used to constrain bond lengths involving hydrogen atoms, and an integration time step of 1.0 fs was used. The protein was fixed during the simulation and other components could move randomly. We provide the NAMD input file for our simulations in Table S2 Supporting Information. A total of six different replicates were used and the first 2.0 ns of each replicate was considered as equilibration. At least 10 ns of production run for each replicate was used to compute properties.

3. Aqueous Protein Interfaces

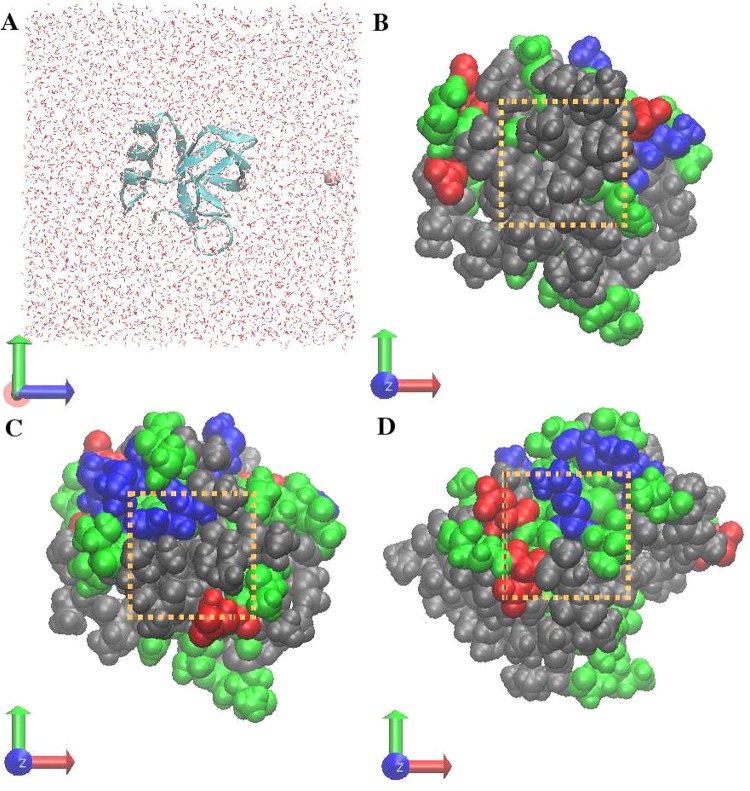
To illustrate the molecular detail and free energetics of Cl^–/I^– approaching the aqueous protein interfaces with different hydrophobicity, we further simulated systems with 6481 TIP3P water molecules and a single Cl^–/I^–, transferring from bulk to the protein interfaces. A representative snapshot of the simulation system can be found in Figure 1A. HFBII protein was arranged in a way that its largest hydrophobic patch, consisting of V18, L19, L21, I22, V24, V54, A61, L62, and L63 (shown in Figure 1B), was nearly perpendicular to the z direction (further quantitative information is in Table S3 Supporting Information) and the whole protein was fixed during the simulation with center of mass located at (x = 0 Å, y = 0 Å, z = 0 Å). A single Cl^–/I^– was added in the solution with one counterion, K⁺, to neutralize the negative charge of the monovalent anion. The K⁺ was fixed at position (x = 0 Å, y = 0 Å, z = −15 Å). Similarly to the liquid–vapor interface situation, for calculation of PMF, we consider the Cartesian z component of the separation between the center of mass of protein and center of mass of the single Cl^–/I^– as the reaction coordinate for the present umbrella sampling molecular dynamics simulations. A single Cl^–/I^– was aligned along the z direction, approaching the specific spot on the patch with position x = 0 Å and y = 0 Å by freezing the orthogonal degrees of freedom along the x axis and y axis via the use of strong restraining potentials. We center on one specific region of the patch, acknowledging that the heterogeneity of the protein surface necessitates some care in interpreting the results, which we will address further below. For a meaningful discussion and interpretation of ion-induced fluctuation (interface fluctuation in addition to the level present in pure water) as the ion approaches the hydrophobic interface, one reference location with fixed position has to be defined. Using NAMD’s “selectConstraints” infrastructure, the x component of the ion was restrained at x = 0 Å and the y component was restrained at y = 0 Å with a force constant of 1000 (kcal/mol)/Ų respectively. Along the z axis, we constructed 46 continuous umbrella sampling “windows” with width 0.2 Å along the positive z-direction ranging from the area around the protein–solvent interface to the bulk water region. The spans of the windows going from interfacial region to bulk region (in Å) were [16.0:16.2], [16.2:16.4], [16.4:16.6] ... [24.4:24.6], [24.6:24.8], [24.8:25.0]. This range of ion position (from 16 to 25 Å) is sufficient to probe the differences of a single ion around the interface and that in the bulk water region, while minimizing the number of windows that is required to construct. In each window, a harmonic restraint potential with force constant of 10 (kcal/mol)/Ų was applied on the Cartesian z component of the ion. Other simulation conditions remain the same as that of the 1 m concentration of the KCl/KI aqueous solution. The first 2 ns was allowed for equilibration before a total of 20 ns production data were generated for each window.

Figure 1.

(A) Representative snapshots of the system used in the study. (B) Representation of the hydrophobic interface defined in this study, including residues L7, V18, L19, L21, I22, V24, V54, A61, L62, and L63. Colors: nonpolar residues, gray; basic residues, blue; acidic residues, red; uncharged hydrophilic residues, green. The dashed orange line roughly selects the region of interest. (C) Representation of the less hydrophobic interface defined in this study, including residues I31, A32, D34, I38, A41, H42, and S45. (D) representation of the hydrophilic interface defined in this study, including residues D25, C26, K27, T28, A58, D59, and Q60.

For comparison, we performed another set of simulations to compute the PMF of the anion approaching the hydrophobic patch using average force integration; in these simulations, both anion and protein are held fixed so as to realize a series of center of mass separation distances; the potential of mean force is obtained by integration of the average force along the reaction coordinate obtained from simulation trajectory analysis. Details about the setup and results of this can be found in the Supporting Information. Furthermore, to attempt to consider effects of protein motion on ion-induced interface fluctuations, we performed simulations with protein under restraint conditions instead of totally fixed. HFBII was placed in the center of box with exactly the same starting structure as in the fixed (rigid) protein case. During the simulation, the protein was strongly restrained to remain in a single orientation and its center of mass at a specific position, chosen as (x = 0 Å, y = 0 Å, z = 0 Å) via the use of strong restraining potentials. Using NAMD’s collective variable infrastructure, HFBII’s center of mass was restrained at (x = 0 Å, y = 0 Å, z = 0 Å) using a force constant of 5000 (kcal/mol)/Ų, and its orientation was restrained about the crystal based orientation using a harmonic restraint potential with a force constant of 5000 (kcal/mol)/Ų. A single Cl^–/I^– was fixed along the positive z axis, starting from z = 16 Å to z = 25 Å, a total of ten continuous windows of width 1.0 Å. We note that PMF calculations will not be concerned in the restrained protein case because it requires extensive simulation time for a well-converged PMF with flexible protein. Instead, we are only interested in the comparison of ion-induced interfacial fluctuations of total fixed protein and restrained moving protein as Cl^–/I^– locates at particular separations along the reaction coordinate. Besides the simulations of a single Cl^–/I^– approaching the most hydrophobic region of the protein, we considered two other scenarios in which single anions approach protein regions with different hydrophobicities. Depending on the nature of residues that are exposed, we defined one patch as a less hydrophobic interface and the other as a hydrophilic interface to distinguish them from the hydrophobic interface we previously described. For these additional two cases, the simulation conditions remained identical to those in the hydrophobic patch calculations, except that the protein was oriented in a different way in the simulation cell. For the simulations in which the anions approach the less hydrophobic region, the interface is composed of residues I31, A32, D34, I38, A41, H42, and S45, arranged perpendicular to the z direction (shown in Figure 1C). Forty-nine (49) continuous windows of width 0.2 Å along the positive z-direction, starting with [15.4:15.6], [15.6:15.8], [15.8:16.0] ... to [24.4:24.6], [24.6:24.8], [24.8:25.0] are constructed. For the hydrophilic interface case, the interface we centered on consists of residues D25, C26, K27, T28, A58, D59, Q60 (shown in Figure 1D). Similarly, this interface was oriented in a way that is perpendicular to the z direction. The window setup ranged from [14.0:14.2], [14.2:14.4], [14.4:14.6] ... [24.4:24.6], [24.6:24.8], [24.8:25.0], a total of 56 windows.

Finally, we address the protocol for simulations where the PMF is computed by an average force integration method. The PMF of a single Cl^–/I^– approaching the protein interface can be calculated by integration of the average forces acting on the anion as shown in eq 1.

1

where ξ₀ is the reaction coordinate taken as the separation distance between the Cl^–/I^– and the center of mass of the protein; ⟨F(ξ₀)⟩ denotes the average forces acting on the anion at each separation along the reaction coordinate. Uncertainties in PMF are determined as⁵⁸

2

where var[G(ξ_N)] is the variance, z̅_i is the mean position of z in the ith window, which can be obtained from block averages.⁵⁹ The standard deviation σ[G(ξ_N)] is then the square root of var[G(ξ_N)].

B. Instantaneous Protein Interface and Interface Fluctuations

We discuss the protocol to construct liquid–vapor interface and protein–solvent interfaces. It has been previously explored by Willard and Chandler¹ that one could construct a coarse-grained solvent density field from the atomic coordinate in individual snapshot. Then the interface related to the solvent is defined as a constant density surface for the coarse-grained field in space. Specifically, in this work, we are interested in the water–vapor interface and water–protein interface. Therefore, the water oxygen density field is constructed as follows: we set up a series of spatial grid points and compute the corresponding coarse-grained densities at space-time point r, t, represented as ρ̅(r,t) by eq 3.

3

where r_i(t) is the ith water oxygen atom’s position in space and summation of each water molecule’s density contribution in the whole space to this point yields the coarse-grained density of the particular grid point. Each water molecule’s density contribution is modeled as a Gaussian function in eq 4.

4

where r is the magnitude of r, ξ is taken as 3.0 Å, and d stands for dimensionality (3 in this case). The final d-dimensional density field will be constructed by acquiring each grid point’s density. Then the interface is determined as the (d – 1)-dimensional manifold with a constant value c. In practice, some differences arise to construct the liquid–vapor interface and liquid–protein interface in this work considering the shape of the liquid–vapor interface is flatter whereas the protein–water interface possesses some curvature. Therefore, we select the Cartesian coordinate system to construct the liquid–vapor interface and spherical coordinate system for the protein–water interface. For the liquid–vapor interface, coordinate (x, y, z) for each grid points in space is set up and the surface is obtained as the manifold by setting ρ(x,y,z) = ρ_bulk/2. That is, for a specific (x, y) coordinate set in 3-dimensional space, it defines a line parallel to the z axis. Along this line, if the water density of one point satisfies the condition ρ(x,y,z) = ρ_bulk/2, then this point is assigned to the interface. This instantaneous surface is denoted as (h_t(x,y), at time t). We can average these instantaneous surfaces to obtain the mean surface ⟨h(x,y)⟩, and furthermore, subtracting the mean values from the h_t(x,y), we obtain δh_t(x,y) as surface height and the height fluctuations ⟨δh²(x,y)⟩. For the protein–water interface, grid points in space are defined by (r, θ, ϕ) and, for a specific (θ, ϕ) coordinate set in the spherical system, it defines a radial vector. r is the radial distance of end point of the radius vector from the origin (0, 0, 0); θ is the polar angle, which is defined as the intersection angle between the radius vector and the positive z vector; and ϕ is the azimuthal angle defined by the positive x vector and orthogonal projection of the radius vector on the xy plane. The spherical coordinates (r, θ, ϕ) of a point could be derived from its Cartesian coordinates (x, y, z) by the following formulas: r = |r| = (x² + y² + z²)^1/2, θ = arccos(x/r) and ϕ = arctan(y/x). Points are defined to belong to the interface if ρ(r₀,θ,ϕ) = 0.6ρ_bulk. We use a different constant value c here compared with the liquid–vapor interface case because this choice will result in a more unambiguous construction of the protein–solvent interface. We note that other parameters, ξ and d, remain the same as in the case of the liquid–vapor interface. Correspondingly, the instantaneous protein interface can be expressed as (h_t(θ,ϕ)), the mean surface as ⟨h(θ,ϕ)⟩, the surface height as δh_t(θ,ϕ), and the height fluctuation as ⟨δh²(θ,ϕ)⟩.

III. RESULT AND DISCUSSION

A. Liquid–Vapor Interface

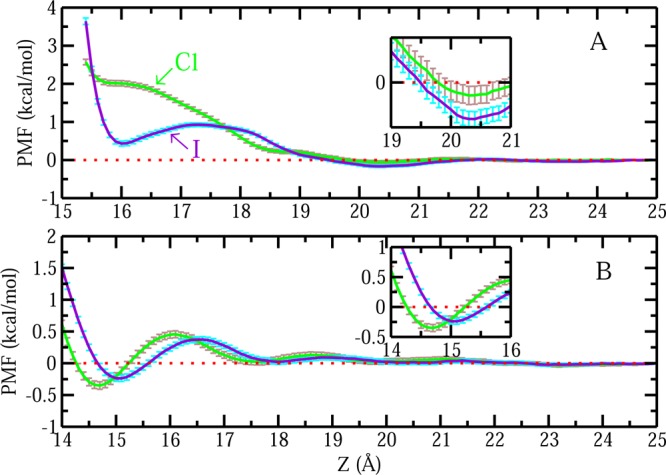
We start to look at the free energetics of a Cl^–/I^– across the liquid–vapor interface. Results of PMF for Cl^– and I^– are shown in Figure 2A. For clarity, we added a vertical offset of 0.1 kcal/mol for the Cl^– case. To better compare the interface stabilities between the two ions, in the large graph of panel A, we emphasized the PMFs around the interfacial region and all PMFs along the reaction coordinate can be found in the small inset. The PMF is defined to be zero in the bulk (which is determined by window z = 10 Å). I^– has a slight PMF minimum (≈0.05 kcal/mol) prior to the GDS (Gibbs dividing surface is around z = ±25.5 Å in this case). Due to the uncertainty reported, whether I^– shows surface stability is ambiguous. However, we notice that there is a barrier (around z = 19 Å) prior to the PMF minimum, which is also observed in other studies;^9,18 as a result, although being less explicit than the interfacial stability reported in experiments and other force fields,^{12,16,18−21} qualitatively we consider that I^– exhibits a surface-stable state in the current simulations. In contrast, Cl^– is repelled from the L–V interface in the current and other force fields.¹⁸ In the Drude polarizable force field, Cl^– shows behavior similar to that of I^–, having a marginal stabilizing/negative free energy minimum state followed by a barrier (from bulk to vapor phase). Unlike the nonpolarizable force fields, the Drude force fields encounter the issues of overpolarization,⁶⁰ which leads to differences in describing the presence of Cl^– at the interface using Drude and nonpolarizable and other polarizable force fields.⁶¹ Consequently, we do not consider Cl^– to be interface stable, and I^– as having liquid–vapor interface stability with the current force field, consistent with previous studies. In this work, we stress that we are not focusing on the exact values of free energetics of a single Cl^–/I^– adsorption at the liquid–vapor interface, but rather we want to emphasize the interfacial stability difference between Cl^– and I^– and related physical and structural properties. More importantly, we would like to connect these ion-specific behaviors at aqueous liquid–vapor interfaces to those of more general aqueous protein hydrophobic interfaces. The nonpolarizable water model and nonpolarizable protein parameters combination would clarify these issues with the benefit of saving computational resources compared with the polarizable force field. In light of this, we argue that the current force field we are applying is sufficiently robust and appropriate.

Figure 2.

(A) PMF of a single Cl^–/I^– approaching the liquid–vapor interface in TIP3P water. (B) Normalized liquid–vapor interface fluctuation at (x = 0, y = 0) as a function of anion restrained position for Cl^– and I^–.

Our previous studies have demonstrated a connection between interfacial stability of Cl^–/I^– around liquid–vapor interface and the magnitude of their induced fluctuations of the interface in SPC/E, TIP4P-FQ, SWM4-NDP, and TIP4P-QDP water models.^18,19 It is found that the species demonstrating an interfacial stability appear to enhance liquid–vapor interfacial fluctuations significantly, whereas those that show no interfacial stability induce no further fluctuation (or may even suppress levels of fluctuations). Here we explore the differences in interfacial fluctuations for the two anions discussed in the current simulations. The fluctuations were computed with the protocol as we state in section IIB. From our previous work,¹⁸ the geometry of the fluctuation surface ⟨δh²(x,y)⟩ is radically symmetric, with the largest value at the center x = 0, y = 0 (right toward the ion). For convenience, we use ⟨δh²(x=0,y=0)⟩ to compare the magnitude of interface fluctuations when Cl^–/I^– are restrained at different z-positions, with the result shown in Figure 2B. The fluctuation profile is normalized by the fluctuation value in pure water (i.e., the system in the absence of the ion, which has a value of 0.77 Ų). Normalization in this manner somewhat accounts for neglecting effects of larger wavelength undulations of the interface and affords a way to compare systems of different lateral dimensions if so needed. In this convention of normalized surface fluctuation (⟨δh_L²⟩) we extract the ion-induced contribution from each species at different z-positions. When ⟨δh_L²⟩ equals 1, the effect of ion is zero; when ⟨δh_L²⟩ > 1, the surface height fluctuation is enhanced relative to pure water with the presence of ion; when ⟨δh_L²⟩ < 1, the surface height fluctuation is suppressed. No obvious enhancement of surface fluctuations is associated with Cl^–; on the other hand, I^– induces larger fluctuation, with the maximum normalized fluctuation value around 1.5 at the location of z = 21 Å, which is before the position of the free energy minimum. Also presented in the inset is the time profile of ⟨δh_L²(x=0,y=0)⟩ for I^– at the window z = 21 Å (which possesses the largest surface fluctuation) to show the convergence of the fluctuation. Previously, by studying a wide variety of force fields (polarizable and nonpolarizable), our results¹⁸ suggest a threshold value of the maximum normalized interfacial fluctuations about 1.5, dividing those ions that are interfacially stable and those that are not. The largest normalized fluctuation and ΔG for I^– are +1.55 (unitless) and −0.03 kcal/mol, just barely placing it on the critical/transitional position in Figure 4 of ref (18). For Cl^–, we found the maximum fluctuation is 1.1 and the corresponding ΔG = 0.52 kcal/mol, which falls in the quadrant for nonsurface stable species. It indicates that in terms of the surface stability, the current force fields for anionic behavior are consistent with other force fields. The differential behavior of the two ions at the pure aqueous liquid–vapor interface, consistent with previous studies, thus provides the control needed to interpret the simulations in a protein context.

We note that the differences in induced interfacial fluctuations by Cl^– and I^– may be attributed to these two types of ions presenting distinct hydration shell environments. The first solvation shell of Cl^– is more rigid and less malleable than that of I^–. The nature of the solvent structure around I^– determines that it is more amenable to inducing fluctuations of the interface as a consequence of a greater disruption of the solvent structure on approach to the interface. This solvation shell property difference between Cl^– and I^– in polarizable water has been discussed previously.⁶² To corroborate that these characteristics are similar when the current nonpolarizable force field is used, we show the radial distribution functions (RDFs) based on water oxygen–single Cl^– and water oxygen–single I^– in Figure S1 of the Supporting Information. Cl^– shows a predominant first solvation peak, and an oscillatory probability function, signifying a substantially structured hydration environment; in contrast, the I^– RDF exhibits a modest peak, and markedly less oscillations, which is consistent with the results we have obtained previously for RDFs in different water models (SPC/E, TIP4P-FQ, SWM4-NDP, and TIP4P-QDP). Overall, with the current force field, we observed ion-specific interfacial behaviors between Cl^– and I^– and also their distinct ability to induce long-ranged perturbations of the aqueous liquid–vapor interface as we have previously discovered in other water models. A further step in this work is that we attempt to extend this investigation from the ideally hydrophobic aqueous liquid–vapor interface to a somewhat more realistic, and certainly more complex, aqueous protein hydrophobic interface.

B. Ion Distributions Around Protein in 1 Molal Aqueous Environment

Here we consider the protein in 1.0 m KCl/KI aqueous solutions, seeking a general overview of the relative stability of Cl^– and I^– around the hydrophobic interface of the protein; superficially, we compare the relative probability of finding an anion of each type in the vicinity of the protein interface. Figure 3 shows spatial distribution of number density of Cl^–/I^– around the hydrophobic interface of HFBII in 1.0 m KCl/KI aqueous solution. The composition of the hydrophobic patch has been discussed in the Method section and roughly the position of the patch is within the range of (−10 Å < x < 10 Å, −10 Å < y < 10 Å, 6 Å < z < 13 Å), so we consider anion density distribution only around this region. The x-axis represents the lateral distance r = (x² + y²)^1/2 (the sign of r depends on that of the x component and the y component: if they are the same, r > 0; if they are different, r < 0), and the y-axis is the z distance from the center of mass of protein located at (0, 0, 0). Comparison of panels A (Cl^– density distribution) and B (I^– density distribution) indicates that I^– has a higher propensity for the hydrophobic protein interface. For a more quantitative comparison, in Figure 4 we show the number of bins (i.e., the effective volume) with Cl^–/I^– densities above certain threshold values around the hydrophobic patch. The bins were constructed in three-dimensional space with size 1 Å × 1 Å × 1 Å, and the ion densities in each bin were computed as normalized values by dividing the numbers of Cl^–/I^– in the bin in the presence of the protein with the number in the absence of protein. Therefore, a normalized density value that is larger than 1 implies that the protein enhances the anion density in the particular site of interest. We consider scenarios with normalized anion densities greater than 3, 4, 5, 6, 7, and 8 for Cl^– and I^–, shown in different panels in the figure. We find that, consistently, at different radii close to the hydrophobic patch and above various thresholds, there is greater enhancement of I^–. Our observation agrees with those of Lund et al.³³ in their simulation study on lysozyme in a mixed aqueous solution of KCl and KI. They observed a specific ion effect around the protein showing that Cl^– has virtually no preference for nonpolar regions, but positively charged residues, whereas I^– accumulates in the vicinity of hydrophobic groups. They explain the behavior of Cl^– as a direct ion pairing interaction, involving small, fully hydrated Cl^– with cationic groups, and I^–’s behavior as solvent-assisted attraction of large, soft, and partially hydrated I^– to a nonpolar protein surface patch. This view of the differences in ion behavior suggests an underlying ligand-substitution theme as well. Chloride must substitute a rigid, strongly held solvation shell with another ligand (this terminology is intentionally used broadly and nonspecifically in this situation); this ligand is a polar or charged entity. The iodide, due to its low charge-density arising from the classical representation of this entity, can accommodate loss of its rather loose, less well-defined solvation shell. For a further atomic level understanding of this solvent-assisted mechanism and a quantitative comparison of the stability of Cl^– and I^– around particular region of HFBII, in the next subsection, we consider the potential of mean force to as a single Cl^–/I^– approaches, from the bulk, a specific point on the hydrophobic interface of HFBII.

Figure 3.

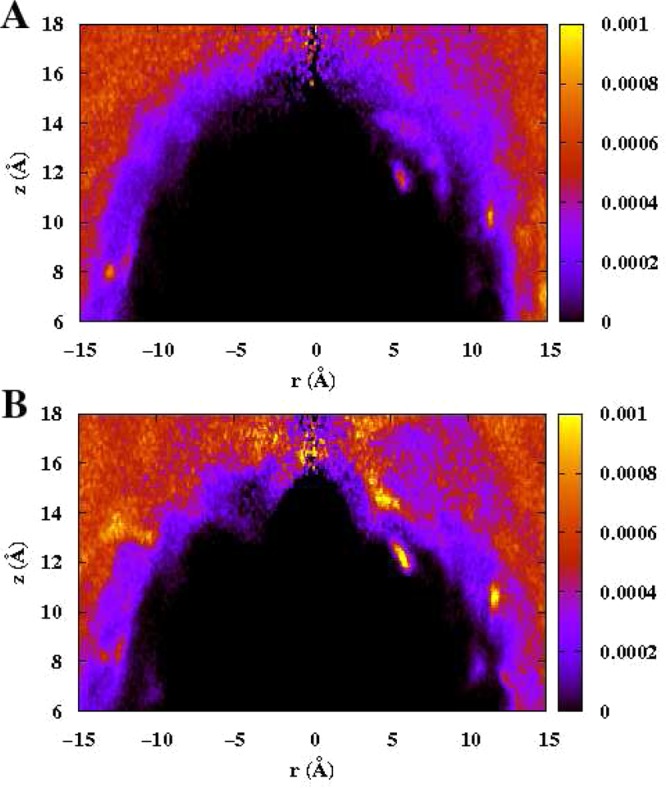
Number density distribution of Cl^–/I^– around the hydrophobic interface of HFBII in 1.0 m KCl/KI aqueous solution: (A) Cl^– density distribution; (B) I^– density distribution. The x axis represents the lateral distance r = (x² + y²)^1/2. r > 0 means the signs of the x component and y component are the same, whereas r < 0 means the signs of x component and y components are different.

Figure 4.

Number of bins that display Cl^–/I^– densities above certain threshold values around the hydrophobic patch of HFBII in 1.0 m KCl/KI aqueous solution: (A) above threshold value 3; (B) above threshold value 4; (C) above threshold value 5; (D) above threshold value 6; (E) above threshold value 7; (F) above threshold value 8.

C. Potential of Mean Force

The umbrella sampling molecular dynamics PMF for both anions approaching the hydrophobic interface are shown in Figure 5A; large values of the x-axis represent large separation of the anion and protein center of mass, and the PMF’s are zeroed at large separation. To assess the convergence of the potential of mean force, we show the time evolution of the minimum of the PMF in Figure S2 Supporting Information. Also, the PMF from this restrained anion protocol is shown to be consistent with the fixed anion approach (average force integration), a comparison of which is shown in Figure S3 Supporting Information.

Figure 5.

(A) PMF for a single Cl^–/I^– approaching the hydrophobic protein–solvent interface. (B) Coordinate water numbers around a single Cl^–/I^– as a function of the reaction coordinate.

For Cl^–, there is a small barrier around z = 19.5 Å, followed by a shallow minimum around z = 18.5 Å; a similar trend is seen for I^–, with a small barrier around z = 20.5 Å and a minimum afterward. For Cl^–, the PMF minimum is −0.06 ± 0.05 kcal/mol; for I^–, it is −0.08 ± 0.04 kcal/mol. In light of the uncertainty estimates, both Cl^– and I^– exhibit little stabilization at the hydrophobic protein interface. However, as the single Cl^–/I^– draws near the interface, significant differences arise. The Cl^– PMF starts to increase monotonically; the I^– PMF shows a slightly more complex trend. Unlike the situation for Cl^–, the PMF profile of I^– shows a second minimum, which is a little higher (0.20 ± 0.04 kcal/mol) than the first one. At this second minimum position, the free energetic difference between Cl^– and I^– is about 0.78 ± 0.09 kcal/mol, even with the consideration of the uncertainty. This implies that close to the hydrophobic protein interface, I^– tends to be more interface stable than Cl^–, although compared with bulk, neither of them displays the stabilization effect around the interface within the context of the specific force field we have chosen to use in this study. We note that the dramatic increase of PMF for both Cl^– and I^– starting around z = 18.5 Å may be related to the change of the number of coordinate water in the first hydration shell around the ion, as it has been shown in Figure 5B. When the ions are close enough to the interface, there will be a decrease of hydration water. Consequently, the favorable interaction between a single anion and water will be lost, entailing the increase of free energy. Because the two anions display distinct free energy profiles nearing the interface, we next consider the induced fluctuations associated with the approach of these ions in the spirit of earlier studies.¹⁸⁻²⁰

The aqueous protein interface was constructed on the basis of the protocol mentioned in IIB. Figure 6 displays the mean protein–solvent interface along with the interface fluctuation. From the color scale, one can judge the magnitude of the fluctuation at each position around the whole protein. Panels A and B represent the situation that a single Cl^–/I^– resides at z = 24 Å, in which case anions are far away from the protein interface and there will be no induced interface fluctuation. These are the inherent fluctuations of the interface, which are completely determined by the structural character of the protein itself. The figure shows that one region manifests larger inherent fluctuation in panels A and B. This region is in fact part of the largest hydrophobic patch of the protein. We will compare and discuss more about the inherent interface fluctuation among different regions of the protein, including hydrophobic, less hydrophobic and hydrophilic patches in the next subsection. As a single Cl^–/I^– approaches the hydrophobic interface, ion-induced perturbations of the aqueous interface around protein surface are more pronounced as reflected in Figure 6C,D. These two figures depict the protein interface fluctuation when a single Cl^–/I^– resides at z = 18 Å. Right above the position (x = 0 Å, y = 0 Å) where a single anion approaches the interface, we notice that fluctuations induced by I^– are much larger than those induced by Cl^–. As single anions move closer to the interface (z = 16 Å), this large difference of fluctuation between Cl^– and I^– lessens, as shown in Figure 6E,F. Due to the heterogeneous features of the protein surface, the extent of induced fluctuation is not perfectly symmetric about (x = 0 Å, y = 0 Å). However, judging from Figure S4 Supporting Information, we could find that (x = 0 Å, y = 0 Å) is a feature point displaying largest induced fluctuations compared with other regions on protein surface as anions reside at various separations.

Figure 6.

Protein–solvent mean interface ⟨h(x,y)⟩ (shown in the z axis) and interface fluctuations ⟨δh²(x,y)⟩ (shown in color scale) in single Cl^–/I^– solution. The color scale represents the interface fluctuations: (A) Cl^– resides at z = 24 Å; (B) I^– resides at z = 24 Å; (C) Cl^– resides at z = 18 Å; (D) I^– resides at z = 18 Å; (E) Cl^– resides at z = 16 Å; (F) I^– resides at z = 16 Å.

To better illustrate the change in interface fluctuation magnitude as single anions move toward the point (x = 0 Å, y = 0 Å), we plot ⟨δh²(x=0,y=0)⟩ along the reaction coordinate in Figure 7A. We stress our intent to discuss the behavior of interfacial fluctuations as the anions move toward the patch; we are not interested solely in the nature of fluctuations when the anions reside at the interface. From the total 20 ns production data, we obtained the fluctuations at this point by using every one nanosecond of data; the values shown here are the average of each one-nanosecond data block and correspondingly, uncertainties were obtained on the basis of the standard deviations. In the bulk region (z ranges from 24 to 25 Å), ⟨δh²(x=0,y=0)⟩ is around 0.2 Ų for both Cl^– and I^–, which corresponds to the protein interface inherent fluctuation in the pure water due to the thermal fluctuations. For the purpose of demonstrating and comparing the fluctuations induced from a single Cl^–/I^–, we defined ⟨δh_L²(x=0,y=0)⟩ as the normalized fluctuation value that is obtained via dividing ⟨δh²(x=0,y=0)⟩ by the inherent fluctuation value, shown in Figure 7B. For the single Cl^– case, fluctuations almost remain the same as in the bulk. At z = 17.5 Å, slight enhancement of fluctuation was observed, with a normalized value of 1.36. In stark contrast, for the case of I^–, the onset of enhanced fluctuation relative to the bulk occurs at z = 22 Å. As I^– moves closer to the hydrophobic patch, induced fluctuations continue increasing and this enhancement reaches a maximum with a normalized value around 3.0 and I^– is located at z = 18 Å. Finally, the fluctuation is lower compared to the bulk when the anion is close to the interface. Comparing the trends of surface fluctuation as a single Cl^–/I^– moves toward the hydrophobic protein interface and liquid–vapor interface, we find that in both cases the fluctuation is enhanced with presence of I^–; however, there is only marginal perturbation of the interface by Cl^–. We stress that this enhancement of interfacial fluctuations occurs as the ions approach the interface, not while they directly reside there.

Figure 7.

(A) Hydrophobic interface fluctuation at (x = 0, y = 0) as a function of anion restrained position for Cl^– and I^–. (B) Normalized interface fluctuation at (x = 0, y = 0) as a function of anion restrained position for Cl^– and I^–.

Again, this originates, we claim, from the fact that Cl^– presents a more rigid hydration environment due to the more effective hydrogen bonding of water, thus decreasing the efficacy of promoting interfacial fluctuations. To visualize these different manners in which the hydration shells of Cl^– and I^– couple with the solvation structure at the hydrophobic protein interface, panels A and B of Figure 8 present the 180° angle-averaged radial water density around Cl^– and I^– as they reside at z = 18 Å, the position of maximum ⟨δh_L²(x=0,y=0)⟩ for the anions. In this map, we only consider the water density distribution along positive z side, because a single anion approaches the protein interface from this side. For the Cl^–, the first hydration shell remains in its entirety as shown in the bright yellow ring. This implies that the hydration shell environment for Cl^– is still quite rigid, well-ordered, and tightly bound to the central anion, which will not cause an increased dynamical perturbation of local solvent (the Cl^– will not give up local solvation water unless there is a sufficiently acceptable ligand to substitute in water’s place); I^–, in contrast, possesses the first hydration shell that is weakly bound and less-ordered, so that it has more tendency to break, as shown in panel B, the bright yellow ring was “broken” at some region. This malleable hydration layer accommodates greater coupling with the solvation shell of the protein interface, consequently, inducing a larger interface fluctuation. For a comparison, we also shown the density map at z = 19 Å in Figure 8C,D, a little ahead of the position of largest fluctuation. In our recent studies, we have demonstrated a connection between L–V interfacial stability of chemical species and the extent to which the presence of these molecular species approaching the interface induces collective fluctuations of the interface in addition to the level inherent in pure water due to thermal motion. Next, we also discuss the induced protein interface fluctuation difference for Cl^– and I^– as a further contribution in explaining their differences in free energy profiles approaching the hydrophobic patch; the contribution arises in the context of a mechanistic view of how the system ultimately finds stability with I^– near the interface. We observe that the iodide anion induces larger fluctuations on approach to the interface; this increases interface entropy (based on refs (18) and (20)). This increased interface entropy may contribute to differentially stabilizing microstates where the iodide is closer to the interface compared to chloride. On the basis of the potentials of mean force of Figure 5, the highest induced fluctuations correspond to barrier states. The fluctuations induced by iodide, being larger than for chloride, may tend to lower the barrier required for the iodide to move to the interface. Thus, the fluctuations provide a mechanism for iodide ultimately presenting at the interface.

Figure 8.

Average water oxygen density around (A) Cl^– at position z = 18 Å, (B) I^– at position z = 18 Å, (C) Cl^– at position z = 19 Å, and (D) I^– at position z = 19 Å. Teh x axis represents the lateral distance (x² + y²)^1/2 and the y axis represents the distance from the positive z direction.

We pause here to address potential artifacts in our algorithm for computing interfacial fluctuations. One may ask whether the instantaneous coarse-grained interface we construct can artificially pass “through” the ion, thus giving rise to artificially large fluctuations. To explore this, we plot the difference in the z-position of the ion center (z_ion) and the z-position of the interface (z_interface) as the ion moves toward the protein along the axis passing through the z-axis; that is, we plot the difference in these positions for different values for each simulation window. Thus, the z-position of the interface is equal to the value of the surface height of the interface at the point (x = 0, y = 0, z_interface), and the z-position of the ion center is identically the z-position of the ion. If the interface is between the ion and the protein, we will see a positive value; if the interface moves “through the ion”, we will get zero; if the ion resides between the interface and the protein, the value will be negative.

In our system, due to the strong restraint applied on the ion, the distribution of the corresponding ion’s z-position (z_ion) in each simulation window is narrow (0.1 Å). Consequently, for each window, by subtracting basically the same z_ion, the distribution of the instantaneous interface’s z-position (z_interface), which correlates with the interfacial fluctuation in our manuscript, essentially has the same width of the distribution for (z_ion – z_interface). The question arises whether the algorithm we use artificially includes all three scenarios (z_ion – z_interface > 0, = 0, < 0) in some simulation windows, and in this way suggesting larger fluctuations. We will show that even when all z_interface values are distributed on one side of the ion (all positive/negative values for z_ion – z_interface), the distribution of z_interface is not necessarily small; i.e., the induced fluctuations are nonartifactual.

Figure S8 of the Supporting Information shows that for just about all positions of I^– greater than 16.5 Å, the interface resides between the protein and the ion. The interface does not pass through the ion center. There are some values less than zero when the ion z-position is 16.5 Å, but at this point, we see suppression of interface fluctuations (Figure 7). Finally, we consider the same analysis by taking the interface position to be the height of the surface at different x and y positions (in addition to a variety of z-positions). This is shown in Figure S9 of the Supporting Information. This again shows the same behavior as Figure S8 of the Supporting Information. On the basis of this analysis and to the best of our ability at this time, we believe the that induced fluctuations we report are reliable and robust.

To close this section, we attempt to evaluate hydrophobic interface fluctuations allowing for protein flexibility. Instead of freezing all protein atoms, we allow modest vibrational degrees of freedom of the protein. Because the real proteins in biological system are not motionless, it is meaningful to address whether the different perturbations of interfacial fluctuations induced by Cl^– and I^– persist in the case of a flexible protein surface. For the convenience of evaluating the interface fluctuation around specific regions of the protein in the external coordinate system without worrying about translation and rotation of the protein in space, translational, and rotational motions of the protein were first removed from the MD trajectory by using “MERGE ORIENT” module of CHARMM. RMSD based on the backbone protein atoms are shown in Figure S5 of the Supporting Information. The RMSD values are less than 2.5 Å in all cases as Cl^–/I^– locate around the protein surface and in the bulk. The aqueous protein interface was constructed using new trajectories on the basis of the same protocol from section IIB in the Method section. Figure 9 shows the hydrophobic interface fluctuation profiles at x = 0 and y = 0 as a function of z-position of Cl^– and I^– approaching the flexible protein. When the single anion is in the bulk, fluctuation is about 0.3 Ų for both anions, higher than the inherent fluctuation of the interface around the fixed protein, which is about 0.2 Ų. This makes sense because inherent fluctuation of the protein interface is derived not only from thermal motion of water but also from that of protein itself. Consistent with the fixed protein outcomes, I^– induces larger fluctuations than Cl^– nearing the patch, with the maximum value of 0.56 Ų higher than that of Cl^– 0.43 Ų at the location of z = 20 Å.

Figure 9.

Hydrophobic interface fluctuation at (x = 0, y = 0) as a function of anion z-position for Cl^– and I^– in the case of flexible protein.

D. Less Hydrophobic and Hydrophilic Protein Interface

We now turn to the process where a single Cl^–/I^– approaches the aqueous protein interfaces with different hydrophobicities. We also start with PMF, representing the reversible work for Cl^–/I^– transferring from the bulk to the regions around the protein–water interfaces that we are interested in. Figure 10A presents the PMF for a single Cl^–/I^– approaching the less hydrophobic protein–solvent interfaces. The PMF shows a minimum of −0.06 ± 0.04 kcal/mol for the single Cl^– and −0.16 ± 0.04 kcal/mol for the single I^– at position around 20 Å for both, which is further emphasized in the small inset. Relative to the state with ion in bulk, there is effectively no stabilization. The main differences in PMF between Cl^– and I^– appear in the range from z = 15.5 Å to z = 17.0 Å. Unlike the Cl^– PMF in this range, which continues increasing, there is a minimum in the PMF profile for I^–. Consistently, the PMF for I^– shows slightly higher stability than that of Cl^– in this range. Figure 10B shows the PMFs for Cl^– and I^– approaching a hydrophilic region. The PMF shows a global minimum of −0.35 ± 0.06 for a single Cl^– and −0.24 ± 0.05 for a single I^– at position 14.7 and 15.1 Å, respectively, as they approach the hydrophilic protein–solvent interfaces (shown more clearly in the inset). They suggest a modest stabilization effect from both Cl^– and I^– as they are in the vicinity of the hydrophilic region around protein interfaces. In summary of the PMF, as a single Cl^–/I^– approaches three different regions on the protein interfaces with different hydrophobicity, we find significant differences arising as a single Cl^–/I^– is close to the interfaces from z = 14 Å to z = 17 Å. For Cl^–, when it is close to the hydrophobic and less hydrophobic regions, there are no free energy minima, and the free energy values are positive. For I^–, although the free energy values are still positive, they are lower (with the largest difference about 1 kcal/mol) than those of Cl^–. Minima are observed in this region for the I^– but not for Cl^–. However, around hydrophilic interfaces, both Cl^– and I^– have minima. This reflects the fact that for both Cl^– and I^–, there are more free energetic advantages as they are close to the hydrophilic regions, compared with the hydrophobic ones of HFBII protein, which may be due to the favorable direct anion-charged residue interactions around the hydrophilic protein interfaces. Interestingly, our results of PMF for Cl^–/I^– when they are around hydrophobic and hydrophilic residues of HFBII protein follow a similar trend for the previous published work by Lund et al.²⁵ They compared the free energetics of F^– and I^– around a spherical model macromolecule. Here, F^– is a small, highly charge-dense and fully hydrated anion similar to Cl^–. They suggest that when the macromolecule is uncharged and considered as a hydrophobic particle, I^– has more free energy advantage than F^– for being near the interface. When the macromolecule is positively charged and considered as a hydrophilic particle, the trend reverses, F^– is more favorable around the macromolecule. Also, comparing the free energetics of the same anion around the hydrophobic and hydrophilic sphere, Lund et al. find that both F^– and I^– are more stable around the hydrophilic particle.

Figure 10.

(A) PMF for a single Cl^–/I^– approaching the less hydrophobic protein–solvent interfaces. (B) PMF for a single Cl^–/I^– approaching the hydrophilic protein–solvent interfaces.

Next, we consider interface fluctuations. First we evaluate the inherent fluctuations (absence of anions) of different interfacial regions of the protein as reference. Figure 11 shows a colored map of the HFBII protein interface based on the magnitude of interface fluctuations in TIP3P water. The color scheme from red to blue represents the fluctuation spectrum from higher to lower values. Because there are no other impurities in the system, the inherent interface fluctuations are derived from the thermal fluctuations of the water. As shown in panel A, regions defined as hydrophobic interfaces (V18, L19, L21, I22, V24, V54, A61, L62, L63) possess the largest fluctuations and the selected hydrophilic interfaces in panel D (D25, C26, K27, T28, A58, D59, Q60) manifest the lowest fluctuations. The less hydrophobic interface (panel C) displays a moderate fluctuation. This suggests that the magnitude of interface fluctuation correlates with the surface hydrophobicity. This is consistent with Garde’s insights³⁸ that density fluctuations are enhanced near hydrophobic surfaces but reduced with increasing hydrophilicity. This enhanced density fluctuation is explained as a consequence of more facile cavity formation, increased compressibility of hydration water, and more favorable binding of hydrophobic solutes. Although in this work the fluctuation we address is based on the aqueous protein interface height, which is not exactly the same as the water density fluctuation Garde et al.³⁸ apply, it reflects similar information about the malleable nature of the water around hydrophobic patch, considering that the aqueous protein interfaces we construct were based on the coarse-grained solvent densities at each space-time point.

Figure 11.

Inherent interface fluctuations of HFBII. For A, B, C, and D, each one depicts one side of the protein interface with a rotation of 90° respectively. Red represents larger fluctuations, and blue represents smaller fluctuations. The highlighted regions in A, C, and D correspond to the hydrophobic, less hydrophobic, and hydrophilic regions that we define in this study.

We now address fluctuations induced by the anions. Parts A and B of Figure 12 show fluctuation profiles as Cl^–/I^– approach the less hydrophobic and hydrophilic protein interfaces, respectively. Compared the fluctuations of distinct protein interfaces as anions in the bulk, in previous section we note this value for hydrophobic region is about 0.2 Ų; in the less hydrophobic interface, it is about 0.1 Ų; and in the hydrophilic interface, it is about 0.07 Ų. These differences correlate with the inherent protein interface fluctuations of Figure 11. As a single Cl^–/I^– moves closer to the less hydrophobic interface, I^– induces more interfacial fluctuation than Cl^–, especially in the range from z = 18 Å to z = 19 Å. The magnitude of the difference is up to 0.2 Ų, similar to the hydrophobic interface value of 0.3 Ų. Comparing this profile with that of the hydrophobic interface in Figure 7A, the induced fluctuations are significant from I^– but marginal from Cl^–; global maxima can be detected in the I^– fluctuation profiles at the location of z = 18.0 and 18.5 Å for hydrophobic interface and less hydrophobic interface, respectively. In the case of the hydrophilic interface, both Cl^– and I^– have an inappreciable effect on hydrophilic interfacial fluctuations. Although I^– may induce a little larger fluctuation compared with Cl^– as it moves closer to the interface, the differences are quite small, with a value of 0.02 Ų, only one-tenth of that from the less hydrophobic interface. In this picture, our suggestion is that the extent of the difference is highly related to the nature of the protein interface. The hydrophilic interface borders a rigid water environment that is difficult to couple with both the hydration shells of Cl^– and I^–. Consequently, Cl^–/I^– approaching the hydrophilic interface induce marginal interfacial fluctuations, and the difference between induced fluctuations of the two anions is less; however, for the hydrophobic interface and less hydrophobic interface we defined, the water shells around these regions are malleable, so they can exchange solvation water with that of I^–, which also possesses a less rigid solvation shell. However, due to the more severe ordering of water around Cl^–, it is not possible for water around hydrophobic interface to perturb the solvent around Cl^–. Therefore, as Cl^– and I^– approach this type of hydrophobic interface, significant differences appear in their ability to induce hydrophobic interfacial fluctuations.

Figure 12.

(A) Less hydrophobic interface fluctuation at (x = 0, y = 0) as a function of anion restrained position for Cl^– and I^–. (B) Hydrophilic interface fluctuation at (x = 0, y = 0) as a function of anion restrained position for Cl^– and I^–.

IV. SUMMARY AND CONCLUSIONS

Building upon the insights gained from the vast studies of specific ion behaviors at aqueous liquid–vapor interfaces, we have presented here a discussion regarding the unique fluctuation inducing properties of two anions for which the degree of induced interfacial fluctuations correlates with stability at the interface. Our major conclusions are for hydrophobic protein–water interfaces, and this particular nature of the interface is chosen as it is a logical extension of the ideally hydrophobic interface presented by the aqueous liquid–vapor context. Our control system, the aqueous liquid–vapor interface, recapitulates earlier specific ion behavior, namely that the less-charge dense, larger iodide anion demonstrates a slight surface propensity as embodied in a free energy stable state compared to chloride. Moreover, our results for the anions at the aqueous liquid–vapor interface recapitulate recent studies correlating to the surface propensity to ability to induce interface fluctuations.¹⁸⁻²⁰ At the interface between a hydrophobic region of a protein, in this case HFBII, and the aqueous solvent, we find that the potential of mean force calculations reveal a lower free energy state for iodide than chloride, the trends qualitatively consistent with those observed at the liquid-vapor interface. Furthermore, we find that the more surface stable iodide also induces significantly larger interface fluctuations on approach to the interface compared to the smaller, more charge-dense chloride; this is again in keeping with observations at the aqueous liquid–vapor interface. These behaviors approaching the hydrophobic interface are related to the coupling of local hydration water in the vicinity of the protein with the hydration water around the individual anions; specifically, the differential ability of the water environments to couple with one another in the case of chloride and iodide leads to the specific-ion behavior as it is related to induced interfacial fluctuations. Approaching interfaces at the other extreme, hydrophilic interfaces, we observe that both anions display similar behaviors in terms of surface stability and induced interface fluctuations. These differences offer a view of the anions as having different characters in different contexts. Where strong local interactions are not dominant, as in the case of hydrophobic surfaces that lead to higher fluctuations in general (i.e., higher solvent density fluctuations³⁷), the anions tend to differentiate themselves on the basis of their “hydrophobicity”; the large, less charge-dense iodide has a higher propensity to associate with hydrophobic regions due to its inherent higher “hydrophobicity”. The smaller, more charge-dense, less hydrophobic chloride is not stable at a hydrophobic interface. The idea of specific-ion behaviors at interfaces being related to hydrophobic solvation has been put forth recently, and we suggest that the current results present another manifestation of the differential hydrophobic character of ions at specific interfaces.¹⁶ In the case of hydrophilic interfaces presenting highly polar and charged species, the strong charge–dipole and charge–charge interactions dominate and equalize the stabilities and interface perturbing effects of both ions.

Supporting Information Available

Supporting Information discusses aspects of verification of LJ parameters, general discussion of potential of mean force, assessment of the convergence of the potentials of mean force, description of another test system with fixed protein and fixed anion simulation, and verification of the fluctuation algorithm. Tables of LJ and NAMD parameters, vector angles, and protein interface fluctuation values. Figures showing radial distribution functions, PMF evolutions, protein surface fluctuations vs θ and ϕ, evolution of protein backbone RMSD, hydrophobic interface fluctuation vs anion restrained position, entropic contributions, and differences between ion position and surface position. This material is available free of charge via the Internet at http://pubs.acs.org

The authors declare no competing financial interest.

Funding Statement

National Institutes of Health, United States