Skip to main content
PMC home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2014 Apr 8;118(17):4461–4470. doi: 10.1021/jp409412g

Structure and Dynamics of a Fusion Peptide Helical Hairpin on the Membrane Surface: Comparison of Molecular Simulations and NMR

Allyn R Brice 1, Themis Lazaridis 1,*
PMCID: PMC4010296  PMID: 24712538

Abstract

graphic file with name jp-2013-09412g_0011.jpg

The conserved N-terminal residues of the HA2 subunit of influenza hemagglutinin (fusion peptide) are essential for membrane fusion and viral entry. Recent NMR studies showed that the 23-residue fusion peptide forms a helical hairpin that undergoes rocking motion relative to the membrane surface on a nanosecond time scale. To compare with NMR and to obtain a detailed molecular picture of the peptide–membrane interaction, we performed molecular dynamics simulations of the fusion peptide in explicit dimyristoylphosphatidylcholine and with the IMM1 implicit membrane model. To account for low and neutral pH conditions, simulations were performed with acidic groups (E11 and D19) protonated and unprotonated, respectively. The hairpin structure was stable in the simulations, with the N-terminal helix buried more deeply into the hydrophobic membrane interior than the C-terminal helix. Interactions between the tryptophans in the fusion peptide and phospholipid residues contribute to peptide orientation. Higher flexibility of the hairpin was observed in the implicit membrane simulations. Internal correlation functions of backbone N–H vectors were fit to the extended Lipari–Szabo model-free approach to obtain order parameters and correlation times. Good agreement with the NMR results was obtained for orientational fluctuations around the hairpin axis (rotation), but those around the perpendicular axis (tilting) were more limited in the simulations than inferred from the NMR experiments.

Introduction

Enveloped virus infection occurs by formation of a channel between the host cell cytoplasm and a virus particle, allowing the release of viral nucleocapsid. Some viruses fuse directly with the host cell membrane, while others, such as influenza A, enter the cell via endocytosis and fuse with the endosome membrane.1−3 The membrane fusion process is facilitated by glycoproteins embedded in the viral envelope. The fusion protein of the influenza virus is hemagglutinin (HA), composed of two polypeptide chains, HA1 and HA2.4,5 HA1 recognizes and binds sialic acid at the host cell membrane, leading to endocytosis, while HA2 facilitates the fusion between the viral and host cell membranes. A decrease in pH within the endosome induces a conformational change in HA, which initiates the fusion process. X-ray crystallography has provided structures of the entire HA ectodomain at neutral pH6 and fragments of the HA2 subunit at acidic pH.7,8 However, only models are available for the structure of the complete protein at low pH.9

The first 23 residues at the N-terminus of HA2, commonly referred to as the fusion peptide (HAFP), are highly conserved across the 16 subtypes of influenza A virus.10 Many mutations in this region have been found to abolish or impair fusion activity.11,12 Connections between fusion activity and structure have been mainly explored for the first 20 residues of HAFP (HAFP20). This peptide has been found to be fusogenic toward synthetic vesicles.13−15 A combined NMR and EPR study reported that the wild-type HAFP20 adopts a kinked, V-shape structure pointing the two termini toward the membrane.16 It was shown that several point mutations of the subtype H3 sequence of HAFP20 that caused loss of fusogenicity also distorted the V-shape structure.17,18 A solid-state NMR study also supported the V-shape conformation.19

The V-shape NMR structure of the HAFP20 peptide has been the subject of numerous computational studies. Early explicit membrane molecular dynamics (MD) simulations reported that the inverted V-shape structure and orientation were stable for the wild type of HAFP20.20,21 Other simulations of wild-type HAFP20 and several point mutants similarly displayed an inverted V-shape structure for the wild-type sequence but a noninserted and/or linear helix conformation for the inactive mutants.22,23 In contrast, implicit membrane simulations found that the inverted V-shape structure is not stable in the membrane and converts to a straight helix, slightly tilted with respect to the membrane,24 not very different from an earlier Poisson–Boltzmann prediction.25 Another implicit membrane study with more extensive conformational sampling found a significant population of kinked conformations but parallel to the membrane surface.26 More recent, longer time scale explicit simulations showed that the HAFP20 actually favors a linear α-helix structure over the inverted V shape.27 A tendency to lose the kink had already been noted in earlier work.28 A coarse-grained model found that the V-shaped HAFP promotes positive bilayer curvature,29 while a very long atomistic simulation study found that the V-shaped HAFP causes more lipid protrusion, which is thought to facilitate fusion.30

Intriguingly, recent NMR work showed that a HAFP peptide that includes the first 23 amino acids adopts a helical hairpin conformation in DPC micelles.31 The structure is stabilized by four CαH–O backbone hydrogen bonds and a favorable interaction of the N-terminal charge with the dipole of the C-terminal helix.32 NOE measurements suggested an interfacial location of the hairpin structure with respect to the lipid surface. NMR relaxation experiments on bicelles revealed wobbling motions of the hairpin with respect to the membrane surface with 2.4–5.1 ns correlation times.33 Lowering the pH from 7 to 4 disrupted the hairpin structure, allowing fluctuation between closed hairpin and open L-shape and extended structures.34 The same authors further showed that hairpin stability is dependent on the length of the peptide, with HAFP20 being mostly open.35 These results raise interesting physical and biological questions: What is the source of stability of the helical hairpin? Why does low pH destabilize the hairpin? Why does the peptide form an intramolecular hairpin instead of an antiparallel dimer? Is the hairpin crucial for the fusion mechanism or circumstantial? Why would formation of the hairpin be crucial if the hairpin eventually needs to open up?

These questions warrant further theoretical studies. Here, we performed 200-ns explicit MD simulations to investigate the structure and orientation of HAFP23 on a dimyristoylphosphatidylcholine (DMPC) bilayer surface. In addition to the explicit simulations, we also performed simulations with the IMM1 implicit membrane model.36 The goal of these simulations was to obtain a molecular picture that would complement the NMR results and a direct comparison of the parameters calculated by the two methods. Computation of NMR parameters from MD simulations has a long history,37−41 but to our knowledge, all previous studies concern soluble proteins. Lorieau and Bax were the first to extract parameters for the motion of a membrane-bound peptide relative to the membrane plane. The nanosecond time scales involved make this an ideal system for comparison with MD simulations.

Methods

Starting Structures

Starting coordinates for the HAFP hairpin were taken from the NMR structure31 (PDB code 2KXA). The HA N-terminal peptide sequence of H1 subtype influenza A includes the following 23 amino acids: GLFGAI AGFIEG GWTGMI DGWYG. In the NMR work,31 a charged C-terminal tag was used to prevent aggregation. The authors found that the presence of the tag did not affect the structure and dynamics of the peptide (Ad Bax, personal communication); therefore, the tag was omitted in the work reported here. Implicit membrane simulations with the tag did not display large effects on hairpin structure (Supporting Information Figure S4). In order to study the peptide under low and neutral pH conditions, simulations were performed with acidic groups (E11 and D19) protonated and unprotonated, respectively. Although these residues may not be fully protonated at the pH of the endosome (∼5), simulating them as protonated ensures that we will observe the maximum possible effect. N- and C-terminal residues were charged in all simulations. The initial membrane depth (average distance from the membrane center) was determined to be 13 Å based on implicit membrane IMM136 simulations. The starting orientations on the membrane surface were similarly determined with IMM1 simulations. To confirm that the explicit MD simulations were unaffected by starting coordinates, initial orientations with the hairpin perfectly parallel to the membrane surface (also at 13 Å depth) were also constructed. These initial orientations are characterized by rotation angles around the x axis equal to 20 and 0° (see Figure 1). We refer to the former simulations as R20 and to the latter as R0.

Figure 1.

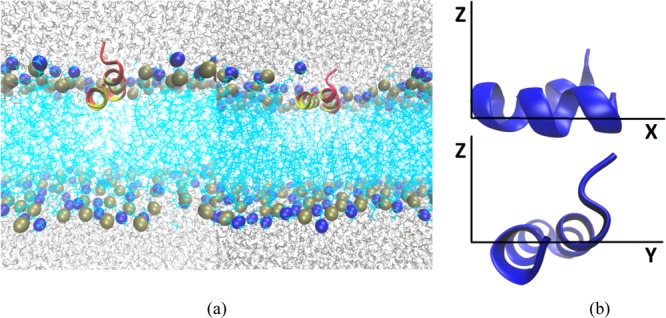
Figure 1

Open in a new tab

(a) Initial structures of explicit DMPC membrane systems with rotation angles of 20° (left) and 0° (right). Hydrophobic groups are highlighted in yellow and hydrophilic groups in red. Nitrogen and phosphorus atoms of the DMPC headgroups are illustrated as blue and tan spheres, respectively, while lipid tails are cyan and water molecules are gray. (b) Illustration of the coordinate system used to describe hairpin motions.

Explicit Membrane Simulations

Explicit membrane simulations of the HAFP hairpin were performed with the NAMD package42 and the CHARMM27 force field.43 Explicit membrane systems were generated with CHARMM-GUI44,45 and then equilibrated. They included 140 pre-equilibrated explicit DMPC lipids, hydrated with 5920 TIP3P water molecules46 for a total of ∼33 500 atoms in a 65 Å × 65 Å × 75 Å cell. The HAFP peptide was inserted at the specified depth (z = 13 Å) and orientation. Lipid molecules overlapping with the peptide were removed (6 lipids for the 20° orientation, 9 lipids for the 0° orientation) using VMD.47 Periodic boundary conditions with particle mesh Ewald48 were applied to account for long-distance electrostatic interactions. Structures were initially minimized with the ABNR algorithm for 5000 steps to remove any atomic clashes. SHAKE was used to constrain all bonds involving hydrogen. A cutoff of 12 Å was used for the van der Waals and electrostatic interactions. The membrane–peptide system was equilibrated at 300 K with a 1 fs time step. Harmonic positional restraints with a force constant of 5.0 kcal/mol were applied to the HAFP and gradually removed over the first 25 ps of equilibration. The simulation was then continued for 200 ns. Nosé–Hoover constant pressure (1 bar) and Langevin constant temperature methods with 1 ps–1 friction coefficient were used to create an isothermal–isobaric ensemble (NPT).42

Implicit Membrane Simulations

The implicit model IMM1 was used,36 which is an extension of the EEF149 model for aqueous proteins. IMM1 represents lipid bilayers as a hydrophobic region centered at z = 0 Å with a specific thickness (T). Here, the value T = 25 Å was used in all implicit membrane simulations. Hairpin structures were simulated with MD in the implicit model. Structures were initially minimized with the ABNR algorithm for 300 steps, and SHAKE was employed to constrain all bonds involving hydrogen. A cutoff of 9 Å was used for the nonbonded interactions. Following minimization, the system was heated from 200 to 300 K, at a rate of 1 K/ps. MD simulations used the Leap Frog Verlet integrator and a time step of 1 fs. Equilibration lasted for 2 ns, and the trajectory over the last 100 ns was used for analysis.

Analysis

The stability of the hairpin during the MD trajectories was assessed through root mean square deviation (rmsd) calculations using the NMR structure as a reference. Rotation angles, as defined in Figure 1b, about the x axis (rotation) and y axis (tilt) as a function of time were calculated along the trajectories. Angles were calculated every 10 ps over the last 50 ns of the 200 ns trajectories. Statistical errors were also calculated over the last 50 ns. The peptide backbone amide bond at residue 13 was used to calculate the rotation angle. The tilt angle was averaged over residues with amide bonds parallel to the N-terminal and C-terminal helix (3 to 10 and 15 to 22).

NMR relaxation rates, order parameters, and correlation times were calculated as follows. Correlation functions, C(t), for the backbone amide bond vectors contain two contributions (eq 1): one from tumbling of the entire protein, C(t)o, and another from internal conformational fluctuations, C(t)I:

graphic file with name jp-2013-09412g_m001.jpg 1
graphic file with name jp-2013-09412g_m002.jpg 2
graphic file with name jp-2013-09412g_m003.jpg 3

where P2 is the second Legendre polynomial (P2(x) = (3x2 – 1)/2), μi(t) is an amide bond vector at time t, and τM is the rotational correlation time. Autocorrelation functions out to 15 ns were calculated over the second half of the 200 ns simulation (the curves become noisy after 15–20 ns). Lorieau et al.33 fitted experimental relaxation data to both the standard and extended Lipari–Szabo (LS) models and determined that the extended LS approach is more applicable to the HAFP hairpin residues. Thus, the extended LS model-free method was also used in the current study:

graphic file with name jp-2013-09412g_m004.jpg 4

where τf and τs are the correlation times for fast and slow internal vector motions, respectively. It is generally assumed that tumbling motions and internal motions can be separately calculated when the time scales greatly differ.50 To specifically calculate internal correlation functions, tumbling motions (C(t)o) are typically removed by translating and orienting the molecule of interest onto a reference structure.40,51 However, since in the current simulations the system cannot tumble, this is not necessary. The NMR module in CHARMM51 was used to obtain relaxation rates, order parameters, and correlation times. Order parameters and correlation times were also obtained by fitting the correlation functions to the extended LS model using MATLAB. The resulting values differed somewhat from those obtained by the NMR module of CHARMM and exhibited less variability among the different simulations. Thus, for S2 and τ, we report the values obtained using MATLAB.

Results

Configurations Observed in the Explicit MD Simulations

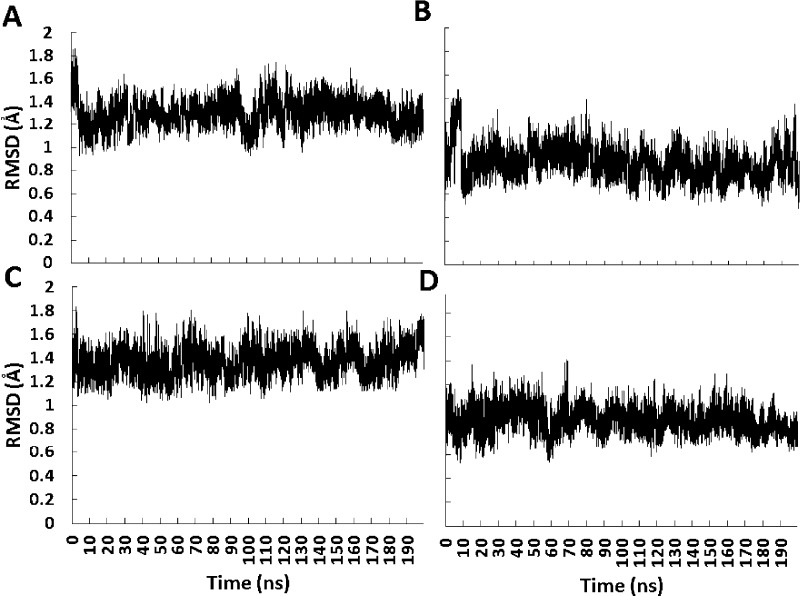
The stability of the HAFP23 hairpin during the simulations was assessed by calculating the rmsd with respect to the initial NMR structure. Figure 2 shows that, regardless of starting orientation or pH, the backbone rmsd remained close to 1 Å; that is, limited conformational changes occurred during 200 ns of explicit membrane simulation. Trajectories at neutral pH (Figure 2B,D) yielded a slightly lower rmsd than the low pH trajectories, which is not surprising since the NMR experiments31 were performed at pH 7.4. However, we did not observe any tendency for opening of the hairpin at low pH,34 probably due to the limited duration of the simulation (see Discussion).

Figure 2.

Figure 2

Open in a new tab

Root mean square deviations from the NMR structure for backbone atoms over MD trajectories in explicit DMPC membrane starting from rotation angles of 20° (top graphs) and 0° (bottom graphs). The low pH systems are shown in A and C, while neutral pH systems are shown in B and D.

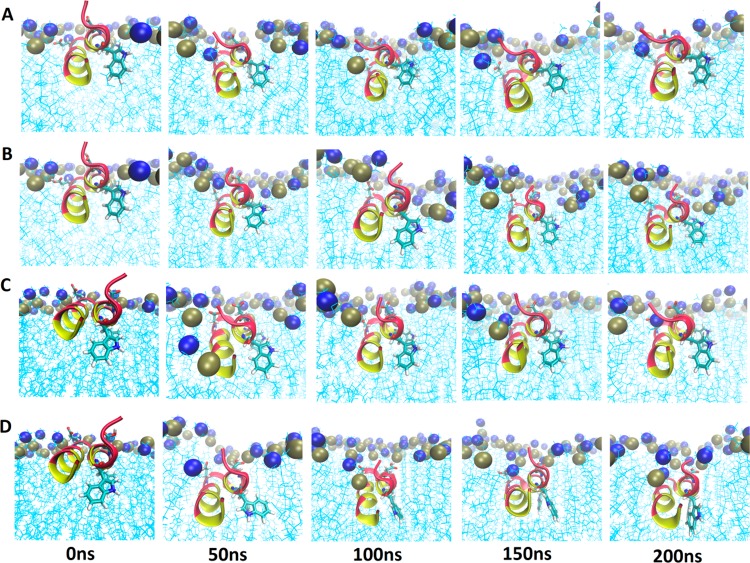
Figure 3 displays snapshots taken from the 200 ns trajectories. The snapshots at 0 ns represent the starting structures R0 and R20. Regardless of starting orientation, the final conformation and orientation are very similar, with the N-terminal helix (residues 1–11) more deeply buried into the nonpolar lipid interior, while the C-terminal helix is more exposed to headgroups and water. Previous explicit membrane studies on the HAFP20 straight helix and the kinked conformations have also demonstrated a more deeply inserted N-terminal end.22,23,27 Despite the deeper burial of the N-terminal helix, the N-terminus is solvent accessible; several water molecules penetrate the membrane interface and interact with it, consistent with the observed high water exchange rates (Figure 3C of ref (31)).

Figure 3.

Figure 3

Open in a new tab

Snapshots of HAFP hairpin from the 200 ns MD simulations on DMPC bilayer for starting orientations with rotation angle 20° (A,B) and 0° (C,D) at neutral pH (A,C) and low pH (B,D). Hydrophobic residues are highlighted in yellow and hydrophilic residues in red. The acidic groups (E11 and D19) are also illustrated. Tan spheres are phosphorus, and blue are nitrogen.

The average orientation of the hairpin is influenced by pH. Structures at neutral pH (Figure 3A,C) display greater rotation than structures at lower pH (Figure 3B,D). This is not surprising since the unprotonated acidic residues E11 and D19 at neutral pH experience repulsive interactions with the negatively charged phosphate groups and are more likely to form hydrogen bonds with water molecules, forcing a larger exposure of the C-terminal helix. Figure S1 (zoomed-in images) reveals interactions between protonated acidic residues at low pH with phosphate headgroups, stabilizing the hairpin just below the membrane surface. These differences in the interactions of protonated and unprotonated residues with their surroundings cause the C-terminal helix to insert more deeply at low pH, lowering the rotation angle. Similarly, previous studies have demonstrated that the HAFP structure is unaffected by changes in pH, while lower pH conditions allow HAFP to insert more deeply into the lipid bilayer.24,26,52

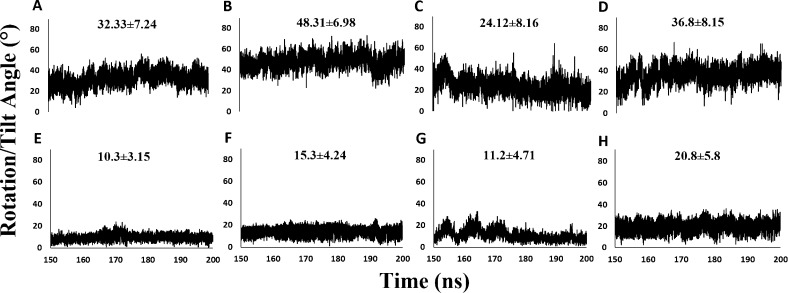
Rotation angles calculated over the trajectories support these qualitative observations (Figure 4). Final rotation angles of the R20 simulations at low pH (23.4°) were much lower than at neutral pH (48.3°). The same effect was observed in R0 simulations, with final rotation angles of 10.5 and 48.7° for low and neutral pH trajectories, respectively. Average values shown in Figure 4 confirm that the hairpin structure is more rotated under neutral pH conditions. To quantify the orientational fluctuations, standard deviations of rotation and tilt angles were also computed from the MD trajectories (Figure 4). Rotation angle fluctuations are larger than tilt angle fluctuations and similar regardless of initial structure. Tilt angle fluctuations were somewhat larger in the R0 simulation.

Figure 4.

Figure 4

Open in a new tab

Analysis of hairpin orientation with respect to the membrane. The angles between N–H bonds and the z axis were calculated over 200 ns MD trajectories. Rotation angles about the x axis are displayed in A–D and tilt angles about the y axis in E–H. Results from R20 simulations are shown in (A) low pH, (B) neutral pH, (E) low pH, and (F) neutral pH. Results from R0 simulations are shown in (C) low pH, (D) neutral pH, (G) low pH, and (H) neutral pH.

Membrane insertion depth (Figure 5) was calculated over the explicit and implicit simulations as the difference between the Cα of each residue in HAFP and the center of the membrane. Implicit membrane simulations show the same pattern, but residue depths are smaller. This is partly due to the value of hydrophobic membrane thickness used in the implicit simulations (25 Å), which is somewhat higher than the experimental thickness of DMPC bilayers (22.353 or 23.0 Å54). However, this accounts for only a small part of the discrepancy; the peptide does insert more deeply in the explicit simulations. Lowering the pH causes only a slightly deeper insertion of the C-terminal region in the explicit simulations.

Figure 5.

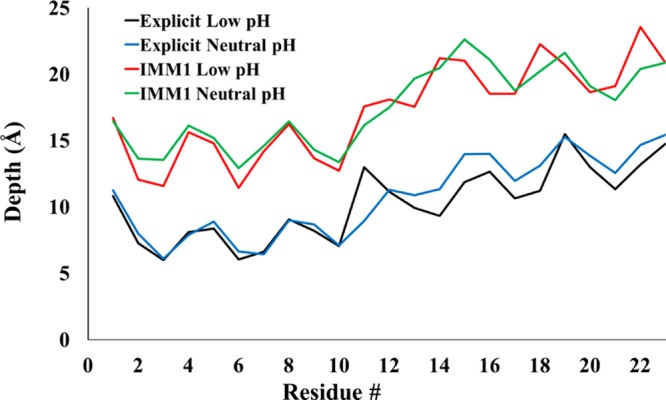
Figure 5

Open in a new tab

Membrane insertion depth (distance from membrane center) per residue calculated over implicit and explicit membrane simulations. Depths for explicit simulations (blue and black) were calculated by subtracting the average z-coordinate of each residue Cα from the average z-coordinate of lipid tail C13 and C14 atoms. Membranes are centered at the origin in implicit simulations; therefore, the average z-coordinate of each Cα is reported.

Lorieau et al. proposed that the hairpin structure is stabilized by interhelical CαH–O H bonds and an interaction between the charged N-terminal G1 with C-terminal backbone carbonyls.31,32 We calculated interaction energies over the last 50 ns of the explicit MD trajectories. The N-terminal and C-terminal helices were represented by residues 2–10 and 14–23, respectively. The average interhelical interaction energy was approximately −36 kcal/mol, of which about −11 kcal/mol is contributed by 8 CαH–OC hydrogen bonds (see Table S1 in Supporting Information). The average interaction energy between G1 and carbonyls of residues 20–23 was approximately −124 kcal/mol. These energies are highly favorable but do not include the desolvation energy, which is typically anticorrelated with Coulombic energy. The same interactions using IMM1 on the NMR structure, including desolvation energy, are more modest: −21 kcal/mol for the interhelical interaction and −12 kcal/mol for the G1 to 20–23 interaction. These calculations confirm the importance of the proposed favorable interactions.

Implicit Membrane Simulations

Using the IMM1 membrane model, membrane binding energies were calculated at various rotated states of the hairpin to determine the most favorable orientation. The NMR hairpin structure was placed at the membrane interface (z = 13 Å) and was rigidly rotated around the x axis in increments of 1° from 0 to 90°. For each configuration, the transfer energy from the membrane to bulk water was calculated. The negatives of these values are plotted in Figure 6 (negative values mean favorable membrane binding). Similar to the explicit DMPC simulations, these calculations show that hairpin structure favors a rotated rather than parallel orientation. The binding energy is most favorable at 31° rotation angle for both low and neutral pH simulations. This energy value (−7 kcal/mol) compares well to previous experimental17 (−7.2 kcal/mol) and theoretical25 (−8 to −10 kcal/mol) studies.

Figure 6.

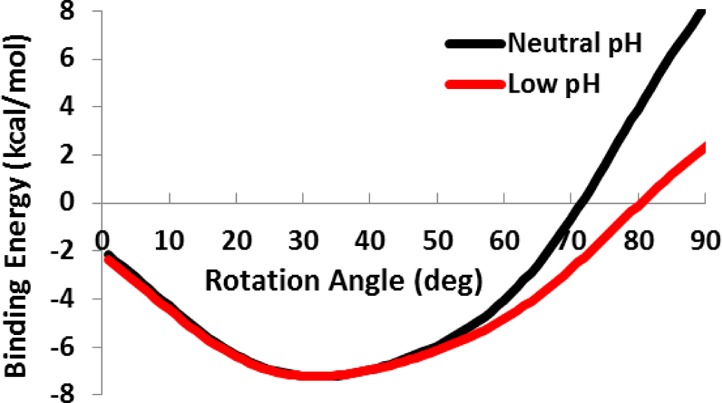
Figure 6

Open in a new tab

Water to membrane transfer energies calculated at rotation angles 0 to 90° at intervals of 1° at low (red) and neutral (black) pH.

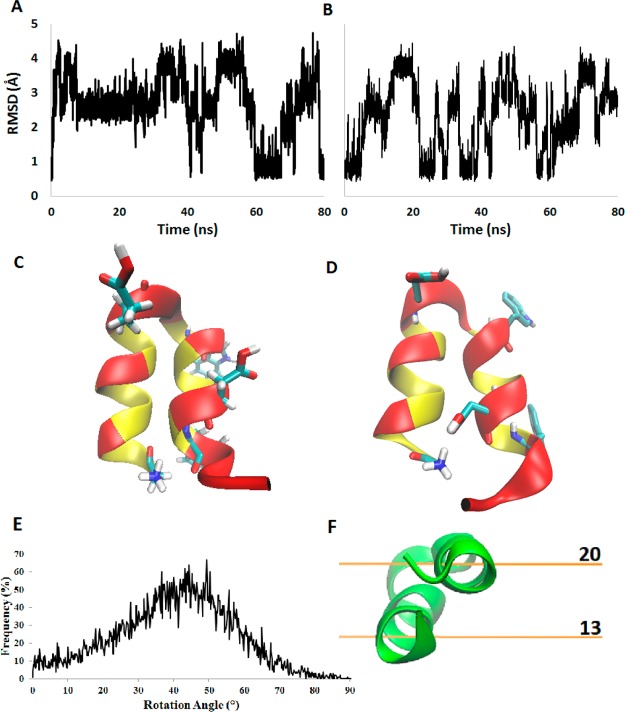
MD simulations of the HAFP23 hairpin structure using the IMM1 implicit membrane offer the opportunity of more extensive sampling of the conformations of the peptide without friction from explicit lipid and solvent molecules. Similar to the explicit DMPC simulations, IMM1 simulations demonstrate significant rotation burying the N-terminal helix (residues 1–11) into the nonpolar lipid interior more than the C-terminal helix (Figure 7F). The rotation angle exhibits a broad distribution, with a peak at about 45° (Figure 7E). Figure 7A,B shows the backbone rmsd over 100 ns of IMM1 MD simulations of the hairpin under low and neutral pH conditions. The deviations from the NMR structure observed here are significantly higher than in the explicit simulations, reaching over 5 Å. A sample structure of the hairpin at these higher rms deviations is shown in Figure 7D, featuring a strong interaction between D19 and G1, which distorts the hairpin. This interaction is more likely to be observed at low pH (Figure 7A), probably because the smaller desolvation cost of Asp at low pH allows it to be buried more deeply in the membrane. In both trajectories, the hairpin returns occasionally to the NMR structure. The strength of the D19–G1 interaction apparently is overestimated by the implicit model. The lack of direct interactions with solvent or membrane atoms can influence thermodynamic ensembles generated from implicit models.55

Figure 7.

Figure 7

Open in a new tab

IMM1 trajectory analysis. Root mean square deviations from the NMR structure over MD trajectories for backbone atoms in the HAFP hairpin. MD trajectories were simulated for 100 ns using the IMM1 implicit membrane with (A) protonated Glu/Asp and (B) unprotonated Glu/Asp. Hairpin structures resulting from (C) a 200 ns explicit simulation and (D) a 100 ns implicit simulation are displayed with acidic residues, tryptophan, and G1 residues highlighted. (E) Population of rotation angle values sampled over the low pH simulation. (F) Hairpin structure shown with relative membrane depth values (z axis).

To test the effect of peptide length on structure, 20 ns IMM1 simulations were performed of 20- and 23-residue peptides starting from either a linear helix or a hairpin. The final structures of these simulations are displayed in Figure S2. Starting from a linear helix, the HAFP20 remains a linear helix but HAFP23 changes to a structure reminiscent of the hairpin. Starting from the hairpin, the HAFP23 remains a hairpin but HAFP20 is much less stable. These results agree with the recent experimental finding that 23 residues are necessary to form a stable hairpin structure.35

Calculation of NMR Parameters

Lorieau et al.32 used 15N NMR relaxation in bicelles of different sizes to extract order parameters (S2), internal correlation times (τ), and relaxation rates (R1 and R2) for motion of HAFP23 with respect to the membrane. They found a rocking motion along the x and y axes with correlation times of 2.4 to 5.1 ns. Here, internal correlation functions (eq 3) of amide bond motion were obtained from the MD trajectories and were used to calculate the same NMR parameters. Order parameters (S2) were obtained from the plateau values, C(∞), of the autocorrelation functions and the correlation times from fitting these functions to the extended LS model (eq 4).

Table 1 compares NMR parameters obtained from the MD simulations to those obtained experimentally. Order parameters range from 0 to 1; a value of 1 corresponds to no internal motion, and a value of 0 indicates unrestrained motion. The S2 values calculated for rotation motions (around the x axis) are all similar (1–6% error) to those measured by NMR. However, S2 values calculated for tilting motions are significantly higher (20–25% error) than the NMR values. In our simulations of HAFP23, there is more rotation than tilting, as can also be observed in the orientation analysis (Figures 3 and 4), whereas the opposite is inferred from the NMR experiments. Correlation times generated from our MD simulations are of the same order of magnitude as the experimental results for both x and y axis rotations. Order parameters calculated from the IMM1 simulations are similar to explicit simulation values for tilting but lower for rotation. The correlation times are of similar order of magnitude. Figure 8 shows correlation functions for rotation around the x axis from the explicit simulations. The curves for the R0 simulations are not completely flat by 15 ns, likely because these simulations started at an orientation far from optimal.

Table 1. NMR Parameters from MD Trajectories.

  x axis
 y axis
  S2 τ (ns) R2 (s–1) R1 (s–1) S2 τ (ns) R2 (s–1) R1 (s–1)
NAMD R20                
low pH 0.88 5.83 42.98 0.26 0.89 5.66 45.78 0.25
neutral pH 0.85 2.53 43.92 0.24 0.88 4.68 45.34 0.25
NAMD R0                
low pH 0.81 5.27 41.92 0.24 0.89 5.66 44.22 0.25
neutral pH 0.86 2.47 43.68 0.25 0.85 7.60 44.6 0.25
IMM1 R20                
low pH 0.71 3.68 31.28 0.06 0.88 6.22 33.71 0.16
neutral pH 0.69 4.57 26.34 0.5 0.85 7.55 36.6 0.67
                 
NMR neutral pH 0.8 2.4 48 0.74 0.71 5.1 34.5 0.8
Open in a new tab

Figure 8.

Figure 8

Open in a new tab

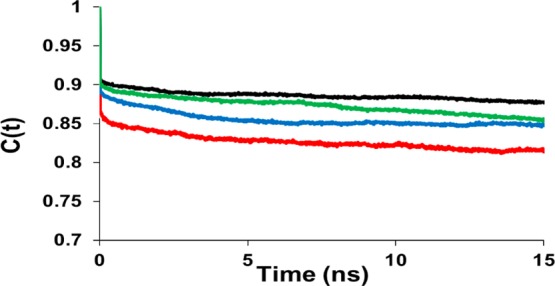
Correlation functions for rotation (x axis). The analysis was carried out for trajectories of R20 at low pH (black) and neutral pH (blue), R0 at low pH (red) and neutral pH (green).

Table 1 includes relaxation rates calculated over explicit and implicit MD trajectories. Calculated R2 relaxation rates from MD simulations are slightly lower than experiment for rotation around the x axis but significantly higher than experiment for rotation around the y axis. Like the S2 parameter, this signifies much lower mobility for tilting than experiment suggests. Lorieau et al. determined R1 to be approximately 0.8 for all amide bonds when the largest bicelle was used (DMPC/DHPC ratio 0.69). The R1 values calculated from MD simulations were significantly lower, around 0.25 for the explicit simulations. R1 rates are more difficult to interpret in terms of motion.

Atomic Contacts and NOE Intensities

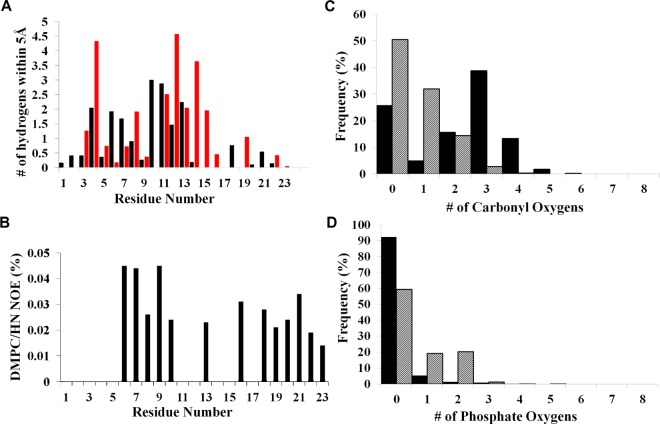
In the NMR experiments, NOE measurements were used to estimate intermolecular distances for interhelical interactions (CαH–O) as well as peptide–lipid interactions in DPC micelles31 and DMPC bicelles.32 These NOE measurements detected contacts between HAFP backbone amide protons and lipid tail protons. Greater intensities with the lipid tail groups of the DPC micelles were observed for backbone amide protons from the N-terminal helix than the C-terminal helix (Figure S5 of ref (31)), which indicates that the N-terminal helix is more inserted in the micelle than the C-terminal helix, consistent with the simulation results. A more detailed comparison can be made between the computational and experimental results in bicelles.32 Interactions between backbone amides of the peptide and hydrophobic tails of the phospholipid molecules were determined over the 200 ns simulations. An approximate estimation was performed for comparison with NMR NOE calculations by counting the number of atoms within 5 Å of backbone amide hydrogens over the last 50 ns of the 200 ns R20 simulations. Calculations are presented for low (black bars) and neutral pH (red bars) simulations (Figure 9A). The atomic contact count reflects the deeper insertion of the hydrophobic N-terminal helix, in agreement with Figure 3. These contact counts correlate to some extent with NOE intensities from NMR measurements of HAFP23 on DMPC bicelles at neutral pH (Figure 9B).32 NOE measurements show that the N-terminal helix exhibits stronger NOE intensities than the C-terminal helix, although the differences seem smaller than those in the contact counts obtained in the simulation.

Figure 9.

Figure 9

Open in a new tab

Interactions between peptide and lipid atoms. (A) Number of atomic contacts between peptide backbone hydrogens and lipid tail hydrogens within 5 Å at low (black) and neutral (red) pH in the simulations. (B) Experimental NOE interaction intensities for the HAFP backbone hydrogen with methylene hydrogen of the DMPC lipid tail.32 (C) Hydrogen bonds between tryptophan indole hydrogens and lipid headgroup carbonyl oxygens. (D) Hydrogen bonds between tryptophan indole hydrogens and lipid headgroup phosphate oxygens. Solid black refers to the simulations at low pH and gray to those at neutral pH.

It is established that TRP residues within membrane proteins form H bonds with polar atoms of phosphocholine headgroups, stabilizing peptides at the water–membrane interface.56,57 Tamm and co-workers demonstrated the significance of residue W14 in the membrane binding energies and fusogenicity of HAFP20.18 Computational studies have shown that the W14A mutant of HAFP20 is more flexible and more likely to vary between a linear, kinked, and hairpin structures.23,27 This suggests that residue W14 is significant in the structural integrity of HAFP and specific interactions formed with the headgroup region. In our analysis of tryptophan interactions with the membrane, we characterized favorable interactions (hydrogen bond or Coulombic) as the number of phosphate or carbonyl oxygen atoms in proximity of the indole hydrogens of W14 and W21. Overall, interactions with the carbonyl oxygens are more frequent than those with the phosphate (Figure 9C,D). In addition, the interactions with the carbonyls increase in the low pH simulations, while those with the phosphate decrease, consistent with a slightly deeper insertion of the C-terminal helix in the low pH simulations (Figure 5).

Discussion

In this work, we aimed to characterize the interaction of the hemagglutinin fusion peptide hairpin structure with the membrane, complementing the recent NMR work from the Bax group.31−35 We performed both explicit and implicit membrane molecular dynamics simulations of the 23 N-terminal residues of HA2 starting from the NMR structure31 with different starting orientations. Our main findings are the following: (a) the hairpin is stable on a time scale of 200 ns, with a backbone rmsd close to 1 Å; (b) the N-terminal helix is buried more deeply in the membrane than the C-terminal helix; and (c) low pH (emulated by protonating E11 and D19) leads to a less rotated structure with deeper insertion of the C-terminal helix.

To our knowledge, this is the first study that compares simulation-derived NMR parameters with experiment for a peptide’s movement with respect to the membrane plane. This comparison for the HAFP hairpin under study here is generally favorable. However, there are some discrepancies. The values of the S2 order parameter for motion around the x axis are quite similar to the NMR results, but the values for motion around the y axis are significantly higher. That is, tilting motion is much more limited in the simulations than the NMR results suggest. This could possibly be explained if the peptide bound to the edges of the bicelle with the y axis perpendicular to the bicelle perimeter. However, there is no evidence to suggest that. In fact, no NOEs were detected between the peptide and the DHPC lipids, which predominantly occupy the bicelle edges (Figure S6 of ref (33)). It is also difficult to imagine how force field deficiencies could be responsible for this discrepancy. Thus, we cannot offer a specific explanation for the overestimation of the y axis S2 parameter at this point, except to point out possible limitations of the model-free formalism.40 There are also some discrepancies in the R1 relaxation rates that are difficult to explain.

Recent work showed that low pH destabilizes the hairpin structure, favoring more open structures.34 Our simulations are too short to detect a slight shift in equilibrium between closed and open structures. The origin of destabilization of the hairpin at low pH is not clear, but it should involve the two acidic residues (the experimental peptide constructs include a basic sequence beyond residue 23, which moves the C-terminus far from the hairpin structure). A weak interaction of E11 and/or D19 with the N-terminus, as seen in the implicit membrane simulations, could explain the destabilization of the hairpin at low pH. Such a structure might correspond to a minor population that does not give rise to NOEs.

The role of tryptophan in orienting proteins in membrane bilayers has been studied extensively.56,58,59 It is established that the W14A mutant is not fusogenic,17 and many studies correlate this lack of function with differences in structure between W14A and wild type.17,18,23,27 NOE measurements detected contacts between TRP indole and choline methyl hydrogens of the DPC micelle.31 Due to conservation of W14 and W21 over the influenza A hemagglutinin subtypes, it was proposed31 that these TRP residues have a role in positioning the fusion peptide at the membrane–water interface. Structures of HAFP23 generated with the present MD simulations are shown in Figure 3, highlighting residues W14 and W21 within the lipid bilayer. The number of contacts formed between the TRP indole hydrogen of residues 14 and 21 and H bond acceptors of the headgroup region is significant, as shown in Figure 9C. The observed HAFP hairpin orientation is likely to be determined in part by these interactions.

The role of peptide structure in the fusion process remains unclear. The recent NMR studies have shown that the more biologically relevant 23-residue HAFP peptide forms a hairpin. The present simulations confirm the stability of the hairpin and add information on its orientation with respect to the membrane. The hairpin, however, is destabilized toward more open structures at pH values relevant to endosomes.34 In addition, the shorter 20-residue peptides, which adopt more extended structures16,35 but also exhibit a minor population of the hairpin,35 exhibit fusogenic activity.13,17,18 This raises the question what is the role of the two structures and whether it is the process of transitioning between the two that plays a role in fusion. A convincing answer to this question is still lacking.

Acknowledgments

This work was supported by the NSF (MCB 1244207). Infrastructure support was provided in part by RCMI Grant 2G12RR03060-26A1/8G12MD007603-27 from NIH. Computing resources of the CUNY HPC center were utilized for the explicit simulations. We are deeply grateful to Dr. Justin Lorieau and Dr. Ad Bax for discussions, sharing unpublished data, and comments on the manuscript. We also thank Dr. Matthias Buck, Dr. Ranajeet Ghose, and Dr. Paul Maragakis for discussions regarding NMR theory and computation of NMR parameters.

Supporting Information Available

Four figures and one table. This material is available free of charge via the Internet at http://pubs.acs.org.

The authors declare no competing financial interest.

Funding Statement

National Institutes of Health, United States

Supplementary Material

jp409412g_si_001.pdf (665.7KB, pdf)

References

  1. White J. M. Membrane Fusion. Science 1992, 258, 917–924. [DOI] [PubMed] [Google Scholar]
  2. Eckert D. M.; Kim P. S. Mechanisms of Viral Membrane Fusion and Its Inhibition. Annu. Rev. Biochem. 2001, 70, 777–810. [DOI] [PubMed] [Google Scholar]
  3. Weissenhorn W.; Hinz A.; Gaudin Y. Virus Membrane Fusion. FEBS Lett. 2007, 581, 2150–2155. [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Skehel J. J.; Wiley D. C. Receptor Binding and Membrane Fusion in Virus Entry: The Influenza Hemagglutinin. Annu. Rev. Biochem. 2000, 69, 531–569. [DOI] [PubMed] [Google Scholar]
  5. Luo M. Influenza Virus Entry. Adv. Exp. Med. Biol. 2012, 726, 201–221. [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Wilson I. A.; Skehel J. J.; Wiley D. C. Structure of the Haemagglutinin Membrane Glycoprotein of Influenza Virus at 3 Å Resolution. Nature 1981, 289, 366–373. [DOI] [PubMed] [Google Scholar]
  7. Bullough P. A.; Hughson F. M.; Skehel J. J.; Wiley D. C. Structure of Influenza Haemagglutinin at the pH of Membrane Fusion. Nature 1994, 371, 37–43. [DOI] [PubMed] [Google Scholar]
  8. Chen J.; Skehel J. J.; Wiley D. C. N- and C-Terminal Resiudes Combine in the Fusion-pH Influenza Hemagglutinin HA2 Subunit To Form an N Cap That Terminates the Triple-Stranded Coiled Coil. Proc. Natl. Acad. Sci. U.S.A. 1999, 96, 8967–8972. [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Madhusoodanan M.; Lazaridis T. Investigation of Pathways for the Low-pH Conformational Transition in Influenza Hemagglutinin. Biophys. J. 2003, 84, 1926–1939. [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. Cross K. J.; Langley W. A.; Russell R. J.; Skehel J. J.; Steinhauer D. A. Composition and Functions of the Influenza Fusion Peptide. Protein Pept. Lett. 2009, 16, 766–778. [DOI] [PubMed] [Google Scholar]
  11. Gething M. J.; Doms R. W.; York D.; White J. Studies on the Mechanism of Membrane Fusion: Site-Specific Mutagenesis of the Hemagglutinin of Influenza Virus. J. Cell Biol. 1986, 102, 11–23. [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Qiao H.; Armstrong R. T.; Melikyan G. B.; Cohen F. S.; White J. M. A Specific Point Mutant at Position 1 of the Influenza Hemagglutinin Fusion Peptide Displays a Hemifusion Phenotype. Mol. Biol. Cell 1999, 10, 2759–2769. [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Lear J. D.; DeGrado W. F. Membrane Binding and Conformational Properties of Peptides Representing the NH2 Terminus of Influenza HA2. J. Biol. Chem. 1987, 262, 6500–6505. [PubMed] [Google Scholar]
  14. Murata M.; Sugahara Y.; Takahashi S.; Ohnishi S. pH-Dependent Membrane-Fusion Activity of a Synthetic 20 Amino-Acid Peptide with the Same Sequence as That of the Hydrophobic Segment of Influenza-Virus Hemagglutinin. J. Biochem. 1987, 102, 957–962. [DOI] [PubMed] [Google Scholar]
  15. Rafalski M.; Ortiz A.; Rockwell A.; Van Ginkel L. C.; Lear J. F.; DeGrado W. F.; Wilschut J. Membrane Fusion Activity of the Influenza Virus Hemagglutinin: Interaction of HA2 N-Terminal Peptides with Phospholipid Vesicles. Biochemistry 1991, 30, 10211–10220. [DOI] [PubMed] [Google Scholar]
  16. Han X.; Bushweller J. H.; Cafiso D. S.; Tamm L. K. Membrane Structure and Fusion-Triggering Conformational Change of the Fusion Domain from Influenza Hemagglutinin. Nat. Struct. Biol. 2001, 8, 715–720. [DOI] [PubMed] [Google Scholar]
  17. Lai A. L.; Park H.; White J. M.; Tamm L. K. Fusion Peptide of Influenza Hemagglutinin Requires a Fixed Angle Boomerang Structure for Activity. J. Biol. Chem. 2006, 281, 5760–5770. [DOI] [PubMed] [Google Scholar]
  18. Lai A. L.; Tamm L. K. Locking the Kink in the Influenza Hemagglutinin Fusion Domain Structure. J. Biol. Chem. 2007, 282, 23946–23956. [DOI] [PubMed] [Google Scholar]
  19. Sun Y.; Weliky D. P. 13C–13C Correlation Spectroscopy of Membrane-Associated Influenza Virus Fusion Peptide Strongly Supports a Helix-Turn-Helix Motif and Two Turn Conformations. J. Am. Chem. Soc. 2009, 131, 13228–13229. [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. Huang Q.; Chen C. L.; Herrmann A. Bilayer Conformation of Fusion Peptide of Influenza Virus Hemagglutinin: A Molecular Dynamics Simulation Study. Biophys. J. 2004, 87, 14–22. [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. Lague P.; Roux B.; Pastor R. W. Molecular Dynamics Simulations of the Influenza Hemagglutinin Fusion Peptide in Micelles and Bilayers: Conformational Analysis of Peptide and Lipids. J. Mol. Biol. 2005, 354, 1129–1141. [DOI] [PubMed] [Google Scholar]
  22. Vaccaro L.; Cross K. J.; Kleinjung J.; Straus S. K.; Thomas D. J.; Wharton S. A.; Skehel J. J.; Fraternali F. Plasticity of Influenza Haemagglutinin Fusion Peptides and Their Interaction with Lipid Bilayers. Biophys. J. 2005, 88, 25–36. [DOI] [PMC free article] [PubMed] [Google Scholar]
  23. Li J. Y.; Das P.; Zhou R. H. Single Mutation Effects on Conformational Change and Membrane Deformation of Influenza Hemagglutinin Fusion Peptides. J. Phys. Chem. B 2010, 114, 8799–8806. [DOI] [PubMed] [Google Scholar]
  24. Sammalkorpi M.; Lazaridis T. Configuration of Influenza Hemagglutinin Fusion Peptide Monomers and Oligomers in Membranes. Biochim. Biophys. Acta 2007, 1768, 30–38. [DOI] [PubMed] [Google Scholar]
  25. Bechor D.; Ben-Tal N. Implicit Solvent Model Studies of the Interactions of the Influenza Hemagglutinin Fusion Peptide with Lipid Bilayers. Biophys. J. 2001, 80, 643–655. [DOI] [PMC free article] [PubMed] [Google Scholar]
  26. Panahi A.; Feig M. Conformational Sampling of Influenza Fusion Peptide in Membrane Bilayers as a Function of Termini and Protonation States. J. Phys. Chem. B 2010, 114, 1407–1416. [DOI] [PubMed] [Google Scholar]
  27. Legare S.; Lague P. The Influenza Fusion Peptide Adopts a Flexible Flat V Conformation in Membranes. Biophys. J. 2012, 102, 2270–2278. [DOI] [PMC free article] [PubMed] [Google Scholar]
  28. Jang H.; Michaud-Agrawal N.; Johnston J. M.; Woolf T. B. How To Lose a Kink and Gain a Helix: pH Independent Conformational Changes of the Fusion Domains from Influenza Hemagglutinin in Heterogeneous Lipid Bilayers. Proteins 2008, 72, 299–312. [DOI] [PubMed] [Google Scholar]
  29. Fuhrmans M.; Marrink S. J. Molecular View of the Role of Fusion Peptides in Promoting Positive Membrane Curvature. J. Am. Chem. Soc. 2012, 134, 1543–1552. [DOI] [PubMed] [Google Scholar]
  30. Larsson P.; Kasson P. M. Lipid Tail Protrusion in Simulations Predicts Fusogenic Activity of Influenza Fusion Peptide Mutants and Conformational Models. PLoS Comp. Biol. 2013, 9, e1002950. [DOI] [PMC free article] [PubMed] [Google Scholar]
  31. Lorieau J. L.; Louis J. M.; Bax A. The Complete Influenza Hemagglutinin Fusion Domain Adopts a Tight Helical Hairpin Arrangement at the Lipid:Water Interface. Proc. Natl. Acad. Sci. U.S.A. 2010, 107, 11341–11346. [DOI] [PMC free article] [PubMed] [Google Scholar]
  32. Lorieau J. L.; Louis J. M.; Bax A. Helical Hairpin Structure of Influenza Hemagglutinin Fusion Peptide Stabilized by Charge-Dipole Interactions between the N-Terminal Amino Group and the Second Helix. J. Am. Chem. Soc. 2011, 133, 2824–2827. [DOI] [PMC free article] [PubMed] [Google Scholar]
  33. Lorieau J. L.; Louis J. M.; Bax A. Whole-Body Rocking Motion of a Fusion Peptide in Lipid Bilayers from Size-Dispersed 15N NMR Relaxation. J. Am. Chem. Soc. 2011, 133, 14184–14187. [DOI] [PMC free article] [PubMed] [Google Scholar]
  34. Lorieau J. L.; Louis J. M.; Schwieters C. D.; Bax A. pH-Triggered, Activated-State Conformations of the Influenza Hemagglutinin Fusion Peptide Revealed by Nmr. Proc. Natl. Acad. Sci. U.S.A. 2012, 109, 19994–19999. [DOI] [PMC free article] [PubMed] [Google Scholar]
  35. Lorieau J. L.; Louis J. M.; Bax A. Impact of Influenza Hemagglutinin Fusion Peptide Length and Viral Subtype on Its Structure and Dynamics. Biopolymers 2013, 99, 189–195. [DOI] [PMC free article] [PubMed] [Google Scholar]
  36. Lazaridis T. Effective Energy Function for Proteins in Lipid Membranes. Proteins 2003, 52, 176–192. [DOI] [PubMed] [Google Scholar]
  37. Lipari G.; Szabo A.; Levy R. M. Protein Dynamics and NMR Relaxation: Comparison of Simulations with Experiment. Nature 1982, 300, 197–198. [Google Scholar]
  38. Palmer A. G.; Case D. A. Molecular-Dynamics Analysis of NMR Relaxation in a Zinc-Finger Peptide. J. Am. Chem. Soc. 1992, 114, 9059–9067. [Google Scholar]
  39. Chatfield D. C.; Szabo A.; Brooks B. R. Molecular Dynamics of Staphylococcal Nuclease: Comparison of Simulation with 15N and 13C NMR Relaxation Data. J. Am. Chem. Soc. 1998, 120, 5301–5311. [Google Scholar]
  40. Chen J. H.; Brooks C. L.; Wright P. E. Model-Free Analysis of Protein Dynamics: Assessment of Accuracy and Model Selection Protocols Based on Molecular Dynamics Simulation. J. Biomol. NMR 2004, 29, 243–257. [DOI] [PubMed] [Google Scholar]
  41. Maragakis P.; Lindorff-Larsen K.; Eastwood M. P.; Dror R. O.; Klepeis J. L.; Arkin I. T.; Jensen M. O.; Xu H. F.; Trbovic N.; Friesner R. A.; et al. Microsecond Molecular Dynamics Simulation Shows Effect of Slow Loop Dynamics on Backbone Amide Order Parameters of Proteins. J. Phys. Chem. B 2008, 112, 6155–6158. [DOI] [PMC free article] [PubMed] [Google Scholar]
  42. Phillips J. C.; Braun R.; Wang W.; Gumbart J.; Tajkhorshid E.; Villa E.; Chipot C.; Skeel R. D.; Kale L.; Schulten K. Scalable Molecular Dynamics with Namd. J. Comput. Chem. 2005, 26, 1781–1802. [DOI] [PMC free article] [PubMed] [Google Scholar]
  43. Klauda J. B.; Venable R. M.; Freites J. A.; O’Connor J. W.; Tobias D. J.; Mondragon-Ramirez C.; Vorobyov I.; MacKerell A. D. Jr.; Pastor R. W. Update of the Charmm All-Atom Additive Force Field for Lipids: Validation on Six Lipid Types. J. Phys. Chem. B 2010, 114, 7830–7843. [DOI] [PMC free article] [PubMed] [Google Scholar]
  44. Jo S.; Kim T.; Iyer V. G.; Im W. CHARMM-GUI: A Web-Based Grraphical User Interface for Charmm. J. Comput. Chem. 2008, 29, 1859–1865. [DOI] [PubMed] [Google Scholar]
  45. Jo S.; Lim J. B.; Klauda J. B.; Im W. CHARMM-GUI Membrane Builder for Mixed Bilayers and Its Application to Yeast Membranes. Biophys. J. 2009, 97, 50–58. [DOI] [PMC free article] [PubMed] [Google Scholar]
  46. Jorgensen W. L.; Chandrasekhar J.; Madura J. D.; Impey R. W.; Klein M. L. Comparison of Simple Potential Functions for Simulating Liquid Water. J. Chem. Phys. 1983, 79, 926–935. [Google Scholar]
  47. Humphrey W.; Dalke A.; Schulten K. VMD: Visual Molecular Dynamics. J. Mol. Graphics Modell. 1996, 14, 33–38. [DOI] [PubMed] [Google Scholar]
  48. Darden T.; York D.; Pedersen L. Particle Mesh Ewald: An N·Log(N) Method for Ewald Sums in Large Systems. J. Chem. Phys. 1993, 98, 10089–10092. [Google Scholar]
  49. Lazaridis T.; Karplus M. Effective Energy Function for Proteins in Solution. Proteins 1999, 35, 133–152. [DOI] [PubMed] [Google Scholar]
  50. Case D. A. Molecular Dynamics and NMR Spin Relaxation in Proteins. Acc. Chem. Res. 2002, 35, 325–331. [DOI] [PubMed] [Google Scholar]
  51. Bruschweiler R.; Roux B.; Blackledge M.; Griesinger C.; Karplus M.; Ernst R. R. Influence of Rapid Intramolecular Motion on NMR Cross-Relaxation Rates: A Molecular-Dynamics Study of Antamanide in Solution. J. Am. Chem. Soc. 1992, 114, 2289–2302. [Google Scholar]
  52. Zhou Z.; Macosko J. C.; Hughes D. W.; Sayer B. G.; Hawes J.; Epand R. M. 15N NMR Study of the Ionization Properties of the Influenza Virus Fusion Peptide in Zwitterionic Phospholipid Dispersions. Biophys. J. 2000, 78, 2418–2425. [DOI] [PMC free article] [PubMed] [Google Scholar]
  53. Rand R. P.; Parsegian V. A. Hydration Forces between Phospholipid Bilayers. Biochim. Biophys. Acta 1989, 988, 351–376. [Google Scholar]
  54. Lewis B. A.; Engelman D. M. Lipid Bilayer Thickness Varies Linearly with Acyl Chain-Length in Fluid Phosphatidylcholine Vesicles. J. Mol. Biol. 1983, 166, 211–217. [DOI] [PubMed] [Google Scholar]
  55. Brice A. R.; Dominy B. N. Examining Electrostatic Influences on Base-Flipping: A Comparison of TIP3P and GB Solvent Models. Commun. Comput. Phys. 2013, 13, 223–237. [Google Scholar]
  56. Kachel K.; Asuncionpunzalan E.; London E. Anchoring of Tryptophan and Tyrosine Analogs at the Hydrocarbon Polar Boundary in Model Membrane-Vesicles: Parallax Analysis of Fluorescence Quenching Induced by Nitroxide-Labeled Phospholipids. Biochemistry 1995, 34, 15475–15479. [DOI] [PubMed] [Google Scholar]
  57. de Planque M. R. R.; Kruijtzer J. A. W.; Liskamp R. M. J.; Marsh D.; Greathouse D. V.; Koeppe R. E.; de Kruijff B.; Killian J. A. Different Membrane Anchoring Positions of Tryptophan and Lysine in Synthetic Transmembrane α-Helical Peptides. J. Biol. Chem. 1999, 274, 20839–20846. [DOI] [PubMed] [Google Scholar]
  58. Sun H.; Greathouse D. V.; Andersen O. S.; Koeppe R. E. The Preference of Tryptophan for Membrane Interfaces: Insights from N-Methylation of Tryptophans in Gramicidin Channels. J. Biol. Chem. 2008, 283, 22233–22243. [DOI] [PMC free article] [PubMed] [Google Scholar]
  59. Al-Abdul-Wahid M. S.; DeMill C. M.; Serwin M. B.; Prosser R. S.; Stewart B. A. Effect of Juxtamembrane Tryptophans on the Immersion Depth of Synaptobrevin, an Integral Vesicle Membrane Protein. Biochim. Biophys. Acta 2012, 1818, 2994–2999. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

jp409412g_si_001.pdf (665.7KB, pdf)

Articles from The Journal of Physical Chemistry. B are provided here courtesy of American Chemical Society

RESOURCES