Skip to main content
PMC home page
NIHPA Author Manuscripts logoLink to NIHPA Author Manuscripts
. Author manuscript; available in PMC: 2014 May 6.
Published in final edited form as: Exp Brain Res. 2011 Mar 3;210(0):643–649. doi: 10.1007/s00221-011-2600-8

Variation in response dynamics of regular and irregular vestibular-nerve afferents during sinusoidal head rotations and currents in the chinchilla

Kyu-Sung Kim 1, Lloyd B Minor 2, Charles Della Santina 2, David M Lasker 2
PMCID: PMC4010622  NIHMSID: NIHMS571868  PMID: 21369854

Abstract

In mammals, primary vestibular afferents that innervate only type I hair cells (calyx-only afferents) respond nearly in phase with head acceleration for high-frequency motion, whereas afferents that innervate both type I and type II (dimorphic) or only type II (bouton-only) hair cells respond more in phase with head velocity. Afferents that exhibit irregular background firing rates have a larger phase lead re head velocity than those that fire more regularly. We wanted to examine what is the cause of the variation in phase lead between regular and irregular afferents at high frequency head rotations. Under the assumption that externally applied galvanic currents act directly on the nerve, we derived a transfer function describing the dynamics of a semicircular canal and its hair cells through comparison of responses to sinusoidally modulated head velocity and currents. All afferent responses were well fit with a transfer function with one zero (lead term). Best-fit lead terms describing responses to current for each group of afferents were similar to the lead term describing responses to head velocity for regular afferents (0.006s + 1). This shows that the pre synaptic/synaptic inputs to regular afferents are pure velocity transducers. However, the variation in phase lead between regular and irregular afferents cannot be explained solely by the ratio of type I to II hair cells (Baird et al. 1988) suggesting that the variation is caused by a combination of pre- (type of hair cell) and post- synaptic properties.

INTRODUCTION

Cupular displacement within the semicircular canals provides a representation of the angular motion of the head. Steinhausen (1933) first proposed that cupular displacement relative to head acceleration could be represented by a torsion-pendulum model based on the fluid dynamics of the semicircular canals. One prediction from this model was that cupular displacement should be in phase with head velocity for a mid-band range of frequencies (~0.2 – 2 Hz in chinchillas). Subsequent studies in mammals (Goldberg and Fernandez, 1971; Anderson et al., 1978; Baird et al., 1988; Sadeghi et al., 2007; Yang and Hullar, 2007; Lasker et al., 2008; Park et al., 2010), fish (Highstein and Baker, 1985; Boyle and Highstein, 1990), reptiles (Brichta and Goldberg, 1998), amphibians (Blanks and Precht, 1976) and birds (Li and Correia, 1998) have shown that at these mid-frequencies of head rotation, some groups of canal afferents do fire nearly in proportion to head velocity as Steinhausen predicted. However, at higher frequencies of head rotation the torsion-pendulum model predicts that the sensitivity of vestibular afferents should begin to decrease and lag head velocity. Single unit experiments have shown that there is a deviation from what canal mechanical models predict and how vestibular afferents actually behave. In mammals, the sensitivity of afferents increases and leads head velocity more than predicted by mechanical models alone, so that they effectively encode a combination of head acceleration and velocity (Goldberg and Fernandez, 1971; Baird et al., 1988; Sadeghi et al., 2007; Lasker et al., 2008; Park et al., 2010). Because of this deviation from what is predicted by the mechanical model and the dynamics of vestibular afferents it has been suggested that this differentiation of cupular motion may be occurring downstream from the mechanical transduction at either the level of the hair cell, synapse or axon.

Intracellular experiments in the toad fish have shown that the high frequency lead appears when stimulating hair cells directly and so the hair cell may be a likely candidate for this lead term. (Highstein et al. 1996). In mammals there are two types of vestibular hair cells. Each of these classes of hair cells has a distinctive pattern of afferent ending onto the hair cell. Type I hair cells are innervated by calyx bearing axons, which are identified by their chalice shape that encloses the body of the hair cell. Type II hair cells are distinguished by bouton endings, which do not surround the hair cell, but rather synapse on to the distal end of the hair cell. These two types of hair cells form three different vestibular-afferent classes. Calyx-only afferents are innervated by type I hair cells, bouton-only afferents innervate only type II hair cells, and dimorphic afferents are innervatedby both hair cell types (Goldberg et al., 1990).

Using a combination of intracellular labeling and extracellular recording, Baird et al. (1988) showed in the chinchilla that there are distinct differences in the physiology between these three afferent classes. One important factor that varies between the different afferent classes is the regularity of the afferent’s resting discharge rate. This regularity of spontaneous activity is measured by the coefficient of variation (CV) which is defined as the standard deviation of the resting interspike interval divided by the mean of the interspike interval of that resting activity. In order to account for the dependence of CV on resting rate, CV has been normalized to a single resting rate (CV*, see Methods and Baird et al. 1988) Calyx-only afferents have action potentials that fire at very irregular rates when firing spontaneously (CV* > 0.2). In addition, these afferents have low sensitivity to angular head velocity at rotations of 2 Hz. Bouton-only afferents have very regular static discharge rates (CV* < 0.1) that also have a low sensitivity to head velocity at 2 Hz. Dimorphic afferents encompass a wide range of static discharge characteristics; some are regularly discharging while others are irregularly discharging. Dimorphic afferents also show a correlation between the discharge regularity and the sensitivity to head velocity at 2 Hz head rotation.

It was later shown in the chinchilla (Hullar et al., 2005) and rhesus monkey (Sadeghi et al., 2007) that the phase lead was largest in calyx-only afferents.. Because calyx-only afferents only innervate type I hair cells, a possible hypothesis is that the type I hair cell is a marker for the mechanism that provides the phase lead with respect to head velocity at high frequencies. Goldberg et al. (1984) have previously shown that externally applied galvanic currents bypass the hair cell and synapse to stimulate the axon directly. Although, recent reports (Aw et al. 2008, 2010, Todd et al. 2010) have conjectured that external current acts on hair cells rather than afferents. We do not believe that this is the case and discuss the implications in the discussion. The goal of this study was to test whether type I hair cells are a marker for the mechanism for increasing phase lead by stimulating the vestibular nerve directly with electric current with high-frequency (2-20 Hz) sinusoidal currents. We then calculated the synaptic output of type I hair cells by dividing the average response of calyx-only afferents with respect to head rotation by the response of calyx-only afferents with respect to current. We show that the synaptic output from type I hair cells innervated by calyx-only afferents have a much larger lead response than the type I hair cells innervated by dimorphic afferents. Because of this a simple linear combination of the synaptic output from type I and II hair cells does not explain the variation in phase lead at high frequencies for the different classes of canal afferents?

METHODS

Surgical Procedures

All surgical and experimental procedures were approved by the Johns Hopkins University School of Medicine Animal Care and Use Committee. Data were obtained from 15 chinchillas anesthetized with 0.3ml/kg solution of 5,5-diallylbarbituric acid (Dial) (Fernandez et al. 1988). The vestibular nerve was approached through a hole through the mastoid bulla. The animals were maintained with a core body temperature of 36 -37° C via an external servomechanism (FHC, model 40-90-8B). During the experiment, saline (5 % of bw) was injected subcutaneously and the heart and respiratory rate was monitored to maintain good physiologic status. An otologic drill was used to access the eighth nerve complex anteromedial to the ampullae of the horizontal and superior semicircular canals. Glass micropipettes (WPI, model M1B100F-4) with impedances of 20-60 MOhms were filled with 3 M NaCl and adjusted into position over the nerve using a minimanipulator (You, model US-3F). In 7 of the 15 animals a silver-stimulating electrode with chloride tip was placed in the perilymphatic space of the vestibule. Electrical stimulating electrodes consisted of silver wire (0.25mm diameter), insulated with Teflon to within 1.0 mm of their tips, which were chlorided. A transtympanic approach was made into the middle ear, the malleus and incus were removed, and a hand-held drill was used to bore a small hole into the bony promontory between the round and oval windows. An uninsulated electrode tip was snugly fitted through the hole and into the perilymphatic space of the vestibule. The distance from the electrode to any end organ was purposely kept large (approx. 2 mm) so as not to interfere with the mechanical operation of the latter. Another advantage of a distant placement was that the galvanic sensitivities of individual axons should not have been greatly influenced by their locations within the various nerve branches or sensory epithelia. A second electrode was placed in the lower part of the middle ear (Baird et al. 1988).

Rotational & Electrical Stimulation

The animal was placed on a superstructure that could tilt in the pitch and roll directions. This superstructure was mounted to a turntable that rotated via a position servomotor (Acutronic model 300) relative to the earth-vertical axis. This minimanipulator could maneuver in three dimensions and was attached to a microdrive (Narishige International USA, model MO-22) mounted on the stereotaxic frame. Signals from the nerve were amplified, band-pass filtered (100 - 3kHz) (Dagan, model 2400A) and threshold detected (Mentor, model N-750). Action potential spike-times were recorded through a digital event channel with a resolution of 100nS (CED, micro1401). In addition the voltage from the microelectrode was digitized with a 16-bit A/D converter with a sample rate 5 kHz for off-line comparison with the spike-times. The angular head position was obtained using a high-resolution digital encoder that was also digitized with a sample rate of 2 kHz. These signals were then recorded on to a PC for off-line analysis. Once an afferent was isolated, a series of static pitches were used to determine whether it innervated a semicircular canal or otolith organ. The resting activity was recorded for 5 sec. in order to obtain a measure of CV*. In the 8 animals without electrode placement canal afferents were studied with sinusoidal rotations at frequencies ranging from 2 – 16 Hz with a peak velocity of 20 deg/sec. In the 7 animals that did have electrodes implanted in the inner ear animals were rotated at 2 Hz. Canal afferents were then electrically stimulated with sinusoidally varying current that ranged in frequency from 2- 20 Hz. Peak current amplitude varied between animals in order to ensure linear responses. Generally, peak amplitude was 50 uAmps. However, if that current caused inhibitory cutoff in neurons we lowered the peak current to 10 uAmps. Conversely, if the responses were small we increased the peak amplitude to 100 uAmps.

Data Acquisition and Analysis

Afferents were classified according to the regularity of their background discharge rate by measuring the coefficient of variation (CV). The coefficient of variation is calculated by dividing the standard deviation of the inter-spike interval by the average inter-spike interval for 5 seconds of resting activity. Because CV is dependent upon the interspike interval, CV was normalized (CV*) with the table developed in Baird et al. (1988). Galvanic sensitivity was normalized in an approach identical to Baird et al. (1988) because of variation in electrode placement from animal to animal. In every animal we normalized galvanic sensitivity so that gG = 1 when CV* = 1.

A cycle histogram was created from records of average spike rates. A least squares fit was performed to the first harmonic of the averaged velocity response and cycle histogram to calculate the sensitivity and phase at each frequency. Cutoff was observed in less than 5% of the afferents recorded for any stimulus condition. In the small subset in which cutoff was observed, the empty bins of the response cycle histogram were treated as regions void of data as described previously (Highstein et al., 1996). The sensitivity was then calibrated using the derived maximum sensitivity vector for that canal plane. Individual transfer functions were then fit to the raw data for each afferent.

Afferents with a CV* ≥0.20 and sensitivity at 2 Hz, 20°/s stimulation (G2Hz) of <1.5 spikes/s per °/s were assigned to the low-gain irregular group as suggested by the morphophysiological results of Baird et al. in the chinchilla (Baird et al. 1988). Regular afferents were identified as having a CV* ≤0.1. All other afferents were identified as dimorphic irregular. No distinction was made in this study between intermediate fibers (0.1 < CV* <0.2) and high-gain irregular fibers.

The responses of vestibular afferents to sinusoidal head velocity and current are described well by a transfer function of the form g·(tzs + 1). The coefficient (g) is a measure of the mid-band sensitivity to either head velocity or current calculated from the fit to the data. More specifically, it is the sensitivity of an afferent within the range of frequencies between the long cupular time constant (tc1) and the time constant associated with the afferent lead term (tz). The coefficient (tz) is a measure of the high frequency lead with respect to the stimulus in the response of an afferent. The higher the value of tz, the lower the frequency in which the response will begin to resemble the derivative of the stimulus.

A phase lead of 90 degrees re head velocity means that the response is aligned with head acceleration (the first derivative of head velocity). Responses of afferents to angular rotations are a combination of head velocity and acceleration. The frequency at which the afferent leads stimulation by 45 degrees is the 3-db point and is equal to 1/(2πtz). It is also the point where the afferent is in phase with a signal that is halfway in between head velocity and head acceleration. The range of frequencies of natural head movements in the chinchilla is likely less than 20 Hz, for the upper portion of this range regular afferents tends to modulate more closely in phase with head velocity whereas calyx-only and dimorphic irregular afferents modulate more closely in phase with head acceleration.

RESULTS

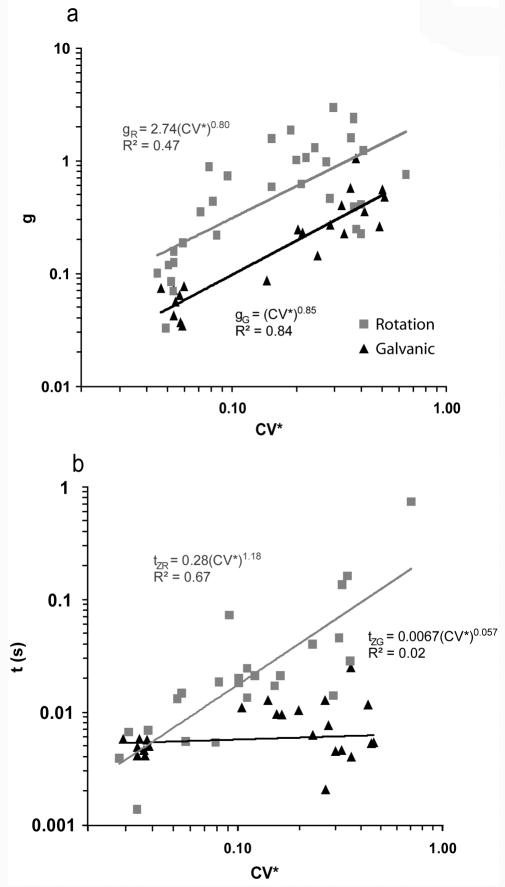
A rise in phase lead with increasing frequency was observed in all afferents. Sensitivity rose with increasing frequency in all irregular afferents and in most regular afferents. Because of this, all afferents were well fit by a transfer function of the form g·(tzs + 1) as stated in the Methods. Figure 1 shows the relationship of g and tz with respect to CV* for each individual afferent during head rotation and compares that relationship to the responses to galvanic stimulation. The mid-band galvanic sensitivity (gG) shows a logarithmic increase with CV* (gG = (CV*)0.85) (r2 = 0.84) whereas the mid-band rotational sensitivity (gR) also shows a logarithmic increase with CV*, however, the correlation coefficient is much smaller (gR = 2.74·(CV*)0.80) (r2 = 0.47). The rotational 1st order lead term (tzR) shows a logarithmic increase with CV* (tzR = 0.28· (CV*)1.18) (r2 = 0.67), whereas the galvanic 1st order lead term (tzG) is relatively flat with respect to CV* (tzG = 0.04· (CV*)0.06) (r2 = 0.01).

Figure 1.

Figure 1

Open in a new tab

Sensitivity (g, panel a) and the time constant (tz, panel b) of the transfer function g·(tzs + 1) are plotted versus CV*for each afferent. The mid-band galvanic sensitivity (gG) shows a logarithmic increase with CV* (gG = (CV*)0.87) (r2 = 0.80) whereas the mid-band rotational sensitivity (gR) is flat with respect to CV* (gR = 0.49·(CV*)0.05) (r2 = 0.002) (a). However, the rotational 1st order lead term (tRz) shows a logarithmic increase with CV* (tRz = 0.28· (CV*)1.18) (r2 = 0.67), whereas the galvanic 1st order lead term (tGz) is relatively flat with respect to CV* (tGz = 0.04· (CV*)0.06) (r2 = 0.01) (b). Fits were made by including all afferent types (Regular, Dimorphic, and Calyx-only). To minimize variation across animals galvanic sensitivities were normalized such that when CV* = 1, gG = 1.

Canal afferents in the chinchilla have been classified into calyx-only, dimorphic and bouton-only groups based on the morphology of their afferents endings as determined from intra-axonal recording and labeling experiments (Baird et al., 1988). In figure 2 we plot the normalized average gain and phase for these three classes of afferents in response to rotations and current. The transfer function fits are listed in table 1.

Figure 2.

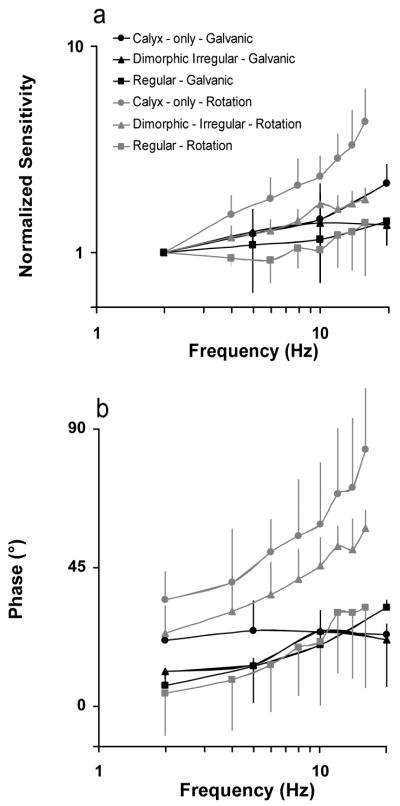
Figure 2

Open in a new tab

The average normalized gain (a) and phase (b) are plotted versus frequency for responses to rotations and current. Each afferent group was normalized so that its sensitivity would equal 1 at 2 Hz. This was to directly compare how each group of afferents varied with frequency regardless of overall magnitude. Gain and phase vary little across frequency for all classes of afferents when the axon is stimulated electrically, whereas there is a large phase lead and gain increase in response to rotations at high frequencies (> 4 Hz). This effect is most evident for calyx-only afferents.

TABLE 1.

Responses to Rotations

Type of Canal Afferent
Afferent Type gR [(sp/sec)/(degrees/sec)] tR (sec)
Calyx-only 0.59 ± 0.37 0.053 ± 0.040
Dimorphic Irregular 1.59 ± 0.77 0.019 ± 0.008
Regular 0.27 ± 0.27 0.006 ± 0.005
Open in a new tab

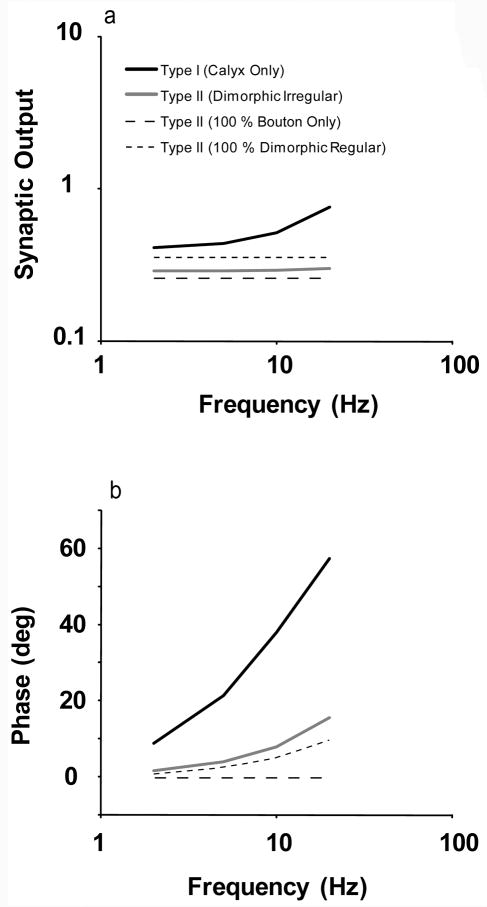
In order to determine if the number and type of hair cell is a primary determinant for the diversity of the high frequency responses from the three classes of afferents we derived an average transfer function representing the synaptic output of type I and II hair cells. In order to do this we need to make two key assumptions; that the output from a hair cell is the same no matter which axon it synapses to and that the individual output from each hair cell is summed linearly with each other (Baird et al. 1988).

We can derive a transfer function of the contribution from type I hair cells by dividing the responses of calyx-only afferents with respect to head rotation by the response of calyx-only afferents with respect to current. In order to get a measure from a single type I hair cell we than divide it by the average number of type I hair cells that synapse on to calyx-only afferents. The average number of hair cells was taken from Baird et al. (1988). The gain and phase is shown in figure 3. The findings indicate that the gain of type I hair cells increases with frequency as does the phase lead. Next, we derive a transfer function for type II hair cells. Because we do not know how many of the regular afferents are bouton-only or dimorphic we have to derive a range of transfer functions that could describe a type II hair cell. This is done by assuming that the regular afferents are either all bouton-only or all dimorphic. This range is also shown in figure 3. Lastly, we derive a transfer function for type II hair cells from the dimorphic irregular data. In Figure 3A we see that the sensitivity of dimorphic irregular type II hair cells falls about half way in between the range of possible sensitivities for type II hair cells. The phase for type II hair cells from dimorphic irregular data increases much more quickly than what is predicted from the regular afferents (Figure 3B).

Figure 3.

Figure 3

Open in a new tab
The derived gain and phase attributed to the average synaptic response from three classes of vestibular afferents. This plot was derived by dividing the average rotational response for each class of afferent by the average galvanic response for the same class of afferents. A 1st order lead term of the form gS·(tSs + 1) was fit to the data for each class of afferent. Values for gS and tS are listed below:
  • Calyx-only; gS = 0.82, tS = 0.078 s
  • Dimorphic Irregular; gS = 7.5, tS = 0.045 s
  • Dimorphic Regular and Bouton-only; gS = 8.9, tS = 0.006 s

DISCUSSION

In our analysis we assumed that stimulating current bypasses hair cells and activates the axon directly. The findings of Goldberg at al. (1984) support this assumption in that in their experiments cathodal currents remained excitatory when moving a stimulating electrode from the perilymphatic to the endolymphatic space in the vestibule. If current were stimulating the hair cells then one would expect a reversal in polarity because cathodal currents which are excitatory for perilymphatic stimulation should have become inhibitory for endolymphatic stimulation. In addition, latencies during short-shock stimulation are too short to involve chemical synaptic transmission (Goldberg et al. 1984).

Recent reports (Aw et al. 2008, 2010, Todd et al. 2010) have shown that externally applied currents delivered by cutaneous electrodes elicit reduced eye responses in human subjects who have been treated with gentamicin. Their findings were interpreted as indicating that external current acts on hair cells rather than afferents. An alternative possibility is that the reduced eye responses are due to loss of type I hair cells, leading secondarily to loss of afferent nerve fibers (Guth et al. 1998, Sadeghi et al. 2007). Histologic data are not available for their human subjects. Considering the results reported by Hirvonen, et al (2005), which showed that intratympanic gentamicin in chinchillas destroyed Type I hair cells and the stereocilia of Type II hair cells but did not reduce responses to applied currents, our assumption that currents bypass the hair cells seems justified. In addition, a partial block of glutamate caused by an injection of CNQX into the anterior semicircular canal in chinchillas reduces the resting rate of vestibular afferents but increases the sensitivity to current (Lasker et al. 2009). Our explanation of this finding is that post-synaptic sensitivity increases in response to reduced hair cell input caused by the glutamate block. If current acts on the hair cells directly then it is likely that afferent sensitivity to current would decrease not increase. Finally, in this study, every afferent shows almost identical dynamics in response to current but a diverse set of responses in response to head velocity. If currents stimulate the hair cells then this diversity of response dynamics must come prior to hair cell transduction which is unlikely based on comparisons of mechanical and electrical stimulation in the toadfish (Highstein et al. 1996).

The results in figure 1 enable us to determine that that the galvanic 1st order lead term (tzG) shows no variation with respect to CV*. This finding is in contrast to the large increase in the rotational 1st order lead term (tzR) showing a logarithmic increase with CV*. This observation suggests that the cause of this increased lead must be occurring prior to the post-synaptic spike-initiation zone. We note that the calyx-only afferents have the largest values of tzR and therefore it might be reasonable to conclude that the type I hair cell is responsible for the increase in the lead operator between regular and calyx-only afferents. Dimorphic units are a combination of type I and type II hair cells and so their lead term is in between the most regular (bouton-only) and the most irregular (calyx-only) afferents.

In Figure 3 we show that the number and type of hair cells innervating an axon is a reasonable proxy for the overall synaptic weight of that cell. However, the same cannot be said for the increasing phase lead at higher frequencies. Although, there is a relatively larger ratio of type II to type I hair cells in dimorphic regular (8:1) as compared to dimorphic irregular afferents (6:1), this difference is not large enough to account for the relatively large difference in phase at higher frequencies between these two groups of units. One possible explanation for this discrepancy is that it is not valid to assume that type I or II hair cells behave the same way throughout the crista but rather vary their contribution depending on the axon they are connected to. Another possibility is that the type I hair cell is merely a marker for other neural processes such as differing transmitter release between the different neurons (Holstein et al., 2004).

It is interesting to note that the transfer functions describing the responses to current of all afferent classes are the same in response to currents, 0.006s +1. This transfer function is the same as what we observe for the rotational response to regular afferents. One possible explanation is that the dynamics of the hair cells that synapse on to regular afferents are effectively pure velocity transducers even at high frequencies. A difficulty with this interpretation is that the regularity of a neuron does not appear to be related to the type of hair cells that innervate it but rather to post-synaptic gain (Baird et al. 1988). There are two major causes for the irregularity of discharge of afferents, the synaptic noise and the trajectory of the after hyper-polarization of the axon (Smith and Goldberg, 1986). Of these two, the after hyper-polarization was estimated to be the greatest contributor to the discharge irregularity (Smith and Goldberg, 1986). In other words, increases in post-synaptic gain (changes in the properties of the after hyper-polarization) will cause an increase of the sensitivity to synaptic noise which will in turn increase the irregularity of firing. Because there is a correlation between the regularity of discharge and the value of tzR, it suggests that there may be a link between the post-synaptic gain of an afferent and the high frequency dynamics of that afferent. The origin of this relationship is not defined in this study, but we can suggest that there is some correlation between the potassium channels that are responsible for the after hyper-polarization and the neural transmitters and/or channels responsible for the increasing phase of calyx-only and dimorphic irregular units at high-frequency head rotations (Risner and Holt 2006, Kalluri et al. 2010).

TABLE 2.

Responses to Currents

Type of Canal Afferent
Afferent Type gG [(sp/sec)/(uA)] tG (sec)
Calyx-only 0.51 ± 0.27 0.005 ± 0.001
Dimorphic Irregular 0.22 ± 0.11 0.009 ± 0.003
Regular 0.06 ± 0.02 0.006 ± 0.003
Open in a new tab

Acknowledgments

This work was supported by NIH R01DC2390.

Reference List

  1. Anderson JH, Blanks RHI, Precht W. Response characteristics of semicircular canal and otolith systems in cat. I. Dynamic responses of primary vestibular nerve fibers. Exp Brain Res. 1978;32:491–507. doi: 10.1007/BF00239549. [DOI] [PubMed] [Google Scholar]
  2. Aw ST, Todd MJ, Aw GE, Weber KP, Halmagyi GM. Gentamicin vestibulotoxicity impairs human electrically evoked vestibulo-ocular reflex. Neurology. 2008;71:1776–82. doi: 10.1212/01.wnl.0000335971.43443.d9. [DOI] [PubMed] [Google Scholar]
  3. Aw ST, Todd MJ, Lehnen N, Aw GE, Weber KP, Eggert T, Halmagyi GM. Does the human electrically-evoked vestibulo-ocular reflex rely on vestibular hair cell transduction? J Vest Res. 2010;20:166. [Google Scholar]
  4. Baird RA, Desmadryl G, Fernandez C, Goldberg JM. The vestibular nerve of the chinchilla. II. Relation between afferent response properties and peripheral innervation patterns in the semicircular canals. J Neurophysiol. 1988;60:182–203. doi: 10.1152/jn.1988.60.1.182. [DOI] [PubMed] [Google Scholar]
  5. Blanks RH, Precht W. Functional characterization of primary vestibular afferents in the frog. Exp Brain Res. 1976;25:369–390. doi: 10.1007/BF00241728. [DOI] [PubMed] [Google Scholar]
  6. Boyle R, Highstein SM. Resting discharge and response dynamics of horizontal semicircular canal afferents of the toadfish,Opsanus tau. J Neurosci. 1990;10:1557–1569. doi: 10.1523/JNEUROSCI.10-05-01557.1990. [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Brichta AM, Goldberg JM. The papilla neglecta of turtles: A detector of head rotations with unique sensory coding properties. J Neurosci. 1998;18:4314–4324. doi: 10.1523/JNEUROSCI.18-11-04314.1998. [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. Goldberg JM, Fernandez C. Physiology of peripheral neurons innervating semicircular canals of the squirrel monkey I. Resting discharge and response to constant angular accelerations. J Neurophysiol. 1971;34:635–660. doi: 10.1152/jn.1971.34.4.635. [DOI] [PubMed] [Google Scholar]
  9. Goldberg JM, Lysakowski A, Fernandez C. Morphophysiological and ultrastructural studies in the mammalian cristae ampullares. Hear Res. 1990;49:89–102. doi: 10.1016/0378-5955(90)90097-9. [DOI] [PubMed] [Google Scholar]
  10. Goldberg JM, Smith CE, Fernandez C. Relation between discharge regularity and responses to externally applied galvanic currents in vestibular nerve afferents of the squirrel monkey. J Neurophysiol. 1984;51:1236–1256. doi: 10.1152/jn.1984.51.6.1236. [DOI] [PubMed] [Google Scholar]
  11. Guth PS, Perin P, Norris CH, Valli P. The vestibular hair cells: post-transductional signal processing. Prog Neurobiol. 1998;54:193–247. doi: 10.1016/s0301-0082(97)00068-3. [DOI] [PubMed] [Google Scholar]
  12. Highstein SM, Baker R. Action of the efferent vestibular system on primary afferents in the toadfish, Opsanus tau. J Neurophysiol. 1985;54:370–384. doi: 10.1152/jn.1985.54.2.370. [DOI] [PubMed] [Google Scholar]
  13. Highstein SM, Rabbitt RD, Boyle R. Determinants of semicircular canal afferent response dynamics in the toadfish, Opsanus tau. J Neurophysiol. 1996;75:575–596. doi: 10.1152/jn.1996.75.2.575. [DOI] [PubMed] [Google Scholar]
  14. Holstein GR, Rabbitt RD, Martinelli GP, Friedrich VL, Jr, Boyle RD, Highstein SM. Convergence of excitatory and inhibitory hair cell transmitters shapes vestibular afferent responses. Proc Natl Acad Sci U S A. 2004;101:15766–15771. doi: 10.1073/pnas.0402824101. [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Hullar TE, Della Santina CC, Hirvonen TP, Lasker DM, Carey JP, Minor LB. Responses of irregularly discharging chinchilla semicircular canal vestibular-nerve afferents during high-frequency head rotations. J Neurophysiol. 2005;93:2777–2786. doi: 10.1152/jn.01002.2004. [DOI] [PubMed] [Google Scholar]
  16. Hirvonen TP, Minor LB, Hullar TE, Carey JP. Effects of intratympanic gentamicin on vestibular afferents and hair cells in the chinchilla. J Neurophysiol. 2005;93:643–55. doi: 10.1152/jn.00160.2004. [DOI] [PubMed] [Google Scholar]
  17. Kalluri R, Xue J, Eatock RA. Ion channels set spike timing regularity of mammalian vestibular nerve afferents. J Neurophysiol. 2010;104:2034–51. doi: 10.1152/jn.00396.2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Lasker DM, Han GC, Park HJ, Minor LB. Rotational responses of vestibular-nerve afferents innervating the semicircular canals in the C57BL/6 mouse. J Assoc Res Otolaryngol. 2008;9:334–348. doi: 10.1007/s10162-008-0120-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Lasker DM, Kim KS, Park HJ, Carey JP, Minor LB. The effect of CNQX on single unit responses of horizontal canal afferents in the chinchilla. ARO MidWinter Meeting; 2009. Abstract 1128. [Google Scholar]
  20. Li W, Correia MJ. Recovery of semicircular canal primary afferent activity in the pigeon after streptomycin ototoxicity. J Neurophysiol. 1998;80:3297–3311. doi: 10.1152/jn.1998.80.6.3297. [DOI] [PubMed] [Google Scholar]
  21. Park HJ, Lasker DM, Minor LB. Static and dynamic discharge properties of vestibular-nerve afferents in the mouse are affected by core body temperature. Exp Brain Res. 2010;200:269–275. doi: 10.1007/s00221-009-2015-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Risner JR, Holt JR. Heterogenous potassium conductances contribute to the diverse firing properties of postnatal mouse vestibular ganglion neurons. J Neurophysiol. 2006;96:2364–76. doi: 10.1152/jn.00523.2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
  23. Sadeghi SG, Minor LB, Cullen KE. Response of vestibular-nerve afferents to active and passive rotations under normal conditions and after unilateral labyrinthectomy. J Neurophysiol. 2007;97:1503–1514. doi: 10.1152/jn.00829.2006. [DOI] [PubMed] [Google Scholar]
  24. Smith CE, Goldberg JM. A stochastic afterhyperpolarization model of repetitive activity in vestibular afferents. Biol Cybern. 1986;54:41–51. doi: 10.1007/BF00337114. [DOI] [PubMed] [Google Scholar]
  25. Todd MJ, Aw ST, Halmagyi GM. The mechanism underlying human electrical vestibular stimulation. J Vest Res. 2010;20:166. [Google Scholar]
  26. Yang A, Hullar TE. Relationship of semicircular canal size to vestibular-nerve afferent sensitivity in mammals. J Neurophysiol. 2007;98:3197–3205. doi: 10.1152/jn.00798.2007. [DOI] [PubMed] [Google Scholar]

RESOURCES