Second Order Total Generalized Variation (TGV) for MRI

Abstract

Total Variation (TV) was recently introduced in many different MRI applications. The assumption of TV is that images consist of areas, which are piecewise constant. However, in many practical MRI situations, this assumption is not valid due to the inhomogeneities of the exciting B1 field and the receive coils. This work introduces the new concept of Total Generalized Variation (TGV) for MRI, a new mathematical framework, which is a generalization of the TV theory and which eliminates these restrictions. Two important applications are considered in this paper, image denoising and image reconstruction from undersampled radial data sets with multiple coils. Apart from simulations, experimental results from in vivo measurements are presented where TGV yielded improved image quality over conventional TV in all cases.

INTRODUCTION

Total Variation (TV) based strategies, which were originally designed for denoising of images (1) have recently gained wide interest for many MRI applications beyond denoising. Examples include regularization for parallel imaging (2, 3), the elimination of truncation artifacts (4), inpainting of sensitivity maps (5), their use as a regularization method for undersampled imaging techniques within the compressed sensing framework (6) as well as in iterative reconstruction of undersampled radial data sets (7,8). TV models have the main benefit that they are very well suited to remove random noise, incoherent noise-like artifacts from random subsampling and streaking artifacts from undersampled radial sampling, while preserving the edges in the image. However, the assumption of TV is that the images consist of regions, which are piecewise constant. Due to inhomogeneities of the exciting B ₁ field of high field systems with 3T and above and of the receive coils, this assumption is often violated in practical MRI examinations. Additionally, even in situations when this is no severe problem, due to the assumption of piecewise constancy, the use of TV often leads to staircasing artifacts and results in patchy, cartoon-like images which appear unnatural.

This paper introduces the new concept of Total Generalized Variation (TGV) as a penalty term for MRI problems. This mathematical theory has recently been developed (9), and while it is equivalent to TV in terms of edge preservation and noise removal, it can also be applied in imaging situations where the assumption that the image is piecewise constant is not valid. As a result, the application of TGV in MR imaging is far less restrictive. It is shown in this work that TGV can be applied for image denoising and during iterative image reconstruction of undersampled radial data sets from phased array coils, and yields results that are superior to conventional TV.

THEORY

The concept of Total Generalized Variation

The Total Generalized Variation introduced in (9) is a functional which is capable to measure, in some sense, image characteristics up to a certain order of differentiation. In this section, we will restrict ourselves to give a short introduction which is not rigorous in the mathematical sense. The reader interested in the mathematical background may find more information in the Appendix.

First, recall the definition of the Total Variation, which is, for a given image u, usually expressed as

$$\mathrm{TV}\left(u\right)={\int }_{\Omega }\mid \nabla u\mid \mathrm{d}x$$ [1]

The Total Generalized Variation of second-order which we will use throughout the paper bases on this definition but is generalized to represent a minimization problem itself:

$${\mathrm{TGV}}_{\alpha }^2\left(u\right)=\underset{v}{\min }{\alpha }_1{\int }_{\Omega }\mid \nabla u-v\mid \mathrm{d}x+{\alpha }_0{\int }_{\Omega }\mid \mathcal{E}\left(v\right)\mid \mathrm{d}x$$ [2]

Here, the minimum is taken over all complex vector fields v on Ω and $\mathcal{E}\left(v\right)=\frac{1}{2}(\nabla v+\nabla v^{\mathrm{T}})$ denotes the symmetrized derivative. Such a definition provides a way of balancing between the first and second derivative of a function (which is controlled by the ratio of positive weights α ₀ and α ₁). In contrast to that, TV only takes the first derivative into account. For compatibility with the usual TV semi-norm we let, α ₁ = 1 throughout the paper. Moreover, according to our experience, the default value α ₀ = 2 is suitable for most applications and does not need to be tuned, hence, one can say that no additional parameters are introduced with TGV.

Let us briefly mention some general properties of the functional. First, as TGV is the semi-norm of a Banach space, associated variational problems fit well into the well-developed mathematical theory of convex optimization problems, especially with respect to analysis and computational realization. Moreover, each function of bounded variation admits a finite TGV value, making the notion suitable for images. This means in particular that piecewise constant images can be captured with the TGV model which even extends the TV model. Finally, TGV is translation invariant as well as rotationally invariant, meaning that it is in conformance with the requirement that images are measured independent from the actual viewpoint.

It turns out that using ${\mathrm{TGV}}_{\alpha }^2$ as a regularizer leads to an absence of the staircasing effect which is often observed in Total Variation regularization. In the following, we like to give an intuitive explanation for this. In smooth regions of a given image u, the second derivative ▽² u is locally “small”. It is therefore beneficial for the minimization of [2] to choose locally v = ▽u in these regions, resulting locally in the penalization of ▽² u. On the other hand, in the neighborhood of edges, ▽² u will be considerably “larger” than ▽u, so it is beneficial for the minimization of [2] to choose locally v = 0 there. This locally results in ${\mathrm{TGV}}_{\alpha }^2$ measuring the first derivative which corresponds to the “jump”, i.e., the difference of the values of u on one side of an edge compared to the other. Of course, this argumentation is only intuitively valid, the values of actual minimizers v may be located anywhere “between” 0 and ▽u. This balancing leads to edges measured in ${\mathrm{TGV}}_{\alpha }^2$ not being more “expensive” than a smooth function, which is similar to TV, but to smooth regions being “cheaper” than staircases in terms of ${\mathrm{TGV}}_{\alpha }^2$, a feature which is absent in TV. Hence, Total Generalized Variation used as a penalty functional prefers images which appear more natural and, as we will see, leads to a more faithful reconstruction of MR images.

Application of TGV in MRI

The effects suggested in the previous subsection can in fact be observed when applied to MRI problems. One example is ${\mathrm{TGV}}_{\alpha }^2$-based denoising which is briefly outlined in the following; for a detailed discussion of the noise suppression characteristics and a comparison with TV-based denoising, we refer to (9). Given a noisy image f ∈ L ²(Ω) and a regularization parameter λ > 0, the denoised version u is computed as the solution of the following problem.

Method 1 (TGV image denoising)

   

$$\underset{u}{\min }\frac{1}{2\lambda }{\int }_{\Omega }{(u-f)}^2\mathrm{d}x+{\mathrm{TGV}}_{\alpha }^2\left(u\right)$$ [3]

We propose [3] to remove noise from MR images which can include smooth signal modulations.

Testing this method with a piecewise affine artificial image (see Fig. 1) clearly reveals its advantage over usual TV-based denoising. Here, the original image consists of regions with vanishing second derivative and since ${\mathrm{TGV}}_{\alpha }^2$ takes into account the second derivative as well as the edges, the method is able to reconstruct almost perfectly.

Figure 1.

Denoising a ramp image with TV and TGV penalty. The noisy test image f (left), its Total-Variation regularization (middle) and its Total-Generalized-Variation regularization [3] (right). The absence of staircasing artifacts for TGV can nicely be observed here.

Besides image denoising, we propose to use ${\mathrm{TGV}}_{\alpha }^2$ for recovering modulated images from incomplete Fourier measurements, which covers in particular the case of subsampled radial data from multiple coils. It bases on the approach analyzed in (10–12), was applied to radial MRI data in (7) and can be described as follows: Denoting the unknown true data by f ∈ L ²(Ω) with Ω being a bounded domain, and by Ξ ⊂ R ^d a non-empty set representing the spatial frequencies (or k-space points) which are measured, we are looking for a solution of

$$\underset{u\in L^2\left(\Omega \right)}{\min }\mathrm{TV}\left(u\right)\text{such that}\widehat{u}\left(\xi \right)=\widehat{f}\left(\xi \right)\text{for all}\xi \in \Xi$$ [4]

with $\widehat{u}$ and $\widehat{f}$ being the Fourier transforms of u and f, respectively. This approach is able to reduce artifacts from the incomplete measurements Ξ which usually appear in the minimum L ²-norm reconstruction. Moreover, surprisingly, for suitable sets Ξ and many piecewise constant f, the solution u of [4] coincides with f (10). However, the tendency of TV to produce staircasing artifacts in piecewise smooth images is again present. We therefore modify the problem to incorporate ${\mathrm{TGV}}_{\alpha }^2$.

$$\underset{u\in L^2\left(\Omega \right)}{\min }{\mathrm{TGV}}_{\alpha }^2\left(u\right)\text{such that}\widehat{u}\left(\xi \right)=\widehat{f}\left(\xi \right)\text{for all}\xi \in \Xi$$ [5]

This approach was tested with a noise-free numerical Shepp-Logan phantom that was modulated with a simulated coil sensitivity generated with the use of Biot-Savart’s law, to simulate the situation of undersampled radial multi channel acquisition. TGV yields again almost perfect reconstruction where conventional TV [4] suffers from staircasing artifacts (see Fig. 2).

Figure 2.

Reconstructions of a Shepp-Logan phantom from undersampled radial k-space data, modulated with a simulated coil sensitivity generated with the use of Biot-Savart’s law. Top row: Original test image of size 256×256 (left) and the corresponding radial sampling pattern with 24 radial spokes (right). Middle row: Conventional NUFFT Reconstruction (left), Minimum-TV-Solution [4] (middle) and Minimum-${\mathrm{TGV}}_{\alpha }^2$-Solution [6] (right). Bottom row: Magnified views from the middle row.

For reconstruction from multiple channel data g ₁, … , g_P, we follow the approach of (7) and assume that there are complex sensitivity estimates σ ₁, … , σ _P such that $\left(\widehat{{\sigma }_{i}u}\right)\approx g_i$ on Ξ. Relaxing the constraint in [5] then leads to

Method 2 (TGV undersampling reconstruction)

   

$$\underset{u\in L^2\left(\Omega \right)}{\min }\sum _{i=1}^P\frac{{\mid \mid \left(\widehat{{\sigma }_{i}u}\right)-g_i\mid \mid }_2^2}{2\lambda }+{\mathrm{TGV}}_{\alpha }^2\left(u\right)$$ [6]

where ∥·∥₂ is a suitable norm on L ²(Ξ) and λ > 0 is a regularization parameter. We apply [6] for undersampled multi-channel radial MR data.

Numerical algorithms

Both the denoising problem [3] and the undersampling reconstruction problem [6] constitute non-smooth convex optimization problems for which several numerical algorithms are available. In order to implement any numerical algorithm on a digital computer, we have to consider the discrete setting of the proposed reconstruction method [6]. For discretization, we use a two dimensional regular Cartesian grid of size M × N and mesh size h > 0. For more information on the discrete setting we refer to (9). From now on we will use the superscript h to indicate the discrete setting. The differential operators div^h, ${\mathcal{E}}^h$, ▽^h are approximated using first order finite differences. These operators are chosen adjoint to each other, i.e.

$${\left({\mathrm{div}}_2^h\right)}^{\ast }=-{\mathcal{E}}^h{\left({\mathrm{div}}_1^h\right)}^{\ast }=-{\nabla }^h$$

With U^h = C ^MN, the discrete version of the denoising problem [3] is given by

$$\underset{u^h\in U^h}{\min }+\frac{1}{2\lambda }{\mid \mid u^h-f^h\mid \mid }_2^2+{\mathrm{TGV}}_{\alpha }^2\left(u^h\right)$$ [7]

where f^h ∈ U^h is the noisy input data and ${\mathrm{TGV}}_{\alpha }^2$ the discrete Total Generalized Variation according to [2] using the corresponding discrete divergence operators. Discretized, problem [7] becomes

$$\underset{u^h\in U^h,v^h\in V^h}{\min }\frac{1}{2\lambda }{\mid \mid u^h-f^h\mid \mid }_2^2+{\alpha }_1{\mid \mid {\nabla }^h{u}^h-v^h\mid \mid }_1+{\alpha }_0{\mid \mid {\mathcal{E}}^h\left(v^h\right)\mid \mid }_1$$ [8]

where V^h = C ^2MN. Note that in this formulation, only first order differential operators are involved.

As recent trends in convex optimization (13, 14) indicate and as they turn out to be suitable for our purposes, it is sensible to use first order algorithms since they are easy to implement, have a low memory print and can be efficiently parallelized. Furthermore, these methods come along with global worst case convergence rates. This allows to estimate the required number of iterations which are needed to reach a certain accuracy. Here, we employ the first-order primal dual algorithm of (15,16). Details about how this method is applied can be found in the Appendix.

A discrete version of the reconstruction problem [6] can be derived as follows: Let R^h = C ^QP represent the vector space associated with Q k-space measurements for P coils and denote by K^h : U^h → R^h and (K^h)* the linear operators which realize the NUFFT and its adjoint on the discrete data, respectively. We assume that K^h is normalized such that ∥K^h∥ ≤ 1. Furthermore, denote by g^h the measured discrete radial sampling data. The continuous problem [6] then becomes

$$\underset{u^h\in U^h}{\min }\frac{1}{2\lambda }{\mid \mid K^h{u}^h-g^h\mid \mid }_2^2+{\mathrm{TGV}}_{\alpha }^2\left(u^h\right)$$ [9]

The main difference to the denoising problem [7] is that the linear operator K^h is involved in the data fitting term. However, the method introduced in (16) can be easily adapted to this setting by introducing an additional dual variable, we refer again to the Appendix for details.

MATERIALS AND METHODS

Application of TGV for denoising

Denoising was the first natural application for TGV. Two different data sets were acquired on a clinical 3T scanner (Siemens Magnetom TIM Trio, Erlangen, Germany). Written informed consent was obtained from all subjects prior to the examinations. The first measurement was a T ₁ weighted 3D gradient echo scan of the prostate with injection of a contrast agent. Sequence parameters were T_R = 3.3 ms, T_E = 1.1 ms, flip angle α = 15°, matrix size (x, y) = (256,256), 20 slices, slice thickness 4 mm, in plane resolution 0.85 mm×0.85 mm. The measurement showed severe signal inhomogeneities due to the exciting B ₁ field and the surface coils used for reception (17). Therefore, the assumption that the images consist of piecewise constant areas is violated.

The other test data set was a T ₂ weighted turbo spin echo scan of the human brain, using a 32 channel receive coil. Sequence parameters were repetition time T_R = 5000 ms, echo time T_E = 99 ms, turbo factor 10, matrix size (x, y) = (256,256), 10 slices with a slice thickness of 4 mm and an in plane resolution of 0.86 mm×0.86 mm. Complex Gaussian noise was then added to the original k-space data. The standard deviation of the added noise was chosen such that the ratio to the norm of the data was 1/15. With this approach, a high SNR gold standard was available which allowed objective comparison of the TV and TGV results. This measurement did not show pronounced signal inhomogeneities, and the goal of the experiments with TGV was to show that even in these cases, TV introduces staircase artifacts which do not represent the underlying signal from the tissue.

Both data sets were exported, and offline denoising was performed with conventional TV, as well as with a Matlab (R2009a, The MathWorks, Natick, MA, USA) implementation of TGV [3].

Image reconstruction of subsampled multicoil radial data with a TGV constraint

Image reconstruction with TV regularization for subsampled radial data sets with removal of the intensity profiles and the phase of the individual coil elements prior to application of TV was first introduced by Block et al. (7). Our TV reference implementation roughly follows this approach. Analogously to (7), it employs, prior to application of TV, for each coil, a reconstruction with a quadratic regularization on the derivative (H ¹-regularization) followed by the convolution with a smoothing kernel. The sensitivities are then obtained by dividing by the sum of squares image for each coil element. All results were also compared to an iterative parallel imaging method of CG-SENSE type (18), using the same coil sensitivities as in the TV experiments.

The fully sampled 32 channel TSE brain data set from the denoising experiments was subsampled retrospectively, to simulate an accelerated acquisition. Data from 32, 24, 16 and 12 radial projections was obtained. As $\frac{\pi }{2}n$ projections (402 for n = 256 in our case) have to be acquired to obtain a fully sampled data set in line with the Nyquist criterion according to the literature (19), this corresponds to undersampling factors of approximately 12, 16, 25 and 33.

Finally, undersampled 2D radial spin echo measurements of the human brain were performed with a clinical 3T scanner (Siemens Magnetom TIM Trio, Erlangen, Germany) using a receive only 12 channel head coil. Sequence parameters were: T_R = 2500 ms, T_E = 50 ms, matrix size (x, y) = (256,256), slice thickness 2 mm, in plane resolution 0.78 mm×0.78 mm. 96, 48, 32 and 24 projections were acquired, and the sampling direction of every second spoke was reversed to reduce artifacts from off-resonances (8). Raw data was exported from the scanner, and image reconstruction was performed offline using a Matlab proof-of-principle implementation of the non-uniform fast Fourier transform (NUFFT) (20) and of the proposed TGV method [6].

Additionally, reconstruction was performed using an implementation which exploits the high parallelization potential of current graphic processing units (GPUs). It uses NVIDIA’s compute unified device architecture (CUDA) framework (21) and leads to a significant acceleration in comparison to the Matlab implementation, which is discussed in the section “Computational requirements”.

RESULTS

Application of TGV for denoising

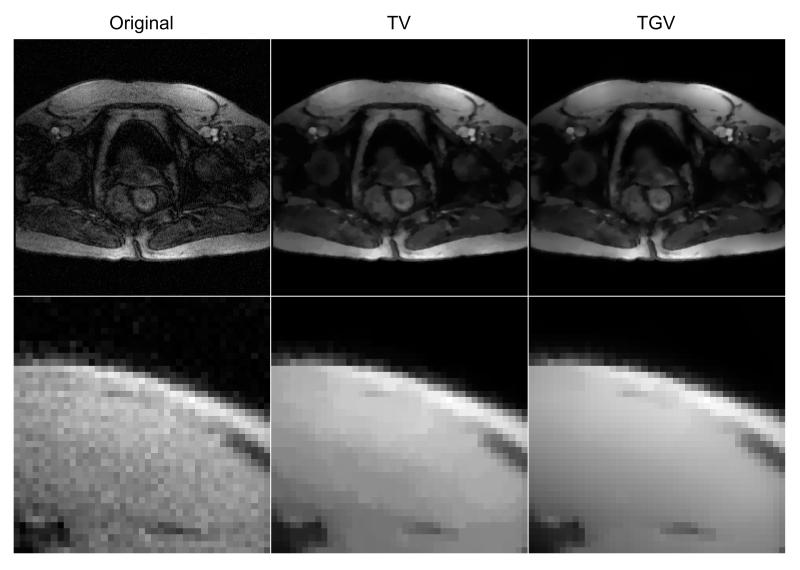
Fig. 3 shows the results from TV and TGV for the T ₁ weighted scan of the human prostate. Both methods remove noise while maintaining sharp edges efficiently. However, in regions where the assumption that the image consists of areas that are piecewise constant is violated, it is not surprising that TV results are significantly corrupted by staircasing artifacts. TGV on the other hand works equally well in these regions, as already pointed out in Fig. 1.

Figure 3.

TV (middle) and TGV (right) denoising results from the contrast enhanced T ₁ weighted prostate scan. The images show smooth modulations due to inhomogeneities of the exciting B ₁ field and the surface coils used for signal reception which lead to significant artifacts when conventional TV is applied.

The original image with high SNR, the noisy image and results with TV and TGV for the T ₂ weighted brain scan are displayed in Fig. 4. Even in this data set, where the assumption that the image consists of areas that are piecewise constant is valid because there are neither severe B ₁ signal inhomogeneities nor modulations from the receive coil, TV introduces additional staircases which cannot be found in the original image. This effect is reduced with TGV.

Figure 4.

Denoising experiments for the T ₂ weighted brain scan. In the top row, the original image with high SNR (left) which has been contaminated with additive Gaussian noise (middle left) is shown. TV (middle right) and TGV (right) denoising results are displayed as well as magnified views of the respective images (middle and bottom rows). An example of an unwanted image feature that is introduced during denoising is highlighted by arrows.

Image reconstruction of subsampled multicoil radial data with a TGV constraint

Fig. 5 and Fig. 8 compare the reconstructions of the undersampled radial imaging experiments from retrospective subsampling and truly accelerated imaging. For comparison, the fully sampled image corresponding to the results of Fig. 5 can be found in Fig. 4.

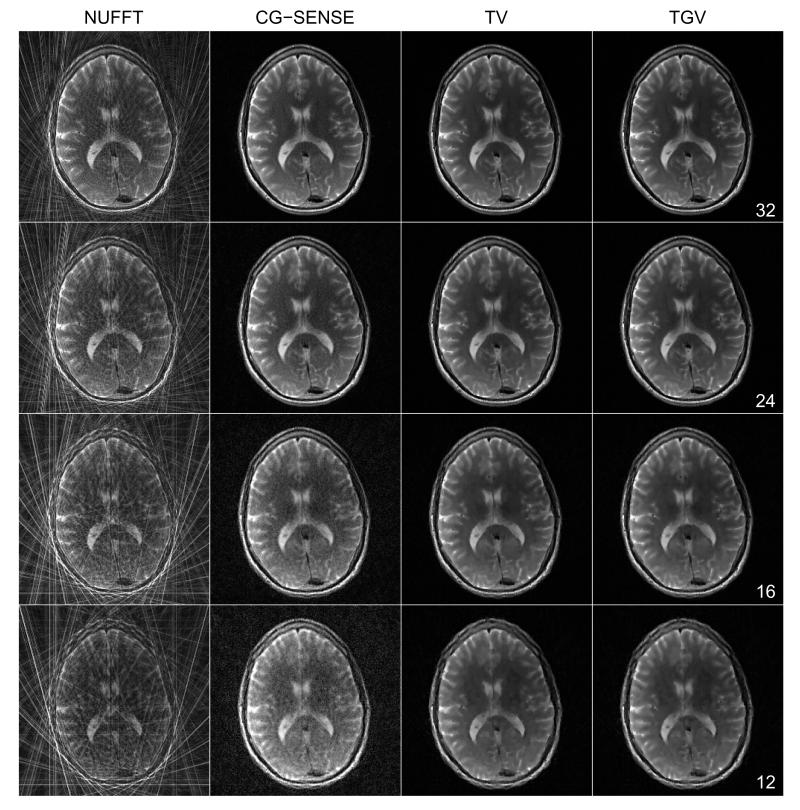
Figure 5.

Results from downsampling experiments of the human brain (256×256 matrix) using 32, 24 16 and 12 radial projections. The columns depict conventional NUFFT reconstructions (left), reconstructions with CG-SENSE (middle left), with a TV constraint (middle right) and with a TGV constraint (right), respectively. The original, fully sampled image is displayed in Fig. 4.

Figure 8.

Radial image reconstructions of the human brain (256×256 matrix) from 96, 48, 32 and 24 projections. The columns depict conventional NUFFT reconstructions (left), reconstructions with CG-SENSE (middle left), with a TV constraint (middle right) and with a TGV constraint (right), respectively.

It is not surprising that conventional NUFFT reconstructions show streaking artifacts which get worse as the number of projections is reduced. Both TV and TGV reconstructions eliminate streaking artifacts efficiently. For moderate subsampling, results with CG-SENSE are of comparable quality. While the results of TV and TGV are of roughly the same quality for all amounts of subsampling in all experiments, magnified views (Fig. 6) again display staircasing artifacts in the TV results. This is also illustrated in Fig. 7, which displays surface plots of the same magnified region as in Fig. 6 for the 32 projections data set. While this is still a level of subsampling where CG-SENSE achieves acceptable results, effects of noise amplification are already visible. The difference between TV and TGV is subtle, but the tendency of TV to introduce staircases which are not present in the fully sampled image is clearly visible, e.g. at the frontal interface of the ventricle.

Figure 6.

Magnified views of the same data as shown in Fig. 5.

Figure 7.

Surface plots of the 32 projections data set of the same magnified region as in Fig. 6. The original fully sampled data, CGSENSE, TV and TGV reconstructions are displayed. The tendency of TV to introduce staircases is clearly visible, e.g. at the frontal interface of the ventricle.

DISCUSSION

The results from this work clearly demonstrate the advantages of TGV over conventional TV for both denoising and for constrained image reconstruction of undersampled data. While this is no real surprise for the results in Fig. 3 because the TV assumption was violated in these cases, it is notable that even with quite homogeneous data sets like in Figs. 4, 5, 6 and 8, TV introduces additional staircasing artifacts which lead to a more blocky, less faithful result when compared to the original image because the underlying assumption of piecewise constancy does not follow the underlying signal from the tissue that well. However, it must be noted that in some situations, the cartoon type, piecewise constant features of TV might actually be desirable. For example, the interfaces between grey and white matter in in the magnified view of Fig. 4 (third row) are artificially enhanced with the use of TV. Although TGV is also edge-preserving (as can be seen by comparing the sharp edges of TV and TGV at the periphery of the brain), this effect gives TV results a slightly “sharper” visual appearance. In the case of image reconstruction this effect can be noticed by a direct comparison of Figs. 6 and 7. Again, the edges and piecewise constant regions introduced in the TV results are more emphasized in comparison to the TGV results and even the original image. In this particular case, the surface plots reveal that the TV result is not closer to the original image, but the described effect may still enhance the diagnostic value, comparable to the use of a postprocessing filter for edge enhancement.

As both TV and TGV introduce model based a-priori information, it is possible that this leads to losses in certain parts of the image, or the introduction of unwanted features. One example is highlighted by arrows in the second row of Fig. 4. In this particular case, noise corruption resulted in a group of bright pixels, which were not eliminated during denoising. Therefore a bright spot remains in the denoised images, which might even be misinterpreted as a lesion. Of course this spot is also visible in the noisy image, but in this case a radiologist would be aware of the low SNR and be reluctant to base a diagnosis on such an image. The same holds true for fine details that are buried below the noise level. While it is possible to eliminate the noise, these features cannot be recovered. Therefore, if denoising is used, radiologists should always have access to the noisy data, too. In this way it is possible to identify wrong image features and missing details more easily, and an unjustified overestimation of the diagnostic value of the images can be prevented.

It is obvious that both variational approaches (TV and TGV based) clearly outperform conventional L ² based parallel imaging. Comparable image quality is only achieved for moderate undersampling (96 projections for the 12 channel data set (Fig. 8), 32 projections in the case of the 32 channel data (Figs. 5, 6). Of course, if the degree of undersampling is too high, some features may be buried without chance of recovery with either method. The cases where extremely high undersampling is performed (e.g. using only 12 projections) in Figs. 5 and 6 demonstrate these limits of the method.

Choice of the regularization parameter

TGV, like TV, needs a proper balancing between the regularization term and the data fidelity term. Overweighting of the TGV term removes image features while underweighting leads to residual noise or streaking artifacts in the image. In our current implementation, the right amount of regularization is determined in the following way. We start with very low regularization and then increase the parameter step by step until noise or artifacts are eliminated from the resulting image. An alternative would be the use of automatic strategies like L-curve (22) or discrepancy principles (23), which is the subject of future investigations. For the calculations of this work, the following weights were used: λ = 0.02 for prostate denoising (Fig. 3), λ = 0.01 for brain denoising (Fig. 4) and λ = 8 10⁻⁵ for all image reconstruction experiments, regardless of undersampling and the selected data set (Figs. 5, 6, 8). Fig. 9 demonstrates the influence of the regularization parameter on the reconstructed images for denoising and image reconstruction. Results with proper regularization, over-regularized (λ_high = 5 · λ_proper) and under-regularized (λ_low = 1/5 · λ_proper) images are shown. In the case of denoising, overweighting causes pronounced losses of object detail while residual noise remains in the image in the underregularized case. In contrast, image reconstruction is much more robust with respect to changes of the regularization parameter, which is an important condition when considering application in clinical practice. This also explains why excellent results were achieved with a “default” parameter for two different data sets and multiple levels of subsampling in the case of image reconstruction, while individual tuning had to be performed for denoising.

Figure 9.

Denoising (top row) and radial image reconstruction with 32 radial projections (256×256 matrix) from the downsampled (middle row), and the in-vivo accelerated (bottom row) experiments. Results with a high regularization weight (left), an appropriate weight (middle) and a low weight (right) are shown.

Computational requirements

The computational load of the proposed TGV models is essentially that of solving the respective minimization problems numerically. These constitute nonsmooth convex optimization problems in high-dimensional spaces with degrees of freedom determined by the number of pixels in the image. Due to the extensive mathematical study of this problem class, efficient and robust abstract algorithms are available.

In our Matlab implementation, which can be run on recent desktop PCs and notebooks, we decided to use rather simple general purpose methods in order to show that the adaptation to TGV does not require much effort in code development. This served as the basis for the CUDA implementation which was designed to run on every PC with a recent NVIDIA graphics processing unit.

While the algorithms for TGV and TV are essentially similar, one minor drawback of TGV in comparison to TV is the slightly higher computational load arising from the need to update more variables in each iteration step compared to the respective TV method. An extensive analysis of the computation times is beyond the scope of this paper. However, our observations are that the NUFFT constitutes the main part of the computational effort and hence, TGV reconstruction needs only slightly more computation time than TV reconstruction (roughly the factor 1.1 in our proof-of-principle implementation). While this means that TGV currently can only be used in applications where offline image reconstruction or postprocessing is acceptable, this is the case for many iterative TV or compressed sensing methods, too.

As it has also been observed for TV based artifact elimination (24), TGV offers great possibilities of acceleration through parallelization. Using our CUDA-based implementation, the TGV reconstruction of the 32 channel data presented in Fig. 5 was performed in roughly 60–100 seconds depending on amount of subsampling. Likewise, the 12 channel data depicted in Fig. 8 needed, due an increase of iteration steps, approximately 80–110 seconds of reconstruction time on an NVIDIA GTX 280 GPU with 1GB of memory.

Extensions

Another advantage of TGV belonging to the well-examined class of convex regularization functionals is its versatile applicability to all kinds of variational problems. Roughly speaking, it can basically be used in all MRI applications in which the image is subject to optimization, in particular those where TV has already shown to work.

It is possible to use TGV as a regularizer that can be applied directly to array coil data of individual receiver channels. Thus, TGV can be used in combination with all parallel imaging reconstruction methods that first generate individual coil images, which are then combined to a single sum of squares image in the last step, like GRAPPA (25). This is not easily possible with conventional TV because prior to the sum of squares combination, the individual coil images are still modulated with the sensitivities of the receiver coils which will lead to considerable staircasing artifacts, as illustrated in Fig. 2.

Radial Sampling was chosen as the primary application for image reconstruction in this paper, but of course it is also possible to use TGV as a penalty term for randomly subsampled data sets or for data that was not acquired with phased array coils, following the approach of compressed sensing (6).

Another promising application for TGV would be diffusion tensor imaging. Currently, TGV is only defined for scalar functions, but as symmetric tensor fields are inherent in the definition, it can be easily extended to higher order tensor fields and could therefore be used as a regularizer to reconstruct the diffusion tensor.

Let us finally mention that the TGV framework is independent of the space dimension and can thus as well be applied to the denoising/reconstruction of 3D image stacks taking full spatial information into account. The implementations can be extended without greater effort, however, an increase in computational complexity in comparison to sequential 2D processing has to be expected, especially in the case of image reconstruction, with 3D regridding being performed in each iteration step. For denoising applications, nevertheless, these kinds of problems do not occur.

CONCLUSIONS

This work presents TGV for MR imaging, a new mathematical framework which is a marked enhancement of the TV method. While it shares the existing desirable features of TV, it is not based on the limiting assumption of piecewise constant images. It is possible to use TGV in all applications where TV is used at the moment, and in the denoising and image reconstruction experiments of this work, it showed its important features to be able to follow the natural continuous signal changes of biological tissues and imaging methods. TGV is based on a solid mathematical theory within the framework of convex optimization, which ensures that numerical implementations are usually straightforward as a variety of numerical algorithms already exist for these types of problems. However, while both TV and TGV are effective penalty functions for denoising and image reconstruction, the use of a-priori information always introduces other biases in the images. This can lead to image content that is missed, as well as to the introduction of false image features. The diagnostic value of TGV-regularized images in clinical practice has to be investigated in future work.

APPENDIX. MATHEMATICAL BACKGROUND OF TGV

One of the main reasons for the use of Total Variation for image processing problems is the fact that the underlying function space allows for images with discontinuities which usually occur on object boundaries. Even though discontinuities do usually not appear in “real world data”, images are often perceived and idealized as having “jumps” at the edges. Since functions are not differentiable at discontinuities, a definition of the Total Variation without derivatives of u is necessary. Such a requirement is realized by setting

$$\mathrm{TV}\left(u\right)=\sup \left\{{\int }_{\Omega }u\mathrm{div}v\mathrm{d}x\mid v\in {\mathcal{C}}_{\mathrm{c}}^1(\Omega ,{\mathbf{C}}^d),{\mid \mid v\mid \mid }_{\infty }\le 1\right\}$$

for a given complex-valued function u on a domain Ω ⊂ R ^d. Note that this definition is informally linked to [1] by v = −▽u/∣▽u∣, the vector field for which the supremum is attained. The definition of the Total Generalized Variation modifies the set of allowed test functions v as follows:

$${\mathrm{TGV}}_{\alpha }^2\left(u\right)=\sup \left\{{\int }_{\Omega }u{\mathrm{div}}^{2}v\mathrm{d}x\mid v\in {\mathcal{C}}_{\mathrm{c}}^2(\Omega ,S^{d\times d}),{\mid \mid v\mid \mid }_{\infty }\le {\alpha }_0,{\mid \mid \mathrm{div}v\mid \mid }_{\infty }\le {\alpha }_1\right\}$$

letting α ₀, α ₁ > 0 and denoting by S ^d×d the set of complex symmetric matrices. The respective definitions for the divergence and norms read as

$${\left(\mathrm{div}v\right)}_i=\sum _{j=1}^d\frac{\partial v_{\mathit{ij}}}{\partial x_j}{\mathrm{div}}^{2}v=\sum _{i=1}^d\frac{{\partial }^2{v}_{\mathit{ii}}}{\partial x_i^2}+2\sum _{i<j}\frac{\partial v_{\mathit{ij}}}{\partial x_i\partial x_j}$$

and

$$\begin{array}{cc}\hfill {\mid \mid v\mid \mid }_{\infty }& =\underset{x\in \Omega }{\sup }{\left(\sum _{i=1}^d{\mid v_{\mathit{ii}}\left(x\right)\mid }^2+2\sum _{i<j}{\mid v_{\mathit{ij}}\left(x\right)\mid }^2\right)}^{1∕2}\hfill \\ \hfill {\mid \mid \mathrm{div}v\mid \mid }_{\infty }& =\underset{x\in \Omega }{\sup }{\left(\sum _{i=1}^d{\mid \sum _{j=1}^d\frac{\partial v_{\mathit{ij}}}{\partial x_j}\left(x\right)\mid }^2\right)}^{1∕2}\hfill \end{array}$$

Again, u needs not to be differentiated. Also, the latter definition can be informally linked, via Fenchel duality theory, with [2] yielding the same values, see again (9).

APPENDIX: ALGORITHM DESCRIPTION

TGV denoising

The primal-dual algorithm we employed for solving the discretization of the TGV-constrained denoising problem [7] bases on the formulation of [8] as a convex-concave saddle-point problem which is derived by duality principles:

$$\underset{u^h\in U^h,v^h\in V^h}{\min }\underset{p^h\in P^h,q^h\in Q^h}{\max }\frac{1}{2\lambda }{\mid \mid u^h-f^h\mid \mid }_2^2+\langle {\nabla }^h{u}^h-v^h,p\rangle +\langle {\mathcal{E}}^h\left(v^h\right),q\rangle$$ [10]

where p^h, q^h are the dual variables. The sets associated with these variables are given by

$$P^h=\{p^h\in {\mathbf{C}}^{2\mathit{MN}}\mid {\mid \mid p^h\mid \mid }_{\infty }\le {\alpha }_1\}{Q}^h=\{q^h\in {\mathrm{C}}^{3\mathit{MN}}\mid {\mid \mid q^h\mid \mid }_{\infty }\le {\alpha }_0\}$$

We denote by proj_P^h $\left({\tilde{p}}^h\right)$ and proj_Q^h $\left({\tilde{q}}^h\right)$ the Euclidean projectors onto the convex sets P^h and Q^h. The projections can be easily computed by pointwise operations

$${\mathrm{proj}}_{\mathit{ph}}\left({\tilde{p}}^h\right)=\frac{{\tilde{p}}^h}{\max \left(1,\frac{\mid {\tilde{p}}^h\mid }{{\alpha }_1}\right)}{\mathrm{proj}}_{Q^h}\left({\tilde{q}}^h\right)=\frac{{\tilde{q}}^h}{\max \left(1,\frac{\mid {\tilde{q}}^h\mid }{{\alpha }_0}\right)}$$

We further denote by ${\mathrm{prox}}_1^{\tau }\left({\tilde{u}}^h\right)$ the proximal map

$${\mathrm{prox}}_1^{\tau }\left({\tilde{u}}^h\right)=\underset{u^h\in U^h}{\mathrm{argmin}}\frac{{\mid \mid u^h-{\tilde{u}}^h\mid \mid }_2^2}{2\tau }+\frac{{\mid \mid u^h-f^h\mid \mid }_2^2}{2\lambda }$$

which can easily identified as the pointwise operation

$${\mathrm{prox}}_1^{\tau }\left({\tilde{u}}^h\right)=\frac{\lambda {\tilde{u}}^h+\tau f^h}{\lambda +\tau }$$

The primal-dual algorithm for the denoising problem [7] reads as follows:

Algorithm 1. (Primal-dual method for TGV denoising).

1: function TGVdenoise(fh)

2: $u^h,{\stackrel{‒}{u}}^h\leftarrow f^h,v^h,{\stackrel{‒}{v}}^h\leftarrow 0,p^h\leftarrow 0,q^h\leftarrow 0$, choose τ, σ > 0

3:  repeat

4: $p^h\leftarrow {\mathrm{proj}}_{P^h}(p^h+\sigma ({\nabla }^h{\stackrel{‒}{u}}^h-{\stackrel{‒}{v}}^h\left)\right)$

5: $q^h\leftarrow {\mathrm{proj}}_{Q^h}(q^h+\sigma {\mathcal{E}}^h{\stackrel{‒}{v}}^h)$

6: $u_{\mathrm{old}}^h\leftarrow u^h$

7: $u^h\leftarrow {\mathrm{prox}}_1^{\tau }(u^h+\tau {\mathrm{div}}_1^h{p}^h)$

8: ${\stackrel{‒}{u}}^h\leftarrow 2u^h-u_{\mathrm{old}}^h$

9: $v_{\mathrm{old}}^h\leftarrow v^h$

10: $v^h\leftarrow v^h+\tau (p^h+{\mathrm{div}}_2^h{q}^h)$

11: ${\stackrel{‒}{v}}^h\leftarrow 2v^h-v_{\mathrm{old}}^h$

12:  until convergence of uh

13:  return uh

14: end function

Note that iterations are very simple and can therefore be efficiently implemented on parallel hardware such as graphics processing units. The algorithm is known to converge for step-sizes $\sigma \tau \le 2h^2∕(16+h^2+\sqrt{32h^2+h^4})$, in particular for mesh-size h = 1, the choice $\sigma =\tau =1∕\sqrt{12}$ leads to convergence, see (16) for details.

TGV undersampling reconstruction

The discrete optimization problem [9] can solved by applying the same primal-dual method. With a straightforward adaptation of Algorithm 1, however, one needs to compute the proximal map with respect to the data fitting term. Such an approach involves the solution of a linear system of equations which is quite costly. In order to circumvent this, we also dualize with respect to the data fitting term. The resulting convex-concave saddle-point problem is obtained as

$$\begin{array}{cc}\hfill \underset{u^h\in U^h,v^h\in V^h}{\min }\underset{p^h\in P^h,q^h\in Q^h,r^h\in R^h}{\max }\langle {\nabla }^h{u}^h-v^h,p^h\rangle & +\langle {\mathcal{E}}^h\left(v^h\right),q^h\rangle \hfill \\ \hfill +& \langle K^h{u}^h-g^h,r^h\rangle -\frac{\lambda }{2}{\mid \mid r^h\mid \mid }_2^2\hfill \end{array}$$ [11]

where r^h ∈ R^h is the dual variable with respect to the data fitting term. Further, let ${\mathrm{prox}}_2^{\sigma }\left({\tilde{r}}^h\right)$ be the proximal map

$${\mathrm{prox}}_2^{\sigma }\left({\tilde{r}}^h\right)=\underset{r^h\in R^h}{\mathrm{argmin}}\frac{{\mid \mid r^h-{\tilde{r}}^h\mid \mid }_2^2}{2\sigma }+\frac{\lambda }{2}{\mid \mid r^h\mid \mid }_2^2\iff {\mathrm{prox}}_2^{\sigma }\left({\tilde{r}}^h\right)=\frac{{\tilde{r}}^h}{1+\sigma \lambda }$$

The primal-dual algorithm for the reconstruction problem [6] is as follows:

Algorithm 2. (PD method for TGV undersampling reconstruction).

1: function TGVreconstruct (gh)

2: $u^h,{\stackrel{‒}{u}}^h\leftarrow 0,v^h,{\stackrel{‒}{v}}^h\leftarrow 0,p^h\leftarrow 0,q^h\leftarrow 0,r^h\leftarrow 0$, choose τ, σ > 0.

3:  repeat

4: $p^h\leftarrow {\mathrm{proj}}_{P^h}(p^h+\sigma {\nabla }^h({\stackrel{‒}{u}}^h-{\stackrel{‒}{v}}^h\left)\right)$

5: $q^h\leftarrow {\mathrm{proj}}_{Q^h}\left(q^h+\sigma {\mathcal{E}}^h{\stackrel{‒}{v}}^h\right)$

6: $r^h\leftarrow {\mathrm{prox}}_2^{\sigma }\left(r^h+\sigma (K^h{\stackrel{‒}{u}}^h-g^h)\right)$

7: $u_{\mathrm{old}}^h\leftarrow u^h$

8: $u^h\leftarrow u^h+\tau \left({\mathrm{div}}_1^h{p}^h-{\left(K^h\right)}^{\ast }{r}^h\right)$

9: ${\stackrel{‒}{u}}^h\leftarrow 2u^h-u_{\mathrm{old}}^h$

10: $v_{\mathrm{old}}^h\leftarrow v^h$

11: $v^h\leftarrow v^h+\tau \left(p^h+{\mathrm{div}}_2^h{q}^h\right)$

12: ${\stackrel{‒}{u}}^h\leftarrow 2v^h-v_{\mathrm{old}}^h$

13:  until convergence of uh

14:  return uh

15: end function

Again, this algorithm is convergent provided that $\sigma \tau <h^2∕(h^2+\sqrt{8}h+8)$, in particular for mesh-size h = 1, the choice $\sigma =\tau =1∕\sqrt{12}$ is sufficient.