Abstract
We compared the powers of the likelihood ratio test (LRT) and the Pearson correlation test (CT) from empirical Bayes estimates (EBEs) for various designs and shrinkages in the context of nonlinear mixed-effect modeling. Clinical trial simulation was performed with a simple pharmacokinetic model with various weight (WT) effects on volume (V). Data sets were analyzed with NONMEM 7.2 using first-order conditional estimation with interaction and stochastic approximation expectation maximization algorithms. The powers of LRT and CT in detecting the link between individual WT and V or clearance were computed to explore hidden or induced correlations, respectively. Although the different designs and variabilities could be related to the large shrinkage of the EBEs, type 1 errors and powers were similar in LRT and CT in all cases. Power was mostly influenced by covariate effect size and, to a lesser extent, by the informativeness of the design. Further studies with more models are needed.
Population pharmacokinetics (PK) is increasingly used in drug development and is based on nonlinear mixed-effect models (NLMEMs).1 Several software algorithms developed to estimate the parameters of these models have been compared, as by Plan et al.2 The first and most popular software is NONMEM and, since version 7, several estimation algorithms have been available, such as first-order conditional estimation with interaction (FOCEI) and stochastic approximation expectation maximization (SAEM). Gibiansky et al.3 compared the performance of NONMEM estimation methods in simulated examples of a target-mediated drug disposition model using either default options or by designing the options to get the best possible results for each algorithm (“expert” options). They demonstrated the importance of the estimation options in the algorithm performance by comparing standard errors of NONMEM estimates with those predicted using PFIM 3.2 optimal design software.4 The SAEM algorithm provided estimates similar to those of FOCEI.
For a given model, when population parameters are estimated, individual parameters from individual observations can be estimated by a Bayesian approach using the maximum a Posteriori method. If the data are from the individuals used to estimate population parameters, the same approach is used, but it is an empirical Bayes estimation. These individual parameter estimates are useful for investigating the influence of the individual's baseline characteristics on the individual parameters.5
Population analysis allows the use of sparse sampling, but the sampling design influences the precision of population estimates.6 The informativeness of a data set in parameter estimation is a function of the number of subjects and of the number and timing of the samples.7 Optimal design methodology allows determination of the most informative design with constraints. It computes a criterion, such as the D-optimality criterion, from the Fisher information matrix (MF), which depends on the structural model, the parameter values, and the design.8
Thus, the design also greatly influences the precision of empirical Bayes estimates (EBEs). For a rich design, the a posteriori distributions of the individual random effects are centered on the true values with small standard deviations. When little information is available for each individual (sparse design), the means of these distributions regress towards the population mean with larger SDs. A formula from linear mixed-effect methodology has been used to predict this shrinkage of EBEs associated with a design.9 This shrinkage should be evaluated before conducting a clinical trial. Using a simulation study, we provide here a good prediction of shrinkage using the Bayesian Fisher information matrix (MBF)9,10, avoiding the use of extensive simulations.
In a study of the impact of shrinkage on model building, Savic and Karlsson11 show that covariate relationships may be masked or falsely induced and that the shape of the true relationship may be distorted when examined using a test of the correlation between the EBEs and the covariates. Savic and Karlsson11 recommend as follows: “When shrinkage is high, other diagnostics and more direct population model estimation need to be employed in model building and evaluation.” They suggest more extensive use of the likelihood ratio test (LRT) test for covariate evaluation and selection when shrinkage is large, which is much more time consuming than selection from EBEs.
However, to our knowledge, no one has compared the power of LRT with the power of the correlation test (CT) with respect to design selection and its expected shrinkage. We therefore compared type 1 errors and power in detecting the effect of a continuous covariate using either the LRT or the CT based on EBEs according to various designs, along with various associated shrinkages.
Through an extensive Monte–Carlo simulation of a simple one-compartment PK model, we compared the performances of FOCEI and SAEM algorithms before evaluating the type 1 errors and powers of the tests to detect covariate influences on individual parameters. We also created several scenarios to vary the informativeness of the PK design and therefore the associated shrinkage.
Results
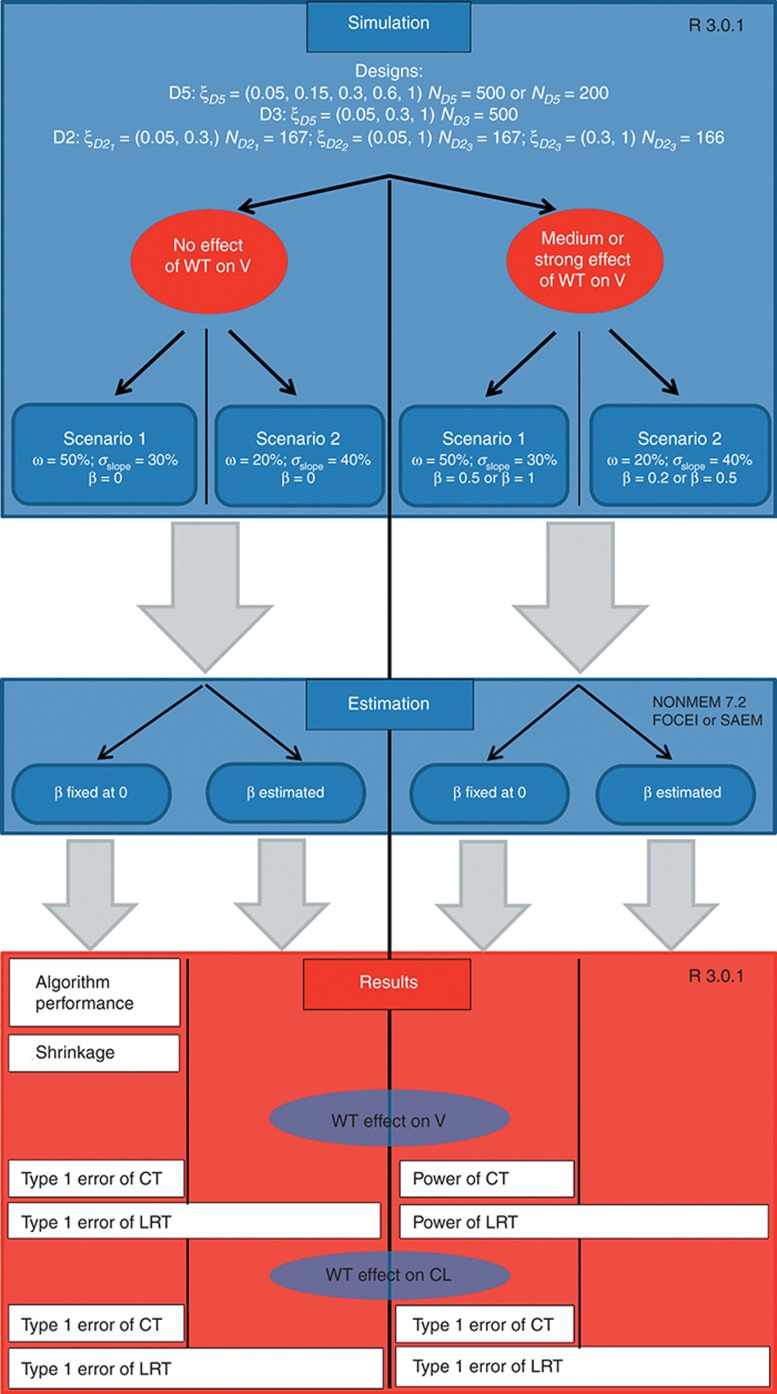
Figure 1 summarizes the different clinical trial simulations performed.
Figure 1.
Global scheme of the clinical trial simulations. CL, clearance; CT, correlation test; FOCEI, first-order conditional estimation with interaction; LRT, likelihood ratio test; SAEM, stochastic approximation expectation maximization; V, volume; WT, weight.
Algorithm performance
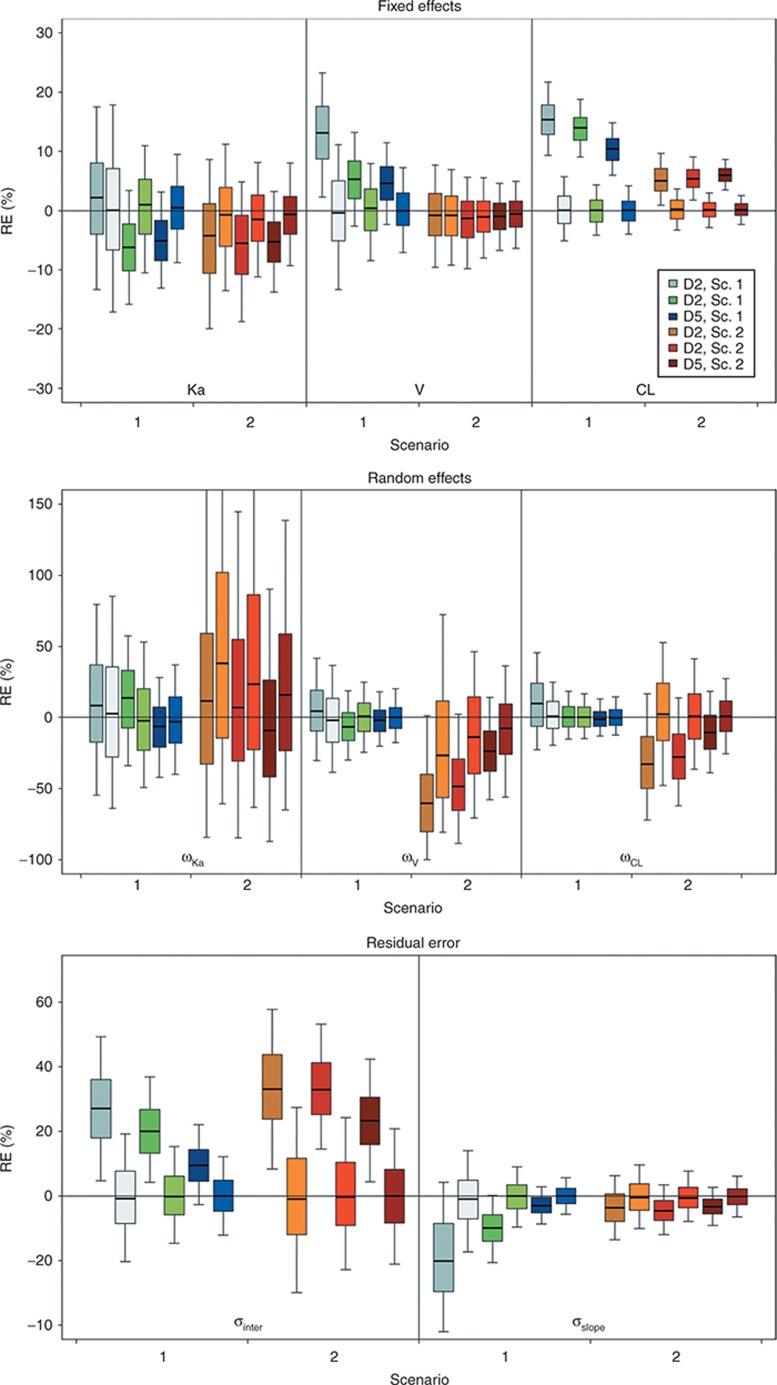
Figure 2 presents, for each scenario and each design with N = 500, the boxplots of relative errors on parameters estimated using either FOCEI or SAEM with NONMEM 7.2. SAEM always provided more accurate estimates than FOCEI, except for ωka in scenario 2. Estimates with the FOCEI algorithm were often slightly biased, mainly for volume (V), clearance (CL), ωV, and ωCL, and for residual error parameters. Bias was more marked for designs D2 and D3. Median values of relative errors using SAEM were less influenced by the design and were always close to 0%.
Figure 2.
Boxplot of relative error (RE; %) on estimated fixed effects (top) without covariate effect, random effects (middle), and residual error parameters (bottom) according to scenario 1 or 2, the design, and the estimation algorithms. Boxplots represent the median, quartiles, and 5–95% percentiles. Colors stand for the design and the scenario. For the same color, the dark areas represent the first-order conditional estimation with interaction algorithm and the pale areas denote the stochastic approximation expectation maximization algorithm. Sc., scenario.
Considering that SAEM gave more accurate estimates than FOCEI, only SAEM power estimates are presented below. FOCEI power estimates are available in the Supplementary Materials online.
Prediction of shrinkage
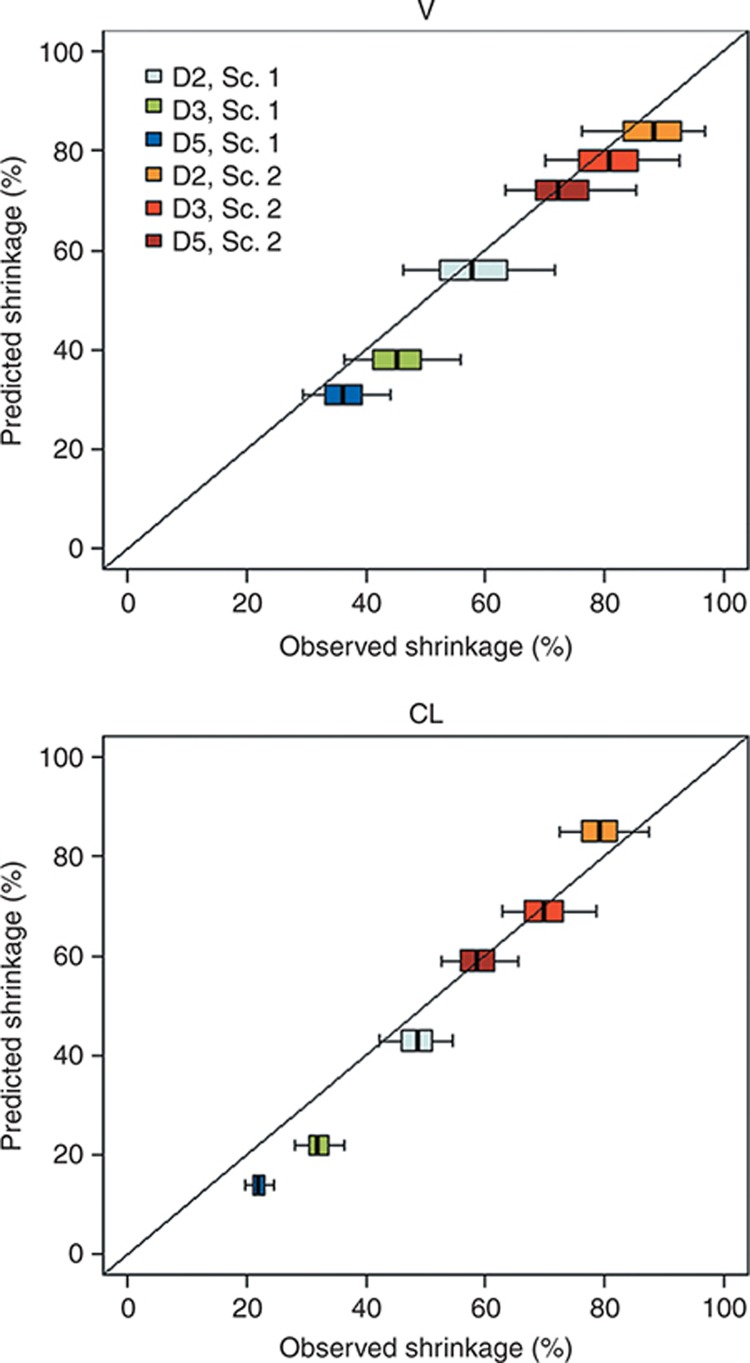
Figure 3 shows predicted shrinkage vs. boxplots of observed shrinkage on V (left) and CL (right) for each design and each scenario without covariate effect. The simulated scenarios generated predicted shrinkage values that increased from D5 to D2. Confirming previous results,9 MBF gave a good prediction of observed shrinkage. The boxplots were closely centered on the identity line, with small deviations for low shrinkages, for which there was a trend to predict lower shrinkages (but by less than or around 10% from median values of observed shrinkage).
Figure 3.
Predicted shrinkage (%) value vs. boxplot of observed shrinkage (%) with the stochastic approximation expectation maximization algorithm for the 1,000 replicates without covariate effect, for parameters volume (V) and clearance (CL), each design, and scenarios 1 or 2. Colors stand for the design and the scenario. Sc., scenario.
Evaluation of tests
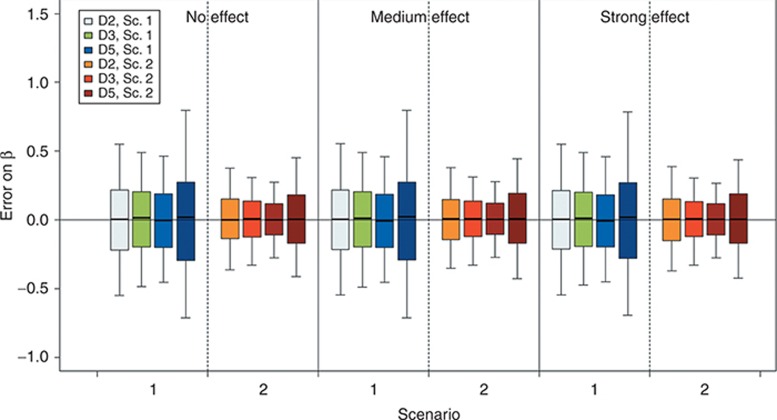
Figure 4 presents the boxplot of the error on β estimates for each scenario, design, and covariate effect. The covariate effect was always correctly estimated. When comparing the effect of the total number of subjects, the boxplots clearly show an increase in the SD of estimates with decrease in number of subjects.
Figure 4.
Boxplot of error on the estimated β value with the stochastic approximation expectation maximization algorithm and for a covariate effect on volume (V), according to scenarios 1 or 2, the design, the simulated covariate effect value, and the number of subjects. Boxplots represent the median, quartiles, and 5–95% percentiles. Colors stand for the design and the scenario. For D5, pale and dark areas are used, respectively, for designs with 500 and 200 subjects. Sc., scenario.
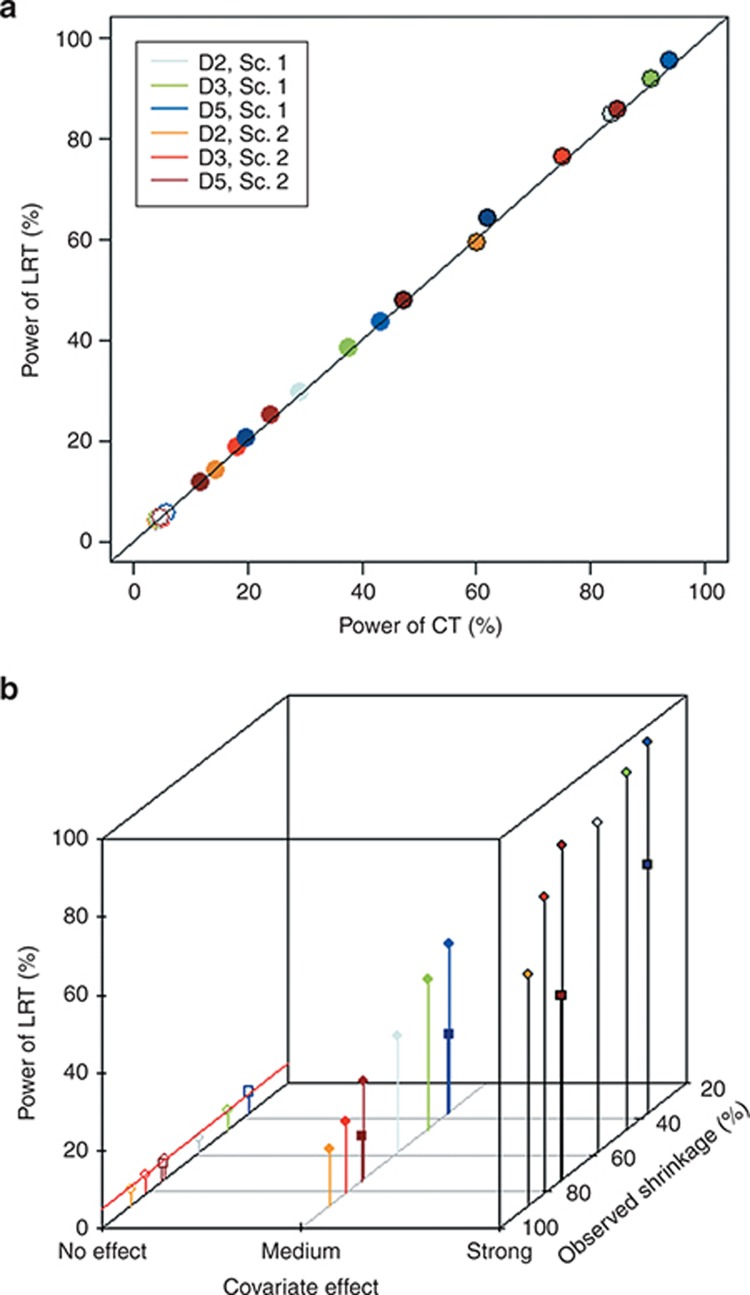
Type 1 errors and the powers of tests between weight (WT) and V are presented in Table 1 for all scenarios and designs and are illustrated in Figure 5. Type 1 error was similar for LRT and CT, even for high values of shrinkage, and in all cases, it was within the prediction interval of 3.65–6.35%. The power of LRT was equal to the power of CT in all scenarios, even with high shrinkage, the greatest difference being 2% for D5 with 200 subjects in scenario 1. Figure 5a illustrates how LRT and CT have very similar type 1 error and power.
Table 1. Type 1 error (%, β = 0), power (%, β ≠ 0) of LRT and CT tests for covariate effect, and predicted shrinkage on V and CL for all scenarios, simulated covariate effect levels, and designs.
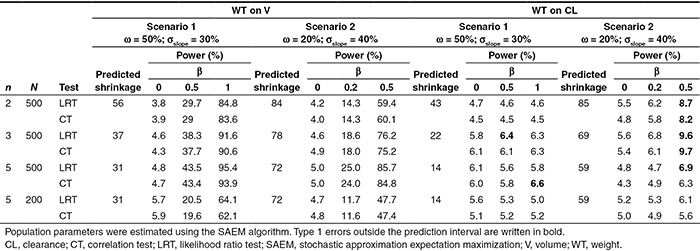
Figure 5.
Power of likelihood ratio test (LRT) between weight (WT) and volume (V) (%), for all scenarios and designs (estimation with stochastic approximation expectation maximization algorithm) vs. (a) correlation test (CT; %; the black line represents the identity line). (b) Observed shrinkage on V (%) and covariate effect. Colors stand for the design and the scenario. Covariate effect is expressed by the background and colors: no effect with a colored line around dots, medium effect with fully colored dots, and strong covariate effect with black line around a colored dot. For D5, pale and dark areas are used respectively for designs with 500 and 200 subjects. Sc., scenario.
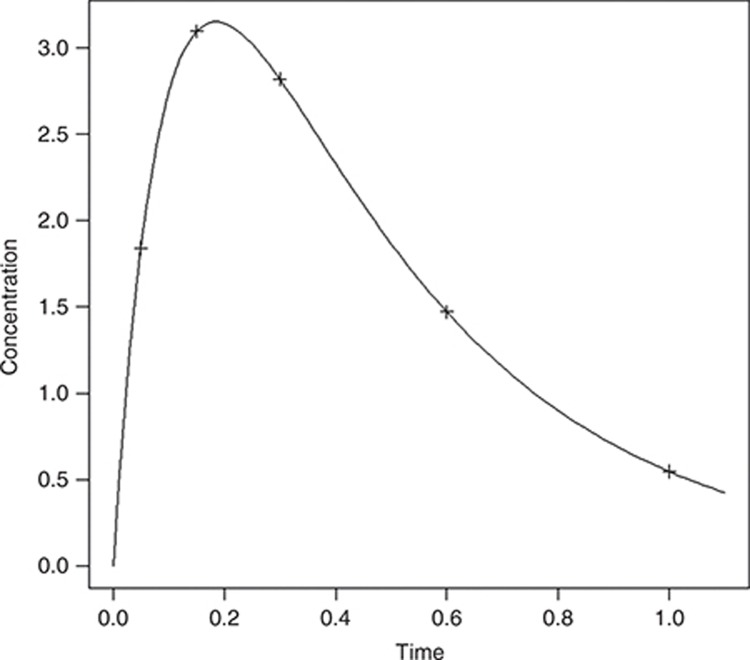
The power was 95% for scenario 1 and 86% for scenario 2, with rich designs and a strong effect of WT. Figure 5b shows the lack of trend between shrinkage and power across scenarios and covariate effects. As expected, the power of tests was directly linked to the covariate effect. For both scenarios, a design modification led to a 25% increase in power when, for a given scenario and design, a change in covariate effect size induced a 50% increase.
When comparing N = 500 with D2 and N = 200 with D5, both with the same total number of samples, power was higher for D2 with a similar type 1 error.
When the covariate effect on CL was explored, type 1 error was similar for LRT and CT in all cases (Table 1). When no covariate effect was simulated on V, type 1 error remained within the range of the prediction interval, around 5%. Surprisingly, this type 1 error increased with the β value, especially in scenario 2. Type 1 errors were in all cases around 5% in scenario 1, except for D3 with β = 0.5 (N = 500, 6.4% for LRT) and for D5 with β = 1 (N = 500, 6.6% for CT). Considering scenario 2, the type 1 error computed for a strong covariate effect led to a significant increase in the type 1 error, for D2 (8.7% for LRT and 8.2% for CT), D3 (9.7% for CT and 9.6% for LRT), and D5 (N = 500, 6.9% for LRT). In this scenario, the increase in type 1 error is linked to higher correlation between individual V and CL. The median correlation was −0.25 for D2 and −0.23 for D3. Median correlation was −0.13 for scenario 2, D5, whereas for scenario 1, almost no correlation in the EBEs was found.
Discussion
We have compared, for different scenarios and different PK sampling designs leading to various amounts of shrinkage, the type 1 error and power of two tests to detect the effect of a continuous covariate on a PK parameter: the LRT, which compares the log-likelihoods of two nested models; and a correlation test between the covariate and the EBEs.
Surprisingly, both tests showed the same power irrespective of the scenario or the design considered. Indeed, even if LRT is based on the fitting of two models to get the two likelihoods, it did not show greater power than a simple CT based on EBEs, even with high shrinkage. As a conclusion, because of its faster execution, we think that the CT should be used in a first screening of the relevant covariates, and then the selected covariates can be tested in a stepwise procedure to build the full covariate model using the LRT.
Savic and Karlsson11 highlighted a possible issue when using the CT to screen covariates when there is high shrinkage in the EBEs and recommended a test that does not rely on EBEs. Our study shows that such a test, the LRT for instance, does not behave differently from the CT, whatever the shrinkage. Indeed, the loss of power associated with high shrinkage in CT has the same influence in the LRT and is linked with less information in the design. It also showed that the size of the covariate effect is the main factor linked to any covariate detection issue. Bertrand et al.12 showed a similar link between power and covariate effect. To a lesser extent, the information in the design also has an impact on the power, which decreases when the number of sampling times per subject decreases. Furthermore, when comparing the two designs with the same number of samples, power was found to be greater for 500 subjects (D2) than for 200 (D5), though the latter has lower shrinkage (Table 1, with β = 1, with WT effect on V). This decrease in power for 200 subjects can be explained by the very challenging conditions we used to simulate the covariate effect (rather small variance of WT and rather small covariate effect). These results are in accordance with the loss of power associated with decreased number of subjects reported by Liu et al.13 and Bertrand et al.14 Nevertheless, even if the LRT was not significant, the covariate effect, β, was always correctly estimated.
Considering the induction of correlation due to high shrinkage, a slight inflation of type 1 error in scenario 2 was found. This inflation could be explained by the EBE correlation between V and CL. The influence of design on EBE correlation should be investigated in future work. Further work is also needed to explore the influence of design on a full covariate modeling process, with several covariates influencing the parameters.
This simulation study also confirms the good prediction of shrinkage using the Bayesian Fisher information matrix, as already shown in ref. 9, when planning clinical studies. This could be helpful in the design of population studies wherein individual estimation of individual parameters with small shrinkage is needed.
As expected, our investigations showed that the SAEM algorithm reliably and accurately estimates population parameters, even for sparse designs. FOCEI gave surprisingly biased results for such a simple model even with rather informative designs. This bias could be explained by the rather large residual error used in our simulations, inducing bias in the linearization during FOCEI.15 This result is not unusual considering previous comparisons of FOCEI and SAEM for continuous data. Girard and Mentré reported that methods without likelihood approximations, such as SAEM (using a version that later became MONOLIX (MOdèles NOn LInéaires à effets miXtes)) perform better than first order or FOCEI.16 Using a previous version of NONMEM (5 and 6β), Dartois et al.17 reported very good estimation of parameters despite some discrepancies in residual error estimates and recommended the use of exact methods such as SAEM instead of FOCEI. At the time of these two studies, SAEM was not implemented in NONMEM. In addition, Ueckert et al.18 and Johannson et al.19 showed the same loss of “robustness” and “precision” of FOCEI compared with SAEM, for continuous data, especially when mu-modeling is used for SAEM in NONMEM 7. Finally, Plan et al.2 compared various algorithms using NONMEM, Statistical Analysis System, MONOLIX, and R and found that FOCEI was in some cases more biased than SAEM, especially for sparse designs, along with issues related to the convergence of the algorithm.
Results for the power of CT and LRT for data sets analyzed using the FOCEI algorithm can be found in the Supplementary Materials online for designs D2 and D5 with N = 500 subjects. Despite some rather biased estimations of population parameters with FOCEI, there was no bias in the estimation of β. Type 1 error and power were similar for FOCEI and SAEM, with only a slight inflation of the type 1 error in scenario 2 for sparse designs. Our selection of the NONMEM 7.2 algorithm and options relied on advice and results presented in ref. 3. Further work is needed to explore the influence of the algorithm options (number of samples and iterations for Monte Carlo importance sampling (IMP) algorithm) on the likelihood computation.
Larger residual error variances than those used in our study may be rather unusual in the field of pharmacometrics. We performed our study for a wide range of shrinkages, and the tests performed similarly whether the generated shrinkage was low or high (Table 1). The use of different error models and the magnitude of those errors could affect the amount of generated shrinkage.9,20 A high residual error would obviously decrease the power of the test. Further work is needed on the extent to which similarities between CT and LRT are influenced by the level and form of residual error.
In our simulation study, we used a rather narrow distribution of covariates and challenging medium covariate effects. This was done on purpose because, for greater covariate distribution and larger covariate effect, the power was very high and we could not investigate the influence of other factors. We studied covariate effects using a power function along with an exponential form of random effects. These forms are the most used in population PK modeling. Studies using other forms of random effects and covariate models are therefore needed.
We only explored the power of covariate detection using LRT and CT with different designs and variabilities. LRT and CT are still the most used in population PK. Future work should focus on other covariate selection methods, such as Generalized Additive Modeling (GAM) analysis21 and Least Absolute Shrinkage and Selection Operator (LASSO),22 but these are mainly used when several covariates are considered. Furthermore, the impact of structural model misspecification could be evaluated along with the effect of design on the covariate selection process.23
The main objective of our work was to compare the performance of CT and LRT for different shrinkages. Although we used a rather simple model, the outcomes provided important information in line with the findings of Savic and Karlsson,11 and the screening of covariates was done with CT instead of the more time-consuming LRT. The next step will be to confirm our results with a more complex model, such as a target-mediated drug disposition model, which involves the use of differential equations and for which use of CT should be all the more beneficial in a model development process, considering the runtime that such a system requires for parameter estimation.
Methods
Models and notations
For a given individual, let yi be the vector of n observed concentrations at n sampling times ξi = {ti,1,…,ti,n} for subject i and f be the known function describing the PK model. So, yi was assumed to be modeled as follows:
 |
where Θi is the p vector of individual PK parameters, Θi = (Θi,1,…,Θi,p)T; εi is the random error, following a normal distribution with zero mean and variance Σ(Θi, ξi). Here, Σ(Θi, ξi) is defined as the variance matrix of a combined error model with an additive component σinter and a proportional one σslope; hence, Σ(Θi, ξi) = diag ((σinter + σslope f(Θi, ξi))2).
Individual parameters Θi are defined as Θi = g(Θ, ηi) where Θ is the vector of p fixed effects and ηi is the vector of p individual random effects ηi = (ηi,1,…,ηi,p)T. Random effects ηi follow a normal distribution with zero mean and variance Ω. For Ω, a diagonal p × p matrix of variances of random effects 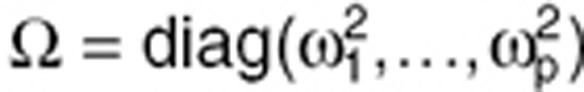 was assumed. For g(Θ,ηi), an exponential model, where
was assumed. For g(Θ,ηi), an exponential model, where 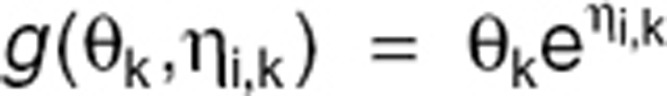 was considered, k = {1,…,p}. The vector Ψ of population parameters is composed of
was considered, k = {1,…,p}. The vector Ψ of population parameters is composed of 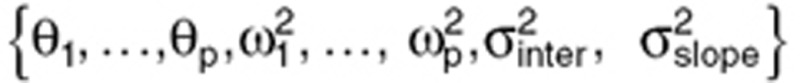 .
.
In PK modeling, population parameters are estimated by the method of maximum likelihood. Individual parameters are estimated by a Bayesian approach using the maximum a Posteriori as follows:
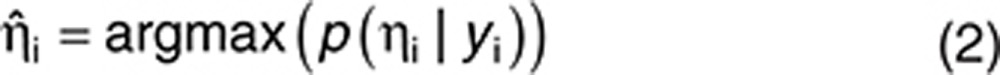 |
where p(ηi|yi) is the probability distribution of ηi given yi, which can be expressed using the Bayes theorem as shown below:
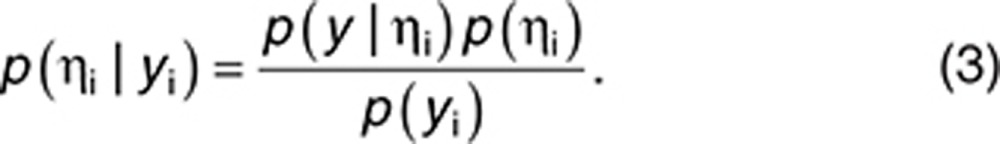 |
To estimate 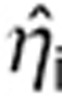 by maximum a Posteriori is equivalent to minimizing, with respect to ηi:
by maximum a Posteriori is equivalent to minimizing, with respect to ηi:
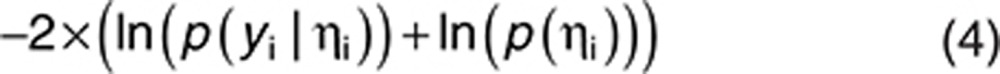 |
This is equal to
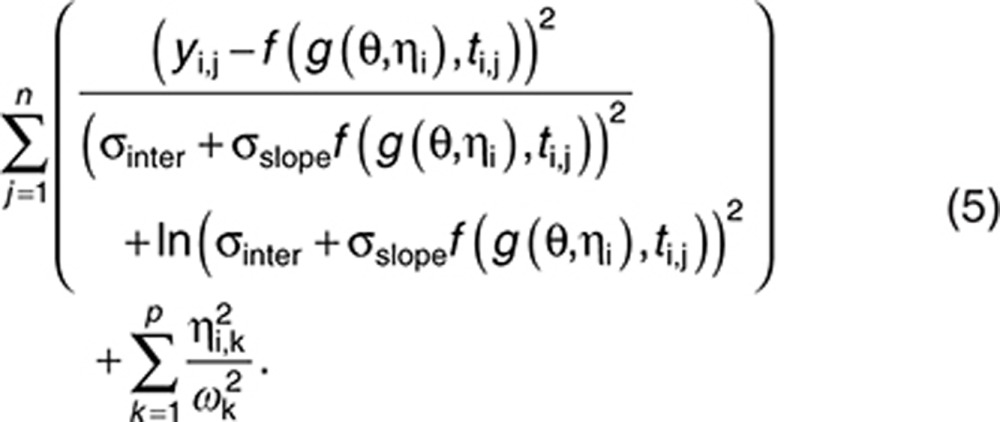 |
PK model of the simulation study
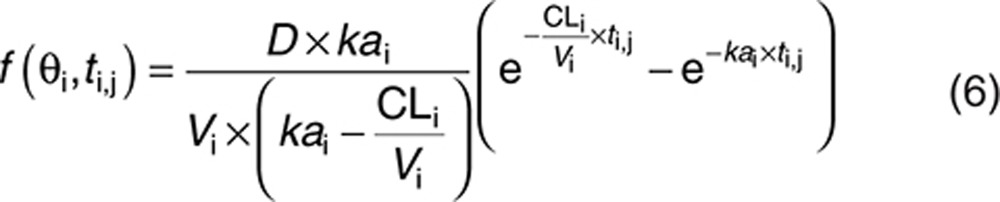
A simulated example involving a one-compartment model with a single oral administration was used. The three parameters are the absorption rate (ka), the apparent volume of distribution (V), and the apparent clearance (CL). For a given dose D, the prediction at time ti,j is shown below:
 |
We chose Θka = 10, ΘV = 0.2, and ΘCL = 0.5 with a dose D = 1. As this model is theoretical, we did not consider any specific units. The PK profile for these typical values of parameters is shown in Figure 6. To explore the influence of shrinkage in various situations, two scenarios were considered: for scenario 1, ω = 50% for each parameter and σslope = 30%;, for scenario 2, ω = 20% and σslope = 40%. Σinter was set to 0.15 in both cases, which is small with respect to the range of concentrations covered by the PK model (see Figure 6 for the mean concentration–time course profile).
Figure 6.
Pharmacokinetic (PK) profile for the mean PK parameters of the simulated example with design D5.
Study design
N = 500 subjects were simulated using three designs. First, a design with five samples (D5) per subject, ξD5 = {0.05, 0.15. 0.3, 0.6, 1}, was simulated and is presented in Figure 6. The simulation code is provided in the Supplementary Materials online. For these sampling times, the most informative design with three samples (D3) was then determined using a D-optimality approach: ξD2 = (0.05,0.3,1}. Finally, from ξD3, a two-sample design (D2) with three groups of one-third of the N subjects each was created: 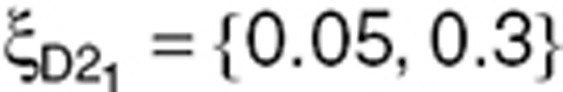 (
(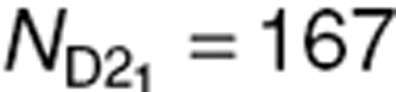 subjects),
subjects), 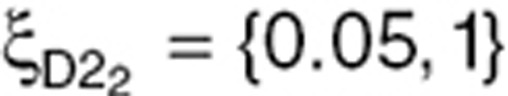 (
( subjects), and
subjects), and 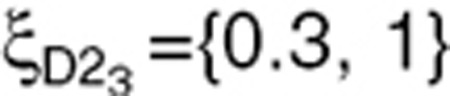 (
(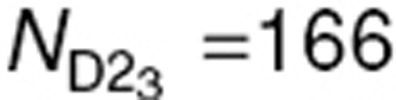 subjects). Design D5 was also evaluated with N = 200 subjects, which corresponds to the same total number of observations as D2 with 500 subjects.
subjects). Design D5 was also evaluated with N = 200 subjects, which corresponds to the same total number of observations as D2 with 500 subjects.
Evaluation of estimation
In the first step, R = 1,000 data sets were simulated without covariate effect for each design (D2, D3, and D5 with N = 500) and each scenario. Each data set was analyzed using NONMEM 7.224 with FOCEI and with SAEM to explore algorithm performances. Expert options inspired by Gibiansky et al.3 were used for the setting of the SAEM algorithm (INTERACTION NBURN=15000 ISAMPLE=3 NITER=5000 SIGL=8 CTYPE=3 CINTERVAL=100). NONMEM codes are available in the Supplementary Materials online. Relative errors of estimations of population parameters, (in percentage), were computed for each component as in Eq. 7:
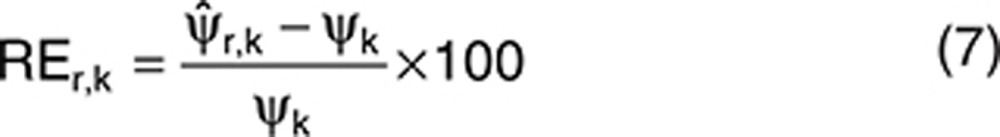 |
where 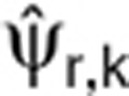 is the kth component of the vector of the estimated population parameter for the rth data set and
is the kth component of the vector of the estimated population parameter for the rth data set and 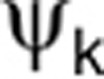 is the value used in the simulation.
is the value used in the simulation.
Prediction of shrinkage
As in the study by Combes et al.,9 the predicted shrinkage is computed as I−W(ξ) where
 |
MBF can be approximated by a first-order linearization of the model25:
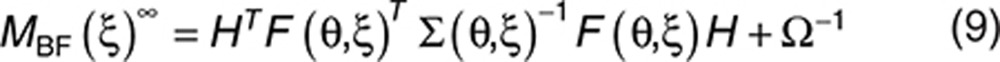 |
where H = diag(Θ1,…,Θp) and 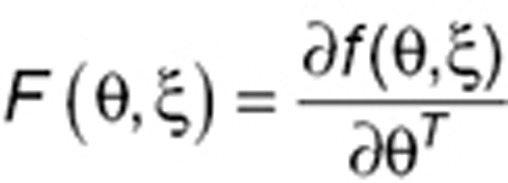 . As Ω is diagonal, the diagonal elements of I−W, given in the Eq. 8, represent the ratio of the predicted variance of estimation using a Bayesian estimation and the a priori variance. When
. As Ω is diagonal, the diagonal elements of I−W, given in the Eq. 8, represent the ratio of the predicted variance of estimation using a Bayesian estimation and the a priori variance. When 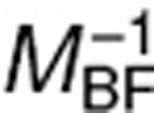 is close to Ω (no information for the individual), I−W is close to I. In that case, shrinkage is expected to be high, close to 100%.
is close to Ω (no information for the individual), I−W is close to I. In that case, shrinkage is expected to be high, close to 100%.
The selected designs and scenarios were chosen to lead to a wide range of predicted shrinkages on V and CL, between 31 and 84% for volume and between 14 to 85% for clearance (see results in Table 1).
For each data set r, the observed shrinkage of each component k was computed as follows:
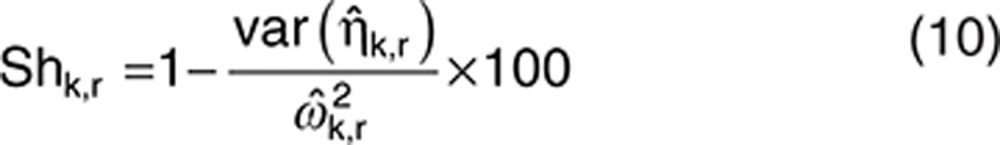 |
The distribution of the 1,000 observed shrinkages from the 1,000 data sets was compared with the predicted shrinkage.
Evaluation of tests for covariate detection
We then considered a covariate model describing the influence of the weight (WT) on volume using a power function:
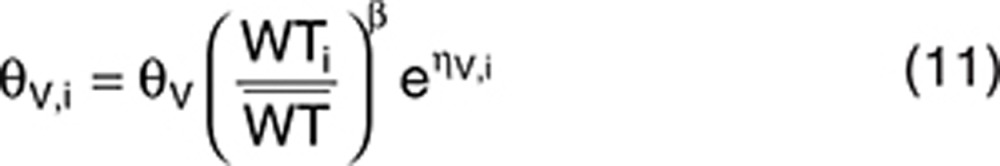 |
We assumed a log-normal distribution of WT with a median 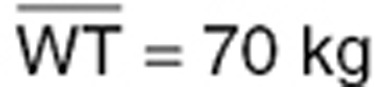 and a coefficient of variation of 10% (quantiles 2.5–97.5%: 57–85 kg). We considered this distribution range so as to avoid a very large distribution, which would contribute to very powerful covariate detection whatever the test and design. Designs involving 500 subjects led to powers close to 100% for LRT and CT, whatever the number of samples per individual.
and a coefficient of variation of 10% (quantiles 2.5–97.5%: 57–85 kg). We considered this distribution range so as to avoid a very large distribution, which would contribute to very powerful covariate detection whatever the test and design. Designs involving 500 subjects led to powers close to 100% for LRT and CT, whatever the number of samples per individual.
R = 1,000 data sets for each design and scenario were simulated. For scenario 1, we first considered a case close to an allometric effect with β = 1. We then considered a smaller value of that effect β = 0.5 (medium effect) and no effect β = 0. Regarding scenario 2, as smaller variances were considered, we reduced the values of β to generate a strong covariate effect (β = 0.5), a medium effect (β = 0.2), or no effect (β = 0).
Using these simulations, we evaluated the properties of two tests in detecting the effect of the weight (WT) on volume (V). First, the LRT, which compares the log-likelihoods of the two nested models (with β fixed to 0 or β on V estimated), was considered significant when the difference in −2 × log-likelihood was greater than 3.84, (the 95% limit of a χ2 distribution with one degree of freedom). The second test was a parametric correlation Pearson test between EBEs of volume from a population analysis with no covariate in the model and weights.
Data sets were analyzed with the SAEM algorithm for population estimation. Likelihood was then computed by importance sampling (algorithm IMP in NONMEM 7.2 with 10 iterations and 3,000 samples).
We first estimated the covariate effect by exploring the error on the estimated β values as the estimated value of β minus the true value used for simulation.
Type 1 error α was then computed as the percentage of significant tests (P value < 0.05) in the R replicates simulated assuming a null hypothesis H0 (β = 0). We computed the 95% prediction interval for a binomial distribution with a probability of 0.05 and 1,000 replicates using the 2.5 and 97.5% percentiles. The prediction interval was 3.65–6.35%. For a test with α = 0.05, we expect the estimated type 1 error to lie within this interval. The power of tests was computed as the percentage of significant tests in the R replicates simulated assuming the alternative hypothesis H1 (β ≠ 0).
Finally, in order to evaluate the risk of induction of covariate effects because of shrinkage,11 the same tests were evaluated for the relationship between WT and CL, although no WT effect was simulated in CL. We computed type 1 error for CT and LRT in the effect of WT on CL. Results (tests, predicted and observed shrinkage) were computed using R 3.0.1.
Author Contributions
F.P.C., N.F., S.R., and F.M. designed the research. F.P.C. performed the research. F.P.C., S.R., and F.M. analyzed the results. F.P.C., S.R., N.F., and F.M. wrote the manuscript.
Conflict of Interest
F.P.C. has a research grant from Roche and the French government. S.R and N.F work for F. Hoffmann-La Roche Ltd, in Pharma Research and Early Development, Clinical Pharmacology. As an associate editor for CPT: PSP, F.M. was not involved in the review or decision process for this manuscript.
Study Highlights

Acknowledgments
During this work, the PhD of F.P.C. was sponsored by a Convention Industrielle de Formation par la Recherche from the French government and the Institut Roche de Recherche et Médecine Translationnelle. The authors thank IFR02 and Hervé Le Nagard for the use of the Centre de Biomodélisation.
Supplementary Material
References
- Pillai G.C., Mentré F., Steimer J.L. Non-linear mixed effects modeling - from methodology and software development to driving implementation in drug development science. J. Pharmacokinet. Pharmacodyn. 2005;32:161–183. doi: 10.1007/s10928-005-0062-y. [DOI] [PubMed] [Google Scholar]
- Plan E.L., Maloney A., Mentré F., Karlsson M.O., Bertrand J. Performance comparison of various maximum likelihood nonlinear mixed-effects estimation methods for dose-response models. AAPS J. 2012;14:420–432. doi: 10.1208/s12248-012-9349-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gibiansky L., Gibiansky E., Bauer R. Comparison of Nonmem 7.2 estimation methods and parallel processing efficiency on a target-mediated drug disposition model. J. Pharmacokinet. Pharmacodyn. 2012;39:17–35. doi: 10.1007/s10928-011-9228-y. [DOI] [PubMed] [Google Scholar]
- Bazzoli C., Retout S., Mentré F. Design evaluation and optimisation in multiple response nonlinear mixed effect models: PFIM 3.0. Comput. Methods Programs Biomed. 2010;98:55–65. doi: 10.1016/j.cmpb.2009.09.012. [DOI] [PubMed] [Google Scholar]
- Bonate P.L. Covariate detection in population pharmacokinetics using partially linear mixed effects models. Pharm. Res. 2005;22:541–549. doi: 10.1007/s11095-005-2492-z. [DOI] [PubMed] [Google Scholar]
- al-Banna M.K., Kelman A.W., Whiting B. Experimental design and efficient parameter estimation in population pharmacokinetics. J. Pharmacokinet. Biopharm. 1990;18:347–360. doi: 10.1007/BF01062273. [DOI] [PubMed] [Google Scholar]
- Retout S., Mentré F., Bruno R. Fisher information matrix for non-linear mixed-effects models: evaluation and application for optimal design of enoxaparin population pharmacokinetics. Stat. Med. 2002;21:2623–2639. doi: 10.1002/sim.1041. [DOI] [PubMed] [Google Scholar]
- Green B., Duffull S.B. Prospective evaluation of a D-optimal designed population pharmacokinetic study. J. Pharmacokinet. Pharmacodyn. 2003;30:145–161. doi: 10.1023/a:1024467714170. [DOI] [PubMed] [Google Scholar]
- Combes F.P., Retout S., Frey N., Mentré F. Prediction of shrinkage of individual parameters using the bayesian information matrix in non-linear mixed effect models with evaluation in pharmacokinetics. Pharm. Res. 2013;30:2355–2367. doi: 10.1007/s11095-013-1079-3. [DOI] [PubMed] [Google Scholar]
- Merlé Y., Mentré F. Bayesian design criteria: computation, comparison, and application to a pharmacokinetic and a pharmacodynamic model. J. Pharmacokinet. Biopharm. 1995;23:101–125. doi: 10.1007/BF02353788. [DOI] [PubMed] [Google Scholar]
- Savic R.M., Karlsson M.O. Importance of shrinkage in empirical bayes estimates for diagnostics: problems and solutions. AAPS J. 2009;11:558–569. doi: 10.1208/s12248-009-9133-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bertrand J., Balding D.J. Multiple single nucleotide polymorphism analysis using penalized regression in nonlinear mixed-effect pharmacokinetic models. Pharmacogenet. Genomics. 2013;23:167–174. doi: 10.1097/FPC.0b013e32835dd22c. [DOI] [PubMed] [Google Scholar]
- Liu M., Lu W., Krogh V., Hallmans G., Clendenen T.V., Zeleniuch-Jacquotte A. Estimation and selection of complex covariate effects in pooled nested case-control studies with heterogeneity. Biostatistics. 2013;14:682–694. doi: 10.1093/biostatistics/kxt015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bertrand J., Comets E., Laffont C.M., Chenel M., Mentré F. Pharmacogenetics and population pharmacokinetics: impact of the design on three tests using the SAEM algorithm. J. Pharmacokinet. Pharmacodyn. 2009;36:317–339. doi: 10.1007/s10928-009-9124-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ge, Z., Bickel P.J., Rice J.A. An approximate likelihood approach to nonlinear mixed effects models via spline approximation. Comput. Stat. Data An. 2004;46:747–776. [Google Scholar]
- Girard P., Mentré F. PAGE (Population Approach Group in Europe) 14.; 16–17 June 2005, Pamplona, Spain; A comparison of estimation methods in nonlinear mixed effects models using a blind analysis. [Google Scholar]
- Dartois C., Lemenuel-Diot A., Laveille C., Tranchand B., Tod M., Girard P. Evaluation of uncertainty parameters estimated by different population PK software and methods. J. Pharmacokinet. Pharmacodyn. 2007;34:289–311. doi: 10.1007/s10928-006-9046-9. [DOI] [PubMed] [Google Scholar]
- Ueckert S., Johansson A.M., Plan E.L., Hooker A., Karlsson M.O. PAGE (Population Approach Group in Europe) 19.; 8–11 June 2010, Berlin, Germany; New estimation methods in NONMEM 7: evaluation of robustness and runtimes. [Google Scholar]
- Johansson A.M., Ueckert S., Plan E.L., Hooker A., Karlsson M.O. PAGE (Population Approach Group in Europe) 19.; 8–11 June 2010, Berlin, Germany; New estimation methods in NONMEM 7: evaluation of bias and precision. [Google Scholar]
- Xu X.S., Yuan M., Karlsson M.O., Dunne A., Nandy P., Vermeulen A. Shrinkage in nonlinear mixed-effects population models: quantification, influencing factors, and impact. AAPS J. 2012;14:927–936. doi: 10.1208/s12248-012-9407-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mandema J.W., Verotta D., Sheiner L.B. Building population pharmacokinetic–pharmacodynamic models. I. Models for covariate effects. J. Pharmacokinet. Biopharm. 1992;20:511–528. doi: 10.1007/BF01061469. [DOI] [PubMed] [Google Scholar]
- Ribbing J., Nyberg J., Caster O., Jonsson E.N. The lasso–a novel method for predictive covariate model building in nonlinear mixed effects models. J. Pharmacokinet. Pharmacodyn. 2007;34:485–517. doi: 10.1007/s10928-007-9057-1. [DOI] [PubMed] [Google Scholar]
- Ribbing J., Jonsson E.N. Power, selection bias and predictive performance of the Population Pharmacokinetic Covariate Model. J. Pharmacokinet. Pharmacodyn. 2004;31:109–134. doi: 10.1023/b:jopa.0000034404.86036.72. [DOI] [PubMed] [Google Scholar]
- Beal S., Sheiner L.B., Boeckmann A., Bauer R.J. (1989–2009), Icon Development Solutions; Ellicott City, Maryland; 2009. NONMEM User's Guides. [Google Scholar]
- Mentré F., Burtin P., Merlé Y., Van Bree J., Mallet A., Steimer, J.L. Sparse-sampling optimal designs in pharmacokinetics and toxicokinetics. Drug Inf. J. 1995;29:997–1019. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.