Simulation of the pharmacokinetics of bisoprolol in healthy adults and patients with impaired renal function using whole-body physiologically based pharmacokinetic modeling

Abstract

Aim:

To develop and evaluate a whole-body physiologically based pharmacokinetic (WB-PBPK) model of bisoprolol and to simulate its exposure and disposition in healthy adults and patients with renal function impairment.

Methods:

Bisoprolol dispositions in 14 tissue compartments were described by perfusion-limited compartments. Based the tissue composition equations and drug-specific properties such as log P, permeability, and plasma protein binding published in literatures, the absorption and whole-body distribution of bisoprolol was predicted using the 'Advanced Compartmental Absorption Transit' (ACAT) model and the whole-body disposition model, respectively. Renal and hepatic clearances were simulated using empirical scaling methods followed by incorporation into the WB-PBPK model. Model refinements were conducted after a comparison of the simulated concentration-time profiles and pharmacokinetic parameters with the observed data in healthy adults following intravenous and oral administration. Finally, the WB-PBPK model coupled with a Monte Carlo simulation was employed to predict the mean and variability of bisoprolol pharmacokinetics in virtual healthy subjects and patients.

Results:

The simulated and observed data after both intravenous and oral dosing showed good agreement for all of the dose levels in the reported normal adult population groups. The predicted pharmacokinetic parameters (AUC, C_max, and T_max) were reasonably consistent (<1.3-fold error) with the observed values after single oral administration of doses ranging from of 5 to 20 mg using the refined WB-PBPK model. The simulated plasma profiles after multiple oral administration of bisoprolol in healthy adults and patient with renal impairment matched well with the observed profiles.

Conclusion:

The WB-PBPK model successfully predicts the intravenous and oral pharmacokinetics of bisoprolol across multiple dose levels in diverse normal adult human populations and patients with renal insufficiency.

Introduction

Bisoprolol is a selective beta-blocker without intrinsic sympathomimetic and membrane-stabilizing activities and has been widely prescribed for the treatment of cardiovascular diseases such as chronic heart failure (CHF), cardiac insufficiency, hypertension, angina pectoris, and cardiac arrhythmias^1,2,3,4,5. Recently, renal impairment has been reported as one of the most important determinants of prognosis in heart failure⁶ and is often associated with CHF⁷. Bisoprolol is eliminated equally by renal and non-renal routes; 50% of the dose is excreted in the urine as the non-metabolized form via the kidneys, and the remaining drug undergoes hepatic biotransformation to inactive metabolites⁸. Therefore, pathological conditions such as renal failure may alter the exposure and disposition of bisoprolol and accordingly cause modifications in the therapeutic efficacy or side effects. These modifications might require dosage adjustment^8,9,10. In light of this need, clinical pharmacokinetic studies of bisoprolol have been undertaken to explore and support the use of bisoprolol in patients with impaired renal function^9,10. However, the changes of the pharmacokinetics in diverse populations were not available before the corresponding clinical studies, which is the time when an accurate approach for clinical pharmacokinetics projection is most needed.

Whole-body physiologically based pharmacokinetic (WB-PBPK) modeling could forecast such changes prior to the corresponding clinical trials. One of the advantages of WB-PBPK models is to extrapolate in vivo pharmacokinetics of drugs to new situations and populations by integrating wide-ranging physiological and biochemical factors and the complex interactions between them^11,12,13,14. This type of model provides a mechanistic approach for studying drug disposition and allows for the incorporation of disease-related changes in physiology and the assessment of these effects on drug disposition^13,14. Therefore, these models have been recognized as a means of bridging healthy adult and patients' studies and for predicting doses and drug exposures in patients.

The aims of the present study were the following: 1) to build and verify a WB-PBPK model that predicts the pharmacokinetics of bisoprolol after oral and intravenous doses in healthy adult populations that differ in age, gender, and ethnicity; 2)to translate the in vivo behaviors of bisoprolol from normal subjects to patients with renal impairment using the validated WB-PBPK model; and 3) to estimate the influence of individual variability on the pharmacokinetics of bisoprolol through stochastic simulations. Prior simulations of the potential exposure and disposition in individuals with renal impairment may help in the selection of a safe and effective dosage regimen.

Materials and methods

Clinical pharmacokinetic data

Clinical pharmacokinetic data for both intravenous and oral administration of bisoprolol in healthy adults and patients with impaired renal function were obtained from the literature^10,15,16,17. The pharmacokinetic studies after intravenous administration of bisoprolol at two doses were conducted in 8 Western female subjects (age 25±3 years)¹⁵ and 12 Western male subjects (age 37±12 years)¹⁶, respectively. The pharmacokinetic studies following single oral administration of 5, 10, and 20 mg of bisoprolol were conducted in 18 Asian male subjects (age 22±1 years)¹⁷, 12 Western male subjects (age 37±12 years)¹⁶, and 5 Western male subjects (age 53±3 years¹⁶, respectively. Mean data in the aforementioned publications were captured by computer digitization and used for development and validation of the WB-PBPK model. Plasma concentration-time profiles of bisoprolol following multiple oral administration in healthy volunteers (age 23±1 years, n=8) and patients with impaired renal function (age 59±5 years, creatinine clearance=28±5 mL/min/1.73 m², n=11) were obtained from the same source¹⁰.

Whole-body physiologically based pharmacokinetic (WB-PBPK) model development

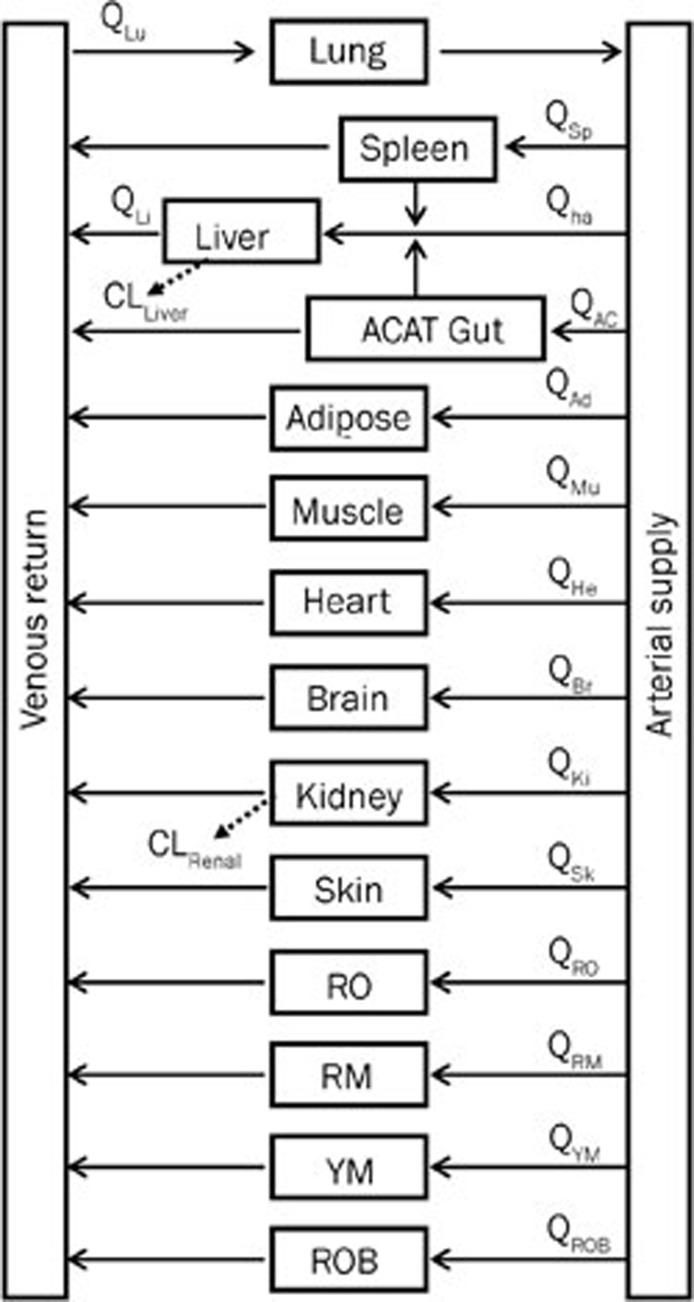
The WB-PBPK model of bisoprolol (Figure 1) was built by GastroPlus version 7.0 (Simulations Plus, Inc, Lancaster, CA, USA) and used for all of the simulations performed in healthy adults and patients with impaired renal function. The PBPK (disposition) model was composed of 14 tissue compartments, including the heart, lung, brain, adipose, muscle, skin, spleen, reproductive, gastrointestinal tract, liver, kidney, yellow marrow, red marrow and rest of the body. These compartments were linked together by venous and arterial blood circulation. All of the tissues except for the liver were supplied from the arterial circulation, and blood exiting of the tissues flows directly into the venous circulation. The liver received its blood supply from the hepatic artery and the portal vein, which itself received the pooled blood supply from the spleen and the gastrointestinal tract. All of the tissues were considered to be well-stirred compartments, and drug distribution into these compartments was driven by perfusion-limited kinetics. The assumption of perfusion-limited kinetics was justified for lipophilic small molecules^18,19. Each compartment was defined by an associated tissue blood flow rate, volume and a tissue-to-plasma partition coefficient. The built-in mass balance differential equations were used in the model. The mass balance for the rate of change in bisoprolol concentration in a non-eliminating tissue was equal to the product of tissue blood flow rate and the difference between the concentrations in the arterial and venous bloods. Here, the venous blood concentration was represented as the tissue concentration divided by tissue-to-plasma partition coefficient (K_p) and then corrected for blood-to-plasma concentration ratio (R_bp). For an eliminating tissue, the mass balance equation must be modified to include a clearance term. Taken together, the mass balance differential equation for a generic tissue compartment, except for lung, had the following form^20,21,22:

Figure 1.

Schematic structure of the whole-body PBPK model used to predict in vivo behaviors of bisoprolol in different human populations. The blood flow rates associatied with the 14 compartments- lung (Lu), liver (Li), spleen (Sp), gut (AC), adipose (Ad), muscle (Mu), heart (He), brain (Br), kidney (Ki), skin (Sk), reproductive organ (RO), red marrow (RM), yellow marrow (YM), rest of body (ROB), — are represented by Q, subscripted with the corresponding compartment. Q_ha is the blood flow rate to the liver via hepatic artery (ha).

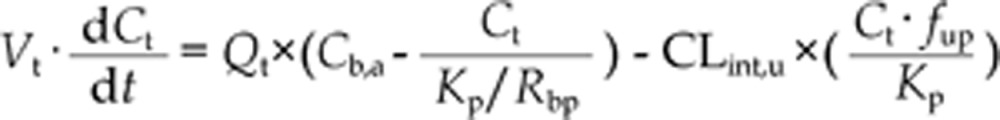where V_t, C_t, Q_t,, K_p, and CL_int,u represent the volume, concentration, blood flow rate, tissue-to-plasma partition coefficient, and unbound intrinsic clearance of the tissue, respectively; C_b,a represents the arterial blood concentration; R_bp represents the blood-to-plasma concentration ratio and f_up represents the fraction unbound in plasma.

The change in mass within the lung was described as^20,21,22:

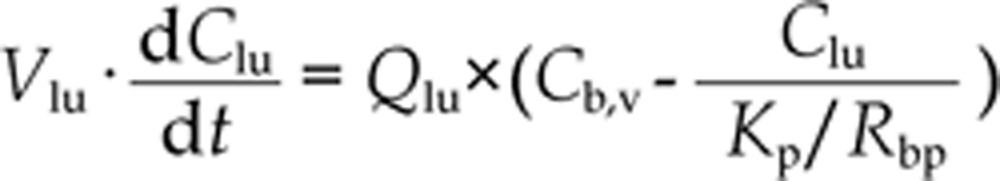where V_lu and Q_lu, are the volume and blood flow rate of lung, respectively. C_b,v is the venous blood concentration.

The mass balance differential equation for arterial blood is^20,21,22:

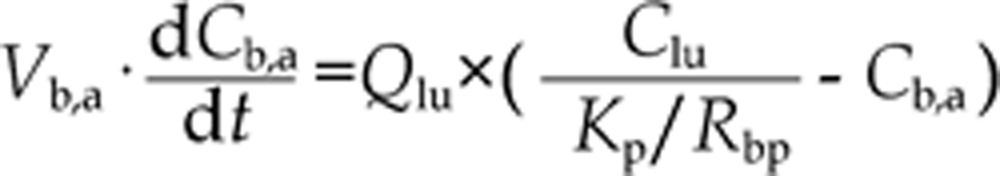where V_b,a is the volume of arterial blood.

For venous blood, the mass balance differential equation is^20,21,22:

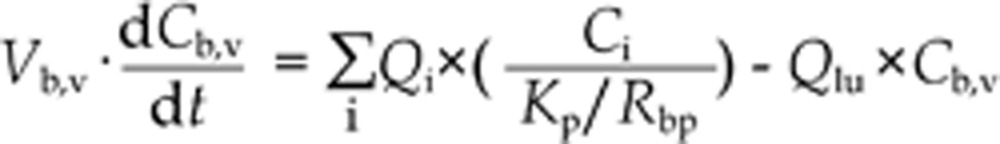where i is adipose, brain, heart, kidney, liver, muscle, red marrow, reproductive organ, rest of body, skin, yellow marrow tissues, and V_b,v is the volume of venous blood.

For bisoprolol, perfusion-limited compartments were adopted to model distribution into tissues. Tissue-to-plasma partition coefficients (K_p) were predicted using established tissue-composition based models^22,23,24. They depend on compound biopharmaceutical properties such as lipophilicity (log P), pK_a, and fraction of free drug in plasma as well as on the composition of lipids, water and proteins in each tissue compartment. The equations used for fraction drug unbound in tissues (f_uT) were derived from the literature²². The steady state volume of distribution (V_ss) was estimated by summing the contributions of all tissue compartments²⁵:

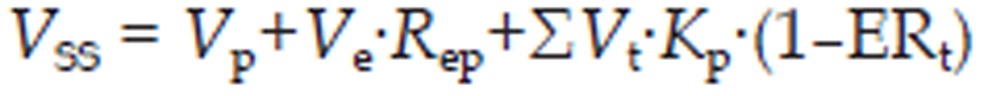where V_p is volume of plasma, V_e is erythrocyte volume, which was computed from the hematocrit of the whole blood, R_ep is erythrocyte-to-plasma concentration ratio, V_t is tissue volume, K_p is the tissue-to-plasma partition coefficient, and ER_t is the extraction ratio in the tissue.

The erythrocyte-to-plasma concentration ratio (R_ep) can be estimated from blood-to-plasma concentration ratio (R_bp) and the hematocrit (45% in human, GastroPlus^TM default value)²⁶:

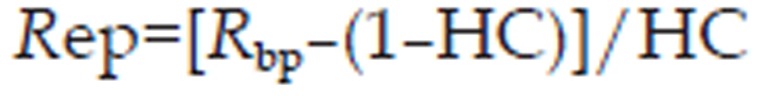where HC is the hematocrit of the whole blood.

The extraction ratio of an organ of elimination (ER_t), based on the well-stirred model, is given by the following equation²⁷:

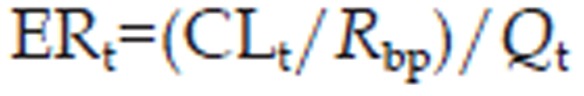where CL_t is the clearance of the tissue of elimination.

As far as the elimination of bisoprolol was concerned, both hepatic metabolic and renal clearances were included in this WB-PBPK approach. The hepatic clearance (CL_liver) was estimated using allometric scaling with a fixed allometric exponent of 0.75 ^14,28.

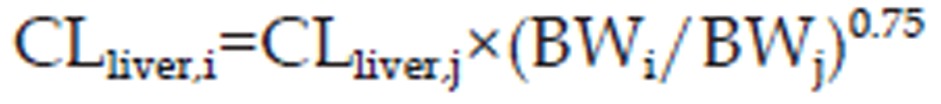where BW is bodyweight. The variables i and j denote human population “i” and population “j”, respectively.

The renal clearance was predicted by Lin's method^29,30:

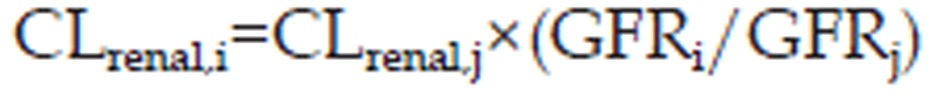where GFR is the glomerular filtration rate. The variables i and j denote human population “i” and population “j”, respectively.

The initial values of human hepatic clearance (5.7 L/h) and renal clearance (7.1 L/h) were obtained from the literature¹⁵ and used in the WB-PBPK model.

The unbound intrinsic clearance (CL_int,u) of the liver and kidney were derived from the plasmatic hepatic and renal clearance, respectively²⁷:

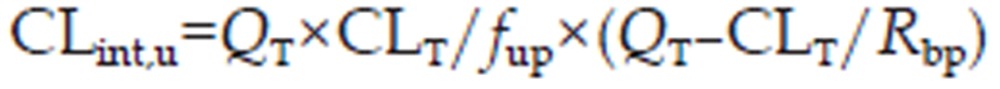For all the other tissues, CL_int,u=0.

The oral absorption of bisoprolol was predicted with the 'Advanced Compartmental Absorption Transit' (ACAT) model implemented in GastroPlus^TM. The ACAT model^31,32,33 has been described in detail previously. Briefly, the ACAT model is a nine-compartment physiologically based absorption model that mimics the transport of compound along the digestive tract as well as through the enterocytes. The kinetics associated with the dissolution and absorption processes are modeled by a system of coupled linear and nonlinear rate equations. The mass balance equations describe the six states of drug substance (unreleased, undissolved, dissolved, degraded, metabolized, and absorbed) in the different regions of the GI tract^31,32. The drug reaches the portal vein followed by distribution in the liver and the other PBPK tissues after it transports through the basolateral membrane of enterocytes.

For immediate release dosage forms, the particle dissolution rate (K_d) in any gastrointestinal compartment, which reflects the entire dissolution profile, is calculated according to the Noyes–Whitney equation^20,34.

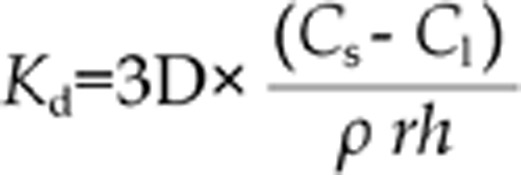where D=diffusion coefficient, which is automatically computed based on molecular weight, ρ=particle density (1.2 g/mL, GastroPlus^TM default value), r=particle radius (25 μm, GastroPlus^TM default value), h= effective diffusion layer thickness, C_s=solubility and C_l= lumen concentration. The effective diffusion layer thickness was taken as equal to the particle radius³⁴.

The absorption rate coefficient (K_a) for each gastrointestinal compartment is the product of the effective permeability (P_eff) and the absorption scale factor for the compartment^20,35,36. The absorption scale factors were used to estimate the changes in permeability as the drug travels along the GI tract^20,35,36. The mean values of GI tract physiology for pH, transit times, volumes, lengths and radius in human fasted state were taken from published data^37,38 and provided by GastroPlus^TM(Table 1). The required drug-specific properties for the absorption model are solubility, logP, pK_a, and effective permeability, which were used as inputs in the absorption model to predict the rate and extent of drug absorption and summarized in Table 2. The ACAT model takes into consideration the biopharmaceutical factors of drugs (eg, pK_a, solubility, and permeability), the human gastrointestinal physiological factors (eg, gastric emptying and intestinal transit rate), and the dosage factors (eg, dosage form and dose in predicting oral drug absorption)³⁹.

Table 1. The mean physiological parameters used in the WB-PBPK absorption models.

Gut compartment	pH	Transit time (h)	Volume (mL)	Length (cm)	Radius (cm)
Stomach	1.3	0.25	50	30	10
Duodenum	6	0.26	48	15	1.6
Jejunum 1	6.2	0.95	175	62	1.5
Jejunum 2	6.4	0.76	140	62	1.34
Ileum 1	6.6	0.59	108	62	1.18
Ileum 2	6.9	0.43	79	62	1.01
Ileum 3	7.4	0.31	56	62	0.85
Caecum	6.4	4.5	53	14	3.5
Ascending colon	6.8	13.5	57	29	2.5

Table 2. Physicochemical properties and in vitro data used in the simulations.

Property	Value	Source
logP	1.87	45
Solubility (mg/mL)	2.639	Estimated by ADMET PredictorTM
pH for solubility	10.66	Estimated by ADMET PredictorTM
Effective permeability (Peff, cm/s)	1.219	Estimated by ADMET PredictorTM
pKa	9.438	Estimated by ADMET PredictorTM
fup (Plasma unbound drug, %)	70	46
Rbp (Blood-to-plasma concentration ratio)	1.1	Estimated, then optimized

WB-PBPK model parameters

Human tissue weights, volumes, and blood perfusion rates were generated by the age-, gender- and body weight-dependent Population Estimates for the Age-Related Physiology (PEAR) module in GastroPlus^TM. The GastroPlus^TM implementation of the PEAR program calculated the human physiologies on the basis of American/Western or Japanese/Asian population databases for males and females aged 1 to 85 years old²⁰. The age- and gender-related population databases for 11039 Americans and 4667 Japanese came from the National Health and Nutrition Examination Survey database⁴⁰ and the Japanese government database⁴¹, respectively. The mean population data for the specific age and gender were used to calculate whole-body tissue estimates for blood flow and organ volume. The mean physiological parameters employed in the model are summarized in Table 1 and Table 3.

Table 3. The mean physiological parameters for different human populations used in the WB-PBPK disposition models.

Physiological parameter	25 years femalea	37 years malea	53 years malea	22 years maleb	23 years malea	59 years malea
Blood flow (mL/s)
Adipose	12.1	9.07	9.84	3.5	7.65	9.07
Arterial supply	75	86.2	81.0	76	87.8	72
Brain	11.1	12.4	11.4	15.2	13.4	10.1
Gut (ACAT)	9.89	12.1	11.3	9.92	12.2	9.84
Heart	3.44	3.33	3.34	2.73	3.35	3.08
Hepatic artery	6.5	6.96	6.47	5.69	6.99	5.65
Kidney	10.1	14.8	13.2	12.1	14.8	11.2
Liver	18.6	21.7	20.2	17.8	21.8	17.7
Lung	75	86.2	81	76	87.8	72
Muscle	7.08	9.02	9.04	7.39	9.06	8.33
Red marrow	4.44	5.06	5.05	4.86	5.23	4.67
Reproductive organ	0.126	0.0976	0.0978	0.0799	0.0981	0.0901
Rest of body	3.45	5.93	4.06	8.22	7.45	3.41
Skin	3.34	3.41	3.42	2.79	3.42	3.15
Spleen	2.18	2.67	2.49	2.19	2.69	2.17
Venous return	75	86.2	81	76	87.8	72
Yellow marrow	1.17	1.41	1.4	1.35	1.46	1.3
Volume (mL)
Adipose	21276	25704	29136	10444	22197	27090
Arterial supply	1103	1782	1765	1908	1912	1596
Brain	1122	1374	1359	1774	1528	1241
Gut (ACAT)	–	–	–	–	–	–
Heart	188	259	259	223	266	233
Hepatic artery	–	–	–	–	–	–
Kidney	165	227	227	196	234	204
Liver	976	1340	1340	1154	1378	1206
Lung	666	914	914	788	941	823
Muscle	12405	17027	17027	14668	17514	15324
Red marrow	777	956	951	965	1012	859
Reproductive organ	31.5	26.3	26.3	22.7	27.1	23.7
Rest of body	4611	9413	6379	15982	12983	4878
Skin	1172	1608	1608	1385	1654	1447
Spleen	110	151	151	130	156	136
Venous return	2206	3565	3530	3816	3825	3193
Yellow marrow	2049	2656	2642	2683	2812	2388

Note: ^a Western population; ^b Asian population; –, not applicable.

Drug-dependent physicochemical and in vitro data

The key physicochemical parameters and in vitro data available for bisoprolol are depicted in Table 2. The logP, pK_a, solubility and effective permeability were obtained using the ADMET Predictor^TM module of GastroPlus, which has been consistently ranked as the most accurate predictive software in quantitative structure-pharmacokinetic relationship models (QSPKR models) of biopharmaceutical properties^42,43,44. Human R_bp (blood-to-plasma concentration ratio) was estimated using the ADMET Predictor^TM module and then fitted to correct for the steady-state volume of distribution (V_ss)¹⁵ within the range 0.81 (ADMET Predictor^TM) and 1.36 (rat value⁴⁵). Human f_up (plasma unbound drug) was obtained from the literature⁴⁶. The tissue-to-plasma partition coefficients (K_p) of biosoprolol were calculated using established tissue-composition based models^22,23,24 (Table 4).

Table 4. The tissue-to-plasma partition coefficients (K_p) of biosoprolol calculated using established tissue-composition based models^22,23,24.

	Ad	Br	He	Ki	Li	Lu	Mu	RM	RO	ROB	Sk	Sp	YM
Kp	0.97	1.98	5.36	10.8	9.96	8.61	4.16	1.99	10.79	7.30	3.41	7.30	0.97

Note: Br, brain; He, heart; Ki, kidney; Li, liver; Lu, lung; Mu, muscle; RM, red marrow; RO, reproductive organ; ROB, rest of body; Sk, skin; Sp, spleen; YM, yellow marrow.

Virtual trial simulations

To investigate the effects of inter-individual differences in the population physiological characteristics and compound variables, virtual trial studies were performed for bisoprolol following multiple oral doses in healthy adults and patients with impaired renal function. Physiological parameters and compound-specific properties were randomly sampled from log-normal distributions via a Monte Carlo method^39,47,48. The coefficient of variation (CV%) values were predefined by GastroPlus^TM based on a priori knowledge of anthropometric distributions obtained from the literature for realistic populations^39,47,48. Virtual subjects of all of the stochastic variables were generated for each simulation. The Monte Carlo-based WB-PBPK model was employed to predict the pharmacokinetic profiles of bisoprolol after multiple doses in 8 healthy subjects and 11 patients with impaired renal function, which is equal to the number of volunteers used in the corresponding real clinical trial^10,47,48.

WB-PBPK modeling strategy

The WB-PBPK prediction strategy in the current work was modified by Jones et al²¹. In this strategy, the first stage was the simulation of the pharmacokinetics in healthy adults after intravenous administration. When a reasonable simulation of the intravenous pharmacokinetic profile in healthy adults was achieved, the second stage was to simulate oral pharmacokinetic profiles at a single dose and then refine the initial model if there were significant mismatches between the observed and the simulated pharmacokinetic data. The model refinement approaches applied in this evaluation for the prediction of the oral pharmacokinetics based on PBPK were summarized by Peters et al^49,50 and Jones et al²¹. If the simulated AUC deviates markedly from that of the observed, the magnitude of permeability or solubility is not representative of the in vivo situation^14,21,51. Additional absorption mechanisms such as transporter-mediated efflux and influx, and intestinal loss such as gut wall first-pass extraction and chemical degradation should be examined and then included in the original model^14,21,49. If the simulated AUC is comparable to that of the observed but the curve shape still does not match, the effect of stomach transit time and intestinal transit time may be explored using a parameter sensitivity analysis⁵⁰. Stomach transit time, which represents gastric emptying time, is a key factor determining the initiation of the absorption phase. It had been reported that stomach transit time has considerable variability^52,53,54. If comparing the observed and simulated oral profiles indicates there is hysteresis of the initial absorption phase between them, the stomach transit time is higher than the average normal value used in the PBPK model and is required to adjust until the simulated profile captures the observed profile shape well⁵⁰ and has a lower value of the mean absolute error (MAE) and root mean square error (RMSE). At the third stage, the refined model was verified at other single oral doses. At the fourth stage, the oral pharmacokinetic profiles after multiple oral administration of bisoprolol in healthy adults and patients with impaired renal function were predicted using the validated WB-PBPK model accounts for the renal function and age dependencies in diverse populations. Finally, the WB-PBPK model coupled with a Monte Carlo simulation was employed for the prediction of bisoprolol pharmacokinetics in virtual healthy subjects and patients with renal impairment.

Assessment of prediction accuracy

The accuracy of the prediction was graphically evaluated by superimposing the concentration-time profile observed in vivo to the simulated ones. Predicted pharmacokinetic parameters were calculated from the simulated plasma concentration–time profiles by non-compartmental analysis using GastroPlus^TM. The area under the plasma concentration–time curve (AUC) and area under the moment curve (AUMC) were calculated by use of the linear trapezoidal rule. The plasma clearance (CL) was calculated as: CL=dose/AUC. The steady-state volume distribution (V_ss) was calculated as: V_ss=CL×AUMC/AUC. The half-life (t_1/2) was computed by the following equation: t_1/2=In2×(V_ss/CL).

The overall accuracy of the predicted pharmacokinetic parameters was assessed from the fold-error (difference between predicted and observed in vivo values), and the prediction was considered successful if the fold-error was less than two^{21,35,43,55,56,57}.

If the observed value is greater than the predicted value, fold-error=observed/predicted;

If observed value is less than the predicted value, fold-error=predicted/observed;

To examine the agreement between the predicted concentrations and the corresponding measured concentrations, the mean absolute error (MAE) and the root mean square error (RMSE), which represent accuracy and precision, were calculated using the following formulas^35,58:

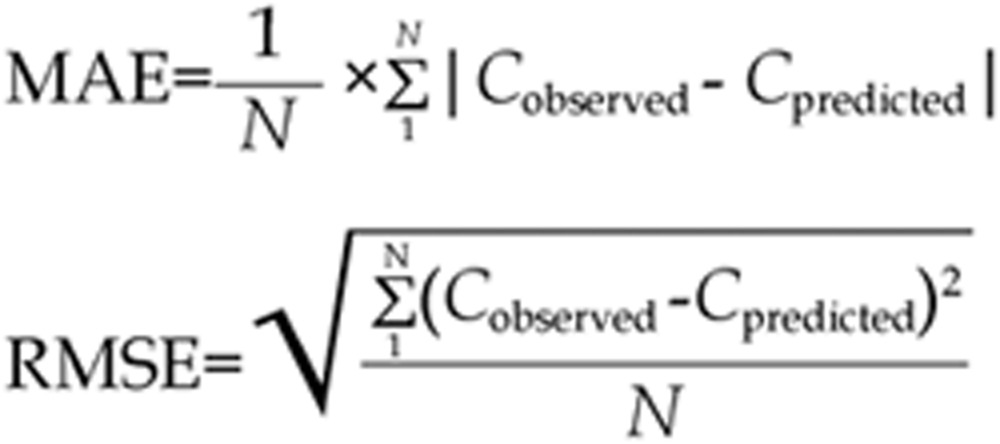Results

Simulation of the intravenous pharmacokinetic profile (Stage 1)

The WB-PBPK model for bisoprolol was constructed according to the scheme presented in Figure 1. Simulations were based on bisoprolol physicochemical and in vitro data (Table 2). Tissue distribution was predicted using established tissue-composition equations. Hepatic and renal bisoprolol clearances were extrapolated to a new population, as described in the methods section.

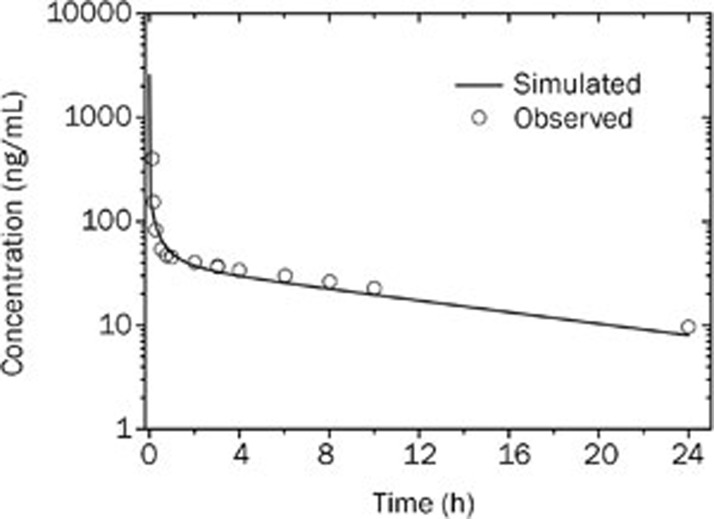
The observed and WB-PBPK model simulated mean plasma concentration-time profiles of bisoprolol in healthy adults after an intravenous bolus of 10 mg are graphically presented in Figure 2. The predicted and observed pharmacokinetic parameters with the prediction accuracy are summarized in Table 5. The simulated intravenous plasma concentration-time profile of bisoprolol by PBPK modeling corresponded well with the observed profile. The predicted pharmacokinetic parameters were reasonably consistent (<1.1-fold error) with the observed values. Therefore, the WB-PBPK model was able to accurately simulate the plasma concentration-time profile following intravenous administration using the in silico data, in vitro data, predicted Kp values and predicted clearances as inputs to the model, as shown in Figure 2 and Table 5.

Figure 2.

Simulated (line) and observed¹⁶ (points) plasma concentration-time profiles of bisoprolol after 10 mg intravenous administration in healthy men (37 years old, Western).

Table 5. Observed and simulated pharmacokinetic parameters of bisoprolol after intravenous administration of 10 mg in healthy adults.

Pharmacokinetic parameters	Observed	Predicted	Fold-error
CLtotal (L/h)	15.6	15.0	1.04
Vss (L)	226	208	1.09
AUC (μg·h/L)	672	664	1.01
t1/2 (h)	10.3	9.6	1.07

Simulation of the single oral pharmacokinetic profile and the refinement of WB-PBPK model (Stage 2)

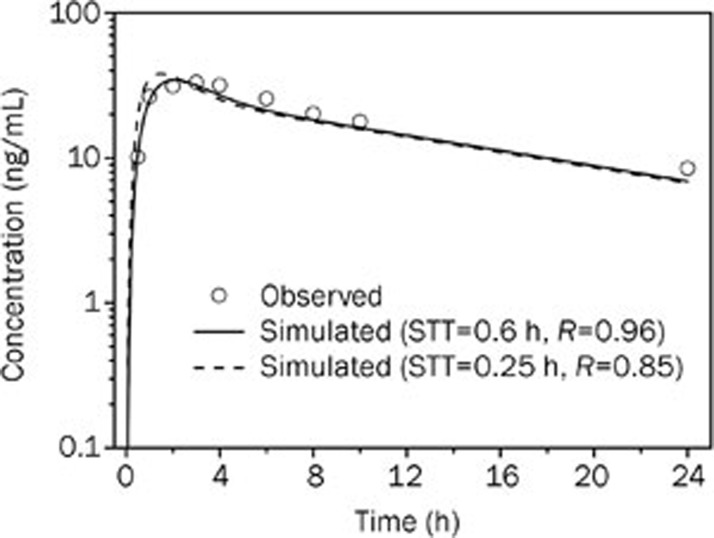
To evaluate the performance of the WB-PBPK model in oral absorption prediction, a simulation for a single oral administration was performed. The input properties used for the intravenous simulation were fixed for the simulation of the oral profile. As shown in Figure 3, the proposed WB-PBPK model allowed for a good simultaneous description of the observed profile in the terminal phase; however, there was a mismatch in the absorption phase between the initial simulated profile (dashed line) and the observed profile. The delayed onset of absorption was found in the observed profile compared to the simulated profile that was generated using typical values of physiological parameters in the WB-PBPK absorption model (Table 1). The AUC and C_max of the initial simulated profile were comparable (<1.2-fold error) to those of the observed profile, but the T_max of the initial simulated profile was slightly underestimated by 2-fold error, as shown in Table 6.

Figure 3.

Simulated (lines) and observed¹⁶ (points) plasma concentration-time profiles of bisoprolol after 10 mg oral administration in healthy men (37 years old, Western). STT, stomach transit time.

Table 6. Observed and simulated pharmacokinetic parameters of bisoprolol after oral administration of 10 mg in healthy adults using different values of stomach transit time.

STT (h)	AUC (μg·h/L)			Cmax (ng/mL)			Tmax (h)
	Observed	Predicted	Fold-error	Observed	Predicted	Fold-error	Observed	Predicted	Fold-error
0.25a	427	380	1.12	33.2	37.3	1.12	3.0	1.5	2.00
0.6b	427	379	1.13	33.2	34.4	1.04	3.0	2.1	1.43

Note: STT, stomach transit time; a The initial value of STT; b The final value of STT was fitted to the observed in vivo data after 10 mg oral dose.

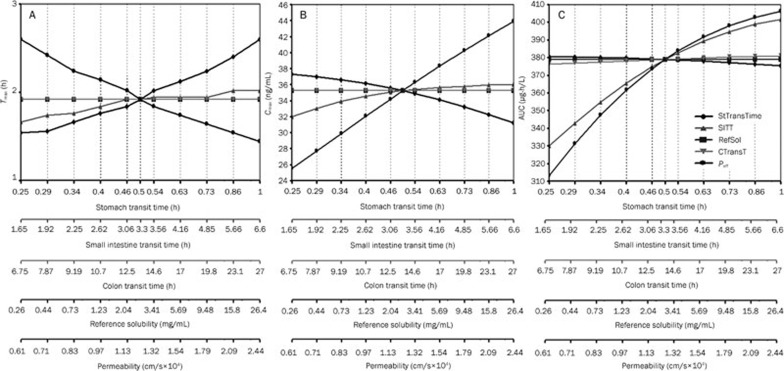
To improve model performance, a parameter sensitivity analysis was conducted to identify the key parameter which significantly influences the absorption phase of bisoprolol. The input parameters that affect the oral plasma concentration-time curve such as solubility, permeability, stomach transit time, small intestine transit time, and colon transit time were varied individually over a wide range of values. Figure 4 shows that T_max is sensitive to changes in the stomach transit time and permeability, with less sensitivity to changes in the small intestine transit time and no sensitivity to the colon transit time and solubility. The AUC and C_max are also markedly affected by permeability. Given the consistency between the initial simulated and observed AUC (Table 6), the stomach transit time was identified as the only parameter that affected the shape of the oral profile and could be altered to match the oral profile. Therefore, the stomach transit time was optimized to match the observed oral pharmacokinetic profile, with a lower RMSE and higher R-square value. It can be observed that WB-PBPK model using the fitted stomach transit time (0.6 h) was able to capture the observed data in both the absorption and disposition phases (Figure 3 and Table 6) and showed a smaller RMSE (2.66) and MAE (2.30).

Figure 4.

Parameter sensitivity analysis for 10 mg bisoprolol single oral administration. StTransTime, stomach transit time; SITT, small intestine transit time; RefSol, reference solubility; CTranT, colon transit time; P_eff=permeability. (A) parameter sensitivity analysis of the T_max; (B) parameter sensitivity analysis of the C_max; (C) parameter sensitivity analysis of the AUC after 10 mg bisoprolol single oral administration.

WB-PBPK model validation (Stage 3)

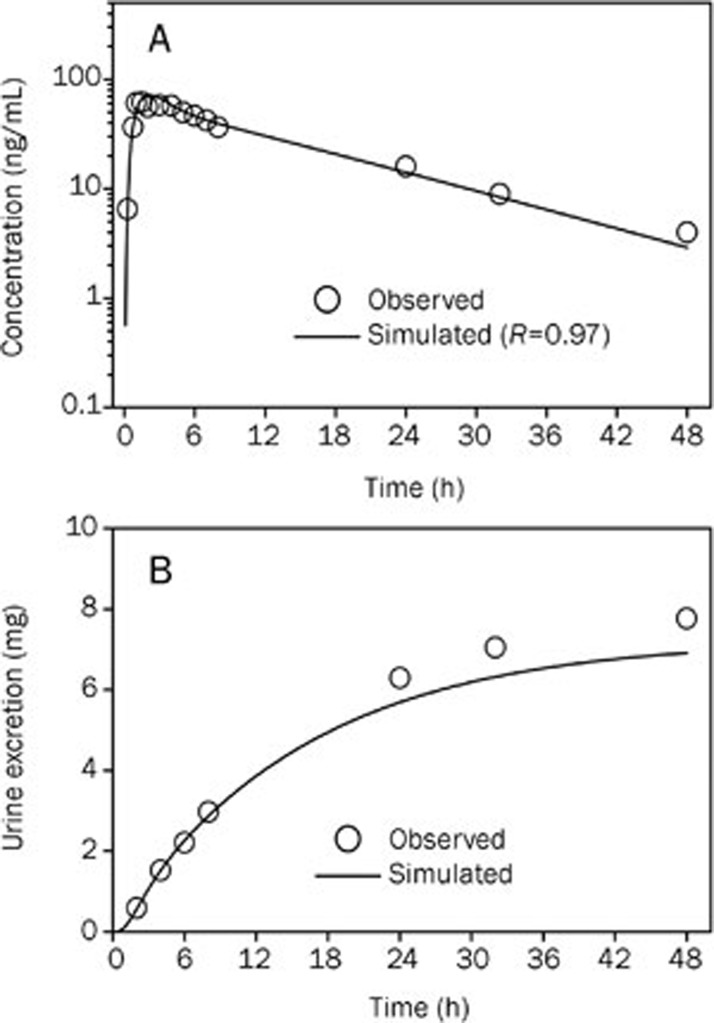
To further validate the model, the refined model was used to predict the oral pharmacokinetics at different single doses. The WB-PBPK model simulated against the observed mean concentration-time profiles of bisoprolol after either a single 20 mg or 5 mg oral dose in different healthy adult populations are shown in Figure 5 and Figure 6, respectively. The predicted pharmacokinetic parameters are compared with the observed data in Table 7. The simulated plasma concentration-time profiles were in line with the observed profiles, as suggested by a small RMSE (1.93) and MAE (1.59). For the 20 mg oral dose, the urine excretion curve was also well simulated. Furthermore, the predicted values of the pharmacokinetic parameters were all within 1.3-fold of the observed values. Overall, these simulations, based on the WB-PBPK model, were close to the observed profiles (RMSE=1.24, MAE=8.39), indicating that the model appropriately describes the processes determining the absorption and disposition of bisoprolol in healthy adult populations of varying age, sex, and ethnicity.

Figure 5.

Simulated (lines) and observed¹⁶ (points) plasma concentration-time profiles (A) and urine excretion-time profile of bisoprolol (B) after 20 mg oral administration in healthy men (53 years old, Western).

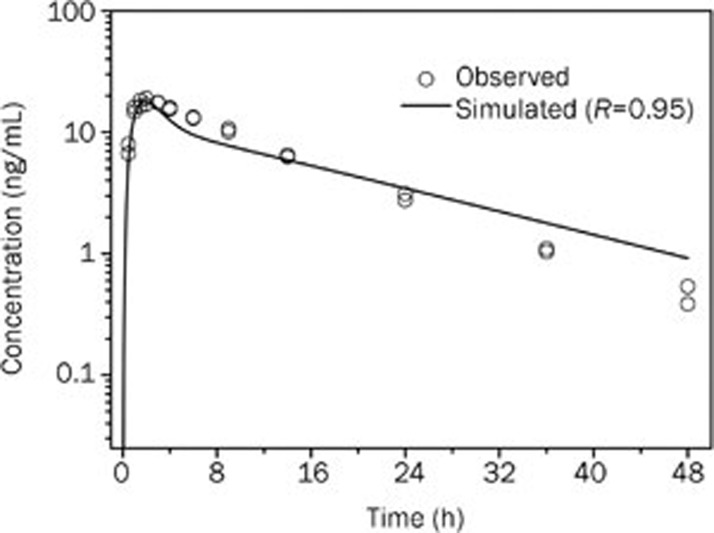
Figure 6.

Simulated (lines) and observed (points)¹⁷ plasma concentration-time profiles of bisoprolol after 5 mg oral administration in healthy men (22 years old, Asian).

Table 7. Observed and simulated pharmacokinetic parameters of bisoprolol after oral administration in healthy adults.

Dose (mg)	AUC (μg·h/L)			Cmax (ng/mL)			Tmax (h)
	Observed	Predicted	Fold-error	Observed	Predicted	Fold-error	Observed	Predicted	Fold-error
20a	1009	974	1.04	61.7	72.2	1.17	1.5	1.9	1.28
5b	244	227	1.07	18.3	18	1.02	2.0	1.9	1.04

Note: ^a Oral administration in healthy men (53 years old, Western); ^b Oral administration in healthy men (22 years old, Asian).

The prediction of oral pharmacokinetics in patients with impaired renal function (Stage 4)

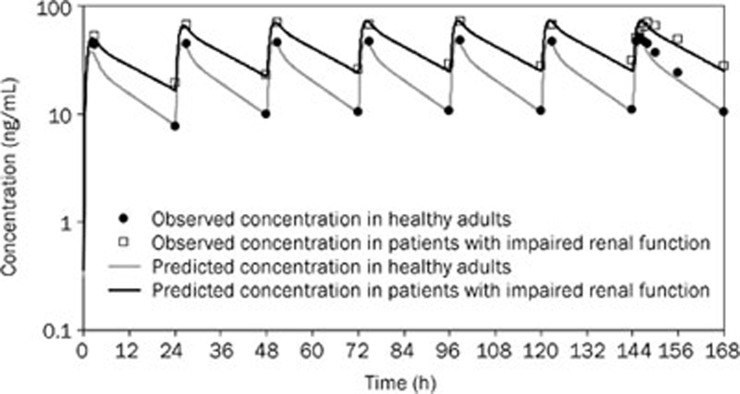
The predictions of the pharmacokinetics of bisoprolol in healthy adults and patients with impaired renal function after the administration of multiple oral doses were further performed. For the prediction in patients with impaired renal function, renal function and age differences were taken into account. The change of creatinine clearance, which reliably reflects the extent of renal impairment, was obtained from the literature¹⁰, and changes in the age-related physiological parameters (Table 3) were based on GastroPlus^TM demographic and physiological databases. These adjustments were incorporated into the WB-PBPK model. Model predictions were compared to the experimental data obtained following 7 d of oral administration of bisoprolol to healthy adults and to patients with impaired renal function. Reasonable predictions of the mean plasma concentration-time curve were achieved not only for the healthy adult population (RMSE=4.51, MAE=3.35), but also for the target patient population (RMSE=5.67, MAE=4.61) (Figure 7).

Figure 7.

Simulated (lines) and observed¹⁰ (points) plasma concentration-time profiles of bisoprolol after 10 mg oral multiple doses in healthy adults and patients with impaired renal function.

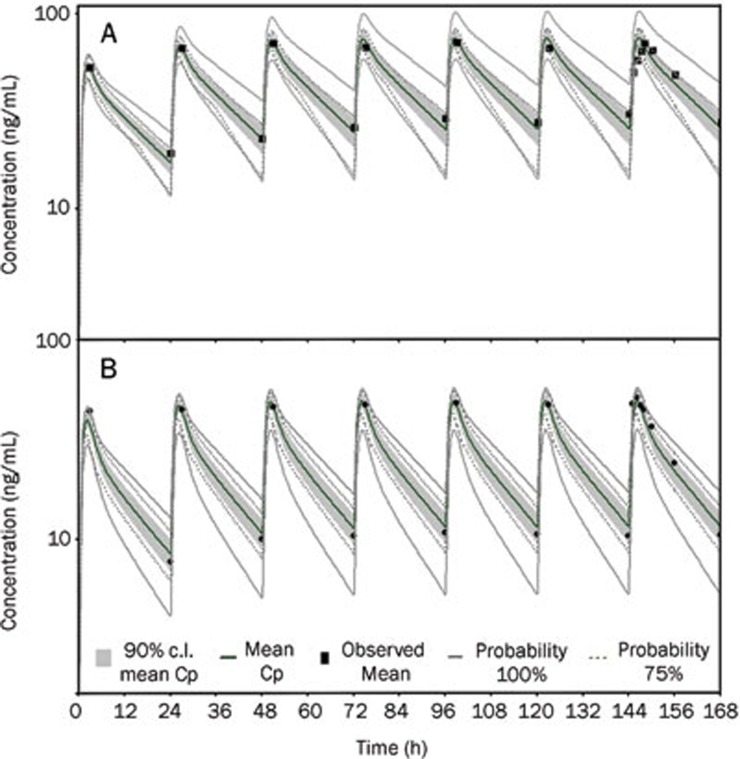
Virtual trial simulations (Stage 5)

Simulations for multiple doses of 10 mg of bisoprolol in 8 virtual healthy subjects and 11 patients with impaired function were compared with the plasma concentration-time curves observed in vivo. The results of these virtual trial simulations are shown in Figure 8. The figure shows the mean plasma concentration-time profile and the clinical observed values, as well as highlighting a grey colored area that represents the 90% confidence intervals around the mean. In addition, the solid lines labeled as 100% probability represent the highest and lowest plasma concentration-time curves from the virtual 8 healthy subjects (Figure 8A) and 11 patients (Figure 8B). The dotted lines represent the corresponding plasma concentration-time curves for 75% probability. In the virtual trial for the 8 healthy subjects, it can be noted that all but one of the clinical observations lie within the 90% confidence intervals of the simulation (Figure 8A). For the 11 virtual patients, it can be noted that all but two of the clinical observations lie within the 90% confidence intervals of the simulation (Figure 8B). Furthermore, it can be seen that the all of the observed data lies within the minimal and maximal individual subject simulations from the virtual trial of the 8 healthy subjects and 11 patients. Figure 8 shows that the observed concentrations are well represented by the generated virtual population concentration-time curves.

Figure 8.

Virtual trial simulation for 8 healthy subjects (A) and 11 patients with impaired renal function (B) after 7-d repeated oral administration of 10 mg bisoprolol. A solid black line adjacent to the middle of the concentration-time profile represents the mean of the predictive values. Solid black squares represent the observed clinical concentration-time data¹⁰. The grey shaded area represents the 90% confidence interval for the simulated data, and the grey solid, and dotted lines represent individual simulated results that include 100% and 75% of the range of simulated individual data.

Discussion

A WB-PBPK model for bisoprolol was developed and applied to predict intravenous and oral pharmacokinetics in diverse population groups of healthy adults and patients with renal impairment. The approach integrated drug-specific parameters such as logP, pK_a, solubility and permeability and in vitro data such as plasma protein binding and blood-to-plasma concentration ratio, was able to simulate the pharmacokinetics of bisoprolol (for both intravenous and oral doses) across multiple dose levels in different human populations with suitable accuracy. The methodology provides a reliable way to understand the mechanisms underlying the pharmacokinetic processes of bisoprolol and to predict its in vivo behavior in patients suffering from renal insufficiency.

WB-PBPK modeling simulates pharmacokinetic profiles on the basis of drug-related physicochemical properties, clearance and a set of relevant physiological parameters, such as organ volumes, tissue composition (water, lipid and protein content) and blood flow rates^21,43,59. To make a WB-PBPK simulation of clinical pharmacokinetics, it is important to predict the distribution and clearance of bisoprolol in different human population groups. An intravenous profile is determined only by the distribution and elimination of bisoprolol. So to start with, the intravenous pharmacokinetics of bisoprolol is simulated using the WB-PBPK model. In the past, WB-PBPK model had been considered difficult to parameterize because of the requirement for measurements of tissue-to-plasma partition coefficient (K_p) for each organ. Experiments for obtaining K_ps are usually difficult and labor-intensive and also require conducting numerous animal studies to ensure accuracy ⁶⁰. Moreover, many tissues are generally omitted due to practical limitations. Recently, these limitations have been solved through in silico estimates, which are based on tissue composition of neutral lipids, phospholipids, and water^23,24. These validated mechanistic equations provide significant opportunities for using WB-PBPK approach in the drug development process^{18,19,35,43,51,61}. For this study, K_ps were estimated from physicochemical characteristics used as input into mechanistic tissue composition equations^22,23,24. Overall, these published tissue composition equations provided accurate estimates of V_ss in humans (Table 5). For the prediction of renal clearance, the filtration clearance (GFR×f_up) was initially evaluated, but underestimations were observed. Furthermore, it had been reported that P-glycoprotein was responsible for the directional transport of bisoprolol in renal epithelial cells⁶². These findings indicated that tubular secretion was involved in the processes of renal elimination of bisoprolol. Given that the filtration clearance contributes up to 70% of renal clearance, the 'GFR ratio approach'^29,30 was used. In the current study, the urinary excretion profile of bisoprolol was well simulated by this renal clearance scaling method (Figure 5B), suggesting this method has reasonable accuracy. For the prediction of hepatic clearance, mechanistic approaches are required to accommodate the maturation rates of drug-metabolizing enzymes in humans younger than two years old; in humans older than two years, allometric scaling is a generally accepted approach¹⁴. Therefore, allometric scaling was used to predict hepatic clearance of bisoprolol. Figure 2 and Table 5 stand as direct evidence for the reliability of these clearance projection methods.

The oral absorption simulations will be proceeded to estimate the rate and extent of oral bisoprolol absorption, as long as a reasonable prediction of the intravenous pharmacokinetics is observed. This stage is necessary to validate and to refine the model. The comparison of the predicted and observed data may offer some insight into refining the model to reproduce the observed profile. If the predicted AUC is not close to the observed value, the permeability or solubility imputed is most likely not representative of the in vivo condition^14,21,51. Other factors such as chemical degradation, gut wall first-pass extraction, transporter-mediated efflux and influx should be considered further^14,21,49. If the predicted AUC is comparable to the observed value but the curve shape still does not match, the effect of stomach transit time may be explored⁵⁰. For bisoprolol, the initial predicted AUC and C_max were well in reasonable agreement with the observed values, but the initial T_max was slightly underpredicted (Figure 3 and Table 6). Thus, a parameter sensitivity analysis was performed to investigate how these three pharmacokinetic parameters were affected by gastrointestinal physiological parameters and biopharmaceutical properties. With the parameter sensitivity analysis, stomach transit time was recognized as the most sensitive parameter, which determines the overall shape of bisoprolol oral pharmacokinetic profile. Stomach transit time is strongly influenced by both volume and composition of gastric contents. It has also been reported that gastric emptying can be inhibited by the drugs themselves, and these drug-induced delayed gastric emptying can be identified through PBPK simulation⁵⁰. Finally, the value of stomach transit time was fitted to match the prolonged T_max in the observed plasma concentration-time data for the 10 mg oral dose. Following our proposed modeling strategy, the refined WB-PBPK model was further verified at other oral doses in different healthy populations to confirm the validity of the assumptions used. Figure 5 and Figure 6 show that the oral pharmacokinetics of bisoprolol after the 20 mg and 5 mg doses in different populations of healthy adults were correctly predicted by adjusting the value of stomach transit time to 0.6 h.

As WB-PBPK modeling allows integration of disease-related changes in physiology, it is valuable for the prediction of differences in the pharmacokinetics between healthy subjects and special patient populations^13,14,63. In the next stage, the validated WB-PBPK model was applied to predict bisoprolol pharmacokinetics in healthy adult subjects and patients with renal impairment after receiving multiple oral doses. GFR and creatinine clearance are accepted as the best overall measurement for assessing renal function⁶⁴. The ratio of creatinine clearance in patients with renal impairment and normal adults was obtained from the original report¹⁰ and then used to scale the renal clearance for the given population of renal-insufficient patients (age 59±5 years). Apart from the renal function, age-dependent physiological changes such as tissue blood flow, tissue volume, and hematocrit were also adjusted to represent the reported patient population. In addition, it was assumed that drug-specific properties, including permeability, unbound fraction in plasma and blood-to-plasma concentration ratio, do not differ substantially between healthy subjects and patients with renal dysfunction. The predictions of the mean plasma concentration-time profiles using the validated WB-PBPK model, which incorporated the corresponding physiological parameters of the target human populations, was in agreement with the observed mean data in healthy humans and patients with renal dysfunction following multiple oral doses, indicating that the model is sufficient to capture the mean pharmacokinetic profiles of bisoprolol in both healthy and patient populations after multiple oral administration.

In terms of the assessment of inter-individual variability, the combination of the WB-PBPK model with a stochastic Monte Carlo approach, which makes use of known variability and distribution functions of physiological parameters and drug-related properties, provides a mechanistic method for predicting population variability in pharmacokinetics. Coupled with a Monte Carlo approach, the PBPK model has been applied to evaluate the quantitative effect of physiological factors on human variability in pharmacokinetics^48,65,66,67. The Virtual Trials feature in GastroPlus allows the user to customize the populations of the in silico subjects that mimic actual healthy adults and patients and can be used to assess pharmacokinetic variability. In our study, two target virtual populations were generated by providing a mix of age ranges, gender ratios, and ethnicities. The inter-individual variability of physiological variables such as organ volume, blood flow, transit times in the various gastrointestinal segments, and pH in all gastrointestinal compartments were assigned to the virtual individuals of the target populations through a Monte Carlo method. Although experimental variability was not shown because of the lack of data in these studies, the mean experimental concentrations in healthy subjects and patients were both well represented by the generated corresponding population concentration-time curves (Figure 8). The advantage of the Monte Carlo-based WB-PBPK approach is that it facilitates the projection of the population mean of the pharmacokinetic characteristics as well as the variability, which will enable us to better anticipate the clinical reality.

In conclusion, a WB-PBPK model for bisoprolol was developed and validated in diverse population groups of healthy adults. The model successfully predicted the intravenous and oral pharmacokinetics of bisoprolol across multiple dose levels in different normal human populations and patients with impaired renal function. This represents a case study that highlights the prospective applications of the WB-PBPK model combined with the Monte Carlo approach to provide clinical pharmacokinetic predictions. From these simulations, the means and variability of the pharmacokinetics of bisoprolol can be obtained before proceeding with clinical studies. Assuming that the exposure-response relationship is similar in subjects with normal renal function and subjects with impaired renal function⁶⁴, the dose and dosing interval can be optimized and incorporated into a clinical trial design. Although more extensive validation is required in the future, the WB-PBPK model developed here is useful to gain the in vivo knowledge from in silico and in vitro studies to enable a priori adjustment of drug dosing for maximal efficacy and minimal toxicity.

Author contribution

Qing-shan ZHENG, Kun WANG, and Guo-fu LI designed the research. Guo-fu LI and Kun WANG performed the research and wrote the paper. Rui CHEN collected the data and revised the paper. Qing-shan ZHENG, Kun WANG, and Hao-ru ZHAO reviewed and revised the paper. Jin YANG discussed the results.