Abstract
Pancreatic cancer is one of the most deadly types of cancer and has extremely poor prognosis. This malignancy typically induces only limited cellular immune responses, the magnitude of which can increase with the number of encountered cancer cells. On the other hand, pancreatic cancer is highly effective at evading immune responses by inducing polarization of pro-inflammatory M1 macrophages into anti-inflammatory M2 macrophages, and promoting expansion of myeloid derived suppressor cells, which block the killing of cancer cells by cytotoxic T cells. These factors allow immune evasion to predominate, promoting metastasis and poor responsiveness to chemotherapies and immunotherapies. In this paper we develop a mathematical model of pancreatic cancer, and use it to qualitatively explain a variety of biomedical and clinical data. The model shows that drugs aimed at suppressing cancer growth are effective only if the immune induced cancer cell death lies within a specific range, that is, the immune system has a specific window of opportunity to effectively suppress cancer under treatment. The model results suggest that tumor growth rate is affected by complex feedback loops between the tumor cells, endothelial cells and the immune response. The relative strength of the different loops determines the cancer growth rate and its response to immunotherapy. The model could serve as a starting point to identify optimal nodes for intervention against pancreatic cancer.
Keywords: Pancreatic cancer, Immune response, Immunotherapy
1. Introduction
Pancreatic cancer is the fourth most common cause of cancer-related death in the United States. It has extremely poor prognosis, with a one-year survival rate of about 25% and a five-year survival rate less than 5% (Hariharan et al., 2008). One reason for its poor prognosis is that pancreatic cancer typically develops over a period of 10–15 years, but most often does not cause symptoms until it is advanced and has metastasized (Corbo et al., 2012). Currently surgery remains the treatment approach with the best chance of cure, but only localized cancer is suitable for surgical intervention. Furthermore only about 20% of patients present with localized disease at the time of diagnosis (Koido et al., 2011; Hackert and Büchler, 2013). The most common histologic subtype of pancreatic cancer, which is the subject of this paper, is pancreatic ductal adenocarcinoma.
The immune system has the capability to detect tumor cells by recognition of their tumor specific antigens and subsequent elimination by cytotoxic CD8+ T cells (CTLs) or natural killer (NK) cells (Fukunaga et al., 2004; Ryschich et al., 2005; Vivier et al., 2011). However, tumor cells may use a variety of means to escape immune recognition and elimination. For example, they may attract myeloid derived suppressor cells (MDSCs), anti-inflammatory macrophages or T regulatory cells to block the activation of CTLs and NK cells, or in some cases induce them to undergo apoptosis (Steer et al., 2010; Liyanage et al., 2002). Tumors also have the ability to render T cells anergic or to engage inhibitory checkpoint ligands (i.e. PD1) on the cell surface (Steer et al., 2010).
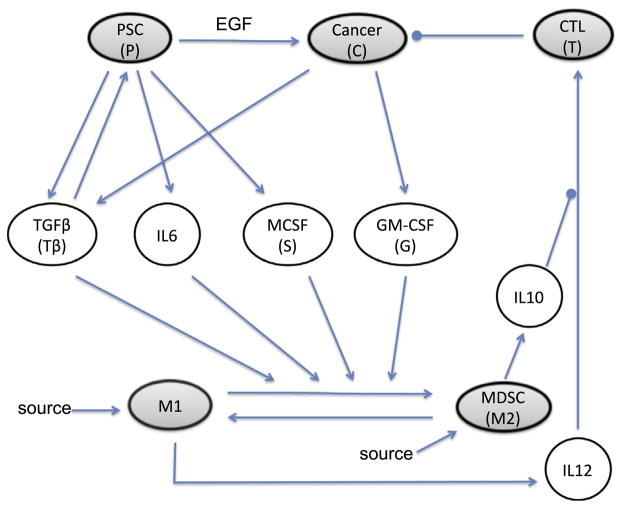
The progression of pancreatic cancer depends on the tumor microenvironment which is dictated not only by pancreatic cancer cells (PCCs) but also by various host cells including but not limited to pancreatic stellate cells (PSCs), CTLs, tumor associated macrophages M1 (pro-inflammatory) and M2 (anti-inflammatory), and MDSCs. These cells communicate with each other through a large array of cytokines and other soluble factors (Fig. 1). For pancreatic ductal adenocarcinoma, PCCs are epithelial cells that have been documented to secrete multiple factors including TGFβ which promotes activity and growth of PSCs (Gaspar et al., 2007; Omary et al., 2007; Apte et al., 1999) and GMCSF which promotes recruitment of MDSC and induces M2 polarization (Bayne et al., 2012; Pylayeva-Gupta et al., 2012). PSCs are myofibroblast-like cells that represent a major component of the tumor-associated stroma. These cells can act to enhance the growth and metastatic properties of tumor cells, and more recently have been recognized as having an immune modulatory potential (Bachem et al., 2008; Mace et al., 2013). These direct tumor-promoting properties may be particularly influenced by the growth factor EGF which promotes the proliferation of PCCs (Phillips, 2012). They also produce cytokines including TGFβ, IL6, and MCSF which enhance MDSC function and M2-polarization and promote an immunosuppressive microenvironment (Shek et al., 2002; Omary et al., 2007; Mace et al., 2013). Tumor-associated macrophages are also highly relevant within the tumor microenvironment. These cells can switch type between pro-inflammatory M1 and anti-inflammatory M2 which have distinct phenotypic characteristics (Kurahara et al., 2011). For example, M1-polarized macrophages typically produce high levels of cytokines such as IL12 and low levels of IL10, whereas M2- polarized macrophages produce high levels of IL10 and low levels of IL12. Together this complex network of cells can act upon CTLs or other cells that elicit cytotoxic activity against tumors. These anti-tumor immune effectors typically displayed upregulated cytotoxic activity upon exposure to IL12 which conversely is down-regulated by IL10. For a recent review see Roshani et al. (2013).
Fig. 1.
Interaction of cells and cytokines in pancreatic cancer. The model contains cells (shaded ellipses) and cytokines (clear ellipses) that operate in different time scales (days/years vs. minutes/hours). Arrows represent activation and circle-heads represent inhibition. Inhibition and activation can have different meanings for different elements. For cytokines, activation represents cytokine production. For tumor cells, inhibition represents the induction of apoptosis, and activation represents cell division. For CTLs activation/inhibition represent function increase/decrease of the killing rate. For macrophages, we assume a homing rate as well as the possibility of switch from one macrophage type to the other. The arrow associated with EGF means that PSCs increase proliferation of cancer cells by producing EGF. MDSC produces IL10 which inhibits activation of CTL by IL12.
Recent data indicate that the M1 to M2 transition may be important for the progression and therapeutic response in patients with pancreatic cancer. Overall, the transition from M1 and M2 is promoted by the cytokines TGFβ, IL6, M-CSF and GM-CSF secreted by PCCs and PSCs (Koido et al., 2011; Bayne et al., 2012; Gnerlich et al., 2010). This results in increased production of cytokines such as IL10, decreased production of IL12, and consequently decreased CTL activity (Koido et al., 2011) and increased cancer growth or metastasis. Together, this diverse collection of cells and soluble factors in the tumor microenvironment can influence the behavior of tumor-associated macrophages (TAMs). In the interaction network described in Fig. 1, we adopted the simplification where MDSC is included together with M2 as one compartment. For example, both cell types produce IL10 which block the activation of CTLs by IL12. However, MDSC can also down-regulate production of IL12 by macrophages (Bunt et al., 2009), and we account for this implicitly by simply decreasing the production rate of IL12.
In recent years, many mathematical models have been developed to describe the interaction between cancer cells and the immune system (de Pillis et al., 2005, 2006, 2013; Galante et al., 2012; Wilson and Levy, 2012; Radunskaya and Hook, 2012; Robertson-Tessi et al., 2012). However, no mathematical model has been developed to address how such interactions lead to cancer growth or regression in the context of pancreatic cancer. In this paper we develop a mathematical model for pancreatic cancer that incorporates the cancer–stroma-immune interaction and use it to explain biomedical and clinical data on clinically-relevant drug treatments that target TGFβ and EGF receptors (Deharvengt et al., 2012; Ellermeier et al., 2013; Kurahara et al., 2011). The resulting model is based on the network in Fig. 1 and describes the dynamic interactions among prominent cells and cytokines in terms of a system of differential equations. The model adequately reproduces multiple observed immunotherapy treatment experiments, but, more importantly, provides a generic insight on the effect of such treatments that may also be applied to other tumors.
The organization of the paper is as follows. In Section 2, we introduce the full model and simplifications of it based on separation of time scales involved in pancreatic cancer growth. In Section 3, we show that our model can explain experimental data on TGFβ silencing therapy and EGFR blocking therapy (Ellermeier et al., 2013; Deharvengt et al., 2012). In Section 4, we show that the model suggests differential responses to drug treatment given different parameters of the immune response. Finally, we discuss our results and open problems in Section 5.
2. The mathematical model
The simplest mathematical model for pancreatic cancer must include PCCs, PSCs, macrophages and T cells. This is so because cancer cells and PSCs affect the phenotype of macrophages (M1→M2), and T cells must be introduced because they are the cells that kill cancer cells and their activation depends on M1 cells. However, in order to understand the underlying biology, we first develop a more detailed model, “the full model”, that also includes primary cytokines by which the above five types of cells communicate with each other. Then we use quasi-steady-state approximation to simplify the full model to the “reduced model” consisting of four ODEs with variables PCCs, PSCs, T, and the ratio of M1 to M2.
2.1. Variables and notations
Based on the interaction network in Fig. 1, we include the following variables for cells and cytokines in the model:
Density of cancer cells: C
Density of pancreatic stellate cells (PSC): P
Density of M1 cells: M1
Density of M2 cells: M2
Density of CTL: T
Concentration of TGFβ: Tβ
Concentration of IL6: I6
Concentration of IL10: I10
Concentration of IL12: I12
Concentration of MCSF: S
Concentration of GMCSF: G
The variables for cells have the unit of number per mL, and the variables for cytokines have the unit of mM.
2.2. The full model
We start by introducing the equations for the tumor cells. Growth of many organisms under normal conditions follows the “universal law”, that is, the total body mass m grows with a rate amp(1−(m/M0)1−p), where the exponent p ≈ 3/4, a is the growth rate and M0 is the maximum size of the organism (West et al., 2001). Recently it was shown that cancer tissue growth can be described similarly, with the exponent p ranges from 2/3 to 1, depending on the growth conditions and the fractal topology of the neoplastic vascular system (Guiot et al., 2006). In this model, we adopt this description and choose p = 3/4 to model the growth of cancer cells; choosing slightly different values of p had no significant effect on the results. In addition, PSC promotes cancer growth through various cytokines, thus we represent the cancer growth rate as the sum of the basal growth rate, kc, and the enhancement by PSC, μcP. We further denote the maximum cancer density by C0. Since IL10 can reduce the ability of CTLs in killing cancer cells (Wang et al., 2011; Itakura et al., 2011), we assume the rate of removal of cancer cells to be a decreasing function of IL10. Based on these considerations, the evolution of the cancer cell density can be described by the following equation:
| (1) |
The first term on the right-hand side (RHS) models cancer growth, and the second term models the removal of cancer cells by T cells.
Pancreatic stellate cells (PSCs) are the resident myofibroblast-like cells in pancreas ducts. PSCs can be activated by cytokines such as TGFβ, and activated PSCs can secrete more TGFβ. Compared to cancer cells, PSCs are more sparse in the pancreas ducts, thus we model their growth using a logistic function. The equation for PSCs is
| (2) |
where kpP(1−P/P0) is the basal growth rate in the absence of TGFβ, (μpTβ/(Kp+Tβ))P(1−P/P0) is the TGFβ induced growth rate, and λp is the death rate of the PSC. The term μpTβ/(Kp+Tβ) is used here to model the saturation limited effect of TGFβ.
The pro-inflammatory and anti-inflammatory macrophages M1 and M2 can be attracted to the site of pancreatic cancer, undergo apoptosis, and switch type. The transition from M1 to M2 is mediated by cytokines such as TGFβ (Tβ), IL6 (I6), MCSF (S), and GMCSF (G). The equations for M1 and M2 are
| (3) |
| (4) |
Here k1 and k2 are the influx rates, λ1 and λ2 are the death rates of M1 and M2 respectively, the transition rate α from M2 to M1 is assumed to be constant, and the transition rate from M1 to M2 is assumed to depend on TGFβ, IL6, MCSF, and GMCSF linearly.
Finally, CTLs in the lymph nodes travel to the cancer site upon a cue. They are then activated by CD4+ T cells, which in turn are activated by IL-12 in conjunction with major histocompatibility complex class II (MHC II) presented on the surface of macrophages, and the latter process is inhibited by IL-10. For simplicity, we model the dynamics of CTLs (T) in pancreatic cancer by the following equation:
| (5) |
We next describe the equations for the cytokines. For simplicity, we assume that the cytokines are produced by corresponding cells at a constant rate, and they undergo a natural decay with constant rates. According to Fig. 1, we have
| (6) |
| (7) |
| (8) |
| (9) |
| (10) |
| (11) |
Here the k’s and μβ are the production rates and the λ’s are the degradation rates. We note that each cytokine is produced by a single cell type, except for TGF-β which is produced by both tumor cells and pancreatic cells. Most parameters in (Eqs. (6)–11) are not known experimentally. However, as we shall see in the next section, these parameters will not appear in our simplified model, because they will be lumped together.
2.3. The reduced model
Pancreatic cancer growth involves multiple time scales: the growth of cancer cells occurs on a time scale of months to years in vivo and weeks to months in vitro; the recruitment of macrophages and T cells occurs on a time scales of days to weeks; and the secretion and decay of cytokines occur on a time scale of seconds to hours. In order to understand the dynamics of cancer growth, we simplify the model using quasi-steady-state approximations for the cytokine concentrations. Under this assumption, Eqs. (6)–(11) become
Substituting these expressions into (Eqs. (1)–5), we obtain the following simplified system for the cell dynamics:
| (12) |
| (13) |
| (14) |
| (15) |
| (16) |
where
Here the combined parameters νc and νp describe the contribution of cancer cells and the PSCs to the growth of the PSC population, and γc and γp describe how the transition from M1 to M2 depends on cancer cells and the PSCs.
We note that the density of PSCs (P) is much smaller than the density of cancer cells (C) in the duct in pancreatic cancer (Feig et al., 2012). We assume that the secretion rate of TGFβ by PSC, kβ, is not bigger than that by cancer cells, μβ. Therefore in Eq. (13) the term νpP is much smaller than νcC and, to simplify the model, we neglect it. By redefining Kp to be Kp/νc, Eq. (13) can be written as
| (17) |
The dynamics of pancreatic ductal adenocarcinoma are affected by the macrophage population types and number. In order to analyze the system, it is more convenient to change variables to represent this dependence. Specifically, the total number of macrophages M =M1+M2, and the fraction of pro-inflammatory macrophages R =M1/M are critical markers of the status of the immune system. Accordingly, we introduce a change of variable from M1 and M2 to M and R. In these new variables, we have
| (18) |
Adding (Eqs. (14) and 15)), and using Eq. (18), we obtain
| (19) |
For R, we can use the chain rule to obtain
| (20) |
Since there are no known differences in macrophages death rates, we assume that λ1 = λ2 = λM and denote kM = k1+k2, then (Eqs. (19) and 20) become
We notice that the total number of macrophages, M, is independent of R and saturates over a period of weeks, which is set by the parameter λM. However, in pancreatic cancer the balance between the two types of macrophages can change slowly, as P and C grow. Based on this observation of separation of time scales, we further simplify the model by approximating M by its quasi-steady-state kM/λM. Thus Eq. (20) becomes
| (21) |
We also simplify (Eqs. (12) and 16) using (18). We set
| (22) |
Using these notations the death term in Eq. (12) becomes
| (23) |
Similarly, the growth term in (16) becomes
| (24) |
Substituting these back into (12) and (16) and dropping the primes for simplicity of notation, the model is then simplified to a system of four ODEs,
| (25) |
| (26) |
| (27) |
| (28) |
where kr = k1λM/kM+α and λr = λM+α. We call this system the reduced model for pancreatic cancer and use it to explain biomedical and clinical data in the next section.
3. Simulation results on drug treatments
In this section, we investigate whether the proposed model shows cancer dynamics that agree with experimental data on treatments that involve immune activation, TGFβ silencing and EGFR silencing.
3.1. Combination of TGFβ silencing and immune activation treatment
Ellermeier et al. (2013) studied the effect of treatments that involve TGFβ silencing and immune activation through RIG-I pathway on pancreatic cancer, and reported the survival time distribution for populations of pancreatic cancer patients without treatments and with different combinations of treatments (see Fig. 2A). For patients without treatments, the mean survival time (MST) is short, the variance of MST is small (black curve). For patients with single treatment using TGFβ silencing or immune activation, the MST increases and its range is broader (orange and green). For patients with both treatments, the MST and its variance are significantly larger than those of single treatments (red).
Fig. 2.
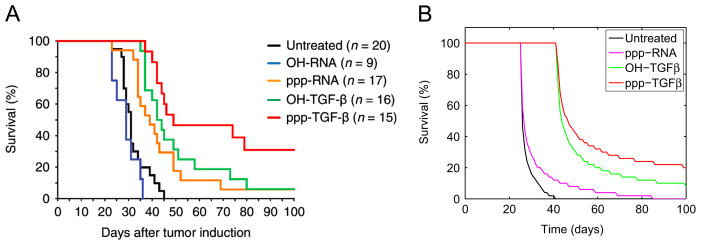
TGFβ silencing and immune activation treatment for pancreatic cancer. (A) Survival data reported in Ellermeier et al. (2013). Reprinted from Cancer Research with permission. Black: no treatments; blue: buffer control; yellow, green, red: immune activation, TGFβ silencing, and both. (B) Simulation of the model on treatments. From left to right: black: no treatment with parameters as in Table 1; magenta: ppp-RNA; green: OH-TGFβ; red: both. (For interpretation of the references to color in this figure caption, the reader is referred to the web version of this article.)
To investigate whether our model agrees with these experimental data, we simulated our model for a population of pancreatic cancer patients and investigated how the survival time distribution depends on the parameters of the model that correspond to TGFβ and immune activation treatments. We assume that the main difference among these patients is the strength of their adaptive immune responses. For each treatment we created a population of 50 patients such that each patient has a different λc which is proportional to the killing rate of cancer cells by CTLs. Specifically, we took these λc’s to be a geometric sequence between 10−9 and 10−6.5. Simulations show that using different distributions of λc yields qualitatively similar results as in Fig. 2B.
For patients without any treatment, we used all parameters as in Table 1; for patients with TGFβ silencing treatment, we reduced γc, γp and μp to 10% of their values in Table 1; and for patients with immune activation, we increased kt to be twice of its value in Table 1. In all simulations, we set the initial cancer cell density to be 200 cells per mL, and initial values for the other three variables at their quasi-steady states. We assumed that the survival time of a patient is the time for the cancer cell density to reach a threshold density and we take this threshold to be 5000 cells per mL. Fig. 2B demonstrates the simulated survival time distribution for different cases of treatments, and the results agree with the experimental data qualitatively.
Table 1.
Parameters for the reduced model.
| Parameter | Value with unit | Notes and references |
|---|---|---|
| C0 | 106 cells/mL | Maximum PCC density, estimated |
| P0 | 105 cells /mL | Maximum PSC density, estimated |
| kc | 7.5 × 10−2 cells1/4mL−1/4day−1 | Estimated |
| μc | 20kc /P0 | Estimated |
| Kc | 0.1 | We assume that the killing rate of cancer increases by a factor of 5, when R increases from 0.1 to 0.9. |
| λc | 10−7 mL per cell per day | In experiments in Seki et al. (2002), 107 CTL cells were found to kill half of the renal cancer cells in about 16 hours. Therefore the maximum rate of CTL in killing cancer cells can be approximated as ln2/16/107 · 24 ≈ 10−7 per cell per day. At the same time, this number is given by λc/(Kc +(1−R)) in a patient. Assume that R is approximately 0.1 in patients, we obtain λc = 10−7 per cell per day. |
| kp | 0.2 per day | Estimated |
| μp | 20 kp | Estimated |
| Kp | C0/100 | Estimated |
| λp | 0.15 per day | The half-life T 1/2 of PSC is 2–5 days. The relation of λp and T1/2 is λp = ln 2/T1/2. |
| kr | 0.2 per day | From the full model, we have kr = α + k1λM/kM. Taking the value that α = 0.2/day, k1 = 40 cells/ml/day (Sichert et al., 2007), kM = 228 cells/ml/day (Sichert et al., 2007; Day et al., 2009), and λM = 0.02/day (Day et al., 2009), we obtain kr ≈ 0.2. |
| λr | 0.22 per day | From the full model, we have λr = λM + α. |
| γp | 0.02λr /Ps | Ps is the PSC density in a healthy person, which satisfies Ps = P0(1−λp/kp). |
| γc | = γp | Estimated |
| kt | 3300 cells per mL per day | Estimated |
| Kt | = Kc | Estimated |
| λt | 0.3 per day | Day et al. (2009) |
3.2. Combinations of EGFR silencing and TGFβ sequestration treatments
In the microenvironment of pancreatic cancer, elevated EGF and its receptor and TGFβ have been observed (Korc, 1998). In a report from Deharvengt et al. (2012) it is shown that concomitant treatment with EGFR silencing RNAs and TGFβ sequestration molecule sTβ RII showed enhanced benefit in controlling ASPC-1 pancreatic cancer cell growth in mice (Fig. 3A). In this section, we use the reduced model to investigate how combinations of treatments of EGFR knockout and TGFβ silencing affect tumor size. As in Deharvengt et al. (2012), we compare four different cases. The first is without any treatment, the second is with EGFR silencing only, the third is with TGFβ sequestration only, and the fourth is with both treatments. For simulations without treatment, we use parameters specified in Table 1. To model EGFR silencing treatment, we take μc to be 0.7 times of the value in Table 1 to take into account the blockage of the enhancement of PCC proliferation by PSC produced EGF. We did not completely block the influence of PSC to PCC because there exists other PSC secreted cytokines in the cancer microenvironment that promote cancer cell growth. To model TGFβ treatment, we set γp = γc = μp = 0 in the reduced model to eliminate the effects of TGFβ. We plot the evolution of the cancer size in these four different cases in Fig. 3B, colored as black, blue, red, and green. These simulations show that combinations of treatment is significantly better than any single treatment and the dynamics of cancer size resulting from our model is in qualitative agreement with experimental data.
Fig. 3.
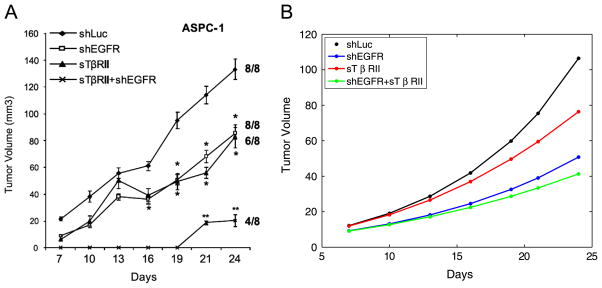
Comparison of different treatments. From top to bottom: no treatment; EGFR knockout; TGFβ silencing; both treatments. (A) Reproduced from Deharvengt et al. (2012). (B) Simulations of the model. For the four curves from top to bottom, the following fold parameters are used: r1 = 1, 0.6, 0.4, 0.3; r2 = 1, 0, 1, 0, where r1 and r2 are fold parameters for γp, γc, μp, and μc. (For interpretation of the references to color in this figure caption, the reader is referred to the web version of this article.)
In Deharvengt et al. (2012), it is also reported that for some other cancer cell lines, e.g., T3M4, the effect of simultaneously targeting EGFR and TGFβ markedly suppressed HER2, resulting in actually larger tumor load than in the case of targeting only EGFR or TGFβ alone. This situation, although not simulated here, can be achieved using our model by changing corresponding parameters that implicitly relate to HER2 expression.
Since some of the parameters of our model are only estimated up to the order of magnitudes, we only claim qualitative fit of our model (Figs. 2B and 3B) to the data in Ellermeier et al. (2013) and Deharvengt et al., 2012 (Figs. 2A and 3A). On the other hand, we shall analyze in the next section how the model results depend on the parameters.
4. Analysis on the drug efficacy and the immune response
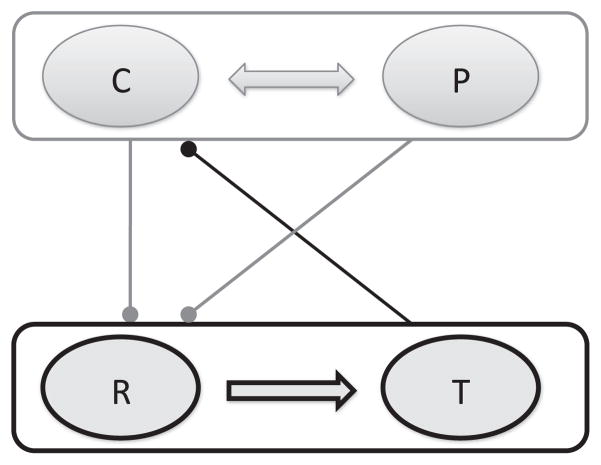
The varied response of patients to drug treatment, as shown, for example, in Section 3.1, is likely due to the varied immune response of patients. In the model (Eqs. (25)–28), the immune system response can be characterized by the parameters γp, γc and λc. In this section, we show that the immune system, characterized by γp, γc, λc is affected by immunotherapy only when these parameters fall within a specific regime, that is, there is a specific “window of opportunity” for an effective immune response. Our analysis is based on the reduced model (Eqs. (25)–28), which highlights two feedback loops as shown in Fig. 4. The first is a positive feedback loop that involves mutual enhancement of PCCs (C) and PSCs (P), and the second is a double negative feedback loop (i.e. a positive feedback loop) involving mutual inhibition of the cancer and the immune system, i.e., the C and P complex (top) and the R and T complex (bottom). Specifically, PCCs and PSCs promote M2 polarization and thus reduce R, and R upregulates T, which in turn down-regulate C.
Fig. 4.
Feedback loops of the reduced model (Eqs. (25)–28). C, P, R and T represent the four variables in the model. C and P enhance each other, and down-regulate R, while R up-regulates T which down-regulates C.
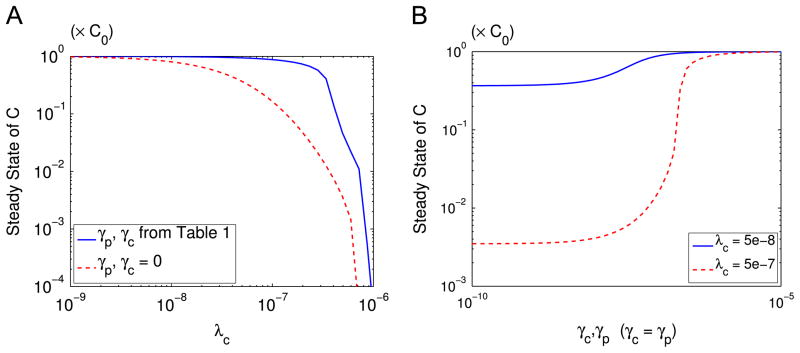
The cancer–immune interaction leads to the sensitive response of the system to the parameters of γc, γp and λc. The parameters γc and γp represent the effect of PCCs and PSCs on the polarization of the macrophages, and λc is the killing rate of cancer cells by T cells. In the absence of the negative feedback from C and P to R, we have γc = γp = 0. In this case, the steady state cancer size slowly decreases as λc increases (Fig. 5A, red dashed). However, in the presence of the negative feedback, the steady state cancer size shows a switch-like behavior as λc increases (Fig. 5A, blue solid): for large λc, the tumor size is small; for small λc, the cytokines have no effect; for intermediate λc, however, there is a sharp change in tumor size. Fig. 5B presents another view of this sensitive response. For small λc = 5e−8, the steady state tumor size remains high regardless of the values of γp and γc (Fig. 5B, blue solid); but for intermediate λc = 5e−7, a decrease of γc and γp leads to significant decrease in cancer size (Fig. 5B, red dashed). For very high value of λc, the tumor size will remain negligible unless γp and γc are unreasonably high (not shown here). For such patients pancreatic cancer may never be observed, since the cancer size remains small for a very long period of time. Similar dynamics also occur if we vary the parameters μc and μp instead of λc.
Fig. 5.
Effect of the immune system on the steady state tumor size. (A) Effect of T cell killing rate λc with (blue solid) and without (red dashed) tumor-induced effect on macrophage polarization represented by different γp, γc values. (B) Effect of cytokines on steady state tumor size for λc =5e−8 (blue solid) and λc = 5e−7 (red dashed). Here C is normalized by C0. (For interpretation of the references to color in this figure caption, the reader is referred to the web version of this article.)
The sensitive response of the system with respect to γc, γp, and λc shown in Figs. 5 have the following implications. First, it suggests that treatments which aim to change these parameters are potentially effective. For example, one can increase λc by boosting the immune response, decrease γp and γc by blocking TGF-beta or IL6, or decreasing μp and μc by blocking EGFR or TGFβ. Second, it suggests that such treatments can only be effective if corresponding parameters are perturbed in the “right” way. For example, if the adaptive immune response is too weak, with λc values in the regime as the blue solid curve in Fig. 5B, no matter how one perturbs γc and γp with treatment, there is no effective control of the cancer growth. On the other hand, if the adaptive immune response is strong enough, with λc in the regime as the red dashed curve in Fig. 5B, a treatment which dramatically decreases γc and γp will have an observable effect in controlling cancer.
To better understand the “switch-like” behavior, we solve the steady-state equations of the reduced model. By explicitly solving the steady states of P, R and T from (26)–(28) and substituting into (25), we obtain that the non-zero steady state cancer size is determined by the nontrivial solution C of the following equation:
| (29) |
with .
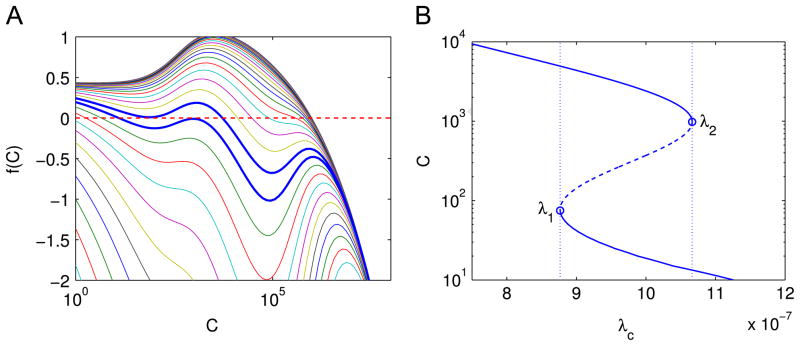
Fig. 6A shows the function f (C) given different λc, and Fig. 6B shows the solution C of f (C) = 0 as a function of λc.
Fig. 6.
(A) The profile of f(C) as a function of C given different values of λc. Each line represents a different value of λc. The parameter λc increases from the top curve to the bottom curve, and the ratio of the λc’s of neighboring two curves is 1.25 fold. The steady state cancer size is where a curve decreases from positive to negative. The two thick blue curves have λc = 8.77e−7 and 1.07e−6 and correspond to λ1 and λ2 in (B). (B) Nonzero solutions of f (C) = 0 as a function of λc. Solid lines: stable steady states of the model; dashed line and open circles: unstable steady states. The dotted lines indicate the values of λ1 and λ2 where the saddle node bifurcations occur. (For interpretation of the references to color in this figure caption, the reader is referred to the web version of this article.)
Bifurcation analysis suggests that two saddle node bifurcations occur near two points of λc, namely, λ1=8.77e−7 and λ2=1.07e−6. For λc < λ1 or λc > λ2, there is only one solution of C, and for λ1 < λc < λ2, there are three solutions. Furthermore, the upper branch (λc < λ2) and the lower branch (λc > λ1) are stable, while the middle branch which connects the two is unstable. The upper branch represents a more aggressive tumor than the lower branch. As λc increases from small values up to λ2, the tumor will remain in the aggressive state. However, as soon as λc exceeds λ2, there is a sharp drop in the size of the steady state cancer, and the system will evolve towards the lower branch. If λc now decreases, the tumor will remain in the nonaggressive state (the lower branch), until λc becomes smaller than λ1, in which case the tumor size will jump back to the aggressive state. This suggests that if we apply a treatment to boost the immune response so that λc increases, the treatment will be most effective if the patient’s parameter λc is near λ2, i.e., a small increase of the immune response will sharply reduce the tumor from the aggressive state to the nonaggressive state; for other values of λc in the upper branch, a small increase in the immune system will provide only minimal improvement.
5. Conclusions and discussion
In this paper we have developed a mathematical model of pancreatic cancer. The model involves PCCs, PSCs, immune cells M1, M2, MDSC and CTL, and cytokines EGF, TGFβ, IL6, MCSF, GMCSF, IL10 and IL12. Although M2 and MDSC are two different types of cells, both suppress the function of CTLs and NK cells. For simplicity we have combined M2 and MDSC into one compartment. We have simulated the model in two cases of treatments, where experimental data were available. We represented the effect of the drug by a change in some of the rate parameters. For example, in EGFR silencing treatment, taking account of the blockage of the enhancement of PCC proliferation by PSC produced EGF, we did not completely block the influence of PSC to PCC because there exist other PSC secreted cytokines in the cancer environment that promotes cancer cell growth, although they were not included explicitly in the model. Thus, this treatment is expressed by decreasing the parameter μc in Eq. (25) to 0.7μc, not by completely eliminating it.
In Section 4 we emphasized the important role of the state of the immune system in drug treatment. If the immune system is weak (e.g., in the sense that the killing rate of CTLs, λc, is small), as in the case of a patient with organ transplant or with HIV/AIDs, or if the immune system is very strong (e.g., λc is very large), then treatment is not effective. Many papers describe the role of cytotoxic chemotherapy (Burrisrd et al., 1997; Von Hoff et al., 2011; Heinemann et al., 2013; Hosein et al., 2013). NAB-Paclitaxel–Gemcitabine perhaps is one of the more promising chemotherapeutic approaches tested to date. Other chemotherapeutic approaches including an intense FOLFIRINOX regimen has proven effective at debulking tumors, to make curative resection more likely (Heinemann et al., 2013; Bekaii-Saab and Goldberg, 2013). As patient data from such treatments become available, our model could be further refined to reflect the results of these treatments, and then be used to develop hypotheses on optimal scheduling of treatments.
The proposed model, as are all such models, is obviously a highly simplified description of the biological complexity. It does not include the spatial structure of the tumor or the metabolic elements limiting the tumor growth. It does not include important aspects of immune response, such as T regulatory cells (Tregs), CD4+ T cells, and the complex interactions between Th1, Th2 and Th17 cells, which may also be relevant to pancreatic cancer development and progression (Beatty et al., 2011). It does not account for stromal cells and hypoxia. We also lumped cytokines into generic groups based on the overall homology in function. Introducing all these cells and their associated cytokines would indeed make the model more comprehensive; however, because of the sparsity of experimental data for pancreatic cancer, not necessarily more useful.
The risk of cancer depends on two factors, growth/proliferation and invasion/metastasis, and the balance of the two primarily depends on the specific cancer. For example, in cutaneous melanoma diagnosed at early stages, growth is a major factor for prognosis: if the tumor is still within the dermis, it can be excised with a reduced chance for relapse; but if the growth has reached the subcutaneous tissue (5 mm depth) then metastasis is more likely and survival may be only a matter of months. Typically, in pancreatic cancer, metastasis has already taken place at the time of diagnosis, and the mean survival time is only a few months (see Fig. 2). Although our mathematical model is described in terms of tumor cell proliferation, it represents, to some extent, the total risk associated with pancreatic cancer, since the more cancer cells there are, the greater the possibility of metastasis is.
HIGHLIGHTS.
Pancreatic cancer is highly effective in evading the immune response.
Model simulations qualitatively agree with data in cancer treatments.
We emphasize the crucial role of the state of the immune system in treatments.
Immuno-modulatory drugs are effective in a narrow window of immune responses.
Acknowledgments
This work is partially supported by the Mathematical Biosciences Institute at the Ohio State University. CX is supported in part by the National Science Foundation in the United States through Grant DMS 1312966. GBL is supported by NIH Grants 1R01 CA169363-01 and 1R21 CA173473-01, and research funding from Prometheus, Inc., Karyopharm Therapeutics, Inc., Oncolytics, Inc., Array Biopharma, Inc. and Bristol Myers-Squibb, Inc.
Footnotes
Parameter estimation
The parameters for the reduced model are listed in Table 1. We note that many of the parameters are presently not measured in pancreatic cancer, and they were estimated from experimental data of other diseases.
References
- Apte MV, Haber PS, Darby SJ, Rodgers SC, McCaughan GW, Korsten MA, Pirola RC, Wilson JS. Pancreatic stellate cells are activated by proinflammatory cytokines: implications for pancreatic fibrogenesis. Gut. 1999;44:534–541. doi: 10.1136/gut.44.4.534. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bachem MG, Zhou S, Buck K, Schneiderhan W, Siech M. Pancreatic stellate cells – role in pancreas cancer. Langenbecks Arch Surg. 2008;393:891–900. doi: 10.1007/s00423-008-0279-5. [DOI] [PubMed] [Google Scholar]
- Bayne LJ, Beatty GL, Jhala N, Clark CE, Rhim AD, Stanger BZ, Vonderheide RH. Tumor-derived granulocyte-macrophage colony-stimulating factor regulates myeloid inflammation and T cell immunity in pancreatic cancer. Cancer Cell. 2012;21:822–835. doi: 10.1016/j.ccr.2012.04.025. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Beatty GL, Chiorean EG, Fishman MP, Saboury B, Teitelbaum UR, Sun W, Huhn RD, Song W, Li D, Sharp LL, Torigian DA, O’Dwyer PJ, Vonderheide RH. CD40 agonists alter tumor stroma and show efficacy against pancreatic carcinoma in mice and humans. Science. 2011;331:1612–1616. doi: 10.1126/science.1198443. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bekaii-Saab T, Goldberg RM. Folfirinox in locally advanced pancreas adenocarcinoma: back to the future? Oncologist. 2013;18:487–489. doi: 10.1634/theoncologist.2013-0157. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bunt SK, Clements VK, Hanson EM, Sinha P, Ostrand-Rosenberg S. Inflammation enhances myeloid-derived suppressor cell cross-talk by signaling through toll-like receptor 4. J Leukoc Biol. 2009;85:996–1004. doi: 10.1189/jlb.0708446. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Burris H, Moore MJ, Andersen J, Green MR, Rothenberg ML, Modiano MR, Cripps MC, Portenoy RK, Storniolo AM, Tarassoff P, Nelson R, Dorr FA, Stephens CD, Von Hoff DD. Improvements in survival and clinical benefit with gemcitabine as first-line therapy for patients with advanced pancreas cancer: a randomized trial. J Clin Oncol. 1997;15:2403–2413. doi: 10.1200/JCO.1997.15.6.2403. [DOI] [PubMed] [Google Scholar]
- Corbo V, Tortora G, Scarpa A. Molecular pathology of pancreatic cancer: from bench-to-bedside translation. Curr Drug Targ. 2012;13:744–752. doi: 10.2174/138945012800564103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Day J, Friedman A, Schlesinger LS. Modeling the immune rheostat of macrophages in the lung in response to infection. Proc Natl Acad Sci USA. 2009;106:11246–11251. doi: 10.1073/pnas.0904846106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- de Pillis L, Gallegos A, Radunskaya A. A model of dendritic cell therapy for melanoma. Front Oncol. 2013:3. doi: 10.3389/fonc.2013.00056. http://dx.doi.org/10.3389/fonc.2013.00056. [DOI] [PMC free article] [PubMed]
- de Pillis LG, Gu W, Radunskaya AE. Mixed immunotherapy and chemotherapy of tumors: modeling applications and biological interpretations. J Theor Biol. 2006;238:841–862. doi: 10.1016/j.jtbi.2005.06.037. http://dx.doi.org/10.1016/j.jtbi.2005.06.037. [DOI] [PubMed] [Google Scholar]
- de Pillis LG, Radunskaya AE, Wiseman CL. A validated mathematical model of cell-mediated immune response to tumor growth. Cancer Res. 2005;65:7950–7958. doi: 10.1158/0008-5472.CAN-05-0564. http://dx.doi.org/10.1158/0008-5472.CAN-05-0564. [DOI] [PubMed] [Google Scholar]
- Deharvengt S, Marmarelis M, Korc M. Concomitant targeting of EGF receptor, TGF-beta and SRC points to a novel therapeutic approach in pancreatic cancer. PLoS One. 2012;7:e39684. doi: 10.1371/journal.pone.0039684. [DOI] [PMC free article] [PubMed] [Google Scholar] [Retracted]
- Ellermeier J, Wei J, Duewell P, Hoves S, Stieg MR, Adunka T, Noerenberg D, Anders HJ, Mayr D, Poeck H, Hartmann G, Endres S, Schnurr M. Therapeutic efficacy of bifunctional siRNA combining TGF-β1 silencing with RIG-I activation in pancreatic cancer. Cancer Res. 2013;73:1709–1720. doi: 10.1158/0008-5472.CAN-11-3850. [DOI] [PubMed] [Google Scholar]
- Feig C, Gopinathan A, Neesse A, Chan DS, Cook N, Tuveson DA. The pancreas cancer microenvironment. Clin Cancer Res. 2012;18:4266–4276. doi: 10.1158/1078-0432.CCR-11-3114. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fukunaga A, Miyamoto M, Cho Y, Murakami S, Kawarada Y, Oshikiri T, Kato K, Kurokawa T, Suzuoki M, Nakakubo Y, et al. Cd8+ tumor-infiltrating lymphocytes together with cd4+ tumor-infiltrating lymphocytes and dendritic cells improve the prognosis of patients with pancreatic adenocarcinoma. Pancreas. 2004;28:e26–e31. doi: 10.1097/00006676-200401000-00023. [DOI] [PubMed] [Google Scholar]
- Galante A, Tamada K, Levy D. B7-h1 and a mathematical model for cytotoxic T cell and tumor cell interaction. Bull Math Biol. 2012;74:91–102. doi: 10.1007/s11538-011-9665-1. http://dx.doi.org/10.1007/s11538-011-9665-1. [DOI] [PubMed] [Google Scholar]
- Gaspar NJ, Li L, Kapoun AM, Medicherla S, Reddy M, Li G, O’Young G, Quon D, Henson M, Damm DL, Muiru GT, Murphy A, Higgins LS, Chakravarty S, Wong DH. Inhibition of transforming growth factor beta signaling reduces pancreatic adenocarcinoma growth and invasiveness. Mol Pharmacol. 2007;72:152–161. doi: 10.1124/mol.106.029025. [DOI] [PubMed] [Google Scholar]
- Gnerlich JL, Mitchem JB, Weir JS, Sankpal NV, Kashiwagi H, Belt BA, Porembka MR, Herndon JM, Eberlein TJ, Goedegebuure P, Linehan DC. Induction of Th17 cells in the tumor microenvironment improves survival in a murine model of pancreatic cancer. J Immunol. 2010;185:4063–4071. doi: 10.4049/jimmunol.0902609. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Guiot C, Delsanto PP, Carpinteri A, Pugno N, Mansury Y, Deisboeck TS. The dynamic evolution of the power exponent in a universal growth model of tumors. J Theor Biol. 2006;240:459–463. doi: 10.1016/j.jtbi.2005.10.006. [DOI] [PubMed] [Google Scholar]
- Hackert T, Büchler MW. Pancreatic cancer: advances in treatment, results and limitations. Dig Dis. 2013;31:51–56. doi: 10.1159/000347178. [DOI] [PubMed] [Google Scholar]
- Hariharan D, Saied A, Kocher HM. Analysis of Mortality Rates for Pancreatic Cancer Across the World. Vol. 10. HPB; Oxford: 2008. pp. 58–62. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Heinemann V, Reni M, Ychou M, Richel DJ, Macarulla T, Ducreux M. Tumour–stroma interactions in pancreatic ductal adenocarcinoma: rationale and current evidence for new therapeutic strategies. Cancer Treat Rev. 2013 doi: 10.1016/j.ctrv.2013.04.004. [DOI] [PubMed] [Google Scholar]
- Hosein PJ, de Lima Lopes G, Pastorini VH, Gomez C, Macintyre J, Zayas G, Reis I, Montero AJ, Merchan JR, RochaLima CM. A phase ii trial of nab-paclitaxel as second-line therapy in patients with advanced pancreatic cancer. Am J Clin Oncol. 2013;36:151–156. doi: 10.1097/COC.0b013e3182436e8c. [DOI] [PubMed] [Google Scholar]
- Itakura E, Huang RR, Wen DR, Paul E, Wünsch PH, Cochran AJ. Il-10 expression by primary tumor cells correlates with melanoma progression from radial to vertical growth phase and development of metastatic competence. Mod Pathol. 2011;24:801–809. doi: 10.1038/modpathol.2011.5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Koido S, Homma S, Takahara A, Namiki Y, Tsukinaga S, Mitobe J, Odahara S, Yukawa T, Matsudaira H, Nagatsuma K, Uchiyama K, Satoh K, Ito M, Komita H, Arakawa H, Ohkusa T, Gong J, Tajiri H. Current immunotherapeutic approaches in pancreatic cancer. Clin Dev Immunol. 2011;2011:267–539. doi: 10.1155/2011/267539. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Korc M. Role of growth factors in pancreatic cancer. Surg Oncol Clin N Am. 1998;7:25–41. [PubMed] [Google Scholar]
- Kurahara H, Shinchi H, Mataki Y, Maemura K, Noma H, Kubo F, Sakoda M, Ueno S, Natsugoe S, Takao S. Significance of M2-polarized tumor-associated macrophage in pancreatic cancer. J Surg Res. 2011;167:e211–e219. doi: 10.1016/j.jss.2009.05.026. [DOI] [PubMed] [Google Scholar]
- Liyanage UK, Moore TT, Joo HG, Tanaka Y, Herrmann V, Doherty G, Drebin JA, Strasberg SM, Eberlein TJ, Goedegebuure PS, et al. Prevalence of regulatory T cells is increased in peripheral blood and tumor microenvironment of patients with pancreas or breast adenocarcinoma. J Immunol. 2002;169:2756–2761. doi: 10.4049/jimmunol.169.5.2756. [DOI] [PubMed] [Google Scholar]
- Mace TA, Ameen Z, Collins A, Wojcik SE, Mair M, Young GS, Fuchs JR, Eubank TD, Frankel WL, Bekaii-Saab T, Bloomston M, Lesinski GB. Pancreatic cancer associated stellate cells promote differentiation of myeloid-derived suppressor cells in a stat3-dependent manner. Cancer Res. 2013 doi: 10.1158/0008-5472.CAN-12-4601. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Omary MB, Lugea A, Lowe AW, Pandol SJ. The pancreatic stellate cell: a star on the rise in pancreatic diseases. J Clin Invest. 2007;117:50–59. doi: 10.1172/JCI30082. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Phillips P. Pancreatic Stellate Cells and Fibrosis. Transworld Research Network; Trivandrum, India: 2012. Pancreatic cancer and tumor microenvironment. [PubMed] [Google Scholar]
- Pylayeva-Gupta Y, Lee KE, Hajdu CH, Miller G, Bar-Sagi D. Oncogenic kras-induced gm-csf production promotes the development of pancreatic neoplasia. Cancer Cell. 2012;21:836–847. doi: 10.1016/j.ccr.2012.04.024. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Radunskaya A, Hook S. New Challenges for Cancer Systems Biomedicine. Springer; 2012. Modeling the kinetics of the immune response; pp. 267–282. [Google Scholar]
- Robertson-Tessi M, El-Kareh A, Goriely A. A mathematical model of tumor–immune interactions. J Theor Biol. 2012;294:56–73. doi: 10.1016/j.jtbi.2011.10.027. [DOI] [PubMed] [Google Scholar]
- Roshani R, McCarthy F, Hagemann T. Inflammatory cytokines in human pancreatic cancer. Cancer Lett. 2013 doi: 10.1016/j.canlet.2013.07.014. [DOI] [PubMed] [Google Scholar]
- Ryschich E, Notzel T, Hinz U, Autschbach F, Ferguson J, Simon I, Weitz J, Frohlich B, Klar E, Buchler MW, et al. Control of T-cell–mediated immune response by HLA class I in human pancreatic carcinoma. Clin Cancer Res. 2005;11:498–504. [PubMed] [Google Scholar]
- Seki N, Brooks AD, Carter CRD, Back TC, Parsoneault EM, Smyth MJ, Wiltrout RH, Sayers TJ. Tumor-specific CTL kill murine renal cancer cells using both perforin and Fas ligand-mediated lysis in vitro, but cause tumor regression in vivo in the absence of perforin. J Immunol. 2002;168:3484–3492. doi: 10.4049/jimmunol.168.7.3484. [DOI] [PubMed] [Google Scholar]
- Shek FWT, Benyon RC, Walker FM, McCrudden PR, Pender SLF, Williams EJ, Johnson PA, Johnson CD, Bateman AC, Fine DR, Iredale JP. Expression of transforming growth factor-beta 1 by pancreatic stellate cells and its implications for matrix secretion and turnover in chronic pancreatitis. Am J Pathol. 2002;160:1787–1798. doi: 10.1016/s0002-9440(10)61125-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sichert D, Aust D, Langer S, Baretton G, Dieter P. Characterization of macrophage subpopulations and microvessel density in carcinomas of the gastrointestinal tract. Anticancer Res. 2007;27:1693–1700. [PubMed] [Google Scholar]
- Steer HJ, Lake RA, Nowak AK, Robinson BWS. Harnessing the immune response to treat cancer. Oncogene. 2010;29:6301–6313. doi: 10.1038/onc.2010.437. [DOI] [PubMed] [Google Scholar]
- Vivier E, Raulet DH, Moretta A, Caligiuri MA, Zitvogel L, Lanier LL, Yokoyama WM, Ugolini S. Innate or adaptive immunity? The example of natural killer cells. Science. 2011;331:44–49. doi: 10.1126/science.1198687. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Von Hoff DD, Ramanathan RK, Borad MJ, Laheru DA, Smith LS, Wood TE, Korn RL, Desai N, Trieu V, Iglesias JL, Zhang H, Soon-Shiong P, Shi T, Rajeshkumar NV, Maitra A, Hidalgo M. Gemcitabine plus nabpaclitaxel is an active regimen in patients with advanced pancreatic cancer: a phase I/II trial. J Clin Oncol. 2011;29:4548–4554. doi: 10.1200/JCO.2011.36.5742. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang R, Lu M, Zhang J, Chen S, Luo X, Qin Y, Chen H. Increased il-10 MRNA expression in tumor-associated macrophage correlated with late stage of lung cancer. J Exp Clin Cancer Res. 2011;30:62. doi: 10.1186/1756-9966-30-62. [DOI] [PMC free article] [PubMed] [Google Scholar]
- West GB, Brown JH, Enquist BJ. A general model for ontogenetic growth. Nature. 2001;413:628–631. doi: 10.1038/35098076. [DOI] [PubMed] [Google Scholar]
- Wilson S, Levy D. A mathematical model of the enhancement of tumor vaccine efficacy by immunotherapy. Bull Math Biol. 2012;74:1485–1500. doi: 10.1007/s11538-012-9722-4. http://dx.doi.org/10.1007/s11538-012-9722-4. [DOI] [PMC free article] [PubMed] [Google Scholar]