High Resolution ¹³C MRI With Hyperpolarized Urea: In Vivo T₂ Mapping and ¹⁵N Labeling Effects

Abstract

¹³C steady state free precession (SSFP) magnetic resonance imaging and effective spin-spin relaxation time (T₂) mapping were performed using hyperpolarized [¹³C] urea and [¹³C, ¹⁵N₂] urea injected intravenously in rats. ¹⁵N labeling gave large T₂ increases both in solution and in vivo due to the elimination of a strong scalar relaxation pathway. The T₂ increase was pronounced in the kidney, with [¹³C, ¹⁵N₂] urea giving T₂ values of 6.3±1.3 s in the cortex and medulla, and 11±2 s in the renal pelvis. The measured T₂ in the aorta was 1.3±0.3 s. [¹³C] urea showed shortened T₂ values in the kidney of 0.23±0.03 s compared to 0.28±0.03 s measured in the aorta. The enhanced T₂ of [¹³C, ¹⁵N₂] urea was utilized to generate large signal enhancement by SSFP acquisitions with flip angles approaching the fully refocused regime. Projection images at 0.94 mm in-plane resolution were acquired with both urea isotopes, with [¹³C, ¹⁵N₂] urea giving a greater than four-fold increase in signal-to-noise ratio [¹³C] over urea.

I. Introduction

Magnetic resonance imaging with hyperpolarized ¹³C-labeled compounds is a powerful tool for molecular imaging in preclinical research with clinical feasibility demonstrated [1]. In the dissolution dynamic nuclear polarization (DNP) experiment [2], the ¹³C-enriched imaging probe is doped with millimolar amounts of an organic radical, cooled to solid state, and irradiated at the electron/nuclear transition frequencies in a high magnetic field. In this manner, nuclear polarizations as high as 70% have been reported [3], or more typically 10%–30%. This represents a gain of four orders-of-magnitude over the Boltzmann polarization at room temperature and high magnetic field. The solid state sample is rapidly dissolved with heated solvents while retaining the polarization into liquid state, creating a new class of injectable MRI contrast agents. The hyperpolarization of endogenous substrates enables minimally invasive monitoring of key specific metabolic pathways and transport processes in vivo [4]–[7] with demonstrated utility in oncological [1], [8]-[11] and perfusion [12]–[16] imaging.

Hyperpolarized MR angiography (MRA) and perfusion imaging have interesting properties differentiating them from conventional MRA methods. Unlike ¹ H MRA which utilizes altered contrast of the water in blood vessels or perfused tissues from radio frequency (RF) preparation pulses, flow-encoding gradients, or the injection of relaxation agents, hyperpolarized ¹³C magnetic resonance allows for direct imaging of the injected compound. Therefore, this method provides background free signal due to the low ¹³C natural abundance (~ 1%) in tissues and the low gyromagnetic ratio (γ) of ¹³C nucleus. This has enabled several intriguing applications including coronary angiography [15] and perfusion assessment within the brain [13], [14] kidney [16], and in preclinical cancer models [17].

Despite the unique advantages of hyperpolarized perfusion imaging, there are several drawbacks. Although the DNP process gives a four order of magnitude gain over Boltzmann polarization, high resolution imaging has been difficult for a number of reasons. First, ignoring the polarization increase, the voltage induced in the receiver coil by a magnetic moment μ will scale as, ε ~ μω₀ ~ γ², while the noise scales as γ. Therefore, the signal-to-noise ratio (SNR) gain from DNP is offset to some by the inherently low SNR from imaging a low γ nucleus. A second significant challenge is the gradient pulse area requirement for a given resolution, which scales as 1/γ and necessitates long encoding pulses on clinical MRI systems.

A novel solution to the resolution and SNR limitations is the use of a long T₂ probe in conjunction with acquisitions employing multiple refocusing pulses [13]. If T₂ is long compared to the imaging time, 180° refocusing RF pulses (preceded by a 90° excitation) are signal-optimal and offer very large SNR improvements. Previously designed hyperpolarized perfusion probes include (bis–1,1–(hydroxy–methyl)–1–¹³C–cyclopropane–d₈) (sometimes abbreviated as HMCP or HP001) and tert butanol, both of which have T₂ values in the range of 1.4–4 s in vivo [13], [18]. Since this is greater than the phase encoding time for a single image, projection images can be acquired at 1 mm in-plane resolution with SNR comparable to ¹H MRI [13].

Another potential solution to the SNR and resolution limitations is the use of endogenous, non toxic imaging probes such as urea [12] which could potentially be injected in very high concentrations. Urea is a normal blood constituent produced by amino acid metabolism, and it is typically found with steady state concentrations of 5.5±2.0mM(33±12 mg/dL) in the blood of healthy humans [19] and rats [20]. Urea has been shown to be well-tolerated intravenously in very large doses even in patients with end stage renal failure on dialysis [21].

Although ¹³C urea is one of the most promising angiographic imaging agents due to its low toxicity, image quality is limited by its comparatively short relaxation times. Scalar coupling of the ¹³C to the fast-relaxing quadrupolar ¹⁴N causes a large T₁ decrease at low fields leading to polarization loss during transport from the polarizer to the imaging magnet [22]. Furthermore, the T₂ range measured in this manuscript (0.09–0.30 s) is approximately an order-of-magnitude lower than that of typical ¹³C compounds measured in vivo [13], [18], [23] and at least two orders-of-magnitude lower than those measured in aqueous solution.

In this study, we found that ¹⁵N labeling the amide groups of [¹³C] urea results in a 250 fold increase in the T₂ in aqueous solution. In vivo T₂ mapping experiments showed that [¹³C, ¹⁵N₂] urea still had a much longer T₂ than [¹³C] urea, although the increases were highly spatially heterogeneous. This difference was most apparent in the kidneys, where T₂ values as high 11 ± 2 s were observed with [¹³C, ¹⁵N₂] urea. The measured T₂ of [¹³C] urea was slightly lower in the kidneys than in the blood, with values of 0.231±0.026 and 0.279±0.027 s respectively. The large T₂ increases associated with ¹⁵N labeling were utilized to extract large SNR gains via steady state free precession (SSFP) imaging with flip angles in the fully refocused regime. [¹³C, ¹⁵N₂] urea projection images depicted the kidney, aorta, and iliac branches in great detail and gave a factor of 4 SNR improvement over [¹³C] urea.

II. Theory

A. SSFP Signal Behavior

The signal behavior of the SSFP sequence applied to hyperpolarized nuclei has been described in detail previously [12], [13], [17], [24]–[26]. Typically, a θ/2 preparation RF pulse is placed TR/2 before the first imaging repetition, and all pulses have alternating polarity. The flip angle θ tunes the degree of T₁ and T₂ weighing and the total image SNR [13], [24], [27], the latter of which is also highly dependent on the relaxation and sequence timing parameters. Assuming a small frequency spread, the analytic model derived by Svensson et al. giving the transverse magnetization at the n^th phase encoding step can be used [13]

$$M_{xy,n}=M_{z,0}\sin \frac{\theta }{2}{\left[{\left(E_1\cos \frac{\theta }{2}\right)}^2+{\left(E_2\sin \frac{\theta }{2}\right)}^2\right]}^{n∕2}$$ (1)

where, E₁ = exp(TR/T₁), E₂ = exp(TR/T₂) The image SNR and pixel blurring can be calculated by

$$\text{signal}=\max \mid h\left(x\right)\mid$$ (2)

$$\text{pixel width}=\mathrm{FWHM}\mid h\left(x\right)\mid$$ (3)

with h(x) = FFT{M_xy} is the point spread function in the phase encoded direction. The simulated signal and pixel width for [¹³C] urea and [¹³C, ¹⁵N₂] urea is shown in Fig. 1 for various T₂ values measured later in this manuscript.

Fig. 1.

Simulated SSFP signal response and pixel width for 96 phase encodes and TR = 15 ms, the values used in projection imaging experiments. The data are plotted as a function of SSFP flip angle for both urea isotopes using the estimated T₂ values.

This model provides a rough estimate of the imaging SNR, since the actual SNR realized will depend also on the k space image and the k space ordering. For N_PE phase encodes and in the long the limit of T₁, T₂ >> N_PETR, the SSFP signal reduces to N_PEM₀ when θ = 180°. In this case, the sequence is similar to the CPMG fast spin echo sequence with the signal given by 1 giving a pure T₂ decay. With T₂ values less than the imaging time N_PETR, a lower value of θ will provide a higher total signal and tighter point spread function. In this regime, signal dropout occurring at ±1/2TR off resonance must also be considered. This effect is simulated in Fig. 2 ignoring relaxation. Clinical MRI systems generally have much stricter requirements on peak gradient amplitude, gradient switching rate, and RF pulse amplitude than high resolution systems designed for animal use. This creates challenges encoding large image matrices with low gyromagnetic ratio (γ) nuclei. Particularly, the TR used for high resolution imaging of low γ nuclei (15 ms for most experiments in this study) was much larger than values used previously for hyperpolarized SSFP on animal systems or for ¹H on clinical systems. This creates a significant challenge for imaging short T₂ compounds since at low flip angles and large TR values, the signal-loss banding occurs close to the resonant frequency.

Fig. 2.

Simulated SSFP signal as a function of frequency excluding relaxation and RF selectivity. Due to the small frequency range simulated, RF spectral profile effects were ignored. The signal loss occurring at ±1/2TR can be detrimental due to the longer TR required on clinical imaging systems. When T₂ is long compared to the imaging time, the banding can be eliminated with use of larger flip angles.

B. Urea Transverse Relaxation

In solution, the measured ¹³C transverse relaxation rate R₂ = 1/T₂ will be the sum of several pathways of varying strength

$$R_2=R_{2,SC}+R_{2,CSA}+\sum _X{R}_{2,CXdd}.$$ (4)

R_2,CXdd is the dipolar relaxation from nucleus X, which, for the ¹³C label of urea, will be primarily from the four amide protons. The ¹⁵N labeled compound will also have some dipolar contributions from the neighboring nitrogens. R_2,CSA is the chemical shift anisotropy contribution which emanates from the variation in Larmor frequency experienced by the carbonyl ¹³C during molecular tumbling. R_2,SC is the pathway which arises from scalar coupling to a fast relaxing (usually quadrupolar) nucleus.

This scalar coupling of the second kind effect was recently shown to attenuate the low-field T₁ of [¹³C] urea at low B₀ due to the strong ¹³C–¹⁴N scalar coupling constant (14 Hz) and fast ¹⁴N relaxation time (T_1,N ~ T_2,N ~1 ms) [28]. This T₁ attenuation becomes negligible at high fields. However, the scalar relaxation pathway affects the T₂ even at high fields [29]

$$R_{2,SC}=\frac{4}{3}{\pi }^2{J}^{2}S(S+1)\left(\frac{1}{R_{1,N}}+\frac{R_{2,N}}{R_{2,N}^2+\Delta {\omega }^2}\right).$$ (5)

Here, Δω = ω_C–ω_N is the difference in Larmor frequency between the ¹³C and ¹⁴N nuclei, J is the coupling constant in Hz, S is the nuclear spin of ¹⁴N. At 3T, the right-hand term in (5) is negligible since Δω = 2π × 22 MHz, and R_2,N ≈ 1 kHz [22], [28]. The left-hand term in the parentheses persists at high fields. This interaction has been used to indirectly estimate the relaxation times of halogens and other quadrupolar nuclei whose relaxation times are difficult to measure directly due to extremely broad line widths [30], [31]. This is possible since R_2,SC scales as 1/T₁ of the quadrupolar nucleus, so the latter parameter can be estimated if the coupling constant is known. Finer et al.. used line broadening due to R_2,SC of the amide protons to estimate the rotation correlation time τ of urea in dilute solution [28]. In an identical manner, the ¹³C scalar coupling relaxation can be derived by substituting the nitrogen quadrupolar relaxation term $R_{1,N}={\omega }_Q^2\tau$ the ¹⁴N nuclear spin S = 1, and summing contributions from both nitrogens giving

$$R_{2,SC}=\frac{16{\pi }^2{J}^2}{3{\omega }_Q^2\tau }.$$ (6)

The ¹³CT₂ due to the scalar coupling effect increases with increasing correlation time τ.

The dipolar and CSA terms can be expressed as

$$R_{2,CSA}+\sum _X{R}_{2,CXdd}=({\alpha }_{CSA}+{\alpha }_{CHdd}+{\alpha }_{CNdd})\tau .$$ (7)

This model assumes the extreme narrowing limit of the spectral density function $(2∕5)\tau ∕(1+{\omega }_0^2{\tau }^2)\sim (2∕5)\tau$. At B₀ = 3 T and using τ = 5 ps estimated in [28] for urea in dilute solution at 17 °C, the product ω₀τ = 10⁻³. The, α_CSA, α_CHdd and α_CNdd terms are the relative strengths of each pathways (in s⁻²). ¹⁵N labeling effectively replaces the R_2,SC term in (4) and (6) with a dipolar term R_2,CNdd from (7). The latter pathway is much weaker, and we found the solution aqueous solution T₂ of [¹³C, ¹⁵N₂] urea (24 ± 4 s) to be at least a factor of 200 greater than that of [¹³C] urea (0.090±.014 s) at 25 °C. From (6), substituting J = 14 Hz, ω_Q = 2π × 2.24 MHz [28], and T_2,SC = 0.090±.014 s gives a correlation time τ = 4.7±0.7 ps, a similar value to that measured using ¹ H NMR linewidth analysis [28].

In vivo T₂ measurements of [¹³C] urea and [¹³C, ¹⁵N₂] urea reported in this manuscript differ considerably from those measured in solution. Particularly, the T₂ of [¹³C, ¹⁵N₂] urea decreases to less than 2 s in blood, while that of [¹³C] urea increases from 0.09 s in solution to 0.28 s in blood. This can be at least partially explained by the high blood viscosity due to hematocrit which increases τ. The slowed rotation will affect [¹³C, ¹⁵N₂] urea and [¹³C] urea in the opposite manner [(7) and (6), respectively]. However, there is likely a strong paramagnetic relaxation enhancement due to deoxygenated hemoglobin; this effect has been extensively studied in ¹ H CPMG experiments. [32]-[34]. Urea is likely to be nearly as prone to this effect as water due to its high permeability through the red blood cell membrane [35], and the intracellular urea pool has been previously observed by ¹³ C NMR via a small (~ 0.2 PPM) frequency shift [36].

III. Methods

A. Sample Preparation

Samples of 6.0 M enriched [¹³C] urea and [¹³C, ¹⁵N₂] urea (Sigma Aldrich, St. Louis, MO, USA) were prepared in a glycerol solution. This mixture was doped with 15 mM of the trityl radical and 1.5 mM Gd-DOTA for polarization enhancement.

B. Hardware

Dynamic nuclear polarization was performed with an Oxford Instruments Hypersense unit (Oxford Instruments, Oxford, U.K.) operating at 1.3 K and 3.35T (ω_e = 94.1 GHz). Imaging and phantom experiments were performed using a custom designed ¹³C/¹H transmit/receive birdcage coil placed in the center of the bore of a 3T (ω_C = 32.1 MHz) clinical imaging system (GE Medical Systems, Waukesha, WI, USA). The scanner gradients had a 4 G · cm⁻¹ peak amplitude, 1.5 G · cm⁻¹ ms⁻¹ peak slew rate.

C. Phantom Measurements

T₁ and T₂ measurements were performed on hyperpolarized [¹³C] urea and [¹³C, ¹⁵N₂] urea in aqueous solution at 37 °C, B₀ = 3 T.T₂ measurements were performed with a CPMG sequence with TR = 2π_CPMG = 10 ms, 2000 repetitions, 10 A/D samples per repetition, total duration 20 s. T₁ measurements used an adiabatic double spin echo sequence [37] with a 5° excitation, TR = 3 s, 64 scans, 192 s total duration. All experiments were repeated three times. Data were fit to a single exponential decay.

T₂ measurements were performed at various bulk viscosity values which were generated by changing ratios of glycerol/water mixtures to approximate the effect of varying the rotation correlation time τ. The viscosity (in cP) was estimated as a function of glycerol fraction and temperature using the empirical relations given by Cheng [38]. Six 2-mL vials were prepared at differing glycerol concentrations, temperature controlled to 37 °C with a water heat bath, mixed with 20 μL hyperpolarized urea solution, and were imaged with the SSFP sequence with θ = 180°. This sequence played the preparation pulse only once, and during the spin echo train, multiple images were phase encoded

(8)

Parameters used were n = 32 phase encodes per image, TR = 12 ms, 384 ms per image, m = 60 total images over 23 s. In an identical manner, T₂ measurements of [¹³C] urea and [¹³C, ¹⁵N₂] urea in 20%, 40%, and 60% fetal bovine serum were performed.

T₂ measurements were also performed in whole rat blood and plasma. Approximately 2 mL venous blood was drawn from anesthetized rats’ lateral tail veins, anticoagulated with K2-EDTA, maintained at 37 °C, injected with hyperpolarized urea solution (< 5% total volume), gently mixed, and measured via nonselective CPMG acquisitions. The time between blood draw and NMR measurement was kept less than 10 min. This experiment was repeated five times for each urea isotope. For an additional two cases, the whole blood samples were centrifuged at 1000 RCF for 10 min, and the plasma supernatant was gently extracted with a pipette. The T₂ of both urea isotopes were measured in the extracted plasma.

D. Animal Imaging Experiments

Animal studies were performed under a protocol approved by the UCSF Institutional Animal Care and Utilization Committee (IACUC). Experiments used male Sprague Dawley rats (400 ± 100 g) anesthetized with an isofluorane/oxygen mixture. Anatomic T₂-weighted ¹H fast spin echo (FSE) images were acquired in the axial and coronal planes. ¹³C transmitter calibrations were performed by finding the null of the signal response of a vial containing 1 mL of 8M ¹³C urea solution placed next to the animal. 107±3 mg samples of urea were polarized for 2.5 h (approximately three buildup-time constants) and then dissolved in 5 mL phosphate buffered saline yielding a final solution of approximately 110 mM. [¹³C] urea samples were transported to the scanner with a bar magnet to avoid signal loss due to low-field T₁ shortening [22]. 3 mL (giving approximately 0.3 millimoles ¹³C) of the hyperpolarized urea solution were injected into a tail vain catheter over 12 s.

1) T₂ Mapping

¹³CT₂ mapping was performed after infusion of hyperpolarized [¹³C] urea and [¹³C, ¹⁵N₂] urea in four different rats. The imaging was initiated 30 s after the beginning of injection (18 s after end of the injection) to ensure a thorough distribution of the contrast agent through the vasculature and kidneys. Furthermore, the long delay time minimized bolus arrival effects during imaging.

As with the phantom experiments, the preparation (excitation) pulse was played only once, and a refocusing pulse train (using SSFP phase cycling) followed in which m dynamic images were acquired (8). Due to the greatly varying T₂ values, the TR and resolution were modified for each isotope. [¹³C, ¹⁵N₂] urea: 64 × 64 encodes over an 8 cm FOV, TR = 12 ms giving 0.768 s per image, m = 20 images acquired over 15 s. [¹³C] urea: 20 × 20 encodes over an 8 cm FOV, TR = 10 ms giving 0.200 s per image, m = 8 images acquired over 1.6 s.

In pixels in which the first time point SNR was greater than 30, the time-decay curves after injection of [¹³C, ¹⁵N₂] urea were fit to the bi-exponential model

$$S(t,x,y)=A_S(x,y)e^{-t∕T_{2,S}(x,y)}+A_L(x,y)e^{-t∕T_{2,L}(x,y)}.$$ (9)

T_2,S, the short T₂ component, was constrained to [0,2] s, and the long component T₂ was constrained to [2, 100] s. Fitting was performed in MATLAB using the trust region algorithm (with the function lsqcurvefit). Single labeled [¹³C] urea was fit to a single exponential decay

$$S(t,x,y)=A(x,y)e^{-t∕T_2(x,y)}$$ (10)

due to the difficulty in bi-exponential fitting with a limited number of data points. As before, fitting was only performed in regions with first time point SNR > 30. After fitting, only pixels with R² > 0.95 were included in analysis. T₂ values from pixels within the aorta, renal cortex and medulla, and renal pelvis (selected using manually-drawn margins) were fit to a normal distribution to estimate mean and variance. The long T₂ component (T_2,L) distributions were highly asymmetric and were fit to a type II generalized extreme value (Frechet) distribution

$$\mathrm{PDF}\left(x\right)=\frac{1}{s}g{\left(x\right)}^{-1-1∕k}\exp \left[-g{\left(x\right)}^{-1∕k}\right]$$ (11)

$$g\left(x\right)=1+k\frac{(x-\mu )}{s}$$ (12)

where μ is the location parameter μ, is the scale parameter, and k shape parameter. This distribution was chosen since it captures the finite lower limit imposed by constrained bi-exponential fitting, the asymmetry of the distribution, and the long observed tails at high T_2,L values. After estimation of s, k, and μ, the means and standard deviations were calculated as μ−s/k + (s/k)g₁ and $(s∕k)\sqrt{g_2-g_1^2}$, respectively, with g_n = Γ(1 − nk ) and $\Gamma \left(z\right)={\int }_0^{\infty }{t}^{z-1}{e}^{-tz}dt$

2) SSFP Imaging SNR Comparison

To measure the improvement in image quality associated with the longer T₂ of [¹³C, ¹⁵N₂] urea, repeat in vivo hyperpolarized imaging experiments with [¹³C] urea and [¹³C, ¹⁵N₂] urea were performed back-to-back in six different animals. All imaging was initiated 20 s after the start of the injection. Similar to previous implementations [13], the acquisition was aligned in the coronal plane with no slice-select gradients (projection mode) and phase encoding set along the right/left dimension to avoid image aliasing. 96 × 96 (n = 4) and 192 × 96 (n = 2) images were acquired with, TR = 15 ms, TE = 7.5 ms, 4.8 ms data acquisition time per TR. All acquisition had a 208 Hz/pixel receive bandwidth. Since this value is much greater than the 19 Hz J-coupling constant of [¹³C, ¹⁵N₂] urea, no imaging SNR loss was expected from the spectral splitting. [¹³C, ¹⁵N₂] urea acquisitions used θ = 180°, and [¹³C] urea acquisitions used θ = 35°. These values were picked to maximize the signal using the aqueous solution T₂ values, and as we will show, the latter value was slightly suboptimal for in vivo T₂ values. One experiment in which [¹³C] urea was imaged with θ = 35°, 50°, 70° and 180° was performed to highlight the need for lower θ values with the short T₂ urea. All experiments used a 3.2 ms time-bandwidth product = 4 windowed sinc pulse which gives a θ = 180° rotation on resonance at 0.6 G.

IV. Results

A. Phantom Measurements

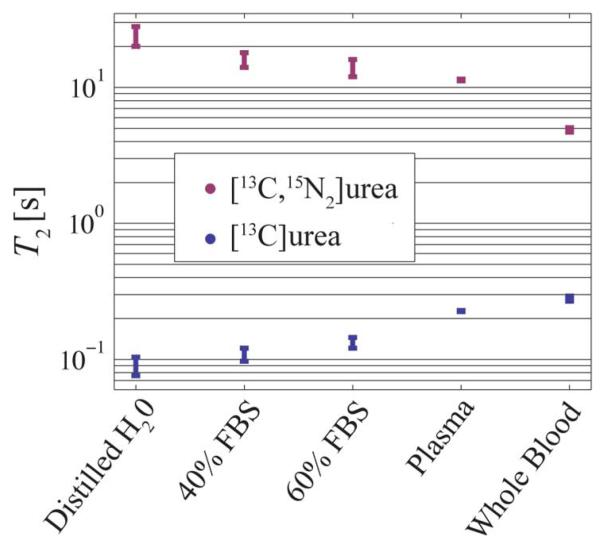
Table I gives aqueous solution T₁, T₂, and polarization measurements. The T₂ values of [¹³C] urea and [¹³C, ¹⁵N₂] urea differed substantially in solution, with the differences being highest in dilute aqueous solutions. Both compounds showed similar T₁ values. The polarization of [¹³C] urea was slightly lower and showed more variability from run to run. Even though the sample was transported with a bar magnet, there was likely some residual scalar coupling T₁ relaxation during transport. Fig. 4 shows the measured T₂ in whole blood, serum, plasma, and water. The blood and plasma values are also listed in Table I. Fetal bovine serum caused some relaxation enhancement of [¹³C, ¹⁵N₂] urea, which is likely due to reduced τ or some degree of protein binding. The [¹³C, ¹⁵N₂] urea T₂ was greatly reduced between plasma and whole blood indicating a strong relaxivity from red blood cells.

TABLE I.

Relaxation and Polarization Measurements in Solution (B₀ = 3T, 37 °C):

	[13C]urea	[13C, 15N2]urea
T1 (aqueous) [s]	46 ± 1	44 ± 1
T2 (aqueous) [s]	.09 ± .01	24 ± 4
T2 (plasma) [s]	.23 ± .01	11 ± 1
T2 (whole blood) [s]	.24 ± .01	4.9 ± .2
Polarization at 25 s	19 ± 5%	22 ± 2%

Fig. 4.

Hyperpolarized urea T₂ values in whole blood, serum, plasma, and water. The [¹³C, ¹⁵N₂] urea T₂ is greaty reduced in whole blood compared to plasma indicating a strong relaxivity effect from red blood cells.

Fig. 3 shows the T₂ behavior of both urea isotopes with modulation of the correlation time via changing the bulk solution viscosity. The scalar coupling pathway clearly dominates the [¹³C] urea T₂. Since the rotational correlation time and viscosity are linearly related for approximately spherical molecules from the Debye–Hückel relation, from (4), (6), and (7) the T₂ of [¹³C, ¹⁵N₂] urea should scale approximately as η⁻¹ and that of [¹³C] urea should scale as η⁺¹. The actual powers measured from fitting the data in Fig. 3 were −0.73 ± 0.20 and 0.87 ± 0.05, respectively. Some deviation of the expected powers of −1 and 1 is expected due to the well known discrepancies between macroscopic and microscopic in solution viscosities [39]. Furthermore, [¹³C] urea will have some weak contribution from dipolar and CSA which will scale as η⁻¹.

Fig. 3.

Hyperpolarized urea T₂ values as a function of macroscopic viscosity. The removal of the scalar relaxation pathway via ¹⁵N labeling gives 13C, ¹⁵N₂] urea a much larger T₂ as well as a differing T₂ dependence on correlation time (which should be approximately linear with viscosity).

B. In Vivo Experiments

1) T₂ Mapping

Results from T₂ mapping experiments are shown in Fig. 5. The [¹³C, ¹⁵N₂] urea experiments showed a largely short scale ~ 1.3 s T_2,S decay throughout the animal which is presumed to be the vascular urea component. Bi-exponential fitting showed the long T_2,L component almost completely isolated to the kidneys. The large mean values of these components are given in Table II. While these values are potentially contaminated by collection of the agent into the inner regions of the kidney during the imaging time, the longer T₂ are believable since signal likely represents that from the glomerular filtrate. Since the filtrate is free from red blood cells and plasma proteins some recovery of the solution T₂ can be expected. The filtered urea in the medulla and cortex is primarily in the tubules and medullary interstitium, so some restriction of motion will likely cause a reduced τ and T₂ shortening compared to that dilute solution. However, in the renal pelvis, the large liquid pool will give a reduced τ and virtually all the solution T₂ is recovered. The short T₂ component observed in the kidney likely arises from blood above and below the kidney (due to the projection imaging mode) and possibly also from the renal vasculature. Some long T₂ component was observed in the inferior aorta and femoral branches. This is likely due to RF transmitter drop-off causing some T₁ contamination to the decay curve. However, slower flow could also be a factor.

Fig. 5.

(a) Single pixel T₂ decay curves each both urea isotopes measured in the aorta, medulla, and renal pelvis. The [¹³C, ¹⁵N₂] urea decay shows a bilinear slope, and the fast decay rate is similar to that measured in the aorta. This is likely due to the blood above and below the kidney. Signal within the blood fit well to single exponential decays. (b) Fitted amplitudes given by (9) and (10). The long T₂ amplitude A_L is almost completely localized to the kidneys. (c) T₂ maps (in ms). The [¹³C, ¹⁵N₂] urea experiments showed extremely long T₂ components in the kidney, with the greatest values measured in the renal pelvis. The T_2,L map was thresholded using the A_L values. The cortex and medulla showed similar values. [¹³C] urea showed slightly lower T₂ values in the kidneys. (d) histograms showing T₂ distributions of all pixels within the medulla, aorta, and renal pelvis for all four rats. T_2,L values approaching the pure solution T₂ of 20 s were detected in some pixels in the renal pelvis.

TABLE II.

T₂ Distributions in Vivo.

	parameter	location	mean±σ [s]	k †
[13C, 15N2]	T 2,L	Pelvis	11.0 ± 1.8	.13 ± .09
	T 2,L	Medulla	6.28 ± 1.27	.13 ± .03
	T 2,S	Pelvis	1.14 ± .38	-
	T 2,S	Medulla	1.15 ±0.42	-
	T 2,S	Aorta	1.31 ± 0.34	-
[13C]	T 2	Kidney	0.231 ± 0.026	-
	T 2	Aorta	0.279 ± 0.027	-

^†Shape Parameter of the Frechet Distribution

Due to the much shorter T₂ of [¹³C] urea, the T₂ mapping images had to be acquired with a much coarser resolution. With the limited number of time samples available, bi-exponential fitting was not possible. However, a slightly shorter mean T₂ within the kidney compared to that measured in the aorta was be observed. This is concordant with solution measurements that show that [¹³C] urea and [¹³C, ¹⁵N₂] urea respond to differences in τ in the opposite manner.

Table II summarizes the histogram fitting of the T₂ mapping experiments. The distributions of [¹³C, ¹⁵N₂] urea T_2,S were approximately normal within the kidney, and the T_2,S measured from the medulla and renal pelvis had very similar mean values. T_2,S values within the aorta were slightly higher. This is potentially due to the fact that the aorta is fed superiorly from the heart, which in these experiments was at the edge of the transmitter. T_2,L distributions within the kidney were highly asymmetric and were fit to a Frechet distribution. T_2,L values had a similar shape parameter k in the medulla and pelvis. Since there was no though-slice localization, it is not possible to determine whether the asymmetry of the distributions represents some geometry factor (stemming from summing all the pixels through the kidney in one dimension), medulla/pelvis partial voluming, or an actual distribution reporting on a physiological parameter. In all likelihood, the decays show more than two characteristic decay times. The reported mean T_2,L in the pelvis of 11.0±1.8 s is likely an underestimate since T_2,L the parameter also incorporated the faster relaxing medulla immediately above and below the pelvis. Determination of all the characteristic decay times is very difficult, however, due to the ill-conditioned nature of multi-exponential fitting.

2) SSFP Imaging Comparisons

In one rat, hyperpolarized [¹³C] urea was imaged with varying τ values. These images are shown in Fig. 7 along with the SNR values measured in the aorta and kidney. With the lower τ necessary for imaging the short T₂ urea at high resolution, the images were susceptible to signal drop-off from banding artifacts. At flip angles sufficiently high to alleviate the banding, the overall signal is greatly decreased due to T₂. The SNR curve resembles its simulated counterpart in Fig. 1, top left, indicating an SNR-optimal τ around 50°. Although the τ = 35° used for imaging comparisons was slightly suboptimal, only an additional 20%–30% signal increase can be expected with use of a higher flip. Furthermore, as indicated in Fig. 1, bottom left, blurring effects will become very problematic in this regime. The image SNR was too low to detect significant blurring, however. A potential solution for yielding favorable signal behavior when the imaging time is much greater than T₂ is the use of progressive flip angle SSFP acquisitions. [40]. This method would require a good estimate of T₂ for flip angle calculations which may introduce difficulty when multiple, greatly varying T₂ values are present.

Fig. 7.

Hyperpolarized [¹³C] urea imaged using an SSFP sequence with multiple θ values (top) highlighting the difficulty in using high flips for the short T₂ urea. Mean SNR values (bottom) are shown with error bars representing standard deviation for the given organ. Only the right kidney SNR values were used due to the banding artifacts (red arrow) in the left kidney. At flip angles sufficiently high to elmininate the banding (yellow arrows), the overall SNR is greatly reduced from a stronger T₂ weighting. The shape of the curves are similar to their simulated counterparts in Fig. 1, top left.

Fig. 6 shows high resolution imaging comparisons of [¹³C] urea and [¹³C, ¹⁵N₂] urea for two different comparisons. Resolution was sufficient to discern the aorta, renal, common and external iliac, medial sacral, and femoral arteries in all [¹³C, ¹⁵N₂] urea images. The kidneys showed a mean SNR of 260 ± 100. [¹³C] urea images had lower SNR expected from the use of lower flip angles; however, in many cases, the SNR difference between [¹³C] urea and [¹³C, ¹⁵N₂] urea images differed substantially more than the factor of ~ 3 expected from simulations (Fig. 1). There was evidence of banding artifact with the use of lower flip angles; this was significant in the image showen Fig. 6, bottom right. In the upper right image in Fig. 6, this artifact is less detrimental but is still present in the region near the iliac branch.

Fig. 6.

Projection imaging at 0.94 mm in-plane resolution. Top: localizer, [¹³C] urea, and [¹³C, ¹⁵N₂] urea images acquired with a 9 cm FOV. Higher SNR and reduced blurring is observed in the [¹³C, ¹⁵N₂] urea image. The [¹³C] urea shows some signal loss due to banding artifact towards the iliac branch. Bottom: [¹³C] urea and [¹³C, ¹⁵N₂] urea images acquired over a 9 × 18 cm FOV. The kidneys were slightly anterior and posterior of the localizer slice. The [¹³C] urea shows much lower SNR also likely due to banding. The [¹³C, ¹⁵N₂] urea image clearly depicts the aorta and its inferior branches. Virtually all [¹³C, ¹⁵N₂] urea images showed signal through the femoral arteries with some enhancement in the knee. Spinal vasculature is also depicted in the bottom center image.

Some differences in contrast are noted in the SSFP images acquired at different flip angles which is expected based on the differing T₂ weighing. SSFP images acquired with lower flip angles tended to have more diffuse background signal; this can be seen in Fig. 6 comparing the bottom two images. The source of this background is unclear, but may it may represent capillary signal with short T₂.

Fig. 8 shows the mean and standard deviation of SNR values measured in the aorta and kidneys of each imaging comparison. Since the dose was not normalized to the animal mass, there is significant subject-to-subject SNR variability. The lower plots in Fig. 8 show the ratio of the SNR values measured in each subject which should normalize to the dose variations. Large variations are observed even in the SNR ratios which is inevitable due to some differences in sample transport time, run-to-run polarization levels, and residual scalar coupling relaxation which diminishes [¹³C] urea polarization. However, all [¹³C, ¹⁵N₂] urea showed at least a doubling in SNR, with a mean increase of 4.9±0.6 in the kidneys and 4.7±1.0 in the aorta.

Fig. 8.

Mean SNR values in the kidney and aorta for each SSFP imaging experiment with error bars representing the standard deviations. The SNR ratios [¹³C, ¹⁵N₂] urea to [¹³C] urea) are shown on the bottom. Although the SNR ratio ideally should normalize for dose variations, large run-to-run variability is still observed likely due to changes in polarizer/scanner transport time and polarization variations.

V. Discussion

The high sensitivity of hyperpolarization is offset by the low intrinsic sensitivity of the ¹³C nucleus, requiring large doses. Therefore, some estimate of the safety of this dose level is warranted to estimate its potential clinical translatability. As mentioned in the introduction, steady state blood urea concentrations of 5.5±2.0 mM(33 ± 12 mg/dL) are typical in healthy humans and rats. For experiments conducted in this study, the estimated blood urea concentration after bolus injection was 12±3 mM(71 ± 20 mg/dL) which was calculated from the 400±100 g mass of the animals used in the study and their estimated blood volumes of 25 ± 6 mL [41]. This value is approximately double the steady state blood urea concentration. The worst-case anticipated safe dose can be inferred from a study by Johnson et al. [21] in which patients with advanced stage renal failure were loaded with urea (added to the dialysate) to maintain steady state blood urea concentrations of 181–600 mg/dL for periods of 7–90 days. Doses of less than 300 mg/dL were well tolerated, while doses from 300–600 mg/dL were associated with malaise, vomiting, and headache [20], [42]. Based on these results, we expect doses at least four times higher than those used in this imaging study to be well tolerated in patients with advanced renal failure. This figure is almost certainly an underestimate since the patients from the Johnson et al. study were maintained at high urea doses for multiple days. Subjects with normal kidney function will also certainly tolerate much larger doses.

In order to extract the large SNR increases from increased T₂, long trains of refocusing pulses were used. The SAR of this sequence compared to that used for ¹H imaging can be roughly estimated by assuming a uniform sphere with diameter long compared to the wavelength (λ = 9.3 m for ¹³C at 3T). Using this model, the power dissipated in the sphere scales as ${\omega }_0^2{B}_1^2$ [43]. Compared to ¹H, ω₀ is reduced by a factor of γ_c/γ_h, the ratio of the gyromagnetic ratios, and the peak B₁ is increased by the same factor for a given flip angle. Therefore, the ¹³C spin echo trains have similar SAR as the ¹H sequence with identical pulse widths, pulse time-bandwidth products, and timing parameters. The large TR values necessary for the larger imaging gradient lobes imply that the SAR is actually lower than that of a typical CPMG imaging sequence for ¹H.

Although all imaging in this manuscript was performed in projection mode so that slice profile effects would not contaminate T₂ and SNR measurements, extension to multi slice or 3D imaging should be straight forward. Multi slice imaging was performed in several previous hyperpolarized SSFP implementations [15]–[17], [24]. For isotropic resolution, 3D imaging should also be possible, but due to the larger number of phase encoding steps, a flip angle less than 180° will likely be required. All T₂ values measured in this manuscript must be considered effective T₂ values due to the numerous factors confounding measurements. Given the SSFP signal response given by (1), RF transmitter variations will deviate θ from 180° thus adding some T₁ weighting to the signal decay. Over a series of spin echo pulses, the net transverse relaxation rate can differ significantly from the true R₂. The diffusion attenuation can be expressed as

$${\tilde{R}}_2=R_2+\frac{b\left(t\right)D}{TR}+\frac{1}{12}D{\gamma }^2{\stackrel{‒}{G}}^{2}T{R}^2$$ (13)

where R₂ is the true rate, ${\tilde{R}}_2$ the observed rate, $b\left(t\right)={\left(2\pi \right)}^2{\int }_0^t{\mid \overrightarrow{k}\left(t^{\prime }\right)\mid }^{2}d{t}^{\prime }$ with $\overrightarrow{k}\left(t\right)=\gamma ∕2\pi {\int }_0^{t}G\left(t^{\prime }\right),d{t}^{\prime }$ is the diffusion weighting due to imaging gradients [24], and the term $(1∕12)D{\gamma }^2{\stackrel{‒}{G}}^{2}T{R}^2$ represents the diffusion through local B₀ variations (modeled as a constant gradient $\stackrel{‒}{G}$) [44]. Although the diffusion term on the left restricts the flip angle choice for hyperpolarized noble gases [24] due to D values in the range of 0.1–2 cm²/s [45], the diffusivity of ¹³C labeled small molecules in solution is between three and five orders of magnitude lower. While this makes liquid state ¹³C diffusion weighted imaging more difficult on a clinical scanner due to the difficulty in achieving large signal attenuation, this is a favorable characteristic for multiple spin echo imaging since the diffusion weighing will not widen the point spread significantly. The apparent diffusion coefficient for urea was measured to be 1.54 × 10⁻³ mm²/s at 27°C [46]. Given the total b value b(N_PETR = 6.5 s/mm² integrated over all frequency and phase encoding pulses over 96 repetitions, the diffusion weighting is exp [b(N_PETR)D]≈ 0.99. Although the imaging gradient weighting is likely negligible, the microscopic diffusion term likely contaminates T₂ measurements to some degree due to the relatively long (10–15 ms) TR values used and the potentially large gradient $\stackrel{‒}{G}$ experienced by the urea molecule in its transport in and out of the red blood cell. This effect is difficult to quantify in vivo; previous studies isolating this effect used T₂ dispersions experiments which measure the dependency of T₂ on TR = 2π_CPMG[32]–[34].

Bulk flow parallel to the imaging gradients will induce some phase, and if this phase not coherent within a voxel, this will lead to some signal loss. The frequency encoding gradients in SSFP sequences are first-moment flow compensated, so constant-velocity flow along the frequency encoded direction is fully rephased. The phase encode gradients had a peak first moment ${\int }_0^{TR}G\left(\tau \right)\tau ,d\tau$ of 0.039 s/cm, leading to a ~ 2° phase shift for a 1 cm/s velocity. Although this value is quoted for the outer k space lines, some destructive interference from phase-induced flow over 96 phase encodes (acquired over 1.4 s) could lead to signal loss. This is very likely the source of the large discrepancy of T₂ values measured in whole blood (Table I) and in vivo (Table II). In addition to the potential signal attenuation due to flow and diffusion effect, there is likely some lengthening of the measured T₂ in the inner regions of the kidney due to collection during the imaging time.

The extremely long T₂ values measured within the kidney is in itself a potential source of interesting imaging contrast. In this study we were not able to definitively attribute the long T₂ component to urea within the filtration and collecting system. However, this seems very likely given the anatomical distributions of the long T₂ component. Relaxation time gradients between the cortex, medulla, and pelvis are well known from ¹H experiments [47], but the direct measurement of urea within the blood and filtered pools could be a powerful tool for assessment of the urea concentrating function of the kidney.

VI. Conclusion

This study demonstrated a greatly increased imaging SNR of hyperpolarized ¹³C urea associated with ¹⁵N labeling of the amide nitrogens. The SNR increase was due to a very large T₂ increase associated with the elimination of a strong scalar coupling relaxation pathway, and this allowed for SSFP acquisitions with flip angles in the fully refocused regime on a clinical scanner with large minimum TR constraints. Projection images were acquired with in-plane resolution of 1 mm with SNR of 230 ± 120 in the aorta and 260 ± 100 in the kidney. In vivo T₂ mapping showed spatially heterogeneous T₂ values, with values of 1.3 s typical in the blood and greater than 10 s observed in the kidney.