Abstract
We report effects of age, age2, sex and additive genetic effects on variability in gray matter thickness, surface area and white matter integrity in 1,010 subjects from the Genetics of Brain Structure and Function Study. Age was primarily associated with gray matter thickness and fractional anisotropy of water diffusion in white matter tracts, while sex was primarily associated with affected gray matter surface area; age2 was only significantly associated with average white matter integrity. Widespread heritability of neuroanatomic traits was observed, suggesting that brain structure is under strong genetic control. Furthermore, our findings indicate that neuroimaging-based measurements of cerebral variability are sensitive to genetic mediation. Further fundamental studies of genetic influence on the brain will help inform gene discovery initiatives in both clinical and normative samples.
Keywords: anatomical MRI, extended pedigrees, imaging genetics, heritability, demographic covariates, aging
Introduction
Despite rapid advancements and widespread interest, neuroimaging-based gene discovery is far from a mature science. To date, candidate genes associated with prevalent disorders attract the lion's share of attention. As a result, a fundamental basis regarding how genetic factors influence basic aspects of the brain has been largely neglected, which is of far greater importance for the maturation of imaging genetics and is critical for a holistic understanding of the brain. Human image-based traits are potentially infinite, yet few, if any, have been linked to cellular mechanisms and ascertainment methods vary widely. In contrast, the genetic search space is finite and defined. Therefore, the greatest limitation is our ability to translate in vivo image-based features into informative phenotypes for genetic research.
An initial step toward bridging this knowledge gap is the characterization of neuroanatomic traits that can be readily derived from magnetic resonance images (MRI). High-resolution T1-weighted images typically contain 105 to 106 voxels, each of which can be used as an independent variable (Stein et al. 2010) or combined to form a plethora of unique sets of variables. For example, the commonly used FreeSurfer pipeline can parcel the cortex into 163,842 surface level vertices per subject (Fischl et al. 1999a). While there are a many modeling approaches to reduce the total number of variables into distinct components (see Chen et al. 2012 for a reduction of 5,124 traits into 12 genetically distant regions), replication of modeled traits often hinders cross-study comparisons. Therefore, we sought two baseline resources for the field: (1) the characterization of common demographic confounds like age and sex with respect to image-based neuroanatomic phenotypes, and (2) heritability estimates of candidate traits derived directly from automated and freely available image-analysis routines.
Results and conclusions reported herein were drawn from testing and applying candidate phenotypic measurements in the Genetics of Brain Structure and Function study (GOBS). Subjects constitute large multi-generation families and phenotypes represent normal variation. Relative pairs of differing degree (Table I) give rise to a precise structure of expected covariance that can be used to create more powerful polygenic models than twin or unrelated samples. Specifically, studies utilizing large extended pedigrees have multiple benefits compared to twin designs, including increased power to detect heritable effects, less confounding of genetic effects with shared environmental effects, greater mathematical power to localize and identify causal quantitative trait loci, and far more power to examine the effects of rare variation (Blangero et al. 2003, Blangero 2004). Because the actions of genes are largely unknown and vary with age, explored phenotypes represent basic neuroanatomic traits with particular emphasis on concomitant effects of age and sex. It is the intention of this report to make progress toward the establishment of a systematic program for basic investigations of candidate phenotypic measures. Such an approach, if adopted by other laboratories, will foster the foundation that is necessary for understanding how genetic mechanisms influence the brain.
Table 1.
Pair–wise relationships within Mexican-American pedigrees of participants in the San Antonio Family Studies (top) and the number of GOBS subjects by decade that participated in the current study.
| Number of Relative Pairs | Familial Relationship |
|---|---|
| 2 | Monozygotic Twins |
| 1004 | Parent-offspring |
| 1192 | Siblings |
| 352 | Grandparent-grandchild |
| 2407 | Avuncular |
| 175 | Half-siblings |
| 7 | Great grandparent-grandchild |
| 675 | Grand-avuncular |
| 361 | Half-avuncular |
| 2783 | 1st cousins |
| 34 | Great grand-avuncular |
| 19 | Half grand-avuncular |
| 2797 | 1st cousins, once removed |
| 402 | Half 1st cousins |
| 343 | 1st cousins, twice removed |
| 10 | Half 1st cousins, once removed |
| 955 | 2na cousins |
| 321 | 2nd cousins, once removed |
| Age Range | Number of subjects |
|---|---|
| < 20 | 55 |
| 20 – 29 | 174 |
| 30 – 39 | 232 |
| 40 – 49 | 221 |
| 50 – 59 | 178 |
| 60 – 69 | 111 |
| 70 – 79 | 34 |
| ≥ 80 | 5 |
Methods
Subjects
GOBS subjects were recruited from two preceding studies: the San Antonio Family Heart Study (Mahaney et al. 1995; Mitchell et al. 1996) and the San Antonio Family Gallbladder Study (Puppala et al. 2006). Family members of individuals who participated in these studies were also recruited. Initially (1992–1995), the San Antonio Family Heart study included 1,431 Mexican-American individuals from 42 extended families. Probands were identified from the Hispanic community in a three-phase process. First, a census tract that occupied low-income neighborhoods of South San Antonio was selected. Although San Antonio is 61% Hispanic, residents of these neighborhoods were of 81% Hispanic ancestry (www.census.gov). Second, all residential addresses within these neighborhoods were identified in the telephone directory. Third, households were approached in random order to determine whether any resident met established proband criteria. A proband had to be Mexican-American, be 40–60 years old, have a spouse willing to participate, and have at least six offspring and/or siblings older than 16 years residing in the San Antonio area. Once a proband was enrolled, all first-, second-, and third-degree relatives of the proband and of the proband's spouse, who were at least 16-years-old, were invited to participate. Mexican-American spouses of these relatives were also invited to participate. Recruitment procedures were similar in the San Antonio Family Gallbladder Study (1998–2001), which included 740 individuals from 39 Mexican-American pedigrees (Duggirala et al. 1999; Puppala et al. 2006). However, probands in the Gallbladder Study were required to have type-2 diabetes and only unilineal relative recruitment was conducted. As type-2 diabetes has a lifetime prevalence approaching 30% in this population, single ascertainment for such a common disease represents effectively random sampling.
The GOBS study (2006–present) recruited individuals from these two cohorts in addition to children and grandchildren of probands that were older than 16 years of age were also invited to participate. Sixty-two percent of the GOBS sample is from the San Antonio Family Heart study, 26% from the San Antonio Family Gallbladder study, and 12% are children or grandchildren of San Antonio Family Heart study participants. Over 80% of all individuals contacted agreed to participate. Thus, participants were pseudo-randomly selected from the community, with the constraints that they must be of Mexican-American ancestry and part of a large family from the San Antonio region. Reported pedigree relationships were verified using PREST (McPeek and Sun, 2000) on available autosomal markers. To date, a total of 1450 subjects from 49 extended pedigrees have participated in the GOBS study and contributed DNA samples; 1035 individuals have been imaged, and 1365 have undergone neurocognitive testing.
In the current report, 838 subjects underwent pointwise analyses, 61% of which were female; 1,010 subjects underwent region-based analyses, 62% of which were female; and 467 subjects underwent DTI analyses, 64% of which were female. Average age across all subjects was 43 years [range: 19–85].
MRI Acquisition
All images were acquired on a research-dedicated, Siemens 3T TIM Treo MR scanner and a high-resolution phase array head coil housed in the Research Imaging Institute, UTHSCSA. Images for gray matter analyses included seven high-resolution T1-weighted 3D turbo-flash sequences with an adiabatic inversion contrast pulse and the following parameters: TE/TR/TI = 3.04/2100/785 ms, flip angle=13°, 800μm isotropic resolution, 200mm FOV, 5-min duration (35-min total; Kochunov et al. 2006). A single-shot single refocusing spin-echo, echo-planar imaging sequence was used to acquire diffusion-weighted data with a spatial resolution of 1.7×1.7×3.0mm (Kochunov et al., 2010). The sequence parameters were: TE/TR=87/8000ms, FOV=200mm, 55 isotropically distributed diffusion weighted directions, two diffusion weighting values, b=0 and 700 s/mm2 and three b=0 (non-diffusion-weighted) images.
Image Processing
Anatomic image processing was based on surface representations of the cortex using the freely available software package FreeSurfer (http://surfer.nmr.mgh.harvard.edu/, Dale et al. 1999, Fischl et al. 1999a) as implemented in our group (Winkler et al. 2010, 2012). First, T1-weighted images underwent inhomogeneity corrections and intensity normalization (Sled et al. 1998), were linearly aligned to a common atlas space (Fischl et al. 2002; 2004a), and were skull-stripped (Segonne et al. 2004). Next, white matter voxels were identified based on location, intensity, and the intensity relative to neighboring voxels. The borders between gray and white matter were defined as the location where the greatest shift in intensity between neighboring voxels occurs according to a six-neighbor connectivity scheme (Dale et al. 1999; Dale and Sereno 1993; Fischl and Dale 2000). The two hemispheres were separated and a tessellated mesh was built around the mass of white matter voxels (Fischl et al. 2001). This mesh was smoothed with an algorithm that accounted for local intensity in the original images; topological defects were corrected (Segonne et al. 2007). The resulting smoothed mesh represented the white surface. The gray matter (pial) surface was generated by expanding the white surface to the gray matter/CSF boundary while constraining surface smoothness. Gray and white matter surfaces were then visually inspected and manually edited if necessary. Next, the pial surface was inflated to a sphere and registered to an atlas based on cortical folding patterns (Fischl et al. 1999b). For pointwise analyses (Fig 1–4), phenotypes were defined by parceling each hemisphere into 40,962 vertices. For regional analyses (Tables II – V), the pial surface was segmented into regions of interest based on gyral and sulcal structure, surface curvature and sulcal depth (Desikan et al. 2006; Fischl et al. 2004b). More specifically, a Bayesian approach was applied to establish the probability that a given vertex belonged to a given label based on a probability atlas. Next, the surface was treated as an anisotropic, non-stationary Markov random field, where the labels for each vertex and its neighbors were considered simultaneously. These processes were iterated until every vertex was assigned a permanent label. Surfaces were parceled into regions of interest defined by the Desikan atlas (2006). Cortical thickness was defined as the average distance between the gray/white boundary and the gray/CSF boundary at each vertex (Fischl and Dale 2000). Subcortical regions were parceled using similar procedures and volumetric measures were calculated (Fischl et al. 2002). All region-based analyses reflect the average of left and right analogous structures. Test-retest reliability of Freesurfer morphometric procedures across scanner manufacturers and field strengths was demonstrated independently by other groups (Han et al. 2006; Reuter et al. 2012), which is crucial for consistency of phenotypes across large-scale studies.
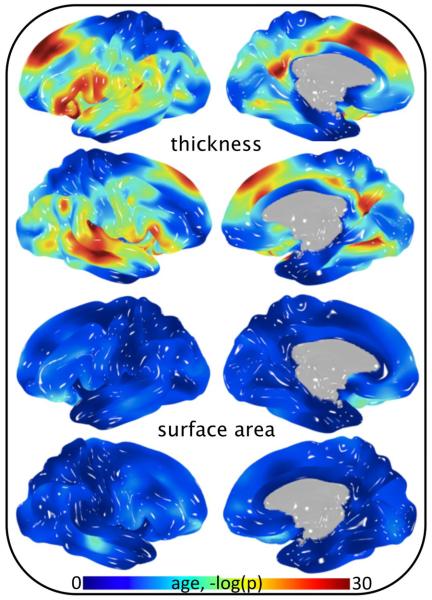
Fig 1.
Significance of age covariance in cortical thickness and surface area analysis of 838 subjects.
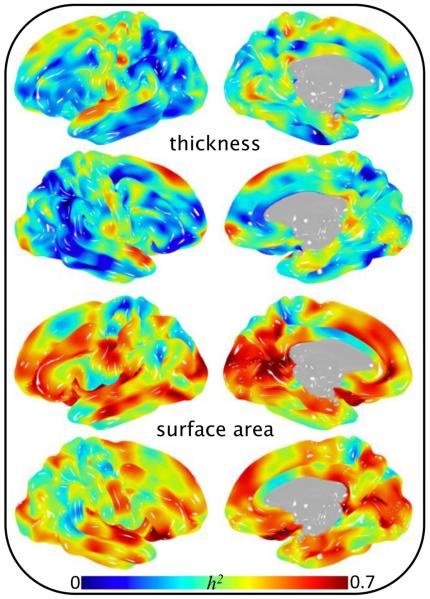
Fig 4.
Heritability of 40,962 pointwise cortical phenotypes in 838 subjects.
Table II.
Statistics from region-based cortical surface area in 1,010 subjects. Brain measurements were averaged across left and right hemispheres prior to genetic analysis. Significant p-values are reported in scientific notation. A negative (positive) β for sex indicates the value of the phenotypic measure was generally smaller in females (males).
| Gyrus/Region Surface Area | h2 (p-value) | Age β (p-value) | Age2 β (p-value) | Sex β (p-value) | Age × Sex β (p-value) | Age2 × Sex β (p-value) |
|---|---|---|---|---|---|---|
| Superior frontal | 0.77 (1.1E-30) | −1.3E-02 (1.4E-07) | −1.2E-04 (0.36) | −0.84 (2.7E-33) | 6.3E-04 (0.85) | −1.6E-04 (0.36) |
| Rostral middlefrontal | 0.67 (3.9E-24) | −1.2E-02 (4.2E-07) | −2.7E-04 (4.3E-02) | −0.94 (2.4E-39) | 1.7E-03 (0.60) | 8.9E-05 (0.62) |
| Caudal middle frontal | 0.63 (2.0E-22) | −8.6E-03 (3.2E-01) | −2.3E-04 (4.7E-04) | −0.62 (3.7E-21) | 1.6E-03 (0.57) | 1.9E-06 (0.70) |
| Pars opercularis | 0.68 (2.4E-26) | −1.4E-02 (1.1E-07) | −1.6E-04 (0.26) | −0.59 (6.3E-15) | 3.1E-03 (0.40) | 1.3E-04 (0.51) |
| Pars triangularis | 0.65 (9.3E-23) | −1.2E-02 (5.7E-06) | −8.2E-05 (0.56) | −0.61 (7.8E-16) | 3.5E-03 (0.34) | −2.4E-04 (0.23) |
| Pars orbitalis | 0.48 (3.1E-13) | −1.3E-02 (1.3E-06) | −8.4E-05 (0.55) | −0.81 (1.9E-26) | 1.3E-03 (0.72) | −1.3E-04 (0.50) |
| Medial orbitofrontal | 0.65 (1.4E-21) | −4.5E-03 (0.080) | −2.5E-04 (0.067) | −0.85 (3.6E-30) | 1.5E-03 (0.67) | 1.9E-05 (0.92) |
| Lateral orbitofrontal | 0.65 (3.1E-23) | −1.8E-02 (1.7E-12) | −2.3E-04 (0.092) | −0.76 (2.0E-25) | 4.8E-03 (0.16) | 9.5E-06 (0.96) |
| Precentral | 0.72 (2.3E-30) | −1.3E-02 (5.6E-07) | −2.0E-04 (0.12) | −0.83 (5.0E-31) | 5.6E-03 (0.10) | −9.1E-05 (0.62) |
| Paracentral | 0.57 (1.1E-16) | −8.8E-03 (1.1E-03) | −1.0E-04 (0.47) | −0.59 (2.0E-14) | 1.7E-03 (0.64) | −2.9E-04 (0.15) |
| Postcentral | 0.68 (2.4E-25) | −1.1E-02 (2.6E-05) | −2.4E-05 (0.86) | −0.89 (3.7E-34) | 4.3E-03 (0.20) | −8.7E-05 (0.64) |
| Superior parietal | 0.73 (6.4E-25) | −1.5E-02 (1.0E-08) | −1.0E-04 (0.45) | −0.85 (1.7E-31) | 2.1E-03 (0.53) | 2.0E-04 (0.29) |
| Supramarginal | 0.64 (6.3E-24) | −1.1E-02 (3.0E-05) | −1.2E-04 (0.39) | −0.87 (1.1E-31) | 1.7E-03 (0.62) | 8.0E-05 (0.67) |
| Inferior parietal | 0.55 (1.5E-21) | −1.6E-02 (1.9E-04) | −1.7E-04 (1.9E-02) | −0.83 (7.1E-32) | 3.9E-04 (0.58) | −6.7E-05 (0.59) |
| Precuneus | 0.70 (2.0E-27) | −1.3E-02 (1.8E-07) | −5.1E-05 (0.70) | −0.82 (1.3E-29) | 1.9E-03 (0.57) | 1.4E-06 (0.99) |
| Caudal anterior cingulate | 0.49 (4.1E-13) | −9.2E-03 (9.9E-04) | −1.6E-04 (0.30) | −0.58 (1.7E-13) | 3.0E-03 (0.42) | −9.9E-05 (0.63) |
| Rostral anterior cingulate | 0.48 (1.2E-11) | −5.5E-03 (4.4E-02) | −2.4E-04 (0.11) | −0.79 (8.3E-24) | 7.3E-04 (0.84) | 2.9E-05 (0.89) |
| Posterior cingulate | 0.65 (2.4E-22) | −1.3E-02 (7.7E-07) | −3.7E-04 (8.4E-03) | −0.72 (2.2E-22) | 1.9E-03 (0.59) | −6.8E-06 (0.97) |
| Isthmus cingulate | 0.65 (3.2E-26) | −3.8E-03 (0.14) | −1.6E-05 (0.91) | −0.84 (9.4E-30) | −3.0E-03 (0.39) | 9.0E-06 (0.96) |
| Superior temporal | 0.75 (4.7E-31) | −7.6E-03 (2.7E-03) | −7.2E-05 (0.59) | −0.81 (2.6E-29) | −1.9E-03 (0.58) | −2.9E-05 (0.88) |
| Middle temporal | 0.67 (3.0E-25) | −1.3E-02 (9.2E-08) | −5.2E-04 (1.1E-04) | −0.91 (2.8E-36) | −2.4E-03 (0.47) | 4.1E-04 (2.8E-02) |
| Inferior temporal | 0.53 (4.6E-19) | −1.7E-02 (8.3E-11) | −9.8E-05 (0.47) | −0.79 (8.0E-27) | 3.0E-03 (0.38) | −1.4E-04 (0.46) |
| Fusiform | 0.63 (4.9E-22) | −1.7E-02 (1.6E-11) | −1.4E-04 (0.30) | −0.80 (2.5E-28) | 2.6E-03 (0.45) | −1.1E-04 (0.57) |
| Parahippocampal | 0.65 (3.4E-24) | −1.7E-02 (1.0E-10) | −3.9E-04 (5.6E-03) | −0.56 (5.1E-14) | 4.6E-03 (0.19) | −7.5E-05 (0.70) |
| Entorhinal | 0.55 (2.9E-20) | 2.1E-03 (0.46) | 7.8E-05 (0.60) | −0.55 (1.6E-12) | −6.7E-04 (0.86) | −3.7E-04 (0.070) |
| Cuneus | 0.64 (4.8E-23) | −1.3E-02 (2.1E-06) | −5.1E-05 (6.7E-03) | −0.82 (3.9E-33) | 1.9E-03 (0.20) | 1.4E-06 (0.17) |
| Lingual | 0.75 (9.2E-26) | −1.3E-02 (1.7E-07) | −3.0E-04 (2.9E-02) | −0.78 (5.2E-26) | 7.9E-04 (0.82) | 2.2E-04 (0.25) |
| Pericalcarine | 0.74 (1.2E-30) | −1.0E-02 (7.7E-05) | −1.6E-04 (0.25) | −0.71 (1.3E-21) | −1.9E-03 (0.59) | 4.8E-05 (0.80) |
| Lateral occipital | 0.69 (1.2E-23) | −1.2E-02 (8.8E-07) | −1.9E-04 (0.14) | −1.09 (4.6E-53) | 1.1E-03 (0.73) | 1.5E-04 (0.38) |
Table V.
Statistics from region-based analysis of white matter FA in 819 subjects. Significant p-values are reported in scientific notation. A negative (positive) β for sex indicates the value of the phenotypic measure was generally smaller in females (males).
| White Matter Tract FA | h2 (p-value) | Age β (p-value) | Age2 β (p-value) | Sex β (p-value) | Age × Sex β (p-value) | Age2 × Sex β (p-value) |
|---|---|---|---|---|---|---|
| R S Longitudinal fasciculus | 0.61 (2.7E-13) | −2.9E-02 (9.6E-20) | 1.0E-05 (0.95) | −0.18 (3.0E-02) | −8.2E-03 (4.73E-02) | 2.7E-04 (0.28) |
| L S Longitudinal fasciculus | 0.59 (2.5E-14) | −2.6E-02 (8.9E-16) | 4.7E-05 (0.80) | −0.03 (0.71) | −1.0E-02 (1.27E-02) | 1.0E-04 (0.69) |
| Corpus callosum-genu | 0.62 (1.2E-14) | −4.1E-02 (6.5E-41) | −3.4E-05 (0.84) | −0.06 (0.41) | 6.9E-03 (0.07) | 7.7E-05 (0.74) |
| Corpus callosum-body | 0.48 (9.5E-12) | −3.7E-02 (1.7E-31) | −1.9E-04 (0.28) | 0.05 (0.54) | 4.9E-03 (0.23) | 6.2E-05 (0.80) |
| Corpus callosum-splenium | 0.62 (8.3E-15) | −3.3E-02 (1.5E-24) | −4.8E-05 (0.79) | −0.18 (2.6E-02) | −2.3E-05 (1.00) | 3.6E-04 (0.15) |
| R Cingulate-Hippocampus | 0.40 (2.1E-06) | −7.9E-03 (2.7E-02) | 4.1E-04 (0.05) | −0.34(2.5E-04) | −5.9E-03 (0.22) | −1.9E-04 (0.51) |
| L Cingulate-Hippocampus | 0.31 (8.0E-05) | −3.8E-03 (0.29) | 3.4E-04 (0.12) | −0.42 (8.3E-06) | −4.8E-03 (0.32) | −2.9E-05 (0.92) |
| R Cingulate | 0.47 (2.8E-09) | −2.8E-02 (2.5E-17) | −4.9E-04 (9.9E-03) | −0.33 (9.2E-05) | −2.2E-03 (0.60) | 4.3E-04 (0.09) |
| L Cingulate | 0.46 (1.1E-08) | −3.0E-02 (4.6E-21) | −3.6E-04 (0.06) | −0.34 (2.8E-05) | −1.7E-03 (0.68) | 3.6E-04 (0.15) |
| R P limb of IC | 0.42 (4.5E-08) | −2.1E-02 (6.3E-10) | 2.2E-04 (0.27) | −0.02 (0.80) | −8.7E-03 (0.05) | 7.0E-05 (0.80) |
| L P limb of IC | 0.44 (4.2E-09) | −1.9E-02 (3.4E-08) | 2.8E-04 (0.17) | 0.02 (0.83) | −7.2E-03 (0.12) | −3.7E-06 (0.99) |
| R A limb of IC | 0.49 (2.3E-10) | −2.6E-02 (8.6E-15) | 1.8E-04 (0.35) | −0.15 (0.08) | −6.4E-03 (0.14) | 6.3E-05 (0.81) |
| L A Iimb of IC | 0.47 (6.3E-10) | −2.4E-02 (9.8E-13) | 2.7E-05 (0.89) | −0.24 (5.8E-03) | −5.2E-03 (0.24) | 1.5E-04 (0.58) |
| R Retrolenticular IC | 0.34 (1.1E-05) | −2.0E-02 (2.3E-09) | 4.0E-04 (4.6E-02) | −0.32 (2.4E-04) | −8.1E-03 (0.07) | 1.9E-04 (0.47) |
| L Retrolenticular IC | 0.30 (6.1E-05) | −2.1E-02 (2.2E-09) | 4.5E-04 (2.6E-02) | −0.16 (0.07) | −9.9E-03 (2.81E-02) | 1.1E-04 (0.70) |
| R External capsule | 0.54 (5.0E-11) | −3.4E-02 (7.2E-27) | 4.6E-05 (0.80) | −0.14 (0.08) | −4.0E-03 (0.33) | 1.0E-04 (0.68) |
| L External capsule | 0.49 (4.8E-10) | −3.3E-02 (5.5E-24) | −1.5E-05 (0.94) | −0.08 (0.34) | −3.2E-03 (0.45) | −8.3E-05 (0.74) |
| R P Thalamic radiations | 0.42 (1.2E-08) | −4.0E-02 (4.3E-35) | −1.7E-04 (0.34) | −0.07 (0.39) | 3.7E-03 (0.36) | 4.1E-04 (0.09) |
| L P Thalamic radiations | 0.46 (4.2E-11) | −3.3E-02 (4.7E-25) | −9.1E-05 (0.62) | 0.07 (0.41) | 3.7E-04 (0.93) | 2.6E-04 (0.30) |
| R S Corona radiata | 0.52 (6.9E-11) | −3.3E-02 (1.6E-24) | 8.7E-05 (0.63) | 0.19 (1.8E-02) | −2.6E-03 (0.53) | −9.4E-05 (0.70) |
| L S Corona radiata | 0.52 (2.7E-12) | −3.1E-02 (6.1E-23) | 5.6E-05 (0.76) | 0.19 (1.9E-02) | −5.1E-03 (0.21) | −1.1E-04 (0.67) |
| R A Corona radiata | 0.55 (2.2E-12) | −4.0E-02 (1.9E-37) | 2.7E-04 (0.13) | −0.03 (0.74) | 5.3E-03 (0.18) | 2.3E-06 (0.99) |
| L A Corona radiata | 0.50 (3.7E-11) | −3.8E-02 (8.4E-34) | −2.4E-05 (0.89) | −0.07 (0.38) | 1.0E-05 (1.00) | 1.4E-04 (0.55) |
| R P Corona radiata | 0.51 (4.2E-12) | −3.2E-02 (4.6E-23) | −1.4E-04 (0.47) | −0.02 (0.79) | 1.1E-03 (0.79) | 9.9E-05 (0.70) |
| L P Corona radiata | 0.42 (1.7E-09) | −3.3E-02 (2.4E-23) | −1.6E-04 (0.41) | 0.08 (0.31) | 3.9E-03 (0.36) | −2.4E-05 (0.93) |
| Mean FA | 0.55 (1.1E-12) | −3.8E-02 (7.8E-34) | −7.4E-05 (0.67) | −0.15 (0.05) | −8.7E-04 (0.82) | 1.9E-04 (0.43) |
FA = fractional anisotropy, R = right, L = left, S = superior, P = posterior, A = anterior, IC = internal capsule
DTI voxel and tract level statistics were estimated for each subject using Tract-Based Spatial Statistics software (Kochunov et al. 2010). Each subject's FA image was nonlinearly aligned to a standard brain space (MNI152). The resulting average FA image was skeletonized to create a white-matter skeleton representing the centers of the major tracts common to the group. Each subject's aligned DTI data was then projected onto the skeleton image where voxel-level FA values were calculated, yielding phenotypes for genetic analyses. Heritability values were projected to a white matter surface rendering.
Quantitative Genetic Analysis
Quantitative genetic analysis was used to partition trait covariance among related individuals into genetic and environmental components. For a trait, the covariance matrix (Ω) in a family (pedigree) of n members was modeled as Ω = 2Φσ2a + Inσ2e, where Φ is the n × n kinship matrix for the pedigree, σ2a is the variance in the trait due to additive genetic effects, In is an n × n identity matrix, and σ2e is the variance due to random environmental effects. The most fundamental genetic parameter is the heritability (h2) of a trait: h2 = σ2a /(σ2a+σ2e). While this model is for the simplest case of only two variance components (additive genetic and environmental), it is readily extendable via the addition of variance terms in the denominator to allow for additional variance components such as those including dominance genetic variance, X-linked genetic variance, mitochondrial effects, and maternal effects (Almasy and Blangero 1998). Age, age2, sex, and their interactions (age × sex, age2 × sex) were included as covariates in all genetic analyses (Fig 4, Tables II–V), meaning h2 = σ2a / [(σ2a+σ2e) − σ2cov], where σ2cov represents variance due to age, age2, sex, and their interactions. Regression terms were estimated for each covariate, and the likelihood of a model in which the covariate effect was estimated was compared to the likelihood of a model in which the covariate effects were constrained to zero. Therefore, each phenotype (p) was modeled as p = μ + Σ βi i + a + e, where μ is the baseline mean of the phenotype, βi represents the regression coefficients, i represents the scaled covariates, “a” represents additive genetic effects, and “e” represents random environmental effects.
Results
Pointwise gray matter traits
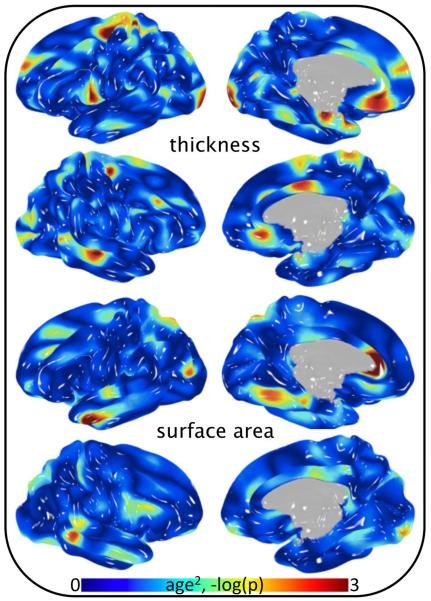
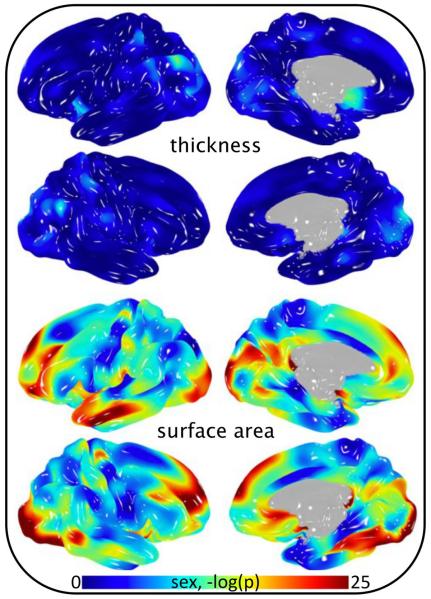
The significance of age as a covariate in analyses of cortical morphology varied by position and metric (Fig 1 and Fig 2). Strong association of age as a linear function was observed when assessing gray matter thickness (Fig 1, top). In contrast, age was not a significant covariate in analyses of surface area (Fig 1, bottom). Localizing any level of association of age2 required a vast reduction in p-value threshold for both surface area and thickness (Fig 2). Interestingly, the significance of sex as a covariate followed the opposite pattern (compare Fig 1 and Fig 3). That is, strong association of sex was observed when assessing gray matter surface area, whereas the effect of sex on gray matter thickness was comparatively small. Heritability of pointwise surface area and thickness ranged from zero to 0.7 and was position and metric dependent (Fig 4). Surface area was predominately more heritable than thickness.
Fig 2.
Significance of age2 covariance in cortical thickness and surface area analysis of 838 subjects.
Fig 3.
Significance of sex covariance in cortical thickness and surface area analysis of 838 subjects.
Region-based gray matter traits
All FreeSurfer derived region-based brain traits (surface area, thickness and volume) were heritable, including measurements of gyri, sulci, Brodmann Areas and subcortical (h2 range = 0.17–0.82, average h2 = 0.53, a subset of the full FreeSurfer trait set is tabulated in Tables II, III and IV). These results demonstrate unequivocal genetic influence on MRI-based phenotypes across the entire brain. Significance of demographic covariates varied widely, similar to effects reported by Winkler and colleagues in 350 fewer GOBS subjects (2010). Effects of age were strongest in cortical thickness phenotypes, while effects of sex were strongest in surface area phenotypes. Interestingly, age2 was generally non-significant in pointwise analyses, but reached significance for many region-based traits. This is potentially attributable to region-based phenotypes representing smoothed measurements with greater signal to noise than individual vertices. Regions that are commonly investigated with volumetric indices are reported in Table IV, which were highly heritable. Age and sex were significantly correlated with each subcortical volumetric trait, while age2 was significantly correlated with hippocampus, amygdala, thalamus and pallidum volume.
Table III.
Statistics from region-based thickness cortical thickness in 1,010 subjects. Brain measurements were averaged across left and right hemispheres prior to genetic analysis. Significant p-values are reported in scientific notation. A negative (positive) β for sex indicates the value of the phenotypic measure was generally smaller in females (males).
| Gyrus/Region Thickness | h2 (p-value) | Age β (p-value) | Age2 β (p-value) | Sex β (p-value) | Age × Sex β (p-value) | Age2 × Sex β (p-value) |
|---|---|---|---|---|---|---|
| Superior frontal | 0.44 (3.0E-12) | −4.0E-02 (1.3E-52) | 1.4E-04 (0.30) | 5.1E-02 (0.46) | 5.0E-03 (0.13) | 3.3E-04 (0.064) |
| Rostral middlefrontal | 0.39 (7.3E-11) | −2.9E-02 (2.3E-24) | −3.9E-05 (0.79) | −1.8E-01 (2.0E-02) | 5.6E-03 (0.13) | 3.7E-04 (0.068) |
| Caudal middle frontal | 0.53 (1.9E-16) | −3.9E-02 (3.6E-47) | 2.4E-04 (0.077) | 3.4E-02 (0.63) | 1.1E-02 (2.1E-03) | −2.7E-05 (0.88) |
| Pars opercularis | 0.38 (1.3E-10) | −4.1E-02 (3.3E-54) | 4.4E-04 (1.0E-03) | −9.8E-02 (0.16) | 7.7E-03 (2.0E-02) | −1.7E-04 (0.37) |
| Pars triangularis | 0.36 (6.5E-10) | −3.8E-02 (3.6E-46) | −3.8E-05 (0.78) | −1.1E-01 (0.11) | 7.2E-03 (3.5E-02) | 2.9E-04 (0.13) |
| Pars orbitalis | 0.34 (3.9E-08) | −3.0E-02 (4.5E-27) | −6.3E-05 (0.67) | −3.2E-02 (0.67) | 6.3E-03 (0.098) | 4.5E-04 (2.6E-02) |
| Medial orbitofrontal | 0.49 (5.2E-14) | −2.5E-02 (1.6E-19) | 3.2E-04 (2.7E-02) | −4.0E-01 (1.2E-07) | −2.1E-03 (0.57) | 3.7E-04 (0.06) |
| Lateral orbitofrontal | 0.40 (3.1E-10) | −3.5E-02 (2.6E-40) | 1.0E-04 (0.46) | −3.4E-01 (2.3E-06) | 3.0E-03 (0.39) | 4.7E-04 (1.2E-02) |
| Precentral | 0.55 (9.6E-17) | −3.6E-02 (3.6E-43) | 9.3E-05 (0.48) | −9.9E-03 (0.89) | 4.9E-03 (0.14) | 8.7E-05 (0.64) |
| Paracentral | 0.61 (7.9E-18) | −2.9E-02 (1.5E-29) | 1.5E-04 (0.26) | 2.4E-01 (6.1E-04) | −3.8E-03 (0.26) | −8.4E-05 (0.65) |
| Postcentral | 0.64 (1.9E-24) | −3.6E-02 (1.1E-43) | 8.3E-05 (0.53) | 2.1E-01 (1.8E-03) | 4.4E-03 (0.18) | −8.4E-05 (0.64) |
| Superiorparietal | 0.42 (1.6E-10) | −3.6E-02 (1.2E-41) | 2.7E-04 (4.7E-02) | 2.5E-01 (4.1E-04) | 6.1E-03 (0.086) | −2.8E-04 (0.15) |
| Supramarginal | 0.46 (4.6E-12) | −4.5E-02 (2.9E-72) | 2.8E-04 (2.2E-02) | 2.1E-01 (1.2E-03) | 7.9E-03 (1.1E-02) | −9.2E-05 (0.59) |
| Inferior parietal | 0.37 (4.4E-10) | −4.6E-02 (2.6E-03) | 3.2E-04 (2.5E-03) | 2.0E-01 (8.6E-40) | 1.0E-02 (0.28) | −1.2E-04 (0.54) |
| Caudal anterior cingulate | 0.38 (3.3E-09) | −2.4E-02 (1.7E-16) | 4.8E-04 (1.5E-03) | 1.0E-01 (0.19) | 6.3E-03 (0.10) | 2.2E-04 (0.30) |
| Rostral anterior cingulate | 0.42 (1.8E-10) | −3.3E-02 (1.9E-35) | 6.0E-04 (1.2E-05) | −2.9E-01 (4.6E-05) | 1.7E-03 (0.63) | 4.0E-04 (3.3E-02) |
| Posterior cingulate | 0.44 (8.0E-12) | −3.8E-02 (5.8E-52) | 3.7E-04 (4.3E-03) | 1.6E-02 (0.80) | −1.2E-03 (0.71) | 2.7E-04 (0.12) |
| Isthmus cingulate | 0.63 (2.8E-23) | −4.0E-02 (5.5E-53) | 9.9E-05 (0.45) | 4.2E-02 (0.54) | 1.0E-02 (2.3E-03) | 1.5E-04 (0.40) |
| Superior temporal | 0.56 (2.0E-18) | −4.5E-02 (6.4E-77) | 1.8E-04 (0.13) | −4.6E-02 (0.46) | 8.9E-03 (3.3E-03) | −2.2E-04 (0.18) |
| Middle temporal | 0.41 (6.2E-11) | −4.2E-02 (3.0E-62) | 3.9E-04 (2.0E-03) | −0.12 (6.3E-02) | 7.7E-03 (1.6E-02) | 6.4E-05 (0.72) |
| Inferior temporal | 0.47 (3.5E-13) | −3.3E-02 (3.4E-34) | 4.6E-04 (9.4E-04) | −1.9E-02 (0.79) | 6.2E-03 (0.079) | 1.5E-04 (0.42) |
| Fusiform | 0.48 (2.5E-11) | −3.8E-02 (8.2E-49) | 2.3E-04 (0.076) | −7.0E-02 (0.31) | 4.2E-03 (0.21) | 9.8E-05 (0.59) |
| Parahippocampal | 0.47 (7.6E-11) | −1.9E-02 (3.8E-11) | 1.6E-04 (0.28) | −8.2E-02 (0.30) | −3.3E-03 (0.39) | −3.7E-05 (0.86) |
| Entorhinal | 0.35 (3.7E-08) | −1.5E-02 (1.3E-07) | −2.6E-04 (0.090) | −4.8E-01 (2.4E-09) | 4.4E-03 (0.25) | 7.1E-05 (0.74) |
| Precuneus | 0.55 (2.5E-17) | −4.3E-02 (3.7E-69) | 2.7E-04 (2.6E-02) | 7.2E-02 (0.25) | 4.2E-03 (0.18) | −2.8E-05 (0.87) |
| Cuneus | 0.43 (4.4E-10) | −4.3E-02 (3.3E-32) | 2.7E-04 (0.39) | 7.2E-02 (4.8E-04) | 4.2E-03 (0.30) | −2.8E-05 (0.44) |
| Lingual | 0.49 (3.2E-12) | −3.9E-02 (2.8E-50) | −9.9E-05 (0.46) | 8.9E-02 (0.19) | 6.6E-03 (4.9E-02) | −1.3E-06 (0.99) |
| Pericalcarine | 0.39 (2.8E-09) | −2.5E-02 (8.6E-19) | −1.4E-04 (0.33) | 3.9E-01 (3.4E-07) | 1.3E-03 (0.72) | −3.1E-04 (0.13) |
| Lateral occipital | 0.49 (4.3E-14) | −3.7E-02 (1.9E-43) | 3.8E-05 (0.78) | 1.7E-01 (1.5E-02) | 1.4E-02 (7.8E-05) | −1.7E-04 (0.37) |
Table IV.
Statistics from region-based analysis of subcortical nuclei in 1,010 subjects. Brain measurements were averaged across left and right hemispheres prior to genetic analysis. Significant p-values are reported in scientific notation. A negative (positive) β for sex indicates the value of the phenotypic measure was generally smaller in females (males).
| Subcortical Nuclei Volume | h2 (p-value) | Age β (p-value) | Age2 β (p-value) | Sex β (p-value) | Age × Sex β (p-value) | Age2 × Sex β (p-value) |
|---|---|---|---|---|---|---|
| Ventral diencephalon | 0.66 (7.9E-28) | −2.8E-02 (1.2E-32) | 5.2E-05 (0.67) | −0.82 (2.9E-36) | 5.4E-04 (0.86) | −1.1E-04 (0.49) |
| Hippocampus | 0.70 (7.6E-33) | −2.5E-02 (5.9E-24) | −3.6E-04 (4.3E-03) | −0.75 (2.7E-27) | 6.0E-03 (0.06) | 7.2E-05 (0.69) |
| Amygdala | 0.73 (1.4E-31) | −2.5E-02 (1.1E-25) | −2.7E-04 (3.2E-02) | −0.70 (1.3E-24) | 9.9E-04 (0.76) | −1.0E-04 (0.55) |
| Thalamus | 0.73 (7.4E-32) | −3.5E-02 (3.8E-53) | −2.9E-04 (1.2E-02) | −0.72 (6.1E-31) | 4.7E-03 (0.11) | −4.4E-06 (0.98) |
| Caudate | 0.74 (5.8E-31) | −1.9E-02 (3.2E-13) | 2.0E-04 (1.3E-01) | −0.65 (1.3E-19) | −1.4E-03 (0.68) | −1.4E-04 (0.45) |
| Putamen | 0.74 (2.8E-28) | −3.5E-02 (2.7E-53) | −9.6E-05 (0.40) | −0.62 (5.9E-24) | 3.5E-04 (0.90) | −7.3E-05 (0.65) |
| Pallidum | 0.59 (4.7E-20) | −2.6E-02 (2.2E-25) | 3.1E-04 (2.0E-02) | −0.72 (1.4E-24) | 3.4E-03 (0.30) | −1.2E-04 (0.49) |
White matter traits
Significant heritability within GOBS subjects was also robust across white matter tracts, in accordance with a previous report by Kochunov and colleagues (2010) (See Table V). Correlation with age was highly significant (page = 7.8×10−34) while correlation with age2 was not significant (page2 = 0.67) for global fractional anisotropy (FA, a measure of white matter integrity (Beaulieu 2002)) averaged across the whole brain. Global FA was highly heritable (h2 = 0.55, p = 1×10−12). Interestingly, age2 was significant in Kochunov et al. 2010, which included 350 fewer GOBS subjects. Table V tabulates heritability estimates across the brain. Age was significant for all tracts except the hippocampal branch of the cingulate, while age2 was only significant for the right cingulate, and the right and left retrolenticular branches of the internal capsule.
Discussion
This is the first brain-wide report of covariate association in the GOBs sample. Results indicate significant location specific correlation of age and sex with cortical thickness and surface area, while age was not significantly correlated with cortical surface area. These results pertain to the linear effect of age, as quadratic effects were seldom significant. Typically, demographic covariates such as age and sex are included by default in genetic analyses. However, age does not appear to be a useful covariate for pointwise analysis of cortical surface area; in contrast age is highly correlated with pointwise cortical thickness. Interestingly, the opposite is appears to be true for sex. Furthermore, when brain traits are partitioned into regions, covariate structure is less consistent. For these reasons, thorough consideration of covariates should be investigated and communicated to aid the replication of imaging-genetic studies across cohorts and ultimately advance the field. Therefore, it is the primary purpose of the current manuscript is to set forth statistics describing the heritability of image-based phenotypes and the correlation with demographic covariates. Notably, the underlying goal is for other laboratories to perform and report analogous investigations.
All image-based phenotypes were influenced by genetic factors. From gray matter comprising neuronal cell bodies and subcortical nuclei to their axonal connections in white matter tracts and ever-present basal activity (Glahn et al. 2010), growing evidence indicates that MRI measures are subject to genetic influence. Furthermore, these techniques provide a powerful, noninvasive means to assess genetic mechanisms driving neurological disease. Future identification of the underlying genes will provide an important vantage point for understanding the brain's inborn architecture and the influence that it has on other domains of neuroscience, including clinical impairment.
Multiple investigations have described changes in cortical anatomy vis-à-vis age and sex. Similarly to the current report, Hogstrom and colleagues (2012) used vertex wise measurements in a cohort of 322 adults to characterize the relationship between age and cortical surface area and cortical thickness (amongst other metrics). Therein, thickness reductions were more significant than surface area (as is the case herein) yet age effects on surface area reached greater statistical significance (p-value) than we report despite a smaller sample size. Sowell and colleagues (2003) reported changes in gray matter density in a sample of 176 subjects that ranged in age from 7–87 years. Notably, significant quadratic effects were reported, potentially due to nonlinear aspects of age related changes that were captured by density metrics but not seen in surface area or thickness analyses. In a later report using the same sample, Sowell and colleagues (2007) reported significant cortical thickness differences between males and females. In this analysis, particular consideration was given to intrinsic brain size differences and the difficulty of inferring age × sex effects. Each of the aforementioned investigations, amongst others (Kochunov et al. 2007; Brun et al. 2009; Bartzokis et al. 2010), provides specific insight regarding the association of cortical measures with age, sex and other demographic measures in relatively large samples.
Similar investigations are seldom reported in imaging-genetic research despite the frequent use of age and sex as demographic covariates in genetic analyses. Going forward, we propose the notion that investigators report the effects of covariates as a matter of course in phenotype development. In time, this will (1) aid the replication of results and principles across increasingly large sample sizes, and (2) aid the establishment of a theoretical basis for genetic influence on the brain so that more informed and consistent gene discovery efforts can be undertaken.
Characterizing the significance of age and sex as covariates and reporting baseline heritability estimates provides critical information necessary before these phenotypic measures can be appropriately applied in genome-wide association studies. Maps of genomic sequence data onto the human brain have not been reported. Reproducible findings of this magnitude would dramatically improve our understanding of how genetic processes influence the brain. This, in turn, would help guide investigations of how these processes are disrupted in neurological disorders and psychiatric illnesses. Thorough reports of baseline heritability estimates and association of demographic variables is the initial step toward these overarching goals.
Over a decade after the 1990s was denoted the decade of the brain (Jones and Mendell 1999) and a decade after the initial sequencing of the human genome (Venter et al. 2001, Lander et al. 2001), many thought more synergistic discovery would have followed. The most glaring nonevent, given the emphasis and allocation of resources, is the general lack of early diagnosis, treatment or prevention of complex brain disorders. To achieve these goals, it is our opinion that priority must shift from categories of illness toward quantitative indices of normal variation in family members. Understanding genetic mechanisms that determine variation in healthy subjects is likely to elucidate how the same mechanisms are disrupted in illness. As a result, investigators will have a means to generate prospective hypotheses based on theoretical deduction rather than observation of clinical populations. Indeed, thoroughly characterized and communicated traits will serve as the foundation to superior gene discovery efforts.
Acknowledgements
We are grateful to the participants in the San Antonio Family Study. Financial support for this study was provided by the National Institute of Mental Health grants MH078143, MH078111 and MH083824; and the National Institute for Heart, Lungs and Blood grant HL045222. The development of the analytical methods and SOLAR software used in this study was supported by National Institute of Mental Health grant R37 MH059490.
References
- Almasy L, Blangero J. Multipoint quantitative-trait linkage analysis in general pedigrees. Am J Hum Genet. 1998;62:1198–211. doi: 10.1086/301844. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bartzokis G, Lu PH, Tingus K, Mendez MF. Lifespan trajectory of myelin integrity and maximum motor speed. Neurobiol Aging. 2010;31(9):1554–1562. doi: 10.1016/j.neurobiolaging.2008.08.015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Beaulieu C. The basis of anisotropic water diffusion in the nervous system - A technical review. NMR Biomed. 2002;15:435–455. doi: 10.1002/nbm.782. [DOI] [PubMed] [Google Scholar]
- Blangero J, Williams JT, Almasy L. Novel family-based approaches to genetic risk in thrombosis. J Thromb Haemost. 2003;1:1391–1397. doi: 10.1046/j.1538-7836.2003.00310.x. [DOI] [PubMed] [Google Scholar]
- Blangero J. Localization and identification of human quantitative trait loci: king harvest has surely come. Curr Opin Genet Dev. 2004;14:233–240. doi: 10.1016/j.gde.2004.04.009. [DOI] [PubMed] [Google Scholar]
- Brun CC, Lepore N, Luders E, Chou Y-Y, Madsen SK, Toga AW, et al. Sex differences in brain structure in auditory and cingulate regions. Neuroreport. 2009;20:930–935. doi: 10.1097/wnr.0b013e32832c5e65. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen CH, Gutierrez ED, Thompson W, Panizzon MS, Jernigan TL, Eyler LT, et al. Hierarchical genetic organization of human cortical surface area. Science. 2012;335:1634–1636. doi: 10.1126/science.1215330. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dale AM, Sereno MI. Improved localization of cortical activity by combining EEG and MEG with MRI cortical surface reconstruction: a linear approach. J Cogn Neurosci. 1993;5:162–176. doi: 10.1162/jocn.1993.5.2.162. [DOI] [PubMed] [Google Scholar]
- Dale AM, Fischl B, Sereno MI. Cortical surface-based analysis. I. Segmentation and surface reconstruction. Neuroimage. 1999;9:179–194. doi: 10.1006/nimg.1998.0395. [DOI] [PubMed] [Google Scholar]
- Desikan RS, Segonne F, Fischl B, Quinn BT, Dickerson BC, Blacker D, et al. An automated labeling system for subdividing the human cerebral cortex on MRI scans into gyral based regions of interest. Neuroimage. 2006;31:968–980. doi: 10.1016/j.neuroimage.2006.01.021. [DOI] [PubMed] [Google Scholar]
- Fischl B, Sereno MI, Dale AM. Cortical surface-based analysis. II: Inflation, flattening, and a surface-based coordinate system. Neuroimage. 1999a;9:195–207. doi: 10.1006/nimg.1998.0396. [DOI] [PubMed] [Google Scholar]
- Fischl B, Sereno MI, Tootell RB, Dale AM. High-resolution intersubject averaging and a coordinate system for the cortical surface. Hum Brain Mapp. 1999b;8:272–284. doi: 10.1002/(SICI)1097-0193(1999)8:4<272::AID-HBM10>3.0.CO;2-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fischl B, Dale AM. Measuring the thickness of the human cerebral cortex from magnetic resonance images. Proc Natl Acad Sci USA. 2000;97:11050–11055. doi: 10.1073/pnas.200033797. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fischl B, Liu A, Dale AM. Automated manifold surgery: constructing geometrically accurate and topologically correct models of the human cerebral cortex. IEEE Trans Med Imaging. 2001;20:70–80. doi: 10.1109/42.906426. [DOI] [PubMed] [Google Scholar]
- Fischl B, Salat DH, Busa E, Albert M, Dieterich M, Haselgrove C, et al. Whole brain segmentation: automated labeling of neuroanatomical structures in the human brain. Neuron. 2002;33:341–355. doi: 10.1016/s0896-6273(02)00569-x. [DOI] [PubMed] [Google Scholar]
- Fischl B, Salat DH, van der Kouwe AJ, Makris N, Segonne F, Quinn BT, et al. Sequence-independent segmentation of magnetic resonance images. Neuroimage. 2004a;23(Suppl 1):S69–84. doi: 10.1016/j.neuroimage.2004.07.016. [DOI] [PubMed] [Google Scholar]
- Fischl B, van der Kouwe A, Destrieux C, Halgren E, Segonne F, Salat DH, et al. Automatically parcellating the human cerebral cortex. Cereb Cortex. 2004b;14:11–22. doi: 10.1093/cercor/bhg087. [DOI] [PubMed] [Google Scholar]
- Glahn DC, Winkler AM, Kochunov P, Almasy L, Duggirala R, Carless MA, et al. Genetic control over the resting brain. Proc Natl Acad Sci USA. 2010;107(3):1223–1228. doi: 10.1073/pnas.0909969107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Han X, Jovicich J, Salat D, van der Kouwe A, Quinn B, Czanner S, et al. Reliability of MRI-derived measurements of human cerebral cortical thickness: the effects of field strength, scanner upgrade and manufacturer. Neuroimage. 2006;32:180–194. doi: 10.1016/j.neuroimage.2006.02.051. [DOI] [PubMed] [Google Scholar]
- Hogstrom LJ, Westlye LT, Walhovd KB, Fjell AM. The Structure of the Cerebral Cortex Across Adult Life: Age-Related Patterns of Surface Area, Thickness, and Gyrification. Cereb Cortex. 2012 doi: 10.1093/cercor/bhs231. doi:10.1093/cercor/bhs231. [DOI] [PubMed] [Google Scholar]
- Jones EG, Mendell LM. Science. 1999;284(5415):739. doi: 10.1126/science.284.5415.739. [DOI] [PubMed] [Google Scholar]
- Kochunov P, Lancaster JL, Glahn DC, Purdy D, Laird AR, Gao F, et al. Retrospective motion correction protocol for high-resolution anatomical MRI. Hum Brain Mapp. 2006;27:957–962. doi: 10.1002/hbm.20235. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kochunov P, Thompson PM, Coyle TR, Lancaster JL, Kochunov V, Royall D, et al. Relationship among neuroimaging indices of cerebral health during normal aging. Hum Brain Mapp. 2007;29:36–45. doi: 10.1002/hbm.20369. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kochunov P, Glahn DC, Lancaster JL, Winkler AM, Smith S, Thompson PM, et al. Genetics of microstructure of cerebral white matter using diffusion tensor imaging. Neuroimage. 2010;53:1109–1116. doi: 10.1016/j.neuroimage.2010.01.078. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lander ES, International Human Genome Sequencing Consortium et al. Initial sequencing and analysis of the human genome. Nature. 2001;409:860–921. doi: 10.1038/35057062. [DOI] [PubMed] [Google Scholar]
- Reuter M, Schmansky NJ, Rosas HD, Fischl B. Within-Subject Template Estimation for Unbiased Longitudinal Image Analysis. Neuroimage. 2012;61:1402–1418. doi: 10.1016/j.neuroimage.2012.02.084. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Segonne F, Dale AM, Busa E, Glessner M, Salat D, Hahn HK, et al. A hybrid approach to the skull stripping problem in MRI. Neuroimage. 2004;22:1060–1075. doi: 10.1016/j.neuroimage.2004.03.032. [DOI] [PubMed] [Google Scholar]
- Segonne F, Pacheco J, Fischl B. Geometrically accurate topology-correction of cortical surfaces using nonseparating loops. IEEE Trans Med Imaging. 2007;26:518–529. doi: 10.1109/TMI.2006.887364. [DOI] [PubMed] [Google Scholar]
- Sled JG, Zijdenbos AP, Evans AC. A nonparametric method for automatic correction of intensity nonuniformity in MRI data. IEEE Trans Med Imaging. 1998;17:87–97. doi: 10.1109/42.668698. [DOI] [PubMed] [Google Scholar]
- Sowell ER, Peterson BS, Thompson PM, Welcome SE, Henkenius AL, Toga AW. Mapping cortical change across the human life span. Nat Neurosci. 2003;6:309–315. doi: 10.1038/nn1008. [DOI] [PubMed] [Google Scholar]
- Sowell ER, Peterson BS, Kan E, Woods RP, Yoshii J, Bansal R, et al. Sex Differences in Cortical Thickness Mapped in 176 Healthy Individuals between 7 and 87 Years of Age. Cereb Cortex. 2007;17:1550–1560. doi: 10.1093/cercor/bhl066. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stein JL, Hua X, Lee S, Ho AJ, Leow AD, Toga AW, et al. Alzheimer's Disease Neuroimaging Initiative: Voxelwise genome-wide association study (vGWAS) Neuroimage. 2010;53(3):1160–1174. doi: 10.1016/j.neuroimage.2010.02.032. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Venter JC, Adams MD, Myers EW, Li PW, Mural RJ, Sutton GG, et al. The sequence of the human genome. Science. 2001;291(5507):1304–1351. doi: 10.1126/science.1058040. [DOI] [PubMed] [Google Scholar]
- Winkler AM, Kochunov P, Blangero J, Almasy L, Zilles K, Fox PT, et al. Cortical thickness or grey matter volume? The importance of selecting the phenotype for imaging genetics studies. Neuroimage. 2010;53:1135–1146. doi: 10.1016/j.neuroimage.2009.12.028. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Winkler AM, Sabuncu MR, Yeo BT, Fischl B, Greve DN, Kochunov P, et al. Measuring and comparing brain cortical surface area and other areal quantities. Neuroimage. 2012;61:1428–1443. doi: 10.1016/j.neuroimage.2012.03.026. [DOI] [PMC free article] [PubMed] [Google Scholar]