Consistent Biomechanical Phenotyping of Common Carotid Arteries From Seven Genetic, Pharmacological, and Surgical Mouse Models

Abstract

The continuing lack of longitudinal histopathological and biomechanical data for human arteries in health and disease highlights the importance of studying the many genetic, pharmacological, and surgical models that are available in mice. As a result, there has been a significant increase in the number of reports on the biomechanics of murine arteries over the past decade, particularly for the common carotid artery. Whereas most of these studies have focused on wild-type controls or comparing controls versus a single model of altered hemodynamics or vascular disease, there is a pressing need to compare results across many different models to understand more broadly the effects of genetic mutations, pharmacological treatments, or surgical alterations on the evolving hemodynamics and the microstructure and biomechanical properties of these vessels. This paper represents a first step toward this goal, that is, a biomechanical phenotyping of common carotid arteries from control mice and seven different mouse models that represent alterations in elastic fiber integrity, collagen remodeling, and smooth muscle cell functionality.

INTRODUCTION

Together with vertebral arteries, common carotid arteries are important conduits of oxygenated blood and nutrients to the brain. Diseases of carotid arteries include stiffening due to hypertension or aging, atherosclerosis (often at or near the carotid bifurcation), and sometimes dissection^38,39,46, hence these vessels demand careful study. Fortunately, its nearly straight, circular, uniform thickness geometry devoid of major branches renders the common carotid artery convenient for biomechanical study, which began in larger animals^6,9 but now often focuses on mice. Despite the increasing number of papers on the biomechanical behavior of mouse carotid arteries, data are typically presented either for wild-type controls or for controls versus a single model of adaptation or disease. Yet, the increased availability of genetic, pharmacological, and surgical models in the mouse has created a special opportunity to compare results more broadly. Only in this way can we exploit this growing data base and identify contributions of particular matrix constituents, cell-matrix interactions, and cellular behaviors to overall arterial stiffness and structural integrity.

One goal of this paper, therefore, is to begin the process of consistent biomechanical phenotyping of common carotid arteries by comparing directly the biaxial mechanical behaviors of normal controls and seven different mouse models. Four of these models have been used to study thoracic aortic disease: fibrillin-1 deficient mice (Fbn1^mgR/mgR), fibulin-5 null mice (Fbln5^−/−), angiotensin-II infused ApoE null mice (Ang-II ApoE^−/−), and smooth muscle α-actin null mice (Acta2^−/−). Two of these models have been used to study effects of muscular dystrophy on arteries: dystrophin deficient mice (mdx) and sarcoglycan-delta null mice (Sgcd^−/−). And one model, surgical banding of the aortic arch, has been used to study longitudinal effects of increased pulse pressure, that is, hypertension. Note, therefore, that the associated eight basic groups of data provide information on alterations to extracellular matrix (Fbn1^mgR/mgR, Fbln5^−/−, Ang-II ApoE^−/−, and Aortic Banding), smooth muscle cell – matrix interactions (mdx and Sgcd^−/−), and smooth muscle contractility (Acta2^−/−, Ang-II ApoE^−/−, and Aortic Banding), and thereby potentially new insights into microstructural contributions to arterial mechanics. Finally, another goal of this paper is to highlight an approach that can facilitate comparisons of data across larger numbers of mouse models based on reports of geometric data and stored energy functions independent of the availability of complete sets of raw biaxial data.

METHODS

Data used herein were compiled from experiments performed at Texas A&M University or Yale University, with approval of the Institutional Animal Care and Use Committee at the appropriate institution. Male mice were euthanized via an intraperitoneal injection of a lethal dose of sodium pentobarbital. The common carotid arteries were then excised, gently cleaned of excess perivascular tissue, cannulated on glass micropipets, and secured with 6-0 silk sutures. The cannulated vessels were placed within a custom computer-controlled biaxial testing system¹⁹ and, in general, equilibrated at 37°C for 30 minutes in a buffered physiologic solution to render the mechanical behavior passive, then preconditioned via 3 cycles of pressurization from 10 to 140 mmHg at an in vivo value of axial stretch that was estimated via the force – pressure relationship (i.e., a constant transducer measured force in response to changes in pressure).

We then performed cyclic pressure-diameter (P-d) tests at multiple fixed lengths (i.e., at the in vivo axial stretch and approximately 5% above and below the in vivo value) and cyclic axial force-length (f-l) tests at multiple fixed pressures (typically 10, 60, 100, and 140 mmHg). Mean in-plane biaxial Cauchy stresses in these up to seven biaxial protocols were estimated via

$${\sigma }_{\vartheta }=\langle t_{\vartheta \vartheta }\rangle =\frac{Pa}{h},{\sigma }_z=\langle t_{zz}\rangle =\frac{f}{\pi h(2a+h)},$$ (1)

where P is the measured distending pressure, f = f_T + πa² P the axial load applied to the closed-end specimen (with f_T representing the axial load measured directly by the force transducer), a the deformed inner radius, and h the deformed thickness. In practice, however, neither a nor h can be measured well on-line. Assuming incompressibility (i.e., isochoric motions) during transient loading, it proves useful to calculate a and h in one of two ways¹⁵. Of these two methods, we now prefer to measure the mean unloaded thickness H via image analysis of cross-sections of intact excised rings (e.g., by averaging values of thickness around the circumference that are determined via radial lines that intersect the unloaded inner and outer contours). After measuring the unloaded outer radius B and unloaded axial length L of the sample, we calculate the mean wall volume V̄ in the unloaded configuration as V̄ = π(B² − (B − H)²)L. Hence, online measurement of the deformed outer radius b and the deformed length l (over which volume was measured) enables calculation of the deformed inner radius a, and thus thickness h, for all subsequent deformations. That is,

$$a=\sqrt{b^2-\overline{V}/(\pi l)},h=b-a.$$ (2)

Finally, the associated mean biaxial wall stretches (i.e., principal components of the left stretch tensor) were estimated via

$${\lambda }_{\vartheta }=\frac{a+h/2}{A+H/2},{\lambda }_z=\frac{l}{L},$$ (3)

where A is the undeformed inner radius and l the deformed overall length, respectively.

In the absence of complete microstructural information throughout the arterial wall, we adopted a previously proposed, microstructurally-motivated, but phenomenological “four-fiber family model” of the passive behavior¹⁵. This model is a straightforward extension of the two-fiber family model of Holzapfel et al.²⁷, which was postulated to capture contributions to overall passive load bearing by an isotropic elastin-dominated matrix and embedded diagonal families of collagen fibers. The four-fiber family model additionally accounts phenomenologically for possible contributions due to passive smooth muscle (typically in the circumferential direction), nearly axially oriented collagen fibers (in the adventitia), and yet unquantified lateral cross-links or effects of physical entanglements; it has proven useful for quantifying the mechanical behavior of diverse murine carotid arteries^{11,14,20,49,50}. The associated strain energy function W has the form

$$W(\mathbf{C},{\mathbf{M}}^i)=\frac{c}{2}(I_C-3)+\sum _{i=1}^4\frac{c_1^i}{4c_2^i}\left\{exp\left[c_2^i{\left({IV}_C^i-1\right)}^2\right]-1\right\},$$ (4)

where c, $c_1^i$ and $c_2^i(i=1,2,3,4)$ are model parameters, with c and $c_1^i$ having units of stress (kPa) and $c_2^i$ dimensionless, C = F^T F the right Cauchy-Green tensor, and F the deformation gradient tensor²⁹. ${\mathbf{M}}^i=(0,sin{\alpha }_o^i,cos{\alpha }_o^i)$ is a unit vector in the direction of the i^th fiber family, where the angle ${\alpha }_o^i$ is computed relative to the axial direction in a reference configuration. Thus, axial and circumferential fiber families are oriented at α_o = 0 and α_o = 90 degrees, respectively. In addition, I_C = trC and ${IV}_C^i={\mathbf{M}}^i·{\mathbf{CM}}^i$ are coordinate invariant measures of deformation, namely

$$I_C={\lambda }_{\vartheta }^2+{\lambda }_z^2+\frac{1}{{\lambda }_{\vartheta }^2{\lambda }_z^2},{IV}_C^i={\lambda }_{\vartheta }^2{sin}^2{\alpha }_o^k+{\lambda }_z^2{cos}^2{\alpha }_o^k,$$ (5)

for F = diag(λ_r, λ_ϑ, λ_z), noting that incompressibility requires λ_r = 1/(λ_ϑ;λ_z).

Independent of the specific form of the strain energy function W, and given the aforementioned assumption of incompressibility under transient loading, the passive Cauchy stress can be determined constitutively in 3-D as

$$\mathbf{t}=-p\mathbf{I}+2\mathbf{F}\frac{\partial W}{\partial \mathbf{C}}{\mathbf{F}}^T,$$ (6)

where p is a Lagrange multiplier that enforces isochoric motions and is determined largely from radial traction conditions²⁹. We calculated p by invoking the common assumption that the radial stress was negligible with respect to the circumferential and axial values. Best-fit values of the eight model parameters were determined from the aforementioned seven biaxial testing protocols for all eight groups of mice using a nonlinear least squares minimization of the error e between the theoretically predicted th and experimentally inferred exp loads, where

$$e_1=\sum _{i=1}^N\left[{\left(\frac{P^{th}-P^{exp}}{{\overline{P}}^{\mathit{exp}}}\right)}_i^2+{\left(\frac{f^{th}-f^{\mathit{exp}}}{{\overline{f}}^{\mathit{exp}}}\right)}_i^2\right],$$ (7)

with the overbar representing an average over all data points N included in the regression. Note, too, that we performed the regressions on data obtained during unloading, which yields information on the stored energy that is available to do work on the blood during elastic recoil (i.e., energy not dissipated during cyclic loading), which thereby captures an important function of a central artery such as the common carotid. Because the linearized stiffness in unloading is as high or higher than that in loading, using data from the unloading curves also provides a conservative estimate of wall stiffness and wall stress.

For comparison, we also tabulate best-fit values of the model parameters that have been reported previously. In some cases, such regressions were accomplished using different biaxial testing protocols and a different objective function, as, for example,

$$\begin{array}{l}{e}_2=\sqrt{\frac{{\sum }_{i=1}^N{\left(P^{th}-P^{exp}\right)}_i^2}{{\sum }_{i=1}^N{\left(P^{exp}\right)}_i^2}}+\sqrt{\frac{{\sum }_{i=1}^N{\left(f^{th}-f^{\mathit{exp}}\right)}_i^2}{{\sum }_{i=1}^N{\left(f^{\mathit{exp}}\right)}_i^2}},\\ e_3=\sqrt{\frac{{\sum }_{i=1}^N{\left({\sigma }_{\vartheta }^{th}-{\sigma }_{\vartheta }^{\mathit{exp}}\right)}_i^2}{{\sum }_{i=1}^N{\left({\sigma }_{\vartheta }^{\mathit{exp}}\right)}_i^2}}+\sqrt{\frac{{\sum }_{i=1}^N{\left({\sigma }_z^{th}-{\sigma }_z^{exp}\right)}_i^2}{{\sum }_{i=1}^N{\left({\sigma }_z^{exp}\right)}_i^2}},\end{array}$$ (8)

where σ again represents the mean stress in the circumferential (ϑ) or axial (z) directions.

Following determination of best-fit values of the model parameters (equation 4) for individual specimens within actual experimental data sets, we then re-created and averaged circumferential and axial Cauchy stress – stretch data for simulated biaxial protocols, that is, for consistently prescribed loaded configurations. Specifically, given a reference configuration defined by the unloaded axial length L, outer radius B, and thickness H, the best-fit model parameters for W, and a prescribed loaded configuration (defined by a physiologic pressure and axial stretch), biaxial stresses were computed by first determining the associated circumferential stretch ratio in the loaded configuration. Rearranging equation 1₁, a Newton-Raphson algorithm was used to solve the following nonlinear equation

$$P\ast -\frac{{\sigma }_{\vartheta }({\lambda }_{\vartheta },{\lambda }_z)h}{a}=0,$$ (9)

for the loaded inner radius a, where P* is the prescribed distending pressure at the loaded configuration, h is the loaded thickness computed via incompressibility, and σ_ϑ(λ_ϑ;λ_z) is the circumferential stress expressed as a nonlinear function of principal stretches. After determining both the inner radius a that minimized equation 9 and the associated circumferential stretch from equation 3₁, the Cauchy stresses were then calculated at each loaded configuration of interest using equation 6 and the best-fit model parameters and associated axial stretches. This procedure was used to test the hypothesis that given complete information on the reference configuration and constitutive properties, one can re-create data for various biaxial testing protocols that can then be used to perform parameter estimations for any constitutive relation of interest. Such a procedure could obviously facilitate a consistent comparison of results from different laboratories provided that the requisite information is available⁴².

Finally, we employed the theory of “small deformations superimposed on large” to compute linearized values of stiffness about a prescribed in vivo state defined by a distending pressure and axial stretch (i.e., an in vivo pair λ_ϑ and λ_z). This linearized stiffness is given by¹

$${\mathrm{C}}_{\mathit{ijkl}}={{\delta }_{ik}{\widehat{t}}_{ij}^o+{\widehat{t}}_{il}^o{\delta }_{jk}+4F_{iA}^o{F}_{jB}^o{F}_{kP}^o{F}_{lQ}^o\frac{{\partial }^2\widehat{W}}{\partial C_{AB}\partial C_{PQ}}|}_{C^o}$$ (10)

where t̂^o are deformation-dependent Cauchy stresses in the finitely deformed configuration about which the linearization is performed, F^o are deformation gradients from an appropriate reference to the same finitely deformed configuration, and C are associated components of the right Cauchy-Green tensor. This appropriately linearized stiffness has multiple advantages. For example, it enables consistent comparisons, given any stored energy function W, in terms fewer parameters than needed in the different nonlinear forms of W and it yields values having in vivo relevance, as needed in fluid-solid-interaction simulations of in vivo mechanics.

To further enable consistent comparisons of results from different laboratories, we mined the literature for correlations between conscious central blood pressures and those collected either using a tail cuff device or under different anesthetics. As shown in the Appendix, such correlations allow reported blood pressures to be adjusted to a common in vivo condition, which can facilitate comparisons of stress, stiffness, or stored energy. Herein, published pressures measured via noninvasive tail cuff (pooled controls, Ang-II ApoE^−/−, Acta2^{− −/−}, and Aortic Banding) and catheterization under isoflurane anesthesia, (mdx, Sgcd^−/−) were adjusted to a conscious central systolic state (Appendix). The reported Fbln5^−/− data were at collected at this preferred state⁵⁴.

RESULTS

Table 1 lists hemodynamic, geometric, and mechanical data (mean ± standard error of the mean) for pooled controls as well as six of the seven different mouse models: Fbn1^mgR/mgR, Fbln5^−/−, Ang-II ApoE^−/−, Acta2^−/−, mdx, and Sgcd^−/−. Many of the same parameters for the Aortic Banding model at 0, 7–10, 10–14, and 35–56 days post-banding are listed in Eberth et al.^12,13 and not repeated here. Note both the considerable similarities and significant differences in the various metrics amongst these seven groups. In particular, a superscript * denotes a statistically different value relative to control based on an ANOVA, with a post-hoc Bonferroni correction, with p < 0.05 considered significant. For example, in vivo wall thickness and outer diameter at systole ranged from 20 to 34 μm and 579 to 680 μm, respectively, with reported systolic pressures ranging from 80 to 157 mmHg. Because these values of blood pressure reflected, in part, the different methods of measurement (e.g., tail cuff or catheter-based) and associated conditions (e.g., conscious or anesthetic used), we also list “adjusted” systolic pressures, which ranged from 81 to 159 mmHg. Of course, associated ratios of a/h at individual systolic pressures, ranging from ~ 7.8 to 14.5, likely contributed to the high systolic values of intramural biaxial stresses (average ~ 170 and 195 kPa in circumferential and axial directions, not including the > 200 kPa stresses in the Sgcd^−/− model that likely resulted in part from its higher axial stretch). Note, in particular, that the in vivo axial stretches ranged from 1.4 to 1.80, with the two elastin compromised models (Fbn1^mgR/mgR and Fbln5^−/−) exhibiting lower values. The most dramatic reduction in axial stretch, to 1.27, was found in the 35–56 day Aortic Banding model^12,13. Values of axial stretch affect values of both circumferential and axial Cauchy stress.

Table 1.

Animal, hemodynamic, and morphological - mechanical data for common carotid arteries for seven different groups: control data pooled from Acta2^+/+ and Fbn1^mgR/+ mice compared with data from fibrillin-1 deficient (Fbn1^mgR/mgR), fibulin-5 null (Fbln5^−/−), angiotensin-II infused ApoE null (Ang-II ApoE^−/−), smooth muscle α-actin null (Acta2^−/−), dystrophin deficient (mdx), and sarcoglycan-δ null (Sgcd^−/−).

	Control	Fbn1 mgR/mgR	Fbln5 −/−	Ang-II ApoE −/−	Acta2 −/−	mdx	Sgcd −/−
n	16	6	5	8	7	5	6
Age (weeks)	9.0 ± 0.4	8.0 ± 0.2	21.2 ± 0.6	12.2 ± 0.1	10.6 ± 0.5	10.0 ± 0.9	10.0 ± 0.8
Body Mass (g)	22.9 ± 0.9	20.1 ± 2.3	33.6 ± 2.2	29.1 ± 1.4	26.3 ± 0.8	29.1 ± 0.5	26.7 ± 0.4
Blood Pressure (mmHg)
Systolic	116 ± 2a,c	131 ± 6b	152 ± 2e	157 ± 7d	82 ± 2a	80 ± 2f	88 ± 1f
Mean	-	107 ± 6b	122 ± 1e	133 ± 2d	-	-	-
Adjusted Systolic†	116	131	152	159	81	106	116
Unloaded Dimensions
Outer Diameter (μm)	394 ± 8	399 ± 6	429 ± 8	429 ± 7*	442 ± 5*	434 ± 7*	419 ± 11
Wall Thickness (μm)	94 ± 4	94 ± 5	70 ± 4*	109 ± 5	78 ± 3	63 ± 2*	62 ± 2*
In-vitro Axial Length (mm)	4.66 ± 0.21	4.14 ± 0.43	5.48 ± 0.35	4.46 ± 0.28	4.30 ± 0.21	4.86 ± 0.26	4.71 ± 0.30
Systolic Dimensions
Outer Diameter (μm)	647 ± 9	656 ± 16	579 ± 9*	680 ± 15	647 ± 7	618 ± 17	619 ± 14
Wall Thickness (μm)	26 ± 1	28 ± 1	33 ± 2*	34 ± 2*	28 ± 1	22 ± 1	20 ± 1*
In-vivo Axial Stretch	1.72 ± 0.02	1.61 ± 0.03	1.40 ± 0.02*	1.60 ± 0.05*	1.63 ± 0.03	1.77 ± 0.02	1.80 ± 0.01
Systolic Cauchy Stresses (kPa)
Circumferential	177.3 ± 5.1	186.8 ± 5.6	160.5 ± 13.7	195.7 ± 11.1	113.9 ± 4.6*	182.8 ± 11.1	219.4 ± 5.7*
Axial	199.7 ± 7.4	164.7 ± 6.3	189.1 ± 23.3	216.6 ± 10.3	182.8 ± 9.3	221.5 ± 10.8	265.4 ± 6.8*
Systolic Stiffness
Circumferential (MPa)	1.46 ± 0.10	1.79 ± 0.11	1.94 ± 0.27	1.86 ± 0.13	0.91 ± 0.11*	1.54 ± 0.13	1.97 ± 0.14
Axial (MPa)	3.03 ± 0.26	2.45 ± 0.29	5.33 ± 0.64*	3.41 ± 0.15	1.62 ± 0.08*	2.52 ± 0.23	2.94 ± 0.19
Pulse Wave Velocity (m/s)	7.74 ± 0.29	8.88 ± 0.31	10.65 ± 0.42*	9.71 ± 0.17*	6.30 ± 0.29*	7.48 ± 0.28	8.07 ± 0.30
Systolic Stored Energy (kPa)	50.4 ± 2.3	36.3 ± 1.5*	26.6 ± 3.6*	48.8 ± 3.5	47.7 ± 3.1	54.4 ± 4.5	63.1 ± 0.9*

Blood pressures (systolic, and mean when available) were compiled from reports in the literature [^a measured by tail-cuff ^{45; b} measured by indwelling catheter^{37; c} measured by tail-cuff ^{24; d} measured by tail-cuff ^{3; e} measured by indwelling catheter^{54; f} measured by left-ventricular catheter under isoflurane anesthesia⁴⁷], but also adjusted to a common central arterial value in the conscious mouse (cf. Appendix) to enable more consistent comparisons of model-specific properties. Actual mechanical data for the Fbn1^mgR/mgR mice were taken from Ferruzzi et al.¹⁴, those for Ang II ApoE^−/− mice from Bersi et al.², and those for the mdx and Sgcd^−/− mice from Dye et al.¹⁰; these data are collected together here for the first time, however, and re-analyzed consistently for purposes of direct comparison. The other mechanical data are new and from the authors’ laboratory. All data are presented as mean ± standard error of the mean. A superscript * denotes a significant difference relative to control based on an ANOVA, with a post-hoc Bonferroni correction, with p < 0.05 considered significant. Finally, albeit not shown, systolic pressures and in vivo axial stretches for the four aortic banding groups were: 120 mmHg and stretch of 1.70 for 0 day, 149 mmHg and 1.46 for 7–10 days, 154 mmHg and 1.37 for 10–14 days, and 125 mmHg and 1.27 for 35–56 days post-banding, respectively, with other information tabulated in Eberth et al.^12,13.

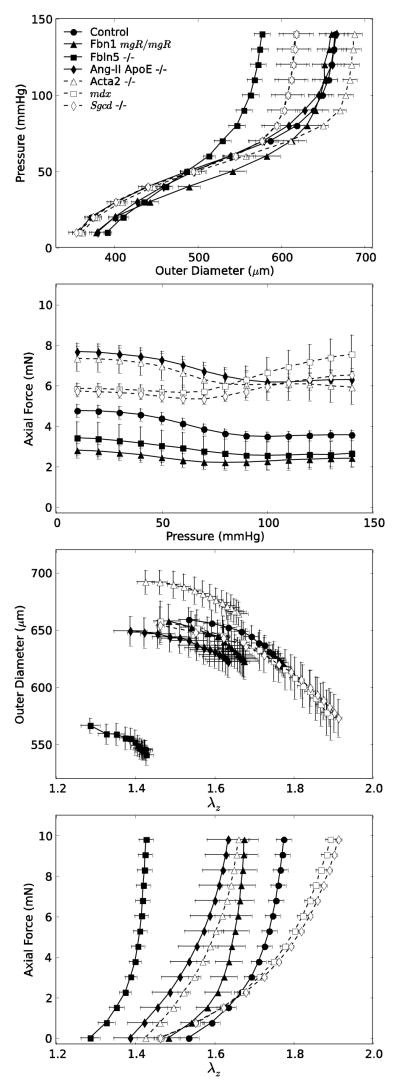
The left panels of Figure 1 show associated P-d and f-P data (also mean ± standard error of the mean) during cyclic pressurization tests at fixed axial stretches near the individual in vivo values (with n ranging from 5 to 8 per group, except for the pooled controls with n = 16). As it can be seen, P-d responses were similar for four of the seven groups, with the mdx and Sgcd^−/− carotids exhibiting an identically reduced distensibility and the Fbln5^−/− carotids exhibiting the lowest distensibility. In contrast, there was greater variation in the transducer-measured axial force f_T needed to maintain fixed the individual values of in vivo stretch during pressurization tests. Similar findings for the Aortic Banding data are again found in Eberth et al.^12,13. Such variations appeared to reflect differences in the in vivo axial stretch (which ranged from 1.4 to 1.8; Table 1). Axial forces were slightly higher for Acta2^−/− and Ang-II ApoE^−/− carotids and similarly for mdx and Sgcd^−/− carotids, each compared with controls; on the other hand, the Fbn1^mgR/mgR and Fbln5^−/− carotids exhibited lower axial forces at their individual in vivo axial stretches, which were amongst the lowest of the seven groups. The right two panels of Figure 1 show data from f–l tests at a constant pressure of 100 mmHg. Note the similar values of loaded outer diameter amongst these seven groups with the exception of the larger diameter Acta2^−/− mice and the much smaller diameter Fbln5^−/− mice. Note, too, that Fbln5^−/− carotids were both the least distensible (in P-d tests) and least extensible (in f–l tests). These observations emphasize the importance of biaxial data in any biomechanical characterization of arterial behavior. Indeed, axial behavior may be particularly important in many arterial adaptations to altered hemodynamics as well as in cases of altered matrix composition or cell-matrix interactions³².

Figure 1.

Mean ± standard error of the mean data for the seven experimental groups listed in Table 1 and collected via P-d tests (left panels) performed at the individually estimated in vivo axial stretches (as determined from the force – pressure responses) and f–l tests (right panels) performed at 100 mmHg. Filled symbols and solid lines show data for controls and extracellular matrix affected mice (Fbn1^mgR/mgR, Fbln5^−/−, Ang-II ApoE^−/−), whereas open symbols and dashed lines show data for smooth muscle cell affected mice (Acta2^−/−, mdx, Sgcd^−/−). Despite a general clustering of circumferential behaviors (cf. top panels), there was greater variation in axial behaviors (bottom panels), which highlights the importance of biaxial comparisons of mechanical properties across different models.

Table 2 lists best-fit values of the eight model parameters (cf. equation 4) for all 11 groups of data (i.e., those in Table 1 plus 4 groups from the Aortic Banding study), which fit reasonably well all of the averaged P-d and f-l data. These parameters were thus used to simulate mean biaxial stress – stretch behaviors. Figure 2 visually compares experimentally derived (filled black symbols) and theoretically simulated (open symbols, with values generated using geometric data in Table 1 and model parameters in Table 2) Cauchy stress – stretch behaviors for three representative genotypes. Because the simulated data were derived from best-fit model parameters, they can be computed consistently over the same range of loading conditions; simulations here represent pressure states ranging from 10 to 140 mmHg in increments of 10 mmHg. Results were similar for the other mouse models, but only three are shown in Figure 2 for clarity. Note that these biaxial simulations consistently agreed well with actual experimental data (i.e., P-d and f-l tests) independent of the mouse model. Moreover, simulated data best matched the actual σ_ϑ–λ_ϑ (top left panel) and σ_z – λ_z (bottom right panel) data (r² > 0.95), whereas it matched the λ_ϑ – λ_z (top right panel) and σ_z – λ_ϑ (bottom left panel) data reasonably well (0.70 < r² < 0.95), with only one outlier (r² < 0.70) in the stretch-stretch plane. Because the best matches to data were for the stress-stretch results, which are of primary interest in terms of understanding material behavior¹⁵, this finding supports the utility of re-creating biaxial data that are not available but are otherwise described by an appropriate nonlinear constitutive relation⁴². Albeit an arbitrary value, we recommend that a goodness of fit to “data” sufficient to justify this approach should yield an r² > 0.95 in terms of the stress – stretch behaviors. Clearly, such an approach could enable in the future a broader biomechanical phenotyping across many mouse models studied by different laboratories. Our goal herein was merely to validate this approach, however, which required us to have the actual experimental data in each case and thereby to focus our attention on a retrospective analysis of the groups reported herein.

Table 2.

Best-fit values of the constitutive parameters for equation 4 for common carotid arteries from the seven groups noted in Table 1 and Figure 1, plus those for the four Aortic Banding groups. Parameters were determined by minimizing objective function e₁ (equation 7) using a mean set of experimental data for each mouse model using methods detailed in Ferruzzi et al.¹⁵.

Group	Elastic Fibers c (kPa)	Axial Collagen		Circumferential Collagen + SMC		Symmetric Diagonal Collagen			Error RMSE
		c11 (kPa)	c21	c12 (kPa)	c22	c13,4 (kPa)	c23,4	α0 (deg)
Control	8.126	9.180	0.151	4.782	0.041	0.015	1.181	29.4	0.099
Fbn1 mgR/mgR	7.015	0.248	1.225	0.938	0.179	1.396	0.564	31.8	0.120
Fbln5 −/−	23.528	1.090	3.321	3.872	1.114	0.044	5.910	30.8	0.082
Ang-II ApoE −/−	7.952	18.671	0.141	5.289	0.058	0.005	1.993	31.8	0.064
Acta 2 −/−	27.171	9.658	0.256	0.350	0.609	0.005	2.204	38.0	0.066
mdx	33.175	0.181	0.547	1.735	0.624	0.113	1.362	42.8	0.082
Sgcd −/−	28.007	2.487	0.216	4.672	0.278	0.165	1.078	42.6	0.086
0d HT	14.574	4.679	0.191	3.561	0.132	0.102	0.971	36.0	0.111
7–10d HT	15.101	0.005	3.020	8.114	0.051	2.834	0.893	37.0	0.093
10–14d HT	8.496	0.010	3.895	8.929	0.015	3.231	0.990	36.7	0.092
35–56d HT	4.025	0.388	9.920	11.579	2.255 × 10–14	13.297	1.102	37.1	0.091

Figure 2.

Comparison of Cauchy stress stretch responses determined experimentally (equation 1) and simulated theoretically (e.g., equation 4) for the same loading conditions (i.e., pressure and axial stretch) as in the experimental protocol. Experimental values are shown by filled symbols (e.g., ●, for controls) and theoretical values by open symbols (e.g., ○, for controls). Observe that our procedure for recreating, or simulating, data captured well the general stress – stretch behaviors across all models (r² > 0.95). Shown here for illustration is a subset of the groups: controls, Fbln5^−/−, and Acta2^−/−. Error bars show the standard error of the mean.

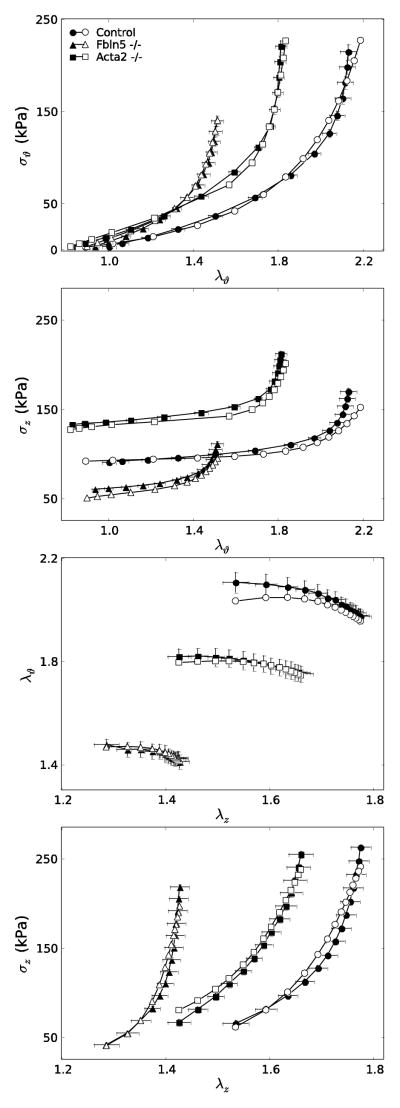
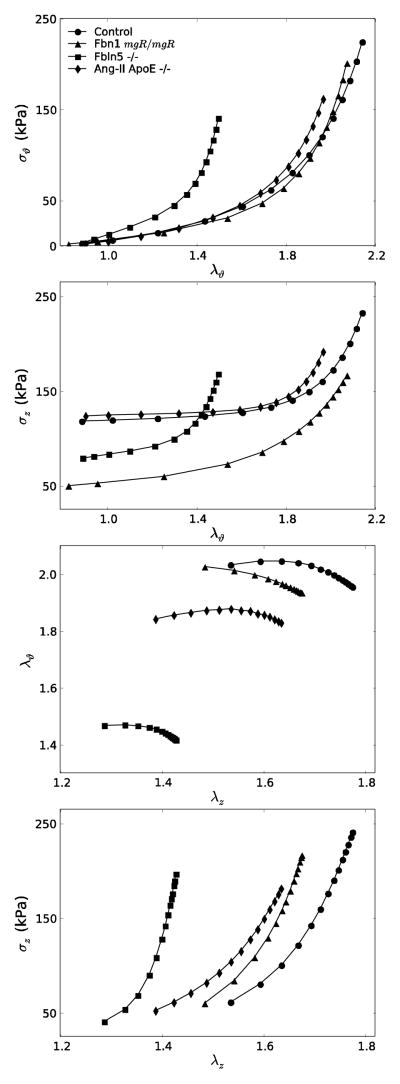
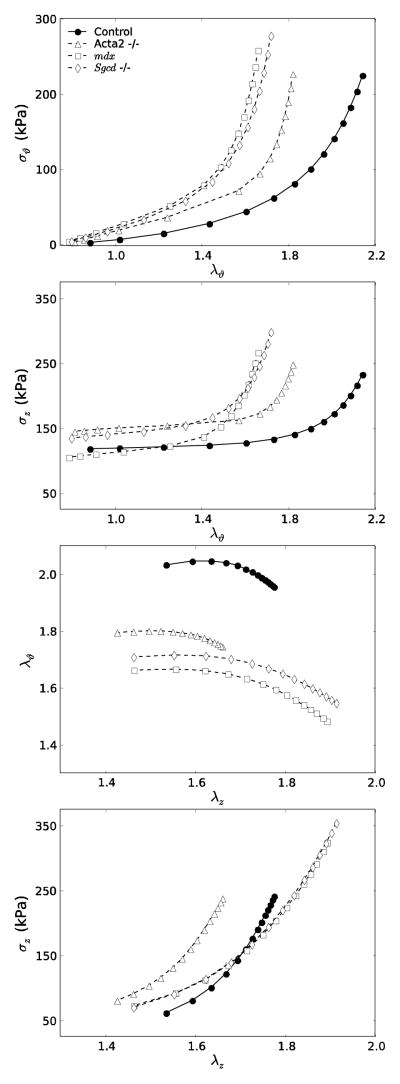
Figures 3 and 4 show simulated mean data for the seven groups of Table 1, the former for models with affected extracellular matrix (Fbn1^mgR/mgR, Fbln5^−/−, Ang-II ApoE^−/−) and the latter for those with affected smooth muscle or smooth muscle – matrix interactions (Acta2^−/−, mdx, Sgcd^−/−). In particular, Figure 3 reveals marked differences in circumferential and axial Cauchy stress – stretch behaviors due to altered matrix: the Fbln5^−/− carotids appeared “stiffest” biaxially (i.e., the least distensible and extensible) whereas Ang-II ApoE^−/−, Fbn1^mgR/mgR and control carotids exhibited similar behaviors. Results for these Fbn1^mgR/mgR and Fbln5^−/− carotids versus controls are similar to prior findings by others^11,49, but this is the first direct comparison of results across multiple models of compromised elastic fiber integrity for the same experimental protocols and methods of data analysis. It appeared that the different “offsets” in axial stress – stretch plots associated, in large part, with the different levels of axial stretch (cf. Table 1). Similarly, Figure 4 shows mean circumferential and axial Cauchy stress – stretch behaviors for the smooth muscle cell affected models. Each of the three models appeared “stiffer” biaxially (i.e., less distensible and extensible) when compared with the controls, with the mdx and Sgcd^−/− carotids appearing slightly stiffer than those from the Acta2^−/− mice.

Figure 3.

Simulated stress – stretch curves for extracellular matrix affected models (Fbn1^mgR/mgR, Fbln5^−/−, Ang-II ApoE^−/−) compared with controls. Note the stiffer circumferential and axial (i.e., less distensible and extensible) behaviors of the Fbln5^−/− carotids as compared with all others. Biaxial simulations were performed using the same loading conditions as in the experiments. Note, too, that the in vivo axial stretches used to recreate the P-d data (left panels) were determined from the crossover point of multiple f–l protocols.

Figure 4.

Simulated stress – stretch curves for smooth muscle cell affected models (Acta2^−/−, mdx, Sgcd^−/−) compared with controls. Each genotype exhibited increased stiffness in axial and especially circumferential directions compared with controls, with the two muscular dystrophy models (mdx and Sgcd^−/−) being similar. As in Figure 3, the biaxial simulations were performed using the same loading conditions as in the experiments and individual in vivo axial stretches were determined from the crossover point of multiple f–l protocols. For clarity, each genotype maintains the same line style (e.g., open symbol with dashed line) as in Figure 1.

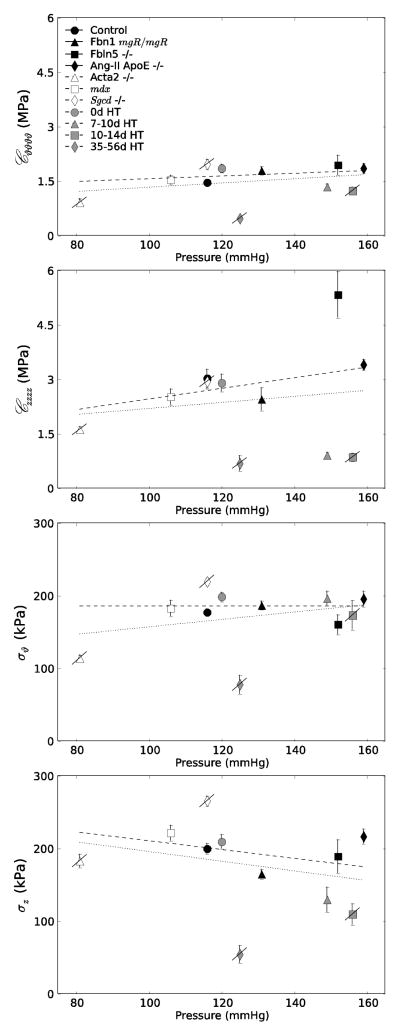
Table 1 also lists values of linearized stiffness at the adjusted systolic pressure and individual in vivo axial stretch. Note that these values, computed from unloading curves, were similar to or slightly higher than those computed from loading curves – for example, for a subset of control carotids (n = 7), the mean circumferential stiffness was 1.238 and 1.249 MPa and the mean axial stiffness was 2.610 and 2.985 MPa, both in loading and unloading, respectively. As it can be seen from the Table, the common carotid appears to be strongly anisotropic, with the axial direction stiffer than circumferential. Moreover, consistent with the stress – stretch plots, the Fbln5^−/− carotids were the stiffest biaxially. Nevertheless, consider Figure 5, which shows circumferential and axial Cauchy stress and linearized stiffness at the individual adjusted systolic pressures and in vivo axial stretches for all 11 sets of data: controls, the six models included in Table 1, and the Aortic Banding model at four times post-surgery (0, 7–10, 10–14, and 35–56 days). As it can be seen (Fig 5, upper panels), with few exceptions, the mean circumferential stress was comparable for most groups at the individual P_sys (slope = 0.001, dark dashed line), whereas the mean axial stress tended to decrease slightly with increasing P_sys (slope = −0.607, dark dashed line). Similarly, with few exceptions, the linearized circumferential stiffness tended to be comparable across groups (slope = 0.004, dark dashed line) whereas the linearized axial stiffness tended to increase slightly with P_sys (slope = 0.015, dark dashed line) (Fig 5, lower panels). The trend toward decreasing axial stress given an increasing axial stiffness may reflect an important compensatory role of reduced axial stretch³². Although axial stiffness is typically not reported, note that a linearized circumferential stiffness at systole of order 1.5 MPa is similar to the incremental value of ~1 MPa (the calculation of which does not account directly for biaxial pre-stresses in vivo) reported by Wagenseil and Mecham (cf. their Fig 9b)⁴⁸. For purposes of comparison, Table 1 also lists estimated values of pulse wave velocity at P_sys and the in vivo axial stretch based on the Moens-Korteweg equation (c² = Eh/2ρa, where c is the pulse wave velocity, ρ the mass density of the fluid (1060 kg/m³), and E the Young’s modulus, which was replaced here with the linearized circumferential stiffness). Although theoretically inappropriate because of the underlying assumptions used in its derivation, the Moens-Korteweg equation nevertheless provides some intuitive insight by combining overall contributions of material stiffness, wall thickness, and luminal radius; it also enables a further comparison of results independent of a particular stored energy function while reflecting an important hemodynamic metric that is easily measured clinically. Consistent with other findings, the highest value of pulse wave velocity at P_sys arose for the Fbln5^−/− carotid (10.65 m/s); values for the Ang-II ApoE^−/− (9.71 m/s) and Fbn1^mgR/mgR (8.88 m/s) carotids were similarly elevated relative to control (7.74 m/s), noting that an elevated value for a Fbn1^mgR/mgR mutation is consistent with measurements in the aorta³⁷. Note, however, that pulse wave velocity not only reflects overall arterial stiffness, it also increases, in general, with increases in blood pressure¹⁷. For example, estimated values of pulse wave velocity were 5.53, 6.15, 6.77, and 7.97 m/s for control carotids at 80, 90, 100, and 120 mmHg transmural pressure (with the associated slope of pulse wave velocity versus pressure similar to that of published values^17,37), again emphasizing the importance of evaluations and cross-comparisons at model-specific mechanical conditions. Values would probably be better compared at mean arterial pressure, but these pressures were not available for all groups of mice.

Figure 5.

Plot of mean circumferential and axial Cauchy stress (upper panels) and linearized stiffness (lower panels) for all 11 groups as a function of the adjusted central systolic blood pressure (cf. Table 1). Error bars show the standard error of the mean. The light dashed line shows the best linear regression of all data whereas the dark dashed line shows the best linear regression if the four apparently “maladaptive” results (Acta2^−/−, Sgcd^−/−, and the 10–14 day and especially the 35–56 day Aortic Banding sets, which are indicated by the slash through the symbol), are excluded from the regression. See text for exclusion criteria.

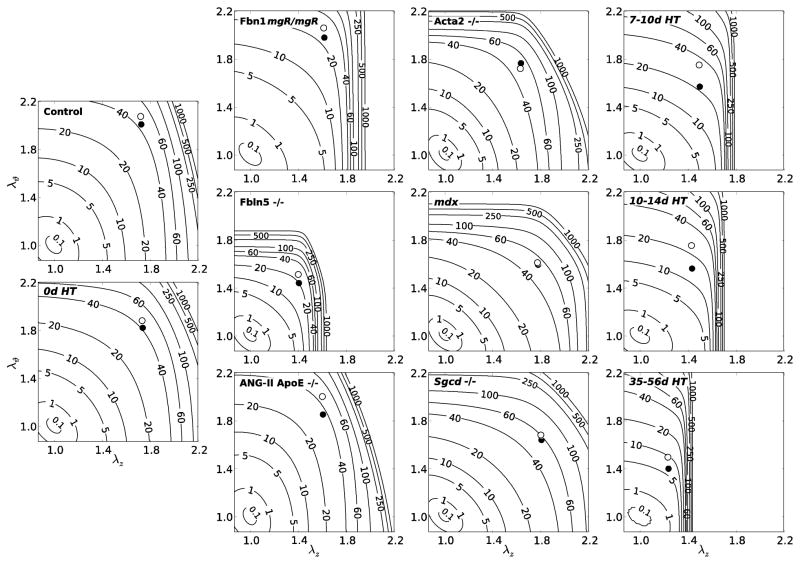
Notwithstanding the importance of quantifying in vivo values of circumferential and axial (material) stiffness for stress analyses and simulations of fluid-solid interactions, one must be careful not to over-interpret stiffness or anisotropy from data that reflect pressurization tests at fixed axial stretches (i.e., data from non-equibiaxial stretching tests)²⁹. For this reason, and because of the difficulty of interpreting differences in eight best-fit model parameters across multiple mouse models (cf. Table 2), we compared the energy W stored as a function of biaxial stretches, including those at the in vivo state. Recall, therefore, that W was computed using model parameters determined from unloading curves, which yielded the energy that is stored during systole and is available to do work on the blood during diastole, a key function of central arteries (of course, calculations of energy stored during loading would similarly be useful when studying cardiac energetics). Figure 6 shows iso-energy contour plots for all 11 groups based on equation 4 and best-fit values of the model parameters listed in Table 2. Note that the two symbols represent specific values of stored energy at particular pressurized states: the filled circle is at a common pressure of 100 mmHg and the open circle is at the adjusted individual systolic pressure noted in Table 1. As it can be seen, the Fbln5^−/− behavior again differed the most of the mutant models. In particular, these carotids exhibited slight anisotropy (i.e., asymmetry in the iso-energy contours), but a marked decrease in distensibility and extensibility (indicated by the stretches) and a marked decrease in energy stored at the in vivo state. Many of these characteristics are similar to those in the dramatic, progressive carotid remodeling that occurred in the Aortic Banding model (denoted by HT for hypertensive)¹², which at 35–56 days post-surgery resulted in extreme anisotropy and a remarkable reduction in axial stretch to 1.27. In particular, the lower energy storage for in the Fbln5^−/− and the long-term hypertensive (HT) carotids at physiologic pressures suggests that less energy would be available for elastic recoil, hence exacerbating the structurally stiffer response with regard to possible effects on the hemodynamics (cf. estimated high values of pulse wave velocity in Table 1). Note, too, that small increases in biaxial stretch could increase significantly the stored energy in these highly nonlinear tissues (reflected by the closeness of the iso-energy contours at modest stretches), which could potentially result in microstructural damage. Finally, note that it was the two models of decreased elastic fiber integrity that showed the stiffest axial responses and lowest energy storage of the mutants. That fibulin-5 null (Fbln5^−/−) carotids exhibited a more dramatic mechanical phenotype than the fibrillin-1 deficient (Fbn1^mgR/mgR) mice was interesting given that the latter have an increased susceptibility to thoracic aortic aneurysms and dissections. There are likely many factors other than overall stiffness that lead to aneurysms and potential dissection, not the least of which would be local rather than global properties³³. Finally, there is a need to compare results regionally¹⁵ and a need to quantify the “biological age” of the vessels, not just the chronological age (noting that the Fbln5^−/− mice were the oldest amongst those studied, though we have found no significant difference in carotid behavior from 5 to 22 weeks of age (unpublished data) and 22 weeks of age is still very young relative to old mice¹⁶).

Figure 6.

Iso-energy contours for the strain energy function W (equation 4) for all 11 groups computed using the best-fit constitutive parameters (Table 2). The leftmost column shows results for controls, the next column shows extracellular matrix affected genotypes, the next column shows smooth muscle cell affected genotypes, and the rightmost column shows Aortic Banding data sets at 7–10, 10–14, and 35–56 days post-banding. The filled symbol (●) represents values at circumferential and axial stretches corresponding to a common pressure of 100 mmHg whereas the open symbol (○) represents values at circumferential and axial stretches corresponding to the adjusted systolic pressures listed in Table 1, all at the individual estimated in vivo axial stretch.

DISCUSSION

The resilience, stiffness, and strength of an artery result primarily from the elastic fibers, fibrillar collagens, and smooth muscle, which in turn depend strongly on cell – matrix and matrix – matrix interactions⁴⁸. Amongst the many mouse models available, we focused on two models of altered elastic fiber integrity (Fbn1^mgR/mgR and Fbln5^−/−), two models of pressure-induced collagen remodeling (Ang-II ApoE^−/− and Aortic Banding), one model of altered smooth muscle contractility (Acta2^−/−), one model of an altered smooth muscle cell cytoskeleton (mdx), and one model of altered smooth muscle – matrix interaction (Sgcd^−/−), each relative to controls. For purposes of completeness, we also list comparable findings from four prior papers based on the four fiber family model (Table 3), one each for the Fbn1^mgR/mgR and Fbln5^−/− models, one on the two muscular dystrophy models, and one on Aortic Banding (i.e., a non-pharmacologically induced hypertension). Of particular note, four of the six models in Table 1 (Fbn1^mgR/mgR, Fbln5^−/−, Ang-II ApoE^−/−, and Acta2^−/−) have been used to study thoracic aortic disease, an area within vascular mechanics that has received far less attention than many others³⁵. Although carotid arteries share a common embryonic lineage with the ascending thoracic aorta and arch (i.e., neural crest derived cells³⁶), they tend not to experience the dilatation or dissection seen in the thoracic aorta when subject to the same genetic mutation. Clearly, there is a pressing need for biomechanical phenotyping of the thoracic aorta in each of these, and other, mouse models¹⁵, yet there is equal motivation to study vessels that do not typically succumb to disease^2,25. In other words, understanding why certain types of arteries do not become diseased while others do may help us to promote arterial health, not just to prevent or treat arterial disease. We thus focused on common carotid arteries in this study.

Table 3.

Similar to Table 2 except showing best-fit parameter values found in the literature for common carotid arteries from diverse mouse models. Note that some of these results were obtained using different objective functions (e_i), protocols, and testing solutions (see original papers for experimental details). Nevertheless, the parameter values tend to be of the same order of magnitude across models, and can be useful in biaxial simulations to recapitulate stresses given information on unloaded dimensions and in vivo pressures and axial stretch, which serves to emphasize the importance of reporting information sufficient to recreate the original results.

Reference	Genotype (Age)	Elastic Fibers c (kPa)	Axial Collagen		Circumferential Collagen + SMC		Symmetric Diagonal Collagen			Obj Fun
			c11 (kPa)	c21	c12 (kPa)	c22	c13,4 (kPa)	c23,4	α0(deg)
Gleason et al. (2008)	C57BL/6J (8–12wks)	21.582	25.028	0.029	12.502	0.137	0.038	1.439	41.4	e2
	mdx (8–12wks)	18.584	20.094	0.075	12.794	0.217	0.644	1.028	35.4
	Sgcd −/− (8–12wks)	17.290	26.838	0.035	12.093	0.167	0.338	0.916	34.8
Eberth et al. (2009)	Fbn1 +/+ (8–14wks)	8.309	2.247	0.791	4.135	0.547	0.577	0.909	35.4	e3
	Fbn1 mgR/+ (8–14wks)	8.024	3.032	0.358	1.514	0.185	2.263	0.484	32.6
	Fbn1 mgR/mgR (8–14wks)	1.018	7.706	0.300	4.069	0.356	1.510	1.185	33.0
Eberth et al. (2011)	C57BL/6J-129Sv (9–10wks)	16.140	0.940	0.690	6.180	0.110	0.372	0.184	43.9	e2
	C57BL/6J-129Sv (9–10wks + 7–10 days HT)	9.710	0.200	1.090	15.500	5.00 × 10–3	7.090	0.658	45.6
	C57BL/6J-129Sv (9–10wks + 10–14 days HT)	6.510	0.200	1.350	16.600	0.064	5.810	0.799	45.7
	C57BL/6J-129Sv (9–10wks + 35–56 days HT)	6.090	0.060	1.540	11.700	1.060	10.900	1.340	46.4
Wan et al. (2011)	Fbln5 +/+ (13 ± 1wks)	25.968	6.450	0.781	2.850	0.278	0.760	0.953	35.6	e1
	Fbln5 −/− (13 ± 5wks)	15.623	4.558	4.186	5.582	0.410	1.828	2.264	34.1

The microfibril fibrillin-1 appears to be important in preserving the long-term structural integrity of elastic fibers (i.e., the extreme half-life), hence rendering these fibers less susceptible to mechanical damage (fatigue) and chemical insult (premature proteolysis). Fbn1^mgR/mgR mice produce normal fibrillin-1 at ~15 to 25% normal levels⁴¹ and thus represent an important model of Marfan syndrome (other models being Fbn1^C1039G/+ and Fbn1^mgΔ/+ mice). Fbn1^mgR/mgR mice tend to die at 2 to 4 months of age from ruptured thoracic aortic aneurysms. The fibulins similarly associate with elastic fibers, although they appear to be involved more in elastogenesis⁵⁵. Whereas Fbln4^−/− and Fbln4^R/R mice also present with thoracic aortic aneurysms or dissections^22,28, Fbln5^−/− mice tend to present with stiff, tortuous arteries⁵⁴. Both fibulin-4 and fibulin-5 mutations have been associated with thoracic aneurysms in humans, however⁵¹.

Angiotensin-II (Ang-II) is a potent vasoconstrictor having pleiotropic activity. Local increases in Ang-II can lead to an increased intramural production of multiple cytokines and chemokines, which in turn can dramatically affect local matrix turnover within the arterial wall. In particular, Ang-II is frequently associated with hypertension, due both to local intramural and systemic renal-controlled changes. It is noteworthy that altered fibrillin-1 has been implicated in the dysregulation of the important cytokine transforming growth factor – beta (TGF-β), and Ang-II and TGF-β have partially overlapping signaling pathways in smooth muscle cells⁴³. Hence, there is motivation to compare results from Fbn1^mgR/mgR and Ang-II infused mice. Apolipoprotein E (ApoE) is an important ligand for receptor mediated removal of lipoproteins from plasma; lack of ApoE causes low density lipoproteins to accumulate within the arterial wall, thus contributing to atherosclerotic plaques²⁶. Although the angiotensin-II infused ApoE^−/− mouse was introduced to study effects of angiotensin on atherosclerosis, it is now one of the most common models of dissecting aortic aneurysms, which typically present in the suprarenal abdominal aorta and exhibit marked regional variations in properties¹⁸. In addition, however, aneurysms also form in the ascending thoracic aorta of the Ang-II ApoE^−/− mouse⁸. The carotids studied herein from Ang-II ApoE^−/− mice were free of atherosclerosis². The aortic arch banding model was introduced to study effects of increased afterload on the heart, but it is also a good model of a mechanically induced increase in common carotid artery pressure¹². Among its advantages, pulse pressure increases in the right common carotid artery without a significant increase in mean arterial pressure, and the left common carotid serves as a natural contralateral control. One limitation, however, is that blood pressure increases abruptly, then decreases slowly toward normal likely due to distal vascular remodeling.

Recent studies show that mutations in Acta2, the gene that codes smooth muscle α-actin, associate with familial thoracic aortic aneurysms and dissections as well as diverse phenotypes in other vessels⁴⁰. Smooth muscle α-actin is fundamental to vascular smooth muscle cell contractility and it is interesting that decreased contractility has been reported in fibrillin-1 deficient^5,11 and fibulin-5 null⁴⁹ mice. Muscular dystrophy is typically thought of as a disease of skeletal muscle, but genetic defects in components of the dystrophin-glycoprotein complex also affect vascular smooth muscle cells. This complex links the actin cytoskeleton to adjacent extracellular matrix and thereby contributes to the structural integrity of smooth muscle cells during contraction and relaxation. The mdx mouse is deficient in the cytoskeletal protein dystrophin whereas the sarcoglycan-δ null (Sgcd^−/−) mouse lacks a key transmembrane protein within the dystrophin-glycoprotein complex. There have been few studies of effects of muscular dystrophy on arterial mechanics¹⁰.

Despite not becoming aneurysmal, most of the common carotid arteries studied herein exhibited apparent geometric adaptations in response to the particular genetic mutation, pharmacologic intervention, or surgical procedure¹, including an altered in vivo outer diameter, thickness, or axial stretch (which may result from a biological lengthening of the vessel), each of which may affect biaxial wall stress and stiffness. Recalling Table 1, therefore, it is clear that consistent reporting of basic information on the mice (e.g., sex, age, body mass, and genotype), the unloaded geometry, and in vivo hemodynamic conditions, as well as in vitro computed intramural stress and material stiffness, is vital for comparing results across different mouse models. In particular, a question of interest is whether a certain artery adapts in response to perturbations in hemodynamic loading or whether compromised cell function leads to a maladaptation. Toward this end, many suggest that normal adaptive changes in arterial caliber and wall thickness tend to restore mean wall shear stress (τ_w = 4μQ /πa³, where μ is viscosity) and mean circumferential stress (σ_θ= Pa / h) toward homeostatic (i.e., original) values in response to sustained changes in volumetric blood flow Q and pressure P, respectively^7,30. If one parameterizes sustained changes in flow and pressure by the scalars ε and γ, respectively, then perturbed values can be written as Q=εQ^o and P=γ P^o, with (^o) denoting original values. It is then easy to show that restored wall shear and circumferential stress would require³¹

$$a={\epsilon }^{1/3}{a}^o,h={\epsilon }^{1/3}\gamma h^o,$$ (11)

and similarly for changes in cross-sectional area, πh(2a+h), which can also be compared with normal values. Taking the pooled control group as homeostatic, with loaded dimensions of a^o = 298 μm and h^o = 26 μm, computed systolic cross-sectional areas for the seven groups in Table 1 ranged from 0.74 (Sgcd^−/−) to 1.36 (Ang-II ApoE^−/−) that of homeostatic, thus indicating marked differences in the in vivo configuration due to either altered hemodynamics or a direct genotypic effect on wall structure (i.e., changes in extracellular matrix organization, smooth muscle cell contractility, or smooth muscle-matrix interactions). Such assessments may complement standard methods of quantification as we biomechanically phenotype arteries from diverse mouse models and seek to correlate changes in structure, function, and properties with specific changes in the mechanobiology of the endothelial cells, smooth muscle cells, and fibroblasts.

Unfortunately, with one exception, there was no information available on carotid flows for the data sets examined. For illustrative purposes, however, we estimated the change in flow rate that would have associated with a perfectly adaptive response for all of the models in Table 1 relative to control. Such a calculation suggested a range from a 36% decrease (Fbln5^−/−) to a 9% increase (Ang-II ApoE^−/−) in common carotid flow relative to normal, which if compared to actual values could provide insight into possible adaptive versus maladaptive changes. Clearly, these estimations reflect the measured values of inner radius at the in vivo state (with Fbln5^−/− and Ang-II ApoE^−/− having the smallest and largest values of a, respectively), noting that homeostatic values of wall shear stress are higher in mice than humans due in large part to the smaller inner radius²¹. Similar to the estimated changes in flow, we also estimated possible changes in pressure from normal based on the observed systolic geometries. For example, values for models in Table 1 implied from a 21% decrease (Sgcd^−/−) to a 48% increase (Fbln5^−/−), which corresponded to systolic pressures of 91 and 172 mmHg respectively. Comparing these geometry-based estimates of pressure with the adjusted measured systolic pressures in Table 1 revealed that the values corresponded well, in general (percent error < 15%). This finding suggests a possible normal, or adaptive, growth and remodeling in response to changes in either genotype or pharmacologic treatment for most of the cases studied, which is consistent with the report by Sather et al.⁴⁴ that arterial caliber was well adapted in an elastin haploinsufficient mouse model (Eln^+/−). A similar analysis of the Aortic Banding model revealed values of ε ranging from 0.83 (0 day) to 1.91 (10–14 day) and γ ranging from 0.94 (0 day) to 2.59 (35–56 day); the actual data suggest a value of ε ~ 2 at the 7–10 day period but only a maximum value of γ ~1.28 at 10–14 days¹².

Note, therefore, that two of the six mutant genotype (Acta2^−/− and Sgcd^−/−) and two of the Aortic Banding (10–14 and 35–56 day) data sets had greater than 15% differences in estimated systolic pressures relative to measured, thus suggesting a possible sub-optimal, or maladaptive, growth and remodeling response in these models with respect to wall shear stress and/or mean circumferential stress. It is interesting that these are the same four models that deviated the most from the other results in Figure 5 (denoted therein by a slash through the symbol). Of these four, the Acta2^−/− mice and 35–56 day Aortic Banding carotids exhibited markedly lower values of circumferential stress and stiffness relative to all other groups, including controls (Figure 5 and Table 1). Note, therefore, that the Acta2^−/− carotids were the only ones that were hypotensive (~81 mmHg) and the 35–56 day banding carotids were the only ones to have experienced an abrupt increase (from 120 to 154 mmHg at 7–14 days), then decrease (to 124 mmHg) in systolic blood pressure. In other words, it appears that “reverse” growth and remodeling (e.g., thinning of the wall) in response to decreases in pressure was much less adaptive than “positive” growth and remodeling in response to increases in blood pressure see, for example, previous results for Eln^+/− carotids⁴⁴ as well as the Fbn1^mgR/mgR, Fbln5^−/−, Ang-II ApoE^−/−, and Aortic Banding models at 7–10 and 10–14 days, all of which only experienced elevated pressures. That central arteries tend to adapt better, or quicker, to increases rather than decreases in pressure has been known since the important work of Wolinsky⁵³ and may have important implications regarding the clinical goal to reverse effects of established hypertension. Nevertheless, the potential utility of evaluating (mal)adaptive responses emphasizes the importance of measuring physiological flows and pressures (e.g., central pressure measurements in the absence of anesthesia) when determining vessel geometry or biaxial stresses at a given in vivo state. Because pulse wave velocity is both a convenient and informative clinical metric, it too should be measured (not estimated via Moens-Korteweg) as part of biomechanical phenotyping. That is, there is clearly a need for increased attention to in vivo ranges of arterial geometry and hemodynamics, not just wall stress and stiffness, across different mouse models as well as across species as we continue to seek to uncover fundamental mechanobiological mechanisms of wall growth and remodeling³⁰.

For purposes of further comparison, we also list in Table 3 the mean values of best-fit model parameters for equation 4 for common carotid arteries from other studies: the original analysis of the two models of muscular dystrophy considered herein (mdx and Sgcd^−/−)²⁰, the Fbn1^mgR/mgR model¹¹, the Aortic Banding model of hypertension¹³, and another study of the Fbln5^−/− mouse⁴⁹. Although based on different experimental protocols and objective functions, it can be useful to compare results in Tables 2 and 3 directly. One particularly interesting observation is that the ratio of $c_1^i/c_2^i$ in the axial direction (i = 1) switched from > 1 for the controls to < 1 for both the Fbln5^−/− carotids (Table 2) and the Aortic Banding carotids (Tables 2 and 3), which suggests a marked change in collagen engagement upon loading (cf. Figure 9 in reference 49). Indeed, the same switching was found in elastase-treated carotids wherein it was discovered that loss of (pre-stretched) elastic fibers can decrease the undulation of associated collagen fibers¹⁴. Again, however, given the different objective functions used in the different papers, it is better to re-create the biaxial data (cf. Figure 2) and to perform a consistent quantification and interpretation (cf. Table 2). As noted before, provided that sufficient information is available, such a procedure could increase access to “data” without the need to document entire experimental data sets for a given mouse model, which could prove invaluable in biomechanically phenotyping different genetic, pharmacological, and surgical mouse models.

Consistent data on arteries from control mice is fundamental to such phenotyping. Note, therefore, that we combined results from two different mouse models, Acta2^+/+ littermates and Fbn1^mgR/+ littermates, to create a larger control data set (n = 16; cf. Tables 1 and 2 and Figures 1 to 6). Carotids from Fbn1^mgR/+ mice were reported to be comparable mechanically to those of their Fbn1^+/+ littermates¹¹ and thus to serve well as control data. The closeness of our control data to the controls used in the Aortic Banding study (C57BL/6J × 129Sv) provides additional confidence in our choice (cf. Figure 5). Nevertheless, given that differences exist even amongst the many different wild-type controls²³, care will be needed when comparing results from different laboratories that use different strains as controls or backgrounds for mutants. For example, compare values of the best-fit parameters for the control Fbln5^+/+ mice in Table 3 with those for the overall controls in Table 2, which were determined using the same objective function. In addition, there is need for caution in the interpretation of results when nonlinear regressions are based on different types of data sets, ranges of pressures or loads used in the tests, or objective functions¹⁵. Herein, we used the objective function proposed by Wan et al.⁴⁹ because it provides a reasonable compromise between the need to fit P-d data at low, but especially high, pressures while capturing well the associated f –P and f –l data. Although there is a need for further work to fit better the low pressure data, the associated predictions of stress stretch behavior needed to quantify the material stiffness, especially in the physiologic range of loading, remain very good¹⁵. Hence, although we previously found that the neoHookean parameter c (motivated by the elastin-dominated amorphous matrix that dominates behavior at lower pressures) correlated well with the mass fraction of elastin in hypertension¹³ and the loss of elastic fiber integrity in the Fbn1^mgR/mgR mouse^11,14, this finding was not borne out exclusively herein (Table 2). Much work remains to identify better constitutive relations and improved methods for regression^4,50. Such a need is highlighted by the present finding that the best-fit value of c may have depended, in part, on the range of circumferential stretches experienced by the vessel note that fits to data for lower values of λ_ϑ (i.e., Acta2^−/− and Fbln5^−/−) tended to have higher values of c and to fit better at low pressures (not shown). Nevertheless, the four-fiber family model continues to yield useful fits and predictions for murine carotid arteries^11,14,20,49. Indeed, this model has been shown to provide a better fit to data than two- and six-fiber family models⁵⁶ and to provide the best fit to murine carotid data of six candidate relations that included four microstructurally based models⁵⁰. Finally, we have shown using a nonparametric bootstrap that the present method of parameter estimation yields robust fixed point estimates for this constitutive relation provided that the estimation is based on appropriate biaxial data¹⁵.

In summary, we demonstrated via direct comparisons to full data sets that properly recreated mean biaxial data are sufficient for consistent comparisons of arterial behaviors across diverse mouse models and we presented the first such comparison of the mechanical behavior of common carotid arteries from multiple mouse models. The former supports the approach of Roccabianca et al.⁴² in which human aortic properties were consistently compared based on data collected from diverse experimental protocols and characterizations in terms of different stored energy functions. The latter revealed, for example, that models of compromised elastic fibers exhibit dramatic reductions in both the in vivo axial stretch and elastic energy storage under systolic conditions (see Figure 6 wherein control carotids stored >40 kPa whereas the Fbln5^−/− and Fbn1^mgR/mgR carotids stored ~20–30 kPa, reminiscent of changes due to extreme hypertension achieved early in the aortic banding model). Lower energy storage suggests less ability to do work on the blood due to elastic recoil during diastole. Indeed, consistent with the qualitative suggestion of Yanagisawa et al.⁵⁴, the Fbln5^−/− mutation appears to result in a particularly severe biomechanical phenotype (i.e., elastopathy), including the most severe phenotype of the six mutant models that were compared herein versus controls. Finally, our findings also suggest, more generally, that biomechanical phenotyping should include a delineation of adaptive versus maladaptive changes in geometry relative to the in vivo hemodynamics, particularly when evaluating possible changes in values of in vivo biaxial stress and stretch, linearized stiffness, and energy storage. Indeed, perhaps the most important, and unexpected, finding was the remarkable consistency in the linearized circumferential stiffness of “adapted arteries” regardless of mouse model and the in vivo level of pressure. This finding may have important mechanobiological implications, perhaps suggesting that intramural cells seek to offset perturbations in hemodynamic loading via changes in structural stiffness while preserving a locally favorable mechanical environment defined by the material stiffness.

Appendix

Reported values of systolic blood pressure summarized in Table 1 were collected using different methods, with data for control, Ang-II ApoE^−/−, and Acta2^−/− mice measured using a noninvasive tail cuff method in the conscious mouse^3,24,45, data for the Fbn1^mgR/mgR and Fbln5^−/− mice measured via an indwelling polyethylene catheter in the conscious mouse^37,54, and data for the mdx and Sgcd^−/− mice measured under isoflurane anesthesia using a left ventricular catheter⁴⁷. To render more consistent the comparison of intramural stress, stiffness, and stored energy across mouse models, these pressures were adjusted to central arterial pressure in the conscious state using published correlations^34,52. Briefly, Whitesall and colleagues simultaneously measured pressure using direct (radiotelemetry) and indirect (noninvasive tail-cuff) methods and reported a linear relationship, P_TC = 0.961×P_C+ 4.203 mmHg, where P_TC and P_c are systolic pressures measured by tail-cuff and telemetry (or central pressure), respectively. Rearranging this equation, tail-cuff measured pressures (i.e., control, Ang-II ApoE^−/−, and Acta2^−/− mice) were adjusted to the conscious central pressure state. In contrast, Janssen and colleagues used an indwelling central artery catheter to evaluate effects of multiple anesthetics on the hemodynamics in mice. They found that isoflurane reduces the measured pressure by 24.3% relative to conscious ambulatory pressures. Hence, we adjusted pressures measured under isoflurane anesthesia (i.e., mdx and Sgcd^−/−) via P_A = 0.757×P_C, where P_A represents the anesthetized pressure. Table 1 thus lists both the value reported in the respective paper and the values adjusted herein.