Evaluation of Estimation Methods and Power of Tests of Discrete Covariates in Repeated Time-to-Event Parametric Models: Application to Gaucher Patients Treated by Imiglucerase

Abstract

Analysis of repeated time-to-event data is increasingly performed in pharmacometrics using parametric frailty models. The aims of this simulation study were (1) to assess estimation performance of Stochastic Approximation Expectation Maximization (SAEM) algorithm in MONOLIX, Adaptive Gaussian Quadrature (AGQ), and Laplace algorithm in PROC NLMIXED of SAS and (2) to evaluate properties of test of a dichotomous covariate on occurrence of events. The simulation setting is inspired from an analysis of occurrence of bone events after the initiation of treatment by imiglucerase in patients with Gaucher Disease (GD). We simulated repeated events with an exponential model and various dropout rates: no, low, or high. Several values of baseline hazard model, variability, number of subject, and effect of covariate were studied. For each scenario, 100 datasets were simulated for estimation performance and 500 for test performance. We evaluated estimation performance through relative bias and relative root mean square error (RRMSE). We studied properties of Wald and likelihood ratio test (LRT). We used these methods to analyze occurrence of bone events in patients with GD after starting an enzyme replacement therapy. SAEM with three chains and AGQ algorithms provided good estimates of parameters much better than SAEM with one chain and Laplace which often provided poor estimates. Despite a small number of repeated events, SAEM with three chains and AGQ gave small biases and RRMSE. Type I errors were closed to 5%, and power varied as expected for SAEM with three chains and AGQ. Probability of having at least one event under treatment was 19.1%.

INTRODUCTION

During evaluation of treatments, one clinical outcome can be the repeated occurrence of the same event. Traditional statistical analyses do not handle these repeated time-to-event (RTTE) data, and often only analysis of the first event is performed in various medical settings.

Nonlinear mixed effect models are the main statistical tool in pharmacometrics (1). RTTE models were first introduced in pharmacometrics by Cox et al. (2) using frailty models. Frailty models (3–6) handle heterogeneity at the individual level, with both fixed and random effect terms (7) and were recently described by Govindarajulu et al. in a tutorial (8). Frailty model are one possible extension to the Cox model (9). In the semi-parametric time-to-event frailty model, the baseline hazard function is unspecified, and the proportionality of the covariate effects on the hazard is assumed. In parametric frailty models, the baseline hazard function is defined as a parametric baseline hazard function. The advantage of a full parametric model is that the clinical trial simulation can be performed. Various methods of estimation for parametric frailty models exist: the likelihood estimation using the Newton–Raphson algorithm, the expectation–maximization (EM) algorithm (10), the penalized likelihood method (11–13), or Bayesian methods (14). Liu et al. (15) proposed a novel adaptive Gaussian quadrature (AGQ) which is implemented in PROC NLMIXED of SAS. Some R packages can also fit frailty model such as Survival, FrailtyPack, or Parfm, and the main disadvantage is their inability to provide standard errors for the estimate of the random effect variance. Algorithms implemented in R are penalized partial likelihood, maximum likelihood, EM with Markov Chain Monte Carlo (MCMC) algorithms, while in SAS are AGQ or EM algorithms.

Some of the software tools used for nonlinear mixed effect models in pharmacometrics can also be used for parametric frailty models, such as MONOLIX or NONMEM (16). MONOLIX was the first proposed software using Stochastic Approximation Expectation Maximization (SAEM) (17). It has been evaluated by simulation for discrete data (18) and count data (19), but not yet for RTTE data. NONMEM implements various algorithms, as the Laplace method and, more recently, SAEM, which can be used for RTTE data. In a previously published simulation study, Karlsson et al. (20) compared EM with importance sampling (IS), Laplace, and SAEM in NONMEM v7. They used an exponential baseline hazard model and a follow-up of 12 days for all patients so did not have any dropout. They found that EM with IS and SAEM are better than Laplace when there are few events; otherwise, they perform equally well. In that simulation, they evaluated parameter estimation but did not evaluate power of the tests to detect impact of discrete covariate in RTTE. In another work, Hirsch and Wienke (21) compared different softwares for gamma and log-normal frailty models and described advantages and limits of each. The different algorithms compared are penalized partial likelihood, EM, and MCMC in R or SAS softwares. In the present study, we evaluated two different software tools and three algorithms: MONOLIX with the algorithm SAEM, PROC NLMIXED with the AGQ, and Laplace algorithms.

Gaucher disease (GD) is a rare (1/100,000 births), autosomal recessive disease characterized by an enzymatic deficit of glucocerebrosidase (22). Clinical endpoints of this disease are bone events (BEs: avascular necrosis of an epiphysis, bone infarct, pathological and/or vertebral compression fracture), splenectomy, and neurological symptoms. The current treatment of Gaucher patients is an enzymatic replacement therapy (ERT) by imiglucerase. Several biomarkers (chitotriosidase, ferritin, angiotensin-converting enzyme, and tartrate-resistant acid phosphatase) are elevated during GD evolution. Their concentrations rise with disease progression and decrease during ERT (23). One main clinical endpoint for evaluation of treatment should be the reduction of repeated occurrence of BE. This needs long-term follow-up data after treatment initiation and a large number of patients. We created the French GD Registry (FGDR) in 2009; it is a complete registry of the disease with long-term follow-up. We have already studied the occurrence of the first BE after ERT initiation and the effect of several covariates. Splenectomy and having a BE before ERT were the two significant covariates found with the traditional log-rank test (24). Here we are interested in the effect of treatment on the occurrence of repeated BEs.

The first objective of the present work was to assess by simulation the estimation performance of the SAEM algorithm in MONOLIX and AGQ and Laplace algorithms in PROC NLMIXED of SAS by simulation with a variation in dropout rate, the number of subjects, and the variability. We also evaluated the power to detect tests of the impact of a binary covariate on the occurrence of events. The second objective was to apply those algorithms to evaluate the occurrence of repeated BE after treatment initiation by imiglucerase in patients from the FGDR.

MODELS AND NOTATIONS

For the ith (i = 1,…, N) patient, let T_ij be the time of the jth (j = 1,…, n_i − 1) event. 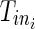is the right censoring time, 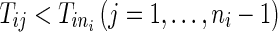, and we defined the censoring indicators as . The hazard function can be expressed with the following frailty model:

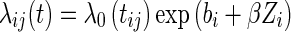where λ₀(t_ij) is the baseline hazard function, Z_i the covariate vectors associated with the vector of regression β, and b_i is the individual random effect, which is assumed to follow a normal distribution with mean 0 and variance equal to ω². Under the parametric approach, the baseline hazard is defined as a parametric function. A common model considered in the literature is the Weibull distribution, λ₀(t_ij) = λαt^α−1, which reduces to an exponential distribution when α = 1.

The vector of parameter-estimated θ is composed of the fixed effects and the variance of the random effects. The log-likelihood for this model is

where p(b_i) is the probability density function of b_i, a normal distribution with mean 0 and variance ω². Because this expression has no closed form, several specific algorithms as described in the Introduction were developed to perform maximum likelihood estimation. To test the impact of covariate, we can use the Wald test, defined by

where is the estimator of the vector of parameter β, and is the estimation variance matrix for the vector of parameter β. The statistic W² is compared with the critical value of a χ² with p degree of freedom where p is the dimension of the vector of parameter β. We can also use the Likelihood Ratio Test (LRT). We estimated the log-likelihood in the model without covariate (i.e., β = 0), L_base, and with covariate (i.e., β estimated), L_cov. The test statistic

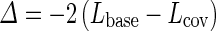is compared with the critical value of a χ² with p degree of freedom.

SIMULATION STUDY

Evaluation of Estimation Performance

The standard simulation scenario was composed of N = 200 patients, an exponential baseline hazard function λ = 2 × 10⁻³ month⁻¹, a standard deviation (sd) of random effect ω = 1 and no covariate. We chose an exponential distribution (10,20,25), a rather simple model, as it is the first evaluation of MONOLIX on RTTE. This choice was based on the real data where events correspond to BEs, with a risk that does not increases over time of study. Furthermore, in these data, Weibull distribution was not significantly better than exponential distribution (e.g., see Results on real data).

The study design observed a maximum follow-up time of 144 months. We defined three levels of dropout, with no dropout corresponding to the end of follow-up. The time of censoring was simulated from an exponential model of parameter γ, with γ = 5 × 10⁻³ month⁻¹, for low dropout, and γ = 1 × 10⁻² month⁻¹, for high dropout.

We varied the number of patients, N = 100, 200, or 400; the value of the hazard function, λ = 2 × 10⁻³ or 4 × 10⁻³; and the sd of the random effect, ω = 0.5, 1, or 2. The variation of λ and ω was only performed for the high dropout condition. K = 100 datasets were simulated in each case. λ and ω were estimated by maximum likelihood in each dataset for each algorithm (SAEM, AGQ, and Laplace) for each scenario.

To assess the statistical properties of an estimator, we computed the relative estimation error on each dataset k, REE_k, as follows:

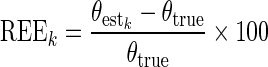where is the estimated parameter value in the kth (k = 1,…, K) dataset, and θ_true is the true parameter value used in the simulation. Each REE_k was expressed in percent. We plotted the box plot of the REE_k with the 10% and 90% percentiles. Then, we computed the relative bias (RB) and the relative root mean square error (RRMSE) values from the REE_k as follows:

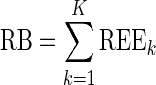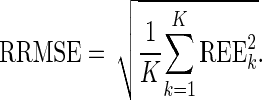Evaluation of Test Performance

We evaluated the power of the test to detect the impact of a dichotomous covariate on the occurrence of events. The standard scenario was defined as before, N = 200 patients, an exponential baseline hazard function λ = 2 × 10⁻³ month⁻¹, and a sd of random effect ω = 1. We defined a dichotomous covariate, Z = 0 in group A and Z = 1 in group B, with 100 patients in each group. We varied the value of the effect of the covariate, exp(β) = 1 (no effect), 1.5, 2, or 3 and the variability of the random effect ω = 1 or 2. K = 500 datasets were simulated in each scenario. We performed two tests: Wald test and LRT. For the Wald test, in the model with covariates, we estimated β and its standard error (se). For the LRT, we estimated the log-likelihood in the model with covariate and in the model without covariate (i.e., β = 0). We computed the number of significant datasets (p value < 0.05). For each estimation method (SAEM and AGQ), each scenario and each test, we estimated the type I error for the simulations under H₀, i.e., exp(β) = 1, and the power for the simulations under H₁, i.e., exp(β) = 1.5, 2, or 3.

To evaluate the gain in studying all the events, we also tested the impact of the covariate on the occurrence of the first event in one hand by a log-rank test and in the other hand by a Wald test and LRT using a standard exponential model.

Software and Algorithms

We estimated the parameter vector θ with MONOLIX and PROC NLMIXED of SAS. The algorithms used are SAEM with one and three chains in MONOLIX, AGQ, and Laplace in PROC NLMIXED. The SAEM algorithm (17,26) belongs to the standard EM algorithm which are characterized by exact likelihood maximization. In the E step, the expectation of the log-likelihood is calculated, and in the M step, new parameters maximizing the likelihood are computed given the likelihood expected in E step. The processus is iterative until a stable parameter value is obtained. In SAEM, the E step is divided into (1) a simulation of individual parameters using a MCMC algorithm, (2) followed by a stochastic approximation of the expected likelihood. In the general case, AGQ is a numerical approximation to the integral over the whole support of the likelihood using Q quadrature points. Laplace (27,28) technique is the simplest AGQ procedure based on the evaluation of the function in one well-chosen quadrature point per random effect. The SE is estimated by a stochastic approach in MONOLIX and is computed from the final Hessian matrix in PROC NLMIXED. Log-likelihood is estimated using importance sampling integration method in MONOLIX and AGQ in PROC NLMIXED. Optimization technique use in PROC NLMIXED is Newton–Raphson algorithm. The analysis of the first event by an exponential model was performed with PROC LIFEREG of SAS and the log-rank test by the PROC LIFETEST of SAS. The estimations were performed using MONOLIX v.4.0, and SAS v.9.3 (SAS Institute, Cary, NC). The specifications of starting values for parameters are the true value used for simulation. Estimation algorithms were utilized with the default settings in the two software tools. Changes from these defaults are listed below. In MONOLIX, standard errors were calculated by stochastic approximation; to estimate the population parameters, we did not use initial simulated annealing; the number of chains was specified as one or three chains, respectively. In SAS, the numbers of quadrature points were specified as 1 or 5 for Laplace and AGQ algorithm, respectively.

The datasets were simulated with R v.2.13 (29).

Results

Figure 1 shows a spaghetti plot of one simulated dataset for the standard scenario with no, low or high dropout. The number of events per patient is small, even the case for no dropout. Figure 1 shows that the probability of having at least one event at 10 years is 27.5% for no and low dropout and 28.6% for high dropout. For low or high dropout, few patients have repeated events (Table I). Twenty-one percent of patients have one event for no dropout and around 15% for low and high dropout. Only 9% of patients have more than one event for no dropout, 7% for low dropout, and 5% for high dropout.

Fig. 1.

Top: Spaghetti plot of the number of events versus time for no (left), low (middle), and high (right) dropout for one simulated dataset of the standard scenario. Circle corresponds to event and plus sign to censure; data of a patient are connected by step functions. Bottom: Kaplan–Meier estimate of the cumulative distribution function for the first event for no (left), low (middle), and high (right) dropout for one simulated dataset of the standard scenario. The dashed lines correspond to 95% pointwise confidence intervals

Table I.

Percent of Patients with No, One, or More than One Event for the Three Levels of Dropout in the Simulation Study for the Standard Scenario (λ = 2 × 10⁻³ and ω = 1)

% of patients	0 event	1 event	More than 1 event
No	70	21	9
Low	77	16	7
High	82	13	5

For the standard scenario, box plots of REE are plotted for λ and ω in Fig. 2, while RB and RRMSE are given in Table II for the three levels of dropout and for different values of the number of subjects. REE were greater for Laplace, mostly negative for λ and positive for ω. RB and RRMSE were greater for Laplace algorithm, with parameters poorly estimated and a systematic bias, even with 400 patients. SAEM with one Markov chain gave also large REE, especially for ω. RB and RRMSE were greater than SAEM with three Markov chains. Because SAEM with one chain and Laplace algorithm had poor estimation properties in the following, we considered only SAEM with three chains and AGQ algorithm with five quadrature points.

Fig. 2.

Box plot of the relative errors (in percent) for three levels of dropout with λ = 2 × 10⁻³ (for λ (left) and ω (right)) and ω = 1 and for various values of the number of patients (N = 100, 200, and 400) for SAEM with one Markov chain (black), SAEM with three Markov chains (white), AGQ (light gray), and Laplace (dark gray)

Table II.

Relative Bias (RB) and Relative Root Mean Square Error (RRMSE) (in Percent) for the Three Levels of Dropout with λ = 2 × 10⁻³ and ω = 1 and for Various Values of the Number of Patients (N = 100, 200, and 400) for SAEM with One and Three Markov Chains, AGQ, and Laplace (LAP) Algorithms

			100				200				400
Parameter	Dropout	N	SAEM 1 chain	SAEM 3 chains	AGQ	LAP	SAEM 1 chain	SAEM 3 chains	AGQ	LAP	SAEM 1 chain	SAEM 3 chains	AGQ	LAP
λ	No	RB	−2.5	18.9	−31.3	−32.2	7.5	1.8	1.6	−31.4	17.5	1.1	1.5	−29.9
		RRMSE	24.3	36.4	33.9	35.2	16.0	20.0	19.9	32.8	20.4	12.7	12.9	30.7
	Low	RB	−11.5	12.8	−0.5	−13.8	5.8	−0.008	1.9	−10.9	18.9	1.8	1.0	−11.3
		RRMSE	26.6	34.6	30.6	35.0	19.3	23.1	23.3	26.0	22.6	16.1	15.6	19.4
	High	RB	−22.9	11.0	−1.2	−19.7	0.4	−1.3	1.5	−17.0	18.5	3.4	1.4	−16.5
		RRMSE	35.0	40.0	39.1	45.9	22.3	27.5	27.1	32.8	23.5	20.6	19.4	25.5
ω	No	RB	−43.0	−22.9	−94.1	−91.3	−52.4	−5.1	−3.6	−94.2	−69.6	−2.1	−2.4	−96.4
		RRMSE	46.2	35.6	96.3	95.5	53.1	22.1	18.5	96.6	70.1	11.6	11.8	97.7
	Low	RB	−30.7	−21.1	−4.4	16.4	−46.2	−3.4	−2.5	15.5	−64.4	−1.4	−1.1	−15.2
		RRMSE	35.6	41.1	35.8	42.6	47.4	27.0	21.3	26.9	65.5	14.6	14.2	20.9
	High	RB	−18.6	−27.1	−9.0	26.1	−40.4	−9.0	−5.9	22.0	−58.8	−3.3	−2.1	22.6
		RRMSE	31.6	49.0	44.8	65.9	42.7	37.3	30.0	39.8	60.7	22.0	21.4	32.0

Results are very close between SAEM with three chains and AGQ, and both algorithms provide good estimates of the parameters λ and ω. For SAEM with three chains and AGQ, RB on λ is low (−2% to 2%), and RB on ω is slightly negative (−9% to −2%); they decrease when N increases for SAEM and AGQ. RRMSE are reasonable and decrease as N increases (<30% with 200 patients and <22% with 400) for SAEM with three chains and AGQ. When N = 100 patients, bias appears in the estimates of λ and ω (Fig. 2). Table III presents REE, RB, and RRMSE for the scenario for high dropout and different values of λ and ω. SAEM with three chains and AGQ provide good estimates of the parameters. When λ increases, RRMSE decrease, and when ω increases, its RRMSE decreases. When ω is small, there is bias in the estimates of both parameters, especially ω.

Table III.

Relative Bias (RB) and Relative Mean Square Error (RRMSE) (in Percent) for High Dropout and N = 200, for Various Values of λ (2 × 10⁻³ and 4 × 10⁻³) and ω (0.5, 1, and 2) for SAEM with Three Chains and AGQ Algorithms

Parameter	λ	ω	0.5		1		2
			SAEM 3 chains	AGQ	SAEM 3 chains	AGQ	SAEM 3 chains	AGQ
λ	2 × 10−3	RB	−9.8	−0.9	−1.3	1.5	1.5	7.0
		RRMSE	19.9	19.9	27.5	27.1	32.4	31.4
	4 × 10−3	RB	−5.2	−0.3	2.2	2.7	7.3	10.1
		RRMSE	16.0	17.0	19.9	20.0	28.2	27.5
ω	2 × 10−3	RB	−51.3	−33.8	−9.1	−5.9	0.1	−3.9
		RRMSE	69.6	74.8	37.3	30.0	12.4	11.1
	4 × 10−3	RB	−32.7	−15.0	−4.2	−3.8	−3.1	−4.5
		RRMSE	62.0	56.2	22.3	19.5	13.3	9.7

We then evaluated the properties of the test for the SAEM with three chains and AGQ algorithm. Figure 3 shows a spaghetti plot for one dataset of the standard scenario, exp(β) = 1 for group A and exp(β) = 2 for group B with high dropout. As expected, there are more events in group B than in group A. In group B, 18% have at least one event and 11% more than one event, compared with 13% and 5% in group A, respectively. Figure 3 shows that the probability of having at least one event at 10 years is higher in group B, 51.6%, than in group A, 24.9%.

Fig. 3.

Top: Spaghetti plot of the number of events versus time for high dropout for one simulated dataset of the standard scenario for groups A and B. Circle corresponds to event and plus sign to censure; data of a patient are connected by step functions. Bottom: Kaplan–Meier estimate of the cumulative distribution function for the first event for high dropout for one simulated dataset of the standard scenario. The dashed lines correspond to 95% pointwise confidence intervals

Figure 4 shows the type I error and the power for the standard scenario and different values of ω and β. The tests have adequate properties for both SAEM with three chains and AGQ; the Wald test and the LRT perform equally well. Type I errors are close to 5%. Powers vary as expected—increasing when β increases and decreasing when ω increases. Figure 5 shows the power of detection of the impact of a covariate using only the first event. Analysis of all the events is more powerful than the log-rank test on the first event.

Fig. 4.

Type I error and power of the Wald test (plus sign) and LRT (asterisk) for the three levels of dropout (the dotted lines indicate no dropout, the dashed lines low dropout, and the solid lines high dropout) for ω = 1 (top) and ω = 2 (bottom) and for SAEM with three Markov chains (left) and AGQ (right). The hatched region represent the 95% prediction interval for the 5% type I error

Fig. 5.

Type I error for the first event and power of the Wald test (plus sign), LRT (asterisk) and log-rank (circle) for the three levels of dropout (the dotted lines indicate no dropout, the dashed lines low dropout, and the solid lines high dropout) for ω = 1 (top) and ω = 2 (bottom). The hatched region represent the 95% prediction interval for the 5% type I error

APPLICATION TO TREATMENT OF GAUCHER PATIENTS

Material and Methods

We used frailty model to analyze data from the FGDR (24). More precisely, we studied the occurrence of repeated BEs in Gaucher patients, since the initiation of treatment (time = 0) by imiglucerase monotherapy. Data were censored at the end of therapy, if it was interrupted for more than 6 months or at the closing date. Several patients presenting repeated BEs, a frailty model with an exponential, or a Weibull distribution were tested.

We estimated the parameters λ, α, and ω. We compared the two distributions, exponential and Weibull, with the Wald test and the LRT, i.e., α = 1 or not. Then, we evaluated, separately, the impact of two covariates on the occurrence of the BEs—the presence of at least one BE before the initiation of treatment and splenectomy as found in the analysis of the first event (24). We next used a multivariate model with backward selection. We estimated exp(β), its standard error, and the p value by the Wald test and the LRT for each covariate. Considering the results of simulation study, data were analyzed using SAEM with three chains and AGQ algorithm.

Results

Among the 185 GD patients treated with imiglucerase, the median (range) follow-up was 6 years (0–13). Figure 6 shows the spaghetti plot of BEs of the treated patients in FGDR as a function of time. Twenty-six patients had BEs with a total number of 36 BEs and a maximum of 4 BEs in one patient. Fifty percent of the patients were females. The median age at first symptoms was 18 years (0–61), and the median age at diagnosis was 23 years (0–67). The median age at initiation of treatment was 37 years (1–76). Figure 6 shows that the probability of having at least one event at 10 years is 19.1%.

Fig. 6.

Top: Spaghetti plot of the number of bone events as a function of time since the initiation of treatment for treated patients in French Gaucher Disease Registry. Circle corresponds to event and plus sign to censure; data of a patient are connected by step functions. Bottom: Kaplan–Meier estimate (black) of the cumulative distribution function for the first event for treated patients in French Gaucher Disease Registry and model prediction of cumulative distribution function by SAEM with three Markov chains with exponential distribution (gray solid lines) and Weibull distribution (gray dashed lines). The black dashed lines correspond to 95% pointwise confidence intervals for the Kaplan–Meier estimate

Table IV shows the values of the estimated parameters for SAEM with three chains and AGQ algorithm and for exponential and Weibull distribution. The results were close for the two algorithms, λ = 1.4 × 10⁻³ (se = 0.5 × 10⁻³)  month⁻¹ and ω = 1.1 (se = 1.1). For both estimation methods, LRT showed that Weibull distribution is not significantly better than exponential distribution. We obtained the same conclusion with the Wald test, and parameter α was not significantly different from 1 (Table IV). Figure 6 shows the Kaplan–Meier estimate of the cumulative distribution function for the first event and the estimate predicted by exponential and Weibull distribution with SAEM algorithm with three chains. Model prediction by SAEM with three chains is close to the Kaplan–Meier curve, in the 95% confidence intervals.

Table IV.

Estimation of the Model Parameters for Bone Events of Treated Patients in French Gaucher Disease Registry for Model Without and with the Covariate, Bone Events Before Treatment and for Two Types of Distribution, and Weibull and Exponential for SAEM with Three Chains and AGQ Algorithms

Model	Covariate	Parameter	SAEM 3 chains	AGQ
Weibull	No	λ month−1 (se)	4.9 × 10−4 (4.8 × 10−4)	5.1 × 10−4 (4.8 × 10−4)
		α (se)	1.2 (0.2)	1.3 (0.3)
		ω (se)	0.9 (0.3)	0.3 (0.2)
		−2 log L	540.9	509.9
Exponential	No	λ month−1 (se)	1.5 × 10−3 (0.6 × 10−3)	1.2 × 10−3 (0.5 × 10−3)
		ω (se)	1.2 (0.2)	1.2 (0.3)
		−2 log L	542.3	512.6
Exponential	Yes	λ month−1 (se)	1.1 × 10−3 (0.3 × 10−3)	1.0 × 10−3 (0.4 × 10−3)
		β (se)	1.1 (0.4)	1.1 (0.4)
		ω (se)	0.9 (0.3)	1.0 (0.3)
		−2 log L	536.1	486.4

The two covariates tested were the presence of BEs before the initiation of treatment and a splenectomy before treatment. As the exponential distribution are adequately fitted the data, the covariates are tested on this model. Among the 185 patients, 48 had BEs before treatment, and 44 had splenectomy before treatment. The two covariates were significant in the univariate model with the LRT. The result obtained, with SAEM with three chains, for BEs before treatment is exp(β) = 3 (se = 1.2), p = 0.01, and that for splenectomy is exp(β) = 1.9 (se = 0.6), p = 0.02. In the multivariate analysis, the BE occurrence before treatment was the only risk factor, and final estimates are given in Table IV. The risk of events was increased three-fold during treatment in patients who already had an event before treatment.

DISCUSSION

We can conclude from this simulation study that SAEM algorithm with three Markov chains (in MONOLIX) and AGQ algorithm with five quadrature points (in PROC NLMIXED of SAS) give rather similar results in the different scenarios evaluated. The Laplace method gives worse results and, in some scenarios, had very poor estimation properties similar to the results obtained by Karlsson et al. (20) in NONMEM. Similarly, SAEM with one Markov chain gave poor results. Therefore, we did not use the SAEM with one chain nor Laplace method for the evaluation test performance and the analysis of real data. This is the first simulation study with MONOLIX (SAEM) for parameters estimation in RTTE models. The performance estimations are good with unbiased estimates, despite the small number of repeated events in the simulation. Some problems occurred with SAEM and AGQ algorithm when there is a small number of subjects or a small variability.

When the number of subjects increases, the precision of estimation increases. The increased proportion of censored patients is the driving force of events. When higher dropout rate is simulated, fewer events are observed. As expected, RRMSE increases when dropout increases. Datasets with N = 400 patients and high dropout rate, or with N = 200 patients and no dropout, lead to the same event rate, 21% of patients with at least one event. These two cases gave similar estimation performance (Table II).

The Wald test and the LRT have adequate properties and give similar results for the test of a binary covariate. Notably, the type I error of 5% is correct. We also performed an additional simulation to evaluate the power of Wald test for dataset with 400 patients and high dropout rate with SAEM with three Markov chains. We found a power of 31.4% very close to the power of 31.2% (Fig. 4) found with 200 patients and no dropout. Those results clearly illustrate that high dropout leads also to loss of power and decreased estimation performance as expected. For the assessment of the first event with a parametric model, the results are close to those for all the events due to the small number of patients with more than one event. The power with the good parametric model for the first event is greater than the power of the log-rank test for the first event.

The runtime with this model was fast with both software programs, MONOLIX and SAS. Laplace algorithm (i.e., AGQ with one quadrature point) or AGQ with three quadrature points did not give adequate results, and five points were needed. Alike, SAEM with three Markov chains was needed.

In the analysis of BEs in Gaucher patients after the treatment initiation by imiglucerase in the FGDR, the two methods SAEM and AGQ gave similar results. Our results confirmed that a BE before ERT increases the risk of a BE during ERT (24). For the next step, we should analyze the complete follow-up of patients, taking into account the initiation of ERT as a time-dependent covariate to test the impact of ERT on the change in BEs occurrence.

We performed the simulation with the simplest exponential distribution, but further analysis should be performed with a more complex one, like the Weibull distribution with more parameters or, also, other parametrisations. On the real data, Weibull distribution was not better than exponential distribution, and using the other usual parametrisation gave similar results (not shown). Further evaluations of models with covariates are also needed. First, the evaluation of a binary covariate that changes over time should be performed. Then, we should also study the impact of a continuous covariate changing or not over time (30).

This study shows that SAEM with three Markov chains in MONOLIX and AGQ in PROC NLMIXED are good estimation methods for analysis of RTTE with parametric frailty models and give similar results. However, SAEM with one Markov chain in MONOLIX and Laplace method is often biased and should not be used.