A Priori Prediction of Tumor Payload Concentrations: Preclinical Case Study with an Auristatin-Based Anti-5T4 Antibody-Drug Conjugate

Abstract

The objectives of this investigation were as follows: (a) to validate a mechanism-based pharmacokinetic (PK) model of ADC for its ability to a priori predict tumor concentrations of ADC and released payload, using anti-5T4 ADC A1mcMMAF, and (b) to analyze the PK model to find out main pathways and parameters model outputs are most sensitive to. Experiential data containing biomeasures, and plasma and tumor concentrations of ADC and payload, following A1mcMMAF administration in two different xenografts, were used to build and validate the model. The model performed reasonably well in terms of a priori predicting tumor exposure of total antibody, ADC, and released payload, and the exposure of released payload in plasma. Model predictions were within two fold of the observed exposures. Pathway analysis and local sensitivity analysis were conducted to investigate main pathways and set of parameters the model outputs are most sensitive to. It was discovered that payload dissociation from ADC and tumor size were important determinants of plasma and tumor payload exposure. It was also found that the sensitivity of the model output to certain parameters is dose-dependent, suggesting caution before generalizing the results from the sensitivity analysis. Model analysis also revealed the importance of understanding and quantifying the processes responsible for ADC and payload disposition within tumor cell, as tumor concentrations were sensitive to these parameters. Proposed ADC PK model provides a useful tool for a priori predicting tumor payload concentrations of novel ADCs preclinically, and possibly translating them to the clinic.

Electronic supplementary material

The online version of this article (doi:10.1208/s12248-014-9576-9) contains supplementary material, which is available to authorized users.

INTRODUCTION

Defining the exposure–response relationship is at the heart of any drug development process. The accuracy and translatability of this relationship depends on the endpoints chosen to represent the exposure and the pharmacological response. Usually, the concentration of drug in the plasma/blood is the preferred exposure endpoint to correlate with efficacy or toxicity. Mainly because it is an easily accessible biological sample, which in many cases very well represents the drug concentration at the site of action (i.e., biophase). However, in many instances, drug concentration in plasma/blood does not represent drug concentration at the site of action (e.g., solid tumor), necessitating either direct measurement of the drug concentration at the site of action or prediction/derivation of the concentration using certain methodology. Mechanism-based pharmacokinetic (PK) models represent one such methodology that can be used to characterize and predict concentration of drug at the site of action, based on the plasma/blood concentration of the drug (1). This manuscript investigates application of one such PK model developed for Antibody–Drug Conjugate (ADC; 2), in terms of its ability to predict the concentrations of drug in animal tumors based on the plasma concentrations.

ADCs are a novel class of targeted chemotherapeutic agents, which consist of a monoclonal antibody (mAb) conjugated to one or more very potent drug molecules (payload) using a chemical linker. Once outside the antigen expressing cell (e.g., cancer cell), the ADC binds to the targeted receptor via mAb and internalizes. Once internalized, depending on the chemical property of the linker, the payload either leaves the mAb during the endolysosomal process or gets liberated in the lysosome following digestion of ADC. Once released, the payload diffuses within the cell and reaches the site of action (e.g., microtubules, DNA), where it elicits the pharmacology. There are more than 30 ADCs currently in the clinical development for the treatment of various malignant disease (3). We are developing a novel ADC that targets 5T4, an oncofetal antigen expressed on tumor initiating cells (TIC), which comprise the most aggressive cell population in the tumor (4). The anti-5T4 ADC is termed A1mcMMAF and comprises the humanized anti-5T4 antibody (A1) linked to the potent microtubule-disrupting agent monomethylauristatin F (MMAF) via a noncleavable maleimidocaproyl (mc) linker. A1mcMMAF has been shown to be highly potent in a variety of tumor models and did not cause any overt toxicity in nonhuman primates at comparable exposures (4). As such, A1mcMMAF is a promising clinical candidate that targets TICs, with the goal of providing long-term therapeutic benefit to patients with cancer.

In order to facilitate the preclinical-to-clinical translation and clinically efficacious dose prediction of A1mcMMAF, it is important to establish the exposure–response relationship for the ADC. However, because the plasma concentration of released payload is significantly lower than tumor concentration (5), plasma concentrations cannot be used as a surrogate for the payload concentration at the site of action. Consequently, it becomes necessary to find out the tumor concentration of released payload (cys-mcMMAF) following ADC administration, as this concentration is responsible for eliciting the pharmacological action. Tumor payload concentrations can either be measured directly or can be predicted based on the plasma ADC concentrations using a PK model. And, since the tumor distribution studies are costly, time-consuming, and not always feasible, we have developed a mechanism-based multi-scale PK model for ADCs that can help predict the tumor concentration of payload based on plasma ADC concentrations (2). Here, we have presented an investigation where we have evaluated the validity of using the ADC PK model for prediction of tumor payload concentration, using two different human tumor xenograft models, i.e., H1975 (non-small cell lung cancer) and MDA-MB-361/DYT2 (breast cancer). We have also presented a systematic investigation of the ADC PK model to better understand the underlying processes responsible for the disposition of ADCs.

MATERIALS AND METHODS

Preparation of A1mcMMAF

Detailed procedure for the synthesis of ADC is presented elsewhere (4). Briefly, mAb was pretreated with 3 equivalents of tris(2-carboxyethyl)phosphine (TCEP) to liberate the thiol residues, and this partially reduced material was exposed to approximately 6 equivalents of maleimidocaproyl-MMAF (mcMMAF). Isolation and purification were accomplished by size exclusion chromatography, and the material was characterized by hydrophobic-interaction chromatography and mass spectrometric analysis under denaturing and non-denaturing conditions.

Cancer Cell Lines

Cancer cell lines were chosen that expressed 5T4 and exhibited reproducible growth curves as tumor xenografts. MDA-MB-361/DYT2 cells were obtained from Dr. D. Yang (Georgetown University, Washington, D.C.), and H1975 cell line was obtained from the American Type Culture Collection (ATCC). Each cell line was cultured in its standard medium as recommended by ATCC, and no further cell line authentication was conducted. MDA-MB-435/5T4 cell line was generated from the control MDA-MB-435/neo cell line after stable transfection of 5T4, as described in (6).

Affinity and Internalization of A1mcMMAF

Detailed protocols to determine the affinity of mAb A1 towards 5T4 antigen and internalization rate of surface bound mAb in 5T4 expressing cell is presented in the supplementary material of (4). Briefly, Biacore® analysis was performed to determine the binding constants between A1 and 5T4 at pH 7.4. The 5T4 proteins used for this analysis consisted of the human 5T4 ectodomain fused to the human IgG1-Fc domain, which was immobilized onto a CM5 chip to measure affinity constants. Various concentrations of the A1 antibody were injected over the surface to generate various binding responses, and the surface was regenerated two times between each injection cycle.

Internalization of surface bound mAb was defined by the loss over time of surface signal, and measured in plate format. 5T4 expressing cells (MDA-MB-435/5T4) seeded in 96-well plates were incubated on ice with 1 μg/mL primary antibody, followed by washes and incubation at 37°C for 0, 1, 4, or 21 h. Cells were then incubated with peroxidase-conjugated Affinity Pure Goat Anti-Human IgG Fc (Jackson ImmunoResearch Labs #109-035-008), washed, and exposed to substrate, Lumiglo (Kirkegard & Perry Labs #54-61-01). Antibody internalization at each time point was expressed as ratio of average relative fluorescence compared to the zero time point.

5T4 Receptor Numbers on Cancer Cells

Antibody binding capacity as a measure of receptor numbers/cell was determined for H1975 cell line using 5T4 antibody clone A3 that binds to the same epitope as the A1 antibody with similar affinity, which was conjugated at 1:1 ratio to phycoerythrin (PE) by flow cytometry. Cells were incubated with increasing concentrations of A3-PE at 4°C for 1 h, and after removal of unbound probe, MFI from the live cells was measured by Flow cytometry using a BD Canto II cytometer. The maximum specific binding was determined by nonlinear regression and converted to binding capacity per cell using a QuantiBRITE bead standard curve generated under the same acquisition conditions as the samples (7). Saturation binding at a single high concentration of 20 μg/mL was used to determine the antibody binding capacity of the MDA-MB-361/DYT2 cells.

Development of Mouse Xenograft

All procedures using mice were approved by the Pfizer Institutional Animal Care and Use Committees according to established guidelines. Athymic female nu/nu mice or SHO mice (6–8 weeks) were obtained from Charles River Laboratories, Wilmington, MA or Taconic, Oxnard, CA. Mice were injected subcutaneously with tumor cells (10 million MDA-MB-361D/YT2 breast cancer tumor cells in 50% matrigel, 8 million H1975 tumor cells, and 7 million MDA-MB-435/5T4 tumor cells), and when animals reached certain pre-determined tumor volume they were randomly divided into different groups to conduct the PK or bio-distribution studies. Tumor size was calculated as: mm3 = 0.5 × (tumor width²) × (tumor length).

A1mcMMAF Mouse PK Study

Single 1 and 10 mg/kg intravenous dose of A1mcMMAF was administered into MDA-MB-435/5T4 tumor (∼300 mm3, +++ expression) bearing or non-tumor bearing mouse (n = 5), and 10 μL mouse blood was collected serially from mice for up to 336 h. Plasma concentrations of total mAb and ADC were quantified using ELISA assay from individual samples, and LC-MS/MS analysis was performed to quantify the released cys-mcMMAF concentration from pooled plasma samples.

A1mcMMAF Tumor Disposition Experiment

For the tumor distribution study, female nu/nu mice (n = 21) inoculated with MDA-MB-361/DYT2 cells (tumor grown to ∼400–500 mg) and female nu/nu mice (n = 21) inoculated with H1975 cells (tumor grown to ∼400–500 mg) were used. Tumor bearing animals were dosed with a single intravenous dose of A1mcMMAF at 3 mg/kg, and plasma and tumor samples were collected at predetermined time points up to 240 h. Plasma and tumor concentrations of total mAb and ADC were quantified using ELISA assay, and LC-MS/MS analysis was performed to quantify the released cys-mcMMAF concentration in plasma and tumor.

LC/MS/MS Assay to Quantify Cys-mc-MMAF

Plasma samples were prepared with solid phase extraction (SPEC 96-well plate C18, Agilent). Tumor tissue samples were weighted and lysis buffer (Sigma-Aldrich, C3228) was added at 100 mg:1 mL ratio to the tissue and homogenized. The supernatants were collected after homogenized samples were centrifuged at 5,000×g for 10 min. Supernatant was aliquot for LBA assay, and the remaining sample was further processed with SPE cartridge for LC/MS/MS analysis.

The LC/MS/MS system consists of Acquity UPLC (Waters) and API 5500 Qtrap (AB Sciex). The column used is Kinetex C18, 2.1 × 100, 1.7 μM (Phenomenex) with 0.1% Formic Acid as Mobile Phase A (formic acid from Fluka) and 0.1% Formic Acid in acetonitrile (Fisher) as mobile phase B. Gradient applied is as following: 0 min at 5%B, 0.5 min at 5% B, 3.8 min at 90% B, 4 min at 90% B, 4.1 min at 5% B, and 5 min at 5% B. The MS/MS transition are CysmcMMAF: 1046.200/428.160, DP = 80, CE = 52; CXP = 22; CysmcMMAD were used as internal standard: 1085.400/428.200, DP = 110, CE = 53, CXP = 20. Data were processed and analyzed by Analyst 1.5 (AB Sciex). The lower limit of quantitation was 0.002 and 0.1 ng/mL for plasma and tumor samples, respectively.

ELISA Assay to Quantify Total mAb (A1) and ADC (A1mcMMAF)

Total mAb and ADC concentrations in mouse plasma and tumor homogenate were determined using an enzyme-linked immunosorbant assay (96-well format) with colorimetric detection. Briefly, the capture protein was recombinant human 5T4 and the detection antibody was a biotinylated goat anti-human kappa chain IgG (Southern Biotech, Birmingham, AL) for the total mAb assay and a biotinylated anti-MMAF antibody (Pfizer, Inc.) for the ADC assay, along with HRP-Streptavidin conjugate (Jackson ImmunoResearch, West Grove, PA). Optical density was measured on a spectrophotometer (Molecular Devices).

Characterizing the Plasma PK of Total mAb, ADC, and Released Payload

Estimating the PK Parameters for Total mAb and Payload Dissociation Rate

Plasma PK of total mAb (A1) and A1mcMMAF ADC in tumor bearing and non-tumor bearing mice, after single intravenous dose of 1 and 10 mg/kg, were simultaneously characterized using a modified 2 compartment model (Fig. 1a) to estimate the PK parameters of total mAb and the payload dissociation rate constant (k_dis). It was assumed that the dissociation rate constant, which is an estimate of the rate at which ADC concentrations drift away from the mAb concentration, will represent the rate of change in average drug antibody ratio (DAR) over the period of time. Equations for the model are provided below:

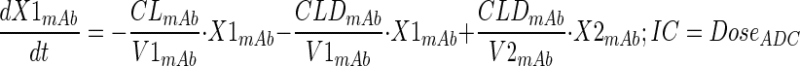1

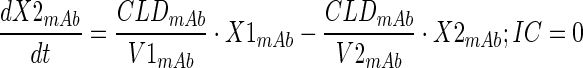2

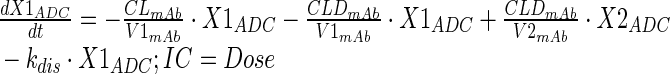3

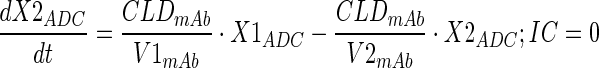4

Fig. 1.

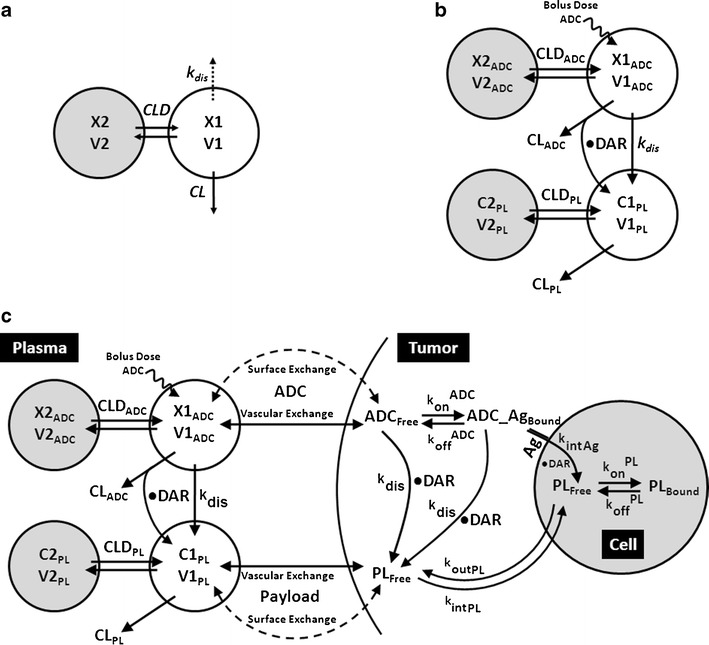
Schematics of the PK models used to characterize the disposition of A1mcMMAF ADC. a A modified two compartment PK model used to characterize the plasma PK of total mAb and ADC simultaneously. b A combined PK model consisting of 2 integrated two compartment models to characterize the PK of ADC and released payload simultaneously. c A multi-scale mechanistic ADC tumor disposition PK model, capable of characterizing and predicting the PK of ADC and released payload in plasma and the tumor compartment. Note: Please refer to the “Materials and Methods” section and Table I for detailed description of the symbols used in the schematics

Description of the symbols and parameters used in above equation are provided in Table I. For the estimation of k_dis, it is assumed that conjugated mAb (i.e., ADC) will have similar clearance and volume of distribution as total mAb, and the dissociation of the payload from mAb will lead to enhanced elimination of ADC cf. mAb.

Table I.

Glossary of the Parameters and Terms Used in Model Equations

Symbol	Definition	Unit
X1mAb, X1ADC	Amount of total mAb and ADC in the central compartment	Nanomole
X2mAb, X2ADC	Amount of total mAb and ADC in the peripheral compartment	Nanomole
CL mAb, CLD mAb	Plasma clearance, and distribution clearance of total mAb	L/day/kg
V1mAb, V2mAb	Total mAb volume of distribution for the central and peripheral compartment	L/kg
k dis	Dissociation rate of payload from ADC	1/day
Dose ADC	Dosing amount of ADC	Nanomole
CL ADC, CLD ADC	Plasma clearance and distribution clearance of ADC	L/day/kg
V1ADC, V2ADC	ADC volume of distribution for the central and peripheral compartment	L/kg
C1PL, C2PL	Concentrations of payload in the central and peripheral compartment	nM
CL PL, CLD PL	Plasma clearance, and distribution clearance, of cys-mcMMAF	L/day/kg
V1PL, V2PL	cys-mcMMAF volume of distribution for central, and peripheral, compartment	L/kg
DAR	Drug antibody ratio i.e. # Payload/# Antibody	Unitless
R Cap, R Krogh	Radius of tumor blood capillary, and an average distance between two capillaries	Μm
P ADC, D ADC	The rate of permeability, and diffusion, of ADC across and around the tumor blood vessels	μm/day, cm2/day
ε ADC	Tumor void volume for ADC	Unitless
ADC FreeTumor _ ExtraCellular, ADC BoundTumor _ ExtraCellular	Free, and antigen bound, ADC concentrations in tumor extracellular space	nM
R Tumor	Radius of the tumor	Cm
k on ADCAntigen, k off ADCAntigen	Association, and dissociation, rate constants between ADC and tumor antigen	1/nM/day, 1/day
Ag Total, ADC_Ag Bound	Total antigen, and ADC bound antigen concentrations	nM
k intAg	Internalization rate of the antigen inside the cell	1/day
PL TumorIntra _ Cellular, PL TumorExtra _ Cellular	Payload concentration inside tumor cells, and in tumor extracellular space	nM
PL BoundTubulin	Concentration of payload bound inside the cell	nM
k intPL	Payload nonspecific uptake rate in cancer cell	1/day
k on PLTubulin, k off PLTubulin	Association, and dissociation, rate constants between payload and unknown cell component	1/nM/day, 1/day
Tubulin Total	Total concentration of payload binding intracellular component	nM
k outPL	Efflux rate of payload from the cell	1/day
P PL, D PL	The rate of permeability and diffusion of payload across and around the tumor blood vessels	μm/day, cm2/day
ε PL	Tumor void volume for cys-mcMMAF	Unitless
DAR 0	Drug antibody ratio for the ADC at time = 0	Unitless

Estimating the PK Parameters for ADC and the Released Payload

Plasma PK of A1mcMMAF and cys-mcMMAF after 1 and 10 mg/kg intravenous dose, from tumor bearing and non-tumor bearing mice, were characterized sequentially using the PK model described in Fig. 1b. In the first step, the PK parameters for ADC were estimated; and in the next step, the PK parameters for cys-mcMMAF were estimated, while keeping the PK of ADC fixed. Equations for the model are provided below:

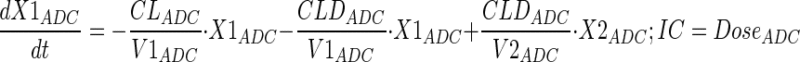5

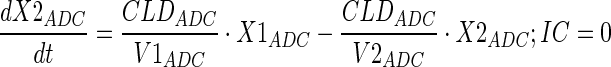6

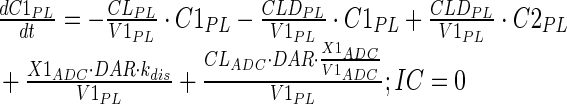7

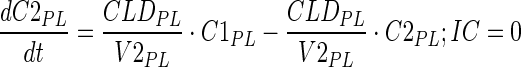8

Description of the symbols and parameters used in above equation are provided in Table I.

Predicting the Tumor PK of Total mAb, ADC, and Released Payload

Tumor concentrations of mAb, ADC, and the released payload were predicted a priori, based on the individually estimated plasma PK of mAb and ADC in each tumor bearing mice, and other biomeasures and chemomeasures (e.g., affinity, internalization rate etc.). Figure 1c displays the diagram of the model that was used to predict the tumor concentration, detailed description of which is provided in reference (2). After systemic administration of A1mcMMAF, it is either allowed to distribute to the peripheral compartment or distribute to the tumor extracellular compartment using the parameters calculated based on the ADC molecular weight and tumor size (8–10). The PK of released payload in the systemic circulation, which is either generated via nonspecific shedding from ADC or via ADC metabolism, or influxed from the tumor, was characterized using the two compartment model and PK parameters generated for cys-mcMMAF in the previous section. Within the tumor, the extracellular ADC is allowed to interact with the cell surface antigen, and the bound ADC is allowed to internalize. Once internalized, it is assumed that each molecule of ADC will generate number of payloads equivalent to the average DAR. The released payload inside the cell is allowed to bind to the intracellular target, and the unbound intracellular payload is allowed to exit the cell. In the extracellular tumor environment, the payload is generated either from the dissociation from ADC or via efflux from the cell. The released payload in the tumor extracellular environment is allowed to distribute to the systemic circulation using the parameters calculated based on the released payload molecular weight and tumor size. Equations for the integrated ADC and payload tumor disposition model are provided below:

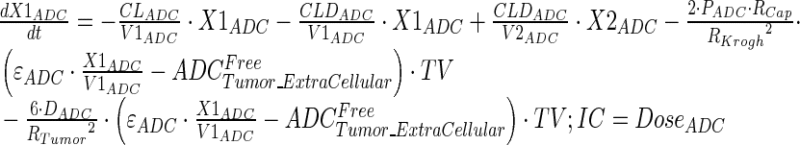9

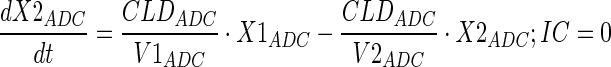10

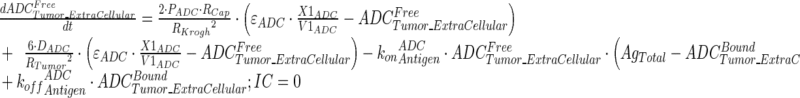11

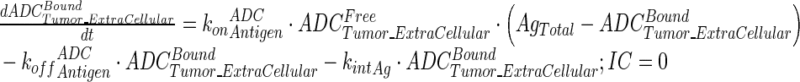12

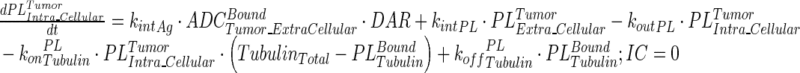13

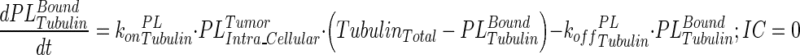14

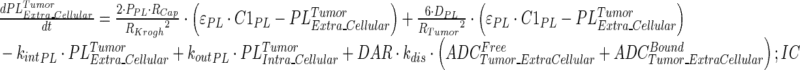15

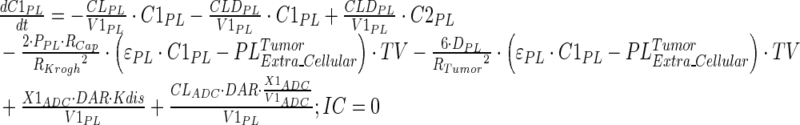16

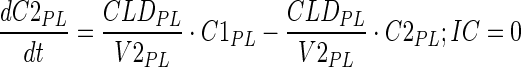17

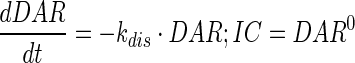18

Description of the symbols and parameters used in above equation are provided in Table I. Above, Equations 9–10 describe the plasma PK of ADC, Equations 11–12 describe the tumor PK of ADC, Equations 13–15 describe the tumor PK of released payload, and Equations 16–17 describe the plasma PK of released payload. Note that Equations 9–12 can also be used to characterize the plasma and tumor PK of total mAb.

In order to evaluate the ability of the ADC PK model to predict the tumor concentrations of total mAb, ADC, and payload, simulations were performed for two different xenograft (MDA-MB-361/DYT2 and H1975) bearing mouse after an intravenous administration of 3 mg/kg dose of A1mcMMAF. Predicted tumor concentration-time profiles for A1, A1mcMMAF, and cys-mcMMAF were compared with experimental data, in the form of area under the curve (AUC), to evaluate the quality of the prediction. For quantitative comparison, percent predictive error was calculated for all the datasets using the following formula: 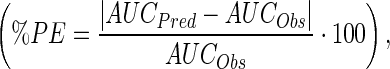where AUC_Pred is the model predicted AUC and AUC_Obs is the observed AUC. To facilitate unit conversion, ADC and mAb were assumed to be of 150 kDa, and the released payload was assumed to be of 1 kDa.

Modeling and Simulation

Models were simulated using the software Berkeley Madonna (University of California at Berkeley, CA) and were fitted to the data using the maximum likelihood (ML) estimation methods in ADAPT-5 software (BMSR, CA). For the model fitting following variance model was used:

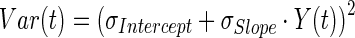19

where Y(t) is the model output at a given time t, and Var(t) is the variance associated with the output. σ_Intercept and σ_Slope are the variance parameters representing a linear relationship between the standard deviation of the model output and Y(t).

Pathway Contributions and Sensitivity Analysis

The ADC tumor disposition model was analyzed in detail to calculate the % contribution of each different pathways responsible for released payload concentration in the plasma, tumor interstitial, and tumor intracellular compartments over the period of time. The % contribution of each pathway was calculated by dividing the input from that pathway by the input from all the pathways involved.

A local sensitivity analysis was performed on the final model and parameter set to assess the sensitivity of the ADC tumor disposition model output to key model parameters. Area under the plasma concentration time curve (AUC) for released payload in different compartments (i.e., plasma, tumor homogenate, tumor interstitial, and tumor intercellular) was chosen as the model output to represent drug exposure. The analysis was conducted by evaluating the percentage change in AUCs with 50% or 200% alteration in the model parameters

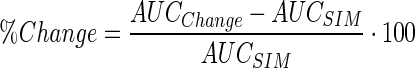20

AUC_SIM refers to the AUC obtained with the optimized set of parameters, and AUC_Change is the AUC obtained following a 50% or 200% change in the parameter value.

RESULTS

Biomeasures and Chemomeasures

Figure 2a shows the internalization profile of A1 antibody in 5T4 expressing cells, with the half life of internalization ∼4 h. The association rate constant and dissociation rate constant between A1 and 5T4 was found to be 0.97 1/nM/h and 0.9 1/h, leading to a dissociation constant value of 0.93 nM. The Anti-5T4 antibody binding capacity per cell, as a measure of receptor number, for MDA-MB-361/DYT2 and H1975 cells were ∼40,000 and ∼62,500, respectively.

Fig. 2.

a The internalization profile of A1mcMMAF in 5T4 expressing cells. b Observed plasma PK of total mAb, ADC, and released payload, obtained after 1 and 10 mg/kg dose of A1mcMMAF, superimposed over each other. c Observed and model described plasma PK of total mAb and ADC, obtained after 1 and 10 mg/kg dose of A1mcMMAF, superimposed over each other. d Observed and model described plasma PK of ADC and released payload, obtained after 1 and 10 mg/kg dose of A1mcMMAF, superimposed over each other

PK Parameters for Total mAb and Payload Dissociation Rate

Since the PK of mAb, ADC, and released payload was not remarkably different between the tumor bearing and non-tumor bearing mice, they were pooled together to perform the parameter estimation. Figure 2b shows the pooled observed PK of total mAb, ADC, and released payload, after 1 and 10 mg/kg dose of A1mcMMAF, superimposed on each other. The PK of total mAb and ADC were dose proportional, and were fit simultaneously (Fig. 2c) using the model shown in Fig. 1a, to estimate the PK parameter for total mAb, and the payload dissociation rate constant. The parameter estimated are provided in Table II.

Table II.

Estimated or Literature Derived Parameter Values Employed for Simulating the ADC Tumor Disposition PK Model

Parameter	Value	Unit	Source
CL mAb	0.021	L/day/kg	Estimated
V1 mAb	0.069	L/kg	Estimated
CLD mAb	0.089	L/day/kg	Estimated
V2 mAb	0.085	L/kg	Estimated
k dis	0.29	1/day	Estimated
CL ADC	0.0426	L/day/kg	Estimated
V1 ADC	0.0666	L/kg	Estimated
CLD ADC	0.0678	L/day/kg	Estimated
V2 ADC	0.0918	L/kg	Estimated
CL PL	74.8	L/day/kg	Estimated
V1 PL	2.22	L/kg	Estimated
CLD PL	485	L/day/kg	Estimated
V2 PL	63.83	L/kg	Estimated
R Cap	8	Μm	From Ref (8)
R Krogh	75	Μm	From Ref (8)
P ADC	334	μm/day	From Ref (8)
D ADC	0.022	cm2/day	From Ref (8)
ε ADC	0.24	Unitless	From Ref (8)
Ag Total	104 (H1975), 66.4 (MDA-MB-361/DYT2)	nM	Measured
k on ADCAntigen	23.2	1/nM/day	Measured
k off ADCAntigen	21.6	1/day	Measured
k intAg	4.2	1/day	Measured
R Tumor	0.5	cm	Measured
P PL	2.1E + 04	μm/day	From Ref (8)
D PL	0.25	cm2/day	From Ref (8)
ε PL	0.44	Unitless	From Ref (8)
k intPL	9.66	1/day	From Ref (2)
k on PLTubulin	0.73	1/nM/day	Based on Kd of 18 nM
k off PLTubulin	13.1	1/day	From Ref (2)
k outPL	1.1	1/day	Assumed similar to MMAE, from Ref (2)
Tubulin Total	65	nM	From Ref (2)
DAR 0	4.0	Unitless	Measured

PK Parameters for ADC and the Released Payload

The plasma concentration-time profiles for ADC obtained after 1 and 10 mg/kg dose of A1mcMMAF in tumor bearing and non-tumor bearing mouse (Fig. 2b), were fitted simultaneously using a two compartment model. The estimated model parameters are provided in the Table II. Subsequently, the plasma concentration-time profiles for ADC and the released payload were characterized simultaneously (Fig. 2d) using the model shown in the Fig. 1b, to estimate the plasma PK parameter for cys-mcMMAF, which are presented in Table II.

Predicting the Tumor PK of Total mAb, ADC, and Released Payload

Plasma PK of total mAb and ADC in H1975 and MDA-MB-361/DYT2 xenograft tumor bearing mice (Fig. 3a, b) were used to predict the tumor concentrations of total mAb, ADC, and released payload. Plasma concentrations of released payload were also simulated for comparison with the observed data. Figure 3c shows the simulated tumor concentrations of mAb, ADC, and released payload, along with model predicted plasma concentrations of released payload, superimposed over the observed results, for H1975 xenograft. Similarly, Fig. 3d shows similar graph generated for MDA-MB-361/DYT2 xenograft. The %PE for tumor mAb and ADC exposure was 3% and 24% for H1975 xenografts, and 10% and 30% for MDA-MB-361/DYT2 xenograft, respectively. The %PE for tumor and plasma payload exposure was 32% and 26% for H1975 xenografts, and 44% and 20% for MDA-MB-361/DYT2 xenograft, respectively. As such, the predictions made by the ADC tumor disposition model were within twofold (i.e., %PE < 100%) of the observed values. Thus, the ADC tumor disposition model was able to a priori predict the tumor concentrations of mAb, ADC, and the released payload reasonably well.

Fig. 3.

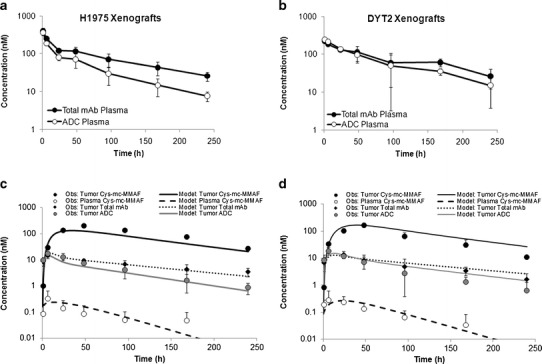
a Observed plasma PK of total mAb and ADC obtained after administration of A1mcMMAF in H1975 tumor bearing mice at 3 mg/kg dose level. b Observed plasma PK of total mAb and ADC obtained after administration of A1mcMMAF in MDA-MB-361/DYT2 tumor bearing mice at 3 mg/kg dose level. c Observed and model predicted tumor PK of total mAb, ADC, and released payload, and plasma PK of released payload, obtained after administration of A1mcMMAF in H1975 tumor bearing mice at 3 mg/kg dose level, superimposed over each other. d Observed and model predicted tumor PK of total mAb, ADC, and released payload, and plasma PK of released payload, obtained after administration of A1mcMMAF in MDA-MB-361/DYT2 tumor bearing mice at 3 mg/kg dose level, superimposed over each other

Pathway Contributions and Sensitivity Analysis

Figure 4a, b, c displays the % contribution of different pathways responsible for released payload concentration in the plasma, tumor interstitial, and tumor intracellular compartments over the period of time. As shown in Fig. 4a, the clearance of ADC seems like a higher contributor of released payload in plasma than the payload dissociated from intact ADC. Payload generated in the tumor does not contribute significantly to the released payload concentration in plasma. Additionally, over the period of time, % contribution of the payload distributing back from the peripheral compartment becomes important. Figure 4b shows that although the released payload distributing from plasma to the tumor contributes notably to tumor interstitial payload concentration at initial time points, the payload generated within the cancer cells is the most dominant source of released payload in tumor interstitial space. The analysis also suggest that the local dissociation of payload from ADC is a very minute contributor to tumor interstitial payload concentration. Figure 4c demonstrates % contribution of different pathways responsible for unbound released payload concentration within the tumor cell compartment. At the initial times the payload brought in the cells by ADC is the predominant contributor, however as the time progress binding of the payload within the cells seems to be the major contributor for retaining unbound payload within the cell, due to the equilibrium binding. Passive influx of the payload within the cell seems to be a very minute contributor.

Fig. 4.

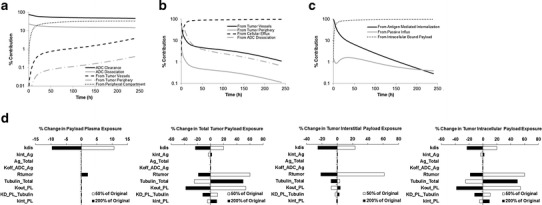
a Analysis of the % contribution of each different pathways responsible for released payload concentration in the plasma over the period of time. b Analysis of the % contribution of each different pathways responsible for released payload concentration in the tumor interstitium over the period of time. c Analysis of the % contribution of each different pathways responsible for unbound released payload concentration in the tumor cells over the period of time. d A local sensitivity analysis evaluating the effect of 50% and 200% change in various model parameters, on the % change in plasma payload exposure, total tumor payload exposure, tumor interstitial payload exposure, and tumor intracellular payload exposure. Here, exposure is measured by calculating the AUC (0-time), and the results are derived after administration of A1mcMMAF in H1975 tumor bearing mice at 3 mg/kg dose level. Note: the sensitivity of parameters is dose dependent, and sensitivity analysis obtained at 0.3 and 30 mg/kg doses are presented in the Supplementary Figure 1

Figure 4d displays the results from a local sensitivity analysis performed on the model to evaluate the effect of change in various model parameters on the exposure of payload in plasma, whole tumor, tumor interstitial, and tumor intracellular compartments. From the analysis, it seems that the payload dissociation rate (k_dis) and tumor size are the most sensitive parameters for exposure of released payload in the plasma. Decreasing k_dis leads to increased plasma exposure, whereas increase in tumor size leads to an increase in plasma payload exposure. Payload exposure in the whole tumor compartment is sensitive to k_dis, tumor size, intracellular payload binding capacity, payload affinity to the binding component, and the influx and efflux of the payload in and out of the cell. Further analysis of the tumor interstitial and intracellular payload exposure reveals that these exposures are sensitive to the same set of parameters to which the payload exposure in whole tumor compartment was sensitive to, though the degree and direction of sensitivity were different. The parameters related to payload binding within the cell and payload exchange in and out of the cell were not as important for tumor interstitial payload exposure, as they were for intracellular payload exposure. In general, decrease in k_dis and tumor size led to increased tumor payload exposure. Increase in payload biding component, and payload influx rate within the cell led to increased whole tumor payload exposure; whereas decrease in payload efflux rate and payload dissociation from its binding component led to increased whole tumor payload exposure. It is important to note that the sensitivity of the parameters is dose-dependent, and the results from the senility analysis performed at different doses are provided in the Supplementary Figure 1. Of note, although the antigen expression and internalization were not sensitive parameters at the 3 mg/kg dose, they became sensitive at the higher dose (Supplementary Figure 1).

DISCUSSION

An ability to predict the drug concentration in the tumor remains a challenge for the development and preclinical-to-clinical translation of small and large molecule drugs. There are various factors (e.g., nonspecific and specific binding of small molecule drugs within the plasma and tumor compartments, and target mediated disposition of large molecules), which makes tumor concentrations notably different than the plasma drug concentrations, preventing us from using the plasma drug concentrations as a surrogate for the tumor drug concentrations. In order to account for the difference between plasma and tumor drug concentration, and to generate a descriptive and predictive tool, scientists have been using PK models that characterizes the tumor drug concentrations by using the plasma drug concentrations as a forcing function (11,12). Although these descriptive PK models work for characterizing tumor drug concentrations within the animal species and dose range that was used to built them, their value for extrapolation beyond the dose range used to built them, and for translation of tumor drug concentrations from one species to the other, is limited. Due to the lack of a mechanistic and translatable framework to predict tumor drug concentrations, ample consideration is not given to how drug concentrations in preclinical tumor models can be used to aid drug development by predicting tumor concentrations in patients or facilitating rational selection of clinical dose and dosing regimens (1). The lack of translatable framework also makes many drug fail in the clinical setting despite of their demonstrated efficacy in preclinical animal models, which in turn makes the animal tumor models appear not translatable.

In order to develop a physiologically relevant and translatable PK model that can characterize and predict the tumor concentration of drug, it is very important to understand and quantify the primary mechanisms responsible for the tumor disposition of drug molecules. Many scientists have spent their entire careers in deciphering the important elements that differentiates tumor tissues from normal tissues, and implementing these differences in a mathematical framework using the principles of engineering (8,13–18). Here, we have employed these findings to develop and validate a multi-scale mechanism-based PK model that can not only help characterize but also predict the tumor concentrations of ADC and payload, using A1mcMMAF as a case study.

Characterizing the PK of ADC brings a unique challenge as one needs to account for the distribution and elimination of a large and a small molecule simultaneously, while also accounting for the generation of the small molecule from the large molecule (5). Since ADC is a heterogeneous molecule consisting of one to several molecules of payload attached to a mAb, one also needs to account for the change in average ratio of the conjugated payload to antibody (i.e., DAR) over the period of time (19). Since ADCs are designed with a mAb that targets tumor cell surface antigen with rapid turnover, one also need to account for degradation of ADC using the targeted antigen and the generation of payload within the cell thereafter. It is also important to account for the binding of small molecule (i.e., payload) within the cell and its efflux from the cell to get an idea about the retention ability of the payload within the cell. Additionally, while accounting for drug distribution into a tumor one also need to pay attention to the size of the tumor, as the diffusion from tumor periphery is the only way for drug entry when tumors are avascular and small, and the diffusion from vasculature takes over as the predominant pathway when the tumor grows in size (18). Considering the high interstitial pressure within the tumor and absence of lymphatics, convection is absent or minimum within the solid tumors, making diffusion the predominant pathway for drug exchange between the tumor and its surrounding. One also needs to consider the size of the molecule being exchanged, and the vascular permeability, tissue diffusion rates, and accessible tissue volume, corresponding to that size (17). All the known mechanisms mentioned above were accounted for by the model presented here, and the ability of this model to predict the tumor concentrations of ADC and released payload was evaluated.

A detailed tumor penetration study with the ADC A1mcMMAF was performed in two different murine xenograft models, and a robust set of data consisting of total mAb, ADC, and released payload concentrations in the plasma and tumor was generated to build and validate the PK model (Figs. 2 and 3). As demonstrated in the Fig. 3, and by the %PE values reported in the results, it is evident that the model did very well in terms of a priori predicting the concentrations of total mAb, ADC, and released payload in the tumor compartment, based on the plasma concentrations of mAb and ADC. These results along with the results from our previous report (2) provides confidence in the model’s ability to predict the tumor concentration of payload following ADC administration, based on data collected from an easily assessable biological matrix, i.e., plasma. In order to gain further confidence in the model’s ability to predict the tumor concentrations of other novels ADCs with a diverse set of target antigens, and to save resources, in the future one can perform a limited scale tumor penetration study and compare the model predictions with the observed data to validate the model. Once validated, the ADC tumor disposition model can be used to predict the tumor payload concentration for myriad of ADCs targeting novel antigens, providing a tool to help triage the ADCs based on the property of the mAb, target antigen, or linker-payload, at the early drug development stage. Since the model is mechanistic and based on the known physiological processes governing the disposition of ADC and payload within the tumor, it is hypothesized that it can also be used to predict tumor concentrations of payload within cancer patients, which will not only aid in the selection of optimum dose and dosing regimen for ADCs in the clinic but will also provide a tool to facilitate precision medicine efforts.

The detailed analysis of the model also provides new insight into the primary factors responsible for the disposition of ADC and the payload, and the parameters that the model outputs were most sensitive to (Fig. 4). It was very interesting to see that the generation of the payload via nonspecific digestion of the ADC was a bigger contributor the plasma payload concentration compared the payload dissociated from the ADC or being generated in the tumor. It was also suggested by the pathway analysis (Fig. 4a) that the distribution of the payload to the peripheral compartment serves as a source for plasma payload concentration once the ADC concentrations have decreased. A detailed analysis of the payload concentration in tumor interstitial space (Fig. 4b) revealed that although initially the payload coming from the central circulation contributes to this compartment, the majority of the time it is the payload coming from the tumor cells (following digestion of ADC) that contributes to the payload concentration in this compartment. Investigation of the tumor intracellular payload concentration revealed that although internalization of the ADC is the primary source of input for the compartment, biding of the payload within the cell is the major contributor for retaining the payload within the cell (Fig. 4c). The local sensitivity analysis conducted at 3 mg/kg dose of A1mcMMAF (Fig. 4d) also provided vital information regarding the sensitivity of several model outputs to a few key parameters. It was discovered that the stability of the payload on the mAb is one of the sensitive parameter, along with the size of the tumor, in determining the payload exposure in plasma. Since the plasma PK of payload follows a formation-rate limited kinetics, the rate of payload formation through dissociation from mAb (i.e., k_dis), and not the intrinsic clearance of payload, determines the systemic payload exposure. And, since the tumor has a capacity to retain ADC within the system, and digest it locally to generate payload that can diffuse out to the systemic circulation, changes in tumor size also results in altered plasma PK of payload. This information is important as it provides a rationale for increasing the stability of the linker, and suggests that one needs to consider the difference in the size of tumor between mouse experimental tumors and clinical patient tumors while translating from preclinical-to-clinical setting. It was also found out that the parameters related to the binding of tubulin within the cell and exchange of payload between the cell and extracellular space are very important determinant for tumor payload concentrations. Surprisingly the antigen expression, antigen internalization, and binding of ADC to the antigen were not very sensitive parameters for tumor payload concentrations at 3 mg/kg dose level, where maximum receptor occupancy for tumor antigen was ∼14%. However, one should be cautious about generalizing these results, as it is shown in the supplementary material that the sensitivity of outputs to the parameters changes with dose. And antigen expression, antigen internalization, and binding of ADC to the antigen become important at higher doses (i.e., 30 mg/kg) where the tumor ADC concentrations are at the saturating level for tumor antigen (maximum receptor occupancy of 100%).

The analysis of ADC tumor disposition model also revealed the importance of conducting fundamental experiments to quantify certain model parameters which the model output is very sensitive to, but we do not have enough confidence in their assumed values. For example, the capacity of the binding component (i.e., tubulin) that binds to the payload, and the affinity of the payload towards the binding component, is very important for accurately quantifying the tumor payload concentration; however our understanding of these basic parameters is very poor. The efflux rate of the payload out of the cells is another parameter that is very important in determining the tumor payload concentration, however our understanding of this parameter is also very poor. In fact, in the current model developed for A1mcMMAF these parameters for the releases payload cys-mcMMAF were assumed to be similar to that of MMAE (from Ref (2)), which may be a reason for the observed deviations between the model predicted and observed PK profile of payload concentrations in the tumor. As such, the model necessitates investigating the processes occurring at the cellular level that may be responsible for the ADC and payload disposition, and quantifying them, which will in turn provide confidence in the value of the parameters being used to drive the PK model, and the predictions made by it.

All in all, this manuscript provides validation for the ADC tumor disposition model, using a novel 5T4 targeting ADC (A1mcMMAF) as a case study. Based on the biomeasures and plasma ADC concentrations, the model was able to predict the total tumor mAb concentrations, tumor ADC concentrations, tumor released payload concentrations, and plasma released payload concentrations reasonably well, in two different xenografts a priori. Thus, taken together with the previously reported performance of the model with brentuximab vedotin (2), results from the present investigation supports the conclusion that the proposed model is applicable to all the ADCs, irrespective of their linker–payload combination. The model was also analyzed to find out the important pathways and parameters that are responsible for payload concentrations in various compartments. The analysis suggested that the stability of the payload on mAb and tumor size are important model parameters. It was also discovered that there is a need to accurately measure poorly understood parameters pertaining to cellular disposition of ADC and payload, as the payload tumor concentrations are very sensitive to them. The model presented here provides a very useful tool for not only predicting the preclinical tumor payload concentrations of novel ADCs, but also for triaging these ADCs, and possibly predicting their concentrations in patient tumors.