A Population Pharmacodynamic Model for Lactate Dehydrogenase and Neuron Specific Enolase to Predict Tumor Progression in Small Cell Lung Cancer Patients

Abstract

The development of individualized therapies poses a major challenge in oncology. Significant hurdles to overcome include better disease monitoring and early prediction of clinical outcome. Current clinical practice consists of using Response Evaluation Criteria in Solid Tumors (RECIST) to categorize response to treatment. However, the utility of RECIST is restricted due to limitations on the frequency of measurement and its categorical rather than continuous nature. We propose a population modeling framework that relates circulating biomarkers in plasma, easily obtained from patients, to tumor progression levels assessed by imaging scans (i.e., RECIST categories). We successfully applied this framework to data regarding lactate dehydrogenase (LDH) and neuron specific enolase (NSE) concentrations in patients diagnosed with small cell lung cancer (SCLC). LDH and NSE have been proposed as independent prognostic factors for SCLC. However, their prognostic and predictive value has not been demonstrated in the context of standard clinical practice. Our model incorporates an underlying latent variable (“disease level”) representing (unobserved) tumor size dynamics, which is assumed to drive biomarker production and to be influenced by exposure to treatment; these assumptions are in agreement with the known physiology of SCLC and these biomarkers. Our model predictions of unobserved disease level are strongly correlated with disease progression measured by RECIST criteria. In conclusion, the proposed framework enables prediction of treatment outcome based on circulating biomarkers and therefore can be a powerful tool to help clinicians monitor disease in SCLC.

Electronic supplementary material

The online version of this article (doi:10.1208/s12248-014-9600-0) contains supplementary material, which is available to authorized users.

INTRODUCTION

The development of individualized therapies is currently a key objective in oncology, yet it poses significant challenges. An essential hurdle to overcome is the early prediction of clinical outcome from a given, newly developed or existing, treatment. KD_LDH and KD_NSE are the first-order rate constants representing the synthesis of LDH and NSE, respectively, promoted by the level of the disease. The difficulty lies in the multitude of factors influencing outcome (e.g., treatment efficacy, toxicity, and development of resistance) and the limited predictive ability of current monitoring techniques.

The Response Evaluation Criteria in Solid Tumors (RECIST) [1] defines current practice to categorize response to treatment, which has limited utility for prediction due to its nonquantitative nature [2, 3]. A proposed solution is the use of quantitative tumor assessment measure. The sum of longest diameters (SLD), a continuous tumor size measurement, has been used in drug development to build predictive models to describe tumor size dynamics [4]; however, despite being a quantitative measurement, it is not widely used in the clinic. An alternative proposed approach to predict clinical outcome is the use of circulating biomarkers. Circulating biomarkers are easily measured in peripheral blood and can be used in conjunction to the aforementioned imaging techniques, which are more limited in their frequency of measurement. Indeed, the use of biomarkers to obtain proof of concept is well-established in drug development [5]. However, there are several factors that might explain the current reluctance to use biomarkers in cancer therapy to evaluate response to treatment in clinical practice. The primary reason is lack of validated tumor-specific biomarkers. However, most validation attempts have been via empirical models which may not properly account for time dependencies between biomarker response and outcome, giving the illusion of poor predictive performance. Proper assessment of the predictive capacity of biomarkers should be in the context of mechanistic models linking their observed levels with clinical outcome. Thus far, there have been few examples using mechanistic models. Nevertheless, recent models involving circulating biomarkers in cancer show that the (semi-) mechanistic approach is feasible [6, 7].

The objective of the current work is to investigate the feasibility of using biomarkers to predict the dynamics of tumor progression. First, we develop a semi-mechanistic model that describes the dynamics of biomarker concentrations in plasma over time. Second, we evaluate the predictive performance of the model by comparing model outcomes with the observed RECIST categories.

We apply this modeling and prediction strategy to data obtained from medical records of patients suffering from small cell lung cancer (SCLC). SCLC, which accounts for 15–20% of all lung cancer diagnoses, is an aggressive and rapidly growing neoplasm. It is highly sensitive to chemotherapy and radiotherapy; however, tumor resistance to these treatments forms very quickly. Early detection of resistance is therefore a high priority in the treatment of SCLC. Several molecules have already been studied as potential tumor markers for SCLC [8, 9]. Among them, neuron specific enolase (NSE) and lactate dehydrogenase (LDH), both circulating enzymes involved in cellular glycolysis processes, appear to be the most promising biomarkers for our purpose. NSE is the most accepted tumor marker in diagnosis and monitoring of SCLC [10, 11]. LDH is a routinely collected biomarker that has been shown to be correlated with tumor size dynamics in several solid cancers [12, 13], including SCLC [10].

METHODS

Patients and Data Collection

Historical data were collected from the medical records of 60 patients diagnosed with SCLC in the University Hospital of Navarra (Pamplona, Spain). All patients included in the dataset had histologically proven SCLC and had received combination therapy of a platinum compound (cisplatin or carboplatin) and etoposide as a first-line treatment. The regimen consisted of an intravenous (IV) infusion of 100 mg/m² etoposide on days 1–3 concomitantly with 75 mg/m² of cisplatin (day 1) or carboplatin AUC 5–6 mg min/mL IV (day 1) every 21 days for six cycles. Blood samples for drug quantification were not available. Patients were staged at diagnosis according to the two-stage system [14] with imaging techniques. Patients were defined as having limited disease (LD) if their tumors were confined to a single hemithorax and regional lymph nodes that could be safely encompassed within a radiation treatment. Patients with metastatic sites that were visibly present outside the thorax were defined as having extensive disease (ED). LD patients also received conformal three-dimensional thoracic irradiation concomitantly with the third and the fourth cycle of chemotherapy. Some ED patients also received thoracic irradiation either as a consolidation therapy, if they had achieved a good response with chemotherapy, or as a palliative treatment for pain or superior cava vein compression syndrome. In addition, 50% of patients received complementary granulocyte colony-stimulating factor (G-CSF). However, data regarding time scheduling and dose administration of G-CSF were not available. Supplementary Table I summarizes patient characteristics of the studied population.

Tumor Assessment

Tumor assessment was performed through computed tomography (CT) scans (Siemens Sensation 64 or Siemens Somation Definition) before the commencement of therapy, between the second and third cycles of chemotherapy, at the end of the entire course of chemotherapy, and every third month thereafter, in follow-up exams. From the CT scan, the calculated sum of the longest diameters was categorized according to modified RECIST criteria where the patient’s response was classified according to the change in total tumor size since the previous CT scan. A detailed description of the tumor assessments obtained for LD and ED patients is shown in Supplementary Table I.

Biomarkers Measurements

Blood samples for measurement of LDH and NSE were collected from each patient before commencement of therapy and when tumor assessment (through imaging techniques) was performed. LDH measurements were also made before the administration of each chemotherapy cycle. For some patients, additional samples were collected between cycles. A total of 369 LDH observations were included in the analysis, where each patient contributed a mean of six samples (range 3–16). A total of 152 NSE concentrations were included in the dataset, where each patient contributed four samples on average (range 1–7). A description of the methods used to quantify LDH and NSE concentrations is provided in the Supplementary material.

Data Analysis

LDH and NSE concentrations measured in plasma were analyzed simultaneously by nonlinear mixed effects (NLME) modeling, also known as the population approach [15]. Tumor assessment measurements were not used for model development and were only used for external validation. An NLME model consists of a structural model, a random effects model, and a covariate model. The structural model describes typical patient-level kinetics and dynamics. The random effects model quantifies interpatient variation in underlying biological processes and also random unexplained variability, including measurement error. These structural and random components together comprise the base model. The covariate model explains interpatient variability, which is quantified by the random effects model using individual patient characteristics. During the analysis, the observations were logarithmically transformed. Interpatient variability was assumed to follow a log-normal distribution. Residual errors were considered to be constant on the log scale (i.e., proportional on the untransformed scale) and were different for each biomarker. The SAEM algorithm, implemented in NONMEM v7.2, was used to estimate model parameters [16]. To cross-check results, we also used the SAEM algorithm implemented in MONOLIX v4.2 [17].

Model Selection

Selection among models was based on the following: (i) log likelihood (denoted −2LL) ratio test (α = 0.05); (ii) precision of parameter estimates; and (iii) visual fit to data, evaluated according to goodness of fit plots.

Base Population Model

Figure 1 shows a typical LDH profile obtained from a patient. The figure reflects the main processes involved in the dynamics of LDH (and in those of NSE): LDH levels increase following treatment onset (1–4 weeks); this might be explained by a delayed drug effect on the biomarker, since the treatment has its effect on the disease rather than directly on the biomarker (which, in the absence of treatment, is expected to increase with tumor size). A subsequent decrease in LDH levels (4–10 weeks) reflects the treatment-related reduction in tumor size, which leads to a decrease in the synthesis rate of the disease biomarkers. Data corresponding to weeks 10–16 show the resistance effects through a continuous increase in LDH, despite the fact that the patient is still undergoing treatment. Finally, the natural disease progression after completion of six cycles of chemotherapy is reflected in weeks 16–25.

Fig. 1.

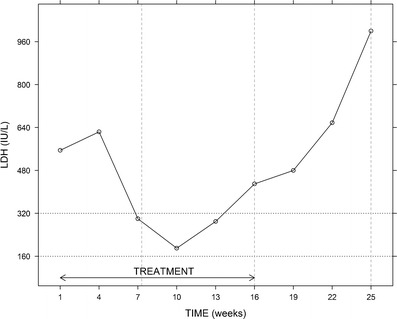
Example of an individual LDH time profile. Treatment (etoposide + platinum compound) consisted of six chemotherapy cycles administered every 3 weeks (i.e., from week 1 (diagnosis) to week 16). The three features identified in most patients are disease progression (weeks 1–4 and weeks 16–25), drug effect (weeks 4–10), and resistance effect (weeks 10–16). Vertical dashed lines represent time points at which tumor size was assessed through CT scans. Horizontal dotted lines correspond to the normal range of values of LDH

Figure 2 shows the schematic representation of the final population model we selected. The main assumptions of the model are the following: (i) the progression of the (unobserved) disease (which can be operationalized, for example, as tumor size) promotes the synthesis of LDH and NSE; (ii) the disease has an inherent progression rate; (iii) chemotherapy and radiotherapy elicit tumor shrinkage; and (iv) there is eventual resistance to treatment effects.

Fig. 2.

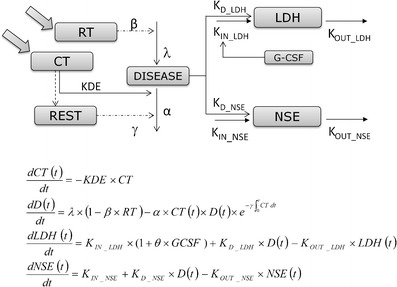
Schematic view of the final model and differential equations used to describe the model. DISEASE is a latent variable that represents disease progression and drives LDH and NSE production. Radiotherapy (RT) and chemotherapy (CT) each affect disease level, where CT decreases its value and RT slows its linear growth. Resistance (REST) is modeled by linking cumulative exposure with a decrease in the drug effect. Granulocyte colony-stimulating factor (G-CSF) increases the physiological LDH synthesis

The model consists of two main components (a) turnover models for biomarkers and (b) a model for a variable we refer to as “disease level”, representing (unobserved) tumor size dynamics. The disease level model itself comprises of four subcomponents: (i) a model for unperturbed disease level; (ii) a model for drug effects; (iii) a model for the effects of resistance to chemotherapy; and (iv) a model for the effect of radiotherapy.

a. Turnover models for biomarkers

LDH and NSE dynamics were described with turnover models [18]. As already mentioned, a fundamental assumption in our model is that increases in biomarker levels are associated with tumor progression, as we can observe in Fig. 1 (weeks 1–4), so turnover models for both biomarkers take the form of Eq. 1:

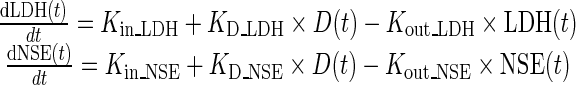1

where LDH(t)  and NSE(t) are the biomarker log concentrations through time, K_{in _ LDH} and K_{in _ NSE} represent the zero-order synthesis rates of LDH and NSE, respectively, and K_{out _ LDH} and K_{out _ NSE} are the first-order rate constants of degradation for the corresponding biomarkers, D represents the disease level, and D(t) reflects the assumption that the disease evolves both in the absence and in the presence of treatment. The expressions corresponding to the initial conditions of LDH and NSE are shown in the Supplementary material.

b. Model for disease level

b.1. Unperturbed model. Equation 2 describes the dynamics of disease level in the absence of perturbation (i.e., treatment). The model corresponds to a linear increase governed by the zero-rate growth constant  λ. This simple choice was driven by the fact that data related to the disease were not used for model building. The value of the disease level at diagnosis (D(0)) was arbitrarily set to 1 in all patients.

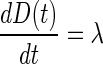2

b.2. Model for drug effects (E_Drug). Due to the lack of pharmacokinetic data, a K-PD approach [19] was used:

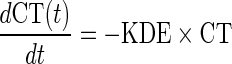3

where CT represents the level of exposure to chemotherapy, and KDE is the first-order elimination rate constant corresponding to exposure to the combined chemotherapeutic compounds (etoposide and platinum). Since the dose of drug combination was identical across patients, a normalized dose of 1 was used to describe the chemotherapy administration for each cycle. Chemotherapy was assumed to induce an irreversible reduction of the disease level, described as a second-order rate process of the form  E_Drug = − α × CT(t) × D(t), where α is a second-order rate parameter accounting for the effectiveness of treatment.

b.3. Model for resistance effect (E_Resistance). A drug resistance term was included in the disease model to account for the resurgence in biomarker concentrations observed in some patients during treatment. We assumed that the resistance was related to the cumulative chemotherapy exposure: 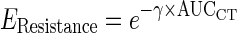, where γ is a parameter that scales the cumulative area under the CT curve (AUC_CT ) from zero to each time point.

b.4. Model for radiotherapy effect (E_Radiotherapy). Radiotherapy works by damaging the DNA of tumor cells, specifically those that are actively dividing. This damage causes cell death and may eliminate localized populations of tumor cells that are resistant to chemotherapy. Radiotherapy effects were included in the model as an irreversible effect on the proliferation rate of the disease of the form E_Radiotherapy = 1 − × RT, where RT is a binary variable that takes the value of 0 before the beginning of radiotherapy and 1 afterwards, and the parameter β, constrained between 0 and 1, accounts for the magnitude of the radiotherapy effects.

The complete model for disease level, incorporating chemotherapy, resistance, and radiotherapy effects was therefore described by the following differential equation:

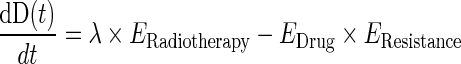4

The final structural model for disease level comprised four of the ordinary differential equations defined above (Eqs. 1, 3, and 4). The model parameters, including those included in  E_Drug, E_Resistance, and E_Radiotherapy , were assumed to be the same for the two biomarkers.

During the development of the base model, we tested all components of the disease model to identify potential areas of improvement. Several different relationships between  E_Drug, E_Resistance, and E_Radiotherapy and the underlying state variables were investigated. Intermediate transit compartments to introduce delays between these terms and state variables were also explored for significance. Different models for disease level were evaluated (exponential, Gompertz, logistic). In addition, we examined a simplified version of the model presented above, which did not include a disease compartment, and in which E_Drug, E_Resistance, and E_Radiotherapy (with proper modifications) were applied directly to the biomarker parameters.

Covariate Selection

Once the base population model was developed, a covariate analysis was performed. The following patient characteristics were considered for inclusion as covariates in the model: the stage of the disease (i.e., LD or ED), number of metastases, age, gender, coadministration of G-CSF, ECOG performance status, and platinum compound received in chemotherapy combination (cisplatin or carboplatin). Covariate selection was performed using stepwise covariate modeling [20], by means of the −2LL ratio test with α = 0.05 for forward inclusion and α = 0.01 for backward deletion.

Model Evaluation

Prediction- and variability-corrected visual predictive checks (pvc-VPCs) [21] were conducted using 1,000 simulated studies to detect notable structural and covariate model misspecifications. Precision of parameter estimates was obtained from the analysis of 1,000 bootstrap datasets. We obtained pvc-VPCs and bootstrap using the software Perl-speaks-NONMEM (PsN) [20].

Model Predictive Performance

Predicted values of disease level were obtained by simulation with the individual parameter values at the exact same times at which CT scans were available (during treatment and all follow-up CT scans), according to the following equation:

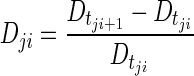5

where 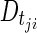is the predicted disease level for patient j at observation point (CT scan) i, and 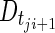is the predicted disease level for patient j at the subsequent observation point (i.e., the following CT scan, approximately 8 weeks later). Changes in disease level between those CT scan times (D_ji) were used to assess the predictive performance of the model through a receiver operating characteristic (ROC) curve [22] and a parametric time-to-progression model.

ROC Analysis

Predictions of D_ji were classified as disease progression or nondisease progression (either response or stable disease) based on different chosen cut-off values. Each chosen cut-off value provides the probability to discriminate disease progression (sensitivity or true positive rate) from nondisease progression (specificity or true negative rate). The ROC curve summarizes the sensitivity and specificity for all discrimination cutoffs. We evaluate the area under the ROC curve (AUC_ROC) as an overall test of the model’s performance. An AUC_ROC value of 0.5 indicates no association between prediction and true outcome, and a value of 1.0 indicates perfect association. Confidence intervals of the AUC_ROC values were computed using 1,000 bootstrap samples. For comparison purposes, the same ROC analysis strategy described for the disease was applied to the model-derived biomarkers and also to LDH and NSE observations (i.e., raw dataset).

Progression-Free Survival (Time-to-Progression)

Different distributions (exponential, Weibull, log-logistic, and Gompertz) were assessed to describe the baseline hazard rate. Changes in the predicted disease level between individual times of CT scans were introduced as predictors of the hazard, as shown in Eq. 6:

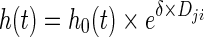6

where h₀(t) is the baseline hazard, δ is a parameter to be estimated, and D_ji  is the predicted change in individual disease level, as defined in Eq. 5.

Model parameters were obtained with the Laplacian method in NONMEM v7.2. This model did not include random effects; however, we accounted for interpatient variability by including the biomarker’s individual predictions regarding changes in disease levels. Model selection and evaluation were based on −2LL and simulation-based diagnostics (i.e. Kaplan-Meier VPC: plots of observed data overlaid with a 95% prediction interval calculated from 1,000 simulations of new patients).

RESULTS

The selected model represented in Fig. 2 successfully described the dynamics of LDH and NSE concentrations in plasma over time. As an example of model fits, Fig. 3a shows the individual predictions of LDH and NSE dynamics in nine representative patients. The estimates of the model parameters are shown in Table I. It is worth noting that in none of the cases, the 95% confidence intervals include the zero value, indicating that the parameters listed were estimated with adequate precision. Data supported the estimation of interpatient variability with regard to λ, α, LDH, and NSE concentrations at time zero (LDH₀ and NSE_0, respectively) which ranged from 53 to 174%, reflecting the high dispersion in the data (Supplementary Figure S1). The remaining parameters were constrained to have a small degree of interpatient variability (15%) to facilitate estimation via the SAEM algorithm. The model seemed to capture well the overall shape and dispersion of the data, as reflected in the pvc-VPCs (Fig. 3b); this suggests an absence of major model misspecification. A low condition number (25.9) provided further evidence that the model was not over-parameterized.

Fig. 3.

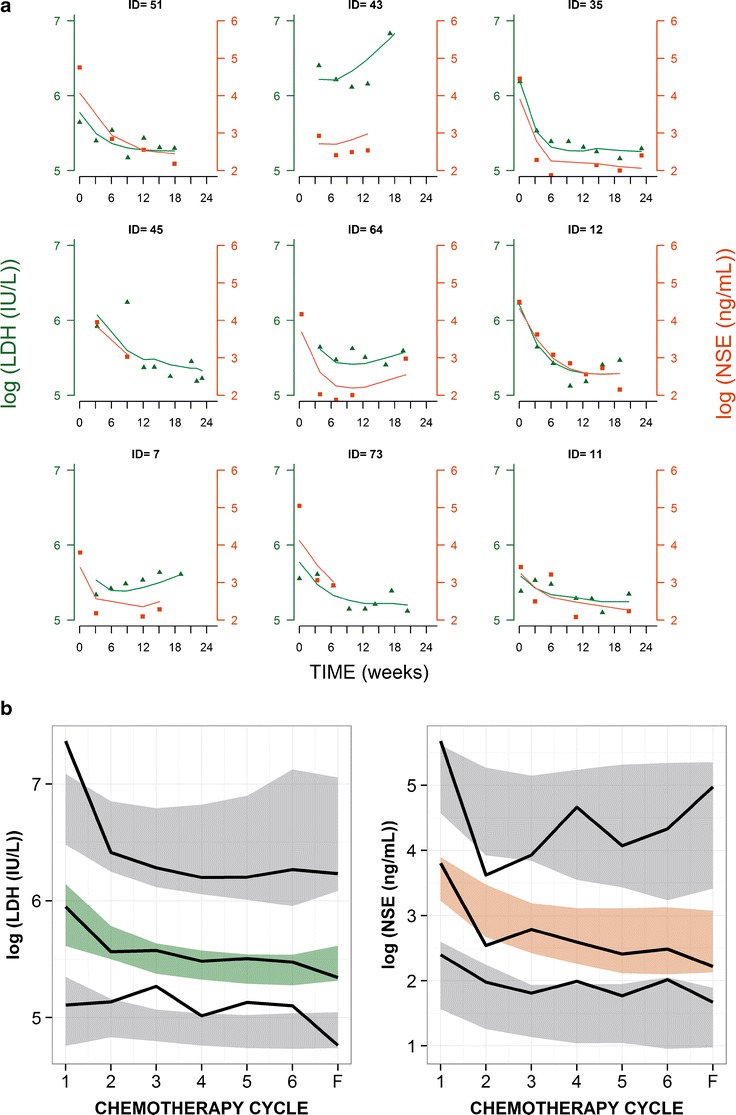
a LDH observations (green circles) with individual predictions (green lines) on the left y axis and NSE observations (orange squares) with the individual predictions (orange lines) on the right y axis for nine selected patients. Observations and predictions for both biomarkers are log-transformed. b pvc-VPC of LDH (left) and NSE (right) for the final model against chemotherapy cycles. Cycle 7 corresponds to follow-up measurement. Solid black lines represent the 5th, 50th, and 95th percentiles of the observed data. Shaded areas are the 95% confidence intervals based on simulated data (n = 1,000) for the corresponding percentiles

Table I.

Model Parameter Estimates Describing LDH and NSE Dynamics

	Parameter (units)	Estimate	95% CI	BSV %	95% CI
Mutual	λ (U weeks−1)	0.0067	0.0004–0.018	213	96.1–292
	ɣ (weeks−1)	0.377	0.294–0.512	15	NE
	KDE (weeks−1)	1.16	NE	54.8	NE
	α (U−1 weeks−1)	1.32	0.905–1.78	47.5	9.87–73.4
	β (weeks−1)	0.831	0.652–0.987	NE	NE
	Correlation (ηLDH0, ηNSE0)	0.684	0.457–0.782	NA	NA
LDH	MRTLDH (weeks)	0.311	0.249–0.519	15	NE
	K in_LDH (IU L−1 weeks−1)a	553	NA	NA	NA
	K in_LDH if GCSF coadministration (IU L−1 weeks−1)a	757	NA	NA	NA
	K D_LDH (IU L−1 weeks−1)a	671	NA	NA	NA
	LDH0 (IU L−1)	352	301–412	61.5	47.3–74.6
	Residual error	0.205	0.182–0.229	NA	NA
NSE	MRTNSE (weeks)	0.301	0.236–0.363	15	NE
	K in_NSE (ng mL−1 weeks−1)a	15.0	NA	NA	NA
	K D_NSE (ng mL−1 weeks−1)a	126	NA	NA	NA
	NSE0 (ng mL−1)	47.7	35.4–62.7	92.1	64.6–120
	Residual error	0.402	0.306–0.506	NA	NA

Abbreviations: λ linear rate of disease progression, ɣ resistance parameter, KDE first-order elimination constant of chemotherapy exposure (KDE and its associated interpatient variability were fixed according to the longest real half-life time of the combination drugs administered to patients [23]), α chemotherapy efficacy parameter, β radiotherapy efficacy parameter, MRT mean residence time (MRT = 1/K _OUT), LDH ₀ LDH values at time = 0, K _{in_LDH} basal (physiological) LDH synthesis, K _{D_LDH} LDH synthesis driven by disease, K _{in_NSE} basal NSE synthesis, K _{D_NSE} NSE synthesis driven by disease, NSE ₀ NSE values at time = 0, BSV between-subjects variability expressed in CV%, Residual error constant on logarithmic scale. NE not estimated, NA not applicable

^aSecondary parameters

Different expressions for disease level provided poorer fit to the data, in terms of −2LL and goodness of fit plots. Similarly, attempts to modify  E_Drug, E_Resistance , and E_Radiotherapy did not improve the fit. In addition, attempts to simplify the final model did not succeed. Baseline disease level was set at 1 for all patients. During model building, we attempted to describe interpatient variability in baseline disease burden. However, its inclusion was not statistically significant as determined by −2LL ratio test. This result suggested that the interpatient variability in initial disease status was accounted for in other model parameters. A model in which the disease variable was excluded fit the data very poorly, yielding a −2LL value that was almost 300 points greater than that obtained with the selected model. Likewise, when we attempted to fit LDH and NSE separately, the corresponding parameter estimates were less precise than those obtained when the two biomarkers were pooled together.

One would expect that the stage of the disease would influence some model parameters. For example, compared with patients with LD, patients with ED might be characterized by faster disease progression (higher values of λ), reduced drug effect (lower values of α), or greater resistance to treatment (higher values of γ). However, the stage of the disease and radiotherapy were confounding covariates, since almost 90% of patients with LD underwent radiotherapy. Separately, each covariate provided a substantial improvement of fit as compared with the base model, as reflected in a decrease of the −2LL; however, the inclusion of radiotherapy provided greater improvement than the inclusion of disease stage. We further evaluated the effects of including the presence of supplementary G-CSF therapy as a covariate on γ (resistance parameter) or on K_{in _ LDH} (physiological LDH synthesis). While inclusion of G-CSF as a covariate on γ did not significantly influence model fit, inclusion of G-CSF as a covariate on K_{in _ LDH} reduced the −2LL by more than 30 points, and therefore, this covariate relationship was kept in the final model. Indeed, among patients who received G-CSF, K_{in _ LDH} values were 36.9% greater than among patients who did not receive G-CSF. No other relationships tested in the covariate analysis showed statistically significant effects.

Given the complexity of the selected model, which involves several nonlinear functions, we sought to gain intuitive insight into the behavior of the different model components. Figure 4a(1–3) shows the drug exposure effect, where typical profile indicates that drug effect is reduced to 50% of its initial value after three to four chemotherapy cycles (3). Figure 4b(1–4) shows that had the model only included terms for drug and/or radiotherapy effects without resistance effects, we would have incorrectly predicted a steady monotonic decline in the disease level (2 and 3), whereas the incorporation of the resistance effect enabled the adequate prediction of a disease nadir level, at approximately the fourth cycle of chemotherapy (4). This tumor reduction corresponds to a median time to disease nadir (i.e., time to the lowest value of predicted disease) of 15.7 weeks (5.02–21.0) and involves disease reduction of 73.9% (34.9–93.4%) from the arbitrary baseline value (95% confidence intervals).

Fig. 4.

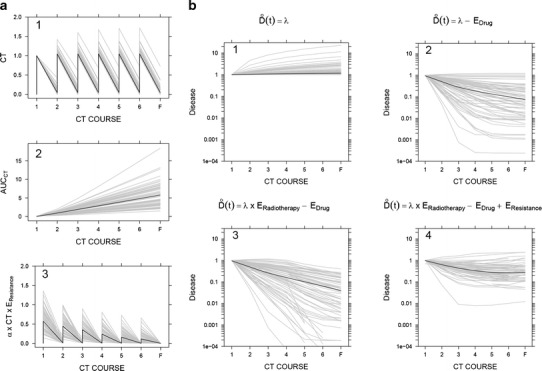
Typical simulated profiles (thick black solid lines) and individual simulated profiles (thin gray lines) from a population of 100 virtual individuals, using the model structure depicted in Fig. 2 and the estimates of model parameters shown in Table I. a Effect of chemotherapy exposure (1), the level of resistance corresponding to AUC_CT (2), and drug effects in the presence of resistance (3). b Predicted disease dynamics in different scenarios: (1) disease level in the absence of any treatment, (2) disease level in presence of chemotherapy, (3) disease level under radiotherapy and chemotherapy, and (4) disease progression as it is described in our model (in the presence of radiotherapy, chemotherapy, and resistance)

ROC Analysis

To create the ROC curve, we used 218 predictions regarding each of three variables—disease level, LDH, and NSE—together with the outcomes of 218 CT scans. Figure 5 shows that the three variables had discriminating ability to differentiate observed disease progression determined from the CT scans (AUC_ROC values are significantly above 0.5), indicating that the disease level and biomarker variables strongly correlate with actual disease progression. Youden’s indices (i.e., cutoffs giving maximum specificity and sensitivity) were +23.5 for disease level, +20.3 for NSE, and +5.3 for LDH. Note that the Youden’s index obtained for disease level (23.5%) is very close to the classificatory criteria of RECIST for disease progression (i.e., 20%) [1].

Fig. 5.

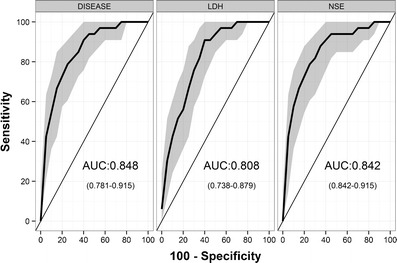
ROC curves (i.e., true positive rate (sensitivity) vs. false positive rate (100-specificity)) for discriminating observed disease progression with simulated biomarker changes. Solid lines correspond to ROC curves, and the shaded area represents the confidence intervals obtained with bootstrapping

Although the AUC_ROC value obtained with the disease level variable was slightly higher than the values obtained with the model-derived LDH and NSE variables (Fig. 5), there was no statistically significant difference among the three AUC_ROC values. To investigate the added value of model-based approaches, we performed the same ROC analysis using raw data instead of model-derived predictions. In the case of LDH, the AUC_ROC value obtained with model-derived LDH values was significantly higher than the AUC_ROC value obtained with LDH observations (p = 0.026) (Table II). Regarding NSE, where only eight instances of observed disease progression (“events”) were included, the AUC_ROC values for model predicted and NSE observations were not significantly different (Table II).

Table II.

Summary of AUC_ROC Values (95% CI) Obtained with the ROC Analysis in Different Scenarios

Included data	Number of CT scans (number of events)	Variable	Model-based (predictions)	Observations (raw data)
All CT scans	218 (33)	LDH	0.856 (0.793–0.920)	NA
		NSE	0.857 (0.785–0.930)	NA
		DISEASE	0.867 (0.801–0.934)	NA
CT scans when LDH observations were available	154 (22)	LDH	0.822 (0.730–0.914)	0.676 (0.548–0.804)
		DISEASE	0.829 (0.727–0.931)	NA
CT scans when NSE observations were available	63 (8)	NSE	0.891 (0.790–0.992)	0.907 (0.760–1.000)
		DISEASE	0.904 (0.810–0.999)	NA

CT computed tomography, NSE neuron specific enolase, LDH lactate dehydrogenase, NA not applicable

Time-to-Progression Model

A log-logistic model best characterized the underlying baseline hazard distribution of time-to-progression, as follows:

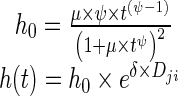7

where μ is the hazard coefficient, estimated to be 4.91 × 10⁻⁶ weeks⁻¹ (CV 14.1%), and ψ is the shape factor, estimated as 3.66 (CV 2.4%). The inclusion of predicted disease changes (D_ji as defined in Eq. 5) in the base hazard equation (Eq. 7) decreased the −2LL by 48 points (δ was estimated to be 0.593, CV 7.04%). Data used to develop the model included biomarker measurements from diagnosis (i.e., time 0) until 25 weeks after diagnosis. Thus, it can be assumed that the individual parameters from the biomarker model used to create D_ji were not affected by shrinkage [24], considering that events occurred mostly after 25 weeks. Median observed time-to-progression was 32.1 weeks (range 13.3–92.0 weeks), and median time-to-progression obtained from a simulation of 1,000 new individuals was 32 weeks (95% CI, 14.4–80.0 weeks). The Kaplan-Meier VPC shows good predictive performance of the time-to-progression model (Fig. 6).

Fig. 6.

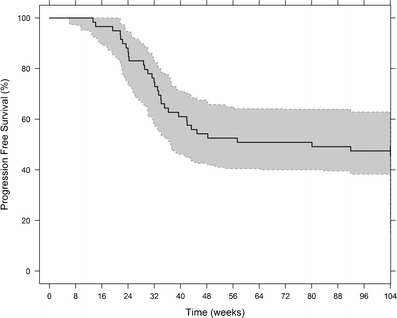
Kaplan-Meier plot of progression-free survival (black line) and 95% prediction intervals (gray shaded area) based on 1,000 simulations. The hazard rate is described by a log-logistic distribution. The baseline hazard is increased by predicted changes in the latent disease variable between CT scan times (approximately 8 weeks)

DISCUSSION AND CONCLUSIONS

The ability to use a biomarker as a surrogate endpoint, defined as “a substitute for a clinically meaningful endpoint [that] is expected to predict the effect of a therapeutic intervention” [25], will potentially benefit oncology practice and drug development. Since the relations between biomarker concentrations and disease progression might not be linear and straightforward, it is necessary to develop mechanistic models to characterize them. Currently, there are available examples of studies that explored the use of biomarkers as surrogate endpoints using different analytical approaches in several cancer indications [26].

Our analysis focused on LDH and NSE, which have not thus far been used extensively to predict clinical outcomes, despite the fact that pretreatment levels of both molecules have been proposed as independent prognostic factors for SCLC. The absence of predictive studies incorporating these biomarkers may, in part, stem from the fact that several studies demonstrating the utility of NSE and LDH for SCLC predictions yielded contradictory conclusions [27–35]. These contradictions may have resulted from the use of empirical data analysis. In addition, lack of specificity with LDH is widely accepted, since variability in circulating LDH can be explained by multiple causal factors. This was also reflected in our data by a low AUC_ROC value (0.676) obtained in the ROC analysis with LDH observations. The advantage of using a mixed effect model-based approach is that non-SCLC related causal factors can be described by random unexplained variability. This approach therefore corrects for the unexplained variation to provide more predictive LDH values. This was reflected by the much larger AUC_ROC (0.822) obtained with model-based individual predictions of LDH. Recent studies have proposed other biomarkers that might be more specific for SCLC, including progastrin-releasing peptide (proGRP) [11, 36] and circulating tumor cells [8]. Nevertheless, our aim here was to provide an example in which the combination of suitable and readily available longitudinal biomarker measurements with modeling approaches can be used to describe tumor dynamics for SCLC.

We have developed a pharmacodynamic model that successfully describes the dynamics of LDH and NSE concentrations in plasma over time, in patients with limited and extensive SCLC disease, treated with first-line chemotherapy and radiotherapy. We focused on developing a model capable of describing our longitudinal data in a biologically consistent manner to maximize predictive capability. The result was a semi-mechanistic model, in which an underlying “disease level” variable was responsible for regulating biomarker concentrations (through its effect on biomarker synthesis rates). We assumed that LDH and NSE enzymes are produced by a constant zero-order rate and cleared at a first-order elimination rate (i.e., indirect or turnover model) in healthy individuals. In addition to the physiological biomarker production, we assumed that the disease level increases LDH and NSE levels. This is consistent with the Warburg effect [37] which is the basis of the use of positron emission tomography (PET) [38] and states that malignant cells chose anaerobic glycolysis even in oxygen-rich conditions although it is less energy efficient [39]. Since both LDH and NSE are glycolytic enzymes, an increase in their synthesis rate allows tumor cells to undergo anaerobic glycolysis. We therefore assumed that the disease level results in an additional zero-order production of LDH and NSE. In fact, several studies show how both enzymes are increased in different cancer cells (for example in [40–42]). Whilst these assumptions are an approximation of the complex biological processes, we believe that they are sufficient to capture the major processes influencing biomarker and disease time courses.

The final model separated SCLC-specific (λ in Eq. 2; K_{D_LDH} and K_{D_NSE} in Eq. 1) and treatment-related parameters (KDE in Eq. 3; α, ɣ, and β in Eq. 4). Our success at describing drug- and system-specific parameters with only routinely collected medical records suggests that similar modeling approaches may work with other treatments and/or cancer types. In our model, a reduction in disease level (i.e., tumor shrinkage due to chemotherapy and to radiotherapy) is reflected in a decrease in the biomarker concentration. Therefore, both chemotherapy and radiation therapy do have effects on LDH and NSE; however, such effects are not direct effects. Chemotherapy and radiotherapy are considered to reduce tumor burden which in turn affects LDH and NSE production. Our use of the cumulative drug dose to model resistance to chemotherapy was consistent with the known pattern of the formation of resistance to platinum compounds [43]. Finally, published studies show that treatment with G-CSF enhances LDH concentrations among healthy individuals [44], noncancer patients [45] and cancer patients [46]. This effect is probably related to the expansion of myeloid cell mass associated with exposure to G-CSF [47]. Our model captures this effect and suggests that the increment might be due to an increase of physiological LDH synthesis.

The model has several limitations. First, the analysis was restricted to data gathered from patients who received the described therapy regimen as first-line treatment. Subsequent treatments administered to patients were much more heterogeneous, with low numbers of patients associated with each treatment and few corresponding LDH and NSE measurements. Nonetheless, further work could expand this model to include second- and third-line treatment. The relationship between treatment and drug effects was established through a K-PD model due to the lack of pharmacokinetic information. Whereas this approach enables a good description of the data, the absence of pharmacokinetic profiles may hamper the interpretation of the variability seen in the response. Although the K-PD approach is certainly an approximation, the simplified pharmacokinetic model was sufficient to build a predictive biomarker and disease model. Another drawback is that the model could not distinguish pharmacokinetic or pharmacodynamic differences between cisplatin and carboplatin, due to lack of data. Similarly, there was insufficient information to take into account different radiotherapy administration schedules.

ROC analysis can be only performed for dichotomized variables. We focused on disease progression, reflecting the clinical objective to identify tumor relapse early on. This identification will allow clinicians to optimize treatment strategy at the individual level. Our model allowed us to predict biomarker levels at any time of interest (exact times where CT scan were also available), thereby increasing the robustness of the ROC analysis (results with small sample size and small number of events should be interpreted with caution). As shown in Table II and described in the “RESULTS” section, in all analyses, the AUC_ROC value obtained with the disease level variable was higher than 0.8 and was higher than the AUC_ROC values obtained with model predictions of either LDH or NSE. This result supports our modeling assumption that the disease level variable is representative of tumor size. This assumption is further supported by the time-to-progression model, which related changes in the disease level to observed time to progression, and allowed us to assess the impact of time on the model’s predictive performance.

In this case study, NSE concentrations had significant predictive value per se in the context of SCLC. However, other biomarkers in SCLC or in other cancer indications might not have similar predictive power. Our semi-mechanistic modeling approach enables the relationships between biomarker dynamics and tumor size dynamics to be properly identified. Our approach highlights the need for proper quantitative analysis in other cancer types and/or different biomarkers and should be considered even in the case of lack of relevant biomarkers, as the building of the current model using the nonspecific biomarker LDH shows.

In conclusion, we have developed a model for biomarker dynamics that, without using tumor size data, is capable of predicting disease progression assessed by CT scans (RECIST data) in SCLC patients. We believe that the proposed modeling framework of circulating biomarkers could constitute a powerful additional strategy for disease monitoring in SCLC patients.