Multiscale Tumor Spatiokinetic Model for Intraperitoneal Therapy

Abstract

This study established a multiscale computational model for intraperitoneal (IP) chemotherapy, to depict the time-dependent and spatial-dependent drug concentrations in peritoneal tumors as functions of drug properties (size, binding, diffusivity, permeability), transport mechanisms (diffusion, convection), spatial-dependent tumor heterogeneities (vessel density, cell density, pressure gradient), and physiological properties (peritoneal pressure, peritoneal fluid volume). Equations linked drug transport and clearance on three scales (tumor, IP cavity, whole organism). Paclitaxel was the test compound. The required model parameters (tumor diffusivity, tumor hydraulic conductivity, vessel permeability and surface area, microvascular hydrostatic pressure, drug association with cells) were obtained from literature reports, calculation, and/or experimental measurements. Drug concentration-time profiles in peritoneal fluid and plasma were the boundary conditions for tumor domain and blood vessels, respectively. The finite element method was used to numerically solve the nonlinear partial differential equations for fluid and solute transport. The resulting multiscale model accounted for intratumoral spatial heterogeneity, depicted diffusive and convective drug transport in tumor interstitium and across blood vessels, and provided drug flux and concentration as a function of time and spatial position in the tumor. Comparison of model-predicted tumor spatiokinetics with experimental results (autoradiographic data of 3H-paclitaxel in IP ovarian tumors in mice, 6 h posttreatment) showed good agreement (1% deviation for area under curve and 23% deviations for individual data points, which were several-fold lower compared to the experimental intertumor variations). The computational multiscale model provides a tool to quantify the effects of drug-, tumor-, and host-dependent variables on the concentrations and residence time of IP therapeutics in tumors.

Electronic supplementary material

The online version of this article (doi:10.1208/s12248-014-9574-y) contains supplementary material, which is available to authorized users.

INTRODUCTION

Intraperitoneal (IP) chemotherapy exposes peritoneal tumors to high drug concentrations due to spatial proximity (1,2), e.g., 20- to 1,000-fold higher peritoneal concentration compared to systemic therapy (3–5). In ovarian cancer, adding IP chemotherapy to intravenous chemotherapy yielded survival advantage of up to 16 months in optimally debulked stage III patients (6–9).

Drug disposition in peritoneal tumors during IP treatments is controlled by kinetic processes connecting several distinct anatomical and physiological compartments (Fig. 1a). Drug is removed from the peritoneal cavity by drainage through the lymphatics or by absorption through peritoneal tissues. Drug can penetrate tumors via diffusion and convection, and, after entering the tumor interstitium, gain entry to blood vessels. The drug absorbed into the systemic circulation is then cleared from the body or recirculates to the tumor. These processes are determined by physiological factors (peritoneal pressure, peritoneal fluid volume), tumor pathology (size, tumor vasculature, perfusion status, microvascular pressure, extracellular matrix composition), and drug properties (molecular size, binding to cellular and extracellular components, clearance from the body). The kinetic processes are often nonlinear, and the variables can have opposing effects. For example, high drug binding to proteins in peritoneal fluid would reduce drug clearance from the peritoneal cavity but would also reduce drug penetration into tumors. Computational tools would be useful to delineate the respective contribution of the various processes to drug transport, delivery, and residence in tumors.

Fig. 1.

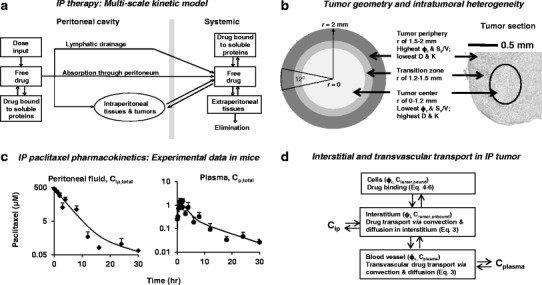
Kinetic models for drug disposition during IP treatment. a Multiscale models for drug distribution and elimination in whole organism. After IP administration, drug disposition in peritoneal tumors is determined by multiple dynamic processes, including drug drainage by lymphatic system, drug absorption into blood circulation through peritoneal tissues, drug clearance from the body, drug redistribution to peripheral tissues including intraperitoneal and extraperitoneal tissues, drug binding to extracellular proteins and cells, and tissue-blood drug exchange. We assumed that only free (unbound) drug is transported. The current model is an expanded version from our earlier model (52). b Geometry of a spherical tumor (4 mm in diameter) comprising three layers: necrotic center of 1.2-mm radius (white area), tumor periphery of 500-μm thickness (dark gray area), and the transition zone (light gray area). c Experimental data of paclitaxel pharmacokinetics in peritoneal fluid and plasma in mice. Nontumor-bearing mice were given an IP injection of paclitaxel (10 mg/kg dissolved in 0.7 mL of 1:1 Cremophor/ethanol); experimental data (squares or circles) were obtained from our previous study (52); lines were the best-fit lines using Eq. 1. Note the different concentration scales for the two profiles. d Transport processes within tumor. Drug transport processes in a peritoneal tumor, which comprises blood vessels, tumor cells, and extracellular matrix, include transvascular and interstitial convective and diffusion transport. These dynamic processes were described by the indicated equations

Several pharmacokinetic (PK) models for IP therapy have been described. A distributed model was introduced in 1980s to predict the drug concentration gradient in peritoneal tissues. This model includes diffusion and convection through tissues, transvascular transport, lymphatic drainage, and the bidirectional mass transport between plasma and peritoneal fluid. Sensitivity analysis using this model identified several determinants of tissue penetration (peritoneal surface area, tissue diffusivity, capillary permeability, interstitial void fraction, hydrostatic and osmotic pressures in tumor capillaries and interstitium). The first-generation distributed model was developed to depict drug disposition in tissues on a macroscale (whole tissue). The investigators have since added tissue pressure gradient to the model to describe the intra-tissue fluid and mass transport for osmotic agents such as glucose in normal parietal and visceral peritoneal tissues (without tumors) (10–12). A second group of investigators developed a theoretical model of cisplatin penetration into peritoneal tumors based on diffusive transport and drug uptake into cells (13). The most recent model by a third investigator group used a hybrid physiologically based PK model to describe the drug transfer between a peritoneal tumor and the systemic circulation (14). This model describes a tumor as a system of concentric layers (total of five) with diffusive drug transfer between individual layers and from individual layers to blood/plasma; the model was used to study the effect of antiangiogenesis on IP topotecan therapy. Convective transport is omitted in the latter two models. None of these earlier models take into account tumor-specific parameters (e.g., elevated interstitial pressure, pressure gradient, heterogeneous tumor vasculature, solute-protein/tissue binding) or deal with intratumor spatial-dependent drug distribution.

Tumors with a size larger than 1–2 cm in diameter typically show a lower density of blood vessels and cells in the center compared to the periphery (15,16). These spatial-dependent variations affect the fluid flow and pressure gradient and thereby alter drug transport in tumor interstitium and across blood vessels, resulting in spatial-dependent drug concentrations. The clinical relevance of spatial drug distribution is indicated by the finding that ovarian cancer patients with tumors larger than 1 cm in diameter do not benefit from IP therapy (17), presumably due to inadequate drug delivery to the inner parts (2).

Computational models to depict the time-dependent and spatial-dependent drug levels (defined as spatiokinetics) in tumors during IP therapy may be useful to elucidate the pharmacodynamics and to evaluate treatment strategies. Multiscale modeling is used in physical sciences to solve problems on multiple scales (e.g., spatial, temporal) and can be used to calculate certain properties on one level (e.g., solid tumor) based on the information from different levels (e.g., whole organism), with each level addressing a phenomenon over a specific window of length and time. The present study describes the first application of multiscale models to depict tumor spatiokinetics as functions of drug-cell biointerface, fluid and mass transport mechanisms, intratumor heterogeneity, IP pressure, and drug-host interactions (absorption, clearance). Model performance was evaluated by comparing the model-predicted results to experimental results in tumor-bearing mice. Sensitivity analysis was performed to evaluate the relative importance of transport and biointerface parameters on tumor spatiokinetics.

METHODS

Overview of Investigation

Model development and validation used paclitaxel as the test drug and comprised three groups of studies: model development, in silico studies, and model performance evaluation.

Model Development: Overview

The tumor spatiokinetic model includes the following components: (a) drug transport in tumor interstitium and across blood vessel (i.e., interstitial and transvascular transport), (b) spatial-dependent transport, and (c) drug disposition in tumor cells. The model considered diffusion and convection as the major transport mechanisms. The interstitial and transvascular diffusion and fluid flow were used together with the drug concentrations in tumor interstitium or tumor blood vessels to calculate the interstitial and transvascular drug flux. The drug concentration-time profiles in peritoneal fluid and systemic blood were used as the boundary conditions (drug source) at the tumor border and tumor blood vessels, respectively, for the calculation of drug concentrations in tumors.

Transport within a tumor is spatial-dependent due to the spatial heterogeneity in several parameters, i.e., vessel density (which determines the blood perfusion and hence the drug supply and removal from tumor), interstitial fluid pressure (which determines the pressure gradient as well as the blood perfusion), and interstitial space volume (which determines the porosity). For example, we and others have shown that increased tumor porosity enhanced the vessel surface area and blood perfusion (18,19). These spatial heterogeneities, which affect the hydraulic conductivity and diffusivity and result in spatial-dependent interstitial and transvascular transport were captured in the model by assigning spatial-dependent parameter values.

We have shown that paclitaxel is extensively bound to cellular components (20–23). To account for the drug disposition within a tumor, the model views a tumor as comprising three subcompartments (i.e., cells to which the drug associates, interstitial space/fluid where the drug undergoes interstitial transport, and vessels where the drug undergoes transvascular transport) and describes changes in the concentrations of the respective drug moiety (i.e., cell-associated drug, unbound drug undergoing interstitial transport, and unbound drug undergoing transvascular transport) as a function of time and spatial positions in a tumor.

Figure 1b depicts a tumor as an isolated spherical tumor (in dimensional form). The selection of a spherical coordinate defined the base vectors (e.g., the radial base vector points outward with center as the origin), as well as the gradient operators (e.g., a vector such as interstitial fluid velocity or diffusive drug flux in the same direction as the base vector had a positive value, and vice versa). The average tumor diameter was set to 4 mm, the size observed in experiments.

Model Development: Assumptions

For transport, we assumed (a) that fluid exchange between tumors, peritoneal cavity, and incoming blood vessels depends on the pressure gradients in these three compartments; (b) that drug transport in tumor interstitium occurred by diffusion and convection, as in a porous gel structure; (c) no lymphatic transport in tumors; and (d) no time- or spatial-dependent changes in vessel permeability, venous pressure, or drug-cell binding parameters. Figure 1d shows the kinetic processes of drug transport in tumor interstitium and across blood vessels via diffusion and convection. The depicted equations are macroscopic models for tumor segments that were much larger compared to the vessel diameter (4 mm vs. 8–45 μm; (24)) and, hence, were minimally affected by the vascular structure. Vessels throughout a tumor were treated as continuously distributed sources for solute and volume transport.

Within the tumor, cell-associated drug was immobilized, and only unbound drug was available for transport. Based on the more extensive drug association with cells compared to extracellular macromolecules (22,23), we assumed negligible drug binding to extracellular macromolecule. This assumption reduced the model complexity and computation time, but was valid only for early time points when the C_ip,total significantly exceeded the average total drug concentration in tumor (C_tumor,total). In addition, we have shown that apoptosis-inducing chemotherapy, by reducing tumor cell density, results in transient expansion of interstitial space and vascular changes between 24 and 96 h (19,25). Accordingly, we limited the present study to the first 6 h, or before the amount of drug bound to extracellular macromolecules became a significant fraction of the total drug amount in tumor and before significant apoptosis developed. We further assumed negligible drug degradation or elimination in tumors. Under these conditions, the three drug entities in a tumor were drug in blood vessels, drug bound to cells, and unbound drug in interstitial space; the corresponding concentration terms were C_plasma,total, C_tumor,bound, and C_{tumor,unbound}.

Model Development: Drug Source and Boundary Conditions

Figure 1d shows the interconnecting kinetic processes between the peritoneal cavity, tumor, and whole organism. In the peritoneal cavity, drug is removed from the peritoneal cavity via lymphatic drainage and/or absorption, processes that are determined by pressure in the peritoneal cavity P_ip, volume of peritoneal fluid V_ip, and drug properties (molecular size, binding to proteins, clearance from the body). The net result of these kinetic processes is reflected in the changes of total drug concentrations in the peritoneal fluid (C_ip,total) over time. In whole organism, drug is cleared from the body (e.g., metabolism, renal excretion) or is recirculated to tissues including the tumor; the net result of these processes is reflected in the changes of total drug concentration in plasma (C_plasma,total) over time. Figure 1c shows the C_ip,total-time and C_plasma,total-time profiles in mice given an IP dose of paclitaxel. The C_ip,total-time profile showed characteristics of two- and three-compartment models. Results of statistical analysis using the Akaike information criterion indicated better data fitting by the two-compartment model compared to the three-compartment model (i.e., a lower Akaike value of 20.1 vs. 25.9). Hence, we selected the two-compartment model for analysis. Similarly, we used a two-compartment model with first-order absorption to analyze the C_plasma,total-time profile. We applied the customary assumption of homogeneous compartments with identical drug concentrations within individual compartments. C_ip,total-time and C_plasma,total-time profiles were analyzed using Eq. 1, to obtain the values of A, B, A′, and B′, the rate constants for the distribution and elimination phases in the C vs. time plots (α_ip, β_ip, α_p, and β_p), and the rate constant for drug absorption into plasma (k_p).

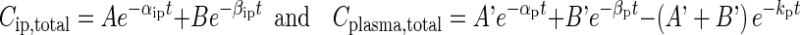1

We specified tumor boundary conditions for fluid flow (P_ip) and solute transport (C_ip,total-time profile as the boundary conditions for the tumor domain and C_plasma,total-time profile for the blood vessels). In view of the relatively small dosing volume (0.7 mL) that was rapidly resorbed within 6 h, P_ip was kept constant over time. For initial conditions when time t equaled 0 (i.e., before the drug gained entry to tumors), C_{tumor,unbound} and C_tumor,bound equaled 0. For the boundary condition at the outer perimeter of the tumor, the boundary pressure P_i equaled P_ip, and the boundary concentration C_{tumor,unbound} equaled the unbound drug concentration in peritoneal fluid. At the tumor center, we used a symmetrical condition, i.e., both interstitial fluid velocity and diffusive drug flux equaled 0.

In the experiments, paclitaxel was administered IP in a micelle solution comprising 4.2% Cremophor (yielded undetectable Cremophor in plasma). We previously found that the free fraction of paclitaxel decreased from 100% in the absence of Cremophor to 23% and 11%, respectively, in 0.25% and 1% Cremophor (26). Assuming a similar reduction in free fraction at the higher Cremophor concentration in the dosing solution (∼50% reduction with four times higher Cremophor), we used a 5% free fraction in the peritoneal fluid. In plasma and in the absence of Cremophor, paclitaxel is bound to soluble proteins such as albumin and alpha-1-acid glycoprotein and shows an average free fraction of about 10% (range, 5 to 13%; (27–31)). Hence, we chose a free fraction of 10% in plasma. Note that a protein-bound drug would be readily transported by the transvascular convective flow. The present model, as the first proof-of-concept study, is limited to the early time points when the plasma drug concentrations are negligible compared to tumor concentrations, and hence, the transvascular transport would not have appreciable effect on the total transport. This assumption was confirmed in a pilot study, which showed minimal changes (<1%) in drug delivery and residence in tumors by using the free plasma concentration instead of the total plasma concentration. With the assumption that only the free (i.e., unbound) drug was transported from the peritoneal fluid or plasma into a tumor, the two boundary conditions were 0.05C_ip,total (at the tumor border) and 0.1C_plasma,total (at tumor vessels).

Model Development: Transport Equations

We described the transvascular and interstitial fluid flow using Starling’s equation and Darcy’s law, respectively, and used a conservation equation to link the two fluid flows (Eq. 2).

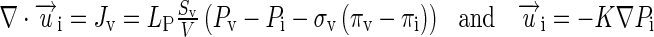2

Definitions of the terms are as follows: u_i, interstitial fluid velocity in the radial direction (from the center to periphery); J_v, rate of fluid moving into or out of blood vessels per unit tumor tissue volume; L_P, hydraulic conductivity of tumor vessel wall; S_v/V, vessel surface area per unit tissue volume; P_v, intravascular pressure; P_i, interstitial fluid pressure; σ_v, reflection coefficient of proteins across tumor vessel wall; π_v and π_i, osmotic pressures in tumor vessel and tumor interstitium, respectively; and K, hydraulic conductivity of tumor tissue. ∇ ⋅ u_i, the divergence of u_i, represents the net flow rate of fluid between the vessels and interstitium. The direction of interstitial fluid flow depends on the pressure gradient and goes outward from the tumor center to tumor periphery when P_i>P_ip (indicated by positive u_i values). The direction of transvascular fluid flow depends on the transvascular pressure difference and goes outward when P_v > P_i (indicated by positive J_v values). The fluid flows were used to depict the convective drug flux.

Equation 3 depicts the total interstitial drug flux J_{s,interstitial} and the total transvascular drug flux J_{s,transvascular}. P_d is the drug permeability of tumor vessel wall. P_ev is the Peclet number or the ratio between transvascular convective flux and transvascular diffusive flux. ∇C_{tumor,unbound} is the unbound concentration gradient. D′ is the effective drug diffusivity in tumor and, because it changes with spatial-dependent volume fractions, is spatial-dependent and hence is placed inside the gradient operator.

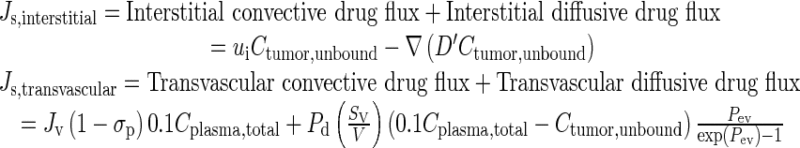3

σ_p is the reflection coefficient of paclitaxel across the tumor vessel wall. The u_i and the two J_s terms are directional: a positive J_{s,transvascular} value indicates a net influx from vessel into tumor interstitium, a positive J_{s,interstitial} value indicates a net influx from tumor interstitium into the peritoneal cavity, and a positive u_i value indicates interstitial fluid flow outward from the tumor center. As shown in the in silico results, the values of these parameters were time- and spatial-dependent.

Equation 4 describes C_tumor,total as the sum of C_plasma,total, C_tumor,bound, and C_{tumor,unbound}. The differential form of the mass conservation equation provides the basis for microscopic analysis of transport phenomena (32); it links the rate of change in extravascular drug concentration at a position within a tumor with the drug flux over the tumor surface area (∇ ⋅ J_{S,interstitial}) and rate of formation or elimination in the tumor (J_{s,transvascular}) (Eq. 5). Drug concentration in tumor interstitium increases when drug in the peritoneal cavity enters the tumor (inward flux through tumor surface) and when drug in the circulating blood exits from the vessels to enter the interstitium. Conversely, the interstitial drug concentration decreases when drug exits from the interstitium to the IP cavity (outward flux through tumor surface) or to blood vessels. Substituting Eq. 4 into 5 yielded Eq. 6 (33,34). B_max is the maximal drug binding capacity to cells. k_assoc and k_dissoc are the respective rate constants of drug association with and dissociation from cells. Equation 6 describes the changes in C_{tumor,unbound} and C_tumor,bound with time and spatial positions. Similar equations were used to depict the transport of antibodies, dopamine, and paclitaxel in normal and tumor tissues (11,33–38).

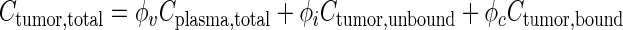4

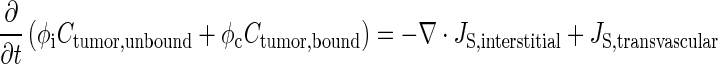5

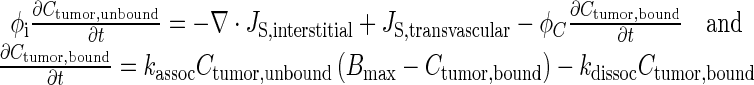6

Model Parameterization

In the model, the tumor was divided into three spatial regions, i.e., tumor periphery, transition zone, and tumor center. The model parameters were either spatial-dependent or spatial-independent.

The spatial-independent parameters include (a) parameters for drug transfer across the vessel wall (L_p, π_v, π_i, σ_p, σ_v, P_d) and drug binding to cells (B_max, k_assoc, k_dissoc), which are determined by properties of tumor and drug, and/or by tumor-drug interaction, and (b) pressure terms P_ip and P_v. The values for L_p, π_v, and π_i were obtained from a previous study (45). The reflection coefficient of plasma proteins and paclitaxel across tumor vessel wall, σ_p and σ_v, respectively, is determined by the ratio of solute radius to vessel pore radius λ (39) and were calculated using Eq. 7 with the assumption that the passage of a spherical solute is through a cylindrical pore. Low σ value indicates high transvascular transport of the solute, and values close to 1 indicate no transvascular transport, e.g., due to the large solute size. The radii of albumin and paclitaxel are about 3.5 and 0.5 nm, respectively (40,41). In view of the literature report that a liposome of 200 nm in radius is transported across the tumor blood vessel wall (42), we used a blood vessel pore radius of 200 nm.

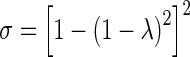7

The tumors used to validate our simulated data were grown on omentum which was mainly perfused by the gastroepiploic vein, which drains to the portal vein. Hence, we used the pressure of portal vein measured in BALB/c mice (equaled 3 mmHg) as P_v (43). P_ip was calculated using the relationship between the IP fluid volume V_ip and P_ip in rats (57) and the experimentally measured changes in V_ip over time in mice.

The drug binding parameters, B_max, k_assoc, and k_dissoc, were calculated using the experimental results of our earlier study that provided data on the cell-bound drug concentration (C_cell-bound) as a function of the extracellular concentration (C_{extracellular}) (22,23). Analysis of this data using Eq. 8 yielded the two binding parameters B_max (maximal saturable binding capacity) and k_d (C_{extracellular} at 50% B_max). k_dissoc, the rate constant for the drug to dissociate from cells, was calculated as (ln 2) divided by (drug efflux half-life, which equaled 1.5 h from our earlier study) (20). k_assoc was calculated from k_dissoc and k_d.

8

The spatial-dependent model parameters that change due to intratumor heterogeneity include the three volume fractions (ϕ_c, ϕ_v, ϕ_i), P_i, and the three related spatial-dependent transport model parameters (D′, K, and S_v/V). We experimentally determined the distribution of the cell volume fraction ϕ_c at different spatial positions in tumors (see “Experimental Section”). Vascular volume fraction ϕ_v was obtained from the literature. Multiple groups of investigators, including our group, have shown that ϕ_v exhibits significant intra- and intertumoral and intersubject heterogeneity (19,44–46). While ϕ_v can vary from 1% to 20% of tumor volume, most studies showed a value of between 2.1% and 5.5%. Accordingly, we chose a tumor-averaged value of 3.5% and arbitrarily assigned a value of 5% in the tumor periphery and 1% in the tumor center. Interstitial volume fraction ϕ_i was calculated using the relationship ϕ_v + ϕ_i + ϕ_c = 1.0.

P_i was determined by P_v and P_ip and was generated during the static model of computation (see “Computation Methods”). For K and S_v/V, we used the values from literature reports as the values in tumor periphery and then calculated the values for the central tumor regions. For the transition zone between tumor center and periphery, we used the piecewise cubic interpolation method to link the values in the tumor center (radial position r of between 0 and 1,200 μm) and periphery (r of between 1,500 and 2,000 μm). S_v/V is a product of microvascular vessel length and vessel perimeter per unit volume; we used the reported value of S_v/V in tumors (Table I) as the value in the tumor periphery. The S_v/V value in tumor center was calculated as the multiplication product of the center-to-periphery ratios for microvascular vessel length and vessel perimeter (0.18-fold and 1.35-fold, respectively) in murine skin melanoma with a 10-mm diameter (16). For hydraulic conductivity K in tumor tissue, we used the value in a previous report (39) as the value for tumor periphery, and, because K is linearly correlated with ϕ_i (47), the K value in the tumor center equaled ϕ_i in the tumor center divided by ϕ_i in the tumor periphery.

Table I.

Values of Model Parameters

From literature reports (references in parenthesis)
K, hydraulic conductivity of tumor tissue in periphery	2.5 × 10−7 cm2/mmHg/s (39)
L p, hydraulic conductivity of vessel wall	1.86 × 10−6 cm/mmHg/s (39)
S v/V, vessel surface area/unit tissue volume in tumor periphery	200 cm2/cm3 (37)
P d, permeability of vessel wall to paclitaxel	2.0 × 10−5 cm/s (68)
P v, microvascular hydrostatic pressure	3.0 mmHg (43)
P ip, pressure in intraperitoneal cavity	−0.2 mmHg (57)
πi, osmotic pressure of interstitial proteins	19.8 mmHg (39)
πv, osmotic pressure of plasma proteins	17.3 mmHg (39)
Calculated
D int, drug diffusion coefficient in tumor interstitium	0.77 × 10−6 cm2/s
D′0, drug diffusion coefficient in tumor periphery	0.27 × 10−6 cm2/s
σ v, reflection coefficient of vessels for plasma protein	0.0012
σ p, reflection coefficient of vessels for paclitaxel	2.5 × 10−5
Experimentally determined
A, intercept of distribution phase in C ip,total vs. time plot	415 μM
B, intercept of elimination phase in C ip,total vs. time plot	7.34 μM
A′, intercept of distribution phase in C plasma,total vs. time plot	7.18 μM
B′, intercept of elimination phase in C plasma,total vs. time plot	0.35 μM
α ip, rate constant of distribution phase in C ip,total vs. time plot	0.41/h
β ip, rate constant of elimination phase in C ip,total vs. time plot	0.16/h
α p, rate constant of distribution phase for C plasma,total vs. time plot	0.67/h
β p, rate constant of elimination phase for C plasma,total vs. time plot	0.09/h
k p, rate constant for drug absorption into blood	0.95/h
B max, maximum cell binding capacity for paclitaxel	81.8 μM
k d, equilibrium concentration for bound paclitaxel	0.281 μM
k dissoc, rate constant of paclitaxel dissociation from cells	0.462/h
k assoc, rate constant of paclitaxel association with cells	1.64/μM/h

Diffusivity in tumor tissue D′ and diffusivity in tumor interstitium D_int were calculated using paclitaxel diffusion coefficient in aqueous solution D_aqueous, radii of paclitaxel (r_s) and interstitial matrix protein fiber (r_f), volume fraction of interstitial matrix F_im, and tortuosity τ (11,34,48), as depicted in Eq. 9. For D_aqueous, we used the average of the two available values in protein-free buffers: 0.766 × 10⁻¹⁰ m²/s (49) and 3.1 × 10⁻¹⁰ m²/s (50), which equaled to 1.933 × 10⁻¹⁰ m²/s. The respective values of F_im, r_f, and r_s were 0.06, 20 nm, and 0.5 nm (51). For tortuosity, we used the value of 2.5 established for rat cerebellum and rat peritoneal tissue (11,33). The calculated D′ value was used as the value in the tumor periphery D′₀. D′ in the tumor center was calculated as for K.

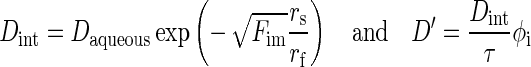9

Experimental Section

The drug concentration-time profiles in the peritoneal fluid and plasma were obtained from our earlier study where nontumor-bearing mice were given an IP dose of paclitaxel (52,53). The C_plasma,total-time profile was obtained by analyzing the drug concentrations in plasma at predetermined times. The determination of C_ip,total-time required several steps. Our earlier study provided the drug amount-time profile (obtained by rinsing the cavity with a known volume of physiological saline and determined the total amount in the rinse). This was necessary because the C_ip,total-time profile could not be directly measured due to the small fluid volume that precluded accurate sampling. In the current study, we measured the V_ip in untreated, nontumor-bearing mice as the difference in the weights of paper tissues before and after being used to blot dry the fluid on the surface of the peritoneum and internal organs (average value of 0.04 mL in five mice). Based on the finding of 7–10-fold increase in V_ip at 4 weeks after IP tumor implantation (53), we estimated a V_ip value of between 0.28 and 0.4 mL in tumor-bearing mice. We further assumed that the change in V_ip from the dosing solution (0.7 mL) was transient based on the rapid resorption of physiological saline in nontumor-bearing mice observed in a pilot study (75% of the injected 0.5 mL was resorbed within 1 h and 87% within 3 h). The rapid fluid absorption is consistent with the previously reported absorption of iso-osmolar albumin solution (0.8 mL in 1 h and 1.3 mL in 3 h) (54). A constant V_ip value of 0.4 mL for tumor-bearing mice was used in subsequent calculations. Drug concentration-time profiles were analyzed using WinNonlin (Pharsight Corp., Mountain View, CA) to obtain the intercompartmental transfer rate constants.

Measurement of ϕ_c in tumors was performed in mice bearing implanted IP tumors. Briefly, human ovarian SKOV3 cancer cells were injected IP. After tumors were established (on day 42, 3–4 mm in diameter), tumors were excised from animals, mounted on glass slide, stained with hematoxylin and eosin, and photographed (×400 magnification); the area occupied by cells was obtained using image analysis (NIH ImageJ) and was divided by the total area to obtain the ϕ_c.

Computation Methods

All model simulations were performed for an isolated peritoneal tumor (i.e., with minimal attachment or adhesion to other tissues or structures, 4 mm in diameter). The finite element mesh for the tumor domain was defined. Equations to describe interstitial and transvascular transport, and drug concentrations in peritoneal fluid, plasma, and tumor interstitium (including unbound drug, cell-associated drug and total drug) were established and solved numerically using the finite element method with the Chemical Engineering software package of COMSOL Multiphysics 3.5 (Los Angeles, CA). Calculations were performed in two stages. The first stage established the steady-state distribution of fluid pressures and fluxes using the static mode of COMSOL. In the second stage, the steady-state pressure and flux distribution was maintained, and drug fluxes and distributions were determined as a time-dependent process in the dynamic mode. The COMSOL output provided the spatial- and time-dependent drug flux and drug concentrations (in tumor interstitium and across blood vessels), in two-dimensional surface plots. Pilot studies were performed to compare the pressure distribution in three geometries (symmetrical circle, axis-symmetrical 12° angle pie-shaped slice, one-dimensional axial line), calculated by the finite element-based COMSOL, with the analytical results calculated using the published equations for a spherical tumor with constant hydraulic conductivity (37). The comparison showed good agreement between the two methods, with maximal deviations of 0.005%, 0.0001%, and 0.00002% for the three respective geometries. Based on these comparison results, the tumor domain was represented as an axis-symmetrical pie-shaped slice in order to reduce computation time, and the drug concentrations and drug flux along the radius (in the middle of the pie slice) at selected time points were collected using the line plot function in COMSOL.

Model Performance Evaluation

Model performance was assessed by comparing the model-predicted spatiokinetics of paclitaxel in peritoneal tumors with an external dataset generated from the experimental results in mice collected in an earlier study (53). Briefly, mice were implanted with IP SKOV3 cells. After tumors were established (on day 42), mice were treated with IP injection of a mixture of ³H-labeled and nonradiolabeled paclitaxel. Tumors located on the omentum were obtained at 6 h after dose administration (one tumor per mouse, total of four) and flash-frozen in liquid nitrogen. Frozen tumors were cut serially with a cryotome into 20 μm-thick sections and thaw-mounted on glass slides (three sections per slide). The first three–five sections, due to the uneven tumor edges, were discarded. Using phosphor imaging plates, autoradioluminography images were captured by exposure of slides with the radiolabeled sections and microscale autoradiography calibration standards (GE Healthcare/Amersham, Piscataway, NJ). The autoradiogram images were digitized to grayscale values using computer-assisted densitometry analysis. After accounting for background noise, the grayscale values were converted to concentration values using the microscale standards to assess drug concentration as a function of distance from the tumor periphery.

Sensitivity Analysis

Sensitivity analysis was performed to evaluate the relative importance of convective and diffusive transport parameters (S_v/V, K, L_p, D′) and drug-cell biointerface parameters (B_max, k_assoc, k_dissoc) on IP tumor spatiokinetics. The values of individual parameters were decreased or increased 3-fold, and the corresponding simulated results were compared to the baseline results obtained with the original parameter values shown in Table I.

RESULTS

Model Parameterization

P_ip is determined by V_ip. The measured V_ip declined from 1.1 mL immediately after IP dose injection to 0.4 mL by 6 h. These volumes, after adjusting for the body weight-surface area ratios in mice and rats, were equivalent to 10 and 3.7 mL in rats (55,56); the corresponding P_ip values were −0.1 and −0.5 mmHg (57). As these P_ip values were below P_v and would not significantly alter the pressure gradient (P_v − P_ip), we elected to use a constant value of −0.2 mmHg over 6 h to reduce the model complexity. The calculated σ_v and σ_p values were 0.0012 and 2.5 × 10⁻⁵, respectively. With respect to drug-cell biointerface parameters, B_max was determined to be 81.8 μM, and k_d equaled 0.281 μM. k_dissoc equaled 0.462/h, and k_assoc equaled 1.64/μM/h.

The experimentally measured ϕ_c was 57 ± 3% (range, 54–63%) in the outermost 510 μm of the tumor and 32 ± 4% (range, 28–35%) in the tumor center (>800 μm) (up to four tumors per location; three fields per tumor). We used ϕ_c values of 60% in the tumor periphery (0–500 μm from the border) and 30% in the necrotic region (>800 μm distance from the border). Using these ϕ_c values and the ϕ_v values stated in “METHODS”, ϕ_i was calculated to be 35% in tumor periphery, increasing to 69% in the center. The S_v/V, K, and D′ values in the tumor center were calculated to be 25% (equaled 1.35 × 0.18), 1.97 and 1.97 times (both equaled 0.69/0.35), respectively, of the values in the tumor periphery.

Other parameters were determined as described in “METHODS”. Table I summarizes the model parameter values, and Fig. 2a shows the spatial distribution of S_v/V, D′, and K, from the tumor periphery to the tumor center.

Fig. 2.

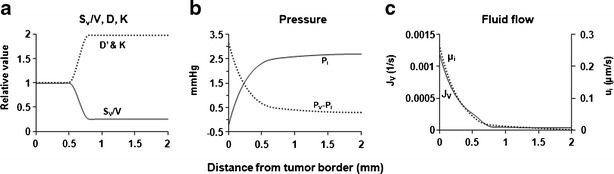
In silico results: intratumoral spatial heterogeneity. a Spatial distribution of S _v/V, D′, and K. b–c Spatial-dependent pressure and fluid flow. Equation 2 was used to simulate P _i, (P _v − P _i), u _i, and J _V, as functions of spatial position. P _ip was set at −0.2 mmHg, and P _v was set at 3.0 mmHg. For P _i, the values increased from the periphery to the center. For (P _v − P _i), positive values indicate vessel-to-interstitium transport, and negative values indicate the opposite interstitium-to-vessel transport. For u _i, the absolute values indicate the velocity (i.e., higher values indicate higher velocity), whereas the flow direction is indicated by its sign (positive values indicate a radial flow away from the center). For J _v, positive values indicate vessel-to-interstitium transport

In Silico Results: Overview

As shown below, the outermost 1.0-mm ring of a tumor, which had the highest S_v/V value and the lowest K and D′ values, displayed the greatest spatial-dependent changes in interstitial and transvascular fluid flow and also the greatest changes in drug flux; the magnitude of changes depended on the pressure and concentration gradients. Accordingly, we focused the in silico studies on the outermost 1 mm of the tumor.

Spatial-Dependent Interstitial and Transvascular Fluid Flow

Figures 2b and 2c show the spatial-dependent changes in the four variables that determine interstitial and transvascular convective transport: P_i, difference between vascular and interstitial pressures (P_v − P_i), u_i, and J_v. Pertinent numerical values and directions of fluid flow are summarized in Table II. The pressure gradient was the highest at the interface between the peritoneal fluid and tumor, leading to the greatest changes in these parameters, increasing or decreasing several folds from the tumor border to reach a nearly constant value at the distance of 0.5–0.75 mm. The direction of u_i reflected the pressure gradient in tumor interstitium and was outward from the tumor center towards the tumor periphery. The direction of J_v, driven by (P_v − P_i), was from tumor vessels into tumor interstitium.

Table II.

Spatial- and Time-Dependent Changes in Transport Flux and Drug Concentration. Total Concentration Represents Volume-Averaged Value and Equals (Sum of Unbound and Bound Concentrations) Divided by Total Volume

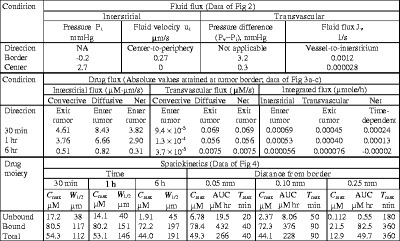
patial- and Time-Dependent Interstitial Convective and Diffusive Drug Flux

Figure 3a shows the interstitial drug flux by diffusion and convection. Over the first 6 h, the convective flux, because P_i exceeded P_ip, was in the tumor center-to-periphery direction, whereas the diffusive flux, because the unbound C_ip exceeded C_{tumor,unbound}, was in the opposite direction.

Fig. 3.

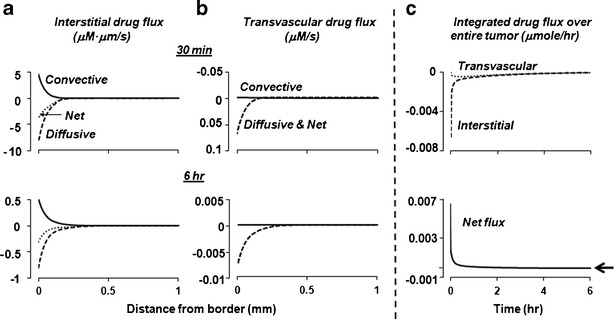
In silico results: interstitial and transvascular drug flux. Equations 1–6 were used to simulate the convective and diffusive drug flux as functions of spatial position, at time points ranging from 1 min to 6 h. P _ip was set at −0.2 mmHg and P _v, at 3.0 mmHg. For interstitial drug flux, positive values indicate flux from the tumor center to periphery. For transvascular drug flux, positive values indicate vessel-to-interstitium transport (entering tumor). In Fig. 3b, the net flux overlapped with the diffusive flux. A positive net flux indicates drug accumulation in tumor, and a negative net flux indicates drug loss from tumor

The results, summarized in Table II, show the drug flux changed with time and spatial position. With respect to spatial position, the greatest changes in interstitial drug flux occurred within the outermost 0.25 mm. The diffusive flux exceeded the convective flux during the first 6 h, in large part due to the greater concentration gradient relative to the pressure gradient in this region. With respect to time, both convective and diffusive fluxes in tumor interstitium were highest at early time points, reduced by ∼25% from 30 min to 1 h, followed by an additional 8-fold decline from 1 to 6 h. The total flux, as the sum of convective and diffusive fluxes, reduced over time by about 12-fold from 30 min to 6 h.

Spatial- and Time-Dependent Transvascular Convective and Diffusive Drug Flux

Figure 3b shows the transvascular drug flux by diffusion and convection; Table II summarizes the numerical results. The transvascular convective flux, driven by (P_v − P_i) and moving fluid from the vessels to interstitium (entering the tumor), was minimal, due to the low C_plasma. In comparison, the diffusive flux in the tumor periphery during the first 6 h, due to the large concentration gradient between C_ip and C_plasma, was consistently in the interstitium-to-vessel direction, exceeding the convective flux by 2–3 orders of magnitude. Hence, the net transvascular flux was nearly identical to the transvascular diffusive flux.

Drug Concentration-Depth-Time Profiles

Figure 4 shows the profiles; the numerical results are summarized in Table II. As discussed below, the directions of concentration changes (i.e., increase or decrease) varied with time and spatial positions and were different for the unbound and cell-associated drug moieties.

Fig. 4.

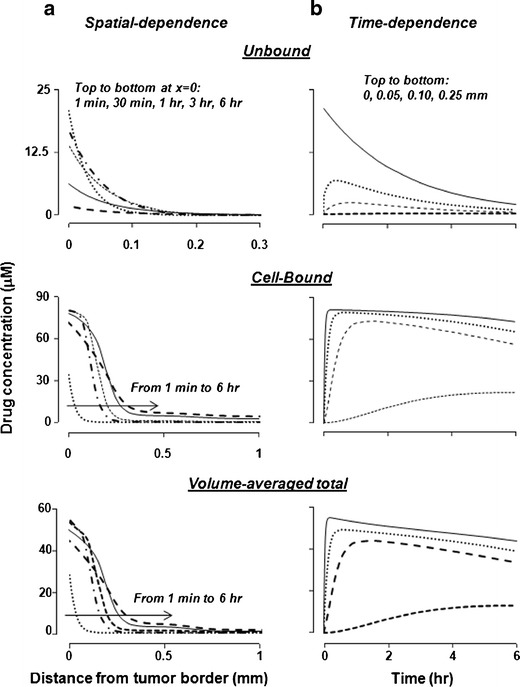
In silico results: tumor spatiokinetics. a Simulated changes of drug concentrations with respect to spatial position in an IP tumor at 1 min to 6 h after dose administration. The volume-average total concentration is (unbound concentration + bound concentration) divided by (tissue volume). For the unbound concentrations, the curves from top to bottom at x = 0 corresponded to 1 min, 30 min, 1 h, 3 h, and 6 h. For the bound- and volume-averaged total concentrations, the lines from left to right along the arrow corresponded to 1 min, 30 min, 1 h, 3 h, and 6 h. Note the different scales for the x-axis. b Simulated changes of drug concentrations with respect to postadministration times at four spatial locations (0, 0.05, 0.10, and 0.25 mm from the tumor border)

For the unbound drug, the maximal concentrations (C_max) at various spatial positions were highest at 1 min and then decreased with time, reflecting the decrease of unbound C_ip with time. The results on the C_{tumor,unbound} values at different spatial positions (Fig. 4a, top panel) showed decreasing C_max values with increasing distance from the tumor border (e.g., C_max decreased by about 60-fold over a 0.2-mm distance from 0.05 to 0.25 mm). However, due to the continuous periphery-to-center drug transport over time, the concentration decline became shallower with time such that the unbound drug concentrations in deeper parts of the tumor at later times exceeded the concentrations at early times (e.g., compare the concentrations at 1 min with the concentrations at 0.5–3 h, at a 0.1-mm distance from the tumor border). A quantitative measure of the steepness of the net concentration change is W_1/2 (distance over which C_{tumor,unbound} values declined by 50%, a longer W_1/2 indicates more shallow concentration decline and deeper penetration); the ∼20% increase in W_1/2 value from 30 min to 6 h reflected the continuous drug transport. With respect to time (Fig. 4b), the C_max in deeper parts of the tumor was reached after a delay, and the time to reach C_max (T_max) increased with increasing distance from the tumor border (9-fold longer T_max at 0.25 mm compared to 0.05 mm). The area under the concentration-time curve or AUC at these locations also decreased with increasing distance (40-fold lower AUC values at 0.25 mm compared to 0.05 mm).

Results of the bound (cell-associated) drug are shown in Fig. 4 middle panels. The changes in the bound concentrations differed from the unbound concentrations in several ways. First, the C_max values for the bound drug at 30 min to 6 h were 4 to 38 times higher compared to the unbound drug; the fold difference between the bound and unbound concentrations increased with distance from the tumor border and time (e.g., from 13-fold at 0.05 mm to 200-fold at 0.25 mm). Similarly, the fold difference in the AUC values of the unbound and bound concentrations increased with distance, from 22-fold at 0.05 mm to 150-fold at 0.25 mm. These changes reflected the time delay in cell binding and the saturable binding. At times of 30 min to 3 h, C_max at the tumor periphery was limited by the B_max value. The ratio of bound and unbound concentrations at equilibrium, which equals B_max/(k_d + C), increased towards the asymptote value of 290 (equals B_max/k_d) as C decreased. Second, the T_max values for the bound concentrations were about 2-fold longer compared to the unbound concentrations. Third, instead of the continuously decreasing C_max values over time observed for the unbound drug, changes in the C_max values for the bound drug initially increased several-fold from 1 min to reach the highest level at 30 min, followed by a slight ∼10% decline at 6 h (e.g., compare Fig. 4a, top and middle panels); the delay to reach C_max reflected the slower rate of drug binding to cells relative to the interstitial transport of the unbound drug, whereas the subsequent declines from 30 min to 6 h were due to the decreasing drug concentrations available for binding. The decreases in the C_max value of the bound drug from 30 min to 6 h were accompanied by increases in W_1/2. The greater increase in W_1/2 for the bound drug relative to the unbound drug (i.e., 68% vs. 18%) was due to the slow drug dissociation from cells that in turn limited the drug removal by interstitial or transvascular transport. Fourth, the greatest difference between bound and unbound concentration-time profiles (Fig. 4b, top and middle panels) was observed at the outer rim of the tumor where the unbound concentration was at the highest level at the earliest time point (time zero), whereas the bound concentration reached the highest level after a delay of 20 to 360 min (see Table II). The delay reflected the relatively slow rate of drug association with cells.

Comparison of the C_max and AUC values for the unbound and bound drugs at different times and different spatial positions indicated that the bound drug was the major drug moiety, especially at deeper parts of the tumor. Due to the much higher C_tumor,bound compared to C_{tumor,unbound}, the changes in C_tumor,total, the volume-averaged total of bound and unbound concentrations (see Eq. 5), mirrored the changes in C_tumor,bound (Fig. 4, bottom panels). For C_tumor,total, the C_max and AUC values decreased with increasing distance from the tumor border by 4- to 5-fold from 0.05 to 0.25 mm, whereas the T_max value increased about 9-fold over the same distance.

Of note is the different kinetics at different spatial positions (Fig. 4b). Both the bound and unbound drug concentrations at the tumor periphery rose rapidly and began to decline after 1 h or sooner, whereas the concentrations at greater distances (e.g., 0.25 mm depth) rose slowly and continued to rise after 6 h. These data indicate a significant lag time for drug penetration into the deeper parts of a tumor, in addition to the substantial spatial-dependent differences in concentrations shown in Fig. 4a.

Interstitial vs. Transvascular Flux Over Whole Tumor

The transvascular and interstitial drug flux had different units and could not be directly compared. Integration of the transport flux over the entire tumor volume yielded the common unit of the total amount of transported drug per unit time or micromoles per second, which enabled the comparison of the relative contribution of interstitial and transvascular flux to the total drug flux.

Two different methods were used to integrate interstitial and transvascular flux. The integration of interstitial drug flux over the entire tumor volume used Gauss’s theorem, which states that the total flux in the entire tissue equaled the multiplication product of flux at the tissue border where the radial position r equaled the tissue radius R and tissue surface area (Eq. 10) (32).

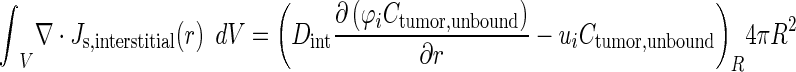10

Integration of the transvascular drug flux over the entire tumor volume was achieved using Eq. 11.

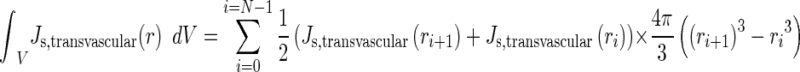11

N is the number of nonuniform concentric segments of the tumor, and i is the radial position of a segment where i = 0 represents the tumor center and i = N represents the tumor border. A tumor was divided into ∼200 segments along the radius and the values of J_{s,transvascular} (r_i) were obtained from the COMSOL analysis output. The multiplication product of average of J_{s,transvascular} (r_i) and J_{s,transvascular} (r_i+1), and volume of segment yielded the J_{s,transvascular} for the segment; summation for all segments yielded the integrated transvascular drug flux for the entire tumor.

The integrated flux changed with time due to time-dependent changes in C_plasma,total and C_ip,total, but, because it represented the value in the whole tumor, was not spatial-dependent. Figure 3c shows the results for the first 6 h after an IP dose. The integrated interstitial drug flux was in the tumor periphery-to-center direction (entering the tumor from peritoneal fluid) and was highest at time 0, followed by a continuous decline by about 110-fold at 6 h (12-fold between 30 min and 6 h). In comparison, the integrated transvascular drug flux was in the tumor interstitium-to-vessel direction (exiting the tumor through vessels). Furthermore, the transvascular flux, due to the lag time for the drug to reach vessels, first increased with time to reach a peak at about 20 min, followed by a slow decline (due to a decrease in unbound C_ip and C_{tumor,unbound}) by about 6-fold at 6 h (Table II).

Figure 3c compares the interstitial drug flux to transvascular drug flux. As a negative interstitial flux indicates drug influx from the peritoneal cavity into the tumor and a positive transvascular flux indicates drug influx from the vessels into the tumor, the net flux into the tumor equals transvascular flux minus interstitial flux. The high interstitial flux compared to low transvascular flux at early time points led to the highest net flux initially. However, the difference between the two fluxes diminished over time, and the transvascular flux became slightly higher compared to the interstitial flux, resulting in a slightly negative net flux after 4 h.

Evaluation of Model Performance

Figure 5a shows the autoradiographic results, and Fig. 5b shows the drug concentration-spatial relationship. The drug concentrations were the highest at the tumor periphery, followed by a decline with increasing distance from the tumor border. The four tumors, in spite of the identical treatments and the identical anatomical location, showed substantial intertumor variations (2-fold for C_max, 3-fold for AUC, up to 15-fold difference for individual data points). In the four tumors, the concentrations were the highest at 0.1 mm from the tumor border (average C_max of 25.1 μM) and declined sharply by 14-fold over 1 mm in distance, with an average W_1/2 of 164 μm.

Fig. 5.

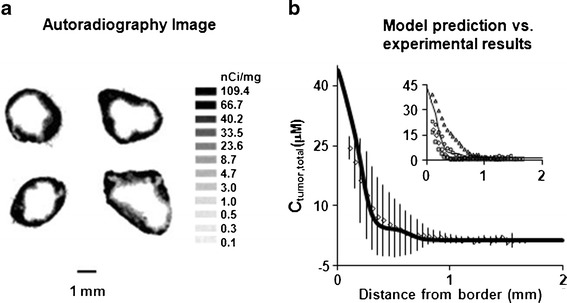
Comparison of experimentally observed and model-simulated spatiokinetics in tumors. Mice bearing implanted IP tumors were treated with a mixture of ³H-paclitaxel and nonradiolabeled paclitaxel. At 6 h posttreatment, tumors were excised and processed for autoradiography (see “METHODS”). Drug concentrations were obtained by converting the grayscale values derived from densitometric analysis of autoradiograms. Results were normalized to a paclitaxel-equivalent dose of 10 mg/kg. a Autoradiograms of four tumors (one per mouse). b Concentration-tumor depth profile at 6 h. Solid line, model-simulated profile; symbols and bars, mean (±1 SD). For the four tumors, the average C _max at 0.1 mm from the tumor border was 25.1 μM (range, 18.5–39.8 μM), and the average W _1/2 value was 164 μm (range, 121–231 μm). Inset, model-simulated (solid line) vs. profiles of individual tumors (symbols)

Separately, we used Eqs. 1–6 to simulate the C_tumor,total-depth profile at 6 h in an IP tumor of a similarly treated mouse, using the experimentally determined C_ip,total-time and C_plasma,total-time data as the boundary conditions. The simulated C_tumor,total-depth results generally agreed with the experimental results. Namely, the simulated and experimental results showed similar C_max values (33.7 vs. 25.1 μM at 0.1 mm), similarly rapid concentration drop, and similar W_1/2 values (126 vs. 164 μm). The deviations between the model-predicted concentrations and the average experimental data averaged 23% for individual data points (range of 0.9% to 44%), which was about 60-fold lower compared to the intertumor variation among animals. The difference in AUC between model-predicted and averaged experimental data was about 1% (7.07 vs. 7.15 μM h).

Sensitivity Analysis

Table III shows the in silico results of altering the convective and diffusive transport and drug-cell biointerface parameter values, by increasing or reducing 3-fold relative to the baseline values, on AUC in a specified position in the tumor (0.1 mm from the tumor border) and C_max in the same position (at a single time point of 6 h).

Table III.

Sensitivity Analysis. In Silico Studies Were Performed to Examine the Effects of Changes in Convective and Diffusive Transport Parameters and Drug-Cell Biointerface Parameters on the Total Drug Exposure (Expressed as AUC), C _max, and Penetration Depth from the Tumor Border (Expressed as W _1/2). Parameter Values Were Increased to Three Times the Baseline Values or Reduced to One-third of the Baseline Values. The Resulting Changes in AUC, C _max, and W _1/2 are Expressed as Percent Change from the Results Obtained with the Baseline Parameter Values Shown in Table I. Simulation Was Performed for the Position of a 0.10-mm Distance from the Tumor Border (See Table II for the Baseline AUC and C _max Values)

At 0.10 mm from tumor border	Convective transport		Diffusive transport	Convective + diffusive	Drug-cell biointerface
	K	L p	D i	S v/V	B max	k dissoc	k assoc
% change from baseline due to 3-time increase in parameter values
AUC	−8.0	−8.2	+16	−28	+167	+1.0	+14
C max at 6 h
Unbound	−33	−34	+194	−69	−39	+2.4	−1.2
Bound	−6.1	−6.3	+7.4	−24	+182	+0.3	+7.5
Total	−6.6	−6.9	+11	−25	+178	+0.5	+7.4
% change from baseline due to 3-time decrease in parameter values
AUC	+4.6	+4.6	−65	+12	−65	−5.5	−25
C max at 6 h
Unbound	+33	+33	−92	+104	+26	−1.2	+3.0
Bound	+2.0	+2.1	−60	+6.0	−66	−5.9	−22
Total	+2.6	+2.7	−60	+7.9	−64	−6.4	−22

As shown above, the net fluid flow and accordingly the transvascular drug flux, due to the pressure gradients, is in the outward direction of blood vessels to tumor interstitium to the peritoneal cavity. On the other hand, the diffusive transport, due to the drug concentration gradient, is in the opposite direction of the peritoneal cavity to tumor interstitium to vessels. Hence, three-fold increases of the two convective transport parameters (K, L_p) reduced the drug entry to tumors, resulting in lower AUC and lower C_max for both unbound and cell-associated drug concentrations. On the contrary, increasing the tumor diffusivity D′ enhanced the AUC and C_max. Interestingly, increasing S_v/V, which affects two transport processes in opposite directions (transvascular convective flux and transvascular diffusive flux), resulted in 2- to 4-fold greater decreases in AUC and C_max compared to L_p. Because S_v/V and L_p are co-multipliers in the equation that describe the transvascular convective flux (i.e., having equal weights, see Eq. 2), the difference is derived from the second effect of S_v/V on transvascular diffusive flux (see Eq. 3). This indicates that the transvascular diffusive transport has a greater effect on removing the drug from tumor interstitium compared to the convective transport. Decreasing these four transport parameters yielded opposite changes in AUC and C_max, albeit to different extents.

Altering drug-cell biointerface parameters also affected the AUC and C_max values. Changes in k_assoc and k_dissoc yielded changes in about the same magnitude as the two convective transport parameters K and L_p, whereas changes in B_max led to much greater changes. Increasing and decreasing B_max led to nearly proportional increases and decreases in AUC and total C_max (with greater changes in the cell-associated C_max relative to the unbound C_max).

The above sensitivity analysis results provide a snapshot of the relative contributions of the various transport and biointerface parameters, at a single position within the tumor and at a single time point. The dynamic nature of these processes and their opposing effects on drug delivery and residence indicate that the relative rank orders of these parameters are likely to depend on time as well as spatial position in the tumor.

DISCUSSION

The present study provided the first-generation multiscale tumor spatiokinetic model for IP therapy, to depict the time- and spatial-dependent drug concentrations within tumors as functions of C_ip,total-time and C_plasma,total-time profiles, drug properties, transport mechanisms, intratumoral heterogeneities, and physiological properties. The in silico results illustrate (a) the interdependent and, at times, opposing effects of many kinetic processes and variables on the interstitial and transvascular drug flux, resulting in changing drug concentrations with time and spatial positions in the tumor; (b) both diffusive and convective transports play a role in tumor spatiokinetics; (c) significant qualitative and quantitative differences in spatiokinetics between cell-associated and unbound drug concentrations; and (d) the importance of drug-cell interaction on drug transport and spatial distribution.

Compared to the earlier models summarized in the “INTRODUCTION,” the current model included several beneficial features: (a) The model includes both diffusive and convective transport mechanisms, thereby enable the studies of situations where pressure-driven transport plays an important role (e.g., due to the presence of fluid such as the 2-L dosing volume used in IP therapy or the ascites fluid accumulation). (b) The model accounts for the intratumor heterogeneities in tumor cell and vessel densities and the spatial-dependent changes in key transport parameters (S_v/V, D′, K). (c) The model accounts for drug association with tumor cells, which represented a major drug depot in tumors. (d) The model uses peritoneal and systemic PK as boundary conditions, which enables the use of these PK data to calculate the spatiokinetics in peritoneal tumors.

A reason that convective transport was omitted in a previous study is because the high interstitial pressure in tumor was expected to result in insignificant contribution of convection relative to diffusion (14). We included convective transport for several reasons. First, results in Fig. 3b indicate negligible transvascular convective drug flux (in the direction of blood to the interstitium) in part due to the low pressure-driven convective flow; this aspect is in agreement with the assumption in the previous study (14). However, because the other cause of the negligible flux is the low C_plasma at early time points, this assumption will not hold, as the contribution of transvascular convective flux increases at later times when C_plasma becomes appreciable relative to C_tumor. Second, the interstitial convective fluid flux, because it is in the direction of exiting from the tumor, counters the flux going from the peritoneal fluid into the tumor and, as shown in Fig. 3a, played a role in determining the overall interstitial drug flux. Third, sensitivity analysis results indicate that 3-fold increases in the values for convective transport parameters (K, L_p) yielded changes in drug delivery and residence time in tumor (AUC and C_max) that were about one-half of the changes derived from increasing D′, indicating that convective transport cannot be ignored. Fourth, excluding convective transport will eliminate the opportunity to examine the effects of changing P_ip (e.g., increase in peritoneal fluid volume due to ascites formation). Fifth, we plan to include normal tissues (e.g., surrounding a tumor) in the next generation models. The higher interstitial pressure in tumors relative to surrounding normal tissues is expected to result in substantial pressure-driven fluid flow at the tumor-normal tissue interface. Sixth, our laboratory has shown that tumor priming by paclitaxel-induced apoptosis resulted in transient changes in tumor vasculature and structure that would enhance both convective and diffusive transport (19). Inclusion of convection transport enables the long-term goal of modeling the effects of the above dynamic processes on tumor spatiokinetics.

The multiscale model in the present study contained a number of simplifying assumptions, including (a) constant P_ip; (b) constant V_ip; (c) no drug degradation in tumors; (d) no temporal effects of paclitaxel on tumor vasculature, tumor cell density, or tumor structure; (e) the amount of paclitaxel bound to extracellular macromolecules in tumor interstitium was insignificant compared to the total drug amount; and (f) no effect of Cremophor micelles on drug transport. Assumption (d) is valid during the early time points (<16–24 h) when drug-induced apoptosis and the related vascular changes are not yet apparent (19). Assumption (e) is also valid at early time points when the drug associated with tumor cells was the major component of C_tumor,total and exceeded the drug binding to extracellular proteins (e.g., collagen, elastin). Comparison of the in silico results with the experimental results on tumor spatiokinetics at 6 h showed close alignment, indicating good performance of the multiscale tumor spatiokinetic model at early time points. Studies are going to evaluate the effects of the drug-induced apoptosis and vascular changes on tumor spatiokinetics at later times, e.g., >16–24 h.

As discussed in our reviews (2,58–61), tumors are highly heterogeneous with respect to size, vascularization, blood flow, growth rate, capillary permeability, extracellular protein contents, and tumor cell density. In addition, many of these properties are dynamic, dependent on the host (e.g., larger tumors in humans than in mice), are patient-dependent (e.g., location in relation to normal tissues, size), diverse in nature, and will change with time (e.g., tumor growth) or with treatments (e.g., apoptosis or necrosis due to chemotherapy or irradiation, changes in vasculature due to antiangiogenic treatment). In addition, changes in one property can affect other properties (e.g., increase in size will affect the vascularization). Such diverse and dynamic tumor properties create uncertainties on drug delivery to target sites. For example, to what extent do treatment-induced changes in vasculature and vessel pore size improve drug delivery? How should one select treatments (dose intensity and dosing interval) in anticipation of intratumoral heterogeneity in the transport mechanisms (diffusion vs. convection) in different parts of a tumor? What are the margins of error if the treatment design/selection does not take into account these dynamic processes? How and when to use antiangiogenic therapy to retard the drug removal from peritoneal tumors, since antiangiogenic therapy has dual and time-dependent effects with initial destruction of less mature vessels and stabilization of other vessels (resulting in temporary increases in tumor blood flow) followed by reduction in blood flow (due to reduced vessel wall permeability P_d and vessel conductivity L_p, reduced vessel density and lowered S_v/V, reduced vessel radius and pore size) (39,62,63). We propose that comprehensive spatiokinetic models that capture the above tumor properties can be used to interrogate, in a quantitative manner, how changes in these diverse and dynamic pathobiological parameters, separately or collectively, affect the target site pharmacokinetics. Such spatiokinetic models would provide a method to evaluate and optimize treatment strategies. For example, Fig. 4a shows the steep concentration decline over a relatively short distance from the tumor border, suggesting (a) inadequate drug delivery to deeper parts of a tumor as a cause of the clinical observation that IP paclitaxel has limited efficacy in patients with bulky tumors (6,17,64–66) and (b) enhancing the inward transport (into tumor) is a potentially useful strategy. The latter may be accomplished by using higher P_ip to reverse the fluid flow from outward direction to inward direction or by increasing interstitial porosity (e.g., using paclitaxel tumor priming) to enhance the diffusivity. Second, results of sensitivity analysis, performed for a single position in the tumor over 6 h, indicate that transvascular diffusive transport is an important mechanism of removing the drug from tumor interstitium. Accordingly, strategies that retard this transport will enhance the drug delivery and residence in tumors. One approach is to diminish the blood flow to tumors; this is in agreement with an earlier in silico study showing that adding the antiangiogenic bevacizumab enhanced the activity of IP topotecan (14). Another possibility is to reduce the transvascular concentration gradient, e.g., by adding intravenous chemotherapy.

Our long-term goal is to extend the current, first-generation spatiokinetic model to a comprehensive model that accounts for time-dependent tumor pathobiological changes and drug-cell-protein interactions. Ideally, this model can be used to simulate the drug concentrations at different locations of a tumor at different times under wide-ranging treatment conditions. Accordingly, an investigator can predict the delivery and residence of a drug at the intended target sites based on the numerical values of model parameters that are readily measured in vitro or ex vivo (e.g., drug-cell-protein interactions can be measured using cultured tumor cells) or in vivo (e.g., whole-body pharmacokinetics). Another area of potential utility is cancer nanotechnologies, as we have shown that the three-dimensional diffusive transport of nanoparticles with different sizes and surface charges in tumor spheroids can be predicted based on biointerface parameters measured in monolayer cultures (51).

CONCLUSION

We have developed, and experimentally verified, a multiscale spatiokinetic model to depict the drug transport and delivery in peritoneal tumors at early times or before drug-induced tumor structural changes, during IP therapy. Spatiokinetic models provide a means to predict the spatial-dependent pharmacokinetics and thereby the pharmacodynamics of a given treatment. The current spatiokinetic model is being applied together with ex vivo pharmacodynamic data to elucidate the role of drug transport in the limited efficacy of IP therapy in patients with bulky tumors (67).

Abbreviations

AUC

area under curve

B_max

maximal cellular binding capacity of paclitaxel

C_ip,total

total drug concentration in peritoneal fluid

C_max

maximal drug concentration in tumor

C_plasma,total

total drug concentration in plasma

C_tumor,bound

concentration of cell-associated drug in tumor

C_tumor,total

total drug concentration in tumor

C_{tumor,unbound}

concentration of unbound drug in tumor

D_aqueous

diffusivity in water

D′

effective tumor diffusivity

D_int

diffusion coefficient in tumor interstitial space

IP

intraperitoneal

J_{s,interstitial}

interstitial drug flux

J_{s,transvascular}

transvascular drug flux per unit volume

J_v

transvascular fluid flux per unit volume

K

tissue hydraulic conductivity

k_assoc

rate constant of paclitaxel association with cells

k_d

paclitaxel binding constant

k_dissoc

rate constant of paclitaxel dissociation from cells

k_p

pharmacokinetic rate constant for systemic absorption

L_p

hydraulic conductivity of vessel wall

P_d

permeability of vessel wall to paclitaxel

P_ev

Peclet number

P_i

interstitial fluid pressure

P_ip

peritoneal pressure

PK

pharmacokinetics

P_v

microvascular pressure

r

radial position in tumor

R

radius of spherical tumor

S_v/V

vessel surface area per unit tissue volume

T_max

time at which C_max is reached

tumor spatiokinetics

time-dependent and spatial-dependent drug concentrations in tumors

u_i

interstitial fluid velocity

V_ip

volume of peritoneal fluid

W_1/2

half width

π_i

osmotic pressure of interstitial proteins

α_ip

α_p, β_ip, β_p, PK rate constants for IP fluid and plasma

ϕ_c

cellular volume fraction

ϕ_i

interstitial volume fraction

ϕ_v

vascular volume fraction

π_v

osmotic pressure of plasma proteins

σ_v

reflection coefficient of vessels for plasma proteins

σ_p

reflection coefficient of vessels for paclitaxel