Synchronization criteria of discrete-time complex networks with time-varying delays and parameter uncertainties

Abstract

This paper is pertained with the synchronization problem for an array of coupled discrete-time complex networks with the presence of both time-varying delays and parameter uncertainties. The time-varying delays are considered both in the network couplings and dynamical nodes. By constructing suitable Lyapunov–Krasovskii functional and utilizing convex reciprocal lemma, new synchronization criteria for the complex networks are established in terms of linear matrix inequalities. Delay-partitioning technique is employed to incur less conservative results. All the results presented here not only depend upon lower and upper bounds of the time-delay, but also the number of delay partitions. Numerical simulations are rendered to exemplify the effectiveness and applicability of the proposed results.

Introduction

Complex networks are composed of a large number of highly interconnected dynamical units and therefore exhibit very complicate dynamics. Undoubtedly, many systems in nature can be described by models of complex networks, which are structures consisting of nodes connected by links. Examples of complex networks include Internet, a network of routes and domains; World Wide Web, a network of websites; Brain, a network of neurons; Social networks, a network of people; Global economy, a network of national economies, which are themselves networks of markets; and markets are themselves networks of interacting producers and consumers; electrical power grids and so on (Wang and Chen 2003; Strogatz 2001; Albert et al. 1999). Since most of the practical systems can be modeled by complex dynamical networks, it has drawn much research attention from various fields. In particular, one of the interesting phenomena in complex networks is the synchronization, which is an important research area with rapidly increasing results (Gao et al. 2006; Wang et al. 2008; Balasubramaniam et al. 2011).

In complex dynamical networks, synchronization of all its dynamical nodes is an important one. Network synchronization phenomena has been found in different forms both in nature and in man-made systems, such as fireflies in the forest, applause, description of hearts, distributed computing systems, routing messages in the internet, etc. In recent years, many researchers develop various efficient synchronization techniques for complex networks, and many profound results are established (Li and Chen 2004; Cao et al. 2006; Delellis et al. 2009).

The characteristic of time-delayed coupling is very common in biological and physical systems, etc, see (Martì and Masoller 2003; Atay et al. 2004; Boccaletti et al. 2006; Wu et al. 2012; Balasubramaniam and Jarina Banu 2013), some of time-delays are trivial so which can be ignored, while some others cannot be ignored. Time-delays occur in complex networks because of the network traffic congestions as well as the finite speed of signal transmission over the links. And it should be pointed out that time-varying delays are more general than the constant ones which are usual in general complex dynamical network.

One significant recent discovery in the field of complex networks is the observation that a number of large-scale and complex networks are scale-free, that is, their connectivity distributions have the power-law form (Barabási et al. 1999a, b). A scale-free network is inhomogeneous in nature. Most nodes have very few connections and only a small number of nodes have many connections. This inhomogeneous feature makes a scale-free network error tolerant but vulnerable to attacks. More precisely, the connectivity of such networks is highly robust. A scale-free network does not have a fixed size but can grow with time. The scale-free networks belongs to the family of networks known as "small-world" networks. The presence of scale-free emerging properties in many real-world networks provides initial evidence that the self-organizing (synchronization) phenomena do not only depend on the characteristics of individual systems, but are general laws of evolving networks.

Recently, synchronization behavior of delayed complex networks have been widely studied. For example, a framework for synchronization of linearly coupled networks of both continuous-time and discrete-time have been investigated in (Gao et al. 2006; Yue and Li 2010; Zhang et al. 2010), whereas the similar topic was also discussed by Lu and Chen (2004); Lu and Ho (2010) without assuming that the coupled configuration matrix is symmetric and irreducible. Wang et al. (2012) investigated the stabilization and synchronization of dynamical networks with different nodes by using decentralized control. The problem of synchronization for an array of coupled stochastic discrete-time neural networks with discrete and distributed time-varying delays have been studied by Wang and Song (2011). Also Yue and Li (2010) have derived the synchronization stability criterion for complex dynamical networks with interval time-varying delays based on a piecewise analysis method and the convexity of matrix inequalities. Fei et al. (2009) revisited the synchronization stability problem for discrete complex dynamical networks with time-varying delay and constructed a new Lyapunov functional by dividing the time-varying delay into a constant part and a variant part. Moreover, the synchronization and state estimation problems for discrete-time complex network by utilizing a time-varying real-valued function and the Kronecker product are investigated by Shen et al. (2011) and the authors provided a novel concept of bounded 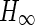synchronization. Synchronization problems have been intensively studied for delayed complex networks with stochastic perturbation (Yu and Cao 2007; Liang et al. 2008a). Recently, some interesting results are reported in the field of synchronization stability. Yang et al. (2013) concerned with input-to-state stability problems for a class of recurrent neural networks model with multiple time-varying delays. Mahdavi and Kurths (2013) studied the synchronization of dynamical neural networks with a neuron of logistic map type and self-coupling connections by utilizing the idea of structured inverse eigen value problem. The oscillations and synchronization problem of two different network connectivity patterns based on Izhikevich model has been investigated by Qu et al. (2013).

Most of the existing results have been concerned with the synchronization problem for continuous-time and deterministic complex networks with or without delays, little progress has been made towards discrete-time complex dynamical networks for details, see (Tang et al. 2010; Park et al. 2009; Cheng and Cao 2011), but discrete-time networks could be more suitable to model digitally transmitted signals in a dynamical way, which have already been applied in a wide range of areas, such as image processing, time series analysis, quadratic optimization problem and system identification. In reality, however, the existence of parameter uncertainties is ubiquitous in a discrete-time fashion. The connection weights of the nodes of complex networks depend on certain resistance and capacitance values that include uncertainties or modeling errors. Motivated by the above discussions, in this paper, we study the synchronization problem for a class of discrete-time complex networks with time-varying delays and parameter uncertainties by constructing new set of Lyapunov functions and employing "delay-partitioning" approach. Therefore, one of the main aims is to reduce the possible conservatism induced by the Lyapunov functional.

The main contributions of this paper can be highlighted as follows: (1) Synchronization criteria for discrete-time complex networks with time-varying delay and parameter uncertainties are developed in terms of LMIs. (2) Delay partitioning approach and reciprocal convex lemma are utilized to reduce possible conservatism. (3) To illustrate the applicability of the proposed results, synchronization of BA scale-free networks and chaotic synchronization of Lorenz system are discussed.

An outline of this paper is as follows. In Sect. 2, the dynamics of complex networks in a discrete-time domain is introduced and some necessary preliminaries are given. In Sect. 3, we establish some synchronization criteria for the discrete-time complex networks by constructing a set of Lyapunov functions. Robust synchronization of uncertain complex dynamical networks are derived in terms of LMIs in Sect. 4. In Sect. 5, some numerical simulations are given to illustrate the theoretical ensues. Concluding remarks are finally stated in Sect. 6.

Notations: Throughout this paper, 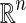and 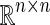denote the n-dimensional Euclidean space and the set of all n × n real matrices respectively. The superscript T and (−1) denote the matrix transposition and matrix inverse respectively. Matrices, if they are not explicitly stated, are assumed to have compatible dimensions. I is an identity matrix with appropriate dimension. The notation * always denotes the symmetric block in one symmetric matrix. 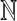denotes the set of all positive integers.

Problem description and preliminaries

Consider the discrete-time complex networks (DCN) with time-varying delays

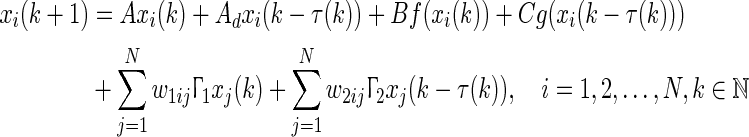1

where 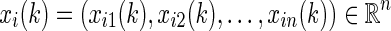is the state vector of the ith node at time k and n denotes the number of nodes in each subsystem. A, A_d, B, and C are known real matrices. 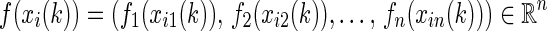and 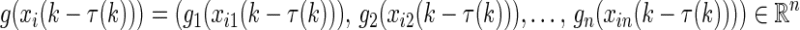are nonlinear vector-valued functions satisfying certain conditions to be given later. The term τ(k) describes the time-varying delay that satisfies

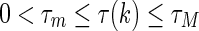2

where 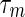and 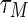are known positive integers representing the minimum and maximum delays. 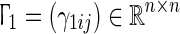and 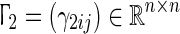are the inner-coupling matrices. If some pairs (i, j), 1 ≤ i, j ≤ n with γ_ij ≠ 0, means that two coupled nodes are linked through their ith and jth state variables. W₁ = (w_1ij)_N × N and W₂ = (w_2ij)_N × N represent the outer-coupling matrices of the networks in which w_sij (s = 1,2) is defined as follows: if there exists a connection between node i and node j (j ≠ i), then w_sij = w_sji = 1, otherwise w_sij = w_sji = 0 (j ≠ i) and the diagonal elements of the matrices w_sii are defined by,

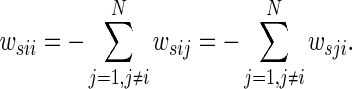3

Suppose that the network (1) is connected in the sense that there are no isolated clusters, that is W₁ and W₂ are irreducible matrices. For the purpose of simplicity, we introduce the following notations

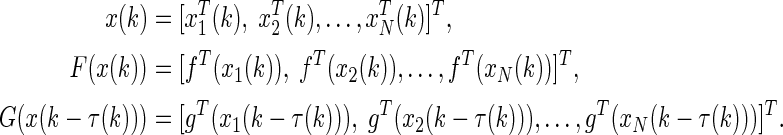By utilizing the Kronecker product of matrices, the DCNs (1) can be written in a more compact form as,

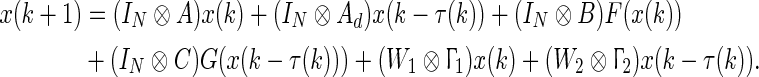4

The initial conditions associated with system (4) are given by

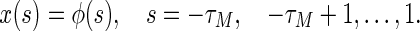5

where ϕ(s) is the initial function of the system.

Assumption 1

For 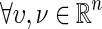, the nonlinear functions 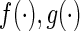are continuous and assumed to satisfy the following sector-bounded conditions

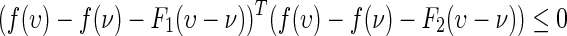6

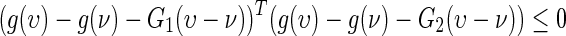7

where F₁, F₂, G₁, and G₂ are known constant real matrices.

Remark 1

The description of nonlinear functions in Assumption 1 are known as the sector-like nonlinearities, which are more general than the commonly used Lipschitz conditions. By adopting such a presentation, it would be possible to reduce the conservatism of the main results.

Before stating the main results, a definition and some lemmas are introduced here.

Definition 1

The discrete-time complex network (1) or (4) is said to be globally synchronized if, for all time-varying delays, the following holds:

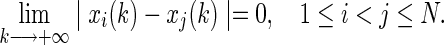Lemma 1

(Horn and Johnson 2001) Let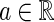andA, B, C, Dbe matrices with appropriate dimensions, the following properties can be proved

1. a(A ⊗ B) = (aA) ⊗ B + A ⊗ (aB)

2. (A ⊗ B)^T = A^T ⊗ B^T

3. (A ⊗ B)(C ⊗ D) = (AC) ⊗ (BD)

4. A ⊗ B ⊗ C = (A ⊗ B) ⊗ C = A ⊗ (B ⊗ C)

Lemma 2

(Park et al. 2011) Let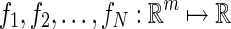have positive values in an open subsetD of 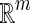. Then, the reciprocally convex combination off_ioverDsatisfies

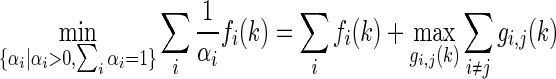subject to

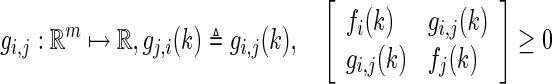Lemma 3

(Boyd et al. 1994) (Schur Complement) Given constant matrices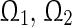and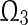with appropriate dimensions, where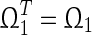and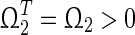, then

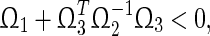if and only if

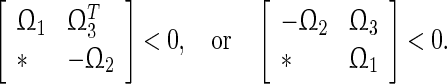Main results

In this section, we deal with the synchronization problem for discrete time-varying complex networks (4). By utilizing new Lyapunov–Krasovskii functionals, we develop an LMI approach to derive sufficient conditions under which the discrete-time complex network (4) is globally synchronized.

Before giving our main results, for the sake of simplicity on matrix representation, we define the following notations

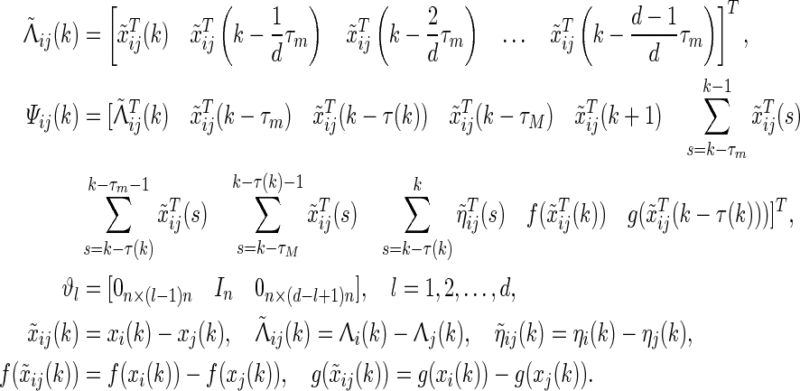Theorem 1

Under Assumption 1, the system (4) is globally asymptotically synchronized if there exist matrices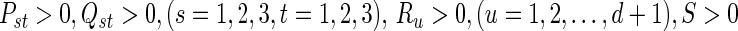and matricesz₁, z₂, F_rv, (v = 1, 2, 3, 4) with appropriate dimensions such that the following LMIs hold

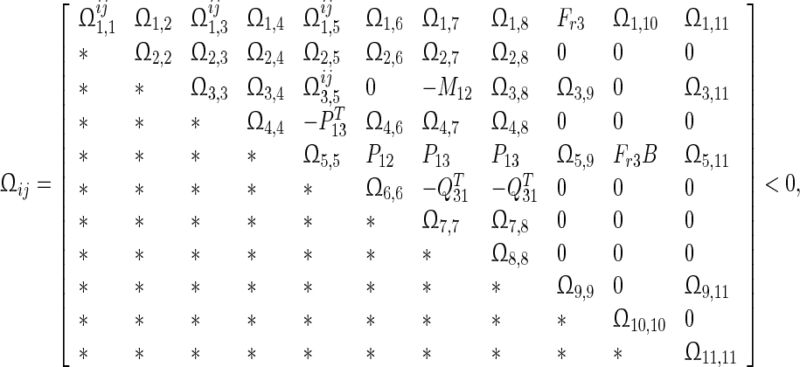8

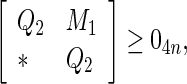9

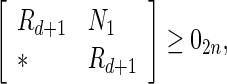10

where

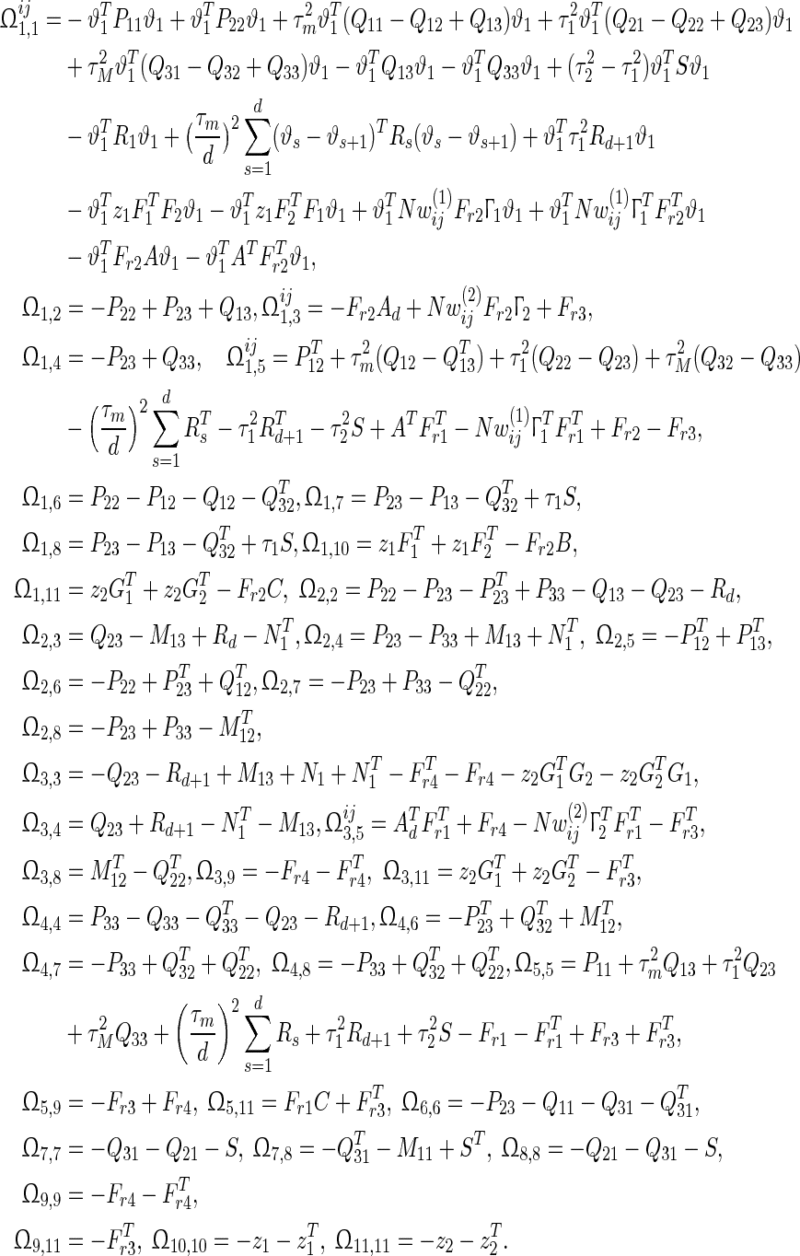Proof

Consider the following Lyapunov functional candidate

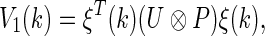11

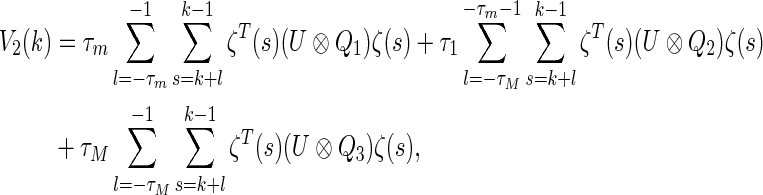12

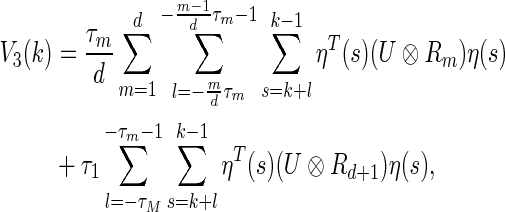13

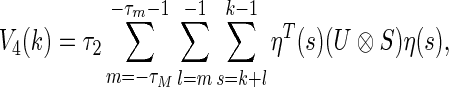14

where

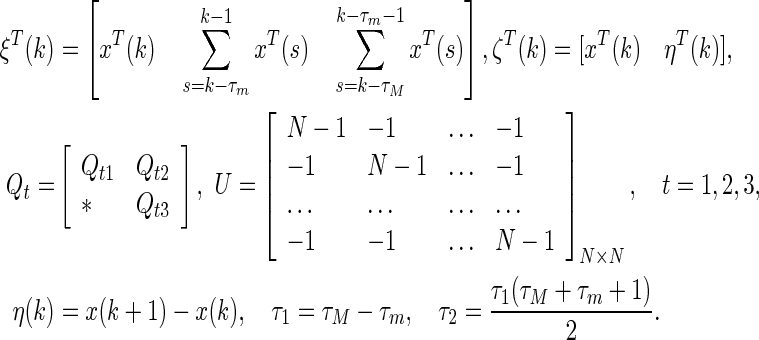Then using the forward difference formula 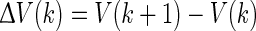along the trajectories of the system (4), we have

15

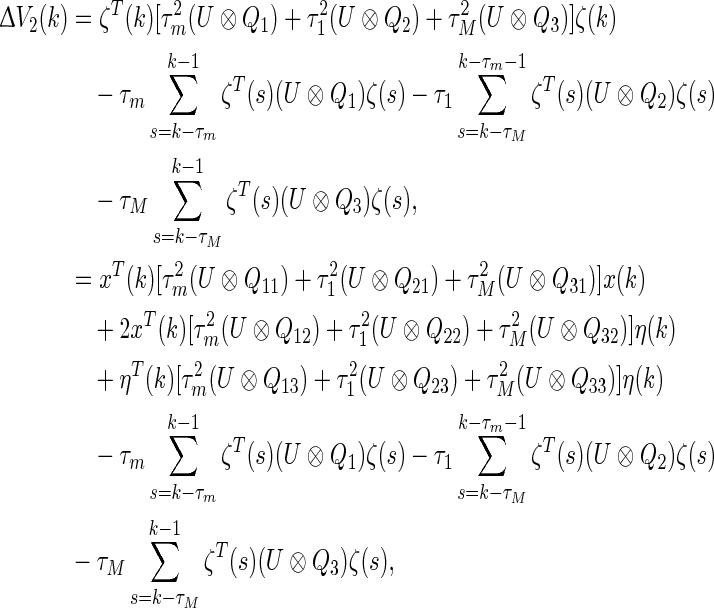16

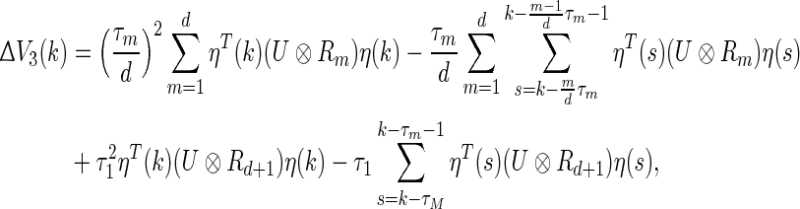17

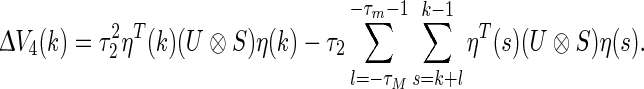18

We have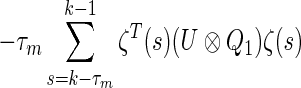

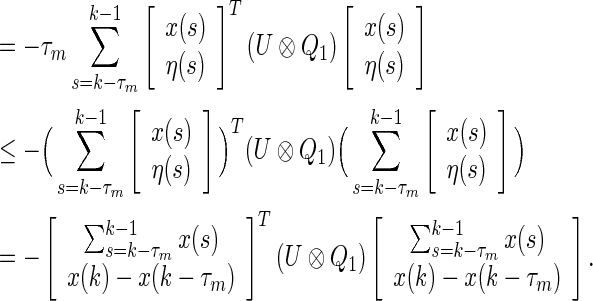19

Similarly,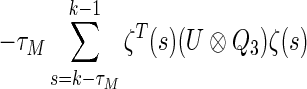

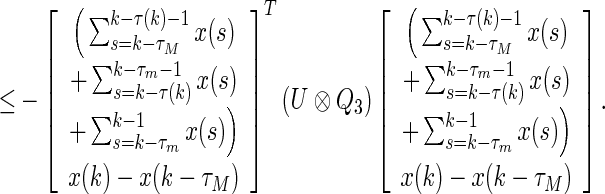20

Since time-varying delay satisfies 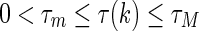, we obtain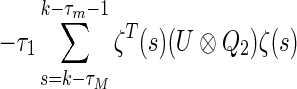

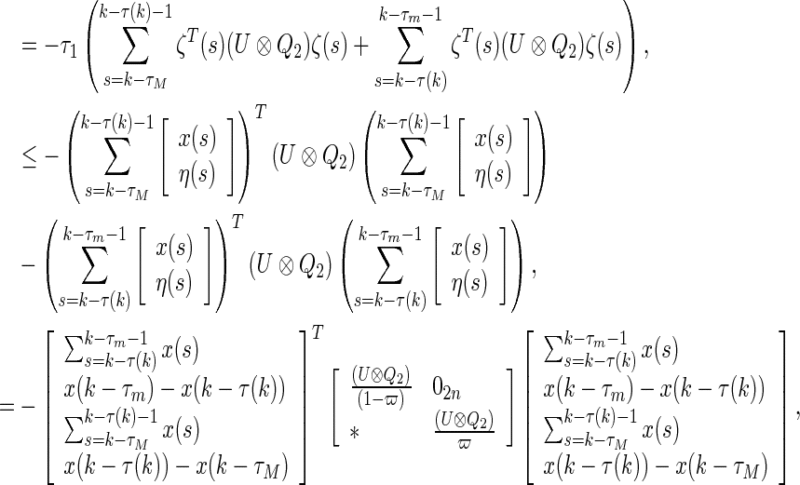where 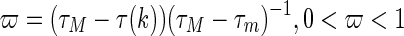. By reciprocal convex Lemma 2, we have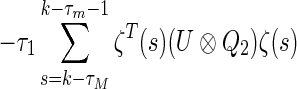

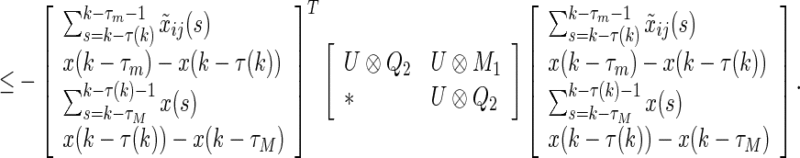21

where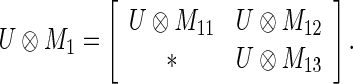

Similarly, we get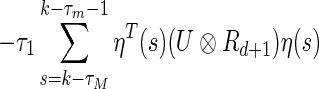

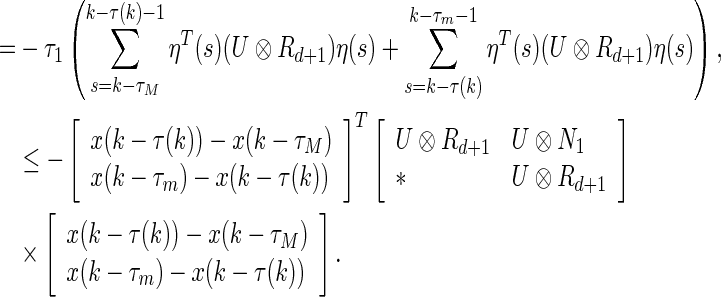22

It should be noted that when 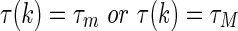, we get 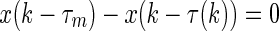or 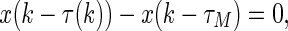respectively. Thus the above inequalities still hold. Also, from 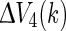we obtain the following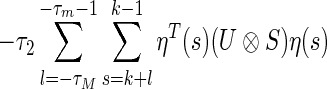

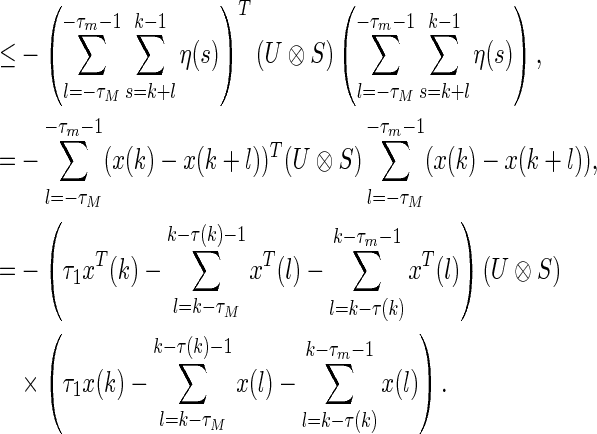23

It follows from (6) and (7), the nonlinear functions satisfy

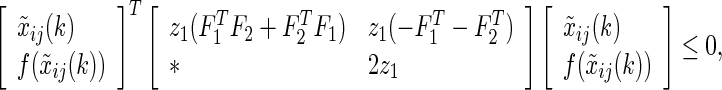24

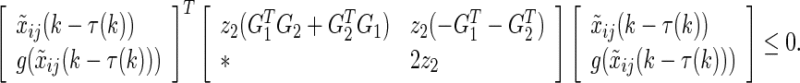25

In addition for any matrices F_r1 and F_r2, the following equality is always true

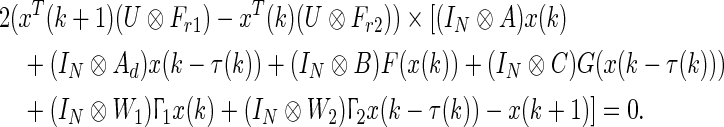26

Given 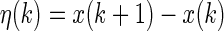. Obviously, 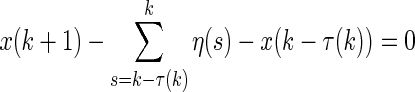, thus, for arbitrary matrices F_r3 and F_r4 of appropriate dimensions, we can obtain that

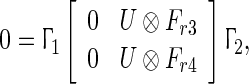27

where 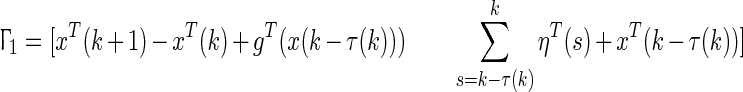and 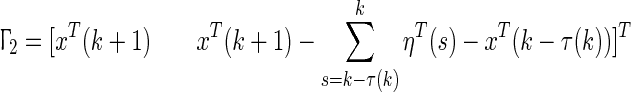. Combining (11)–(27), it can be concluded that,

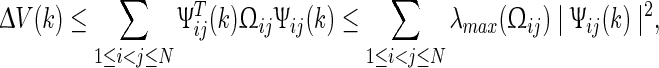28

where 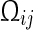is defined as in (8). Noticing that 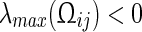and letting

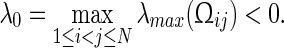29

It follows from (28) that

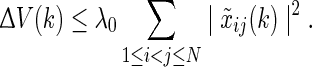30

One can easily conclude from the above that

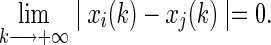31

According to Definition 1, system (4) is stable. This completes the proof.

Assuming that the network evolves with neither state delay and the nonlinear part 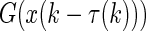, then the networks (4) degenerate as

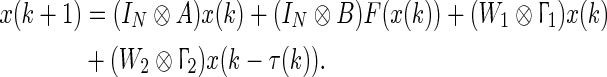32

Similar to Theorem 1, the synchronization criteria can be derived for the above system.

Corollary 1

Under Assumption 1, the discrete-time complex network (32) is globally asymptotically synchronized if there exist matrices 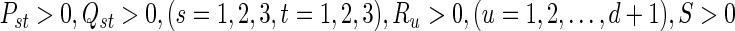and matricesz₁, F_rv, (v = 1, 2, 3, 4) with appropriate dimensions such that the following LMIs hold

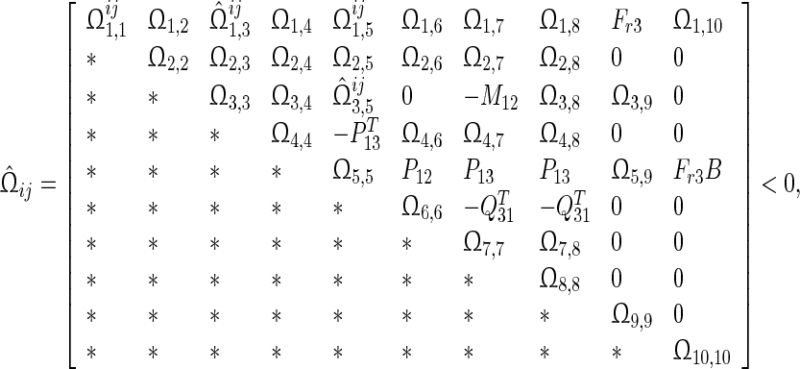33

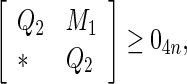34

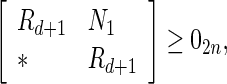35

where

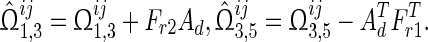and the other parameters are defined as in Theorem 1.

Case 2 Now, we consider the case when there is neither state delay and state coupling, the system (4) reduces to the following

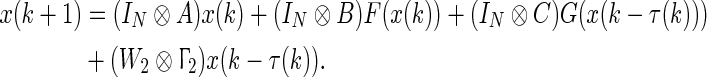36

The synchronization criterion for the above system can be easily accessible from Corollary 2.

Corollary 2

Under Assumption 1, the discrete-time complex network (36) is globally asymptotically synchronized if there exist matrices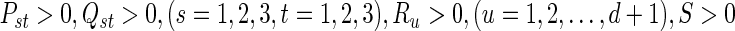and matricesz₁, z₂, F_rv, (v = 1, 2, 3, 4) with appropriate dimensions such that the following LMIs hold

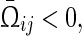37

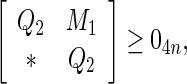38

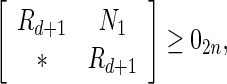39

where

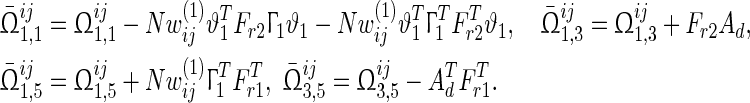and the other parameters are defined as in Theorem 1.

Case 3 Consider system (4) in the absence of both state delay and coupling delay. Then (4) becomes

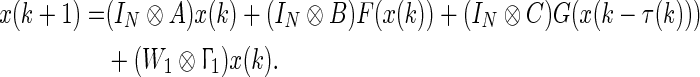40

It is easy to obtain the synchronization criterion for the above system (40), which is given in the following corollary.

Corollary 3

Under Assumption 1, the system (40) is globally asymptotically synchronized if there exist matrices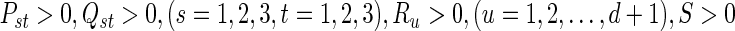and matricesz₁, z₂, F_rv, (v = 1, 2, 3, 4) with appropriate dimensions such that the following LMIs hold

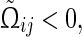41

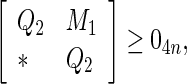42

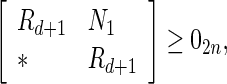43

where 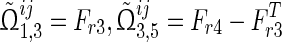and other parameters are defined as in Theorem 1.

Norm-bounded uncertainties

In this section, we will discuss the delay-dependent robust synchronization criteria for the uncertain system

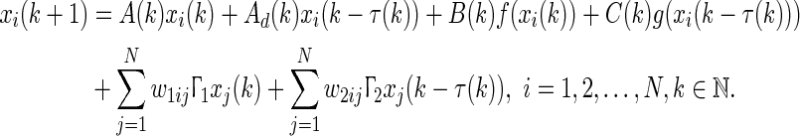44

Here A(k), A_d(k), B(k), and C(k) are time-varying matrices defined by

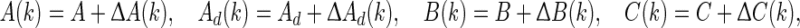where the constant matrices A, A_d, B, and C are known an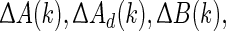d and 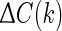are unknown matrices representing the time-varying parameter uncertainties which are assumed to satisfy the condition

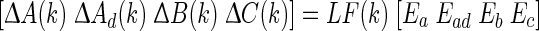45

where E_a, E_ad, E_b, E_c and L are constant matrices of appropriate dimensions. F(k) is an unknown time-varying real matrix satisfying

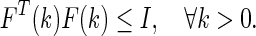46

Using Kronecker product, we can rewrite system (44) into a more compact form as

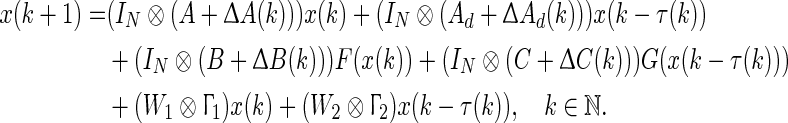47

The initial condition associated with the system (47) is given by

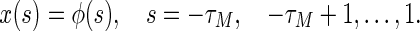48

The following lemma can be utilized to derive the results.

Lemma 4

(Petersen 1987) Given matrices χ = χ^T, G, Hwith appropriate dimensions, then

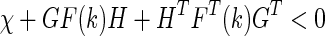for allF(k) satisfyingF^T(k)F(k) ≤ I, if and only if there exists an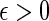such that

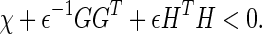Delay-dependent robust stability criterion for the system (47) is derived in the following theorem.

Theorem 2

Under Assumption 1, the uncertain system (47) is globally robustly asymptotically synchronized if there exist matrices 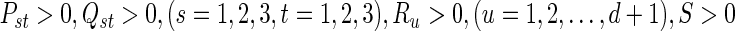, z₁, z₂, F_rv, (v = 1, 2, 3, 4) with appropriate dimensions and positive scalars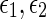such that the following LMIs hold

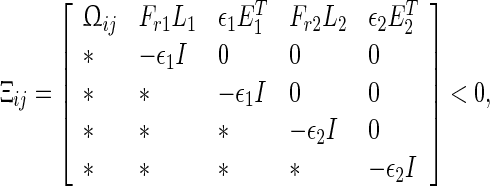49

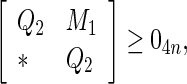50

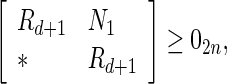51

where

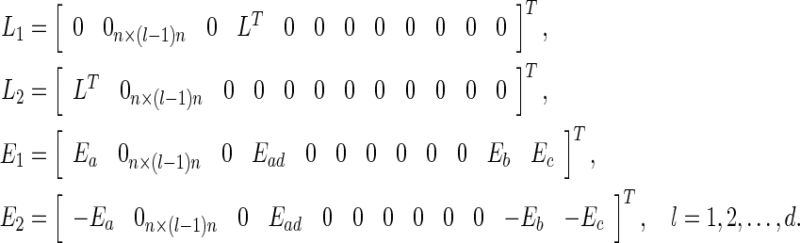Remark 2

Li and Chen (2004) have derived both delay-independent and delay-dependent asymptotic stability criteria in terms of LMIs for network synchronization in which the time-delay assumed to be constant. Synchronization of a linear array of identical logistic maps have been studied by Martì and Masoller (2003) and the coupling delay proportional to the distance between the maps. Park et al. (2013) has proposed some delay-dependent synchronization criterion for the coupled discrete-time neural networks with time-varying delays in network couplings. Finsler’s lemma has been utilized to derive LMIs. Based on piecewise analysis method and Lyapunov functional method, authors investigated the synchronization problem for continuous/discrete complex dynamical networks with time-varying delays in the dynamical nodes and the coupling term (Yue and Li 2010). However, these results were restricted to constant delay or non parameter uncertainties. In this paper, both time-varying coupling delays and parameter uncertainties are considered which can describe more realistic complex networks. By implementing delay-partitioning technique and reciprocal convex lemma, conservative results are developed in terms of LMIs. It is noted that the conservatism of the given condition is reduced as the number of delay partitioning grows.

Remark 3

In (32), if the parameter uncertainties are taken into account, then the networks become

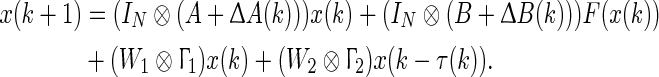52

The following corollary provides the sufficient condition for synchronization of the networks (52).

Corollary 4

Under Assumption 1, the uncertain system (52) is globally robustly asymptotically synchronized if there exist matrices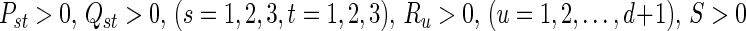, z₁, z₂, F_rv, (v = 1, 2, 3, 4) with appropriate dimensions and positive scalars 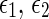such that the following LMIs hold

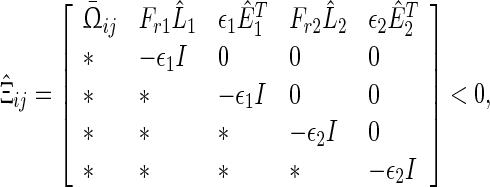53

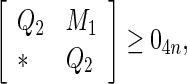54

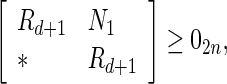55

where

and 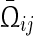is defined as in Corollary 1.

Remark 4

Consider the networks (36) with parameter uncertainties, that is

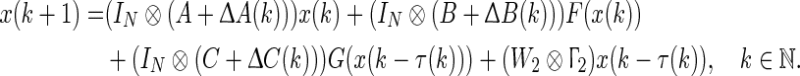56

The following corollary provides the delay-dependent synchronization criteria for the uncertain discrete-time complex networks (56).

Corollary 5

Under Assumption 1, the uncertain system (56) is globally robustly asymptotically synchronized if there exist matrices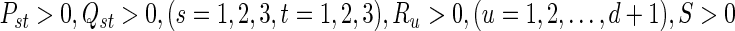, z₁, z₂, F_rv, (v = 1, 2, 3, 4) with appropriate dimensions and positive scalars 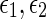such that the following LMIs hold

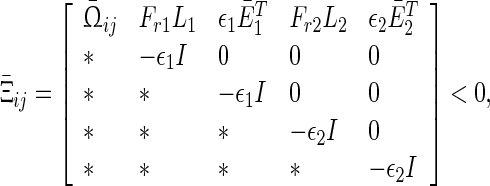57

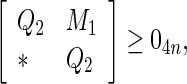58

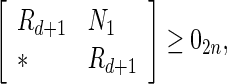59

where

and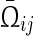is defined as in Corollary 2.

Remark 5

If parameter uncertainties are considered in the system (40), the system becomes

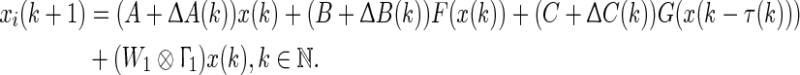60

The following corollary provides sufficient synchronization criteria for the uncertain discrete-time complex networks (60).

Corollary 6

Under Assumption 1, the uncertain discrete-time complex network (60) is globally robustly asymptotically synchronized if there exist matrices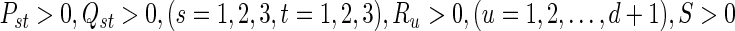, z₁, z₂, F_rv, (v = 1, 2, 3, 4) with appropriate dimensions and positive scalars 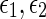such that the following LMIs hold

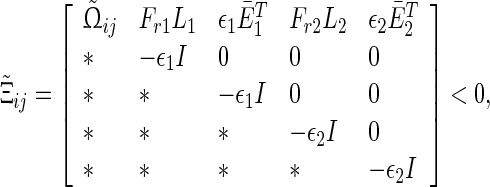61

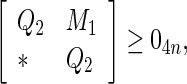62

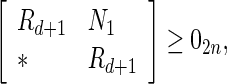63

where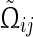is given in Corollary 3.

Remark 6

Park et al. (2009, 2013) considered the synchronization problem of discrete-time delayed complex networks. In both papers, the parameter uncertainties have not been taken into consideration. Since the connection weights of the nodes of complex networks depend on certain resistance and capacitance values, it includes uncertainties in complex networks. Therefore, it is necessary to analyze the synchronization problem of complex networks with uncertainties. Corollary 5 and Corollary 6 provide sufficient synchronization criterion for complex networks with time-varying delay and parameter uncertainties, respectively. Moreover, synchronization for discrete-time complex networks with randomly occurring information deserves our future investigation.

Numerical examples

In this section, numerical examples are provided to substantiate the theoretical results.

Example 1

Consider the discrete-time complex networks with 4-node which is modeled as in Fig. 1. The parameters are given as

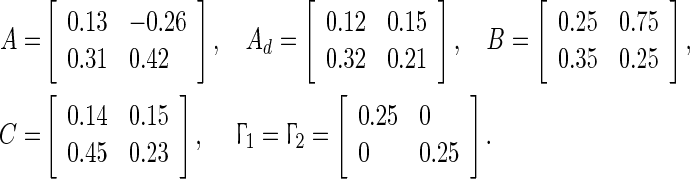Fig. 1.

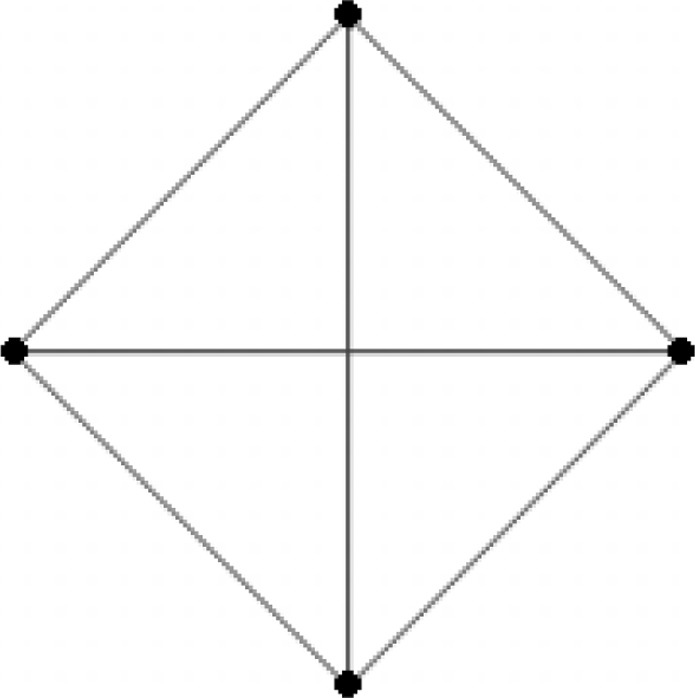
Structure of discrete-time complex networks with 4-nodes

Let the nonlinear vector-valued functions be given by

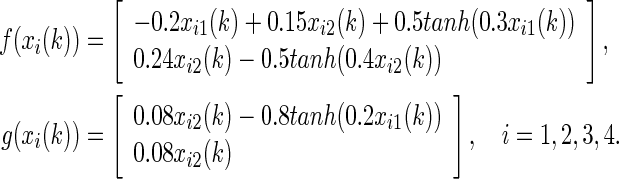Then, Assumption 1 is satisfied with the matrices

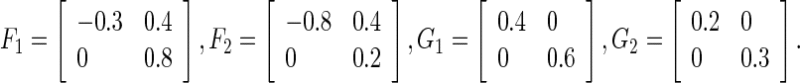The outer-coupling matrices are described as

Generally, κ_i × W_i (i = 1, 2) describes the coupling structure and strength information in symmetric networks, where κ_i is called the coupling strength. The discrete time-varying delay is assumed as 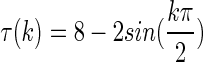. It can be verified that, the lower and upper bounds of the time-delay are 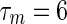and 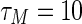, respectively.

Choose d = 3. By using Matlab LMI toolbox, Theorem 1 can be solved with set of feasible solutions given as

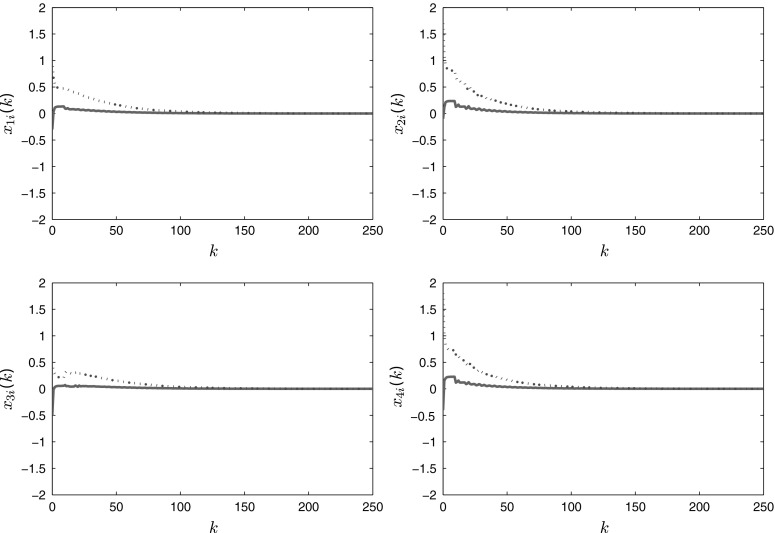
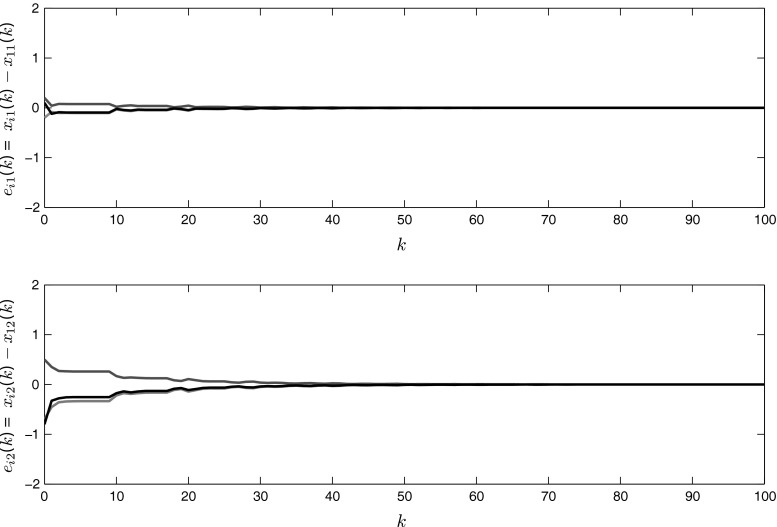
Then, it follows from Theorem 1 that the system (1) with given parameters achieves synchronization, which is further verified by the simulation results shown in Figs. 2 and 3. Figure 2 provides the state trajectories x_i1(k), x_i2(k) of the system (1) and Fig. 3 shows that the error trajectories e_i1(k) = x_i1(k) − x₁₁(k), e_i2(k) = x_i2(k) − x₁₂(k), (i = 2, 3, 4) of the system (1) which converges zero asymptotically.

Fig. 2.

State responses of System (1)

Fig. 3.

Synchronization errors e _ij(k) of System (1), i = 2, 3, 4, j = 1, 2

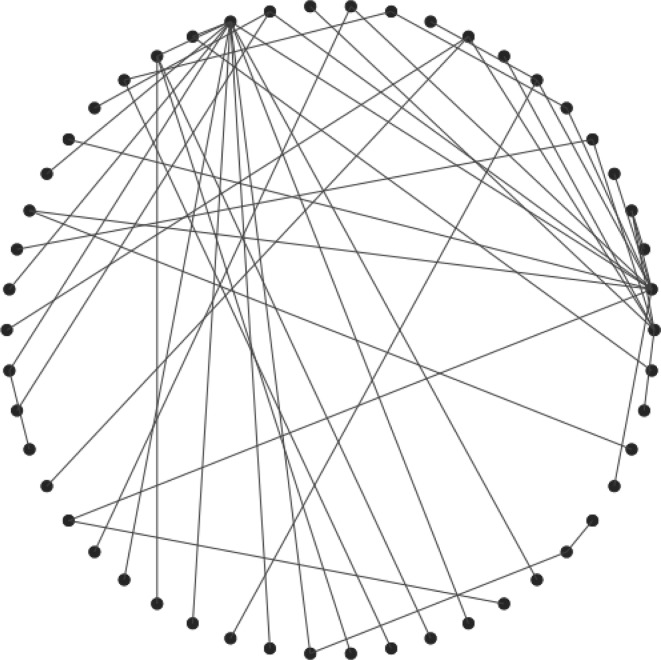
Example 2

The scale-free networks model is considered as a significant discovery because it has been successfully applied to many complex real-world networks. Here, we consider a scale-free networks with 50 dynamical nodes, and the coupling matrix W₂ of the networks can be randomly generated by BA scale-free model (Fig. 4), where each node is the discrete-time dynamical delayed system (36) with the following parameters

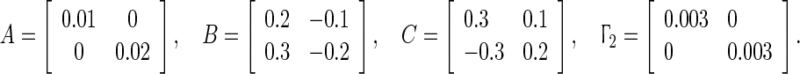The nonlinear vector-valued functions are defined as

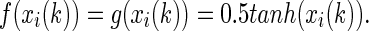Fig. 4.

Structure of BA Scale-free complex networks with dynamical nodes N = 50

Then, by using Matlab toolbox, a set of feasible solutions for the LMIs given in Corollary 2 can be obtained as follows

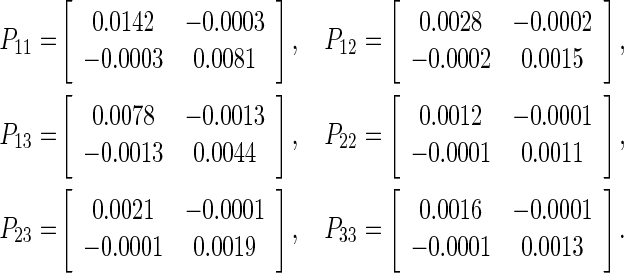Figure 5 depicts the synchronization errors for system (36) with randomly chosen initial conditions. The maximum upper bound 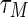of the time-varying delay for different values of 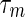are listed in Table 1. Generally, given the dynamics of an isolate node and the inner linking structural matrix, synchronization of the dynamical network with respect to a specific coupling configuration, is said to be strong if the network can synchronize with a small value of the coupling strength. From Table 1, it can be observed that conditions given in Corollary 2 are less conservative than the results obtained by Park et al. (2013).

Fig. 5.

Error trajectories e _ij(k) of System (36),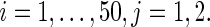

Table 1.

Allowable upper bound τ_M for different values of lower bound τ_m

τm	1	5	10	20
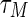
	24	45	73	98

Example 3

Consider complex dynamical networks with three linearly coupled identical nodes which describe the discrete-time version of multiple Lorenz chaos systems (Lorenz 1963) coupled via complex networks. This chaos system has quite complex and abundant property, such as homoclinic bifurcation, period doubling phenomena, pre-turbulence, intermittent chaos (Chacon 1998; Fradkov and Pogromsky 1998; Sparrow 1982). The dynamic equation of such networks is described by (52) with the following parameters

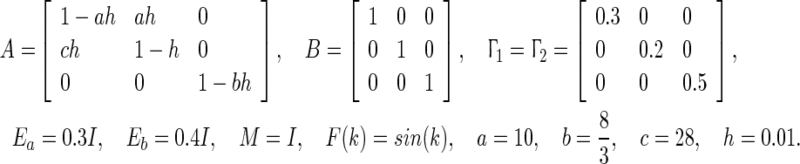The nonlinear function is defined as

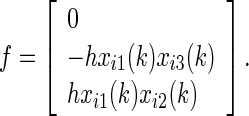The outer coupling matrices are of the form

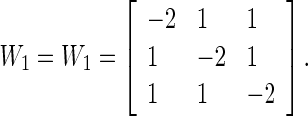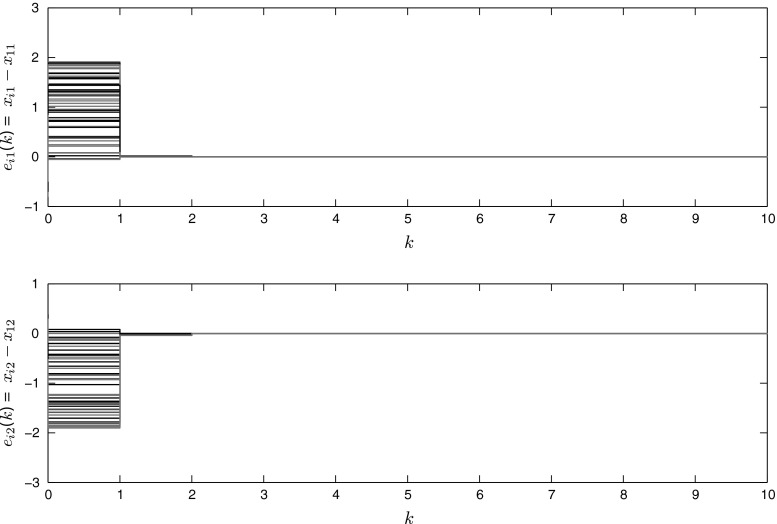
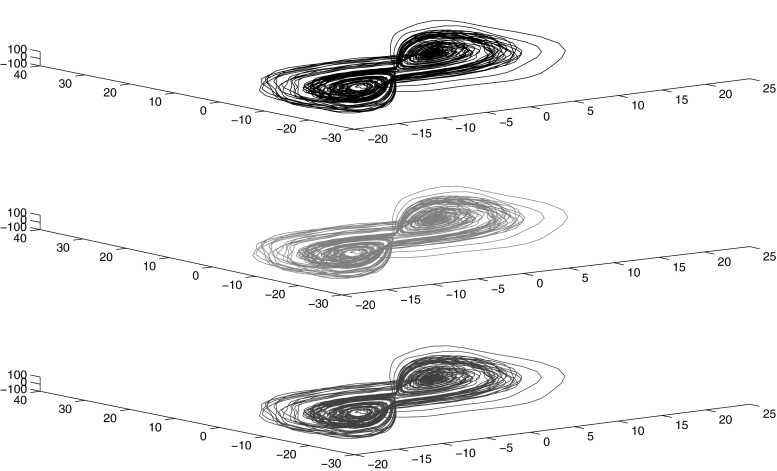
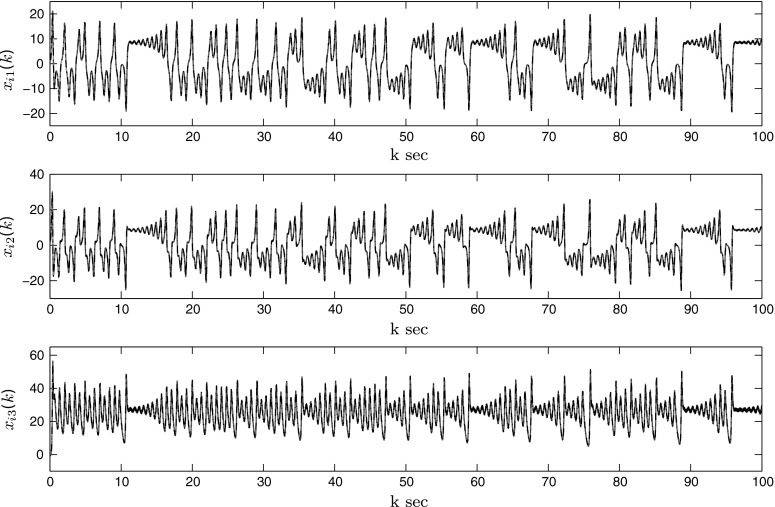
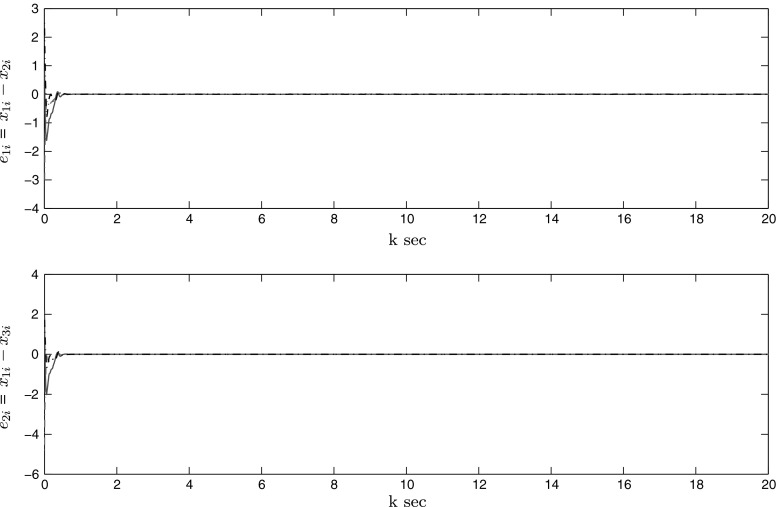
For the above system, a set of feasible solutions can be obtained by solving the LMIs in Corollary 4. Then, it follows that the system (52) with given parameters achieves synchronization, which is further verified by the simulation results shown in Figs. 6, 7 and 8. The chaotic behavior of the system can be realized from Fig. 6, which depicts the state trajectories of the system (52). Figure 7 represents that states of the 2nd and 3rd system are synchronized with states of 1st system and Fig. 8 represents that the synchronization errors approach zero asymptotically. Thus, the numerical simulation affirms the theoretical results.

Fig. 6.

Phase-space trajectories of Lorenz system (52) with 3 nodes

Fig. 7.

State trajectories of Lorenz system (52)

Fig. 8.

Synchronization errors

Example 4

Consider an example for the model (60) with the following parameters

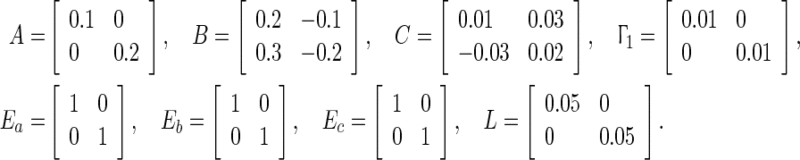The nonlinear vector-valued functions are defined as

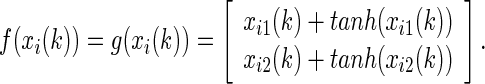The time-varying delays are assumed to be 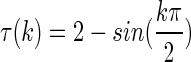, then 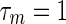and 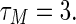If we take the asymmetric outer coupling matrix as

Then using Matlab LMI Toolbox, we can obtain the feasible solution of Corollary 6 which is given by

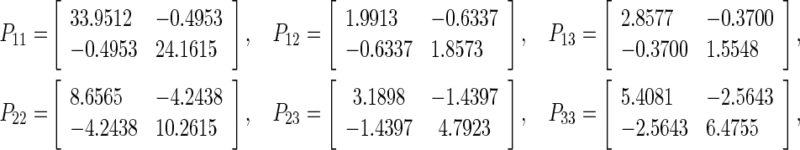with scalars 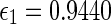and 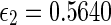. Thus, by assuming d = 1 the maximum delay bound 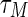is 30 whereas in (Wang and Song 2011) it is 4. This shows the conservatism of our result. Also, it should be noted that the criteria proposed by Liang et al. (2008b) fail to solve this synchronization problem with the above parameters for both symmetric and asymmetric coupled matrix.

Conclusions

This paper described the problem of synchronization for discrete-time complex dynamical networks with time-varying delays in the dynamical nodes and the coupling term. The parameter uncertainties are imbedded in the network state. Rather than the commonly used Lipschitz condition, a more general sector-like nonlinear condition has been employed to describe the nonlinearities which exist in the network. By utilizing Lyapunov–Krasovskii functional, Kronecker product and free-weighting matrix approach sufficient delay-dependent synchronization criteria are derived by a set of linear matrix inequalities. Moreover, delay-partitioning technique and convex reciprocal lemma are exploited to obtain less conservative results. Finally, numerical examples are provided to demonstrate the effectiveness of the derived criteria. The obtained results can lead to less conservative results than those obtained from the existing methods.