Convergence analysis of fully complex backpropagation algorithm based on Wirtinger calculus

Abstract

This paper considers the fully complex backpropagation algorithm (FCBPA) for training the fully complex-valued neural networks. We prove both the weak convergence and strong convergence of FCBPA under mild conditions. The decreasing monotonicity of the error functions during the training process is also obtained. The derivation and analysis of the algorithm are under the framework of Wirtinger calculus, which greatly reduces the description complexity. The theoretical results are substantiated by a simulation example.

Introduction

The theoretical studies and practical implementations of complex-valued neural network (CVNN) have attracted considerable attention in signal processing, pattern recognition, and medical information processing (Fink et al. 2014; Hirose 2012; Nitta 2013). Based on different choices of the activation function, there are two main CVNN models: the split CVNN (Nitta 1997) and the fully CVNN (Kim and Adali 2003). The split CVNN uses a pair of real-valued functions to separately process the real part and the imaginary part of the neuron’s input signal. This strategy can effectively overcome the singularity problem during the training procedure. In contrast, activation functions of the fully CVNN are fully complex-valued, which helps the network make fully use of the phase information and thus achieve better performance in some applications. As one of the most popular training methods for neural networks, backpropagation algorithm (BPA) has been extended from the real domain to the complex domain in order to train the CVNN. Accordingly, there are two types of complex BPA: one is the split-complex BPA (SCBPA) (Nitta 1997) for split CVNN, and another is the fully complex BPA (FCBPA) (Li and Adali 2008) for fully CVNN.

Convergence is the precondition for any iteration algorithm to be used in real applications. (Wei et al. 2013; Osborn 2010) The convergence of the BPA has been extensively studied in literature (Wu et al. 2005, 2011; Zhang et al. 2007, 2008, 2009; Shao and Zheng 2011), where the boundedness and differentiability of the activation function are usually two necessary conditions for the convergence analysis. However, as stated by the Liouvilles theorem (an entire and bounded function in the complex domain is a constant), the complex activation function can not be both bounded and analytic. The conflict between the boundedness and differentiability of the activation function makes the theoretical convergence analysis for the complex BPA more difficult than that for the BPA. Fortunately, as the activation functions of the split CVNN can be split into two bounded and differential real-valued functions, the convergence analysis of SCBPA can then be conducted in the real domain. For the corresponding convergence results, we refer to (Nitta 1997; Zhang et al. 2013; Xu et al. 2010). However, though FCBPA has been widely used in many applications and has been experimentally shown to be convergent for some kinds of activation functions (Kim and Adali 2003), the theoretical convergence analysis remains challengeable.

Despite the challenge posed by the Liouville‘s theorem, another challenge for the theoretical convergence analysis of FCBPA is that the traditional mean value theorem, which is vital for the convergence analysis of BPA, dos not hold in the complex domain. (For example: $f(z)=e^z\text{with}{z}_2=z_1+2\mathit{\pi }i$. We have f(z₂) − f(z₁) = 0 but $(z_2-z_1)f^{\prime }(w)=2\mathit{\pi }i{e}^w\ne 0$ for all w.) By expanding the analytic function with Taylor series and omitting the high order terms, some local stability results for complex ICA are obtained (Adali et al. 2008). Under the assumption that the activation function is a contraction, the convergence of the complex nonlinear adaptive filters is proved (Mandic and Goh 2009). However, to the best of our knowledge, the theoretical convergence results of the FCBPA has not yet been established. This becomes the main concern of this paper. Specifically, we make the following contributions:

• By introducing a mean value theorem for a holomorphic function (Mcleod 1965), we will prove both the weak convergence and the strong convergence of FCBPA.

• Instead of dropping the high order terms of the Taylor series (Adali et al. 2008), we give an accurate estimation for the difference of the error function between two iterations using the mean value theorem. As a result, our results are of global nature in that they are valid for arbitrarily given initial values of the weights.

• The restrictive condition that the activation function is a contraction is not needed in our analysis.

• The derivation and analysis of the algorithm are under the framework of Wirtinger calculus, which greatly reduces the description complexity.

The remainder of this paper is organized as follows. The network structure and the derivation of the FCBPA based on Wirtinger calculus are described in the next section. “Main results” section presents the main convergence theorem of the paper. The detailed proof of the theorem is given in Section Proofs. In “Simulation result” section we use a simulation example to support our theoretical results. The paper is concluded in “Conclusion” section.

Network structure and FCBPA based on Wirtinger calculus

We consider a single hidden layer feedforward network consisting of p input nodes, q hidden nodes, and 1 output node. Let ${\mathbf{w}}_0={(w_{01},w_{02},\cdots ,w_{0q})}^T\in {\mathbb{C}}^q$ be the weight vector between all the hidden units and the output unit, and ${\mathbf{w}}_l={(w_{l1},w_{l2},\cdots ,w_{lp})}^T\in {\mathbb{C}}^p$ be the weight vector between all the input units and the hidden unit l$(l=1,2,\cdots ,q)$. To simplify the presentation, we write all the weight parameters in a compact form, i.e., $\mathbf{w}={({\mathbf{w}}_0^T,{\mathbf{w}}_1^T,\cdots ,{\mathbf{w}}_q^T)}^T\in {\mathbb{C}}^{q+pq}$ and we define a matrix $\mathbf{V}={({\mathbf{w}}_1,{\mathbf{w}}_2,\cdots ,{\mathbf{w}}_q)}^T\in {\mathbb{C}}^{q\times p}$.

Given activation functions $f,g:\mathbb{C}\to \mathbb{C}$ for the hidden layer and output layer, respectively, we define a vector function $\mathbf{F}(\mathbf{x})={(f(x_1),f(x_2),\cdots ,f(x_q))}^T$ for $\mathbf{x}={(x_1,x_2,\cdots ,x_q)}^T\in {\mathbb{C}}^q$. For an input $\mathit{z}\in {\mathbb{C}}^p$, the output vector of the hidden layer can be written as $\mathbf{F}(\mathbf{V}\mathit{z})$ and the final output of the network can be written as

$$y=g({\mathbf{w}}_0·\mathbf{F}(\mathbf{V}\mathit{z})),$$ 1

where ${\mathbf{w}}_0·\mathbf{F}(\mathbf{V}\mathit{z})$ represents the inner product between the two vectors w₀ and $\mathbf{F}(\mathbf{V}\mathit{z})$.

Suppose that ${\{{\mathit{z}}^k,d^k\}}_{k=1}^K\subset {\mathbb{C}}^p\times \mathbb{C}$ is a given set of training samples, where ${\mathit{z}}^k$ is the input, and d^k is the desired output. The aim of the network training is to find the appropriate network weights ${\mathbf{w}}^{★}$ that can minimize the error function

$$E(\mathbf{w})=\sum _{k=1}^K(d_k-y_k)(\overline{d_k}-\overline{y_k}),$$ 2

where

$$y_k=g({\mathbf{w}}_0·\mathbf{F}(\mathbf{V}{\mathit{z}}^k))$$ 3

and the notation ⁻ denotes the complex conjugation.

As noted by Adali et al. (2008), any function h(z) that is analytic in a bounded zone |z| < R with a Taylor series expansion with all real coefficients in |z| < R satisfies the property $\overline{h(z)}=h(\overline{z})$. Examples of such functions include polynomials and most trigonometric functions and their hyperbolic counterparts, which are qualified activation functions of CVNNs (Kim and Adali 2003). As a result, we suppose both the activation functions $f(·)$ and $g(·)$ satisfy $\overline{f(z)}=f(\overline{z})$, $\overline{g(z)}=g(\overline{z})$. Therefore,

$$\overline{y_k}=g(\overline{{\mathbf{w}}_0}·\mathbf{F}(\overline{\mathbf{V}}\overline{{\mathit{z}}^k})).$$ 4

E(w) can be viewed as a function of complex variable vector w and its conjugate $\overline{\mathbf{w}}$. According to the Wirtinger calculus (Brandwood 1983; Bos 1994), we can define two gradient vectors ∇_wE (by taking partial derivatives with respect to w at the same time treating $\overline{\mathbf{w}}$ as a constant vector in E) and ${\nabla }_{\overline{\mathbf{w}}}E$ (by taking partial derivatives with respect to $\overline{\mathbf{w}}$ at the same time treating w as a constant vector). Then the gradient ${\nabla }_{\overline{\mathbf{w}}}E$ defines the direction of the maximum rate of change in E(w) with respect to w. As the output node y_k does not explicitly contain the variable vector $\overline{\mathbf{w}}$, we can conclude ${\nabla }_{\overline{\mathbf{w}}}{y}_k=0$. Thus, by the chain rule of the Wirtinger calculus, we have

$$\frac{\mathit{\partial }E(\mathbf{w})}{\mathit{\partial }\overline{{\mathbf{w}}_0}}=\sum _{k=1}^K(y_k-d_k)g^{\prime }(\overline{{\mathbf{w}}_0}·\mathbf{F}(\overline{\mathbf{V}}\overline{{\mathit{z}}^k}))\mathbf{F}(\overline{\mathbf{V}}\overline{{\mathit{z}}^k}),$$ 5

$$\frac{\mathit{\partial }E(\mathbf{w})}{\mathit{\partial }\overline{{\mathbf{w}}_l}}=\sum _{k=1}^K(y_k-d_k)g^{\prime }(\overline{{\mathbf{w}}_0}·\mathbf{F}(\overline{\mathbf{V}}\overline{{\mathit{z}}^k}))\overline{w_{0l}}{f}^{\prime }(\overline{{\mathbf{w}}_l}·\overline{{\mathit{z}}^k})\overline{{\mathit{z}}^k},l=1,2\cdots ,q.$$ 6

Obviously,

$${\nabla }_{\overline{\mathbf{w}}}E(\mathbf{w})={\left({\left(\frac{\mathit{\partial }E(\mathbf{w})}{\mathit{\partial }\overline{{\mathbf{w}}_0}}\right)}^T,{\left(\frac{\mathit{\partial }E(\mathbf{w})}{\mathit{\partial }\overline{{\mathbf{w}}_1}}\right)}^T,\cdots ,{\left(\frac{\mathit{\partial }E(\mathbf{w})}{\mathit{\partial }\overline{{\mathbf{w}}_q}}\right)}^T\right)}^T.$$ 7

Starting from an arbitrary initial value w⁰, the BPA based on Wirtinger calculus updates the weights {wⁿ} iteratively by

$${\mathbf{w}}^{n+1}={\mathbf{w}}^n-\mathit{\eta }{\nabla }_{\overline{\mathbf{w}}}E({\mathbf{w}}^n),$$ 8

where $\mathit{\eta }>0$ is the learning rate.

Main results

The following assumptions are needed in our convergence analysis.

• (A1) There exists a constant c₁ > 0 such that $\Vert {\mathbf{w}}_l^n\Vert \le c_1$ for all $l=0,1,\cdots ,q$, $n=0,1,\cdots$;

• (A2) The functions f(z) and g(z) are analytic in a bounded zone |z| < R with a Taylor series expansion with all real coefficients in |z| < R, where R > max{c₂,c₃} (c₂ and c₃ are defined in (17) below).

• (A3) The set ${\mathrm{\Phi }}_1=\{\mathbf{w}:{\nabla }_{\overline{\mathbf{w}}}E(\mathbf{w})=0\}$ contains only finite points.

Remark 1

Assumption (A1) is the usual condition for the convergence analysis of the gradient method for both the real-valued neural networks (Zhang et al. 2007, 2008) and the CVNNs (Xu et al. 2010) in literature. As noted by Adali et al. (2008), Assumption (A2) is satisfied by quite a number of functions which are qualified as activation functions of the fully CVNNs. Assumption (A3) is used to establish a strong convergence result.

Now we present our convergence results.

Theorem 1

Suppose that the error function is given by (2), that the weight sequence {wⁿ} is generated by the algorithm (8) for any initial valuew⁰, that$0<\mathit{\eta }<\frac{1}{L}$, whereLis defined by (27) below, and that Assumptions (A1) and (A2) are valid. Then we have

1. $$E({\mathbf{w}}^{n+1})\le E({\mathbf{w}}^n),n=0,1,2,\cdots ;$$ 9
2. $$Thereis{E}^{★}>0suchthat\underset{n\to \infty }{lim}E({\mathbf{w}}^n)=E^{★};$$ 10
3. $$Thereholdstheweakconvergence\text{:}\underset{n\to \infty }{lim}∥{\nabla }_{\overline{w}}E(w^n)∥=0.$$ 11

   Moreover, if Assumption (A3) is valid, then there holds the strong convergence: there exists a point${\mathbf{w}}^{★}\in \mathrm{\Phi }$such that
4. $$\underset{n\to \infty }{lim}{\mathbf{w}}^n={\mathbf{w}}^{★}.$$ 12

Proofs

Lemma 1

[see Theorem 10 in by Mcleod (1965)] Suppose h is a holomorphic function defined on a connected open set G in the complex plane. Ifz₁andz₂are points in G such that the segment joining them is also in G then

$$h(z_2)-h(z_1)=(z_2-z_1)({\mathit{\lambda }}_1{h}^{\prime }({\mathit{\xi }}_1)+{\mathit{\lambda }}_2{h}^{\prime }({\mathit{\xi }}_2))$$ 13

for some ξ₁and ξ₂on the segment joiningz₁andz₂and some nonnegative numbers${\mathit{\lambda }}_1$and${\mathit{\lambda }}_2$such that${\mathit{\lambda }}_1+{\mathit{\lambda }}_2=1$.

Lemma 2

Suppose Assumptions (A1) and (A2) are valid, then${\nabla }_{\overline{\mathbf{w}}}E(\mathbf{w})$satisfies Lipschitz condition, that is, there exists a positive constantL₁, such that

$$\Vert {\nabla }_{\overline{\mathbf{w}}}E({\mathbf{w}}^{n+1})-{\nabla }_{\overline{\mathbf{w}}}E({\mathbf{w}}^n)\Vert \le L_1\Vert {\mathbf{w}}^{n+1}-\mathbf{w}{}^n\Vert .$$ 14

Similarly, there exists a positive constantL₂, such that

$$\Vert {\nabla }_{\mathbf{w}}E({\mathbf{w}}^{n+1})-{\nabla }_{\mathbf{w}}E({\mathbf{w}}^n)\Vert \le L_2\Vert {\mathbf{w}}^{n+1}-\mathbf{w}{}^n\Vert .$$ 15

Proof

For simplicity, we introduce the following notations:

$${\mathbf{F}}^{n,k}=\mathbf{F}({\mathbf{V}}^n{\mathbf{z}}^k),{\overline{\mathbf{F}}}^{n,k}=\mathbf{F}(\overline{{\mathbf{V}}^n}\overline{{\mathbf{z}}^k}),$$ 16

for $n=1,2,\cdots ,k=1,2,\cdots ,K$.

By Assumption (A2), f and g have differentials of any order in the zone {z: |z| < R}. In addition, recalling ${\{z^k,d^k\}}_{k=1}^K$ is finite and {wⁿ} is bounded, we can define c₂ and c₃ such that

$$c_2=\underset{l,n,k}{sup}|\overline{{\mathbf{w}}_l^n}·\overline{{\mathbf{z}}^k}|,c_3=\underset{n,k}{sup}|\overline{{\mathbf{w}}_0^n}·\mathbf{F}(\overline{{\mathbf{V}}^n}\overline{{\mathbf{z}}^k})|,$$ 17

$$c_4=\underset{|z|<max\{c_2,c_3\}}{sup}\{|f(z)|,|g(z)|,|f^{\prime }(z)|,|g^{\prime }(z)|,|g^{″}(z)|\}.$$ 18

Using (18), Lemma 1 and the Cauchy-Schwartz Inequality, for any 1 ≤ k ≤ K and $n=0,1,\cdots$, we have that

$$\begin{array}{cc}\hfill \Vert {\mathbf{F}}^{n+1,k}-{\mathbf{F}}^{n,k}\Vert & =∥\left(\begin{array}{c}f({\mathbf{w}}_1^{n+1}·{\mathbf{z}}^k)-f({\mathbf{w}}_1^n·{\mathbf{z}}^k)\\ ⋮\\ f({\mathbf{w}}_q^{n+1}·{\mathbf{z}}^k)-f({\mathbf{w}}_q^n·{\mathbf{z}}^k)\end{array}\right)∥\hfill \\ & =∥\left(\begin{array}{c}({\mathbf{w}}_1^{n+1}·{\mathbf{z}}^k-{\mathbf{w}}_1^n·{\mathbf{z}}^k)({\mathit{\lambda }}_{11}{f}^{\prime }({\mathit{\xi }}_{11})+{\mathit{\lambda }}_{12}{f}^{\prime }({\mathit{\xi }}_{12}))\\ ⋮\\ ({\mathbf{w}}_q^{n+1}·{\mathbf{z}}^k-{\mathbf{w}}_q^n·{\mathbf{z}}^k)({\mathit{\lambda }}_{q1}{f}^{\prime }({\mathit{\xi }}_{q1})+{\mathit{\lambda }}_{q2}{f}^{\prime }({\mathit{\xi }}_{q2}))\end{array}\right)∥\hfill \\ & \le c_5∥\left(\begin{array}{c}{\mathbf{w}}_1^{n+1}-{\mathbf{w}}_1^n\\ ⋮\\ {\mathbf{w}}_q^{n+1}-{\mathbf{w}}_q^n\end{array}\right)∥\hfill \\ & \le c_5\sum _{l=1}^q\Vert {\mathbf{w}}_l^{n+1}-{\mathbf{w}}_l^n\Vert ,\hfill \end{array}$$ 19

where $c_5=\sqrt{q}{c}_4\underset{k}{sup}\Vert {\mathbf{z}}^k\Vert ,{\mathit{\lambda }}_{l1}\ge 0,{\mathit{\lambda }}_{l2}\ge 0,{\mathit{\lambda }}_{l1}+{\mathit{\lambda }}_{l2}=1$, ξ_l1 and ξ_l2 lie on the segment joining ${\mathbf{w}}_l^{n+1}·{\mathbf{z}}^k$ and ${\mathbf{w}}_l^n·{\mathbf{z}}^k$, $l=1,\cdots ,q$.

Similarly, we have

$$\Vert {\overline{\mathbf{F}}}^{n+1,k}-{\overline{\mathbf{F}}}^{n,k}\Vert \le c_5\sum _{l=1}^q\Vert {\mathbf{w}}_l^{n+1}-{\mathbf{w}}_l^n\Vert .$$ 20

By (18), (19), Lemma 1 and the Cauchy-Schwartz Inequality we have that for any 1 ≤ k ≤ K and $n=0,1,\cdots$

$$\begin{array}{cc}\hfill \Vert y_k^{n+1}-y_k^n\Vert & =\Vert g({\mathbf{w}}_0^{n+1}·{\mathbf{F}}^{n+1,k})-g({\mathbf{w}}_0^n·{\mathbf{F}}^{n,k})\Vert \hfill \\ & =\Vert ({\mathbf{w}}_0^{n+1}·{\mathbf{F}}^{n+1,k}-{\mathbf{w}}_0^n·{\mathbf{F}}^{n,k})({\mathit{\eta }}_1{g}^{\prime }({\mathit{\zeta }}_1)+{\mathit{\eta }}_2{g}^{\prime }({\mathit{\zeta }}_2))\Vert \hfill \\ & \le c_4(\Vert {\mathbf{w}}_0^{n+1}-{\mathbf{w}}_0^n\Vert \Vert {\mathbf{F}}^{n+1,k}\Vert +\Vert {\mathbf{w}}_0^n\Vert \Vert {\mathbf{F}}^{n+1,k}-{\mathbf{F}}^{n,k}\Vert )\hfill \\ & \le \sqrt{q}{c}_4^2\Vert {\mathbf{w}}_0^{n+1}-{\mathbf{w}}_0^n\Vert +c_1{c}_4{c}_5\sum _{l=1}^q\Vert {\mathbf{w}}_l^{n+1}-{\mathbf{w}}_l^n\Vert \hfill \\ & \le c_6\Vert {\mathbf{w}}^{n+1}-{\mathbf{w}}^n\Vert ,\hfill \end{array}$$ 21

where $c_6=\sqrt{q+1}max\{\sqrt{q}{c}_4^2,c_1{c}_4{c}_5\}$, ${\mathit{\eta }}_1\ge 0,{\mathit{\eta }}_2\ge 0,{\mathit{\eta }}_1+{\mathit{\eta }}_2=1$, ${\mathit{\zeta }}_1$ and ${\mathit{\zeta }}_2$ lie on the segment joining ${\mathbf{w}}_0^{n+1}·{\mathbf{F}}^{n+1,k}$ and ${\mathbf{w}}_0^n·{\mathbf{F}}^{n,k}$.

In the same way, we can prove that

$$\Vert g^{\prime }(\overline{{\mathbf{w}}_0^{n+1}}·{\overline{\mathbf{F}}}^{n+1,k})-g^{\prime }(\overline{{\mathbf{w}}_0^n}·{\overline{\mathbf{F}}}^{n,k})\Vert \le c_6\Vert {\mathbf{w}}^{n+1}-{\mathbf{w}}^n\Vert .$$ 22

With (18), (20), (22), and Cauchy-Schwartz Inequality we obtain

$$\begin{array}{cc}& \Vert g^{\prime }(\overline{{\mathbf{w}}_0^{n+1}}·{\overline{\mathbf{F}}}^{n+1,k}){\overline{\mathbf{F}}}^{n+1,k}-g^{\prime }(\overline{{\mathbf{w}}_0^n}·{\overline{\mathbf{F}}}^{n,k}){\overline{\mathbf{F}}}^{n,k}\Vert \hfill \\ & =\Vert (g^{\prime }(\overline{{\mathbf{w}}_0^{n+1}}·{\overline{\mathbf{F}}}^{n+1,k})-g^{\prime }(\overline{{\mathbf{w}}_0^n}·{\overline{\mathbf{F}}}^{n,k})){\overline{\mathbf{F}}}^{n+1,k}+g^{\prime }(\overline{{\mathbf{w}}_0^n}·{\overline{\mathbf{F}}}^{n,k})({\overline{\mathbf{F}}}^{n+1,k}-{\overline{\mathbf{F}}}^{n,k})\Vert \hfill \\ & \le |g^{\prime }(\overline{{\mathbf{w}}_0^{n+1}}·{\overline{\mathbf{F}}}^{n+1,k})-g^{\prime }(\overline{{\mathbf{w}}_0^n}·{\overline{\mathbf{F}}}^{n,k})|\Vert {\overline{\mathbf{F}}}^{n+1,k}\Vert +|g^{\prime }(\overline{{\mathbf{w}}_0^n}·{\overline{\mathbf{F}}}^{n,k})|\Vert ({\overline{\mathbf{F}}}^{n+1,k}-{\overline{\mathbf{F}}}^{n,k})\Vert \hfill \\ & \le c_6\sqrt{q}{c}_4\Vert {\mathbf{w}}^{n+1}-{\mathbf{w}}^n\Vert +c_4{c}_5\sum _{l=1}^q\Vert {\mathbf{w}}_l^{n+1}-{\mathbf{w}}_l^n\Vert \hfill \\ & \le \sqrt{q}{c}_4(c_5+c_6)\Vert {\mathbf{w}}^{n+1}-{\mathbf{w}}^n\Vert \hfill \end{array}$$ 23

Combining (18), (21), (23), and the Cauchy-Schwartz Inequality we can conclude

$$\begin{array}{cc}& \Vert \frac{\mathit{\partial }E({\mathbf{w}}^{n+1})}{\mathit{\partial }\overline{{\mathbf{w}}_0}}-\frac{\mathit{\partial }E({\mathbf{w}}^n)}{\mathit{\partial }\overline{{\mathbf{w}}_0}}\Vert \hfill \\ & =\Vert \sum _{k=1}^K(y_k^{n+1}-d_k)g^{\prime }(\overline{{\mathbf{w}}_0^{n+1}}·{\overline{\mathbf{F}}}^{n+1,k}){\overline{\mathbf{F}}}^{n+1,k}-\sum _{k=1}^K(y_k^n-d_k)g^{\prime }(\overline{{\mathbf{w}}_0^n}·{\overline{\mathbf{F}}}^{n,k}){\overline{\mathbf{F}}}^{n,k}\Vert \hfill \\ & =\Vert \sum _{k=1}^K((y_k^{n+1}-y_k^n)g^{\prime }(\overline{{\mathbf{w}}_0^{n+1}}·{\overline{\mathbf{F}}}^{n+1,k}){\overline{\mathbf{F}}}^{n+1,k}\hfill \\ & +(y_k^n-d_k)(g^{\prime }(\overline{{\mathbf{w}}_0^{n+1}}·{\overline{\mathbf{F}}}^{n+1,k}){\overline{\mathbf{F}}}^{n+1,k}-g^{\prime }(\overline{{\mathbf{w}}_0^n}·{\overline{\mathbf{F}}}^{n,k}){\overline{\mathbf{F}}}^{n,k}))\Vert \hfill \\ & \le \sum _{k=1}^K(|(y_k^{n+1}-y_k^n)g^{\prime }(\overline{{\mathbf{w}}_0^{n+1}}·{\overline{\mathbf{F}}}^{n+1,k})|\Vert {\overline{\mathbf{F}}}^{n+1,k}\Vert \hfill \\ & +|y_k^n-d_k|\Vert g^{\prime }(\overline{{\mathbf{w}}_0^{n+1}}·{\overline{\mathbf{F}}}^{n+1,k}){\overline{\mathbf{F}}}^{n+1,k}-g^{\prime }(\overline{{\mathbf{w}}_0^n}·{\overline{\mathbf{F}}}^{n,k}){\overline{\mathbf{F}}}^{n,k}\Vert )\hfill \\ & \le \sum _{k=1}^K(c_4^2\sqrt{q}|y_k^{n+1}-y_k^n|+(c_4+sup{d}_k)\Vert g^{\prime }(\overline{{\mathbf{w}}_0^{n+1}}·{\overline{\mathbf{F}}}^{n+1,k}){\overline{\mathbf{F}}}^{n+1,k}-g^{\prime }(\overline{{\mathbf{w}}_0^n}·{\overline{\mathbf{F}}}^{n,k}){\overline{\mathbf{F}}}^{n,k}\Vert )\hfill \\ & \le L_3\Vert {\mathbf{w}}^{n+1}-{\mathbf{w}}^n\Vert \hfill \end{array}$$ 24

where $L_3=K\sqrt{q}{c}_4(c_4{c}_6+(c_4+sup{d}_k)(c_5+c_6))$.

Similarly, there exists a Lipschitz constants L₄ such that for $l=1,\cdots ,q$

$$\Vert \frac{\mathit{\partial }E({\mathbf{w}}^{n+1})}{\mathit{\partial }\overline{{\mathbf{w}}_l}}-\frac{\mathit{\partial }E({\mathbf{w}}^n)}{\mathit{\partial }\overline{{\mathbf{w}}_l}}\Vert \le L_4\Vert {\mathbf{w}}^{n+1}-{\mathbf{w}}^n\Vert .$$ 25

Hence, (7), (24), and (25) validate (14) by setting L₁ = L₃ + qL₄.

Equation (15) can be proved in a similar way to (14). □

Now, we proceed to the proof of Theorem 2 by dealing with Equations (9)-(12) separately.

Proof of (9)

By the differential mean value theorem, there exists a constant $\mathit{\theta }\in [0,1]$, such that

$$\begin{array}{cc}& E({\mathbf{w}}^{n+1})-E({\mathbf{w}}^n)\hfill \\ & ={({\nabla }_{\mathbf{w}}E({\mathbf{w}}^n+\mathit{\theta }\mathrm{\Delta }{\mathbf{w}}^n))}^T\mathrm{\Delta }{\mathbf{w}}^n+{({\nabla }_{\overline{\mathbf{w}}}E({\mathbf{w}}^n+\mathit{\theta }\mathrm{\Delta }{\mathbf{w}}^n))}^T\overline{\mathrm{\Delta }{\mathbf{w}}^n}\hfill \\ & ={({\nabla }_{\mathbf{w}}E({\mathbf{w}}^n))}^T\mathrm{\Delta }{\mathbf{w}}^n+{({\nabla }_{\overline{\mathbf{w}}}E({\mathbf{w}}^n))}^T\overline{\mathrm{\Delta }{\mathbf{w}}^n}\hfill \\ & +{({\nabla }_{\mathbf{w}}E({\mathbf{w}}^n+\mathit{\theta }\mathrm{\Delta }{\mathbf{w}}^n)-{\nabla }_{\mathbf{w}}E({\mathbf{w}}^n))}^T\mathrm{\Delta }{\mathbf{w}}^n\hfill \\ & +{({\nabla }_{\overline{\mathbf{w}}}E({\mathbf{w}}^n+\mathit{\theta }\mathrm{\Delta }{\mathbf{w}}^n)-{\nabla }_{\overline{\mathbf{w}}}E({\mathbf{w}}^n))}^T\overline{\mathrm{\Delta }{\mathbf{w}}^n}\hfill \\ & \le 2Re({\nabla }_{\mathbf{w}}E{({\mathbf{w}}^n)}^T\mathrm{\Delta }{\mathbf{w}}^n)\hfill \\ & +(\Vert {\nabla }_{\mathbf{w}}E({\mathbf{w}}^n+\mathit{\theta }\mathrm{\Delta }{\mathbf{w}}^n)-{\nabla }_{\mathbf{w}}E({\mathbf{w}}^n)\Vert +\Vert {\nabla }_{\overline{\mathbf{w}}}E({\mathbf{w}}^n+\mathit{\theta }\mathrm{\Delta }{\mathbf{w}}^n)-{\nabla }_{\overline{\mathbf{w}}}E({\mathbf{w}}^n)\Vert )\Vert \mathrm{\Delta }{\mathbf{w}}^n\Vert \hfill \\ & \le -2\mathit{\eta }Re({({\nabla }_{\overline{\mathbf{w}}}E({\mathbf{w}}^n))}^H{\nabla }_{\overline{\mathbf{w}}}E({\mathbf{w}}^n))+(L_1+L_2)\mathit{\theta }{\Vert \mathrm{\Delta }{\mathbf{w}}^n\Vert }^2\hfill \\ & =(-2\mathit{\eta }+(L_1+L_2)\mathit{\theta }{\mathit{\eta }}^2){\Vert {\nabla }_{\overline{\mathbf{w}}}E({\mathbf{w}}^n)\Vert }^2\hfill \end{array}$$ 26

To make (9) valid, we only require the learning rate η to satisfy

$$0<\mathit{\eta }<L,$$ 27

where $L=\frac{2}{(L_1+L_2)\mathit{\theta }}$. □

Proof of (10)

Equation (10) is directly obtained by (9) and $E({\mathbf{w}}^n)>0(n=1,2,\cdots )$.

Proof of (11)

Let β = 2η − (L₁ + L₂)θη². By (26), we have

$$\begin{array}{cc}& E({\mathbf{w}}^{n+1})\le E({\mathbf{w}}^n)-\mathit{\beta }{\Vert {\nabla }_{\overline{\mathbf{w}}}E({\mathbf{w}}^n)\Vert }^2\hfill \\ & \le \cdots \le E({\mathbf{w}}^0)-\mathit{\beta }\sum _{t=0}^n{\Vert {\nabla }_{\overline{\mathbf{w}}}E({\mathbf{w}}^t)\Vert }^2.\hfill \end{array}$$ 28

Considering E(wⁿ⁺¹) > 0, let $n\to \infty$, then we have

$$\mathit{\beta }\sum _{t=0}^{\infty }{\Vert {\nabla }_{\overline{\mathbf{w}}}E({\mathbf{w}}^t)\Vert }^2\le E({\mathbf{w}}^0)<\infty .$$ 29

This immediately gives

$$\underset{n\to \infty }{lim}\Vert {\nabla }_{\overline{\mathbf{w}}}E({\mathbf{w}}^n)\Vert =0.$$ 30

□

The following lemma, which will be used in the proof of (12), is a generalization of Theorem 14.1.5 by Ortega and Rheinboldt (1970) from the real domain to the complex domain. The proof of this lemma follows the same route as (Ortega and Rheinboldt 1970) and we omit it here.

Lemma 3

[22] Let$\mathit{\phi }:\mathrm{\Phi }\subset {\mathbb{C}}^k\to \mathbb{C}(k\ge 1)$be continuous for a bounded closed region$\mathrm{\Phi }$, and${\mathrm{\Phi }}_0=\{\mathbf{z}\in \mathrm{\Phi }:\mathit{\phi }(\mathbf{z})=0\}$.Suppose the set${\mathrm{\Phi }}_0$contains only finite points and the sequence {zⁿ} satisfy:

• (i)${lim}_{n\to \infty }\mathit{\phi }({\mathbf{z}}^n)=0$;
• (ii)${lim}_{n\to \infty }\Vert {\mathbf{z}}^{n+1}-{\mathbf{z}}^n\Vert =0$.

Then, there exists a unique${\mathbf{z}}^{★}\in {\mathrm{\Phi }}_0$such that$\underset{n\to \infty }{lim}{\mathbf{z}}^n={\mathbf{z}}^{★}$.

Proof of (12)

Obviously ${\nabla }_{\overline{\mathbf{w}}}E(\mathbf{w})$ is continuous under the Assumption (A2). Using (8) and (11), we have

$$\underset{n\to \infty }{lim}\Vert {\mathbf{w}}^{n+1}-{\mathbf{w}}^n\Vert =\mathit{\eta }\underset{n\to \infty }{lim}\Vert {\nabla }_{\overline{\mathbf{w}}}E({\mathbf{w}}^n)\Vert =0.$$ 31

Furthermore, the Assumption (A3) is valid. Thus, applying Lemma 3, there exists a unique ${\mathbf{w}}^{★}\in \mathrm{\Phi }$ such that $\underset{n\to \infty }{lim}{\mathbf{w}}^n={\mathbf{w}}^{★}$. □

Simulation result

In this section we illustrate the convergence behavior of the FCBPA by the problem of one-step-ahead prediction of the complex-valued nonlinear signals. The nonlinear benchmark input signal is given by (Mandic and Goh 2009)

$$z(t)=\frac{z(t-1)}{1+z^2(t-1)}+n^3(t),$$ 32

where n(t) is a complex white Gaussian noise with zero mean and unit variance.

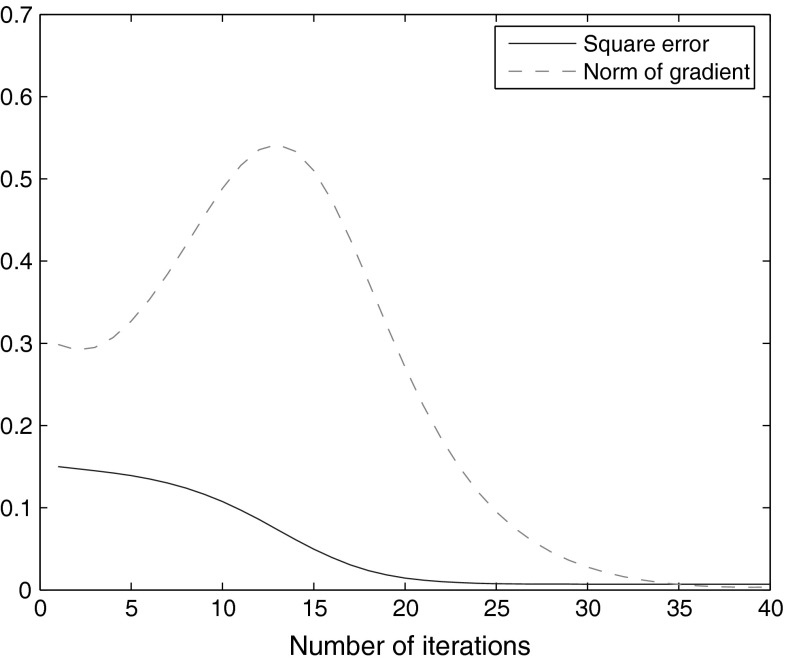
This example uses a network with one input node, five hidden nodes, and one output node. We set the activation function for both the hidden layer and output layer to be $sin(·)$, which is analytic in the complex domain. The learning rate η is set to be 0.1. The test is carried out with the initial weights (both the real part and the imaginary part) taken as random numbers from the interval [−0.1, 0.1]. The simulation results are presented in Fig. 1, which shows that the gradient tends to zero and the square error decreases monotonically as the number of iteration increases and at last it tends to a constant. This supports our theoretical findings.

Fig. 1.

Convergence behavior of FCBPA

Conclusion

In this paper, under the framework of Wirtinger calculus, we investigate the FCBPA for fully CVNN. Using a mean value theorem for holomorphic functions, under mild conditions we prove the gradient of the error function with respect to the network weight vector satisfies the Lipschitz condition. Based on this conclusion, both the weak convergence and strong convergence of the algorithm are proved. Simulation results substantiate the theoretical findings.