Evaluating influence of microRNA in reconstructing gene regulatory networks

Abstract

Gene regulatory network (GRN) consists of interactions between transcription factors (TFs) and target genes (TGs). Recently, it has been observed that micro RNAs (miRNAs) play a significant part in genetic interactions. However, current microarray technologies do not capture miRNA expression levels. To overcome this, we propose a new technique to reverse engineer GRN from the available partial microarray data which contains expression levels of TFs and TGs only. Using S-System model, the approach is adapted to cope with the unavailability of information about the expression levels of miRNAs. The versatile Differential Evolutionary algorithm is used for optimization and parameter estimation. Experimental studies on four in silico networks, and a real network of Saccharomyces cerevisiae called IRMA network, show significant improvement compared to traditional S-System approach.

Introduction

The increased interest in systems biology, e.g., reverse-engineering of GRNs, is primarily due to the availability of genome wide expression data. While static expression data allows the learning of only the network structure, the time-course data enables the modeling of intricate system dynamics over time. The GRN inference methods can be broadly classified into three major groups, namely co-expression network, Bayesian network and differential equation approach. Co-expression network (Butte and Kohane 2000) are coarse-scale, simplistic models that employ pairwise association measures for inferring the interactions between genes. Due to the low computational complexity these methods can be scaled up to thousand gene network (Basso et al. 2005), but suffer from their inability of modeling system dynamics. Bayesian networks (BN), and its extension, the dynamic Bayesian network (DBN), are more sophisticated models based on the strong foundations of probability and statistics. In this model, the dependencies between nodes are represented using directed edges and conditional probability distributions. In addition, DBNs allow the modeling of system dynamics in discrete time.

Amongst the other group of reverse engineering techniques, i.e., co-expression network and Bayesian network, this paper focuses on differential equation based approaches, which belong to a sophisticated and well established class of methods for modeling biochemical phenomena, including GRNs (Gardner et al. 2003). The differential equation based approach has the ability to accurately model system dynamics in continuous time. Of several linear and non-linear types of differential equation models employed for reconstructing GRNs, the S-System model (Savageau 1976) has gained popularity recently (Chowdhury et al. 2012; Kikuchi et al. 2003; Kimura et al. 2005; Noman and Iba 2006, 2007). This model is considered to provide the necessary balance between model complexity and mathematical tractability: it is complex enough to represent a wide range of dynamics, yet is simple enough to allow certain analytical studies. Other than the above mentioned three major groups, recently proposed approaches for GRN construction methods deal with either stability of the network or stochastic delayed regulations or both (He and Cao 2008; Luo et al. 2010; Ye and Cui 2010; Wang et al. 2009).

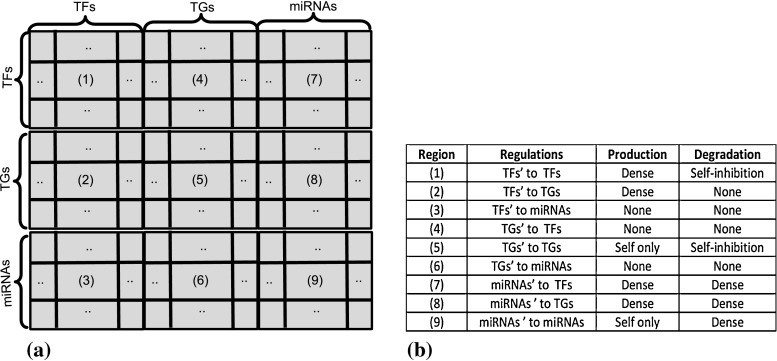
Besides the transcriptional level interactions between transcription factors (TFs) and target genes (TGs), at the post transcriptional control, a large and growing class of ∼22 nucleotide-long non-coding RNAs, namely micro RNA (miRNA), have been observed to negatively regulate gene expression and function as repressor in genomes. In brief, we can state that the gene expression profiles are controlled not only by TFs but also by miRNAs (He and Hannon 2004; Chen and Rajapaksy 2007), where miRNAs contribute only towards gene degradation. In Fig. 1a, we show different categories of regulations by dividing the possible interactions into 9 regions, while the nature of the regulations between two genes belonging to any of the 9 regions are listed in Fig. 1b. Since current microarray technology is unable to capture miRNA expression level, all the existing methods for reverse engineering genetic network from microarray data ignore the presence of miRNAs and only consider various TF–TG interactions in GRNs to estimate the model parameters. In this paper, adapting the existing S-System model for reverse engineering GRN, we propose a new technique for GRN reconstruction by incorporating the influence of miRNAs’ regulations on genes. For modeling the influences of miRNAs’ interactions, the regulations among genes are restricted to self-inhibition in the degradation phase. This is a biological relevant assumption (Chen and Rajapaksy 2007) and it helps to reduce the number of parameters to be estimated. The proposed method iREGARD (improved version of REGARD (Chowdhury et al. 2012) possesses the following key contributions:

• Developing a method that considers the biological knowledge of Regulatory (i.e., TFs) and Regulated (i.e., TGs) genes, and miRNAs. Although, the data for miRNA expression profiles are not available with microarray data, the expression profiles of TFs and TGs include the influence of miRNAs. The proposed iREGARD is developed with the consideration of this biological substantiation by improving the previously proposed method and fitness function. While reconstruction is performed using TFs’ and TGs’ expression data, the biological facts on miRNA regulations are deemed to be legitimate and optimization is performed taking into account this consideration.

• The S-System based modeling algorithms (Chowdhury et al. 2012; Kikuchi et al. 2003; Kimura et al. 2005; Noman and Iba 2006, 2007) learn the full-set of S-System parameters (2*N*(N + 1)) for N genes, which reduces to 2*(N + 1) with decoupled equations. The incorporation of biological knowledge in iREGARD has greatly reduced the number of parameters further. This is done by exploiting the fact that, a transcription factor can regulate itself during the degradation phase, and any other regulations are considered biologically unrealistic. Thus we eliminate learning (N − 1) regulatory parameters in the degradation phase (represented by h in the S-System). Hence the total number of parameters to learn in S-System using the proposed iREGARD becomes 2*(N + 1) − (N − 1) = N + 3.

Fig. 1.

a Regions of interactions among TFs, TGs, and miRNAs (possible interactions in a GRN). b Classification of parameters related to interactions among TFs, TGs, and miRNAs

Preliminaries

The S-System model

For a network of N genes, the existing S-System model is given by the following set of ordinary differential equations (ODEs):

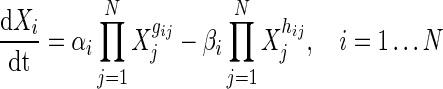1

Here, for any ith gene, X_i is the expression level, 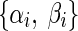’s are the rate constants, and {g_ij, h_ij}’s being the the kinetic orders represent the regulations in RNA synthesis/production and degradation, respectively. To infer a GRN of N genes using the S-System model, 2N(N + 1) parameters must be estimated. To reduce computational complexity, method of Voit and Almeida (2004) approximated the original problem as N decoupled sub-problems, each of having 2(N + 1) parameters. The canonical S-System model (Eq. 1) requires enormous computation time to converge properly. However, decoupled S-System can infer the parameters of the target network much quickly, albeit with some approximation, compared to the canonical S-System model.

Fitness criteria

In order to assess the goodness of S-System models, previous works commonly employed the squared relative error (SRE) as criterion for model evaluation. As the parameters for each gene in the decoupled S-System are learned independently of the others, the SRE for ith gene is given as:

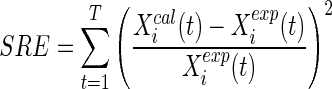2

Here t denotes a specific time-stamp (TS) in the observed time series of T sample points. X^cal_i(t) and X^exp_i(t) denote the calculated and observed expression value of gene-i at time-stamp t respectively. Due to decoupling, this SRE criterion for each gene can be minimized independently. The solution for this optimization problem is normally dense, i.e., it has many non-zero parameter values corresponding to many regulators for each gene. However, due to salient features of GRNs, i.e., the sparsity and following the scale-free topology (Guelzim et al. 2002; Sheridan et al. 2010), Kimura et al. (2005) added a regularized penalty term for model complexity introducing the concept of maximum in-degree (I). Noman and Iba (2007) improved that regularized term of Kimura et al. (2005) and obtained good results. However, both the fitness functions (Kimura et al. 2005; Noman and Iba 2007) apply this I as global parameter while in-degrees vary from gene to gene. Unlike the previous methods with fixed I, recently proposed method REGARD (Chowdhury et al. 2012) introduce the concept of min in-degree and calculate the error according to the following equation:

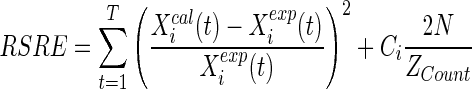3

Here, Z_Count is the total number of non-regulations for the ith gene (= 2N- total regulations) and, C_i is the scaling factor for the ith gene defined as:

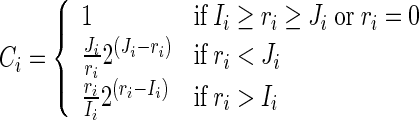4

Here, r_i is the number of regulations, and {I_i, J_i} indicate the in-degrees of gene-i. The values of I_i and J_i are initialized to N and 0 (in-degrees of the entire network), respectively and adapt themselves based on population statistics. Details about this fitness function are available in Chowdhury et al. (2012). We call the Eq. (3) as regularized squared relative error (RSRE) as it is essentially a regularized version of the initial proposal (Eq. 2). This fitness function was designed by ignoring the absence of miRNAs in the network (hence in the microarray data), that work on large search space during the optimization. In this paper, we have adapted this fitness function to fit in the absence of miRNAs and adjusted the optimization accordingly.

The proposed technique: iREGARD

The model

Among the N genes in a gene regulatory network, let N₁ be the total number of regulatory (TFs) and regulated/target genes (TGs) which we denote as RRG (regulatory and regulated genes), while N₂ are miRNAs. Here, 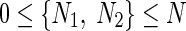and N₁ + N₂ = N. We rewrite the S-System model equations accordingly:

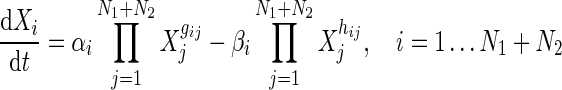5

Now, we form four groups by combining the regions of Fig. 1 in order to separate the in-out regulations of miRNAs. Table 1 shows these four groups along with corresponding S-System parameters for each group. However, due to the non-availability of miRNAs’ expression data with the current microarray technology, only N₁ expression profiles (for N₁ RRGs) are available for reverse engineering. As a result, these N₁ expression profiles can only be applied to reconstruct the regulatory networks having N₁ RRGs. Thus, the resulting S-System parameter model becomes:

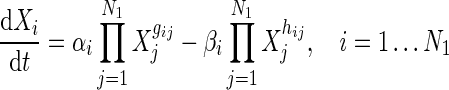6

which represents the interactions in Group A only. Thus, in the decoupled form for Group A genes (RRGs), we estimate 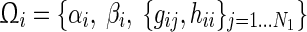parameters (i.e., N + 3 in total for each gene with decoupled equation) for every ith gene.

Table 1.

Possible groups, with regulations, in the S-System model along with corresponding parameter values

Groups	Regions	Possible regulations	Parameter values
Group A	(1), (2), (4), (5)	Regulations among RRGs
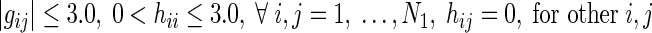
Group B	(7), (8)	Regulations on RRGs from miRNAs
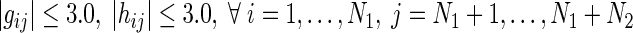
Group C	(9)	Regulations among miRNAs
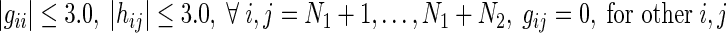
Group D	(3), (6)	Regulations on miRNAs from RRGs

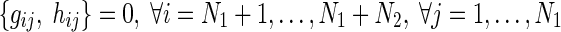
The inference method

In the optimization phase, we use Differential Evolution (DE), an evolutionary algorithm proposed by Price et al. (Storn and Price 1997) for learning the S-System parameters. The proposed iREGARD starts with a cardinality based initial population generation technique that incorporates the biological knowledge about the interactions. In the initial population, 10 % individuals are initialized with all the g values set to zero, however, initialize the single 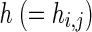value to a random positive value. For each of the remaining 90 % individuals, we randomly select I positions from g vector and initialize them with a random value. The remaining N − I positions are initialized to 0. This initialization allows 90 % individuals to start with exactly I randomly selected regulations. In GRNs, it is well known that the transcription factors and target genes generally have effects only on the production of their target genes, but not their degradation. The messenger RNA (mRNA) degradation is affected by either a self-degradation rate specific to each gene, and/or by miRNAs and some proteins with mRNA degradation functions (Shyu et al. 2008). Thus we initialize the only h to a positive value (i.e., h_i,i for ith gene), indicating the self-inhibition of the RRGs.

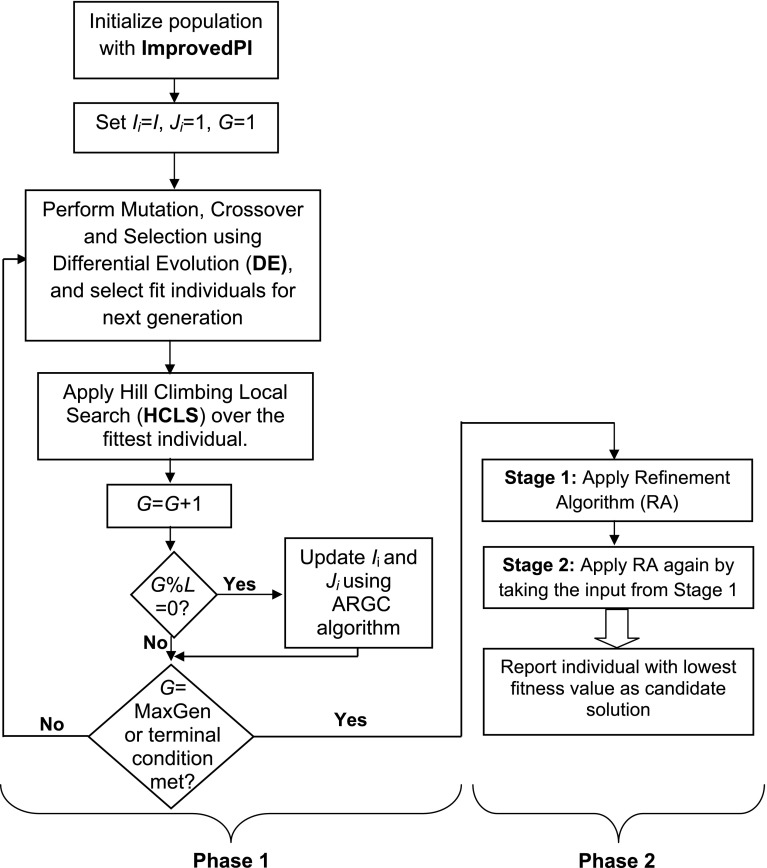
Once the initialization is completed, we start the iteration of the evolutionary algorithm. In each generation, we apply mutation, crossover and selection operations to produce the individuals for next generation. Once the individuals for the next generation are created, we apply hill-climbing local search algorithm (Noman and Iba 2007) over the fittest individual. Further, in each Lth iteration, we update the cardinality parameters I_i (max in-degree) and J_i (min in-degree) for ith gene (as we are using decoupled S-System) based on papulation statistics. Details about this adaptation algorithm, known as Adaptive Regulatory Genes Cardinality (ARGC), can be found in Chowdhury et al. (2012). These two parameters I_i and J_i are initialized to I and 1, respectively, where I is the maximum in-degree for the network. Finally, we apply the multistage refinement algorithm (MRA) for pruning the low-weighted regulations that are less than the predefined threshold (ψ). It should be noted that, due to the absence of miRNA data in the reverse engineering process, the effects of miRNA regulations (to and from) have to be treated as noise in the expression profiles of given microarray data (only for RRGs’ regulations). Hence, we lowered this threshold from REGARD to avoid pruning the true regulations that are inferred with relatively low values than target values. The inference method of the proposed iREGARD is shown as a flow-chart in Fig. 2.

Fig. 2.

The flow-chart of the proposed iREGARD. I indicates the maximum in-degree of the network, where I _i and J _i, respectively indicate the maximum and minimum in-degrees of ith gene. L denotes the frequency to update the cardinalities using ARGC algorithm

Experimental results and discussions

The performance of iREGARD is studied by investigating four synthetic networks and a real network of Saccharomyces cerevisiae (yeast) called IRMA (Cantone et al. 2009). The proposed algorithm is implemented in C++ using a 2.16 GHz Dual-core CPU PC with 3 GB of RAM. This code and data for all the networks can be made available upon request. The parameter values for the DE algorithm were set as follows: Mutation Rate F = 0.5, Crossover Factor CF = 0.8, population size Pop= 5*(number of parameters), which is 5*(N + 3), where N is the size of the network. The maximum in-degree (I) for the network were set to N, while the cardinality parameters for each genes are updated in every Lth = 50th generation. We have executed the proposed iREGARD for 850 generations in the first phase while in the second phase, MRA is executed for 250 generations. Finally, the pruning factor ψ = 0.10 was used for the multi-stage refinement algorithm. For each of the four synthetic networks, M = 10 datasets are generated from 10 different initial conditions.

The four in silico GRNs are designed taking into account the presence of miRNA in various ratio with respect to regulatory and regulated genes (RRGs). The proposed technique assumes the presence of N₂ miRNAs (=N₁ + N₂ genes in total) in the GRNs, while the reconstruction will estimate the parameters for N₁ RRGs, considering the non-availability of expression profiles for miRNAs. Since the data are created considering all N₁ + N₂ genes and only N₁ RRGs are provided for reverse engineering, the influences of the N₂ genes (miRNAs) on those N₁ RRGs can be considered to be acting as noise. The first three networks (Net-1, Net-2, and Net-3) are designed with the inevitable presence of miRNAs in the GRN. On the other hand, Net-4 is a widely used 20-gene synthetic network (Noman and Iba 2007) composed of RRGs only, hence the time-series data for this network does not have any influence of miRNAs. The number of RRGs and miRNAs for all four synthetic networks are summarized in Table 2. For all the synthetic networks, we have compared the performances of iREGARD with our previously developed algorithm REGARD (Chowdhury et al. 2012). With the 5-gene real-life network of IRMA, it has time-responses available for two modes, i.e., ON and OFF. In the ON dataset, there are 16 time-samples which were evenly sampled in every 20 min. On the other hand, in the OFF dataset, there are 21 time-samples which were evenly sampled in every 10 min. The ON dataset corresponds to the shifting of the growth medium from glucose to galactose while the OFF dataset corresponds to the shifting of the growth medium from galactose to glucose. Similar to Net-4, all five genes (in both ON and OFF modes) are assumed to be RRGs during the optimization. The performances of iREGARD for IRMA are compared with six state-of-the-art algorithms, where two of them [i.e., REGARD (Chowdhury et al. 2012) and ALG (Noman and Iba 2007)] are S-System based methods and remaining four are non-S-System based methods [i.e., TDARACNE (Zoppoli et al. 2010), ARACNE (Margolin et al. 2006), NIR & TSNI (Della et al. 2008), and BANJO (Yu et al. 2004)]. The uniform parameter values were considered for REGARD (Chowdhury et al. 2012), ALG (Noman and Iba 2007) and iREGARD, except the pruning factor ψ in REGARD was set to 0.25 as proposed in (Chowdhury et al. 2012). On the other hand, ALG (Noman and Iba 2007) was executed for 5 trials in the first phase and the best result from each trial were used in the second phase. In the second phase, remaining P-5 individuals were initialized randomly and a separate trial were performed with the parameter settings similar to the first phase. In both the phases, 850 iterations were performed for every single run. More details about the REGARD and ALG can be found in Chowdhury et al. (2012) and Noman and Iba (2007), respectively. Regarding the four non-S-System based methods: ARACNE (Margolin et al. 2006) is an information theoretic approach that calculates the influence of one gene over other using Mutual Information. Zoppoli et al. (2010) improved the ARACNE, by incorporating time-delays, which is also an information theoretic approach that defines two threshold τ_up = 1.2 and τ_down = 0.83 while measuring the initial change of expression of a gene. On the other hand, NRI & TSNI (Della et al. 2008) is an integrated experimental and computational approach that uses ordinary differential equation to represent the network and regulations. Finally, dynamic Bayesian network based method BANJO (Yu et al. 2004) is developed with probability equations that measures the performance based on their developed influence score metric. We have shown the best case results for all these four methods that are reported in the original papers (Margolin et al. 2006; Della et al. 2008; Yu et al. 2004; Zoppoli et al. 2010). More about the above mentioned four methods can be found in the corresponding original papers (Margolin et al. 2006) (ARACNE), (Zoppoli et al. 2010) (TDARACNE), (Della et al. 2008) (NIR & TSNI) and (Yu et al. 2004) (BANJO). We consider four performance measures i.e., sensitivity (S_n), specificity (S_p), precision (P_r) and F-score (F − score) for network evaluation, where best, average (AVG) and standard deviation (STD) are reported.

Table 2.

Summary of four synthetic networks

Net name	Total genes	RRGs (N 1)	miRNAs (N 2)
Net-1	5	3	2
Net-2	8	5	3
Net-3	12	8	4
Net-4	20	20	0

Synthetic networks

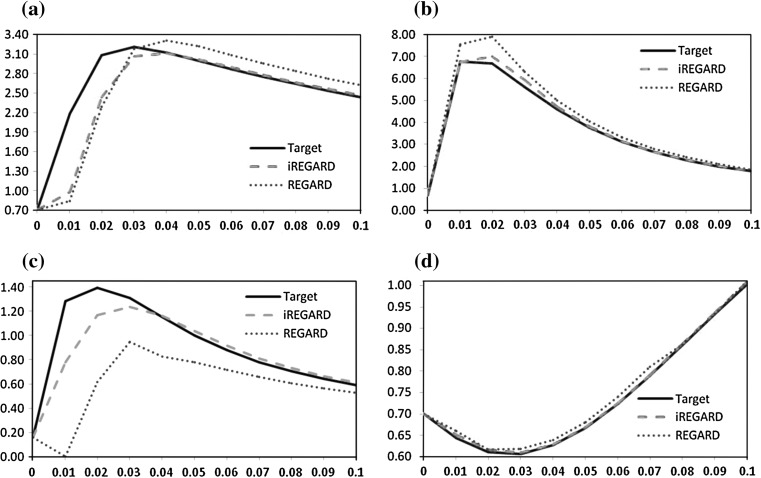
The evaluation of iREGARD for the 4 synthetic networks are shown in Table 3, and compared with recently proposed method REGARD (Chowdhury et al. 2012). For all the four synthetic networks, we observe excellent performance of iREGARD in all four performance metrics (i.e., 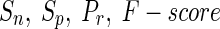). On the other hand, although the performances of the existing method REGARD (Chowdhury et al. 2012) are satisfactory, yet remarkably inferior to that of iREGARD. The synthetic networks are designed for the experiment in such a way that ratio of RRGs and miRNAs should vary in each network, so that we can evaluate the influence of miRNAs’ in the learning process. We observe that, the performance of REGARDS improves with the increase of ratio between RRGs and miRNAs Apart from inferring the RRGs with very high accuracy, the expression profiles for the genes in all four networks estimated by iREGARD are either closely overlapping or completely follow the trends of the target expression patterns. The expression profiles of four genes, one from each of the four networks, for the target, iREGARD, and REGARD are shown in Fig. 3.

Table 3.

Experimental results for all four synthetic networks

	Net-1				Net-2
	S n	S p	P r	F − score	S n	S p	P r	F − score
iREGARD (Best)	0.89	1.00	1.00	0.94	0.94	0.94	0.88	0.91
iREGARD (AVG ± STD)	0.78 ± 0.11	0.96 ± 0.06	0.94 ± 0.07	0.85 ± 0.09	0.91 ± 0.03	0.93 ± 0.01	0.86 ± 0.03	0.88 ± 0.03
REGARD (Best)	0.56	0.89	0.83	0.67	0.81	0.82	0.68	0.74
REGARD(AVG ± STD)	0.48 ± 0.06	0.85 ± 0.06	0.76 ± 0.06	0.60 ± 0.05	0.71 ± 0.05	0.80 ± 0.01	0.62 ± 0.03	0.69 ± 0.04

	Net-3				Net-4
iREGARD (Best)	0.96	0.82	0.59	0.73	1.00	1.00	1.00	1.00
iREGARD (AVG ± STD)	0.89 ± 0.06	0.82 ± 0.01	0.57 ± 0.02	0.69 ± 0.03	0.98 ± 0.01	0.98 ± 0.01	0.83 ± 0.09	0.89 ± 0.06
REGARD (Best)	0.74	0.60	0.28	0.41	0.98	0.90	0.37	0.53
REGARD (AVG ± STD)	0.72 ± 0.02	0.57 ± 0.01	0.31 ± 0.01	0.43 ± 0.01	0.96 ± 0.01	0.90 ± 0.005	0.35 ± 0.01	0.52 ± 0.01

Fig. 3.

Target and inferred expression profiles (with iREGARD and REGARD) for one gene from all four networks. Horizontal and vertical axis indicate time and expression level, respectively. a Net-1—Gene 1. b Net-2—Gene 1. c Net-3—Gene 4. d Net-4—Gene 20

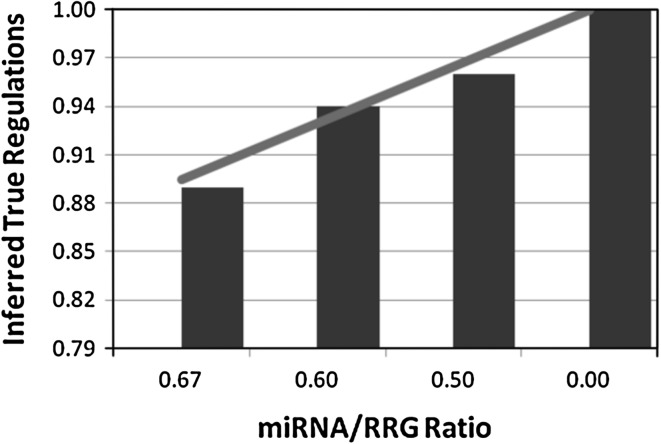
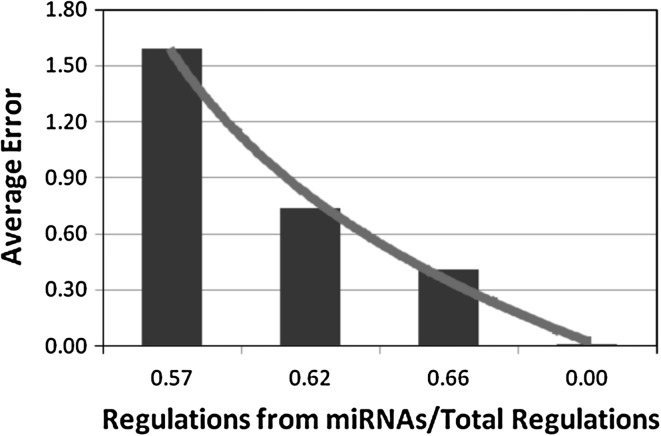
Investigating the proposed iREGARD for four synthetic networks, we observe a reciprocal relationship between the number of inferred true regulations and the ratio of miRNAs/RRGs. In contrast, the average error (defined in Chowdhury et al. 2012) is decreased with the decrease of ratio between regulations from miRNAs and total regulations. The first observation is shown in Fig. 4, where the increase in inferred true regulations can be represented by a trendline of increasing linear function. On the other hand, the observation on average error, shown in Fig. 5, can be mapped to an approximate logarithmic trendline.

Fig. 4.

miRNA/RRG ratio vs inferred true regulations graph

Fig. 5.

Total regulations from miRNAs/ total regulations vs average error graph

IRMA real network

The proposed technique is next applied to a real-life biological network of Saccharomyces cerevisiae (yeast) called IRMA (Cantone et al. 2009). This network is composed of five genes (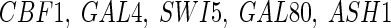), regulating each other. We test both the networks considering the presence of RRGs by allowing the self-inhibitions only in the degradation phase during the optimizations. The four performance measures for iREGARD are compared with state-of-the-art algorithms, namely ALG (Noman and Iba 2007), REGARD (Chowdhury et al. 2012), TDARACNE (Zoppoli et al. 2010), ARACNE (Margolin et al. 2006), NIR and TSNI (Della et al. 2008), and BANJO (Yu et al. 2004). The results are shown in Table 4. It can be observed that, S_n of iREGARD for ON dataset is best as compared to other methods, where only the method ALG (Noman and Iba 2007) reached the same S_n. Although, the specificity (S_p) is not the best among all, this value is still promising and close to the so-far best result reported in the table. The two other performance metrics are also competitive and better than most of the methods. While investigating the OFF dataset, it is excellent to observe that, 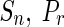, and F − score for iREAGARD obtained the best results among all other techniques reported in this paper. The other performance measure S_p was also found to be very competitive with other methods.

Table 4.

Performance comparison with IRMA real network

Methods	IRMA ON				IRMA OFF
	S n	S p	P r	F − score	S n	S p	P r	F − score
iREGARD (Best)	0.77	0.86	0.67	0.71	0.85	0.81	0.61	0.71
iREGARD (AVG ± STD)	0.74 ± 0.04	0.84 ± 0.03	0.62 ± 0.04	0.67 ± 0.03	0.79 ± 0.07	0.77 ± 0.02	0.55 ± 0.04	0.65 ± 0.05
REGARD (Chowdhury et al. 2012)	0.69	0.83	0.60	0.64	0.77	0.76	0.53	0.63
ALG (Noman and Iba 2007)	0.77	0.27	0.27	0.40	0.76	0.56	0.38	0.57
TDARACNE (Zoppoli et al. 2010)	0.63	0.88	0.71	0.67	0.60	–	0.37	0.46
ARACNE (Margolin et al. 2006)	0.60	–	0.05	0.54	0.33	–	0.25	0.28
NIR & TSNI (Della et al. 2008)	0.50	0.94	0.80	0.63	0.38	0.88	0.60	0.47
BANJO (Yu et al. 2004)	0.24	0.76	0.33	0.29	0.38	0.88	0.60	0.46

Conclusion

In this paper, a new gene regulatory network (GRN) modeling technique is proposed to demonstrate the influence of micro RNAs (miRNAs) in the GRNs. We have taken into account the non-availability of expression profiles for miRNAs and reconstructed the GRN of transcription factors (TFs) and target genes (TGs). The proposed method iREGARD adapts the traditional S-System equations by grouping its parameters according to the biological knowledge of interactions among miRNAs, TFs and TGs. The observation shows that, despite the absence of miRNA expression profiles in microarray and yet influencing the other expression profiles, genetic regulatory network of TFs and TGs can still be reconstructed with reasonable accuracy. The investigations carried out on multiple synthetic networks of varying scale and realistic IRMA network show that the new approach outperforms the state-of-the-art methods in well-known performance measures.