SNP2GO: Functional Analysis of Genome-Wide Association Studies

Abstract

Genome-wide association studies (GWAS) are designed to identify the portion of single-nucleotide polymorphisms (SNPs) in genome sequences associated with a complex trait. Strategies based on the gene list enrichment concept are currently applied for the functional analysis of GWAS, according to which a significant overrepresentation of candidate genes associated with a biological pathway is used as a proxy to infer overrepresentation of candidate SNPs in the pathway. Here we show that such inference is not always valid and introduce the program SNP2GO, which implements a new method to properly test for the overrepresentation of candidate SNPs in biological pathways.

GENOME-WIDE association studies (GWAS) allow researchers to identify the portion of the genetic variants associated with a complex trait. The typical output of GWAS consists of a set of noncandidate and candidate single-nucleotide polymorphisms (SNPs), which are supposedly associated with the trait. How to identify a candidate SNP is still under discussion and different statistical approaches have been suggested (Evangelou and Ioannidis 2013). In addition, biological information, such as linkage, genotype, and mutation effects (e.g., missense SNPs in coding regions) can also help to deal with the heterogeneity associated with the experimental design and reduce the number of false (positive) candidate SNPs (Wang et al. 2012).

At some point, and regardless of the classification criterion, the researcher ends up with a set of candidate and noncandidate SNPs. To gain a deeper biological insight into the candidate SNPs, a pathway analysis is carried out to identify the genes and mechanisms that are involved in the expression of the trait under study (Holmans 2010; Wang et al. 2012). One rationale of such analysis is that if a biological pathway (i.e., a group of related genes) is involved in the expression of the trait, then it is likely that the candidate SNPs will be enriched among the genes of the pathway (Holmans 2010). Here, we focus on the Gene Ontology (GO) as a paradigm of a structured and controlled way to associate genes according to their cellular roles (Ashburner et al. 2000).

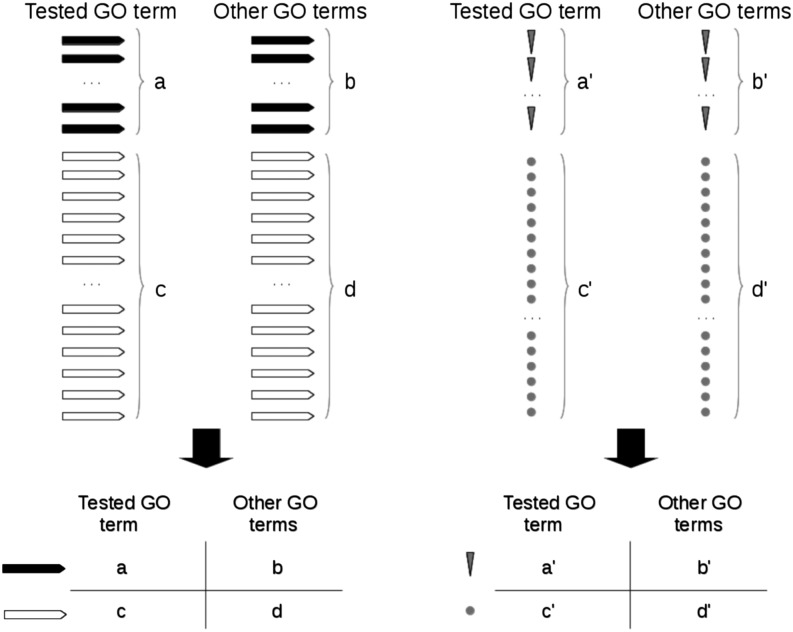
Strategies to identify significant GO terms are typically based on the concept of gene list enrichment (Wang et al. 2007; Chasman 2008; Guo et al. 2009; Holmans et al. 2009; Medina et al. 2009; Chen et al. 2010; Nam et al. 2010; Zhang et al. 2010; Turner et al. 2011; Jones et al. 2012; Kofler and Schlötterer 2012) (to cite a few). Originally developed for the analysis of differentially expressed genes (Wang et al. 2012), the idea is to test whether the number of candidate genes (i.e., genes having at least one candidate SNP) linked to a GO term is higher than expected (enriched) in the respective GO term (Holmans 2010; Wang et al. 2012). If candidate genes are significantly overrepresented, then one typically concludes that the GO term also contains an overrepresentation of candidate SNPs. While this may be true in many instances, it is certainly not always the case. Figure 1 illustrates the conceptual difference between gene list enrichment and candidate SNP enrichment. Let us call π₁ the probability to obtain a candidate gene associated with one GO term and π₂ the probability to obtain a candidate gene associated with the other GO terms. The null hypothesis of homogeneity, H₀, states that π₁ = π₂, which is tested against the alternative hypothesis H₁: π₁ > π₂ (Agresti 1992). If H₀ is rejected in favor of H₁, it is inferred that the tested GO term has an overrepresentation of candidate genes. However, the conclusion that the tested GO term has also an overrepresentation of candidate SNPs is true only when π₁ = π′₁ and π₂ = π′₂, where π′₁ is the probability to obtain a candidate SNP associated to the GO term, and π′₂ is the probability to obtain a candidate SNP associated to the other GO terms. When these equalities do not hold, then rejection of H₀: π₁ = π₂ may not entail rejection of H₀: π′₁ = π′₂, and vice versa.

Figure 1.

Illustration comparing gene list enrichment (left) and candidate SNP enrichment (right) methods. Solid and open bars represent candidate genes (i.e., genes having at least one candidate SNP) and noncandidate genes, respectively. Arrowheads and circles represent candidate and noncandidate SNPs, respectively. π₁ = a/(a + c); π₂ = b/(b + d); π′₁ = a′/(a′ + c′); π′₂ = b′/(b′ + d′); see main text for details.

To better illustrate the conceptual difference, we discuss an example. To this end, we randomly classified 1.6 million nucleotide positions across the Drosophila melanogaster genome as noncandidate SNPs and 2000 positions as candidate SNPs. The apportionment is based on recent population genetics studies on this species (Orozco-Terwengel et al. 2012). Next, we ran Gowinda (Kofler and Schlötterer 2012) (snp mode), a program based on the gene list enrichment concept, on the simulated data and compared the results with the SNP2GO results. Because candidate genes are defined as a function of candidate SNPs, we expect π₁ = π′₁ and π₂ = π′₂ in most cases. In agreement with this, we found a significant correlation between the P-values calculated by Gowinda and SNP2GO for each GO term (Spearman’s ρ = 0.924, P < 2.2 10⁻¹⁶). However, these equalities do not always hold. GO:0000981 and GO:0006915 constitute representative examples. GO:0000981 is an arbitrary GO term in which Gowinda found a significant overrepresentation of candidate genes (P-value = 0.009). Thus, from the Gowinda analysis, one would conclude that, because candidate genes are significantly overrepresented, GO:0000981 has an overrepresentation of candidate SNPs. However, SNP2GO estimated a P-value of 0.133, indicating that there is no overrepresentation of candidate SNPs in GO:0000981. On the other hand, GO:0006915 has a significant overrepresentation of candidate SNPs according to SNP2GO (P-value = 0.038), while this result does not necessarily imply a significant overrepresentation of candidate genes (P-value = 0.848, according to Gowinda). At this point, it is worth clarifying that GO:0000981 and GO:0006915 are not examples of false positive and false negative errors found by Gowinda. The examples illustrate that gene list enrichment methods do not test for overrepresentation of candidate SNPs and that in some instances the test outcomes may be very different. Therefore, SNP2GO complements standard gene list enrichment tests.

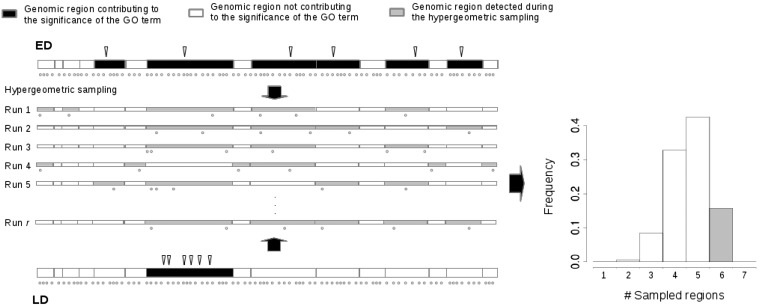
To add more complexity to the problem, a GO term may be significant due to different reasons: (1) only few genomic regions accumulate most or even all candidate SNPs associated with the GO term (as in Linkage Disequilibrium (LD) in Figure 2) or (2) the candidate SNPs are “evenly” distributed in the genomic regions associated with a GO term and equally contribute to the significance of the GO term (Even Distribution (ED) in Figure 2). In the latter case, one may conclude that the GO term is involved in the expression of the trait (Holmans 2010), whereas in the former case, the significance may be due to the positional neighborhood of the SNPs. A third case, not usually considered in GWAS, is the overdispersion of candidate SNPs, in which the number of genomic regions carrying at least one candidate SNP is larger than expected. Therefore, detection of a local genomic effect on the SNP distribution is of special interest as it might help researchers to properly interpret their results. In some cases, mainly in humans, linkage or haplotype data are available, and this information can be used to detect enrichment of candidate SNPs due to LD (see, for instance, Raychaudhuri et al. 2009). However, in many others, such information is not available or cannot be inferred (e.g., if allele frequencies are analyzed from pooled sequencing data). In addition, the enrichment of candidate SNPs may be due to other genomic local effects, such as clustering of genes with the same function (Hong et al. 2009) or heterogeneity in mutation and evolutionary rates across the genome (Eyre-Walker 1993; Hwang and Green 2004; Singh et al. 2005; Duret and Arndt 2008; Tanay and Siggia 2008). We have, therefore, developed SNP2GO to detect such local genomic effects. Importantly, SNP2GO does not require genotype data and can be easily used in studies on any organism. Our method is especially useful in the aforementioned cases, typically found in population genetics and experimental evolution studies (Atwell et al. 2010; Hancock et al. 2011; Turner et al. 2011; Fabian et al. 2012; Jones et al. 2012; Orozco-terWengel et al. 2012; Turner and Miller 2012; Bastide et al. 2013) (to cite a few).

Figure 2.

Test for local effects. Here we represent the distribution of candidate and noncandidate SNPs in the 15 genomic regions associated with the GO term GO:0005548. This term was significant using random SNP positions in the D. melanogaster genome, as explained in the main text. In ED (actual result, with expected distribution of candidate SNPs), g = 6 while in LD (a hypothetical scenario) all candidate SNPs occur in a single genomic region (g = 1). In both ED and LD examples, candidate SNPs (c) = 6 and noncandidate SNPs (nc) = 1497 (not all shown). Run 1 . . . Run r display typical outcomes of the sampling. Genomic regions with at least one sampled SNP are shaded. After r runs, the empirical distribution (right side) is used to test whether g is higher or lower than expected. For ED we estimated P(g ≥ 6) = 0.16 (shaded bar in the histogram), while for LD, P(g ≤ 1) < 10⁻⁵.

In the next section, we introduce SNP2GO, a candidate SNP enrichment analysis method for GWAS that also provides a strategy to detect local genomic effects in the candidate SNP distribution.

Candidate SNP Enrichment Analysis and Detection of Local Genomic Effects

SNP2GO can be applied to pathway databases such as the Kyoto encyclopedia of genes and genomes (Kanehisa et al. 2004), Panther (Mi et al. 2013), GO (Ashburner et al. 2000), or other BioOntologies (Smith et al. 2007), although here we focus on GO. SNP2GO answers two questions: (1) Does a particular GO term show an overrepresentation of candidate SNPs? (2) Is the number of genomic regions contributing to the significance of a GO term different from expectation?

We briefly describe the workflow. SNP2GO takes the genome annotation of the organism of interest (i.e., the gene coordinates), the associated GO terms, and the list of candidate and noncandidate SNPs as defined by the user as input. To avoid decreasing the power of the tests when parental GO terms and children GO terms are compared, SNP2GO carries out an inclusive analysis of the GO terms (Al-Shahrour and Dopazo 2005). For a selected node level, the SNPs are assigned to the genomic regions associated with the GO term (i.e., genes or genes plus or minus a given amount of nucleotides up and down the gene) and a Fisher’s exact test for 2 × 2 contingency tables is done (Figure 1). Correction of P-values for multiple testing follows the Benjamini and Hochberg (1995) false discovery rate adjustment. This part of SNP2GO answers the first question.

To answer the second question, SNP2GO carries out an additional analysis of significant GO terms based on the hypergeometric sampling. Figure 2 shows an instance where all candidate SNPs belong to a single genomic region and another example where exactly one candidate SNP belongs to one genomic region. To determine significant spatial patterns, we count the number, g, of genomic regions in the selected GO term containing at least one candidate SNP and the number, c, of candidate SNPs contained in these regions. Then we sample without replacement c SNPs from all the SNPs associated with the GO term and count the number of genomic regions to which the SNPs belong. After r runs (100,000 by default), the resulting distribution of genomic regions with at least one SNP serves as a null distribution to test whether g deviates significantly from the simulated distribution. If g is small, then the candidate SNPs cluster in a few genomic regions (LD in Figure 2); if g is large, then the candidate SNP distribution is overdispersed (not shown).

This hypergeometric sampling is conceptually similar to the genome-wide permutation approaches typically applied to preserve the LD structure in the data (e.g., Guo et al. 2009; Holmans et al. 2009; Atwell et al. 2010; Kofler and Schlötterer 2012). However, our sampling space is defined by the genomic regions associated with the significant GO term, instead of the whole genome. In other words, SNP2GO does not assume that the level of LD between SNPs is, on average, equal across GO categories, and therefore it is released from violations of this general assumption (Holmans et al. 2009).

Results

As previously mentioned, our method is especially useful in population genetics studies where there is no a priori biological knowledge about linkage, haplotypes, or where this information cannot be inferred. To show the relevance of SNP2GO in such studies, we analyzed the SNPs identified from the comparison between the base and the middle experiment in Orozco-Terwengel et al. (2012). In this study, the authors found 2000 candidate SNPs (of 1.6 million) potentially involved in the thermal adaptation of D. melanogaster and wanted to find the biological pathways potentially implicated in the process. We ran SNP2GO on these data and found 135 significant GO terms (false discovery rate <0.05), with at least 10 genes associated to each of these terms (supporting information, Table S1). Typically, one would conclude that these cellular processes and molecular functions are involved in thermal adaptation in Drosophila. However, SNP2GO found that the number of genomic regions in the corresponding GO terms contributing to the significance of 120 of the 135 significant GO terms was lower than expected by chance (P < 0.05, according to the empirical null distribution). In other words, only a few genomic regions per GO term caused the significance. Hence, according to SNP2GO, one should be careful about the interpretation of the significance of these GO terms, since local genomic effects are probably clustering the candidate SNPs.

Therefore, we further studied the genomic distribution of the SNPs found in Orozco-Terwengel et al. (2012) and analyzed the location of the candidate SNPs on the chromosomes. We found that 1568 of the 2000 candidate SNPs (i.e., 78%) are located on the chromosomal arm 3R (expected 23%, according to the size of the chromosomal arm). In agreement with this observation, we also found that the chromosomal arm 3R contributes on average 2.6 more than expected to the significance of the GO terms (Figure 3). This leads to a simpler, nonadaptive, biological explanation for the significance of these GO terms. The Drosophila populations that Orozco-Terwengel et al. (2012) studied segregate the cosmopolitan inversion ln(3R)Payne, which covers a region of ∼8 Mb on the chromosomal arm 3R. Since suppression of recombination expands beyond the inversion region (Evans et al. 2007), LD is expected to affect more than one-third of this chromosomal arm, explaining the unique contribution of the genes located in this genomic region, as SNP2GO reported. This observation was recently corroborated by Tobler et al. (2013).

Figure 3.

Observed/expected ratio number of genes contributing to the significance of the GO terms. 3R, autosomal arm 3R; Rest, other chromosomes.

Conclusions

Originally developed for the analysis of gene expression data, gene list enrichment is currently being applied by researchers to test whether a particular pathway/GO term has an overrepresentation of candidate SNPs. While a big effort has been made to find the best criteria to define candidate SNPs and to detect whether LD is causing the significance of the pathway (Holmans 2010; Wang et al. 2012; Evangelou and Ioannidis 2013), the appropriateness of gene list enrichment methods in GWAS has not been discussed. Here we show that gene list enrichment tests are not generally applicable to test for the overrepresentation of candidate SNPs. Thus, we propose a candidate SNP enrichment analysis that is implemented in the program SNP2GO. SNP2GO tests on the basis of the number of candidate SNPs and noncandidate SNPs in a GO term. In addition, it allows testing for the spatial distribution of candidate SNPs and addresses the potential biological meaning for the significant overrepresentation.

An R package that implements our method (i.e., the inclusive analysis of GO terms, candidate SNPs enrichment analysis, and a test for local effects) can be found at http://www.cibiv.at/software/snp2go/index.shtml.